Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия
Поиск по сайту:
| Справочник по математике | Геометрия (Планиметрия) | Треугольники |
| Тип утверждения | Фигура | Рисунок | Формулировка |
| Определение | Равнобедренный треугольник | Равнобедренным треугольником называют треугольник, у которого две стороны равны. Равные стороны называют боковыми сторонами равнобедренного треугольника, третью сторону называют основанием равнобедренного треугольника. | |
| Свойство | Углы при основании равнобедренного треугольника | Если треугольник является равнобедренным треугольником, то углы при его основании равны. | |
| Признак | Два равных угла треугольника | Если у треугольника два угла равны, то этот треугольник является равнобедренным треугольником. | |
| Свойство | Медиана, биссектриса и высота, проведённые к основанию равнобедренного треугольника | В равнобедренном треугольнике медиана, биссектриса и высота, проведённые из вершины, противолежащей основанию, совпадают. | |
| Признак | Высота треугольника, совпадающая с медианой | Если в треугольнике высота совпадает с медианой, то этот треугольник является равнобедренным | |
| Признак | Высота треугольника, совпадающая с биссектрисой | Если в треугольнике высота совпадает с биссектрисой, то этот треугольник является равнобедренным | |
| Признак | Биссектриса треугольника, совпадающая с медианой | Если в треугольнике биссектриса совпадает с медианой, то этот треугольник является равнобедренным |
| Определение: равнобедренный треугольник | |
Равнобедренным треугольником называют треугольник, у которого две стороны равны. Равные стороны называют боковыми сторонами равнобедренного треугольника, третью сторону называют основанием равнобедренного треугольника. | |
| Свойство: углы при основании равнобедренного треугольника | |
Если треугольник является равнобедренным треугольником, то углы при его основании равны. | |
| Признак: два равных угла треугольника | |
Если у треугольника два угла равны, то этот треугольник является равнобедренным треугольником. | |
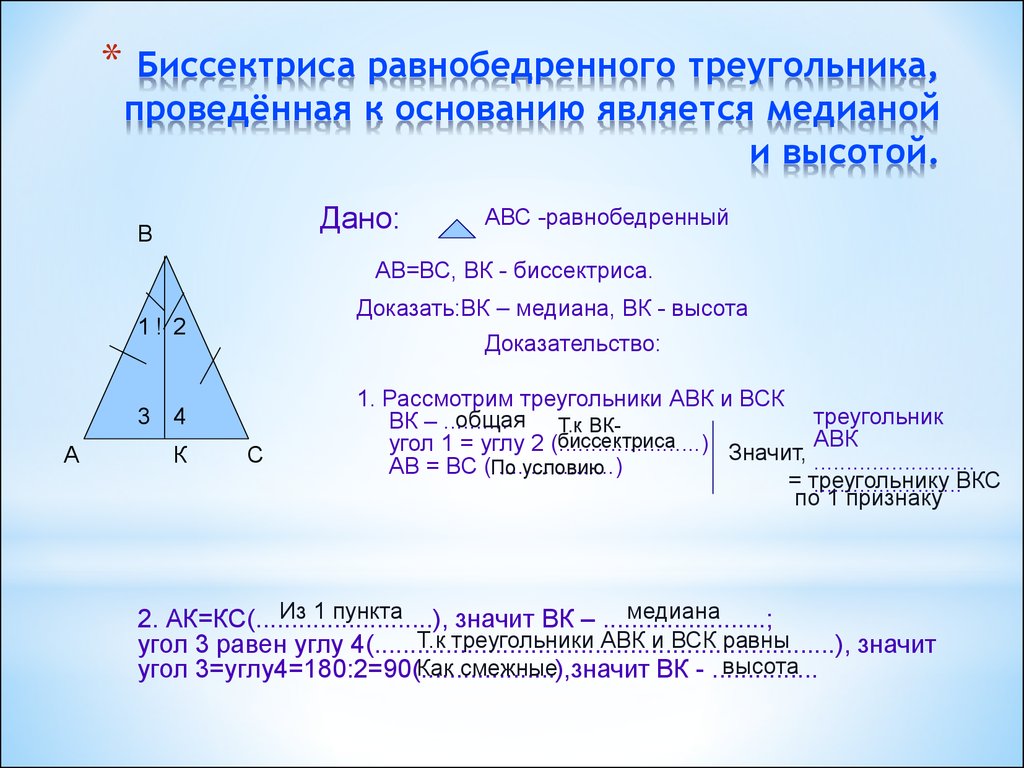
| Свойство: медиана, биссектриса и высота, проведённые к основанию равнобедренного треугольника | |
| В равнобедренном треугольнике медиана, биссектриса и высота, проведённые из вершины, противолежащей основанию, совпадают. | |
| Признак: высота треугольника, совпадающая с медианой | |
Если в треугольнике высота совпадает с медианой, то этот треугольник является равнобедренным | |
| Признак: высота треугольника, совпадающая с биссектрисой | |
Если в треугольнике высота совпадает с биссектрисой, то этот треугольник является равнобедренным | |
| Признак: биссектриса треугольника, совпадающая с медианой | |
Если в треугольнике биссектриса совпадает с медианой, то этот треугольник является равнобедренным | |
| Определение равнобедренного треугольника |
Определение: Равнобедренным треугольником называют треугольник, у которого две стороны равны. Равные стороны называют боковыми сторонами равнобедренного треугольника, третью сторону называют основанием равнобедренного треугольника. |
| Свойство углов при основании равнобедренного треугольника |
Свойство: Если треугольник является равнобедренным треугольником, то углы при его основании равны. |
| Признак равнобедренного треуголька: два равных угла треугольника |
Признак: Если у треугольника два угла равны, то этот треугольник является равнобедренным треугольником. |
| Свойство медианы, биссектрисы и высоты, проведённых к основанию равнобедренного треугольника |
Свойство: В равнобедренном треугольнике медиана, биссектриса и высота, проведённые из вершины, противолежащей основанию, совпадают. |
| Признак равнобедренного треугольника: высота треугольника, совпадающая с медианой |
Признак: Если в треугольнике высота совпадает с медианой, то этот треугольник является равнобедренным |
| Признак равнобедренного треугольника: высота треугольника, совпадающая с биссектрисой |
Признак: Если в треугольнике высота совпадает с биссектрисой, то этот треугольник является равнобедренным |
| Признак равнобедренного треугольника: биссектриса треугольника, совпадающая с медианой |
Признак: Если в треугольнике биссектриса совпадает с медианой, то этот треугольник является равнобедренным |
На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
| До ЕГЭ по математике осталось | |||
| дней | часов | минут | секунд |
|
Каким является треугольник? Самостоятельная работа 10. Вариант 2. № 2 ГДЗ Геометрия 9 класс Зив Б.Г. – Рамблер/класс
Каким является треугольник? Самостоятельная работа 10. Вариант 2. № 2 ГДЗ Геометрия 9 класс Зив Б.Г. – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
Остроугольным, прямоугольным или тупоугольным является треугольник, стороны которого равны 4, 5, 6?
ответы
Найдем угол против большей стороны:
α — острый => остроугольный треугольник.
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
Экскурсии
Мякишев Г.Я.
Досуг
Химия
похожие вопросы 5
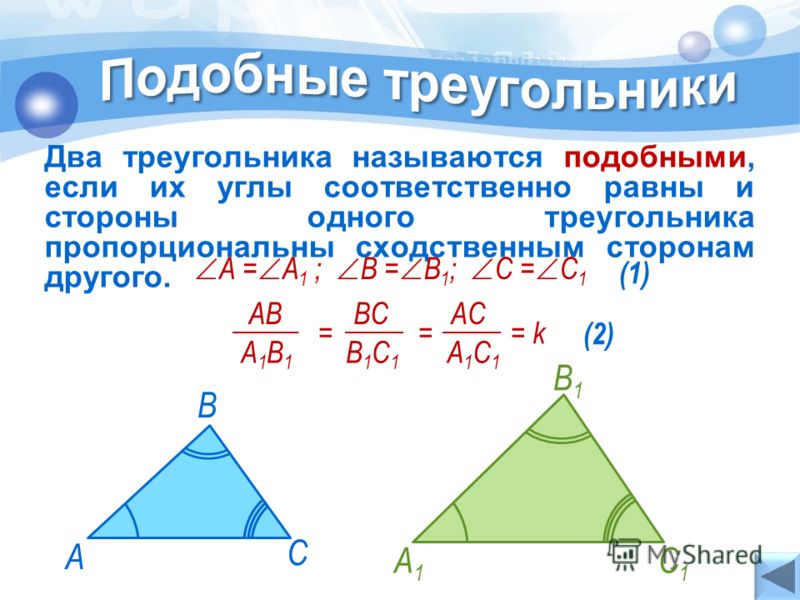
Докажите, что треугольники подобны. Вопросы и задачи 64, Геометрия, 10-11 класс, Атанасян Л.С.
Привет. Запуталась при решении, нужна помощь знатоков!!!
Три прямые, проходящие через одну точку и не лежащие в одной (Подробнее…)
ГДЗГеометрия11 класс10 классАтанасян Л.С.
Самостоятельная работа 19. Вариант 2. № 2 ГДЗ Геометрия 9 класс Зив Б.Г. Помогите доказать, используя параллельный переносИспользуя параллельный перенос, докажите, что углы при основании равнобедренной трапеции равны между собой.
ГДЗЭкзаменыГеометрия9 классЗив Б. Г.
Дадут ли аттестат после второй пересдачи.?
Мне сказала подруга,что аттестат не дадут после второй пересдачи,дадут только справку и всё,так ли это?
9 класс
Ребята нужны ответы на пересдачу по математике 9 класс 11 регион. Срочно!
ГИА9 класс
9. Определите ряд, в котором в обоих словах пропущена одна и та же буква. ЕГЭ-2017 Русский язык Цыбулько И. П. ГДЗ. Вариант 12.
9.
Определите ряд, в котором в обоих словах пропущена одна и та же буква. Выпишите
ГДЗРусский языкЕГЭЦыбулько И.П.
Что такое треугольник? (Определение, свойства и примеры)
Написано
Малкольм МакКинси
Проверка по фактам
Paul Mazzola
.
который замыкается в пространстве. Он использует линии, сегменты линий или лучи (в любой комбинации), чтобы сформировать три стороны. Когда три стороны формируются и встречаются, они создают три вершины или угла.Углы внутри треугольника являются внутренними углами. Углы вне треугольника являются внешними углами.
Слово «треугольник» буквально означает три угла, «три» — это латинская приставка к трем, например трицикл (три колеса), трио (три члена группы) или трицепс (три мышцы в группе).
Представьте стену, на которую опираетесь. Стена имеет высоту 20 футов и образует одну из двух сторон прямоугольного треугольника. Лестница имеет высоту 30 футов и образует наклонную гипотенузу. Расстояние от стены до лестницы и есть основание нашего треугольника.
Наш прямоугольный треугольник называется △ESP . Он имеет три стороны:
ES — 20 футов (стена)
SP — 22,36 футов (расстояние от нижней части стены до ноги лестницы)
PE — 30 футов (гипотенуза; сама лестница)
Имеет три угла:
∠E , острый угол составляет около 41°
тий , прямой угол, измерение ровно 90 °
↑P , еще одно острой угол, измерение около 48 °
Triangle
Triangle
Triangle
Triangle
Triangle
.
быть его основанием . Вы выделяете основание только тогда, когда планируете построить высоту или высоту для своего треугольника. В большинстве случаев база представлена вам горизонтально, но это не обязательно. Везде, где построена высота, сторона, которую она пересекает, является основанием.Высота треугольника (высота)
Помните наклонную лестницу у побега заключенных? Стена тюрьмы была высотой; лестница была гипотенузой, которая длиннее высоты прямоугольного треугольника. Высота или высота треугольника находится путем построения перпендикулярной линии от одной стороны треугольника к противоположному углу.
В прямоугольном треугольнике у вас есть две готовые высоты, две стороны, которые являются , а не , гипотенузой.
В △ESP сторона ES — это высота того, как сейчас выглядит треугольник. Если мы повернем всю картинку на 90° , сторона SP станет высотой. Если бы мы повернули треугольник так, чтобы гипотенуза (сторона лестницы) была горизонтальной, мы могли бы построить высоту от этой гипотенузы до ∠S .
Мы обнаружим, что эта высота равна 14,91 фута высоты.
Высота, или высота, всегда перпендикулярно основанию и всегда пересекает противоположный угол. Каждый треугольник имеет три высоты. Только в равностороннем треугольнике все три высоты будут равны.
Противоположный угол
У каждой стороны есть свой противоположный угол. Гипотенуза PE имеет противоположное ∠S ; сторона ES имеет противоположное значение ∠P , а сторона SP имеет противоположное значение ∠E .
Это также означает, что каждый угол имеет противоположную сторону. ∠S имеет противоположную сторону PE , гипотенуза и так далее.
Смежные стороны
Выберите любую сторону треугольника. Две стороны, соприкасающиеся с ним, являются смежными , что означает, что они соприкасаются. Таким образом, для стороны PE стороны ES и SP являются смежными.
Выберите любой угол треугольника.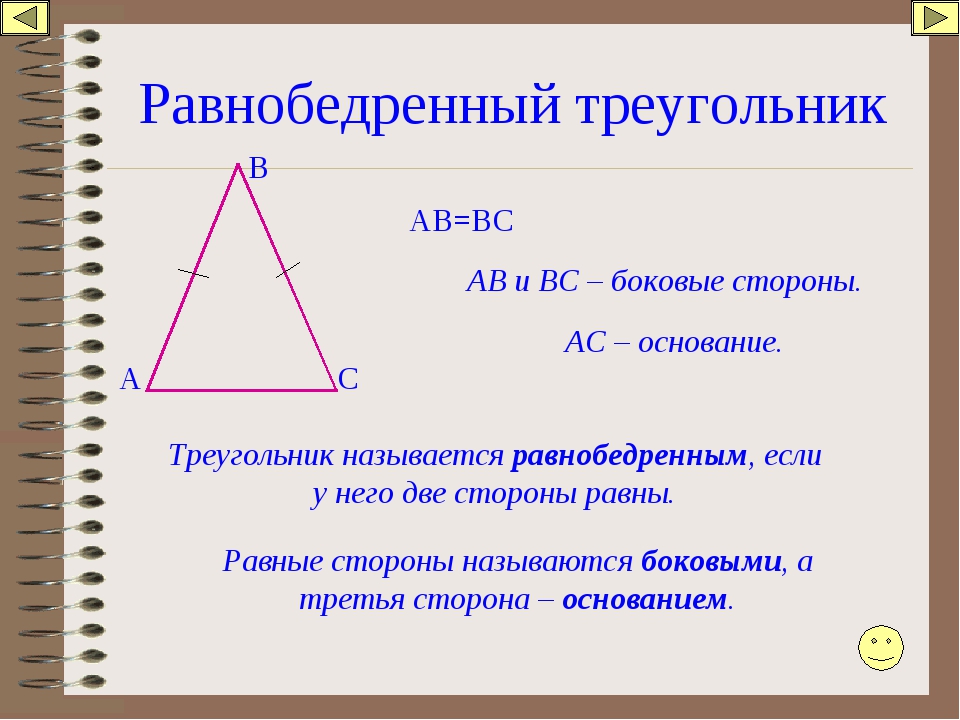
Две стороны, образующие его, являются его смежными сторонами. Таким образом, для ∠E стороны ES и PE являются смежными.
Итоги урока
Теперь, когда вы внимательно прочитали урок и изучили видео и рисунки, вы можете вспомнить и определить характеристики треугольника, определить три стороны и три угла треугольника, распознать и определить основание и высоту (или высоту) треугольника, и найдите противоположный угол для данной стороны и найдите смежные стороны для данной стороны или угла.
Что такое треугольник? | House of Math
Энциклопедия>Геометрия>Плоские фигуры>Треугольники>Атрибуты треугольника>Что такое треугольник?
Фигура с тремя сторонами (или ребрами) и тремя углами (или вершинами) называется треугольником. Ниже вы видите пять разных треугольников.
Как видите, стороны треугольника могут иметь разную длину, поэтому одни треугольники большие, а другие маленькие. Некоторые треугольники заметно наклонены, а другие довольно прямые.
Некоторые треугольники высокие и узкие, а другие короткие и толстые.
Несмотря на то, что эти треугольники выглядят по-разному, все они имеют три стороны и три угла. Проверьте, все ли приведенные выше треугольники имеют три стороны и три угла. Если вы посчитаете и обнаружите, что у одного из них есть что-то отличное от трех сторон и углов, посчитайте еще раз! Все они треугольники.
Некоторые треугольники обладают особыми свойствами, за что им даны особые имена. Давайте посмотрим на них.
Равносторонние треугольники
Треугольник называется равносторонним, если все его стороны имеют одинаковую длину. Все углы в равностороннем треугольнике имеют одинаковую величину.
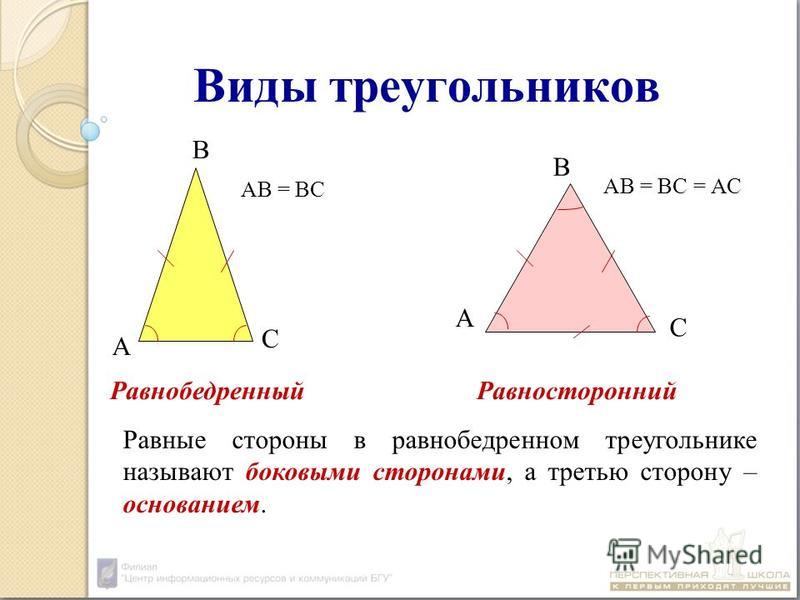
Равнобедренные треугольники
Треугольник называется равнобедренным, если две его стороны имеют одинаковую длину. Два угла в равнобедренном треугольнике имеют одинаковую величину.
Прямоугольные треугольники
Треугольник называется прямоугольным, если один из его углов прямой (90°).