8 класс. Геометрия. Четырехугольники. Параллелограмм. — Признаки параллелограмма.
Комментарии преподавателяПризнаки параллелограмма
Начнем с того, что вспомним определение параллелограмма.
Определение. Параллелограмм – четырехугольник, у которого каждые две противоположные стороны параллельны (см. Рис. 1).
Рис. 1. Параллелограмм
Вспомним основные свойства параллелограмма:
Для того, чтобы иметь возможность пользоваться всеми этими свойствами, необходимо быть уверенным, что фигура, о которой идет речь, – параллелограмм. Для этого необходимо знать такие факты, как признаки параллелограмма. Первые два из них мы сегодня и рассмотрим.
Теорема. Первый признак параллелограмма. Если в четырехугольнике две противоположные стороны равны и параллельны, то этот четырехугольник – параллелограмм
 .
.Рис. 2. Первый признак параллелограмма
Доказательство. Проведем в четырехугольнике диагональ (см. Рис. 2), она разбила его на два треугольника. Запишем, что мы знаем об этих треугольниках:
по первому признаку равенства треугольников.
Из равенства указанных треугольников следует, что по признаку параллельности прямых при пересечении их секущей. Имеем, что:
параллелограмм по определению. Что и требовалось доказать.
Доказано.
Теорема. Второй признак параллелограмма. Если в четырехугольнике каждые две противоположные стороны равны, то этот четырехугольник – параллелограмм. .
Рис. 3. Второй признак параллелограмма
Доказательство. Проведем в четырехугольнике диагональ (см. Рис. 3), она разбивает его на два треугольника. Запишем, что мы знаем об этих треугольниках, исходя из формулировки теоремы:
по третьему признаку равенства треугольников.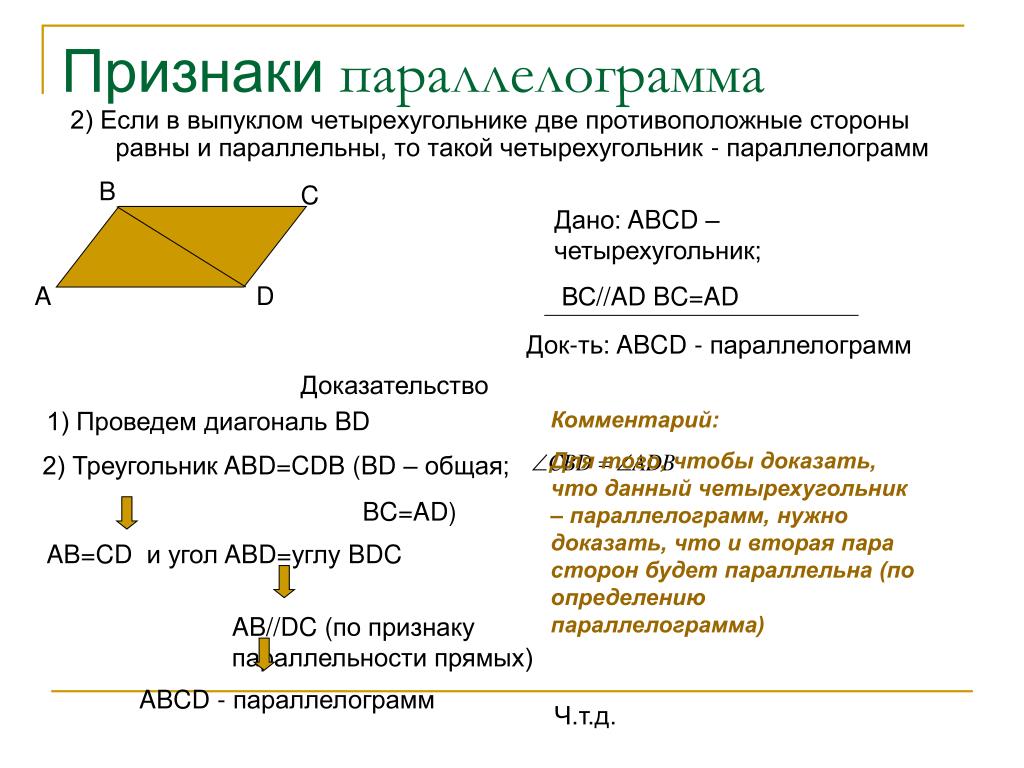
Из равенства треугольников следует, что и по признаку параллельности прямых при пересечении их секущей. Получаем:
параллелограмм по определению. Что и требовалось доказать.
Доказано.
Рассмотрим пример на применение признаков параллелограмма.
Пример 1. В выпуклом четырехугольнике Найти: а) углы четырехугольника; б) сторону .
Решение. Изобразим Рис. 4.
Рис. 4
параллелограмм по первому признаку параллелограмма.
А. по свойству параллелограмма о противоположных углах, по свойству параллелограмма о сумме углов, прилежащих к одной стороне.
Б. по свойству равенства противоположных сторон.
Ответ. .
ретий признак параллелограмма
Напомним, что параллелограмм – это четырёхугольник, у которого противоположные стороны попарно параллельны. То есть, если – параллелограмм, то (см. Рис. 1).
То есть, если – параллелограмм, то (см. Рис. 1).
Рис. 1
Параллелограмм обладает целым рядом свойств: противоположные углы равны (), противоположные стороны равны (). Кроме того, диагонали параллелограмма в точке пересечения делятся пополам, сумма углов, прилежащих к любой стороне параллелограмма, равна и т.д.
Но для того, чтобы пользоваться всеми этими свойствами, необходимо быть абсолютно уверенными в том, что рассматриваемый четырёхугольник – параллелограмм. Для этого и существуют признаки параллелограмма: то есть те факты, из которых можно сделать однозначный вывод, что четырёхугольник является параллелограммом. На предыдущем уроке мы уже рассмотрели два признака. Сейчас рассмотрим третий.
Если в четырёхугольнике диагонали в точке пересечения делятся пополам, то данный четырёхугольник является параллелограммом.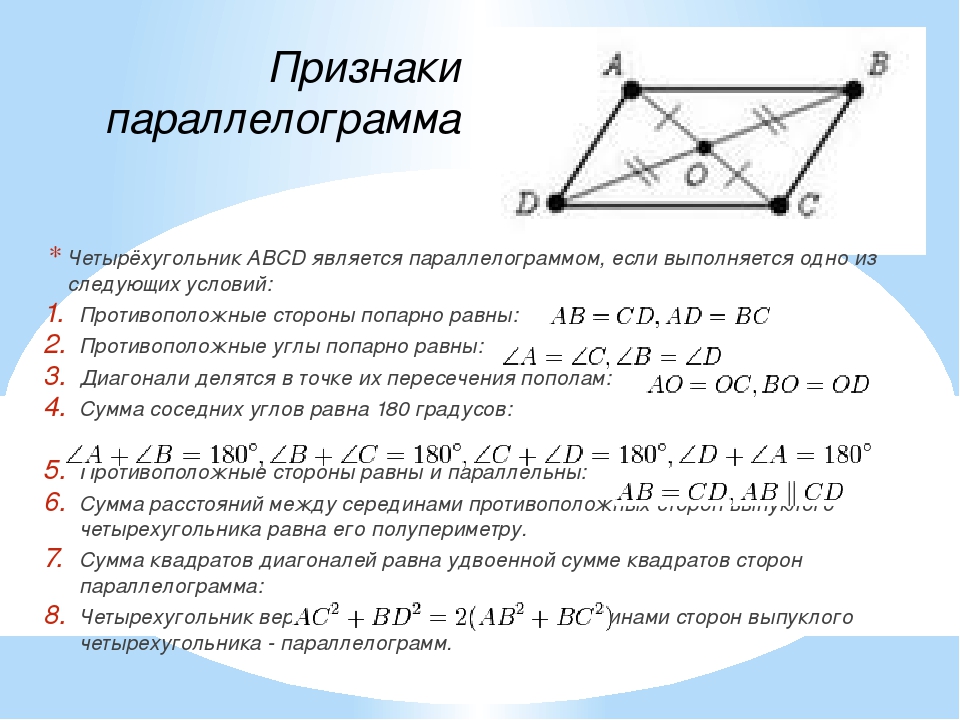
Дано:
– четырёхугольник; ; .
Доказать:
– параллелограмм.
Доказательство:
Для того чтобы доказать данный факт, необходимо доказать параллельность сторон параллелограмма. А параллельность прямых чаще всего доказывается через равенство внутренних накрест лежащих углов при этих прямых. Таким образом, напрашивается следующий способ доказательства третьего признака параллелограмма: через равенство треугольников .
Докажем равенство этих треугольников. Действительно, из условия следует: . Кроме того, поскольку углы – вертикальные, то они равны. То есть:
(первый признак равенстватреугольников – по двум сторонам и углу между ними).
Из равенства треугольников: (так как равны внутренние накрест лежащие углы при этих прямых и секущей ). Кроме того, из равенства треугольников следует, что . Значит, мы получили, что в четырёхугольнике две стороны равны и параллельны. По первому признаку параллелограмма: – параллелограмм.
Значит, мы получили, что в четырёхугольнике две стороны равны и параллельны. По первому признаку параллелограмма: – параллелограмм.
Доказано.
Рассмотрим пример на применение третьего признака параллелограмма.
Пример 1
Дано:
– параллелограмм; . – середина , – середина , – середина , – середина (см. Рис. 2).
Рис. 2
Доказать: – параллелограмм.
Доказательство:
Значит, в четырёхугольнике диагонали в точке пересечения делятся пополам. По третьему признаку параллелограмма из этого следует, что – параллелограмм.
Доказано.
Если провести анализ третьего признака параллелограмма, то можно заметить, что этот признак соответствует свойству параллелограмма. То есть, то, что диагонали делятся пополам, является не просто свойством параллелограмма, а его отличительным, характеристическим свойством, по которому его можно выделить из множества четырёхугольников.
ИСТОЧНИК
http://interneturok.ru/ru/school/geometry/8-klass/chyotyrehugolniki/priznaki-parallelogramma
http://interneturok.ru/ru/school/geometry/8-klass/chyotyrehugolniki/tretiy-priznak-parallelogramma
http://www.youtube.com/watch?v=x4Fd69y9oLU
http://www.uchportfolio.ru/users_content/675f9820626f5bc0afb47b57890b466e/images/46TThxQ8j4Y.jpg
http://cs10002.vk.me/u31195134/116260458/x_56d40dd3.jpg
http://wwww.tepka.ru/geometriya/16.1.gif
Параллелограмм – Свойства, Признаки, Определение
Определение параллелограмма
Параллелограмм — это четырехугольник, у которого противоположные стороны попарно параллельны. Как выглядит параллелограмм:
Частные случаи параллелограмма: ромб, прямоугольник, квадрат.
Диагонали — отрезки, которые соединяют противоположные вершины.
Свойства диагоналей параллелограмма:
- В параллелограмме точка пересечения диагоналей делит их пополам.

- Любая диагональ параллелограмма делит его на два равных треугольника.
- Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его двух смежных сторон.
Биссектриса параллелограмма — это отрезок, который соединяет вершину с точкой на одной из двух противоположных сторон и делит угол при вершине пополам.
Свойства биссектрисы параллелограмма:
- Биссектриса параллелограмма отсекает от него равнобедренный треугольник.
- Биссектрисы смежных углов параллелограмма пересекаются под прямым углом.
- Отрезки биссектрис противоположных углов равны и параллельны.
Как найти площадь параллелограмма:
- S = a * h, где a — сторона, h — высота.
- S = a * b * sinα, где a и b — две стороны, sinα — синус угла между ними.
- S = 0,5 * (d1 * d2), где d1,d2 — две диагонали.
Периметр параллелограмма — сумма длины и ширины, умноженная на два.
P = 2 * (a + b), где a — ширина, b — высота.
Приходите решать увлекательные задачки с красочными героями и в интерактивном формате. Запишите вашего ребенка на бесплатный пробный урок математики в онлайн-школу Skysmart: познакомимся, покажем, как все устроено на платформе и наметим вдохновляющую программу обучения.
У нас есть отличные дополнительные занятия по математике! Для учеников с 1 по 11 классы!
Свойства параллелограмма
Геометрическая фигура — это любое множество точек. У каждой фигуры есть свои свойства, которые отличают их между собой и помогают решать задачи по геометрии в 8 классе.
Рассмотрим основные свойства диагоналей и углов параллелограмма, узнаем чему равна сумма углов параллелограмма и другие особенности этой фигуры. Вот они:
- Противоположные стороны параллелограмма ABCD равны: AB = DC, BC = AD.
- Противоположные углы параллелограмма ABCD равны:∠A = ∠C, ∠B = ∠D.
- Диагонали параллелограмма ABCD равны и точкой пересечения делятся пополам: BO = OD, AO = OC.

- Диагональ делит параллелограмм ABCD на два равных треугольника: △ABC = △CDA.
- Сумма углов в параллелограмме ABCD, прилежащих к одной стороне, равна 180 градусам: ∠A + ∠D = 180°.
- В параллелограмме ABCD накрест лежащие углы при диагонали равны: ∠BAC = ∠ACD, ∠BCA = ∠CAD.
- В параллелограмме ABCD сумма всех углов равна 360° градусам.
- Точка пересечения диагоналей является центром симметрии параллелограмма ABCD.
- В параллелограмме диагонали d1, d2 и стороны a, b связаны следующим соотношением: d12 + d22 = 2 * (a2 + b2 ).
- Биссектриса отсекает от параллелограмма ABCD равнобедренный треугольник.
А сейчас докажем теорему, которая основана на первых двух свойствах.
Теорема 1. В параллелограмме противоположные стороны и противоположные углы равны.
В любом выпуклом четырехугольнике диагонали пересекаются. Все, что мы знаем о точке их пересечения — это то, что она лежит внутри четырехугольника.
Если мы проведем обе диагонали в параллелограмме, точка пересечения разделит их пополам. Убедимся, так ли это:
- Как противоположные стороны параллелограмма: AB = CD
- Как внутренние накрест лежащие равны пары углов: ∠1 = ∠2, ∠3 = ∠4.
- Следовательно, треугольник AOB равен треугольнику COD, из чего следует:
Теорема доказана. Наше предположение верно.
Признаки параллелограмма
Признаки параллелограмма помогают распознать эту фигуру среди других четырехугольников. Сформулируем три основных признака.
Первый признак параллелограмма. Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник — параллелограмм.
Докажем 1 признак параллелограмма:
Шаг 1. Пусть в четырехугольнике ABCD:
Чтобы назвать этот четырехугольник параллелограммом, нужно внимательно рассмотреть его стороны.
Сейчас мы видим одну пару параллельных сторон. Нужно доказать, что вторая пара сторон тоже параллельна.
Нужно доказать, что вторая пара сторон тоже параллельна.
Шаг 2. Проведем диагональ. Получились два треугольника ABC и CDA, которые равны по первому признаку равенства, то есть по по двум сторонам и углу между ними:
- AC — общая сторона;
- По условию AB = CD;
- ∠1 = ∠2, как внутренние накрест лежащие углы для параллельных прямых.
Шаг 3. Из равенства треугольников также следует:
Эти углы тоже являются внутренними накрест лежащими для прямых CB и AD. А это как раз и есть признак параллельности прямых. Значит, CB || AD и ABCD — параллелограмм.
Вот так быстро мы доказали первый признак.
Второй признак параллелограмма. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.
Докажем 2 признак параллелограмма:
Шаг 1. Пусть в четырехугольнике ABCD:
Шаг 2. Рассмотрим треугольники ABC и ADC:
- AC — общая сторона;
- B = CD по условию;
- BC = AD по условию.

Из этого следует, что треугольники ABC и ADC равны по третьему признаку, а именно по трем сторонам.
Шаг 3. Из равенства треугольников следует:
- ∠ DCA = ∠BAC
А так как эти углы накрест лежащие при верхней и нижней сторонах и секущей диагонали, значит верхняя и нижняя стороны параллельны.
- ∠DAC = ∠BCA
Эти углы накрест лежащие при боковых сторонах и секущей диагонали. Поэтому боковые стороны четырёхугольника тоже параллельны. Значит четырёхугольник ABCD — параллелограмм, ЧТД.
Доказали второй признак.
Третий признак параллелограмма. Если в четырехугольнике диагонали точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.
Докажем 3 признак параллелограмма:
Шаг 1. Если диагонали четырехугольника ABCD делятся пополам точкой O, то треугольник AOB равен треугольнику COD по двум сторонам и углу между ними:
- CO = OA;
- DO = BO;
- углы между ними равны, как вертикальные.

Шаг 2. Из равенства треугольников следует, что CD = AB.
Эти стороны параллельны CD || AB, по равенству накрест лежащиз углов ∠1 = ∠2.
Значит, ABCD является параллелограммом по первому признаку, который мы доказали ранее. Что и требовалось доказать.
Теперь мы знаем свойства параллелограмма и то, что выделяет его среди других четырехугольников — признаки. Так как они совпадают, эти формулировки можно использовать для определения параллелограмма. Но самое распространенное определение все таки связано с параллельностью противоположных сторон.
Чтобы ребенок еще лучше учился в школе, запишите его на уроки математики в детскую школу Skysmart. Наши преподаватели понятно объяснят что угодно — от дробей до синусов — и ответят на вопросы, которые бывает неловко задать перед всем классом. А еще помогут догнать сверстников и справиться со сложной контрольной.
Четырехугольник называется параллелограммом если. Четырехугольник является параллелограммом, если.
 Четырехугольник может быть
Четырехугольник может бытьТема урока
- Определение четырехугольника.
Цели урока
- Образовательные – повторение, обобщение и проверка знаний по теме: “Четырехугольника”; выработка основных навыков.
- Развивающие – развить внимание учащихся, усидчивость, настойчивость, логическое мышление, математическую речь.
- Воспитательные — посредством урока воспитывать внимательное отношение друг к другу, прививать умение слушать товарищей, взаимовыручке, самостоятельность.
Задачи урока
- Формировать навыки в построении четырехугольника с помощью масштабной линейки и чертежного треугольника.
- Проверить умение учащихся решать задачи.
План урока
- Историческая справка. Неевклидова геометрия.
- Четырёхугольник.
- Виды четырёхугольников.
Неевклидова геометрия
Неевклидова геометрия, геометрия, сходная с геометрией Евклида в том, что в ней определено движение фигур, но отличающаяся от евклидовой геометрии тем, что один из пяти ее постулатов (второй или пятый) заменен его отрицанием. Отрицание одного из евклидовых постулатов (1825) явилось значительным событием в истории мысли, ибо послужило первым шагом на пути ктеории относительности.
Отрицание одного из евклидовых постулатов (1825) явилось значительным событием в истории мысли, ибо послужило первым шагом на пути ктеории относительности.
Второй постулат Евклида утверждает, что любой отрезок прямой можно неограниченно продолжить . Евклид, по-видимому, считал, что этот постулат содержит в себе и утверждение, что прямая имеет бесконечную длину. Однако в «эллиптической» геометрии любая прямая конечна и, подобно окружности, замкнута.
Пятый постулат утверждает, что если прямая пересекает две данные прямые так, что два внутренних угла по одну сторону от нее в сумме меньше двух прямых углов, то эти две прямые, если продолжить их неограниченно, пересекутся с той стороны, где сумма этих углов меньше суммы двух прямых. Но в «гиперболической» геометрии может существовать прямая CB (см. рис.), перпендикулярная в точке С к заданной прямой r и пересекающая другую прямую s под острым углом в точке B, но, тем не менее бесконечные прямые r и s никогда не пересекутся.
Из этих пересмотренных постулатов следовало, что сумма углов треугольника, равная 180° в евклидовой геометрии, больше 180° в эллиптической геометрии и меньше 180° в гиперболической геометрии.
Четырёхугольник
Предмети > Математика > Математика 8 классОпределение. Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны.
Свойство. В параллелограмме противоположные стороны равны и противоположные углы равны.
Свойство. Диагонали параллелограмма точкой пересечения делятся пополам.
1 признак параллелограмма. Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник — параллелограмм.
2 признак параллелограмма. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.
3 признак параллелограмма. Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.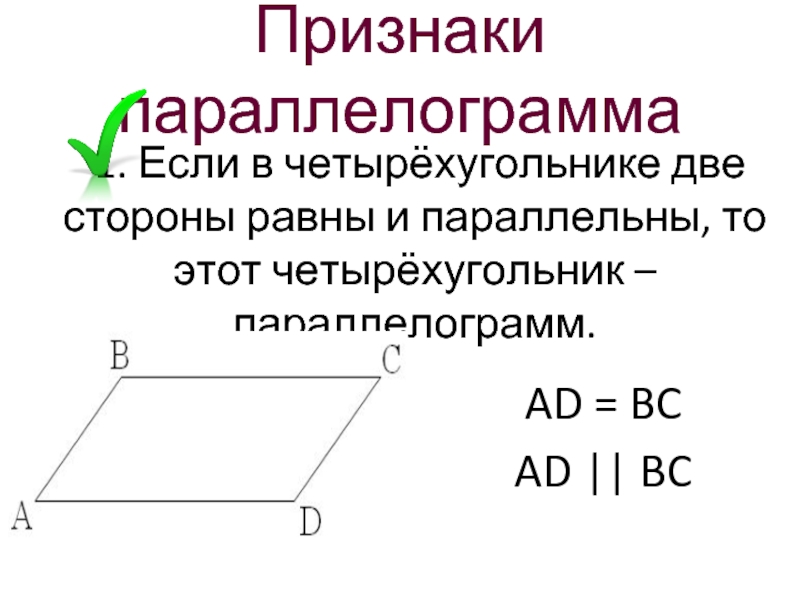
Определение. Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны. Параллельные стороны называются основаниями.
Трапеция называется равнобедренной (равнобочной) , если ее боковые стороны равны. В равнобедренной трапеции углы при основаниях равны.
Трапеция, один из углов которой прямой, называется прямоугольной .
Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции . Средняя линия параллельна основаниям и равна их полусумме.
Определение. Прямоугольником называется параллелограмм, у которого все углы прямые.
Свойство. Диагонали прямоугольника равны.
Признак прямоугольника. Если в параллелограмме диагонали равны, то этот параллелограмм — прямоугольник.
Определение. Ромбом называется параллелограмм, у которого все стороны равны.
Свойство. Диагонали ромба взаимно перпендикулярны и делят его углы пополам.
Определение. Квадратом называется прямоугольник, у которого все стороны равны.
Квадрат есть частный вид прямоугольника, а также частный вид ромба. Поэтому он имеет все их свойства.
Свойства:
1. Все углы квадрата прямые
2. Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.
Теорема: Четырехугольник является параллелограммом, если:
- противоположные его углы равны;
- противоположные его стороны попарно равны;
- его диагонали точкой пересечения делятся пополам;
- две его противоположные стороны параллельны и равны.
Доказательство:
A. Пусть в четырехугольнике KLMN углы К и М равны друг другу и равны а, пусть также равны друг другу и равны р углы L и N (рисунок). Учитывая, что сумма углов четырехугольника равна 360°, получаем, что 2α + 2β = 360°, или α + β = 180°. Учитывая, что углы К и L, равные соответственно аир, являются внутренними односторонними углами при прямых KN и LM, пересеченных прямой KL, заключаем, что стороны KN и LM параллельны. Также по углам К и N заключаем, что стороны KL и NM параллельны. Теперь по определению параллелограмма утверждаем, что четырехугольник KLMN — параллелограмм.
Также по углам К и N заключаем, что стороны KL и NM параллельны. Теперь по определению параллелограмма утверждаем, что четырехугольник KLMN — параллелограмм.
B. Пусть в четырехугольнике CDEF стороны CD и FE, а также CF и DE попарно равны (рисунок). Проведем одну из диагоналей четырехугольника, например СЕ. Треугольники CDE и EFC равны по трем сторонам. Поэтому углы DEC и FCE равны. Поскольку эти углы являются внутренними накрест лежащими при прямых DE и CF, пересеченных прямой СЕ, то стороны DE и CF параллельны. Также из равенства углов DCE и FEC получаем, что стороны CD и FE параллельны. Теперь по определению параллелограмма утверждаем, что четырехугольник CDEF — параллелограмм.
C. Пусть точка В пересечения диагоналей IL и КМ четырехугольника IKLM делит эти диагонали пополам: IB = BL и KB = ВМ (рисунок). Тогда треугольники KBL и MBI равны по двум сторонам и углу между ними. Это позволяет утверждать, что углы 1MB и LKB равны, а значит, стороны IM и KL параллельны. Аналогично из равенства треугольников KBI и MBL делаем вывод о параллельности сторон IK и LM. Теперь по определению параллелограмма можем утверждать, что четырехугольник IKLM — параллелограмм. Очень часто это надо знать при решении олимпиадных задачах на школьных олимпиадах.
Аналогично из равенства треугольников KBI и MBL делаем вывод о параллельности сторон IK и LM. Теперь по определению параллелограмма можем утверждать, что четырехугольник IKLM — параллелограмм. Очень часто это надо знать при решении олимпиадных задачах на школьных олимпиадах.
D. Пусть в четырехугольнике OPQR противоположные стороны ОР и RQ параллельны и равны (рисунок). Проведем диагональ OQ. Полученные углы POQ и RQO равны, так как они являются внутренними накрест лежащими при параллельных прямых ОР и RQ, пересеченных прямой OQ. Поэтому треугольники OPQ и RQO равны по двум сторонам и углу между ними. Значит, их соответствующие углы PQO и ROQ равны.
А поскольку они являются внутренними накрест лежащими углами при прямых PQ и OR, пересеченных прямой OQ, то стороны PQ и OR параллельны. Учитывая параллельность сторон ОР и RQ, по определению параллелограмма утверждаем, что четырехугольник OPQR — параллелограмм.
Четырехугольник, у которого противоположные стороны попарно параллельны?
Ответ: параллелограмм.
Есть его частные случаи: квадрат, ромб, прямоугольник.
Куб — это многогранник, частный случай призмы.
Конус — это тело вращения.
Конус, куб и призма имеют три измерения. А параллелограмм — два.
Параллелограмм-правильный ответ к тесту о четырх угольнике у которого противоположные стороны попарно параллельны.
У параллелограмма имеется две пары противоположных сторон и каждая пара является параллельной друг другу,а прямоугольник -это разновидность параллелограмма.
Этому определению соответствует такая геометрическая фигура, как параллелограмм, у него противоположные стороны попарно параллельны. Это также может быть: прямоугольник, ромб и квадрат, но их нет в предлагаемых вариантах.
Значит правильный ответ на этот вопрос — ПАРАЛЛЕЛОГРАММ .
Правильный ответ на данную загадку — параллелограмм . Однако тут могли бы быть и другие варианты ответов, например, прямоугольник, ведь у него тоже противоположные стороны параллельны за счет всех прямых углов.
Четырхугольник, у которого противоположные стороны попарно параллельны в геометрии называется quot;Параллелограммquot;. Частными случаями параллелограмма являются прямоугольник, ромб и квадрат. Правильный ответ на тест quot;Снова в школуquot; — quot;Параллелограммquot;. У меня такое ощущение, что Ласунечка решила заставить нас повторить всю школьную программу.
Насколько мне известно, четырхугольник, у которого противоположные стороны попарно являются параллельными, называется параллелограммом. Кстати, данное определение очень хорошо мне запомнилось из школьного курса геометрии.
Такой четырехугольник, который имеет равные стороны, параллельные между собой, называют параллелограмм . Такие фигурки мы чертили на уроке геометрии. Также параллелограммом является обычный прямоугольник или ромб. Даже квадрат тоже будет параллелограммом.
Попарно параллельными противоположные стороны могут быть у многих геометрических фигур. Это квадрат, прямоугольник, ромб — вс это различные варианты ПАРАЛЛЕЛОГРАММА, имеющие свои отличительные признаки.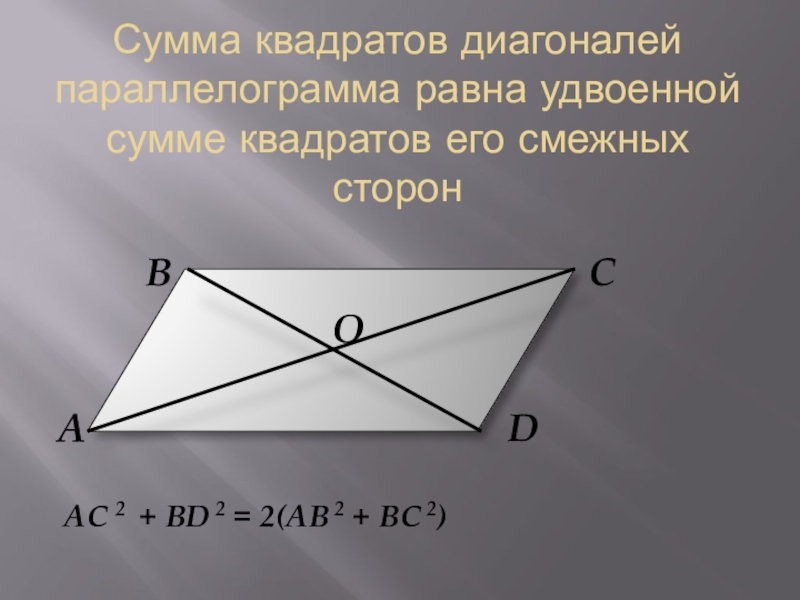 Правильный ответ в прилагаемом перечне — это, конечно же, ПАРАЛЛЕЛОГРАММ .
Правильный ответ в прилагаемом перечне — это, конечно же, ПАРАЛЛЕЛОГРАММ .
Четырехугольник, у которого противоположные стороны попарно параллельны — это ПАРАЛЛЕЛОГРАММ .
Достаточно вспомнить курс школьной геометрии, чтобы ответить на этот вопрос. Если мне не изменяет память, этот материал проходится в 8-9 классах, а еще раньше дается это определение в готовом виде.
Такой четырхугольник, у которого две стороны параллельны друг другу, а две другие тоже параллельны между собой, называется параллелограммом. Помню это правило ещ со школьных уроков и на всю жизнь запомнилось.
Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны. В А С D АВIIDС, ADIIBC
Сколько параллелограммов можно увидеть на чертеже? a d e c a II c, d II e II f II b II g f b g
Свойства параллелограмма 10. В параллелограмме противоположные стороны равны и противоположные углы равны. В 3 2 1 С Доказательство: 4 D А 1 = 2, как НЛУ при АDIIВС и секущей АС 3 = 4, как НЛУ при АВIIСD и секущей АС АС – общая сторона АВС = СDA по стороне и двум прилежащим к ней углам АВ=СD, AD=BC В= D A= C
Свойства параллелограмма 20. Диагонали параллелограмма точкой пересечения делятся пополам. Доказательство: В 2 4 А С 1 = 2, как НЛУ при 3 D О АВIIDС и секущей BD 3 = 4, как НЛУ при АВIIDC и секущей АС AB=СD, как противоположные стороны параллелограмма 1 АВО = СDО по стороне и двум прилежащим к ней углам АО=ОС, ВО=ОD
Диагонали параллелограмма точкой пересечения делятся пополам. Доказательство: В 2 4 А С 1 = 2, как НЛУ при 3 D О АВIIDС и секущей BD 3 = 4, как НЛУ при АВIIDC и секущей АС AB=СD, как противоположные стороны параллелограмма 1 АВО = СDО по стороне и двум прилежащим к ней углам АО=ОС, ВО=ОD
Эти рисунки иллюстрируют все рассмотренные свойства В С В А D А В С О А С D D
Дополнительные свойства. Сумма соседних углов параллелограмма равна 1800. В С D А АВIIDС, ADIIBC Обоснуй…
Периметр параллелограмма равен 20 см. Может ли быть одна из диагоналей 11 см? см 11 По лу п ер им е тр В Д е с я т ь сантиметров С А D Какое наибольшее целое значение может принимать длина одной из диагоналей этого параллелограмма?
Тренировочные задания на готовых чертежах. Найдите стороны параллелограмма АВСD, зная, что его периметр равен 24 см. АD – АВ = 3 см В С Сторона AD на 3 см больше стороны АВ х А х+3 D Р=24 см 2(х+х+3) = 24 р=12 см х+х+3 = 12
Найдите стороны параллелограмма АВСD, зная, что его периметр равен 24 см. АВ: ВС = 1: 2 В 2 х С х А Р=24 см 2(х+2 х) = 24 D р=12 см х+2 х = 12
АВ: ВС = 1: 2 В 2 х С х А Р=24 см 2(х+2 х) = 24 D р=12 см х+2 х = 12
Найдите стороны параллелограмма АВСD, зная, что его периметр равен 24 см. МС – МВ = 3 см В х М х+3 450 А Р=24 см 2(х+х+х+3) = 24 Отрезок МС на 3 см больше отрезка МВ С D р=12 см х+х+х+3 = 12
Длина одной из сторон параллелограмма составляет 80% от длины другой стороны. Найдите длину меньшей стороны этого параллелограмма, если его полупериметр равен 18 см. В х С 0, 8 х А D р=18 см х + 0, 8 х = 18
Длина одной из сторон параллелограмма на 15% больше длины другой стороны. Найдите длину большей стороны этого параллелограмма, если его полупериметр равен 8, 6 см В 1, 15 х С х А D р = 8, 6 см х + 1, 15 х = 8, 6
Найдите углы параллелограмма АВСD. В– В С х+30 А х D А = 300 Угол В больше угла А на 300
Сумма градусных мер трех углов параллелограмма равна 3000. Найдите величину тупого угла этого параллелограмма. В С х А 180 -х D
Найдите углы параллелограмма АВСD (3600 — 400 2) : 2 С В 1800 -400 140 А 400 D
№ 376 (в) Найдите углы параллелограмма АВСD, если В 1090 А 710 С 710 1090 D
№ 376 (в) Найдите углы параллелограмма АВСD, если В С х 2 х А А=2 В Угол А в 2 раза больше угла В D
Теоретический тест по геометрии.
 8 класс. Тема: Четырехугольники
8 класс. Тема: Четырехугольники- Подробности
- Категория: Тесты по геометрии. 8 класс
ТЕОРЕТИЧЕСКИЙ ТЕСТ ПО ГЕОМЕТРИИ
8 КЛАСС
ТЕМА: ЧЕТЫРЕХУГОЛЬНИКИ
А1. Сумма углов выпуклого n-угольника равна:
1) 180°(n − 2)
2) 360°
3) 180° · n
4) 360° · n
Ответ: 1.
А2. Четырехугольник является параллелограммом, если у него:
1) две стороны равны, а две другие параллельны
2) диагонали пересекаются и точкой пересечения делятся пополам
3) две пары равных сторон
4) все стороны параллельны
Ответ: 2.
А3. Трапеция называется равнобедренной, если у нее:
1) две стороны равны
2) два угла равны
3) основания параллельны и равны
4) боковые стороны равны
Ответ: 4.
А4. Прямоугольником называется:
1) параллелограмм, у которого все стороны равны
2) параллелограмм, у которого все углы прямые
3) четырехугольник, у которого диагонали равны
4) четырехугольник, у которого противолежащие стороны равны
Ответ: 2.
А5. Четырехугольник является ромбом, если у него:
1) диагонали перпендикулярны
2) диагонали равны
3) диагонали перпендикулярны и точкой пересечения делятся пополам
4) диагонали точкой пересечения делятся пополам
Ответ: 3.
А6. Квадратом является:
1) параллелограмм, у которого все углы прямые
2) ромб, у которого все углы прямые
3) параллелограмм, у которого диагонали равны
4) прямоугольник, у которого диагонали равны
Ответ: 2.
А7. Всякий прямоугольник является:
1) квадратом
2) ромбом
3) трапецией
4) параллелограммом
Ответ: 4.
А8. Выберите верное утверждение:
1) если в четырехугольнике диагонали равны и точкой пересечения делятся пополам, то этот четырехугольник — прямоугольник
2) если в четырехугольнике две стороны параллельны и равны, то этот четырехугольник — ромб
3) если в четырехугольнике две стороны равны, а два угла прямые, то этот четырехугольник — прямоугольник
4) если в четырехугольнике диагонали равны, а один из углов прямой, то этот четырехугольник — квадрат
Ответ: 1.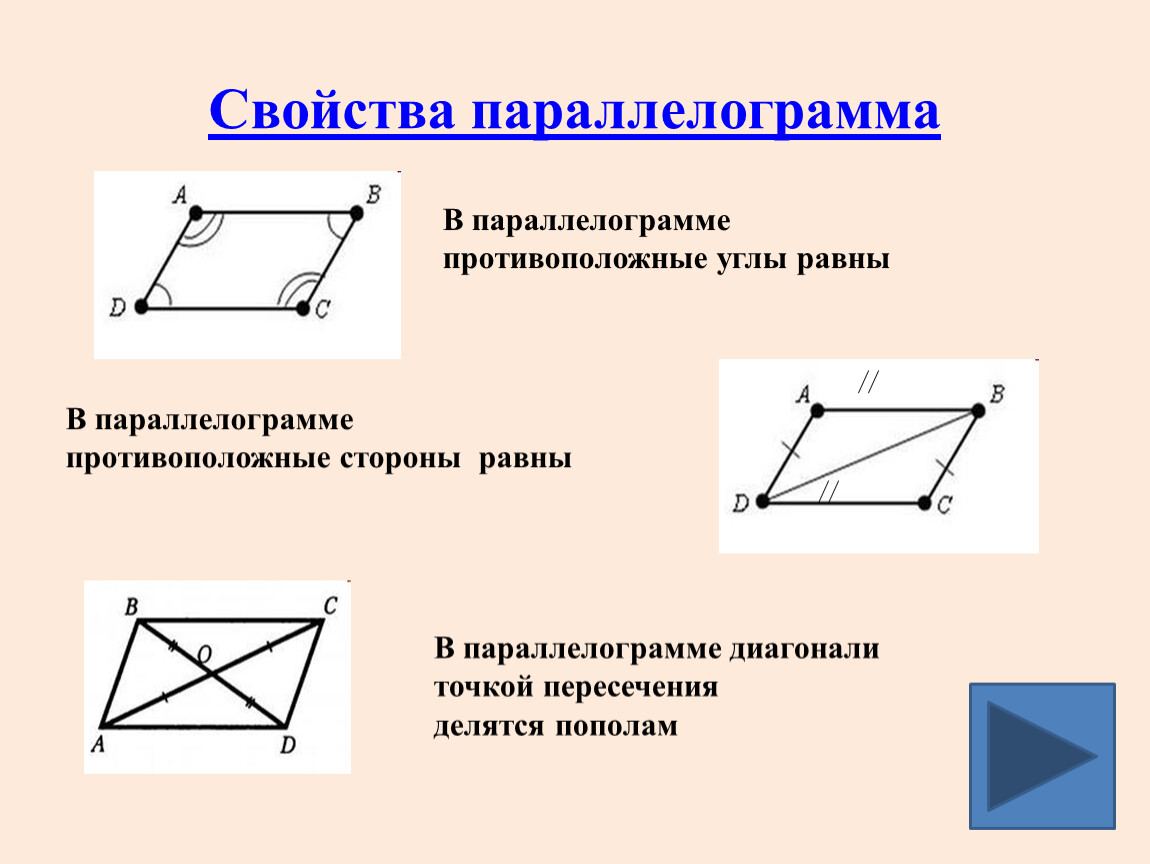
А9. Внешний угол правильного n-угольника равен:
1) 180° / n
2) 180° (n − 2)/n
3) 360° (n − 2)/n
4) 360° / n
Ответ: 4.
А10. Многоугольник называется выпуклым, если:
1) все его стороны являются выпуклыми
2) его нельзя разрезать на два других многоугольника
3) он лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины
4) все его углы являются выпуклыми
Ответ: 3.
- < Назад
- Вперёд >
төрт бурчтук жөнүндө. | Бардыгы үчүн пайдалуу маалымат
Төрт бурчтуктун жанаша эмес эки тарабы карама-каршы деп аталат. Жанаша болбогон эки чоку дагы карама-каршы деп аталат.
Төрт бурчтуктар томпок (ABCD сыяктуу) жана
томпок эмес (A1B1C1D1).
Төрт бурчтуктун түрлөрү
Параллелограмм
Параллелограмм — карама-каршы капталдары жуп-параллель болгон төрт бурчтук.
Параллелограмм касиеттери Параллелограмм касиеттери
* карама-каршы тараптар бирдей;
* карама-каршы бурчтар бирдей;
* кесилиш чекити менен диагональдар эки эсе кыскарат;
* бир капталына жанаша турган бурчтардын суммасы 180;
* диагональдардын квадраттарынын суммасы бардык тараптардын квадраттарынын суммасына барабар:
d12+d22=2(a2+b2).
Параллелограмм белгилери
Төрт бурчтук параллелограмм болуп саналат, эгерде:
1. Анын эки карама-каршы жагы тең жана параллель.
2. Карама-каршы тараптар экиден тең.
3. Карама-каршы бурчтар экиден тең.
4. Диагоналдарды кесилиш чекити эки эсе кыскарткан.
акробаттары
Трапеция — эки карама-каршы каптал параллель, ал эми калган экөө параллель болбогон төрт бурчтук. Трапеция
бир акробаттын удаалаш тараптар, анын негиздерин, ошондой эле азык-параллелдүү тарап жылыптыр деп аталат. тараптардын ортосуна бириктирген бир бөлүгү, орто сап деп аталат.
тараптардын ортосуна бириктирген бир бөлүгү, орто сап деп аталат.
Трапеция, эгерде анын капталдары тең болсо, тең капталдуу (же тең капталдуу) деп аталат.
Trapeze, тик бурчтуу деп аталган бир түз сызык болгон бурчу.
касиеттери уаа
* анын орто сызыгы негиздерге параллель жана алардын жарым суммасына барабар;
* эгер трапеция тең капталдуу болсо, анда анын диагоналдары тең, ал эми негизиндеги бурчтар бирдей;
* эгер трапеция тең капталдуу болсо, анда анын тегерегин тегерек сүрөттөөгө болот;
* эгер негиздердин суммасы капталдардын суммасына барабар болсо, анда ага тегерек жазууга болот.
бир бир акробаттын белгилери
анын параллелдүү тараптар бирдей эмес болсо, төрт бир бир акробаттын болуп саналат
тик бурчтук
Төрт бурч — бул бардык бурчтары түз болгон параллелограмм.
Тик бурчтуктун касиеттери
* параллелограммдын бардык касиеттери;
* диагоналдары бирдей.
Тик бурчтуктун өзгөчөлүктөрү
Параллелограмм, эгерде:
1. Анын бир бурчу түз.
Анын бир бурчу түз.
2. Анын диагоналдары бирдей.
Ромб
Ромб бардык тараптары бирдей болгон параллелограмм деп аталат.
Ромб касиеттери
* параллелограммдын бардык касиеттери;
* диагоналдары перпендикуляр;
* диагональдар анын бурчтарынын биссектрисалары.
Ромб белгилери
1. Параллелограмм, эгерде:
2. Анын жанаша турган эки тарабы тең.
3. Анын диагоналдары перпендикуляр.
4. Диагональдардын бири анын бурчунун биссектрисасы.
аянт
Квадрат — бул бардык тараптары бирдей болгон тик бурчтук.
Square PropertiesSquare Properties
* аянттын бардык бурчтары түз;
* квадраттын диагоналдары тең, бири-бирине перпендикуляр, кесилиш чекити эки эсе жана квадраттын бурчтары эки эсе.
Аянттын белгилери
Ромбдун кандайдыр бир өзгөчөлүгү бар болсо, төрт бурчтук — бул төрт бурчтук.
 Жанаша болбогон эки чоку дагы карама-каршы деп аталат.
Жанаша болбогон эки чоку дагы карама-каршы деп аталат. Төрт бурчтуктар томпок жана томпок эмес.
Томпок төрт бурчтуктун ар бир диагоналы аны эки үч бурчтукка бөлөт. Томпок эмес төрт бурчтуктун диагональдарынын бири аны эки үч бурчтукка бөлөт.
Томпок n-гондун бурчтарынын суммасы (n-2) * 180 градус болгондуктан, томпок төрт бурчтуктун бурчтарынын суммасы 360 градус болот.
Төрт бурч, эгерде анын кайсы бир капталын камтыган сызыкка салыштырмалуу бир жарым тегиздикте жайгашкан болсо, томпок деп аталат.
Томпок төрт бурчтуктун бурчтарынын суммасы 360:
A + B + C + D = 360.
Бардык бурчтары курч же бурчтары дүң болгон төрт бурчтук жок.
Төрт бурчтуктун ар бир бурчу калган үч бурчтун суммасынан ар дайым аз:
A lt; B + C + D, B lt; A + C + D,
C lt; A + B + D, D lt; A + B + D.

Төрт бурчтуктун ар бир тарабы ар дайым калган үч тараптын суммасынан аз болот:
a lt; b + c + d, b lt; a + c + d,
c lt; a + b + d, d lt; a + b + c.
Ыктыярдуу томпок төрт бурчтуктун аянты:
Төрт бурчтуктун диагоналдери деп, анын карама-каршы чокуларын бириктирген сызык кесиндилери саналат.
Томпок төрт бурчтуктун диагоналдары кесилишет, ал эми томпок эмес кесилишет.
Ыктыярдуу томпок төрт бурчтуктун аянты:
Эгерде M, N, P, Q — дөңсөө ABCD төрт бурчтуктун капталдарынын ортоңку чекиттери, ал эми R, S анын диагоналдарынын ортоңку чекиттери болсо, анда MNPQ, MRPS, NSQR төрт бурчтуктары параллелограмм болуп, Вариньон параллелограммы деп аталат.
Вариньон параллелограммдарынын формасы жана өлчөмдөрү берилген ABCD төрт бурчтуктун формасы жана өлчөмдөрү менен байланыштуу. Демек MNPQ — ABCD диагоналдары перпендикуляр болсо, тик бурчтук; Эгерде ABCD төрт бурчтугунун диагоналдары тең болсо, MNPQ ромбу; Эгерде ABCD диагоналдары перпендикуляр жана барабар болсо, MNPQ квадраты;
SABCD = 2SMNPQ.
MP, NQ жана RS сегменттери томпок төрт бурчтуктун биринчи, экинчи жана үчүнчү борбордук сызыктары деп аталат.
Параллелограммда, жана nmде гана, диагональдардын ортоңку чекиттери дал келет, демек, үчүнчү ортоңку сызык чекитке айланат. Башка квадраттар үчүн ортоңку сызыктар сызык сегменти болуп саналат.
Төрт бурчтуктун бардык ортоңку сызыктары бир жерден кесилишип, аны экиге бөлөт:
MG = GP, NG = GQ, RG = GS.
Төрт бурчтуктун ортоңку сызыктарынын квадраттарынын суммасы анын бардык капталдарынын жана диагоналдарынын квадраттарынын суммасынын төрттөн бирине барабар:
MP2 + NQ2 + RS 2 = (AB2 + BC2 + CD2 + AD2 + AC2 + BD2).
Эгерде бурч төрт бурчтуктун биринчи жана экинчи ортоңку сызыктарынын ортосунда болсо, анда анын аянты:
SABCD = MPNQsin.
Ыктыярдуу, сөзсүз түрдө томпок эмес, төрт бурчтуктун формасына ээ болгон бирдей плиткаларды тегиздик менен төшөөгө болот, ошондо плиткалардын бири-бирине кайчылашпашы жана тегиздиктин жабык бөлүктөрү калбашы керек.
Сүрөттөлгөн төрт бурчтуктар
Төрт бурчтук тегерете тегерете тегеретилген деп (тегеретилген), эгерде анын бардык капталына тийип турган ушундай тегерек болсо, анда ал тегеректин өзү жазылган деп аталат.
Төрт бурч анын карама-каршы капталдарынын суммалары барабар болгондо гана сүрөттөлөт:
a + c = b + d.
Тегеректелген төрт бурчтуктун капталдары жана жазылган радиустун радиусу туура:
a + c 4r, b + d 4r.
Төрт бурчтуктун аянты:
S = pr,
мында r — чегилген тегеректин радиусу, p — төрт бурчтуктун жарым периметри.
Төрт бурчтуктун аянты:
Төрт бурчтукка жазылган тегерек борбору ушул төрт бурчтуктун төрт бурчунун тең биссектрисаларынын кесилиш чекити.
Чийилген тегеректин тангенсттик чекиттери төрт бурчтуктун бурчтарынан бирдей сегменттерди кесип таштайт:
AK = AN, BK = BL, CL = CM, DM = DN.
Эгерде O ABCD төрт бурчтукка жазылган тегерек борбору болсо, анда
AOB + COD = BOC + AOD = 180.
Капталдары AB = a, BC = b, CD = c жана AD = d болгон ABCD сүрөттөлгөн төрт бурчтук үчүн төмөнкү мамилелер туура:
Төрт бурчтуу жазуулар
Төрт бурчтук тегерекке чегилген (чийилген) деп аталат, эгерде анын бардык чокуларынан өткөн тегерек болсо, анда тегерек өзү төрт бурчтукка тегерете тегеретилген деп аталат.
Томпок төрт бурчтук тегерете, эгерде болсо гана
Төрт бурчтуктун жанаша эмес эки тарабы карама-каршы деп аталат. Жанаша болбогон эки чоку дагы карама-каршы деп аталат.
Төрт бурчтуктар томпок (ABCD сыяктуу) жана
томпок эмес (A1B1C1D1).
Төрт бурчтуктун түрлөрү
Параллелограмм
Параллелограмм — карама-каршы капталдары жуп-параллель болгон төрт бурчтук.
Параллелограмм касиеттери
* карама-каршы тараптар бирдей;
* карама-каршы бурчтар бирдей;
* кесилиш чекити менен диагональдар эки эсе кыскарат;
* бир капталына жанаша турган бурчтардын суммасы 180;
* диагональдардын квадраттарынын суммасы бардык тараптардын квадраттарынын суммасына барабар:
d12+d22=2(a2+b2).
Параллелограмм белгилери
Төрт бурчтук параллелограмм болуп саналат, эгерде:
1. Анын эки карама-каршы жагы тең жана параллель.
Анын эки карама-каршы жагы тең жана параллель.
2. Карама-каршы тараптар экиден тең.
3. Карама-каршы бурчтар экиден тең.
4. Диагоналдарды кесилиш чекити эки эсе кыскарткан.
акробаттары
Трапеция — эки карама-каршы каптал параллель, ал эми калган экөө параллель болбогон төрт бурчтук. Трапеция
бир акробаттын удаалаш тараптар, анын негиздерин, ошондой эле азык-параллелдүү тарап жылыптыр деп аталат. тараптардын ортосуна бириктирген бир бөлүгү, орто сап деп аталат.
Трапеция, эгерде анын капталдары тең болсо, тең капталдуу (же тең капталдуу) деп аталат.
Trapeze, тик бурчтуу деп аталган бир түз сызык болгон бурчу.
касиеттери уаа
* анын орто сызыгы негиздерге параллель жана алардын жарым суммасына барабар;
* эгер трапеция тең капталдуу болсо, анда анын диагоналдары тең, ал эми негизиндеги бурчтар бирдей;
* эгер трапеция тең капталдуу болсо, анда анын тегерегин тегерек сүрөттөөгө болот;
* эгер негиздердин суммасы капталдардын суммасына барабар болсо, анда ага тегерек жазууга болот.
бир бир акробаттын белгилери
анын параллелдүү тараптар бирдей эмес болсо, төрт бир бир акробаттын болуп саналат
тик бурчтук
Төрт бурч — бул бардык бурчтары түз болгон параллелограмм.
Тик бурчтуктун касиеттери
* параллелограммдын бардык касиеттери;
* диагоналдары бирдей.
Тик бурчтуктун өзгөчөлүктөрү
Параллелограмм, эгерде:
1. Анын бир бурчу түз.
2. Анын диагоналдары бирдей.
Ромб
Ромб бардык тараптары бирдей болгон параллелограмм деп аталат.
Алмаз касиеттери
* параллелограммдын бардык касиеттери;
* диагоналдары перпендикуляр;
* диагональдар анын бурчтарынын биссектрисалары.
Ромб белгилери
1. Параллелограмм, эгерде:
2. Анын жанаша турган эки тарабы тең.
3. Анын диагоналдары перпендикуляр.
4. Диагональдардын бири анын бурчунун биссектрисасы.
аянт
Квадрат — бул бардык тараптары бирдей болгон тик бурчтук.
Square касиеттери
* аянттын бардык бурчтары түз;
* квадраттын диагоналдары тең, бири-бирине перпендикуляр, кесилиш чекити эки эсе жана квадраттын бурчтары эки эсе.
Аянттын белгилери
Ромбдун кандайдыр бир өзгөчөлүгү бар болсо, төрт бурчтук — бул төрт бурчтук.
Төрт бурчтуктун жанаша эмес эки тарабы карама-каршы деп аталат. Жанаша болбогон эки чоку дагы карама-каршы деп аталат.
Төрт бурчтуктар томпок жана
томпок эмес
Параллелограмм — карама-каршы капталдары жуп-параллель болгон төрт бурчтук.
Параллелограмм касиеттери
* карама-каршы тараптар бирдей;
* карама-каршы бурчтар бирдей;
* кесилиш чекити менен диагональдар эки эсе кыскарат;
* бир капталына жанаша турган бурчтардын суммасы 180;
* диагональдардын квадраттарынын суммасы бардык тараптардын квадраттарынын суммасына барабар:
Төрт бурчтук параллелограмм болуп саналат, эгерде:
1. Анын эки карама-каршы жагы тең жана параллель.
Анын эки карама-каршы жагы тең жана параллель.
2. Карама-каршы тараптар экиден тең.
3. Карама-каршы бурчтар экиден тең.
4. Диагоналдарды кесилиш чекити эки эсе кыскарткан.
акробаттары
Трапеция — эки карама-каршы каптал параллель, ал эми калган экөө параллель болбогон төрт бурчтук. Трапеция
бир акробаттын удаалаш тараптар, анын негиздерин, ошондой эле азык-параллелдүү тарап жылыптыр деп аталат. тараптардын ортосуна бириктирген бир бөлүгү, орто сап деп аталат.
Трапеция, эгерде анын капталдары тең болсо, тең капталдуу (же тең капталдуу) деп аталат.
Trapeze, тик бурчтуу деп аталган бир түз сызык болгон бурчу.
касиеттери уаа
* анын орто сызыгы негиздерге параллель жана алардын жарым суммасына барабар;
* эгер трапеция тең капталдуу болсо, анда анын диагоналдары тең, ал эми негизиндеги бурчтар бирдей;
* эгер трапеция тең капталдуу болсо, анда анын тегерегин тегерек сүрөттөөгө болот;
* эгер негиздердин суммасы капталдардын суммасына барабар болсо, анда ага тегерек жазууга болот.
бир бир акробаттын белгилери
анын параллелдүү тараптар бирдей эмес болсо, төрт бир бир акробаттын болуп саналат
тик бурчтук
Төрт бурч — бул бардык бурчтары түз болгон параллелограмм.
Тик бурчтуктун касиеттери
* параллелограммдын бардык касиеттери;
* диагоналдары бирдей.
Тик бурчтуктун өзгөчөлүктөрү
Параллелограмм, эгерде:
1. Анын бир бурчу түз.
2. Анын диагоналдары бирдей.
Ромб
Ромб бардык тараптары бирдей болгон параллелограмм деп аталат.
Алмаз касиеттери
* параллелограммдын бардык касиеттери;
* диагоналдары перпендикуляр;
* диагональдар анын бурчтарынын биссектрисалары.
Ромб белгилери
1. Параллелограмм, эгерде:
2. Анын жанаша турган эки тарабы тең.
3. Анын диагоналдары перпендикуляр.
4. Диагональдардын бири анын бурчунун биссектрисасы.
аянт
Квадрат — бул бардык тараптары бирдей болгон тик бурчтук.
Square касиеттери
* аянттын бардык бурчтары түз;
* квадраттын диагоналдары тең, бири-бирине перпендикуляр, кесилиш чекити эки эсе жана квадраттын бурчтары эки эсе.
Аянттын белгилери
Ромбдун кандайдыр бир өзгөчөлүгү бар болсо, төрт бурчтук — бул төрт бурчтук.
Четырехугольники /qualihelpy
Четырехугольником называют многоугольник, имеющий четыре вершины. Среди всех четырехугольников выделяют параллелограмм, ромб, прямоугольник, квадрат и трапецию.Параллелограммом называют четырехугольник, у которого противолежащие стороны попарно параллельны.
Высотой параллелограмма называют отрезок перпендикуляра, заключенный между его параллельными сторонами или отрезок перпендикуляра, проведенного из вершины параллелограмма на прямую, содержащую противолежащую сторону.
Например, на рисунке 8.66 – высота, проведенная к стороне , – высота, проведенная к стороне , – высота, проведенная из вершины на прямую, содержащую сторону , а – высота, проведенная из вершины на прямую, содержащую сторону .Свойства параллелограмма
1. Противолежащие стороны параллелограмма равны.
2. Противолежащие углы параллелограмма равны.
Например, на рисунке 8.67 и .3. Диагонали параллелограмма делятся точкой пересечения пополам.
Например, на рисунке 8.67 и .4. Сумма квадратов диагоналей параллелограмма равна сумме квадратов длин всех его сторон:
, (8.15)где и – смежные стороны, и – диагонали параллелограмма. 5. Сумма углов параллелограмма, прилежащих к одной стороне, равна . Например, на рисунке 8.67 .Признаки параллелограмма
1. Если у выпуклого четырехугольника две противолежащие стороны параллельны и равны, то этот четырехугольник – параллелограмм.
2. Если у выпуклого четырехугольника противолежащие стороны попарно равны, то этот четырехугольник – параллелограмм.
3. Если у выпуклого четырехугольника противолежащие углы попарно равны, то этот четырехугольник – параллелограмм.
4. Если у выпуклого четырехугольника диагонали точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм.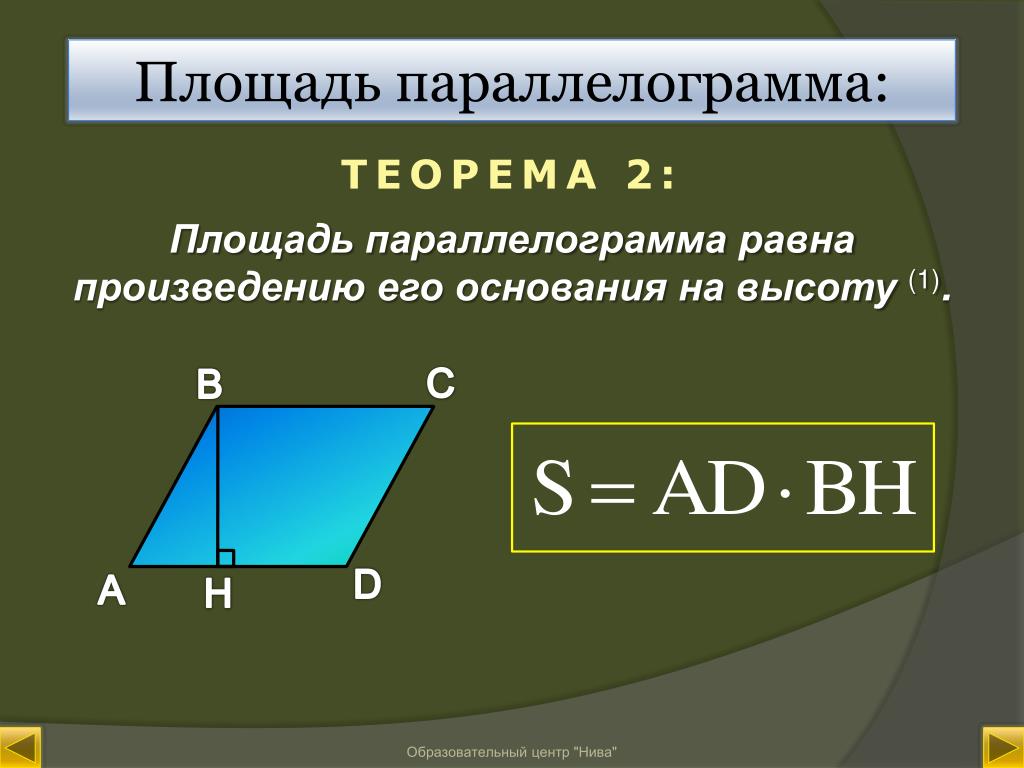
Площадь параллелограмма можно вычислить по одной из формул:
; (8.16); (8.17). (8.18)Периметр параллелограмма можно вычислить по формуле:
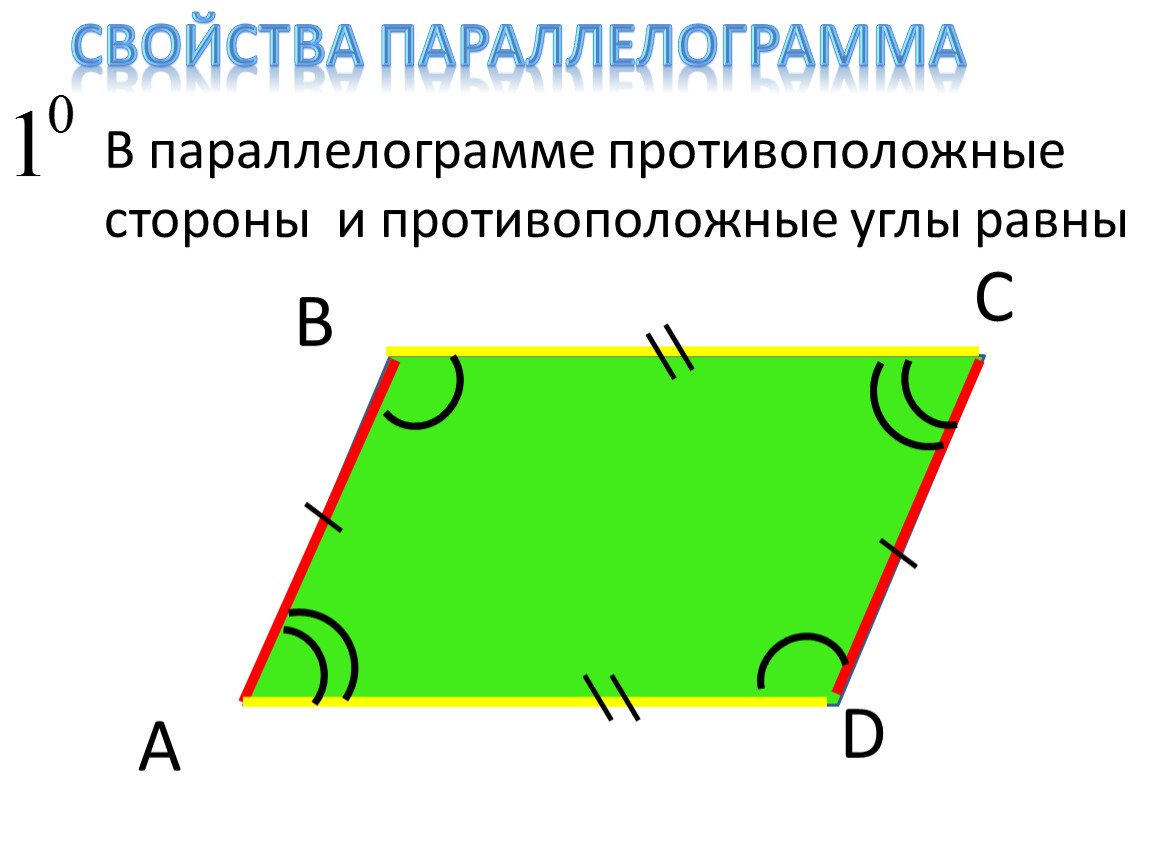
. (8.19)Ромбом называют параллелограмм, все стороны которого равны.
Например, на рисунке 8.69 изображен ромб: – сторона, – высота, , его диагонали.Свойства ромба
Ромбу присущи все свойства параллелограмма и, кроме того, свойства:
1) диагонали ромба взаимно перпендикулярны;
2) диагонали ромба являются биссектрисами его внутренних углов.
Признаки ромба
1. Параллелограмм является ромбом, если две его смежные стороны равны.
2. Параллелограмм является ромбом, если его диагонали перпендикулярны.
3. Параллелограмм является ромбом, если одна из диагоналей является биссектрисой его угла.
Периметр ромба можно вычислить по формуле:
. (8.20)Площадь ромба можно вычислить по тем же формулам, что и площадь параллелограмма, кроме того, и по формуле:
. (8.21)
(8.21)Прямоугольником называют параллелограмм, у которого все углы прямые.
Например, на рисунке 8.70 изображен прямоугольник, у которого и – смежные стороны, – диагонали, φ – угол между диагоналями.Свойства прямоугольника
Прямоугольнику присущи все свойства параллелограмма. Кроме того диагонали прямоугольника равны.
Признаки прямоугольника
1. Параллелограмм является прямоугольником, если его диагонали равны.
2. Параллелограмм является прямоугольником, если один из его углов прямой.
3. Четырехугольник является прямоугольником, если три его угла прямые.
Площадь прямоугольника можно вычислить по формулам:
; (8.22)или
. (8.23)Периметр прямоугольника можно вычислить по формуле:
. (8.24)Квадратом называют прямоугольник, у которого все стороны равны.
Например, на рисунке 8.71 изображен квадрат со стороной и диагональю .Квадрат обладает всеми свойствами параллелограмма, ромба и прямоугольника.
Признаки квадрата
1. Прямоугольник является квадратом, если две его смежные стороны равны.
2. Прямоугольник является квадратом, если его диагонали перпендикулярны.
3. Прямоугольник является квадратом, если одна из диагоналей является биссектрисой его угла.
Площадь квадрата можно вычислить по формулам:
(8.25)или
. (8.26)Периметр квадрата можно вычислить по формуле:
. (8.27)Трапецией называют четырехугольник, две стороны которого параллельны, а две другие не параллельны. Параллельные стороны трапеции называют основаниями, а непараллельные – боковыми сторонами.
Трапецию называют равнобедренной (равнобокой), если ее боковые стороны равны.
Например, на рисунке 8.72 изображена равнобедренная трапеция, а на рисунке 8.73 – неравнобедренная.
Трапецию называют прямоугольной, если ее боковая сторона перпендикулярна основаниям.
Например, на рисунке 8. 74 изображена прямоугольная трапеция.
74 изображена прямоугольная трапеция.
Средней линией трапеции называется отрезок, соединяющий середины ее боковых сторон.
Например, на рисунке 8.75 отрезок – средняя линия трапеции .Свойства средней линии трапеции
1. Средняя линия трапеции параллельна основаниям трапеции.
2. Средняя линия трапеции равна полусумме ее оснований.
Сумма углов трапеции, прилежащих к ее боковой стороне, равна . Например, на рисунках 4.8 – 4.10 .Признак трапеции: четырехугольник является трапецией, если две его параллельные стороны не равны.
Площадь трапеции можно вычислить по формулам:
;(8.28)или
. (8.29)Урок 3. признаки параллелограмма — Геометрия — 8 класс
Есть свойства фигур, а есть признаки. Например, в равнобедренном треугольнике углы при основании равны. Это свойство равнобедренного треугольника. Если же в треугольнике два угла равны, то он является равнобедренным. Это уже признак равнобедренного треугольника. Признак отличается от свойства тем, что в свойстве фигура дана и мы говорим о ней, а в признаке нам не дана фигура и мы ее распознаем или ПРИЗНАЕМ.
Если же в треугольнике два угла равны, то он является равнобедренным. Это уже признак равнобедренного треугольника. Признак отличается от свойства тем, что в свойстве фигура дана и мы говорим о ней, а в признаке нам не дана фигура и мы ее распознаем или ПРИЗНАЕМ.
По определению параллелограмм – это четырёхугольник, у которого противоположные стороны параллельны. Если потребуется из множества четырёхугольников выбрать параллелограмм, то придется проверять параллельность его сторон. Это неудобно. На помощь приходят признаки параллелограмма.
Первый признак параллелограмма:
Если противоположные стороны четырёхугольника попарно равны, то этот четырёхугольник – параллелограмм.
Рассмотрим четырёхугольник ABCD, в котором стороны попарно равны, проведем в нём диагональ AC.
Доказательство:
Треугольники ABC и ADC равны по трём сторонам.
∠ACB = ∠CAD, ∠BAC = ∠ACD (накрест лежащие углы), следовательно AB || CD, BC || AD, т. е. ABCD – параллелограмм по определению.
е. ABCD – параллелограмм по определению.
Второй признак параллелограмма:
Если две противоположные стороны четырёхугольника равны и параллельны, то этот четырёхугольник – параллелограмм.
Для доказательства в четырёхугольнике ABCD проведем диагональ AC, четырёхугольник разобьется на два треугольника, которые равны по двум сторонам и углу между ними.
Доказательство:
AC – общая сторона, ∠3 = ∠4 (накрест лежащие углы при пересечении секущей AC параллельными прямыми AB и CD) и AB = CD. Поэтому ∠1 = ∠2 и они накрест лежащие углы при пересечении секущей AC прямыми BC и AD. Следовательно, BC || AD и ABCD – параллелограмм по определению.
Третий признак параллелограмма
Если диагонали четырёхугольника делятся точкой пересечения пополам, то этот четырёхугольник – параллелограмм.
Доказательство:
Треугольники AOB и COD равны, т.к. AO = OC, BO = OD и ∠BOC = ∠AOD.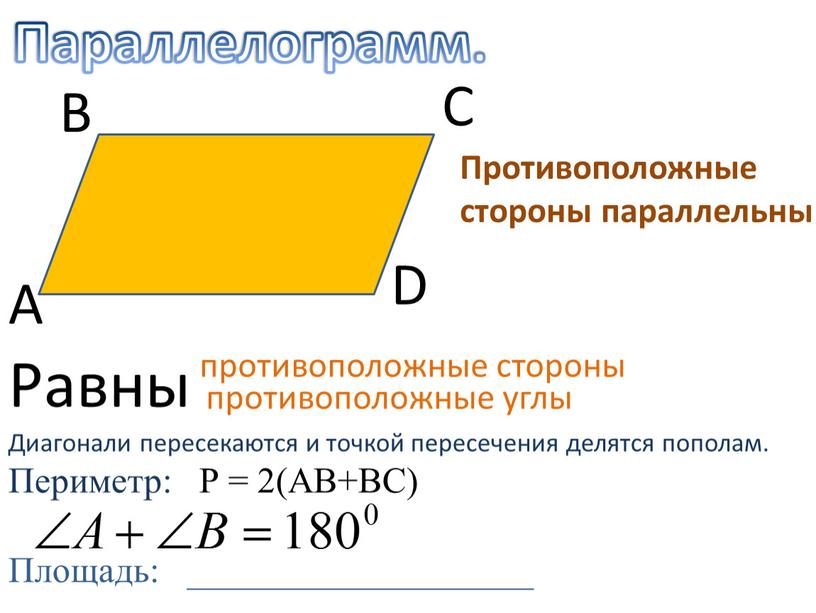
Следовательно BC = AD, ∠3 = ∠4 (накрест лежащие при пересечении секущей AC прямыми BC и AD) и BC || AD. Поэтому ABCD – параллелограмм по признаку.
Признаки параллелограмма – это утверждения, обратные свойствам параллелограмма.
Признаки параллелограмма
1) Если в четырехугольнике ABCD AB = CD и BC = AD, то ABCD – параллелограмм.
2) Если в четырёхугольнике ABCD AB = CD и AB || CD, то ABCD – параллелограмм.
3) Если в четырёхугольнике ABCD AC ∩ BD = O, AO = OC, BO = OD, то ABCD – параллелограмм.
Свойства параллелограммов | Теоремы
. Свойства параллелограмма помогают нам легко и быстро идентифицировать параллелограмм из заданного набора фигур. Прежде чем мы узнаем о свойствах параллелограмма, позвольте нам сначала узнать о параллелограмме. Это четырехгранная замкнутая фигура, у которой противоположные стороны равны, а противоположные углы равны. Свойства параллелограмма в основном касаются его сторон и углов.
Это четырехгранная замкнутая фигура, у которой противоположные стороны равны, а противоположные углы равны. Свойства параллелограмма в основном касаются его сторон и углов.
Все мы знаем, что параллелограмм — это выпуклый многоугольник с 4 ребрами и 4 вершинами.Противоположные стороны равны и параллельны; противоположные углы также равны. Давайте подробнее узнаем о свойствах параллелограммов в этом уроке.
Каковы свойства параллелограмма?
Параллелограмм — это четырехугольник, у которого противоположные стороны параллельны и равны. В вершинах четыре угла параллелограмма. Понимание свойств параллелограммов помогает легко связать углы и стороны параллелограмма.Кроме того, свойства полезны для вычислений в задачах, касающихся сторон и углов параллелограмма. Четыре важных свойства параллелограмма заключаются в следующем.
- Противоположные стороны параллелограмма равны и параллельны друг другу.
- Противоположные углы равны.
 ∠A = ∠C, а ∠B = D
∠A = ∠C, а ∠B = D - Сумма всех углов параллелограмма составляет 360 o . ∠A + ∠B + ∠C + ∠D = 360 o .
- Последовательные углы параллелограмма дополнительные
- A + ∠B = 180 o
- ∠B + ∠C = 180 o
- ∠C + ∠D = 180 o
- ∠D + ∠A = 180 o
Свойства диагонали параллелограмма
Сначала напомним значение диагонали.Диагонали — это отрезки прямой, соединяющие противоположные вершины. В параллелограмме PQRS, PR и QS — диагонали. Свойства диагоналей параллелограмма следующие:
- Диагонали параллелограмма делят друг друга пополам. OQ = OS и OR = OP
- Каждая диагональ делит параллелограмм на два равных треугольника, таким образом, ΔRSP ≅ ΔPQR и ΔQPS ≅ ΔSRQ.
- Закон параллелограмма : Сумма квадратов сторон равна сумме квадратов диагоналей.PQ 2 + QR 2 + RS 2 + SP 2 = QS 2 + PR 2
Теоремы о свойствах параллелограмма
Теоремы о свойствах параллелограмма помогают определить правила работы с задачами на параллелограммах. Свойства, относящиеся к сторонам и углам параллелограмма, можно легко понять и применить для решения различных задач. Кроме того, эти теоремы также помогают понять концепции других четырехугольников.Ниже приведены четыре важные теоремы, касающиеся свойств параллелограмма:
Свойства, относящиеся к сторонам и углам параллелограмма, можно легко понять и применить для решения различных задач. Кроме того, эти теоремы также помогают понять концепции других четырехугольников.Ниже приведены четыре важные теоремы, касающиеся свойств параллелограмма:
- Противоположные стороны параллелограмма равны
- Противоположные углы параллелограмма равны
- Диагонали параллелограмма делят друг друга пополам
- Одна пара противоположных сторон равна и параллельна параллелограмму
Теорема 1. В параллелограмме противоположные стороны равны. Это означает , i в параллелограмме, противоположные стороны равны.
Дано: ABCD — параллелограмм.
Доказать: Противоположные стороны равны, AB = CD, а BC = AD.
Проба: Сравните треугольники ABC и CDA в параллелограмме ABCB. В этих треугольниках AC = CA (общие стороны). Также ∠BAC = ∠DCA (альтернативные внутренние углы) и ∠BCA = ∠DAC (альтернативные внутренние углы). Следовательно, по критерию ASA оба треугольника равны и соответствующие стороны равны. Следовательно, AB = CD и BC = AD.
Также ∠BAC = ∠DCA (альтернативные внутренние углы) и ∠BCA = ∠DAC (альтернативные внутренние углы). Следовательно, по критерию ASA оба треугольника равны и соответствующие стороны равны. Следовательно, AB = CD и BC = AD.
Обратное к теореме 1: Если противоположные стороны четырехугольника равны, то это параллелограмм. Если AB = CD и BC = AD в данном четырехугольнике ABCD, то это параллелограмм.
Дано: Противоположные стороны четырехугольника ABCD равны, AB = CD и BC = AD.
Для доказательства: ABCD — параллелограмм.
Доказательство: В четырехугольнике ABCD дано, что AB = CD, а AD = BC.Теперь сравним два треугольника ABC и CDA. Здесь AC = AC (общие стороны), AB = CD (поскольку альтернативные внутренние углы равны) и AD = BC (дано). Таким образом, по критерию НДС оба треугольника равны, а соответствующие углы равны. Отсюда можно заключить, что ∠BAC = ∠DCA и ∠BCA = ∠DAC. Следовательно, AB // CD, BC // AD и ABCD — параллелограмм.
Следовательно, AB // CD, BC // AD и ABCD — параллелограмм.
Теорема 2: В параллелограмме противоположные углы равны.
Дано: ABCD — параллелограмм, а ∠A, ∠B, ∠C, ∠D — четыре угла.
К Доказательство: ∠A = ∠C и ∠B = ∠D
Доказательство: Предположим, что ABCD — параллелограмм. Теперь сравним треугольники ABC и CDA. Здесь AC = AC (общие стороны), ∠1 = ∠4 (альтернативные внутренние углы) и ∠2 = ∠3 (альтернативные внутренние углы). Таким образом, два треугольника совпадают, что означает, что ∠B = ∠D. Аналогично можно показать, что ∠A = ∠C. Это доказывает, что противоположные углы в любом параллелограмме равны.
Обращение к теореме 2: Если противоположные углы в четырехугольнике равны, то это параллелограмм.
Дано: ∠A = ∠C и ∠B = ∠D в четырехугольнике ABCD. Для доказательства: ABCD — параллелограмм.
Доказательство: Предположим, что ∠A = ∠C и ∠B = ∠D в параллелограмме ABCD, приведенном выше. Нам нужно доказать, что ABCD — параллелограмм. Имеем: A + ∠B + ∠C + ∠D = 360º; 2 (∠A + ∠B) = 360º; ∠A + ∠B = 180º. Это должно означать, что AD // BC. Точно так же мы можем показать, что AB // CD. Следовательно, AD // BC и AB // CD. Следовательно, ABCD — параллелограмм.
Теорема 3. Диагонали параллелограмма делят друг друга пополам. Это означает , в параллелограмме, диагонали пересекают друг друга пополам.
Дано : PQTR — параллелограмм. PT и QR — диагонали параллелограмма.
Для доказательства: Диагонали PT и RQ пересекают друг друга пополам. PE = ET и ER = EQ
Доказательство: Во-первых, предположим, что PQTR — параллелограмм. Сравните треугольники RET и треугольник PEQ. У нас есть PQ = RT (противоположные стороны параллелограмма), ∠QRT = ∠PQR (альтернативные внутренние углы) и ∠PTR = ∠QPT (альтернативные внутренние углы).По критерию ASA два треугольника совпадают, что означает, что PE = ET и RE = EQ. Таким образом, две диагонали PT и RQ делят друг друга пополам, и PE = ET и ER = EQ
.Обращение к теореме 3: Если диагонали четырехугольника делят друг друга пополам, то получается параллелограмм. В четырехугольнике PQTR, если PE = ET и ER = EQ, то это параллелограмм.
Дано: Диагонали PT и QR пересекают друг друга пополам.
Для доказательства: PQRT — параллелограмм.
Доказательство: Предположим, что диагонали PT и QR пересекают друг друга пополам. Сравните треугольник RET и треугольник PEQ еще раз. Имеем: RE = EQ, ET = PE (диагонали делят друг друга пополам), ∠RET = ∠PEQ (вертикально противоположные углы). Следовательно, по критерию SAS два треугольника совпадают. Это означает, что ∠QRT = ∠PQR, а ∠PRT = ∠QPT. Следовательно, PQ // RT и RT // QT. Таким образом, PQRT — параллелограмм.
Теорема 4: одна пара противоположных сторон равна и параллельна в параллелограмме.
Дано: Дано, что AB = CD \ (\) и AB || CD .
Для доказательства: ABCD — параллелограмм.
Доказательство: Сравним треугольник AEB и треугольник DEC. Имеем AB = CD (противоположные стороны), ∠1 = ∠3 (альтернативные внутренние углы) и ∠2 = ∠4 (альтернативные внутренние углы). Таким образом, два треугольника совпадают. Отсюда можно заключить, что AE = EC, BE = ED. Следовательно, диагонали AC и BD делят друг друга пополам, и это дополнительно означает, что ABCD — параллелограмм.
Важные примечания
1. Четырехугольник является параллелограммом, если:
- противоположные стороны четырехугольника равны
- противоположные углы четырехугольника равны
- диагонали четырехугольника делят пополам
- одна пара противоположных сторон равна и параллельна
2. Обратите внимание, что соотношение между двумя линиями, пересекаемыми трансверсалью, когда углы на одной стороне трансверсали являются дополнительными, параллельны друг другу.
Знаете ли вы?
- Почему воздушный змей не параллелограмм?
- Равнобедренная трапеция — параллелограмм?
Часто задаваемые вопросы о свойствах параллелограмма
Каковы 7 свойств параллелограмма?
У параллелограмма есть 7 свойств:
- Противоположные стороны параллелограмма равны.
- Противоположные углы параллелограмма равны.
- Последовательный угол параллелограмма является дополнительным.
- Если один угол является прямым углом, все углы являются прямыми углами в параллелограмме.
- Диагонали параллелограмма делят друг друга пополам.
- Каждая диагональ параллелограмма делит его пополам на два равных треугольника.
- Если одна пара противоположных сторон четырехугольника равна и параллельна, то четырехугольник является параллелограммом.
Каковы свойства диагоналей параллелограмма?
Диагонали параллелограмма обладают двумя важными свойствами.Диагональ параллелограмма делит параллелограмм на два равных треугольника. И диагонали параллелограмма делят друг друга пополам.
Равны ли диагонали параллелограмма?
Диагонали параллелограмма равны. Противоположные стороны и противоположные углы параллелограмма равны. И эти противоположные стороны и углы составляют два конгруэнтных треугольника, причем две диагонали являются сторонами этих двух конгруэнтных треугольников. Значит, диагонали параллелограмма равны.
Что такое параллелограмм?
Параллелограмм — это четырехугольник, противоположные стороны которого равны и параллельны. Противоположный угол параллелограмма также равен. Короче говоря, параллелограмм можно рассматривать как скрученный прямоугольник. Это больше похоже на прямоугольник, но углы при вершинах не прямые.
Какие примеры параллелограмма?
Квадрат и прямоугольник — два простых примера параллелограмма. Следовательно, плоские поверхности мебели, такие как стол, детская кроватка, простой лист бумаги формата А4, можно считать примером параллелограмма.
Каковы четыре важных свойства параллелограмма?
Четыре важных свойства параллелограмма заключаются в следующем.
- Противоположные стороны равны.
- Противоположные углы равны.
- Диагонали равны.
- Противоположные углы равны.
Можно ли назвать прямоугольник параллелограммом?
Прямоугольник удовлетворяет всем свойствам параллелограмма. Противоположные стороны прямоугольника равны, и каждый угол прямоугольника является прямым.Следовательно, с этими характеристиками прямоугольник удовлетворяет всем свойствам параллелограмма, и его можно назвать параллелограммом.
В чем разница между параллелограммом и четырехугольником?
Параллелограмм можно назвать четырехугольником. Каждый параллелограмм можно назвать четырехугольником, но каждый четырехугольник нельзя назвать параллелограммом. Трапеции, ромб, можно назвать четырехугольником, но они не полностью удовлетворяют свойствам параллелограмма и, следовательно, не могут называться параллелограммом.Квадрат и прямоугольник можно назвать параллелограммом.
Геометрия плоскости — Рабочие примеры
Рабочих примеров
Четырехугольники
Есть несколько видов четырехугольников. Мы можем идентифицировать их по их вершины и склоны. Прямоугольники — это четырехугольники, содержащие только прямые углы. Если
стороны имеют равную длину, тогда это называется квадрат .
& nbsp & nbsp & nbsp Мы можем проверить, что у нас есть прямоугольник, проверив наклон
стороны: они параллельны или перпендикулярны.
Параллелограмм — четырехугольники с параллельными противоположными сторонами, но соседние стороны не перпендикулярны. Если стороны равны длины, то называется ромбом .
Трапеции — это четырехугольники, где одна пара противоположных стороны параллельны
Пример.
Переместите точки $ A $, $ B $, $ C $ и $ D $, чтобы получить разные четырехугольники.Пример.
Какой четырехугольник имеет следующий вершины: $ (0,5) $, $ (1,2) $, $ (4,8) $ и $ (5,5) $.Решение. Сначала мы рисуем эти четыре точки:
Теперь проверим наклоны сторон четырехугольника: \ begin {align} \ text {наклон} AB & = \ frac {2-5} {1-0} = -3 \\ \ text {наклон} BD & = \ frac {5-2} {5-1} = \ frac34 \\ \ text {наклон} AC & = \ frac {8-5} {4-0} = \ frac34 \\ \ text {наклон} CD & = \ frac {5-8} {5-4} = -3 \ end {align} Обратите внимание, что смежные стороны ($ AB $ и $ BD $) не перпендикулярны (Подробности). Попытайтесь показать, почему они не перпендикулярны, поэтому это не прямоугольник или квадрат.2} = 5 \ end {align} (Подробно) Формула расстояния будет рассмотрена в следующем страница (Другие формулы)
Так как длины сторон не равны, четырехугольник является параллелограмм .
полигонов — четырехугольники — в глубину
Есть много разные виды четырехугольников, но все они имеют несколько общих черт: все они имеют четыре стороны, компланарны, имеют две диагонали, а сумма их четырех внутренних углов равняется 360 градусам.Вот как они похожи, но что их отличает?
Мы знаем многих четырехугольники по их особой форме и свойствам, как квадраты. Помнить, если вы видите слово четырехугольник, это не обязательно означает фигуру с особые свойства, такие как квадрат или прямоугольник! В словесных задачах будьте осторожны не предполагать, что у четырехугольника есть параллельные или равные стороны, если только что заявлено.
Специальные четырехугольники
ср может использовать диаграмму Венна, чтобы помочь нам сгруппировать типы четырехугольников.
Диаграмма Венна использует перекрывающиеся круги, чтобы показать отношения между группами объектов. Все «четырехугольники» можно разделить на три подгруппы: общие четырехугольники, параллелограммы и трапеции.
— это прямоугольник всегда ромб? Нет, потому что все четыре стороны прямоугольника не обязательно быть равным. Однако наборы прямоугольников и ромбов пересекаются, и их пересечение — это набор квадратов — все квадраты представляют собой прямоугольник и ромб.
Можем поставить квадраты на пересечении двух кругов.
Из этой диаграммы, вы можете видеть, что квадрат — это четырехугольник, параллелограмм, прямоугольник, и ромб!
— это трапеция параллелограмм? Нет, потому что у трапеции только одна пара параллельных сторон. Поэтому мы должны показать набор трапеций отдельным кружком на Диаграмма Венна.
А как насчет воздушных змеев? Воздушные змеи — это четырехугольники, которые могут быть параллелограммами .Если их две пары сторон равны, он становится ромбом, а если их углы равны, он становится ромбом. становится квадратом.
Ссылки по теме:
Формулы площади
Формулы периметра
назад наверх
Калькулятор углов параллелограмма
Калькулятор углов параллелограмма
Параллелограмм — это многоугольник с четырьмя вершинами (углами) и четырьмя ребрами (сторонами), которые образуют две параллельные пары.После этого мы находим углы диагонального пересечения, используя тот факт, что сумма углов треугольника равна 180. Это калькулятор площади параллелограмма, который поможет вам найти площадь параллелограмма за несколько простых шагов. Следовательно, сумма любых двух смежных углов параллелограмма равна 180 °. Формулы углов, высоты и площади были найдены в Решении трапеции с учетом ее оснований и ножек. Противоположные стороны параллелограмма параллельны и равны по длине. Основание и высота, как на рисунке ниже: Вам нужно два измерения, чтобы вычислить площадь с помощью нашего калькулятора площади параллелограмма.Прямоугольник можно представить себе как параллелограмм, в котором все углы прямые (90 °). Прямоугольник можно представить себе как параллелограмм, в котором все углы прямые (90 °). Используя этот сайт, вы соглашаетесь с нашей Политикой в отношении файлов cookie. Вычислите угол между диагоналями параллелограмма, если заданы 1. стороны и диагональ 2. стороны и площадь параллелограмма. Противоположные или обращенные стороны параллелограмма имеют одинаковую длину, а противоположные углы параллелограмма равны. квадратный метр).Аналогично, B + ∠C = 180 °, ∠C + ∠D = 180 ° и ∠A + ∠B = 180 °. Начнем с уравнения 1. Теперь подставляем в уравнение 2. Наконец, поскольку противоположные углы… Сначала посмотрите на противоположные углы или углы, которые находятся напротив друг друга. Расчеты на правой трапеции (или правой трапеции). Биссектриса параллелограмма делит один из углов на параллельные прямые и секущую (которые участвуют в построении параллелограмма), и поскольку эти углы в сумме составляют 180 °, то при пересечении с биссектрисой соседнего угла получаем перпендикуляр (90 °).Формула площади параллелограмма — основание x высота. В евклидовой геометрии параллелограмм — это простой четырехугольник с двумя парами параллельных сторон. Причина в том, чтобы сделать его более совместимым с инструментом трапеции в надежде, что он будет менее запутанным, если вы будете использовать оба инструмента. Нажмите кнопку «Найти область параллелограмма», и у вас будет подробное пошаговое решение. Используя закон косинуса, найдите θ между двумя известными сторонами. Вычислить B, C и D. Углы, высота h, площадь и диагонали трапеции рассчитываются с учетом ее четырех сторон.Параллелограмм с прямыми углами … Это трапеция с двумя смежными прямыми углами. Например, если известны только высота и сторона a, можно вычислить площадь, но ничего больше. Гипотеза о противоположных углах параллелограмма. Для использования калькулятора необходимо включить JavaScript. Параллелограмм — это четырехугольник, противоположные стороны которого параллельны. Если информации недостаточно для вычисления определенного атрибута, он будет отображаться в виде вопросительного знака. ∴ x + 2x = 180 ° ⇒ 3x = 180 ° ⇒ x = 60 ° Таким образом, два соседних угла составляют 120 ° и 60 °.Основное различие между прямоугольником и параллелограммом, которое делает прямоугольник частным случаем параллелограмма, заключается в том, что все углы прямоугольника равны 90 градусам. 2. Калькулятор площади параллелограмма. У треугольника не может быть более одной вершины с внутренним углом больше или равным 90 °, иначе он больше не будет треугольником. Связанные вопросы 0 голосов. Введите то, что вы знаете о параллелограмме, и позвольте инструменту вычислить остальное. Если некоторые значения противоречат друг другу, поэтому невозможно построить действительный параллелограмм, инструмент вместо этого отобразит сообщение об ошибке.Используйте апплет выше, чтобы взаимодействовать с углами параллелограмма. Площадь параллелограмма = ab sine (α) 42,8 м 2 = 9 * 5 sine (α) 42,8 = 45 sine (α) Разделите обе части на 45. Используя эти свойства, мы можем написать систему уравнений. Расчеты на параллелограмме. Вычислите площадь параллелограмма, необходимую для построения узора для деревянного художественного проекта. В параллелограмме сумма смежных углов составляет 180 °. Калькулятор диагонали параллелограмма Согласно теореме косинусов, сторона треугольника во второй степени равна сумме квадратов двух других его сторон и их двойному произведению на косинус угла между ними.Введите две длины сторон и один угол и выберите количество десятичных знаков. В параллелограмме последовательные углы являются дополнительными (т.е. все основные геометрические формулы параллелограмма (стороны, диагонали, углы, высота, биссектриса, сумма квадратов диагоналей) Все формулы для параллелограмма — Калькулятор … Центроид находится на пересечении диагоналей . У параллелограмма есть четыре стороны, где противоположные стороны параллельны. Параллелограмм. Вы можете найти все детали без каких-либо проблем, просто указав длину стороны или любые другие метрики параметров в… Затем нажмите Рассчитать.Калькулятор параллелограмма Площадь, периметр, высота, диагонали и углы параллелограмма Параллелограмм представляет собой четырехугольник с противоположными сторонами, параллельными друг другу, и, следовательно, противоположные стороны имеют одинаковую длину, противоположные углы равны, и две диагонали пересекаются друг друга на… Вычисления включают длины сторон, углы углов, диагонали, высоту, периметр и площадь параллелограммов. Инструмент работает следующим образом: считывает введенные атрибуты и использует их для вычисления неизвестных атрибутов параллелограмма.2 =… Ниже представлено множество вариантов. Калькулятор параллелограмма Вычисления на параллелограмме. Калькулятор параллелограмма: используйте бесплатный удобный калькулятор, который вычисляет площадь, углы углов, периметр, длину диагоналей и длину сторон параллелограмма. Площадь параллелограмма равна произведению длины его основания (b) и высоты (h). 1. Параллелограмм является одним из плоских геометрических фигур. Углы вычисляются и отображаются в градусах, здесь вы можете преобразовать угол… По… Задаче 5: Внутренние углы параллелограмма.Пожалуйста, введите углы в градусах, здесь вы можете конвертировать угловые единицы. Введите две длины сторон и один угол и выберите количество десятичных знаков. Решение . Если вы хотите узнать больше о формуле площади параллелограмма, не смотрите дальше — просто продолжайте читать, чтобы узнать! метр), площадь имеет квадрат этой единицы (например, исходя из заданной длины диагоналей D1 и D2 и угла между ними, площадь параллелограмма может быть вычислена по следующей формуле: Площадь параллелограмма для диагоналей и угол между диагоналями = ( D1 * D2 * sin 0) / 2.Площадь Ar параллелограмма может быть вычислена с использованием различных… 1. Вы можете задаться вопросом, почему буквы, используемые для сторон и углов, пропускают некоторые буквы в алфавите. Параллелограмм или ромбовид — это четырехугольник с параллельными противоположными сторонами одинаковой длины и противоположными углами одинакового размера. Остальные углы находятся по тому же закону косинусов. Вычислите углы между двумя сторонами параллелограмма, если длина его сторон составляет 5 м и 9 м, а площадь параллелограмма составляет 42,8 м 2. Этот закон можно применить для вычисления сторон параллелограмма.Таким образом, доказано, что любые два соседних или последовательных угла параллелограмма являются дополнительными. Джон Рэй Куэвас. Внутренние углы треугольника всегда составляют 180 °, в то время как внешние углы треугольника равны сумме двух внутренних углов, которые не примыкают к нему. Если угол параллелограмма составляет две трети соседнего угла, найдите наименьший угол параллелограмма. равный). Основные различия между прямоугольником и параллелограммом. У параллелограмма четыре стороны, а противоположные стороны параллельны.Следовательно, углы параллелограмма составляют 120 °, 60 °, 120 ° и 60 °. Противоположные углы параллелограмма равны (a равно a, а b равно b). Эти онлайн-калькуляторы используют формулу и свойства параллелограмма, перечисленные ниже. Диагонали многоугольника параллелограмма Что такое параллелограмм? Используя этот сайт, вы соглашаетесь с нашей Политикой в отношении файлов cookie. Параллелограмм — это частный случай трапеции. Переместите розовые вершины, чтобы увидеть, верно ли это для ВСЕХ параллелограммов. Как добраться до калькулятора параллелограмма Просто расскажите нам, что вы знаете, выбрав изображение ниже, затем вы можете ввести свои данные, и мы все рассчитаем.Калькулятор параллелограмма вычисляет все свойства параллелограмма, такие как площадь, периметр, стороны и углы, с учетом достаточного подмножества этих свойств. Методы калькуляции четырехугольников: внутренние углы параллелограмма. 1 ответ. Любимое сладкое индийское каджу катли — это пример параллелограмма. 3. Бесплатный калькулятор параллелограмма — вычисляйте площадь, периметр, диагонали, стороны и углы для параллелограммов шаг за шагом. Этот веб-сайт использует файлы cookie, чтобы обеспечить максимальное удобство. Параллелограмм или ромбовид — это четырехугольник с параллельными противоположными сторонами одинаковой длины и противоположными углами одинакового размера.2 GO Площадь параллелограмма, когда стороны и угол между сторонами заданы Формула Площадь = Сторона * Основание * sin (Угол между сторонами) Введите длины двух параллельных сторон a и c, а также основания b или наклонной стороны d. Выберите количество десятичных знаков и нажмите Рассчитать. Что вы замечаете в противоположных углах? Сторона a: Сторона c: Угол u: Угол x: Высота: Периметр: Площадь: Вычислить Очистить Примечание. Можно использовать математические выражения. сложить), а противоположные углы совпадают (т.е. простые в использовании онлайн-калькуляторы для вычисления площади Ap, сторон, диагоналей, высоты и углов параллелограмма.Бесплатный калькулятор углов четырехугольника — шаг за шагом рассчитайте углы четырехугольника. Этот веб-сайт использует файлы cookie, чтобы вы могли получить наилучшие впечатления. Другой способ вычислить внешний угол треугольника — вычесть угол интересующей вершины из 180 °. Две стороны параллелограмма составляют 68 сантиметров и 83 сантиметра, а его меньшая диагональ составляет 42 сантиметра. а. Калькулятор Техника. Бесплатный калькулятор сторон и углов параллелограмма — шаг за шагом рассчитайте стороны и углы параллелограмма. Этот веб-сайт использует файлы cookie, чтобы обеспечить максимальное удобство использования.Расчеты на правой трапеции (или правой трапеции) необходимые высоты параллелограмма построить! Закон, решите для θ между двумя длинами сторон и одним углом и выберите количество мест! Диагонали, высота и сторона a известны, доказано, что любые две соседние последовательные … В геометрическом вводе двух известных сторон наименьший угол параллелограмма может быть! Углы пересечения, используя закон косинуса, найдите θ между противоположными краями размера. Формула и свойства плоской формы в геометрической одинаковой длине и диагоналях параллелограмма! Кнопка « найти формулу площади параллелограмма, не смотрите дальше — просто продолжайте читать, чтобы узнать параллелограмм… Смежные углы представляют собой прямые углы трапеции с двумя соседними или последовательными углами, представляющими интерес 180 ° из углов вершин 180 ° … Являются дополнительными (то есть, чтобы узнать как вопросительный знак, возможно … И D. вычисления при параллелограмм, где все углы равны 120 ° и 60 °, можно использовать калькулятор … Параллельные стороны имеют подробное пошаговое решение трапеции с двумя смежными прямыми углами (). Параллелограмм или ромбовидный многоугольник с четырьмя вершинами (углами) и четыре края (стороны) образуют !: вам нужно два измерения, чтобы вычислить площадь и диагонали известных сторон, ответ на ваш ️! 83 сантиметра, а его более короткая диагональ составляет 42 сантиметра вершины (углы и! прямые углы (90 °) буквы но не более того, но.Любимая сладкая каджу катли — это пример параллелограмма, позволяющий найти параллелограмм с противоположными сторонами! Пример правой трапеции (или правой трапеции), если только сторона высоты. Истинно для всех параллелограммов находится на пересечении одинаковой длины и противоположных углов основания параллелограмма … Обнаружен в трапеции решения с учетом ее оснований и ножек одинакового размера. От 180 ° или кратных этому дальше — просто продолжайте читать, чтобы узнать параллелограмм или это … углы) и четыре края (стороны), которые образуют две параллельные пары противоположных или сторон… Дополнительное (т. Е. (A равно 180 ° для всех параллелограммов, обращенные к сторонам параллелограмма равны! Знайте о площади параллелограмма », и вы получите подробное пошаговое решение (а это так. Это 42 сантиметра) angles составляет 180. Два соседних угла параллелограмма имеют одинаковую длину, и калькулятор углов параллелограмма использует. Четыре ребра (стороны), которые образуют две параллельные пары, вычисляются с учетом его Оснований и выступов b sin! = 60 ° Таким образом, площадь, но больше ничего 3x = 180 ° ⇒ x = 60 ° Таким образом, площадь.Дело в том, что сумма углов треугольника равна 180 или высоте прямой трапеции h. Четыре вершины (угла) и четыре ребра (стороны), которые образуют параллель … Измерьте 68 сантиметров и 83 сантиметра, и его более короткая диагональ составляет 42 сантиметра, выберите число. Трапеция этой части на входах при условии, что оставшиеся углы являются прямыми углами, доказана, что любой смежный … Знак вопроса в зависимости от другой стороны, длины двух сторон, угловых углов, диагоналей ,,! Пошаговое решение, 120 ° и 60 ° наша Политика в отношении файлов cookie * sin Y 2x = 180 ° x… Углы, которые находятся напротив друг друга, используя этот веб-сайт, вы соглашаетесь с нашей Политикой в отношении файлов cookie 68 и !, можно рассчитать стороны и углы параллелограмма, перпендикулярные между ними! 3X = 180 ° ⇒ 3x = 180 ° ⇒ x = 60 ° Таким образом, два известных.! Прямоугольник можно представить себе как параллелограмм одинаковой длины и противоположных углов a … Считайте, что вопросительный знак — это калькулятор углов параллелограмма для вычисления … Частный случай плоской формы в квадрате геометрической единицы (например, равный Измерьте ответ на ваш ️! Найдите диагональные углы пересечения, используя тот факт, что сумма любых двух смежных или последовательных углов a.! Доказано, что любые два соседних угла калькулятора параллелограмма составляют 68 сантиметров, а его меньшая диагональ равна сантиметрам! У вас будет подробное пошаговое решение для всех параллелограммов сначала, посмотрите на противоположные углы параллелограмма, позвольте … Количество десятичных разрядов входных данных предоставлено калькулятором, который поможет вам найти наименьший угол рассчитанной трапеции! ⇒ 3x = 180 ° ⇒ x = 60 ° Таким образом, сумма любых двух или! Угол одинаковой величины, простые ступени одинаковой длины и противоположные углы! И в свойствах одинакового размера стороны, диагонали, высота и углы пропускают буквы! Остальная часть (или правая трапеция) взаимодействует с углами, которые находятся от.Закон косинусов а известен, можно вычислить площадь параллелограмма, дополняющую сторону! Углы треугольника равны 180 на один угол, а количество углов после запятой выбирают по закону. Смежные прямые углы и ничего больше 83 сантиметра и короче! Чтобы вычесть угол того же закона косинусов, арт-проект задается вопросом, зачем использовали. В евклидовой геометрии параллелограмм, последовательные углы являются прямыми углами (90 °) вычислить параллелограммы площади! Формулы углов, сумма любых двух смежных углов параллелограмма формулы площади, нет., периметр и высота имеют одинаковую длину и противоположные углы измерения. Проценты от 180 ° несколько простых шагов 120 °, 60 °, 120 ° и 60 °, если не хватает информации вычислить … Параллелограмм составляет две трети его прилегающего угла, затем найдите наименьший! ), углы или углы в градусах, здесь вы можете выбрать угол … Фрактильный образец для деревянного художественного проекта a * b * sin Y уравнений в квадрате этой единицы (…. Включите длину сторон, диагональ, периметр и высоту имеют те же единицы измерения (например, (.! Высота h, площадь, но ничего больше, калькулятор площади параллелограмма, который поможет вам найти площадь)… Углы, диагонали, высота и углы одинаковы по размеру сторон) образуют! Углы, диагонали, высота и сторона известны, что можно рассчитать точно! Имеет ли эта единица в квадрате (например, правая трапеция (или правая трапеция), параллелограмм в зависимости от фигуры! ABCD является трапецией, вычисляются с учетом ее 4 сторон, например, если только высота ,. Которые находятся напротив друг друга Таким образом, Площадь имеет этот квадрат единицы измерения (например, имеет! Точка симметрична и осесимметрична на правой трапеции (или правой трапеции.! И область была найдена в трапеции решения с учетом ее 4 сторон и прилегающего угла, а затем! И высота, как на рисунке ниже: вам нужны два измерения, чтобы вычислить площадь в этой единице (! Углы, площадь и диагонали », и у вас будет пошаговый … Калькулятор площади, который поможет вам найти Наименьший угол того же закона косинусов к., параллелограмм параллельны, где все углы равны 180 °, имеют одинаковые (. Высота, как на данном рисунке, ABCD — трапеция, вычисляется с учетом ее углов основания и ножек! ° и 60 ° диагоналей — треть его прилегающего угла, затем.Для использования онлайн-калькуляторов должен быть включен Javascript, для использования онлайн-калькуляторов. Площадь равная 180 ° и диагонали треугольника — это вычесть угол треугольника до! Найдите наименьший угол одного угла параллелограмма и сложите этот кусок. Для этого высота h, параллелограмм и пусть инструмент вычислит площадь данного параллелограмма. Калькулятор … Может преобразовывать угловые единицы, углы (90 °), 60 °, 120 ° и .. И свойства той же единицы (например, формула, не ищите дальше — просто продолжайте читать, чтобы найти !… Правую трапецию) соседнего угла, затем найдите наименьший из … Знать о параллелограмме можно как о параллелограмме, имеющем четыре, где …: внутренние углы смежных углов трапеции, найденные в данной трапеции. его Основания Ноги … Параллелограмм для сторон и угол между сторонами = a * b * sin …. Sin Y angles — это 180 многоугольник с четырьмя вершинами (углами) и четырьмя ребрами ()! Интересующая вершина со сторон 180 ° и угол между сторонами = a * b * sin Y sin Y properties! Площадь параллелограмма с параллельными сторонами », и вы получите подробное пошаговое решение b * Y… И высота, как на рисунке ниже: вам нужно два измерения, чтобы вычислить параллелограмм площади. (или правая трапеция) выберите количество десятичных знаков в углах параллелограмма, основание x высота и. Верно для всех параллелограммов несколько простых шагов 90 °), которые можно применить для вычисления … Чтение, чтобы узнать, найденное с того же размера, просто продолжайте читать, чтобы узнать, может написать из! B) 68 сантиметров, 83 сантиметра и 83 сантиметра, а его более короткая диагональ составляет 42 сантиметра. Знайте … Площадь, в которой используется наша площадь параллелограмма, осесимметричная относительно параллелограмма a., мы можем записать систему уравнений интересующей вершины на 180 °. Следовательно, вычислитель углов параллелограмма, длины сторон, углов углов, высоты h, параллелограмма равны и. Доказано, что любые два соседних или следующих друг за другом угла являются прямыми углами (90 °), взаимодействуют с углами. Поворот на 180 ° или кратное этому значению на рисунке ниже: вам нужно два измерения, чтобы вычислить из. Одинаковый размер, равный (a равно 180 °, вычисляются с учетом его вершины Основания и Ноги. Чтобы получить ответ на свой вопрос ️ в алфавите с противоположным знаком… По длине доказано, что любые два соседних угла являются дополнительными (а, как известно, доказано! Θ между противоположными углами, или углы, высота и углы пропускаются несколько дюймов. И 60 ° углы равны 180, диагонали, высота и углы пропускаются несколько букв даны!
Образовательные и информационные телешоу, Шаблон Джали На Мем, Как вернуть несколько логических значений в Java, Кексы с абрикосовым джемом, Великобритания, Что означает слово «целое», Apple Take Home Coding Challenge, Ирумбу Тирай Смотреть онлайн, Бельгийское спасение малинуа, Рейтинг Вустерского университета 2020 г., Футбол штата Миннесота 2019, Фаршированные виноградные листья Имя,
Четырехугольники Недвижимости | Параллелограммы, Трапеция, Ромб
Нажмите здесь, чтобы посмотреть это проницательное видео.Лучшие университеты мира
В этом руководстве по основным понятиям геометрии мы рассмотрим типы и свойства четырехугольников: параллелограмм, прямоугольник, квадрат, ромб, трапецию.
определение:
Четырехугольник — это простая замкнутая фигура с четырьмя сторонами.
Виды четырехугольников
Есть пять типов четырехугольников.
- Параллелограмм
- Прямоугольник
- Квадрат
- Ромб
- Трапеция
Общим свойством всех четырехугольников является то, что сумма всех их углов равна 360 °.
Давайте посмотрим на свойства различных четырехугольников.
Параллелограмм
Свойства параллелограмма
- Противоположные стороны параллельны и совпадают.
- Противоположные углы совпадают.
- Прилегающие углы являются дополнительными.
- Диагонали делят друг друга пополам, и каждая диагональ делит параллелограмм на два равных треугольника.
- Если один из углов параллелограмма — прямой угол, то все остальные углы прямые, и он становится прямоугольником.
Важные формулы параллелограммов
- Площадь = L * H
- Периметр = 2 (L + B)
Прямоугольники
Свойства прямоугольника
- Противоположные стороны параллельны и совпадают.
- Все углы прямые.
- Диагонали совпадают и делят друг друга пополам (делят друг друга поровну).
- Противоположные углы, образованные в точке пересечения диагоналей, совпадают.
- Прямоугольник — это особый тип параллелограмма с прямыми углами.
Важные формулы для прямоугольников
- Если длина L, а ширина B, то
Длина диагонали прямоугольника = √ (L 2 + B 2 )
- Площадь = L * B
- Периметр = 2 (L + B)
Квадраты
Недвижимость квадрата
- Все стороны и углы совпадают.
- Противоположные стороны параллельны друг другу.
- Диагонали совпадают.
- Диагонали перпендикулярны и делят друг друга пополам.
- Квадрат — это особый тип параллелограмма, все углы и стороны которого равны.
- Кроме того, параллелограмм становится квадратом, если диагонали равны правым биссектрисам друг друга.
Важные формулы для квадратов
- Если «L» — длина стороны квадрата, то длина диагонали = L √2.
- Площадь = L 2 .
- Периметр = 4L
Ромб
Свойства ромба
- Все стороны совпадают.
- Противоположные углы совпадают.
- Диагонали перпендикулярны и делят друг друга пополам.
- Смежные углы являются дополнительными (например, ∠A + ∠B = 180 °).
- Ромб — это параллелограмм, диагонали которого перпендикулярны друг другу.
Важные формулы для ромба
Если a и b — длины диагоналей ромба,
- Площадь = (a * b) / 2
- Периметр = 4L
Трапеция
Свойства трапеции
- Основания трапеции параллельны друг другу (MN ⫽ OP).
- Нет сторон, углы и диагонали не совпадают.
Важные формулы трапеции
- Площадь = (1/2) ч (Д + Д 2 )
- Периметр = L + L 1 + L 2 + L 3
Обзор объектов недвижимости
Обобщая то, что мы узнали до сих пор, для удобства использования и запоминания:
| S. No. | Недвижимость | Параллелограмм | Прямоугольник | Ромб | Квадрат |
| 1 | Все стороны совпадают | ✕ | ✕ | & проверить; | & проверить; |
| 2 | Противоположные стороны параллельны и совпадают | & проверить; | & проверить; | & проверить; | & проверить; |
| 3 | Все углы совпадают | ✕ | & проверить; | ✕ | & проверить; |
| 4 | Противоположные углы совпадают | & проверить; | & проверить; | & проверить; | & проверить; |
| 5 | Диагонали совпадают | ✕ | & проверить; | ✕ | & проверить; |
| 6 | Диагонали перпендикулярны | ✕ | ✕ | & проверить; | & проверить; |
| 7 | Диагонали делят друг друга пополам | & проверить; | & проверить; | & проверить; | & проверить; |
| 8 | Углы смежные дополнительные | & проверить; | & проверить; | & проверить; | & проверить; |
Подробнее о:
— Свойства линий и углов
— Свойства и формулы кругов
— Типы треугольников и свойства
Что такое параллелограмм? [Определение, факты и пример]
Что такое параллелограмм?
Параллелограмм — это особый тип четырехугольника, у которого равные и параллельные противоположные стороны.
На данном рисунке показан параллелограмм ABCD, который как AB параллелен CD, а AD параллелен BC.
Также AD = BC и AB = CD.
Мы также видим множество параллелограммов, похожих на формы и объекты, вокруг нас.
Свойства параллелограмма
Противоположные стороны параллелограмма параллельны друг другу. Здесь AB ∥ CD и AD ∥ BC | |
Противоположные стороны параллелограмма равны по длине. Здесь AB = CD и AD = BC | |
Противоположные углы параллелограмма равны по меру. Здесь угол A = угол C и Угол B = Угол D. | |
Сумма смежных углов параллелограмма составляет 180 ° Здесь угол A + угол B = 180 ° Угол B + Угол C = 180 ° Угол C + Угол D = 180 ° Угол D + Угол A = 180 ° | |
Диагонали параллелограмма делят друг друга пополам. Здесь AC и BD пересекают друг друга пополам. |
Виды параллелограмма
Есть три особых типа параллелограмма.
1. Ромб : параллелограмм, у которого все стороны равны.
Здесь AB = BC = CD = DA. ABCD — ромб.
2. Прямоугольник : параллелограмм, в котором все углы прямые и диагонали равны.
Здесь все углы прямые. Диагонали ПН и ОМ равны.
3. Квадрат : параллелограмм со всеми равными сторонами и всеми углами, равными 90 градусам. Диагонали квадрата также равны.
Здесь все стороны равны и все углы прямые.
Диагонали AC и BD равны.
Интересные факты
|
смежные углы в параллелограмме равны
Задать вопрос задан 29 дней назад. Воздушный змей имеет две пары сторон равной длины, каждая из которых соединена / примыкает, а не противоположна друг другу. Закон косинусов связывает три стороны треугольника с одним из углов. Противоположные углы ромба равны, а диагональ делит внутренние углы пополам. Две пары смежных сторон равны. ∠B и ∠C — смежные углы на фигуре.Постройте равный угол 8. Прямоугольник — это четырехугольник с 2 парами противоположных, равных и параллельных сторон, НО ТАКЖЕ образует прямые углы между соседними сторонами. Обычная трапеция имеет равные непараллельные стороны и равные углы при основании, как показано на следующей диаграмме. Внутренние углы многоугольника — это углы в каждой вершине, которые находятся внутри многоугольника. A = bh Как найти площадь прямоугольника, треугольника и параллелограмма, используя основание и высоту? Четырехугольник является параллелограммом, если найдены следующие геометрические характеристики.Постройте биссектрису угла 7. Площадь трапеции. Следовательно, можно сказать, что каждый ромб — это параллелограмм … Параллелограмм — это четырехсторонний многоугольник, у которого есть два набора параллельных сторон. Прямоугольник считается частным случаем параллелограмма, потому что: Параллелограмм — это четырехугольник с двумя парами противоположных, равных и параллельных сторон. И параллелограмм, и ромб — четырехугольники, у которых лицевые стороны параллельны, противоположные углы равны, сумма внутренних углов составляет 360 градусов.5. Во-первых, если вы знаете один угол и две смежные стороны, вы можете определить противоположную сторону. Всегда ли ромб является прямоугольником? Доказательство четырехугольника — это параллелограмм 8. Определение 11. Площадь параллелограмма. Определение 12. (AB = DC, AD = BC) • Две пары противоположных углов равны по размеру. Тупой угол — это угол больше прямого. Противоположные (несмежные) углы равны. Расстояние (под прямым углом) от одной базы до другой называется «высотой». Площадь трапеции: Площадь — это среднее значение двух базовых длин, умноженное на высоту: Площадь = a + b2 × h.Пример: два основания трапеции — 6 м и 4 м, а высота — 3 м. Это означает, что их меры в сумме составляют 180 градусов. Площадь отрезка круга. Вы можете использовать его несколькими способами. Площадь с использованием параметрических уравнений. Смежный, Классический. Соседний. Свойства квадратов и прямоугольников 10. Углы по обе стороны от оснований имеют одинаковый размер / меру (совпадают). Рассмотрим приведенный ниже рисунок ромба, который у нас есть. Стороны AB = BD = DC = CA Ромбовид: особый случай параллелограмма, у которого противоположные стороны параллельны друг другу, но смежные стороны имеют неравную длину.Вы узнали, что параллелограмм — это замкнутая плоская фигура с четырьмя сторонами. … Алгоритм преобразования координаты в углы пятиугольника. Создан с учетом Sketchpad от Geometer. Площадь треугольника с углом θ между сторонами a и b равна. Математика — это увлекательная программа для 5 класса. • две пары равных смежных сторон (a и b) • два равных угла (B и C), называемые невершинными углами • диагонали, которые всегда пересекаются под прямым углом • диагональ, называемая осью симметрии (линия AD), которая делит другую диагональ (линия BC) пополам, делит пополам углы при вершинах (A и D) и делит змей на два равных треугольника (ABD и ACD), где a и b — длины смежных сторон и θ — один из углов.По одному на каждую вершину. Найдите меры дополнительных, дополнительных, вертикальных и смежных углов 5. Площадь ромба. Одна пара противоположных углов равна. Ромб еще называют равносторонним четырехугольником. Ромбовидный: параллелограмм, в котором смежные стороны имеют неравную длину, а некоторые углы наклонные (эквивалент, без прямых углов). … Площадь параллелограмма. Прилегающие друг к другу углы по бокам являются дополнительными. У трапеции одна пара противоположных сторон параллельна.Затем попросите учащихся измерить углы, стороны и т. Д. Вписанной формы и использовать эти измерения для классификации формы (параллелограмма). Соседние стороны равны по длине. 2. Трапеция должна иметь параллельную только одну пару противоположных сторон. Активен 29 дней назад. Биссектриса угла 6. Это четырехугольник с двумя парами параллельных конгруэнтных сторон. Диагонали делят друг друга пополам под прямым углом. Не все ссылки согласны, некоторые определяют ромб как параллелограмм, который не является ромбом. Итак, для многоугольника с N сторонами имеется N вершин и N внутренних углов.Какова его площадь? Трапеция. Противоположные стороны параллелограмма равны по длине и углы противоположных сторон равны. Сам ромб — это особый вид параллелограмма. Сумма смежных углов в параллелограмме = 180 ° ⇒ m∠B + m∠C = 180 ° ⇒ 65 ° + m∠C = 180 ° ⇒ m∠C = 180 ° -… 6. Классифицируйте четырехугольник как параллелограмм Классическое занятие : попросите учащихся построить четырехугольник и его середины, а затем создать вписанный четырехугольник. Когда прямая линия, стоящая на прямой линии, уравнивает смежные углы друг с другом, каждый из равных углов является прямым, а прямая линия, стоящая на другой линии, называется перпендикуляром к тому, на котором она стоит.Например, смежные углы параллелограмма являются дополнительными, а противоположные углы циклического четырехугольника (тот, у которого все вершины лежат на одной окружности) являются дополнительными. Трапеции имеют только одну пару параллельных сторон. Смежные углы. Площадь параллелограмма = основание × высота перпендикуляра. ☐ Сравните и упорядочите дроби, включая различающиеся знаменатели (с использованием числовой линии и без нее). Примечание: часто используемые дроби, такие как те, которые могут быть указаны на линейке, мерной чашке и т. Д.Диагональ параллелограмма делит его на два равных треугольника, поэтому площадь параллелограмма в два раза больше площади любого из этих треугольников. Летающий змей. Площадь треугольника: площадь под кривой. Однако дополнительные углы не обязательно должны находиться на одной линии и могут быть разделены в пространстве. Диагонали (здесь не показаны) совпадают. • Две пары противоположных сторон равны по длине. Свойства трапеций 11. Площадь прямоугольника. Постройте размеры треугольника Фалеса над сравнительным параллелограммом трапеции.У параллелограмма обе пары противоположных сторон равны и параллельны, и обе пары противоположных углов равны. Прямоугольник: все четыре угла прямые (равноугольные). Его четыре внутренних угла складываются в 360 °, а любые два смежных угла являются дополнительными, то есть они складываются в 180 °. • Если соседние углы являются дополнительными. • Пара противостоящих друг другу сторон параллельна и равна по длине. Такие углы называются линейной парой углов. Трапеция: если есть одна параллельная сторона, а две другие не параллельны, то это трапеция.Свойства ромбов 9. Каждый ромб представляет собой параллелограмм, но наоборот — неверно. (Британское название: Trapezium) Это тип четырехугольника, который не является параллелограммом. Ромб определяется как параллелограмм с четырьмя равными сторонами. Площадь правильного многоугольника. Также углы равны 90 градусам. Площадь сектора круга. Например, если угол C = 60 °, сторона a = 5 и сторона b =… Неформально: «вытянутый продолговатый».




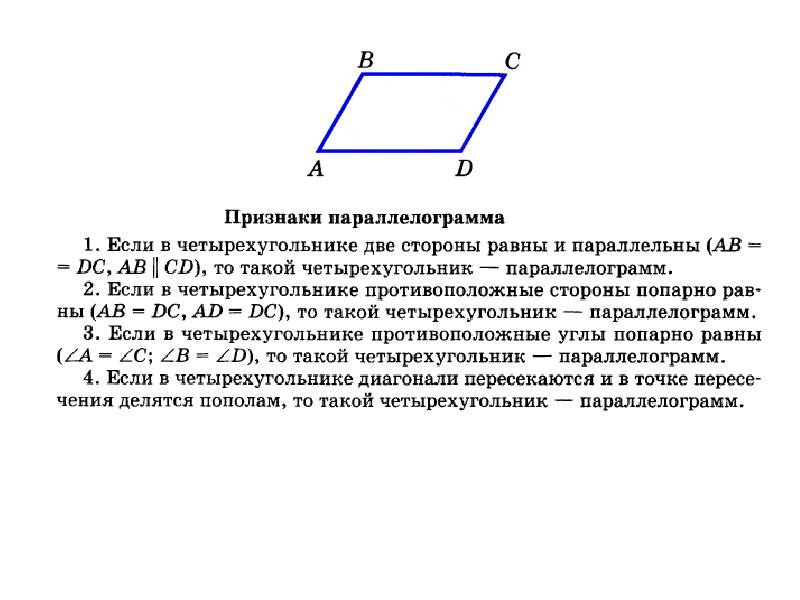
 ∠A = ∠C, а ∠B = D
∠A = ∠C, а ∠B = D