Z i 2: Mathway | Популярные задачи

Калькулятор онлайн — Решение комплексных чисел: сумма, разность, произведение, частное, n-ая степень и корень n-ой степени (с подробным решением)

С помощью данного калькулятора вы можете сложить, вычесть, умножить, и разделить комплексные числа.
Программа решения комплексных чисел не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс нахождения решения.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Правила ввода действительной и мнимой части

Примеры подробного решения >>

Введите действительную и мнимую части чисел \( z_1 \) и \( z_2 \).
У каждого числа нужно ввести как минимум одну часть — действительную или мнимую.

Обнаружено что не загрузились некоторые скрипты, необходимые для решения этой задачи, и программа может не работать.
Возможно у вас включен AdBlock.
В этом случае отключите его и обновите страницу.

Сообщение отправлено. Спасибо.

Понятие комплексного числа

Определение.
Комплексными числами называют выражения вида а + bi где а и b — действительные числа, а i — некоторый символ, для которого по определению выполняется равенство i² = -1.

Название «комплексные» происходит от слова «составные» — по виду выражения а + bi. Число а называется действительной частью комплексного числа а + bi, а число b — его мнимой частью. Число i называется мнимой единицей. Например, действительная часть комплексного числа 2-3i равна 2, мнимая часть равна -3. Запись комплексного числа в виде а + bi называют алгебраической формой комплексного числа.

Равенство комплексных чисел

Определение.
Два комплексных числа а + bi и c + di называются равными тогда и только тогда, когда а = с и b = d, т. е. когда равны их действительные и мнимые части.

Сложение и умножение комплексных чисел

Операции сложения и умножения двух комплексных чисел определяются следующим образом.

Определения.
Суммой двух комплексных чисел а + bi и c + di называется комплексное число (a + c) + (b + d)i, т.е.
(a + bi) + (c + di) = (a + c) + (b + d)i.
Произведением двух комплексных чисел а + bi и c + di называется комплексное число (ac — bd) + (ad + bc)i, т. е.
(а + bi)(с + di) = (ас-bd) + (ad + bc)i.

Из двух предыдущих формул следует, что сложение и умножение комплексных чисел можно выполнять по правилам действий с многочленами. Поэтому нет необходимости запоминать эти формулы, их можно получить по обычным правилам алгебры, считая, что i² = -1.

Основные свойства сложения и умножения комплексных чисел

1. Переместительное свойство
\( z_1 + z_2 = z_2 + z_1 , \qquad z_1z_2 = z_2z_1 \)

2. Сочетательное свойство
\( (z_1 + z_2) + z_3 = z_1 + (z_2 + z_3) , \qquad (z_1z_2)z_3 = z_1(z_2z_3) \)

3. Распределительное свойство
\( z_1(z_2 + z_3) = z_1z_2 + z_1z_3 \)

Комплексно сопряженные числа

Определение.
Сопряженным с числом z = a + bi называется комплексное число а -bi, которое обозначается \( \overline{z} \), т. е.
\( \overline{z} = \overline{a+bi} = a-bi \)

Например, \( \overline{3 + 4i} = 3-4i, \qquad \overline{-2-5i} = -2+5i, \qquad \overline{i} = -i \)

Отметим, что \( \overline{a-bi} = a+bi \), поэтому для любого комплексного числа z имеет место равенство
\( \overline{(\overline{z})} = z \)

Равенство \( \overline{z} = z \) справедливо тогда и только тогда, когда z — действительное число.

Модуль комплексного числа

Определение.
Модулем комплексного числа z = а + bi называется число \( \sqrt{a^2+b^2} \), т.е.
\( |z|=|a+bi| = \sqrt{a^2+b^2} \)

Из данной формулы следует, что \( |z| \geq 0 \) для любого комплексного числа z, причем |z|=0 тогда и только тогда, когда z=0, т.е. когда a=0 и b=0.

Вычитание комплексных чисел

Определение.
Комплексное число (–1)z называется противоположным комплексному числу z и обозначается –z.
Если z = a+bi, то –z = –a–bi. Например, –(3–5i) = –3+5i. Для любого комплексного числа z выполняется равенство
z+(–z) = 0.

Вычитание комплексных чисел вводится как операция, обратная сложению: для любых комплексных чисел z₁ и z₂ существует, и притом только одно, число z, такое, что
z + z₂ = z₁,
т.е. это уравнение имеет только один корень.

Деление комплексных чисел

Деление комплексных чисел вводится как операция, обратная умножению: для любых комплексных чисел \( z_1 \) и \( z_2 \neq 0 \) существует, и притом только одно, число \( z \), такое, что \( zz_2=z_1 \) т.е. это уравнение относительно z имеет только один корень, который называется частным чисел \( z_1 \) и \( z_2 \) и обозначается \( z_1:z_2 \), или \( \frac{z_1}{z_2} \), т.е. \( z=z_1:z_2 = \frac{z_1}{z_2} \)

Комплексное число нельзя делить на нуль.

Частное комплексных чисел \( z_1 \) и \( z_2 \neq 0 \) можно найти по формуле
\( \large \frac{z_1}{z_2} = \frac{z_1 \cdot \overline{z_2}}{|z_2|^2} \)

Каждое комплексное число z, не равное нулю, имеет обратное ему число w, такое, что z*w = 1, где
\( \large w= \frac{1}{z} = \frac{a}{a^2+b^2}-\frac{b}{a^2+b^2}i \)

Если z₁ = a₁ + b₁i, z₂ = a₂ + b₂i, то формулу частного комплексных чисел можно представить в виде
\( \large \frac{z_1}{z_2} = \frac{a_1+b_1i}{a_2+b_2i}= \frac{(a_1+b_1i)(a_2-b_2i)}{a^2_2+b^2_2} = \frac{a_1a_2+b_1b_2}{a^2_2+b^2_2}+ \frac{a_2b_1-a_1b_2}{a^2_2+b^2_2}i \)

Геометрическая интерпретация комплексного числа. Комплексная плоскость

Действительные числа геометрически изображаются точками числовой прямой. Комплексное число а + bi можно рассматривать как пару действительных чисел (а; b). Поэтому естественно комплексные числа изображать точками плоскости.

Пусть на плоскости задана прямоугольная система координат. Комплексное число z = a + bi изображается точкой плоскости с координатами (а; b), и эта точка обозначается той же буквой z.

Такое соответствие между комплексными числами и точками плоскости взаимно однозначно: каждому комплексному числу а + bi соответствует одна точка плоскости с координатами (а; b) и, наоборот, каждой точке плоскости с координатами (а; b) соответствует одно комплексное число a + bi. Поэтому слова «комплексное число» и «точка плоскости» часто употребляются как синонимы. Так, вместо слов «точка, изображающая число 1 + i» говорят «точка 1 + i». Можно, например, сказать «треугольник с вершинами в точках i, 1+i, -i».

При такой интерпретации действительные числа a, т.е. комплексные числа а+0i, изображаются точками с координатами (а; 0), т.е. точками оси абсцисс. Поэтому ось абсцисс называют действительной осью. Чисто мнимые числа bi = 0+bi изображаются точками с координатами (0; b), т.е. точками оси ординат, поэтому ось ординат называют мнимой осью. При этом точка с координатами (0; b) обозначается bi. Например, точка (0; 1) обозначается i, точка (0; -1) — это -i , точка (0; 2) — это точка 2i. Начало координат — это точка O. Плоскость, на которой изображаются комплексные числа, называют комплексной плоскостью.

Отметим, что точки z и -z симметричны относительно точки 0 (начала координат), а точки \( z \) и \( \overline{z} \) симметричны относительно действительной оси.

Комплексное число z = a+bi можно изображать вектором с началом в точке 0 и концом в точке z. Этот вектор будем обозначать той же буквой z, длина этого вектора равна |z|.

Число z₁ + z₂ изображается вектором, построенным по правилу сложения векторов z₁ и z₂ а вектор z₁-z₂ можно построить как сумму векторов z₁ и -z₂.

Геометрический смысл модуля комплексного числа

Выясним геометрический смысл модуля комплексного числа |z|. Пусть z = а+bi. Тогда по определению модуля \( |z|= \sqrt{a^2+b^2} \). Это означает, что |z| — расстояние от точки 0 до точки z.

Например, равенство |z| = 4 означает, что расстояние от точки 0 до точки z равно 4. Поэтому множество всех точек z, удовлетворяющих равенству |z| = 4, является окружностью с центром в точке 0 радиуса 4. Уравнение |z| = R является уравнением окружности с центром в точке 0 радиуса R, где R — заданное положительное число.

Геометрический смысл модуля разности комплексных чисел

Выясним геометрический смысл модуля разности двух комплексных чисел, т.е. |z₁—z₂|.
Пусть z₁ = a₁+b₁i, z₂ = a₂+b₂i.
Тогда \( |z_1-z_2| = |(a_1-a_2) + (b_2-b_2)i| = \sqrt{(a_1+a_2)^2 + (b_1+b_2)^2} \)

Из курса геометрии известно, что это число равно расстоянию между точками с координатами (а₁; b₁) и (a₂; b₂).

Итак, |z₁-z₂| — расстояние между точками z₁ и z₂.

Тригонометрическая форма комплексного числа. Аргумент комплексного числа

Определение
Аргумент комплексного числа \( z \neq 0 \) — это угол \( \varphi \) между положительным направлением действительной оси и вектором Oz. Этот угол считается положительным, если отсчет ведется против часовой стрелки, и отрицательным при отсчете по часовой стрелке.

Связь между действительной и мнимой частями комплексного числа z = а + bi, его модулем r=|z| и аргументом \( \varphi \) выражается следующими формулами:
\( \left\{ \begin{array}{l} a=r \cos \varphi \\ b=r \sin \varphi \end{array} \qquad (1) \right. \)

\( \left\{ \begin{array}{l} \cos \varphi =\frac{a}{\sqrt{a^2+b^2}} \\ \sin \varphi =\frac{b}{\sqrt{a^2+b^2}} \end{array} \qquad (2) \right. \)

Аргумент комплексного числа z = a+bi ( \( z\neq 0 \) ) можно найти, решив систему (2). Эта система имеет бесконечно много решений вида \( \varphi =\varphi_0+2k\pi \), где \( k\in\mathbb{Z} , \;\; \varphi_0 \) — одно из решений системы (1), т.е. аргумент комплексного числа определяется неоднозначно.

Для нахождения аргумента комплексного числа z = а+bi ( \( z\neq 0 \) ) можно воспользоваться формулой
\( tg \varphi = \large \frac{b}{a} \normalsize \qquad (3) \)

При решении уравнения (3) нужно учитывать, в какой четверти находится точка z = а+bi.

Запись комплексного числа в тригонометрической форме

Из равенства (1) следует, что любое комплексное число z = a+bi, где \( z\neq 0 \), представляется в виде
\( z = r(\cos\varphi +i\sin\varphi ) \qquad (4) \)
где \( r=|z|=\sqrt{a^2+b^2} \) — модуль комплексного числа z, \( \varphi \) — его аргумент. Запись комплексного числа в виде (4), где r>0, называют тригонометрической формой комплексного числа z.

Умножение и деление комплексных чисел, записанных в тригонометрической форме

С помощью тригонометрической формы записи комплексных чисел удобно находить произведение и частное комплексных чисел z₁ и z₂. Если два комплексных числа записаны в тригонометрической форме:
\( z_1 = r_1(\cos\varphi_1 +i\sin\varphi_1), \quad z_2 = r_2(\cos\varphi_2 +i\sin\varphi_2) \) то произведение этих комплексных чисел можно найти по формуле:
\( z_1z_2 = r_1r_2(\cos(\varphi_1+\varphi_2) +i\sin(\varphi_1+\varphi_2)) \)

Из этой формулы следует, что при перемножении комплексных чисел их модули перемножаются, а аргументы складываются.

Формула для нахождения частного комплексных чисел:
\( \frac{z_1}{z_2} = \frac{r_1}{r_2}(\cos(\varphi_1-\varphi_2) +i\sin(\varphi_1-\varphi_2)) \)

Из этой формулы следует, что модуль частного двух комплексных чисел равен частному модулей делимого и делителя, а разность аргументов делимого и делителя является аргументом частного.

Формула Муавра

Для любого \( n \in \mathbb{Z} \) справедлива формула
\( z^n = r^n(\cos \varphi + i \sin \varphi)^n = r^n(\cos (n\varphi) + i \sin (n\varphi) ) \) которую называют формулой Муавра.

Mathway | Популярные задачи

1	Найти точное значение	sin(30)
2	Найти точное значение	sin(45)
3	Найти точное значение	sin(60)
4	Найти точное значение	sin(30 град. )
5	Найти точное значение	sin(60 град. )
6	Найти точное значение	tan(30 град. )
7	Найти точное значение	arcsin(-1)
8	Найти точное значение	sin(pi/6)
9	Найти точное значение	cos(pi/4)
10	Найти точное значение	sin(45 град. )
11	Найти точное значение	sin(pi/3)
12	Найти точное значение	arctan(-1)
13	Найти точное значение	cos(45 град. )
14	Найти точное значение	cos(30 град. )
15	Найти точное значение	tan(60)
16	Найти точное значение	csc(45 град. )
17	Найти точное значение	tan(60 град. )
18	Найти точное значение	sec(30 град. )
19	Преобразовать из радианов в градусы	(3pi)/4
20	График	y=sin(x)
21	Преобразовать из радианов в градусы	pi/6
22	Найти точное значение	cos(60 град. )
23	Найти точное значение	cos(150)
24	Найти точное значение	tan(45)
25	Найти точное значение	sin(30)
26	Найти точное значение	sin(60)
27	Найти точное значение	cos(pi/2)
28	Найти точное значение	tan(45 град. )
29	График	y=sin(x)
30	Найти точное значение	arctan(- квадратный корень 3)
31	Найти точное значение	csc(60 град. )
32	Найти точное значение	sec(45 град. )
33	Найти точное значение	csc(30 град. )
34	Найти точное значение	sin(0)
35	Найти точное значение	sin(120)
36	Найти точное значение	cos(90)
37	Преобразовать из радианов в градусы	pi/3
38	Найти точное значение	sin(45)
39	Найти точное значение	tan(30)
40	Преобразовать из градусов в радианы	45
41	Найти точное значение	tan(60)
42	Упростить	квадратный корень x^2
43	Найти точное значение	cos(45)
44	Упростить	sin(theta)^2+cos(theta)^2
45	Преобразовать из радианов в градусы	pi/6
46	Найти точное значение	cot(30 град. )
47	Найти точное значение	arccos(-1)
48	Найти точное значение	arctan(0)
49	График	y=cos(x)
50	Найти точное значение	cot(60 град. )
51	Преобразовать из градусов в радианы	30
52	Упростить	( квадратный корень x+ квадратный корень 2)^2
53	Преобразовать из радианов в градусы	(2pi)/3
54	Найти точное значение	sin((5pi)/3)
55	Упростить	1/( кубический корень от x^4)
56	Найти точное значение	sin((3pi)/4)
57	Найти точное значение	tan(pi/2)
58	Найти угол А	tri{}{90}{}{}{}{}	
59	Найти точное значение	sin(300)
60	Найти точное значение	cos(30)
61	Найти точное значение	cos(60)
62	Найти точное значение	cos(0)
63	Найти точное значение	arctan( квадратный корень 3)
64	Найти точное значение	cos(135)
65	Найти точное значение	cos((5pi)/3)
66	Найти точное значение	cos(210)
67	Найти точное значение	sec(60 град. )
68	Найти точное значение	sin(300 град. )
69	Преобразовать из градусов в радианы	135
70	Преобразовать из градусов в радианы	150
71	Преобразовать из радианов в градусы	(5pi)/6
72	Преобразовать из радианов в градусы	(5pi)/3
73	Преобразовать из градусов в радианы	89 град.
74	Преобразовать из градусов в радианы	60
75	Найти точное значение	sin(135 град. )
76	Найти точное значение	sin(150)
77	Найти точное значение	sin(240 град. )
78	Найти точное значение	cot(45 град. )
79	Преобразовать из радианов в градусы	(5pi)/4
80	Упростить	1/( кубический корень от x^8)
81	Найти точное значение	sin(225)
82	Найти точное значение	sin(240)
83	Найти точное значение	cos(150 град. )
84	Найти точное значение	tan(45)
85	Вычислить	sin(30 град. )
86	Найти точное значение	sec(0)
87	Упростить	arcsin(-( квадратный корень 2)/2)
88	Найти точное значение	cos((5pi)/6)
89	Найти точное значение	csc(30)
90	Найти точное значение	arcsin(( квадратный корень 2)/2)
91	Найти точное значение	tan((5pi)/3)
92	Найти точное значение	tan(0)
93	Вычислить	sin(60 град. )
94	Найти точное значение	arctan(-( квадратный корень 3)/3)
95	Преобразовать из радианов в градусы	(3pi)/4
96	Вычислить	arcsin(-1)
97	Найти точное значение	sin((7pi)/4)
98	Найти точное значение	arcsin(-1/2)
99	Найти точное значение	sin((4pi)/3)
100	Найти точное значение	csc(45)

Комплексные числа

Напомним необходимые сведения о комплексных числах.

Комплексное число — это выражение вида a + bi, где a, b — действительные числа, а i — так называемая мнимая единица, символ, квадрат которого равен –1, то есть i² = –1. Число a называется действительной частью, а число b — мнимой частью комплексного числа z = a + bi. Если b = 0, то вместо a + 0i пишут просто a. Видно, что действительные числа — это частный случай комплексных чисел.

Арифметические действия над комплексными числами те же, что и над действительными: их можно складывать, вычитать, умножать и делить друг на друга. Сложение и вычитание происходят по правилу (a + bi) ± (c + di) = (a ± c) + (b ± d)i, а умножение — по правилу (a + bi) · (c + di) = (ac – bd) + (ad + bc)i (здесь как раз используется, что i² = –1). Число 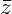 = a – bi называется комплексно-сопряженным к z = a + bi. Равенство z ·  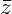= a² + b² позволяет понять, как делить одно комплексное число на другое (ненулевое) комплексное число:

.

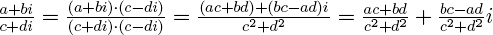(Например, .)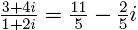

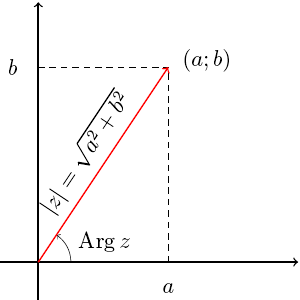
У комплексных чисел есть удобное и наглядное геометрическое представление: число z = a + bi можно изображать вектором с координатами (a; b) на декартовой плоскости (или, что почти то же самое, точкой — концом вектора с этими координатами). При этом сумма двух комплексных чисел изображается как сумма соответствующих векторов (которую можно найти по правилу параллелограмма). По теореме Пифагора длина вектора с координатами (a; b) равна 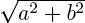. Эта величина называется модулем комплексного числа z = a + bi и обозначается |z|. Угол, который этот вектор образует с положительным направлением оси абсцисс (отсчитанный против часовой стрелки), называется аргументом комплексного числа z и обозначается Arg z. Аргумент определен не однозначно, а лишь с точностью до прибавления величины, кратной 2π радиан (или 360°, если считать в градусах) — ведь ясно, что поворот на такой угол вокруг начала координат не изменит вектор. Но если вектор длины r образует угол φ с положительным направлением оси абсцисс, то его координаты равны (r · cos φ; r · sin φ). Отсюда получается тригонометрическая форма записи комплексного числа: z = |z| · (cos(Arg z) + i sin(Arg z)). Часто бывает удобно записывать комплексные числа именно в такой форме, потому что это сильно упрощает выкладки. Умножение комплексных чисел в тригонометрической форме выглядит очень просто: z₁ · z₂ = |z₁| · |z₂| · (cos(Arg z₁ + Arg z₂) + i sin(Arg z₁ + Arg z₂)) (при умножении двух комплексных чисел их модули перемножаются, а аргументы складываются). Отсюда следуют формулы Муавра: zⁿ = |z|ⁿ · (cos(n · (Arg z)) + i sin(n · (Arg z))). С помощью этих формул легко научиться извлекать корни любой степени 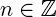из комплексных чисел. Корень n-й степени из числа z — это такое комплексное число w, что wⁿ = z. Видно, что 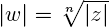, а 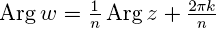, где k может принимать любое значение из множества {0, 1, …, n – 1}. Это означает, что всегда есть ровно n корней n-й степени из комплексного числа (на плоскости они располагаются в вершинах правильного n-угольника).

Далее: Фрактальные размерности

Mathway | Популярные задачи

1	Найти точное значение	sin(30)
2	Найти точное значение	sin(45)
3	Найти точное значение	sin(60)
4	Найти точное значение	sin(30 град. )
5	Найти точное значение	sin(60 град. )
6	Найти точное значение	tan(30 град. )
7	Найти точное значение	arcsin(-1)
8	Найти точное значение	sin(pi/6)
9	Найти точное значение	cos(pi/4)
10	Найти точное значение	sin(45 град. )
11	Найти точное значение	sin(pi/3)
12	Найти точное значение	arctan(-1)
13	Найти точное значение	cos(45 град. )
14	Найти точное значение	cos(30 град. )
15	Найти точное значение	tan(60)
16	Найти точное значение	csc(45 град. )
17	Найти точное значение	tan(60 град. )
18	Найти точное значение	sec(30 град. )
19	Преобразовать из радианов в градусы	(3pi)/4
20	График	y=sin(x)
21	Преобразовать из радианов в градусы	pi/6
22	Найти точное значение	cos(60 град. )
23	Найти точное значение	cos(150)
24	Найти точное значение	tan(45)
25	Найти точное значение	sin(30)
26	Найти точное значение	sin(60)
27	Найти точное значение	cos(pi/2)
28	Найти точное значение	tan(45 град. )
29	График	y=sin(x)
30	Найти точное значение	arctan(- квадратный корень 3)
31	Найти точное значение	csc(60 град. )
32	Найти точное значение	sec(45 град. )
33	Найти точное значение	csc(30 град. )
34	Найти точное значение	sin(0)
35	Найти точное значение	sin(120)
36	Найти точное значение	cos(90)
37	Преобразовать из радианов в градусы	pi/3
38	Найти точное значение	sin(45)
39	Найти точное значение	tan(30)
40	Преобразовать из градусов в радианы	45
41	Найти точное значение	tan(60)
42	Упростить	квадратный корень x^2
43	Найти точное значение	cos(45)
44	Упростить	sin(theta)^2+cos(theta)^2
45	Преобразовать из радианов в градусы	pi/6
46	Найти точное значение	cot(30 град. )
47	Найти точное значение	arccos(-1)
48	Найти точное значение	arctan(0)
49	График	y=cos(x)
50	Найти точное значение	cot(60 град. )
51	Преобразовать из градусов в радианы	30
52	Упростить	( квадратный корень x+ квадратный корень 2)^2
53	Преобразовать из радианов в градусы	(2pi)/3
54	Найти точное значение	sin((5pi)/3)
55	Упростить	1/( кубический корень от x^4)
56	Найти точное значение	sin((3pi)/4)
57	Найти точное значение	tan(pi/2)
58	Найти угол А	tri{}{90}{}{}{}{}	
59	Найти точное значение	sin(300)
60	Найти точное значение	cos(30)
61	Найти точное значение	cos(60)
62	Найти точное значение	cos(0)
63	Найти точное значение	arctan( квадратный корень 3)
64	Найти точное значение	cos(135)
65	Найти точное значение	cos((5pi)/3)
66	Найти точное значение	cos(210)
67	Найти точное значение	sec(60 град. )
68	Найти точное значение	sin(300 град. )
69	Преобразовать из градусов в радианы	135
70	Преобразовать из градусов в радианы	150
71	Преобразовать из радианов в градусы	(5pi)/6
72	Преобразовать из радианов в градусы	(5pi)/3
73	Преобразовать из градусов в радианы	89 град.
74	Преобразовать из градусов в радианы	60
75	Найти точное значение	sin(135 град. )
76	Найти точное значение	sin(150)
77	Найти точное значение	sin(240 град. )
78	Найти точное значение	cot(45 град. )
79	Преобразовать из радианов в градусы	(5pi)/4
80	Упростить	1/( кубический корень от x^8)
81	Найти точное значение	sin(225)
82	Найти точное значение	sin(240)
83	Найти точное значение	cos(150 град. )
84	Найти точное значение	tan(45)
85	Вычислить	sin(30 град. )
86	Найти точное значение	sec(0)
87	Упростить	arcsin(-( квадратный корень 2)/2)
88	Найти точное значение	cos((5pi)/6)
89	Найти точное значение	csc(30)
90	Найти точное значение	arcsin(( квадратный корень 2)/2)
91	Найти точное значение	tan((5pi)/3)
92	Найти точное значение	tan(0)
93	Вычислить	sin(60 град. )
94	Найти точное значение	arctan(-( квадратный корень 3)/3)
95	Преобразовать из радианов в градусы	(3pi)/4
96	Вычислить	arcsin(-1)
97	Найти точное значение	sin((7pi)/4)
98	Найти точное значение	arcsin(-1/2)
99	Найти точное значение	sin((4pi)/3)
100	Найти точное значение	csc(45)

Аргумент и модуль комплексного числа

Вычислить аргумент и модуль комплексного числа.
Аргументом комплексного числа z называется угол φ в радианах радиус-вектора точки, соответствующей данному комплексному числу и обозначается Arg(z) = φ

Аргументом комплексного числа z называется угол φ в радианах радиус-вектора точки, соответствующей данному комплексному числу и обозначается Arg(z) = φ

Из определения следуют следующие формулы:

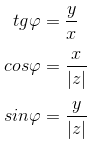
Для числа z = 0 аргумент не определен.

Главным значением аргумента называется такое значение φ, что 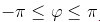. Обозначается: arg(z).

Свойства аргумента:

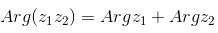	— аргумент от произведения двух комплексных чисел равен сумме аргументов этих чисел
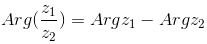	— аргумент частного двух комплексных чисел равен разности аргументов этих чисел
	— аргумент от сопряженного комплексного числа равен отрицательному значению аргумента от этого числа.

Модулем комплексного числа z = x + iy называется вещественное число |z| равное:

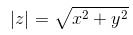
Для любых комплексных чисел z, z₁, z₂ имеют место следующие свойства модуля:

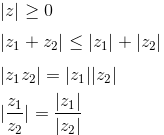для пары комплексных чисел z1 и z2 модуль их разности |z1 − z2| равен расстоянию между соответствующими точками комплексной плоскости.

Mathway | Популярные задачи

Mathway | Популярные задачи

Популярные задачи

Элементарная математика Основы алгебры Алгебра Тригонометрия Основы мат. анализа Математический анализ Конечная математика Линейная алгебра Химия

Для функционирования Mathway необходим javascript и современный браузер.

Этот веб-сайт использует cookie файлы, чтобы сделать использование нашего ресурса максимально удобным для вас.

Убедитесь, что ваш пароль содержит не менее 8 символов и как минимум один из следующих символов:

• число
• буква
• специальный символ: @$#!%*?&

90000 90001,, 90002 90003 90004 90005 90006 90007 90008 90009 90010 90005 90012 z1 = + i 90009 90010 90005 90012 z2 = + i 90009 90010 90005 90006 90007 90008 90009 90010 90005 90012 90027 z1 + z2 z1 — z2 z1 * z2 z1 / z2 90028 90009 90010 90005 90006 90009 90010 90005 90006 90009 90010 90039 90000 90005 90003 90000 90005 90045 90009 90003 90007, 90008 90009 90010 90005 90053 .90009 90010 90005 90053 , 90009 90010 90039 90009 90003 90009 90003 90000 90005 90045 90009 90003 90007, 90008 90009 90010 90005 90053 .90009 90010 90005 90053 , 90009 90010 90039 90009 90010 90005 90086 90009 90010 90005 90003 90000 90005 90045 90009 90003 90007, 90008 90009 90010 90005 90053 .90009 90010 90005 90053 , 90009 90010 90039 90009 90003 90009 90003 90000 90005 90045 90009 90003 90007, 90008 90009 90010 90005 90053 .90009 90010 90005 90053 , 90009 90010 90039 90009 90010 90005 90086 90009 90010 90005 90003 90000 90005 90045 90009 90003 90007 90008 90009 90010 90005 90053 n.90009 90010 90005 90053 90009 90010 90039 90009 90003 90009 90003 90000 90039 90009 90010 90039 90009 90039.90000. ().,, 90001 90002 90003 90004 90003 () 90004 -,: 90007 x 90008 90007 + 90008 90007 iy 90008, 90007 x 90008 90007 y 90008 -, 90007 i 90008 — (,: 90007 i 90008 90007 90022 2 90023 90008 90007 = -1 90008). 90027 90002. 90027 90002 90027 90002 90003 90004 () -,. . 90027 90002 90027 90002 90003 90004: 90027 90002 90043 90027 90002 90027 90002,: 90027 90002 90027 90002,,, 90027 90002,,, 90027 90002,,,.90027 90002 90027 90002 90027 90002 90027 90063. 90064 90002 90007 a 90008 90007 + 90008 90007 bi 90008 90007 = 90008 90007 c 90008 90007 + 90008 90007 di 90008 90027 90002, 90007 a 90008 90007 = 90008 90007 c 90008 90007 b 90008 90007 = 90008 90007 d 90008 (2,). 90027 90002 90007 (a + bi) + (c + di) = (a + c) + (b + d) i 90008. 90027 90002 1: 90007 z 90008 90007 90103 1 90104 90008 90007 + 90008 90007 z 90008 90007 90103 2 90104 90008 90007 = 90008 90007 z 90008 90007 90103 2 90104 90008 90007 + 90008 90007 z 90008 90007 90103 1 90104 90008 -.90027 90002: 90027 90002 2 90007 z 90008 90007 90103 1 90104 90008 90007 = 1 + 3 90008 90007 i 90008 90007, 90008 90007 z 90008 90007 2 = 4 — 5 90008 90007 i 90008 90007. 90008 90027 90002 2: 90027 90002 90027 90002 90007 (a + bi) — (c + di) = (a — c) + (b — d) i. 90008 90027 90002: 90027 90002 90007 z 90008 90007 90103 1 90104 90008 90007 — 90008 90007 z 90008 90007 90103 2 90104 90008 90007 z 90008 90007 90103 2 90104 90008 90007 — 90008 90007 z 90008 90007 90103 1 90104 90008,, 90007 z 90008 90007 90103 1 90104 90008 90007 = -2 + 90008 90007 i 90008,.90027 90002,,, -: 90027 90002 90027 90002 90027 90002, 2, 3. :. :. 90027 90002 2: 90027 90002 90027 90002 90043 :. 90027 90002 «»:. . 90027 90002 90007 (a + bi) (c + di) = ac + bci + adi + bdi 90022 2 90023 = (ac — bd) + (bc + ad) i. 90008 90027 90002: 90027 90002, 90027 90002: 90027 90002 90027 90002,. ,. 90027 90002: 1. 90027 90002: 90027 90002 90027 90002,.90027 90002,:. 90027 90002 2. 90027 90002 90027 90002 90027 90002 90007 a + bi 90008 () 90007 c + di 90008 () — 90007 e + fi 90008 (), 90007 c + di 90008, 90007 a + bi 90008. 90027 90002, 90027.90000 90001 90002 90003 90000 90005 90003 90007 90003 90007 90003 90007 90012 90005 90014 90007 90012 90005 90003 90007 90003 90007 90003 90007 90012 90005 90014 90007 90012 90005 90003 90007 90003 90007 90003 90000 90005 90037 90007 90003 90040.(). 90041 90007 90012 90005 90045 (),: X + iy, x y, i (,: i 2 = -1). 90007 90012 90005 90045 . (). 90007 90012 90052 90007 90012 90005 90014 90007 90012 90059 90052 90007 90052.