Z2 z1 z: : z1 = -2 + 5i z2 = 3 — 4i. : ) z1 + z2; ) z2

Множество комплексных чисел — презентация онлайн

Множество
комплексных
чисел.
Комплексным числом называется выражение
вида а + bi, в котором а и b – действительные числа,
а i – некоторый символ такой, что
i
1
Действительное число a называется действительной
2
частью z=a+bi (Re z), а число b-мнимой частью (Im z)
Комплексное число z=a+bi изображают точкой
плоскости с координатами (a;b)
Точка М(a;b), соответствующая комплексному числу
z=a+bi, называется аффиксом данного числа z.
Два комплексных числа (a; b) и (c; d) называются
равными, если а = с и b = d.
Комплексное число a-bi называется
комплексно сопряженным с числом a+bi
z
и обозначается через
z a bi= a-bi
Комплексные числа вида a+bi и –a-bi называются
противоположными.
Арифметические операции над
комплексными числами
Свойство умножения: Произведение двух комплексных чисел z1=a+bi и z2=c+di будет комплексное число вида z=z1 z2=
a+bi
c+di
=
ac−bd
+(ad+bc)i
Сумма двух комплексных чисел z1=a+bi и z2=c+di
будет комплексное число вида
z=z1+z2=a+bi+c+di=a+c+(b+d)i
Разностью двух комплексных чисел z1=a+bi и
z2=c+di будет комплексное число вида
z=z1−z2=a+bi−c+di=a−c+(b−d)i
Произведение двух комплексных чисел z1=a+bi и
z2=c+di будет комплексное число вида
z=z1*z2=(a+bi)*(c+di) =ac−bd+(ad+bc)i

5.

Частное двух комплексных чисел z1=a+bi и z2=c+di будет комплексное число вида z=z2/z1= (a+bi)/(c+di)= (ac+bd)/(c2+d2)+(bc−ad)*i/(c2+d2)

6. Нахождение степеней числа i

Если показатель степени i делится на 4, то
значение степени равно 1, если при делении
показателя на 4 в остатке получается 1, то
значение степени равно i, если при делении
показателя на 4 остаток равен 2, то значение
степени равно -1, если в остатке при делении
показателя на 4 будет 3, то значение степени
равно –i.
• Вычислить: 1) i
Решение:
1) i66
66
, 2) i143 , 3) i216 ,4)i137
66:4=16(2). Остаток равен 2, значит i66=-1
2)i143
143 :4=35(3).В остатке 3, значит i 143=-i
,
3)i216
216:4=54(0).в остатке 0, значит i216=1
4)i137
137:4=34(1).В остатке 1, значит i137=i
Пример 1
Вычислить:
3 2
i
(
1
2
i)i
1
i
1
)(
1
2
i)i
i
2
i
2
i
2
3
2
i (3
2
i)(
1
i) 3
2
i
3
i
2
i 3
5
i
215
2
)
i
2
1
i (
1
i)(
1
i)
1
i
1
1 22
2
15 53
3
)(
2
i)
i
i
22 22
Геометрический смысл комплексного
числа
Каждой точке М плоскости с координатами (a,b)
соответствует один и только один вектор
OM z
с началом в точке z = 0 и концом в точке z=a+bi
y
M(a;b)
b
0
a
x
Если комплексное число Z= a+bi трактовать как
точку M (a,b) плоскости xOy, то модуль Z равен
расстоянию точки M (a,b) от начала координат
z a b
2
2
Если на плоскости ввести полярные координаты
(r,φ), где φ аргумент числа z (φ=argz) — угол
между действительной осью ОХ и вектором ОМ,
то а = r COS φ, b = r SIN φ
В силу этого комплексное число Z можно
записать в форме z = r(COS φ+iSIN φ),
где r – модуль числа Z, φ – угол (в рад. ), который
составляет вектор OM с положительным
направлением оси ox
Тригонометрическая форма
комплексного числа
Тригонометрической формой комплексного числа
называют его запись в виде:
z = r(cosφ + isinφ), где r a2 b2 — модуль, а
φ – аргумент числа z, связанный с а и b формулами:
cos
sin
a
a b
b
2
2
a2 b2
;
Угол φ из промежутка ; называется главным
аргументом. Все остальные значения угла φ могут быть
получены прибавлением к главному аргументу значений
2 n, где n – любое целое число.
Пример2.
Записать в тригонометрической форме:
Сначала находим модуль числа:
r (
23
)
2
4
2
Далее, согласно формулам (*),
имеем:
2
3 3
2
1
cos
;
sin
4 2
4
2
Учитывая, что угол
2 3 2i
; 5
5
5
Итак, z
4
cos
isin
6
6
6
2
Действия над комплексными числами,
заданными в тригонометрической форме
При умножении/делении комплексных чисел,
заданных в тригонометрической форме, их модули
перемножаются /делятся, а аргументы складываются
(вычитаются).
z
z
r
r
(cos(
)
i
sin(
))
1
2
1
2
1
2
1
2
(1)
z
1 r
1
(cos(
)
i
sin(
))
1
2
1
2
z
(2)
2 r
2
Пример3. Выполнить действия:
1
2
2
4
cos
i
sin
*
cos
i
sin
10
3
3
6 6
Используя формулу (1), находим:
4
2
2
2
2
cos
i
sin
cos
i
sin
i
10
6
3
6
3
5
2
2
5
При возведении комплексного числа
z = r (Cosφ + iSinφ) в натуральную степень
n
модуль данного числа возводится в эту
степень,
а аргумент умножается на показатель степени:
формула Муавра
z r (cos n i sin n )
n
n
Корень n-й степени из комплексного
числа z = r (Cosφ + iSinφ) имеет n различных
значений, которые находятся по формуле :
n
2
2
z r cos
i sin
n
n
n
Здесь к = 0, 1, 2, … n-1
Пример4. Решить уравнение
z 4 0
2
Корнями данного уравнения являются все значения
Для числа — 4 имеем r =2,
2
Согласно формуле,
находим:
2
2
4 2 cos
i sin
2
2
Если к = 0, то 1
2 cos i sin
2
2
2i
3
3
i sin
2i
Если к = 1, то 2 2 cos
2
2
4
Показательная форма комплексного
числа. Формула Эйлера
Если комплексному числу(cos i sin )
, модуль которого равен 1, поставить в соответствие
показанное выражение e i , то получим соотношение
i
cos i sin e ,
то получим соотношение которое называется формулой
Эйлераz.
Любое комплексное число можно записать в
виде
z re
i
Эта форма записи комплексного числа
называется показательной формой.
.
Пример: Записать число
в показательной
форме.
3
3
z 3(cos
i sin
)
2
2
3
Решение: Здесь r 3,
2
тогда показательная форма числа имеет вид
.
z 3e
3
i
2
Пример: Записать число z 5i в показательной
форме.
z
Решение. Что бы представить число
в виде
z
z re
i
нужно найти модуль и аргумент числа
3
2
2
2
,
Здесьa 0, b 5; тогда r a b 0 5 5,
2
лежит на мнимой оси комплексной плоскости.
так как точка
r и
.
Зная
z
, получим
.
z 5e
3
i
2
•Действия над комплексными числами,
заданными в показательной форме
Если комплексные числа записаны в показательной
форме, то умножение, деление, возведение в степень
производится по правилам действий со степенями.
Так, для произведения и частного комплексных чисел
i 2
i 1
и
z 2 r2 e справедливы формулы
z re
1
1
z1 z 2 r1 r2 e
i 1 2
z1
r1
e i 1 2
z2
r2
а для n-й степени комплексного числа используется
n
n i n
•формула z
r e
Для вычисления корня из комплексного числа
z re
i
используется формула
2 k
n
z re
n
n
где k принимает n значений: 0,1,2,…,n-1.

24. Понятие функции комплексного переменного и отличие от действительного анализа

Пусть D – некоторая область на комплексной плоскости
Определение. Функцией комплексного аргумента с
областью определения D называется соответствие,которое
любому комплексному числу
сопостовляет
z D
одно или несколько комплексных значений.
Таким образом, в отличие от действительного анализа, в
комплексном анализе допускаются многозначные функции.
Например,
f(z)=az+b (a, b – фиксированные комплексные числа)однозначная функция;
f ( z ) z 2 — однозначная функция
f ( z)
n
z — n-значная функция;
f ( z ) Argz -бесконечнозначная функция.
Если функция однозначна,то она может быть
задана в виде отображения f : D C В таком
случае функция называется однолистной .В
дальнейшем, если не указано особо,будем
рассматривать однолистные функции.
Пример: Для функции
z2 1
f ( z)
1найти
2i
f (i )
Решение: Подставим в место z значение i в функцию
i 1
1 1
f (i)
1
1 0 1 1
2i
2i
2
Ответ:
f(i)=1

27.

Компоненты функцииПусть дана функция , f (z ) z D Представим z в
z x iy Значение f(x)алгебраической форме
f ( z ) C,которое также можем
комплексное число,т.е.
f ( z ) u ( z ) iv,где
( z)
представить в алгебраической форме
u (z-действительные
)
v( z )
и
функции комплексного
аргумента,но задание я эквивалентно заданию
пары(x,y).Окончательно,любую функцию комплексного
аргумента можно представить в виде
f ( z ) u ( x, y ) iv ( x, y ),где
и v ( x, y ) действительные функции двух действительных
переменных.Функции u и v называются компонентами
функции f(z),u- действительная компонента,v-мнимая
компонента.Пишут :
u ( x, y )
u Re f ( z ) v Im f ( z )
f ( z ) ( x iy ) 4i
2
Пример: Для функции
z x iy
Где
мнимую часть.
найти ее действительную и
Решение:
(x+iy)2+4i=x2+2ixy-y2+4i=(x2-y2)+(2xyi+4i)=(x2-y2)+i(2xy+4).
Тогда действительная часть функции f(z) — x2-y2,а
мнимая — 2xy+4.
Re( f ( z )) x y
2
2
Im( f ( z )) 2 xy 4
Понятие непрерывности определяется аналогично
действительному случаю.
f ( z) f ( z0 ) 0 ( )
z0 lim
z z
z z0 f ( z) f ( z0 )
Так как это определение
формально совпадает с обычным ,то все свойства
непрерывной функции комплексного аргумента
совпадают дословно со свойствами действительных
функций.
F(z)-непрерывна в точке
0

Sony Xperia Z2, Z1, Z, L получили Android 5 Lollipop AOSP – видео и скриншоты

Прошивки

На чтение 2 мин Просмотров 26 Опубликовано 12.11.2014

Компания Sonyпланирует гарантировано обновить всё свое семейство смартфонов линейки “Xperia Z” до новой версии операционной системы Android 5. 0 Lollipop, о чем мы уже писали ранее. В свою очередь была выпущена версия системы для разработчиков, которая позволяет испытывать её на смартфонах искать баги и оптимизировать под неё приложения и сервисы. На форуме разработчиков XDA были опубликованы сборки Android 5 Lollipop для моделей Sony Xperia Z2, Xperia Z1, Xperia Z и даже старичка Xperia L. Все пользователи, кто хоть что-то понимает в установке прошивок из вне, могут опробовать их на своих смартфонах, но для этого необходимо иметь на устройстве разблокированный загрузчик.

Стоит учитывать, что данные версии нестабильны и, например, для модели Xperia L работает практически все, кроме беспроводных соединений включая сеть, так что вы сможете лишь познакомиться с новым интерфейсом и не более – для ежедневного использования они не годятся.

Xperia Z2 Android 5.0 Lollipop AOSP ROM

Версия все ещё находится в стадии разработки, дисплей, большинство параметров, Wi-Fi и вибро работают. Скачать версию системы и узнать о ней более детально можно непосредственно на XDA.

 

Xperia Z1 Android 5.0 Lollipop AOSP ROM

Сборка системы для данной модели поддерживает в рабочем состоянии Bluetooth, вызовы, SMS, звук, вибро, полное функционирование дисплея и тачскрина, однако в ней не работает передача данных, камера и масса других функций.

 

Xperia Z Android 5.0 Lollipop AOSP ROM

Тестовая прошивка для данной модели в нынешнее время самая функциональная и стабильная: работает Bluetooth, Wi-Fi, дисплей и такчскрин, вибро и аудио, камеры, NFC, GPS, все датчики и прочее.

 

Xperia L Android 5.0 Lollipop AOSP ROM

Одной из первых появилась версия прошивки для разработчиков для Иксперия Л, и количество работающих функций также велико: дисплей и тачскрин, аппаратное ускорение, аудио, декодеры, все датчики, включая вибро, GPU рендеринг, камеры, внешняя и внутренняя память, индикатор, но нефункционирующими остаются GPS, Wi-Fi, Bluetooth, RIL.

Расчеты комплексных чисел с заданными значениями для z1 и z2

$\begingroup$

У меня вопрос:

Учитывая, что $z_1 = 4 — 3i$ и $z_2 = -3 + 4i$, определить:
a) $2z_1 — z_2$
b) $z_1z_2$
c) $z_1\overline{z_1}$

Вот моя попытка. Это правильно?

а) $$\begin{align}2z_1 — z_2&=2(4-3i)-(-3+4i)\\&=8-6i+3-4i\\&=8+3-6i-4i\\&= 11-10i\end{выравнивание}$$

9*)=i(25)=25i$

$\endgroup$

1

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Интерпретация Z1 Z2 | Решенные примеры | Числа

Пусть \({z_1}\) и \({z_2}\) представляют собой две фиксированные точки комплексной плоскости. Существует очень удобный способ интерпретации выражения \(\left| {{z_1} — {z_2}} \right|\). Рассмотрим следующий рисунок, который геометрически изображает вектор \({z_1} — {z_2}\):

Однако обратите внимание, что этот вектор также равен вектору, проведенному из точки \({z_2}\) в точка \({z_1}\):

Таким образом, \(\left| {{z_1} — {z_2}} \right|\) представляет собой длину вектора, проведенного из \({z_2}\) в \({z_1}\). Другими словами, \(\left| {{z_1} — {z_2}} \right|\) представляет собой расстояние между точками \({z_1}\) и \({z_2}\).

Возьмем пример. Рассмотрим

\[\begin{align}&{z_1} = 1 + i\\&{z_2} =  — 3i\end{align}\]

Выражение \(\left| {{z_1} — {z_2 }} \right|\), как мы пришли к выводу, представляет собой расстояние между точками \({z_1}\) и \({z_2}\), равное \(\sqrt {17} \), как видно из следующий рисунок:

Мы можем проверить это алгебраически:

\[\begin{align}&{z_1} — {z_2} = \left( {1 + i} \right) — \left( { — 3i } \right) = 1 + 4i\\&\Стрелка вправо \,\,\,{z_1} — {z_2} = \sqrt {1 + 16}  = \sqrt {17} \end{align}\]

Эта интерпретация выражения \(\left| {{z_1} — {z_2}} \right|\) как расстояния между точками \({z_1}\) и \({z_2}\) чрезвычайно полезна и мощный.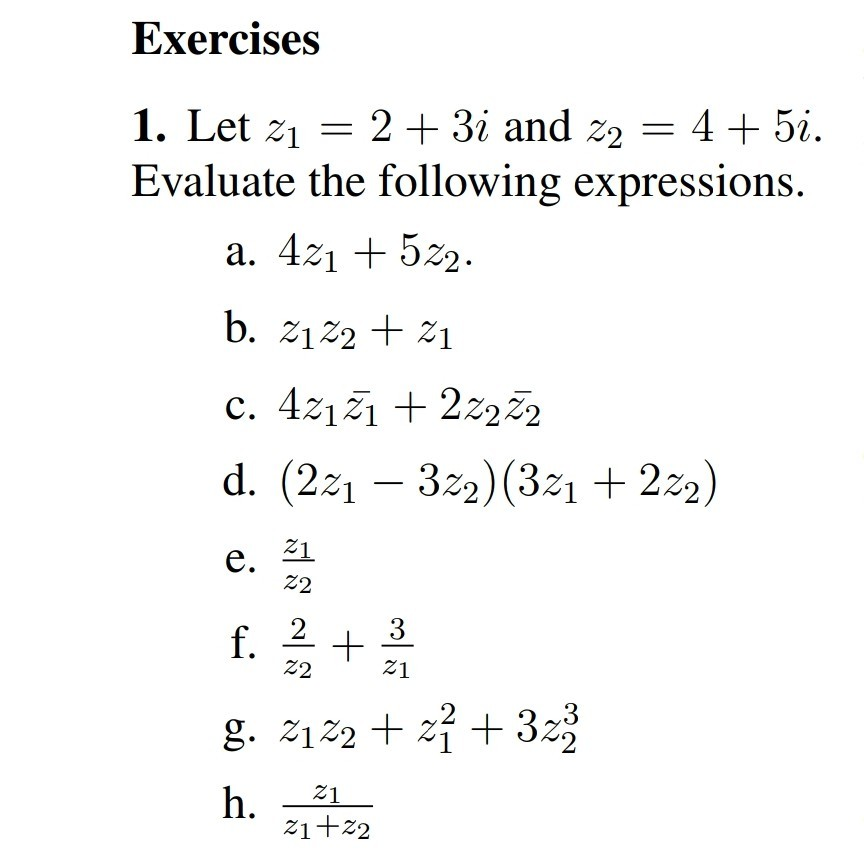 Давайте посмотрим, как.

Предположим, что z — переменная точка комплексной плоскости такая, что \(\left| {z — i} \right| = 3\). Что такое геометрическое место z ? Другими словами, какой путь прослеживает z , удовлетворяя при этом этому ограничению?

Мы можем интерпретировать \(\left| {z — i} \right|\) как расстояние между переменной точкой z и фиксированная точка i . Уравнение \(\left| {z — i} \right| = 3\) говорит о том, что переменная точка z движется так, что всегда находится на постоянном расстоянии 3 единицы от фиксированной точки i . Таким образом, z описывает окружность на плоскости с центром в точке i и радиусом 3 единицы:

Возьмем другой пример. Рассмотрим уравнение

\[\left| {г — 1 + я} \право| = 2\]

Запишем это уравнение как

\[\left| {z — \left( {1 — i} \right)} \right| = 2\]

Это говорит о том, что расстояние z от фиксированной точки \(\left( {1 — i} \right)\) всегда равно 2 единицам. Таким образом, z описывает на плоскости окружность с центром в точке \(\left( {1 — i} \right)\) и радиусом, равным 2 единицам:

Пример 1:   z — переменная точка на плоскости, такая что

\[\left| {z — 2 + 3i} \право| = 11\]

Постройте геометрическое место z.

Решение: Перепишем данное уравнение в виде

\[\left| {z — \left( {2 — 3i} \right)} \right| = 1\]

Таким образом, z описывает окружность радиусом 1 единицу с центром в точке \(\left( {2 — 3i} \right)\):

Пример 2:  A переменная точка z всегда удовлетворяет

\(\left| {z — i} \right| = \left| {z + i} \right|\)

Когда z движется, какой путь она проследит в самолет?

Решение: Во-первых, мы перепишем данное уравнение как

\[\left| {г — я} \право| = \ влево | {z — \left( { — i} \right)} \right|\]

Это уравнение говорит, что расстояние z от точки \(i\) равно расстоянию

z от точки точка \(\влево( { — i} \вправо)\).