Задачи круги эйлера с решением: описание, примеры, для дошкольников, для школьников

Множества. Решение задач с помощью кругов Эйлера. 5, 6, 7 класс

Братунова Вера Дмитриевкна,

преподаватель математики и информатики,

Гимназия-детсад им. С. Демиреля, мун. Комрат, АТО Гагауз Ери, Республика Молдова

 

Множества. Решение задач с помощью кругов Эйлера

 

Классы: 5, 6, 7

Ключевые слова: круги Эйлера

 

Пояснительная записка

 

Очень часто решение задачи помогает найти рисунок. Использование рисунка делает решение простым и наглядным.

В данной разработке приведены примеры решения задач с помощью кругов Эйлера. Это не просто занимательная и интересная штука, но и весьма полезный метод решения задач. Они помогают быстро и просто решить даже достаточно сложные или просто запутанные на первый взгляд задачи.

С данным способом решения задач учащихся можно познакомить как на уроках, так и на кружковых занятиях.

Главной целью этой работы является помощь учителям математики для подготовки учащихся к олимпиадам, а также к экзаменам.

 

Основные понятия

Понятие множества − одно из первичных в математике. Поэтому очень трудно дать ему какое-либо определение, которое бы не заменяло слово «множество» каким-нибудь равнозначным выражением, например, совокупность, собрание элементов и т.д. Элементы множества − это то, из чего это множество состоит, например, каждый ученик вашего класса есть элемент множества школьников.

 

Пересечение множеств в теории множеств — это множество, которому принадлежат те и только те элементы, которые одновременно принадлежат всем данным множествам.

Круги Эйлера — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления. Изобретены Леонардом Эйлером. Используется в математике, логике, менеджменте и других прикладных направлениях.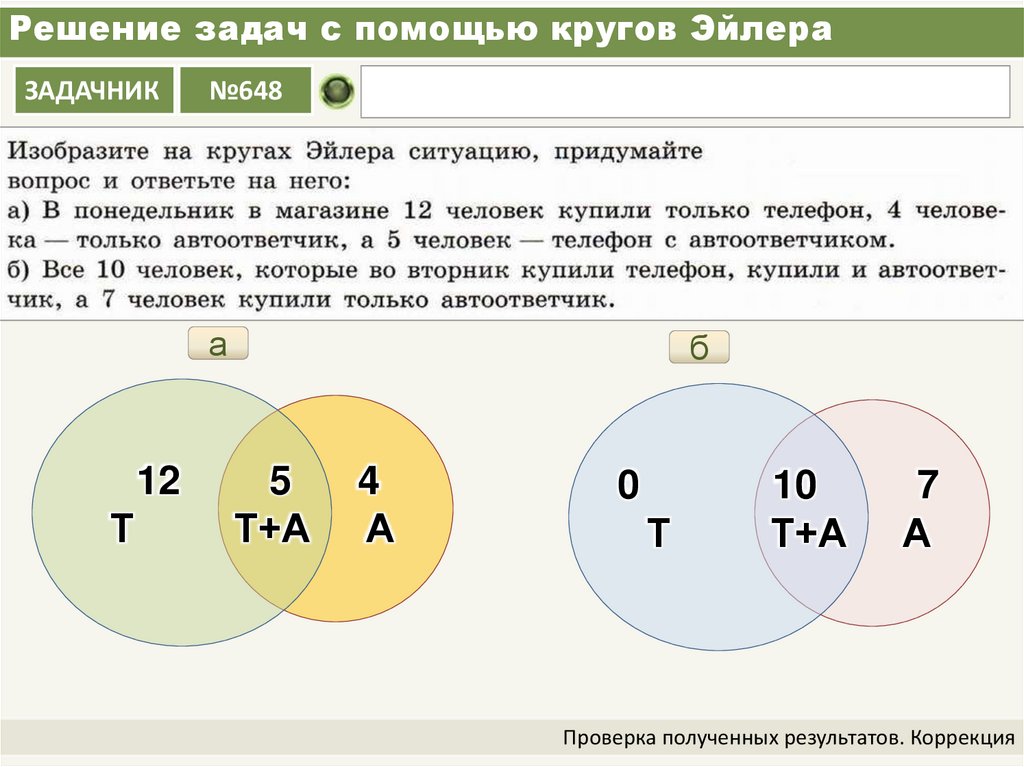

 

2. Решение задач с помощью кругов Эйлера

 

2.1. «Обитаемый остров» и «Стиляги»

Некоторые ребята из нашего класса любят ходить в кино. Известно, что 15 ребят смотрели фильм «Обитаемый остров», 11 человек — фильм «Стиляги», из них 6 смотрели и «Обитаемый остров», и «Стиляги». Сколько человек смотрели только фильм «Стиляги»?

 

Решение:

Чертим два множества таким образом:

6 человек, которые смотрели фильмы «Обитаемый остров» и «Стиляги», помещаем в пересечение множеств.

1. 15 — 6 = 9 — человек, которые смотрели только «Обитаемый остров»,

2. 11- 6 = 5 — человек, которые смотрели только «Стиляги».

Получаем:

Ответ: 5 человек.

 

2.2. Задача про библиотеки

Каждый из 35 шестиклассников является читателем, по крайней мере, одной из двух библиотек: школьной и районной. Из них 25 человек берут книги в школьной библиотеке, 20 — в районной.

Сколько шестиклассников:

1.     Являются читателями обеих библиотек;

2.     Не являются читателями районной библиотеки;

3.     Не являются читателями школьной библиотеки;

4.     Являются читателями только районной библиотеки;

5.     Являются читателями только школьной библиотеки?

 

Решение:

Чертим два множества таким образом:

1) 20+ 25 — 35 = 10 (человек) — являются читателями обеих библиотек. На схеме это общая часть кругов. Мы определили единственную неизвестную нам величину. Теперь, глядя на схему, легко даем ответы на поставленные вопросы.

2) 35 — 20 = 15 (человек) — не являются читателями районной библиотеки,

3) 35 — 25 = 10 (человек) — не являются читателями школьной библиотеки,

4) 35- 20 = 10 (человек) — являются читателями только районной библиотеки,

5) 35- 20 = 15 (человек) — являются читателями только школьной библиотеки.

Очевидно, что вопросы 2 и 5, а также 3 и 4 — равнозначны и ответы на них совпадают.

Ответ: 10 человек; 15 человек; 10 человек; 10 человек; 15 человек.

 

2.3. Гарри Поттер, Рон и Гермиона

На полке стояло 26 волшебных книг по заклинаниям, все они были прочитаны. Из них 4 прочитал и Гарри Поттер, и Рон. Гермиона прочитала 7 книг, которых не читали ни Гарри Поттер, ни Рон, и две книги, которые читал Гарри Поттер. Всего Гарри Поттер прочитал 11 книг. Сколько книг прочитал только Рон?

 

Решение:

Учитывая условия задачи, сделаем чертеж:

Так как Гарри Поттер всего прочитал 11 книг, из них 4 книги читал Рон и 2 книги — Гермиона, то 11 — 4 — 2 = 5 — книг прочитал только Гарри.

Следовательно, 26 — 7 — 2 — 5 — 4 = 8 — книг прочитал только Рон.

Ответ: 8 книг.

 

2.4. Задача про любимые мультфильмы

Шестиклассники заполняли анкету с вопросами об их любимых мультфильмах. Оказалось, что большинству из них нравятся «Белоснежка и семь гномов», «Губка Боб Квадратные Штаны» и «Волк и теленок». В классе 38 учеников. «Белоснежка и семь гномов» нравится 21 ученику. Причем трем среди них нравятся еще и «Волк и теленок», шестерым — «Губка Боб Квадратные Штаны», а один ребенок одинаково любит все три мультфильма. У «Волка и теленка» 13 фанатов, пятеро из которых назвали в анкете два мультфильма. Надо определить, скольким же шестиклассникам нравится «Губка Боб Квадратные Штаны».

 

Решение:

Чертим три круга, таким образом:

Из условия знаем, что трем ученикам нравиться и «Белоснежка и семь гномов», и «Волк и теленок», шестерым — «Белоснежка и семь гномов» и «Губка Боб Квадратные Штаны», а один ребенок одинаково любит все три мультфильма.

Мы помним, что по условиям задачи среди фанатов мультфильма «Волк и теленок» пятеро ребят выбрали два мультфильма сразу, т.е. 5 — 3 = 2 — ученика выбрали «Волк и теленок» и «Губка Боб Квадратные Штаны».

1) 21 — 3 — 1 — 6 = 11 — учеников выбрали только «Белоснежка и семь гномов»,

2) 13 — 3 — 1 — 2 = 7 — учеников выбрали — «Волк и теленок»,

3) 38 — (11 + 3 + 1 + 2 + 6 + 7) = 8 — ребят выбрали «Губка Боб Квадратные Штаны».

 

 

4) 8 + 2 + 1 + 6 = 17 — человек выбрали мультик «Губка Боб Квадратные Штаны».

Ответ: 17 учеников.

 

2.5. Задача про Крейсер и Линкор

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети интернет.

Запрос	Найдено страниц, тыс.
Крейсер и Линкор	7000
Крейсер	4800
Линкор	4500

Какое количество страниц (в тысячах) будет найдено по запросу Крейсер и Линкор? (Считается, что все вопросы выполняются практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.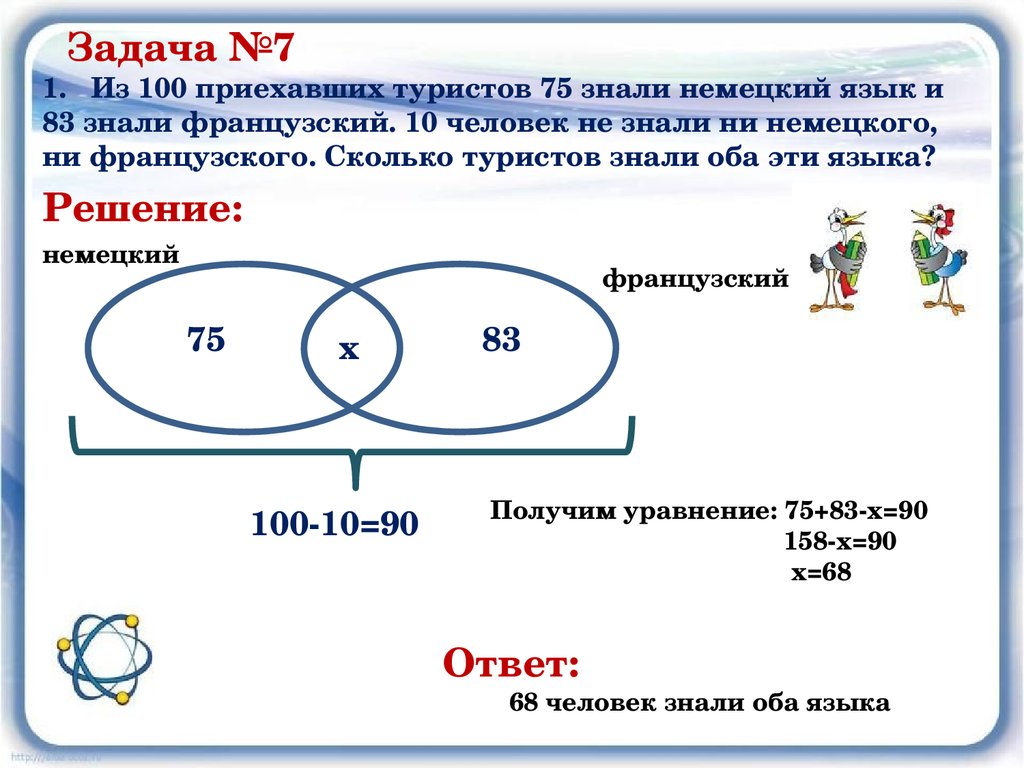

)

 

Решение:

При помощи кругов Эйлера изобразим условия задачи.

1) 4800 + 4500 — 7000 = 2300 (тыс. страниц) — найдено по запросу Крейсер и Линкор,

2) 4800 — 2300 = 2500 (тыс. страниц) — найдено по запросу Крейсер,

3) 4500 — 2300 = 2200 (тыс. страниц) — найдено по запросу Линкор.

Ответ: 2300 тыс. страниц.

 

2.6. Задача про блондинок

Каждый ученик класса — либо девочка, либо блондин, либо любит математику. В классе 20 девочек, из них 12 блондинок, но одна блондинка любит математику. Всего в классе 24 ученика — блондина, математику из них любят 12, а всего учеников (мальчиков и девочек), которые любят математику, 17, из них 6 девочек. Сколько учеников в данном классе?

 

Решение:

Изобразим с помощью кругов Эйлера данные из задачи:

1) 12 — 1 = 11 (учеников) — девочек блондинок,

2) 12 — 1 = 11 (учеников) — блондины и любят математику,

3) 6 — 1 = 5 (учеников) — девочек, которые любят математику,

 

4) 20 — 11 — 1 — 5 = 3 (ученика) — девочки,

5) 24 — 11 — 1 — 11 = 1 (ученик) — блондин,

6) 17- 5 — 1 — 11 = 0 (учеников) — любят математику,

7) 3 + 1 + 0 + 5 + 11 + 11 + 1 = 32 (ученика) — всего в классе.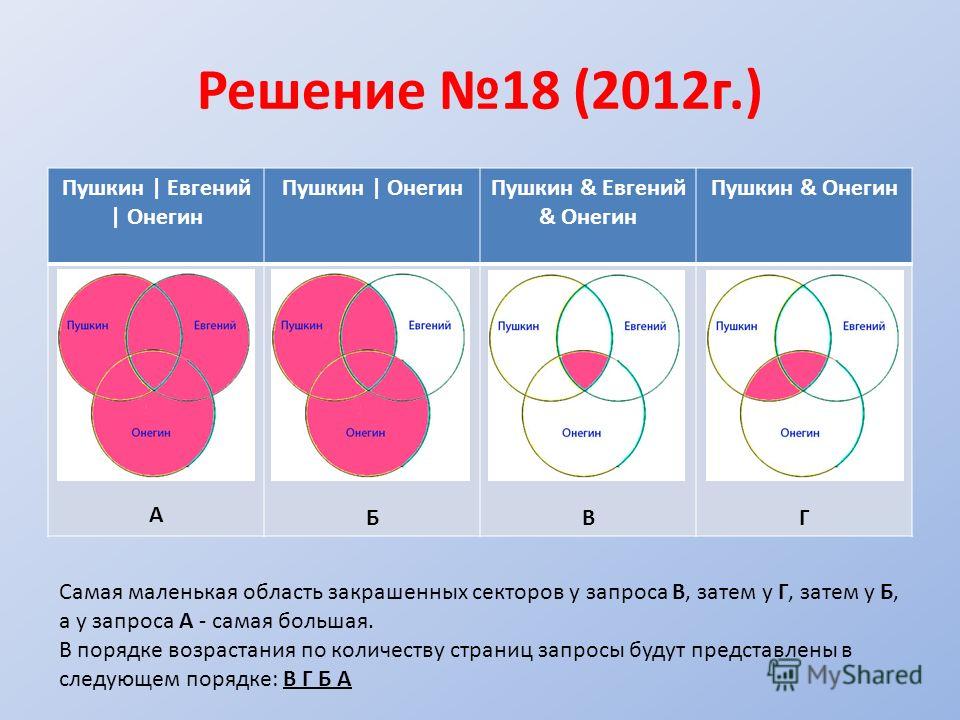

Ответ: 32 ученика.

 

2.7. Задача про кружки

В трёх седьмых классах 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют в хоре, не увлекаются спортом и не занимаются в драмкружке? Сколько ребят заняты только спортом?

 

Решение:

Учитывая условия задачи, сделаем чертеж:

 

1) 10 — 3 = 7 (ребят) — посещают драмкружок и хор,

2) 6 — 3 = 3 (ребят) — поют в хоре и занимаются спортом,

3) 8 — 3 = 5 (ребят) — занимаются спортом и посещают драмкружок,

4) 27 — 7 — 3 — 5 = 12 (ребят) — посещают драмкружок,

5) 32 — 7 3 — 3 = 19 (ребят) — поют в хоре,

6) 22 — 5 — 3 — 3 = 11 (ребят) — увлекаются спортом,

 

7) 70 — (12 + 19 + 11 + 5+ 7 + 3 + 3) = 10 (ребят) — не поют в хоре, не увлекаются спортом и не занимаются в драмкружке.

 

Ответ: 10 человек и 11 человек.

 

 

 

 

 

 

 

 

 

Задачи для самостоятельного решения

 

1.     На фирме работают 67 человек. Из них 47 знают английский язык, 35 — немецкий язык, а 23 — оба языка. Сколько человек фирмы не знают ни английского, ни немецкого языков?

2.     Из 40 учащихся нашего класса 32 любят молоко, 21 — лимонад, а 15 — и молоко, и лимонад. Сколько ребят в нашем классе не любят ни молоко, ни лимонад?

3.     12 моих одноклассников любят читать детективы, 18 — фантастику, трое с удовольствием читают и то, и другое, а один вообще ничего не читает. Сколько учеников в нашем классе?

4.     Из тех 18 моих одноклассников, которые любят смотреть триллеры, только 12 не прочь посмотреть и мультфильмы. Сколько моих одноклассников смотрят одни «мультики», если всего в нашем классе 25 учеников, каждый из которых любит смотреть или триллеры, или мультфильмы, или и то и другое?

5.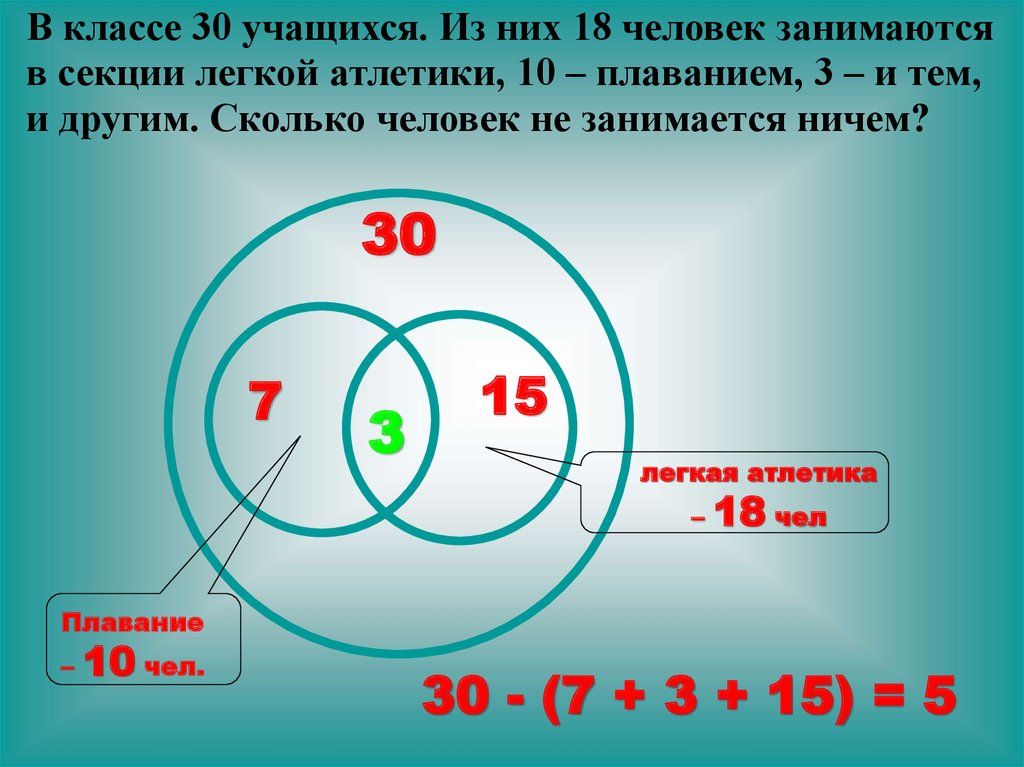      Из 29 мальчишек нашего двора только двое не занимаются спортом, а остальные посещают футбольную или теннисную секции, а то и обе. Футболом занимается 17 мальчишек, а теннисом — 19. Сколько футболистов играет в теннис? Сколько теннисистов играет в футбол?

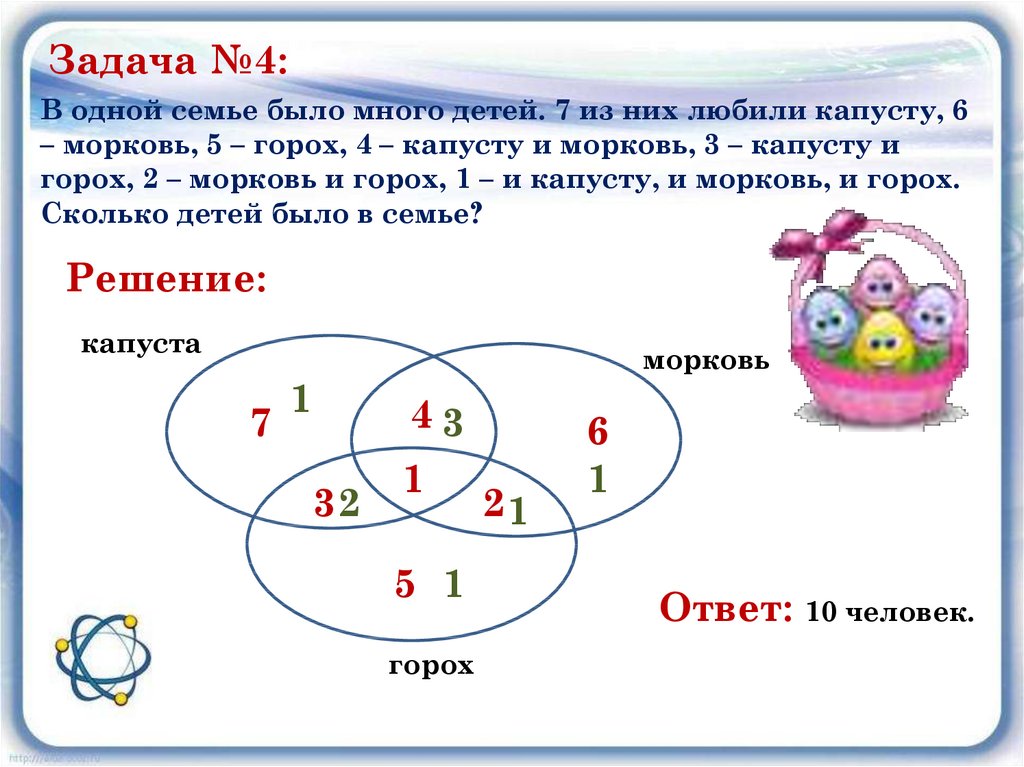
6.     В одном классе 25 учеников. Из них 7 любят груши, 11 — черешню. Двое любят груши и черешню; 6 — груши и яблоки; 5 — яблоки и черешню. Но есть в классе два ученика, которые любят все и четверо таких, что не любят фруктов вообще. Сколько учеников этого класса любят яблоки?

7.     В конкурсе красоты участвовали 22 девушки. Из них 10 было красивых, 12 — умных и 9 — добрых. Только 2 девушки были и красивыми, и умными; 6 девушек были умными и одновременно добрыми. Определите, сколько было красивых и в то же время добрых девушек, если я скажу вам, что среди участниц не оказалось ни одной умной, доброй и вместе с тем красивой девушки?

8.     В нашем классе 35 учеников. За первую четверть пятерки по русскому языку имели 14 учеников; по математике — 12; по истории — 23. По русскому и математике — 4; по математике и истории — 9; по русскому языку и истории — 5. Сколько учеников имеют пятерки по всем трем предметам, если в классе нет ни одного ученика, не имеющего пятерки хотя бы по одному из этих предметов?

9.     Из 100 человек 85 знают английский язык, 80 — испанский, 75 — немецкий. Все владеют, по крайней мере, одним иностранным языком. Среди них нет таких, которые знают два иностранных языка, но есть владеющие тремя языками. Сколько человек из этих 100 знают три языка?

10. Из сотрудников фирмы 16 побывали во Франции, 10 — в Италии, 6 — в Англии; в Англии и Италии — 5; в Англии и Франции — 6; во всех трех странах — 5 сотрудников. Сколько человек посетили и Италию, и Францию, если всего в фирме работают 19 человек, и каждый из них побывал хотя бы в одной из названных стран?

 

Список использованных источников

 

1. Баженов И.И, Порошкин А.Г., Тимофеев А.Ю., Яковлев В.Д. Задачи для школьных математических кружков: учеб. пособие / Сыктывкар: Сыктывкарский университет, 2006.

2. Марков И.С. Новые олимпиады по математике — Ростов н/Д: Феникс, 2005.

3. https://ru.wikipedia.org/wiki/

4. http://logika.vobrazovanie.ru

5. http://www.otvet-prost.ru/load/diskretnaja_matematika/na_krugi_ehjlera/zadacha_na_krugi_ehjlera/18-1-0-22

6. http://urok.1sept.ru/articles/550092/

7. http://www.tutoronline.ru/blog/reshit-zadachu-pomogut-krugi-jejlera

 

Решение задач кругами Эйлера — презентация онлайн

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. Занятие 1

Решение задач кругами Эйлера

2. Разминка

Сложили 123 тысячи, 123 сотни и 123
единицы. Какое число получилось?
Ответ:
123000
12300
123
135423

3. Разминка

В числе 456 798 702 134 вычеркните 4
цифры так, чтобы оставшиеся цифры в
том же порядке составили наибольшее
число.
Ответ:
98 702 134

4. Историческая справка Леонард Эйлер (1707-1783)

Л.
Эйлер
–
один
из
величайших
ученых.
Его
именем названы более 20 (!)
формул математики. В день
200-летия со дня рождения
этого великого математика
на родине, в Швейцарии, было
издано все его наследие,
которое состояло из 72 томов
по 600 страниц. 30 томов
посвящено математике.

5. Задача 1 Пересчитай математиков!

В классе 35 учеников, 12 занимаются в
математическом кружке, 9 занимаются в
биологическом, а 16 ребят не посещают
эти кружки. Сколько биологов увлекаются
математикой?

6. Задача 1 Решение

Решим задачу с помощью кругов Эйлера.
35
М 12
Б9
16
М — математики
Б — биологи

7. Задача 1 Решение

Внутри большого круга 35
учеников, внутри кругов М и Б:
35-16=19 учеников, внутри круга
М — 12 ребят, значит, в той части
круга Б, которая не имеет
ничего общего с кругом М,
находится 19-12=7 учеников,
следовательно, в МБ находится
2 ученика (9-7=2). Таким
образом, 2 биолога увлекаются
математикой.

8. Задача 2

В туристической группе из 100 человек 75
человек знают немецкий язык, 65 человеканглийский язык, а 10 человек — не знают ни
немецкого, ни английского языка. Сколько
туристов знают два языка?

9. Задача 2 Решение

10
А 65
Н 75
А – англ. язык
Н – немецкий
Ответ: 50

10. Задача 3

В классе 35 учеников, каждый из которых
любит футбол, волейбол или баскетбол. 24 из
них любят футбол, 18 – волейбол и 12 –
баскетбол. 10 учеников одновременно любят и
футбол, и волейбол, 8 – футбол и баскетбол, а
5 – волейбол и баскетбол. Сколько учеников
этого класса любят все три вида спорта?

11. Задача 4

В классе 38 учеников. Из них 16 играют в
баскетбол, 17 – в хоккей, 18 – в волейбол.
Увлекаются только двумя видами спорта –
баскетболом и хоккеем – 4, баскетболом и
волейболом – 3, волейболом и хоккеем – 5.
Трое учеников ничем не увлекаются.
Сколько ребят увлекается одновременно
тремя видами спорта?
Сколько ребят увлекается лишь одним из
этих видов спорта?

12. Задачи со спичками

Нужно переложить одну спичку так, чтобы
получилось верное равенство:
Ответ:

13. Задачи со спичками

Из
семи
спичек
1/
выложено
число
7.
Превратите
эту
дробь
в число 1/3, не прибавляя
и не убавляя спичек.
Ответ:

14. Домашнее задание

Чтобы открылись ворота в сказочный город,
необходимо в свободных клетках на табло при
въезде набрать числа так, чтобы сумма чисел,
стоящих в любых трех последовательных
клетках, равнялась 20. Попробуйте открыть
ворота.

English     Русский Правила

Подать заявку – Euler Circle

Право на участие

При нормальных обстоятельствах учащиеся не должны заканчивать среднюю школу к началу курса. Официального нижнего возрастного предела нет, но мы ожидаем, что учащиеся будут иметь математическую зрелость старшеклассников.

Стоимость обучения

Стоимость каждого курса средней продолжительности составляет 1000 долларов США. Однако, если вы не в состоянии заплатить или если это вызовет финансовые трудности, сообщите нам об этом (только после того, как вас примут), и мы, возможно, сможем организовать некоторую финансовую помощь.

Заявка

Чтобы подать заявку в Euler Circle, пожалуйста, заполните форму ниже. В рамках вашего заявления, пожалуйста, введите имя и адрес электронной почты учителя математики, с которым мы можем связаться, если у нас возникнут какие-либо вопросы. Это может быть учитель из школы, или из математического лагеря или другой внеклассной программы.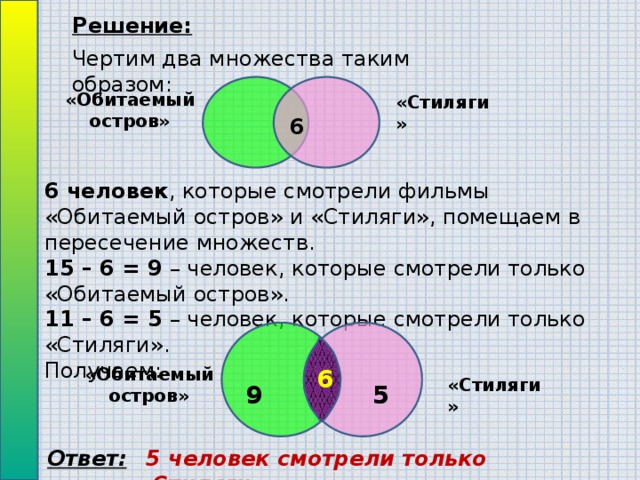 Мы не обязательно свяжемся с вашим учителем.

Сейчас мы принимаем заявки на весенние и летние курсы 2023 года. Весной у нас будет промежуточное занятие по переходу к доказательствам в анализе, занятие по основам высшей математики на уровне между средним и продвинутым с упором на точечно-множественную топологию и углубленное занятие по дифференциальной тополгое. Эти занятия можно будет пройти онлайн или лично. Вам не нужно жить в районе залива Сан-Франциско, чтобы посещать онлайн-занятия; приветствуются студенты со всего мира. Вот даты и время трех занятий:

Класс	Дата начала	Дата окончания	Все	Онлайн	Лично
Переход к доказательствам	3 апреля	7 июня	Понедельник 17:00–18:00	Вторник 17:00–19:00	Среда 18:30–20:30
Основы высшей математики	3 апреля	7 июня	Понедельник 17:00–18:30	Среда 17:00–19:00	Среда 18:30–20:30
Дифференциальная топология	3 апреля	7 июня	Понедельник 18:30–20:30	Вторник 17:00–19:00	Среда 18:30–20:30

Заявки на зимние курсы принимаются 19 февраля . После этого мы продолжим принимать заявки по мере поступления, пока остаются места.

Форма заявления о переходе весной 2023 г. на 9 класс доказательств0005

Заявка на весенний 2023 курс основ высшей математики

Заявление на весенний 2023 класс дифференциальной топологии

Летом у нас будет два продвинутых класса. На первой летней сессии у нас будет независимый класс по исследованию и написанию статей, а на второй летней сессии у нас будет класс по математике Эйлера. Летние занятия будут проходить полностью онлайн.

Вот даты и время летних занятий:

Класс	Дата начала	Дата окончания	раз
Независимые исследования и написание статей	12 июня	14 июля	Понедельник, вторник, четверг и пятница с 17:00 до 19:00
Математика Эйлера	17 июля	18 августа	Понедельник, вторник, четверг и пятница с 17:00 до 19:00

Прием заявок на летние курсы 9 апреля . После этого мы продолжим принимать заявки, пока места остаются на постоянной основе.

Заявка на летние занятия 2023

Нравится:

Нравится Загрузка…

Нажмите здесь, чтобы подписаться на рассылку!

кругов, Базельская проблема и кажущаяся яркость звезд

В День числа числа Пи 2016 года я написал в этом посте о замечательном факте, открытом Эйлером, что вероятность того, что два случайно выбранных целых числа не имеют общих простых множителей, равна . Доказательство использует известное тождество, часто называемое «проблемой Базеля», которое также принадлежит Эйлеру. В посте 2016 года я представил оригинальное решение Эйлера для Базельской проблемы с использованием разложения в ряд Тейлора для .

В честь Дня Пи 2018 я хотел бы объяснить простое и интуитивно понятное решение Базельской проблемы, предложенное Йоханом Вестлундом. (Статья Вестлунда находится здесь; см. также это видео на YouTube, где я впервые услышал об этом подходе — спасибо Фрэнсису Су за то, что он поделился им на Facebook!) Подход Вестлунда мотивирован физическими соображениями (закон обратных квадратов, который управляет яркость источника света) и использует только базовую евклидову геометрию и тригонометрию.

План доказательства

Краткий план аргументации Вестлунда выглядит следующим образом:

Шаг 1: С помощью некоторых простых алгебраических манипуляций достаточно доказать эквивалентную формулу . Это, в свою очередь, следует (устанавливая ) из следующего более общего факта:

Теорема: Для каждого действительного числа, которое не является целым числом, мы имеем

Шаг 2: Пусть четно, и думать о (что, без ограничения общности, мы можем предположить, удовлетворяет) как точка на прямой с действительными числами. Расположите на числовой прямой звезды одинаковой яркости, по одной звезде в каждой целой (т. е. «решетчатой») точке полуоткрытого интервала. Тогда, по закону обратных квадратов, мы можем интерпретировать частичную сумму как полную видимую яркость в -звездной системе.

Шаг 3: Мы можем аппроксимировать (с любой желаемой точностью) точки решетки равноотстоящими точками по периметру окружности очень большого радиуса, которая касается прямой с действительными числами в точке .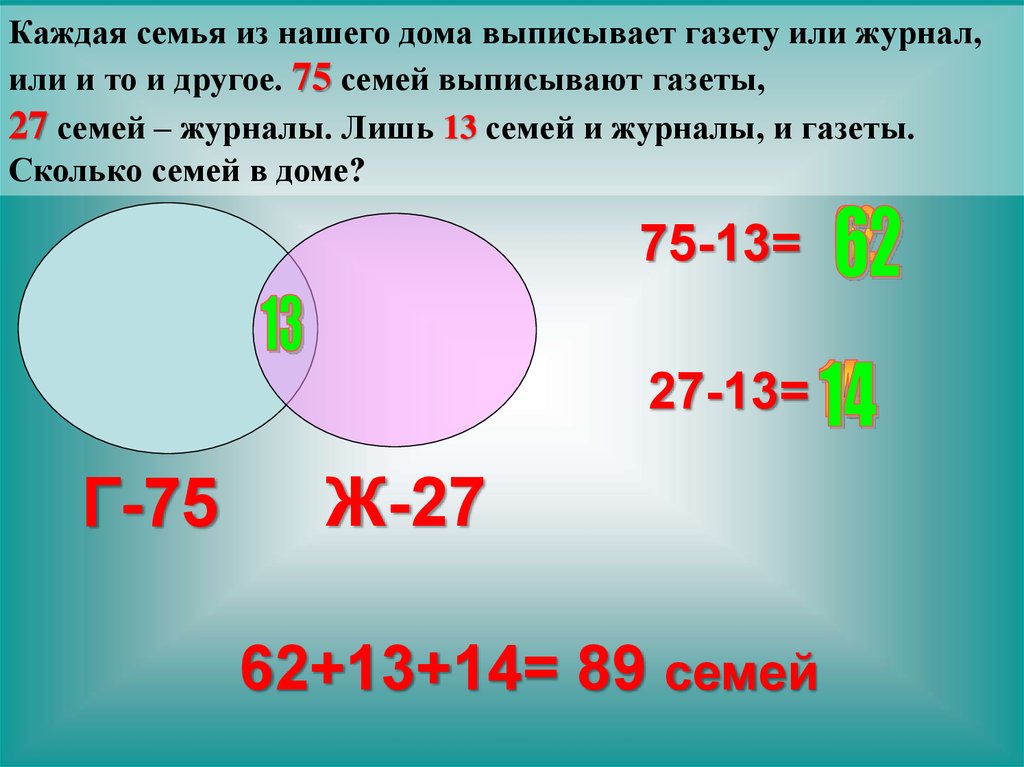 Поэтому мы можем заменить нашу систему звезд на прямой системой звезд, лежащих на некоторой дуге с центром внутри большого круга (подобно синим точкам на рис. 1).

Рисунок 1

Шаг 4: Предположим, мы размещаем звезды одинаковой яркости на одинаковом расстоянии друг от друга по всему периметру окружности и измеряем общую видимую яркость в некоторой точке окружности, имеющей расстояние (измеряемое по окружности) от ближайшей звезды (см. рис. 2).

Рисунок 2

Тогда закон обратных квадратов подразумевает, что для «большая часть» (в точном количественном смысле) этой яркости исходит от звезд, ближайших к .

Шаг 5: Итерируя это наблюдение, обозначим общую видимую яркость ближайших звезд к моменту, когда мы размещаем равноотстоящие звезды по периметру окружности, причем ближайшая звезда находится на расстоянии дуги от (снова см. Рисунок 1) . Затем .

Шаг 6. С помощью элегантного геометрического рассуждения, связанного с «обратной теоремой Пифагора» (см. рис. 3), получается, что для каждого имеем . Другими словами, мы можем заменить систему равноотстоящих звезд вдоль окружности , касательной к реальной линии в точке , системой равноотстоящих звезд вдоль окружности , также касательной к реальной линии в такой таким образом, что общая видимая яркость при остается неизменной.

Рисунок 3

Отсюда по индукции следует, что для всех натуральных чисел . Объединив это с предыдущим шагом, мы получаем .

Шаг 7: В частности, если сама является большой степенью двойки, то примерно для всех . Когда также большой, примерно (где как раньше). Следует, что .

Шаг 8: По элементарной тригонометрии имеем , что доказывает теорему.

Немного евклидовой геометрии

Важнейшей и самой инновационной частью аргумента является факт из шага 6, что . Легче всего это объяснить для , хотя доказательство в общем случае по существу такое же. Итак, давайте посмотрим, как Вестлунд доказывает это.

Аргумент основан на «обратной теореме Пифагора», которая является утверждением, что в условиях рисунка 4 (где ACB — прямой угол) мы имеем .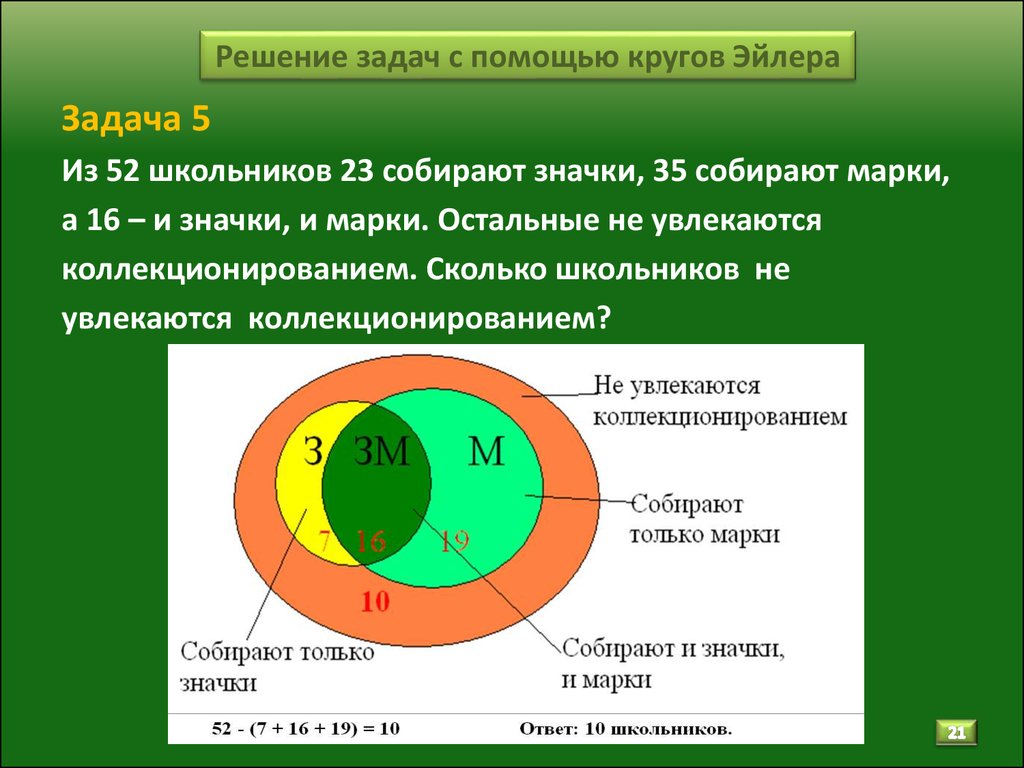

Рисунок 4

Вывести это из обычной теоремы Пифагора — элементарное упражнение.

Имея единственную звезду (обозначенную красной точкой R на рисунке 5) на окружности радиуса 1, касательной к реальной линии в точке , мы можем заменить ее двумя равноотстоящими звездами (синие точки и ) на окружности радиуса 2, также касательной к реальной линии в , таким образом, что видимая яркость красной звезды в равна сумме видимых яркостей двух голубых звезд в .

Рисунок 5

Построение и из происходит следующим образом. Пусть будет центром меньшего круга, и пусть будет центром большего круга. Тогда и две точки, где линия пересекает больший круг.

Так как это диаметр меньшего круга, это прямой угол. Формула, выражающая равенство между видимой яркостью в красной и синей звездных системах, будет немедленно следовать из обратной теоремы Пифагора, как только мы покажем, что расстояние по дуге (против часовой стрелки) от до равно расстоянию по дуге (против часовой стрелки) от до .

Чтобы убедиться в этом, сначала обратите внимание, что произведение дугового расстояния от до равно величине (в радианах) центрального угла . И умноженное на расстояние по дуге от до, равно 2 (длина окружности большего круга), умноженное на меру  центрального угла . Так что достаточно показать это. Это следует из того, что , которая пересекает ту же дугу малого круга, что и центральный угол .

Аналогичным образом, заменив каждую красную звезду двумя синими звездочками, как на рисунке 3 выше, следует, что для всех .

Базовый случай (Шаг 8)

В базовом случае количество равно где окружность окружности 1 (и, следовательно, радиус ), точки, на которых находятся на расстоянии, измеренном по окружности , и обозначает евклидово (хордальное) расстояние между и . Это элементарное упражнение по тригонометрии, чтобы показать это (см. рис. 6). Рисунок 60005

Остальные технические подробности

Теперь покажем, что когда большое, приблизительно равно .

Рассмотрим звездную систему по окружности окружности (и радиусом ). Суммарная яркость при по определению равна . Теперь удалите звезды, наиболее удаленные от , и посчитайте суммарную яркость оставшихся звезд. Поскольку каждая из вычеркнутых звезд имеет расстояние не менее , отсюда следует, что .

Аналогичным образом, если мы начнем с -звездной системы на круге радиуса и удалим все звезды, кроме ближайших к , и обозначим через общую яркость оставшихся звезд, мы получим

С другой стороны, геометрически ясно (поскольку радиусы окружностей стремятся к бесконечности), что

По неравенству треугольника разница между и ограничена

Принимая за произвольно большую степень числа 2 и применяя предложение 1, теперь получаем теорему 1 (в частном случае , но из этого легко следует общий случай).

Заключительные замечания

1. Приведенные выше оценки можно использовать для доказательства апостериорных того, что для все положительных целых чисел , а не только степени двойки.

   No related posts.