Графы. Применение графов к решению задач
Разделы: Внеклассная работа
1. Методические рекомендации к теме “Графы”.
Понятие графа целесообразно вводить после того, как разобрано несколько задач, подобных задаче 1, решающее соображение в которых – графическое представление. Важно, чтобы ученики сразу осознали, что один и тот же граф может быть нарисован разными способами. Строгое определение графа, на мой взгляд, давать не нужно, т.к. оно слишком громоздко и это только затруднит обсуждение. На первых порах хватит и интуитивного понятия. При обсуждении понятия изоморфизма можно решить несколько упражнений на определение изоморфных и неизоморфных графов. Одно из центральных мест темы – теорема о четности числа нечетных вершин. Важно, чтобы ученики до конца разобрались в ее доказательстве и научились применять к решению задач. При разборе нескольких задач рекомендую не ссылаться на теорему, а фактически повторять ее доказательство. Чрезвычайно важно также понятие связности графа. Содержательным соображением здесь является рассмотрение компоненты связности, на это необходимо обратить особое внимание. Эйлеровы графы – тема почти игровая.
Первая и главная цель, которую нужно преследовать при изучении графов, –научить школьников видеть граф в условии задачи и грамотно переводить условие на язык теории графов. Не стоят рассказывать обе всем на нескольких занятиях подряд. Лучше разнести занятия по времени на 2–3 учебных года. (Прилагается разработка занятия “Понятие графа. Применение графов к решению задач” в 6 классе).
2. Теоретический материал к теме “Графы”.
Введение
Графы – замечательные математические объекты, с их помощью можно решать очень много различных, внешне не похожих друг на друга задач. В математике существует целый раздел – теория графов, который изучает графы, их свойства и применение. Мы же обсудим только самые основные понятия, свойства графов и некоторые способы решения задач.
Понятие графа
Рассмотрим две задачи.
Задача 1. Между девятью планетами солнечной системы установлено космическое сообщение. Рейсовые ракеты летают по следующим маршрутам: Земля – Меркурий; Плутон – Венера; Земля – Плутон; Плутон – Меркурий; Меркурий – Вене; Уран – Нептун; Нептун – Сатурн; Сатурн – Юпитер; Юпитер – Марс и Марс – Уран. Можно ли долететь на рейсовых ракетах с Земли до Марса ?
Решение: Нарисуем схему условия: планеты изобразим точками, а маршруты ракет – линиями.
Теперь сразу видно, что долететь с Земли до Марса нельзя.
Задача 2. Доска имеет форму двойного креста, который получается, если из квадрата 4×4 убрать угловые клетки.
Можно ли обойти ее ходом шахматного коня и вернуться на исходную клетку, побывав на всех клетках ровно по одному разу ?
Решение: Занумеруем последовательно клетки доски:
А теперь с помощью рисунка покажем, что такой обход таблицы, как указано в условии, возможен:
Мы рассмотрели две непохожие задачи. Однако решения этих двух задач объединяет общая идея – графическое представление решения. При этом и картинки, нарисованные для каждой задачи, оказались похожими: каждая картинка – это несколько точек, некоторые из которых соединены линиями.
Такие картинки и называются графами. Точки при этом называются вершинами, а линии – ребрами графа. Заметим, что не каждая картинка такого вида будет называться графом. Например. если вас попросят нарисовать в тетради пятиугольник, то такой рисунок графом не будет. Будем называть что рисунок такого вида, как в предыдущих задачах, графом, если есть какая-то конкретная задача для которой такой рисунок построен.
Другое замечание касается вида графа. Попробуйте проверить, что граф для одной и той же задачи можно нарисовать разными способами; и наоборот для разных задач можно нарисовать одинаковые по виду графы. Здесь важно лишь то, какие вершины соединены друг с другом, а какие – нет. Например, граф для задачи 1 можно нарисовать по-другому:
Такие одинаковые, но по-разному нарисованные графы, называются изоморфными.
Степени вершин и подсчет числа ребер графа
Запишем еще одно определение: Степенью вершины графа называется количество выходящих из нее ребер. В связи с этим, вершина, имеющая четную степень, называется четной вершиной, соответственно, вершина, имеющая нечетную степень, называется нечетной вершиной.
С понятием степени вершины связана одна из основных теорем теории графов –теорема о честности числа нечетных вершин. Докажем ее мы немного позднее, а сначала для иллюстрации рассмотрим задачу.
Задача 3. В городе Маленьком 15 телефонов. Можно ли их соединить проводами так, чтобы каждый телефон был соединен ровно с пятью другими ?
Решение: Допустим, что такое соединение телефонов возможно. Тогда представим себе граф, в котором вершины обозначают телефоны, а ребра – провода, их соединяющие. Подсчитаем, сколько всего получится проводов. К каждому телефону подключено ровно 5 проводов, т.е. степень каждой вершины нашего графа – 5. Чтобы найти число проводов, надо просуммировать степени всех вершин графа и полученный результат разделить на 2 (т.к. каждый провод имеет два конца, то при суммировании степеней каждый провод будет взят 2 раза). Но тогда количество проводов получится разным . Но это число не целое. Значит наше предположение о том, что можно соединить каждый телефон ровно с пятью другими, оказалось неверным.
Ответ. Соединить телефоны таким образом невозможно.
Теорема: Любой граф содержит четное число нечетных вершин.
Доказательство:
Количество ребер графа равно половине суммы степеней его вершин. Так как количество ребер должно быть целым числом, то сумма степеней вершин должна быть четной. А это возможно только в том случае, если граф содержит четное число нечетных вершин.Связность графа
Есть еще одно важное понятие, относящееся к графам – понятие связности.
Граф называется связным, если из любые две его вершины можно соединить путем, т.е. непрерывной последовательностью ребер. Существует целый ряд задач, решение которых основано на понятии связности графа.
Задача 4. В стране Семерка 15 городов, каждый из городов соединен дорогами не менее, чем с семью другими. Докажите, что из каждого города модно добраться в любой другой.
Доказательство: Рассмотрим два произвольных А и В города и допустим, что между ними нет пути. Каждый из них соединен дорогами не менее, чем с семью другими, причем нет такого города, который был бы соединен с обоими рассматриваемыми городами (в противном случае существовал бы путь из A в B). Нарисуем часть графа, соответствующую этим городам:
Теперь явно видно, что мы получили не менее различных 16 городов, что противоречит условию задачи. Значит утверждение доказано от противного.
Если принять во внимание предыдущее определение, то утверждение задачи можно переформулировать и по-другому: “Доказать, что граф дорог страны Семерка связен.”
Теперь вы знаете, как выглядит связный граф. Несвязный граф имеет вид нескольких “кусков”, каждый из которых – либо отдельная вершина без ребер, либо связный граф. Пример несвязного графа вы видите на рисунке:
Каждый такой отдельный кусок называется компонентой связности графа. Каждая компонента связности представляет собой связный граф и для нее выполняются все утверждения, которые мы доказали для связных графов. Рассмотрим пример задачи, в которой используется компонента связности:
Задача 5. В Тридевятом царстве только один вид транспорта – ковер-самолет. Из столицы выходит 21 ковролиния, из города Дальний – одна, а из всех остальных городов, – по 20. Докажите, что из столицы можно долететь в город Дальний.
Доказательство: Понятно, что если нарисовать граф ковролиний Царства, то он может быть несвязным. Рассмотрим компоненту связности, которая включает в себя столицу Царства. Из столицы выходит 21 ковролиния, а из любых других городов, кроме города Дальний – по 20, поэтому, чтобы выполнялся закон о четном числе нечетных вершин необходимо, чтобы и город Дальний входил в эту же самую компоненту связности. А так как компонента связности – связный граф, то из столицы существует путь по ковролиниям до города Дальний, что и требовалось доказать.
Графы Эйлера
Вы наверняка сталкивались с задачами, в которых требуется нарисовать какую-либо фигуру не отрывая карандаш от бумаги и проводя каждую линию только один раз. Оказывается, что такая задача не всегда разрешима, т.е. существуют фигуры, которые указанным способом нарисовать нельзя. Вопрос разрешимости таких задач также входит в теорию графов. Впервые его исследовал в 1736 году великий немецкий математик Леонард Эйлер, решая задачу о Кенигсбергских мостах. Поэтому графы, которые можно нарисовать указанным способом, называются Эйлеровыми графами.
Задача 6. Можно ли нарисовать изображенный на рисунке граф не отрывая карандаш от бумаги и проводя каждое ребро ровно один раз ?
Решение. Если мы будем рисовать граф так, как сказано в условии, то в каждую вершину, кроме начальной и конечной, мы войдем столько же раз, сколько выйдем из нее. То есть все вершины графа, кроме двух должны быть четными. В нашем же графе имеется три нечетные вершины, поэтому его нельзя нарисовать указанным в условии способом.
Сейчас мы доказали теорему об Эйлеровых графах:
Теорема: Эйлеров граф должен иметь не более двух нечетных вершин.
И в заключение – задача о Кенигсбергских мостах.
Задача 7. На рисунке изображена схема мостов города Кенигсберга.
Можно ли совершить прогулку так, чтобы пройти по каждому мосту ровно 1 раз?
3. Задачи к теме “Графы”
Понятие графа.
1. На квадратной доске 3×3 расставлены 4 коня так, как показано на рис.1. Можно ли сделав несколько ходов конями, переставить их в положение, показанное на рис.2?
Рис. 1 | Рис. 2 |
Решение. Занумеруем клетки доски, как показано на рисунке:
Каждой клетке поставим в соответствие точку на плоскости и, если из одной клетки можно попасть в другую ходом шахматного коня, то соответствующие точки соединим линией. Исходная и требуемая расстановки коней показаны на рисунках:
При любой последовательности ходов конями порядок их следования, очевидно, измениться не может. Поэтому переставить коней требуемым образом невозможно.
2. В стране Цифра есть 9 городов с названиями 1, 2, 3, 4, 5, 6, 7, 8, 9. Путешественник обнаружил, что два города соединены авиалинией в том и только в том случае, если двузначное число, образованное названиями городов, делится на 3. Можно ли долететь по воздуху из города 1 в город 9 ?
Решение. Поставив в соответствие каждому городу точку и соединив точки линией, если сумма цифр делится на 3, получим граф, в котором цифры 3, 5, 9 связаны между собой, но не связаны с остальными. Значит долететь из города 1 в город 9 нельзя.
Степени вершин и подсчет числа ребер.
3. В государстве 100 городов к из каждого города выходит 4 дороги. Сколько всего дорог в государстве.
Решение. Подсчитаем общее количество выходящих городов дорог – 100 . 4 = 400. Однако при таком подсчете каждая дорога посчитана 2 раза – она выходит из одного города и входит в другой. Значит всего дорог в два раза меньше, т.е. 200.
4. В классе 30 человек. Может ли быть так, что 9 человек имеют по 3 друга, 11 – по 4 друга, а 10 – по 5 друзей ?
Ответ. Нет (теорема о четности числа нечетных вершин).
5. У короля 19 вассалов. Может ли оказаться так, что у каждого вассала 1, 5 или 9 соседей ?
Ответ. Нет, не может.
6. Может ли в государстве, в котором из каждого города выходит ровно 3 дороги, быть ровно 100 дорог?
Решение. Подсчитаем число городов. Число дорог равно числу городов х, умноженному на 3 (число выходящих из каждого города дорог) и разделенному на 2 (см. задачу 3). Тогда 100 = Зх/2 => Зх=200, чего не может быть при натуральном х. Значит 100 дорог в таком государстве быть не может.
7. Докажите, что число людей, живших когда-либо на Земле и сделавших нечетное число рукопожатий, четно.
Доказательство непосредственно следует из теоремы о четности числа нечетных вершин графа.
Связность.
8. В стране из каждого города выходит 100 дорог и из каждого города можно добраться до любого другого. Одну дорогу закрыли на ремонт. Докажите, что и теперь из любого города можно добраться до любого другого.
Доказательство. Рассмотрим компоненту связности, в которую входит один из городов, дорогу между которыми закрыли. По теореме о четности числа нечетных вершин в нее входит и второй город. А значит по-прежнему можно найти маршрут и добраться из одного из этих городов в другой.
Графы Эйлера.
9. Имеется группа островов, соединенных мостами так, что от каждого острова можно добраться до любого другого. Турист обошел все острова, пройдя по каждому мосту розно 1 раз. На острове Троекратном он побывал трижды. Сколько мостов ведет с Троекратного, если турист
а) не с него начал и не на нем закончил?
б) с него начал, но не на нем закончил?
в) с него начал и на нем закончил?
10. На рисунке изображен парк, разделенный на несколько частей заборами. Можно ли прогуляться по парку и его окрестностям так, чтобы перелезть через каждый забор розно 1 раз?
6.03.2007
urok.1sept.ru
1 | Было 4 мальчика: Ваня, Петя, Стас и Гоша. На каждом из них были перчатки разных цветов: оранжевые, черные, белые и красные. Известно, что на Пете были черные перчатки, на Гоше не оранжевые и не белые, а на Стасе не белые. Какого цвета перчатки у каждого мальчика? (Чачкова Дарья, 5Б) |
2 | Маша, Петя , Ира и Миша ходят в разные школы ( №111, №304, №125, №31). Маша и Петя знакомы с учеником школы №111, школа №304 только для мальчиков. Маша не знает школу №304, школа Иры находится между школами №111, №31. Петя проходит через школы №125 и №31. Кто в какой школе учится? (Щербина Кристина, 5Б) |
3 | Женя, Ваня, Дима и Даня были в кинотеатре. Показывали четыре жанра : боевик, комедия, мультик и драма, которую сегодня впервые показывают на экранах. Известно, что Женя любит комедии, но на этот жанр сегодня не пошел. Даня и Дима не любят мультфильмы и комедии. Дима сказал, что пойдет на фильм, который уже смотрел, ведь он ему очень понравился. На каком жанре кино был каждый мальчик? (Черных Даниил, 5Б) |
4 | Три друга были в театре в белом, красном и голубом смокингах. Их туфли были тех же трех цветов. Только у Глеба цвета смокинга и туфель совпадали. Алеша был в белых туфлях. Ни туфли, ни смокинг Дани не были красными. Определите цвета смокинга и туфлей друзей. (Гергаиа Ника, 5Б) |
5 | Четыре мальчика Дима Костя, Вова и Кирилл собирают разные предметы: жетоны, марки, значки и монеты. Друзья Дима и Костя не собирают жетоны. Любитель значков не знает Костю. Вова и Дима ничего не знают о марках. Кирилл не собирает жетоны. Кто из мальчиков что коллекционирует? (Петрик Максим, 5Б) |
6 | Три брата Иван, Дмитрий и Сергей преподают дисциплины в университетах Москвы, Санкт-Петербурга и Киева. Иван работает не в Москве, а Дмитрий – не в СПб. Москвич преподает не историю. Тот, кто работает в СПб, преподает химию. Дмитрий преподает не биологию. Какую дисциплину преподает каждый из братьев и в каком городе? (Федичева Валерия, 5Б) |
7 | Саша, Коля и Ваня пошли в кафе. Мальчики купили сок, лимонад и чай. Саша спросил у друга: «Зачем ты купил холодный сок, у тебя же горло болит?» А третий друг ответил: «Коля, надо было покупать горячий чай, как я». Кто что купил? (Новиков Игорь, 5Б) |
multiurok.ru
Задачи для 5 — 6 классов на развитие логического, пространственного мышления. Математические игры
Программа занятий для математического кружка для 5 — 6 классов
Программа математического кружка носят преимущественно игровой, занимательный характер. Это не только решение задач, но и работа с графами, с чертежами, практическое моделирование, интеллектуальные игры. Основной целью занятий является привитие интереса к математике, а так же развитие мышления учащихся. Как известно, у младших школьников преобладает наглядно-образный характер мышления; и для учеников 5-6-х классов кружковые занятия послужат «мостиком» от наглядного к активному развитию абстрактного мышления; в работу включается пространственное мышление и пространственное воображение, развивается логическое и эвристическое мышление, формируется креативность мышления.
Создание геометрической мозаики в стиле Маурица Эшера.
Знакомство с понятиями «граф», «вершины и ребра графа», «изолированная вершина», «полный граф», решение задач с помощью графов.
Знакомство с понятиями «путь» и «цикл в графе, «степень вершины», «дерево», «лес»; решение задач с помощью «деревьев».
Знакомство с понятиями «эйлеров цикл» и «эйлеров путь»; решение задач по рисованию графов, не отрывая карандаша от бумаги.
Знакомство с понятиями «гамильтонов путь» и «гамильтонов цикл» в графах; решение задач.
Анализ развития игры с помощью «деревьев».
Знакомство с понятиями «цветной граф», «правильная раскраска графа»; решение задач на раскраску графов, турнир раскрасчиков.
Геометрическое моделирование: создание действующей модели флексагона.
Решение логических задач с помощью графов.
Решение логических задач с помощью таблиц.
www.zaesenok.ru
Открытый урок математики по теме «Графы вокруг нас». 5-й класс
Разделы: Математика
Цели урока:
- дидактические: ввести понятие «граф»; рассмотреть примеры использования графов в различных областях знаний; отрабатывать умение решать текстовые задачи на применение теории графов
- развивающие: развитие внимания, памяти, логического мышления, аргументированной математической речи;
- воспитательные: воспитывать чувства уверенности, последовательности, дисциплинированности, умение слушать.
Оборудование: проектор, экран, раздаточный материал (Приложение 1), презентация (Приложение 2)
Ход урока
1. Организационный момент
Сегодня мы познакомимся с математическим понятием «граф»; рассмотрим примеры использования графов в различных областях знаний; задачи по теории графов. Работа на уроке будет проходить в группах. Надеюсь, что наша работа будет продуктивной.
2. Этап усвоения новых знаний
1. Рассмотрим задачу. В первенстве класса по настольному теннису 6 участников: Артем, Булат, Влад Батыршин, Глеб, Дмитрий и Ермошин Влад. Первенство проводится по круговой системе– каждый из участников играет с каждым из остальных один раз. К настоящему моменту некоторые игры уже проведены: Артем сыграл с Булатом, Глебом и Ермошиным; Булат, как уже говорилось, с Артемом и еще с Глебом; Влад – с Глебом, Дмитрием и Ермошиным; Глеб – с Артемом и Булатом; Дмитрий – с Владом и Ермошин – с Артемом и Владом. Сколько игр проведено к настоящему моменту и сколько еще осталось?
Решение демонстрируется на доске. Изобразим данные задачи в виде схемы. Участников будем изображать точками: Андрея – точкой А, Бориса – точкой Б и т.д. Если двое участником уже сыграли между собой, то будем соединять изображающие их точки отрезками. Получается схема, которая называется графом.
2. Определение. Графом называют конечное множество точек, которые соединены отрезками прямых. Точки называются вершинами графа, а отрезки – ребрами графа.
Прежде всего стоит сказать о том, что графы, о которых пойдет речь, к аристократам былых времен никакого отношения не имеют. Наши «графы» имеют корнем греческое слово «графо», что значит «пишу». Тот же корень в словах «график», «биография», «голография», география.
Точки А, Б, В, Г, Д, Е называются вершинами графа, соединяющие их отрезки – ребрами графа.
Число игр, проведенных к настоящему моменту, равно числу ребер, т.е. 7. Чтобы найти число игр, которые осталось провести, построим еще один граф с теми же вершинами, но ребрами будем соединять тех участников, которые еще не играли друг с другом. Ребер у этого графа осталось 8. Значит, осталось провести 8 игр.
Сейчас почти в любой отрасли науки и техники встречаешься с графами.
Внимание на доску.
Примеры графов:
- схема метро;
- генеалогическое древо;
- кристаллическая решетка;
- электрическая схема и другие.
Придумайте свои примеры графов.
В качестве примеров ученики могут привести следующие примеры: схемы железных и автомобильных дорог, тепло– и электросети, дерево каталогов, планы выставок и другие.
Графы широко используются в современной математике и программировании. С теорией графов связаны не только математические головоломки, но и такие серьезные науки, как теория отношений и теория групп. Графы находят все новые приложения в теории планирования и управления, теории расписаний, социологии, математической лингвистике, биологии и медицине.
Теория графов содержит большое количество нерешённых проблем и пока не доказанных гипотез, это сравнительно молодая наука: во времена Ньютона такой науки еще не было, хотя и были «генеалогические деревья», представляющие собой разновидности графов.
3. Этап закрепления новых знаний
1. Рассмотрим задачу: 5 друзей при встрече обменялись рукопожатиями (каждый пожал руку каждому по одному разу). Обменяйтесь, пожалуйста, рукопожатиями. Сколько всего рукопожатий было сделано?
Решение демонстрируется на доске. Задача легко решается с помощью теории графов.
Изобразите в тетради 5 точек: А, Б, В, Г, Д.
Сколько всего рукопожатий было сделано?
К решению можно прийти чисто логически. Но графы придали наглядность, упростили решение.
Если подвести итог, то можно утверждать: если полный граф имеет n вершин, то количество ребер будет равно n(n — 1)/2.
2. Хочу предложить вам решить задачу – загадку. Перед вами граф – «распечатанное письмо». Попробуйте начертить этот граф не отрывая карандаша от бумаги и не проводя по одной линии дважды.
Тот, у кого получилось, может выйти к доске и записать маршрут обхода.
В какой вершине вы начали движение? В какой закончили? (Начала в А, закончила в Е)
Есть другие варианты? (Да, я начал в Е, закончил в А)
Не расстраивайтесь. Мы сейчас с вами выведем алгоритм для решения этой задачи. Для этого нам нужно будет перенестись на более чем 200 лет назад и оказаться вместе с великим математиком Леонардом Эйлером в городе Кенигсберге (сейчас этот город называется Калининград).
На доске портрет Леонарда Эйлера. Что вы знаете о Леонарде Эйлере?
3. Историческая справка (сообщение ученика)
Леонард Эйлер (1707-1783) – математик, механик, физик и астроном. Ученый необычайной широты интересов. Автор свыше 800 работ по математическому анализу, дифференциальной геометрии, теории чисел, приближенным вычислениям, небесной механике, математической физике, оптике, баллистике, кораблестроению, теории музыки и других, оказавших значительное влияние на развитие науки. Леонард Эйлер по происхождению швейцарец. В 1726г. был приглашен работать в Петербург, в 1727г. переехал жить в Россию. Являлся академиком, а затем почетным членом Петербургской академии наук.
Первая работа по теории графов принадлежит именно ему (1736), хотя термин «граф» впервые ввел в 1936 году венгерский математик Денеш Кениг. В начале 20 века наряду с термином «граф» употреблялись другие термины, например карта, комплекс, диаграмма, сеть, лабиринт.
4. Задача о Кёнигсбергских мостах.
Бывший Кёнигсберг расположен на реке Прегель. В пределах города река омывает два острова. С берегов на острова были перекинуты мосты. Старые мосты не сохранились, но осталась карта города, где они изображены. Жители города предлагали приезжим следующую задачу: пройти по всем мостам и вернуться в начальный пункт, причем на каждом мосту следовало побывать только один раз. До Эйлера никто не мог этого сделать, но и доказать, что это невозможно, тоже ни у кого не получалось. Как поступил Эйлер?
Попробуйте найти нужный ответ и выдвиньте свою гипотезу. Через 3 минуты слушаем гипотезы.
Прогуляться по городским мостам предложили и Эйлеру. После безуспешной попытки совершить нужный обход он начертил упрощенную схему мостов. Получился граф, вершины которого – части города, разделенные рекой, а ребра – мосты.
Попробуйте провести линии по всем ребрам -«мостам», не отрывая карандаша от бумаги. У кого получилось? Таких нет? У Эйлера тоже не получилось.. А вы знаете почему? Оказывается все дело в числе ребер, сходящихся в вершине. Давайте посчитаем, сколько ребер сходится в каждой вершине графа. Напишите рядом с каждой вершиной число, отражающее количество ребер, в ней сходящихся, и назовем вершину четной или нечетной в зависимости от того, какое число, четное или нечетное, стоит рядом. Итак, в вершине А сходится 5 ребер, в вершине В-3, в вершине С-3, в вершине Д-3. Какими являются все эти вершины? (Нечетными.)
Леонард Эйлер сформулировал правило:
Обход возможен:
- ЕСЛИ все вершины – четные, и его можно начать с любого участка.
- ЕСЛИ 2 вершины – нечетные, но его нужно начать с одной из нечетных вершин.
Обход невозможен если нечетных вершин больше 2.
Во время прогулки по городу нельзя пройти по всем семи мостам, проходя по каждому только один раз.
5. Давайте вернемся к задаче «распечатанное письмо» и применим правило Эйлера.
– Сколько ребер сходится в каждой вершине? (В вершине А сходится 3 ребра, в вершине В-4, в вершине С-2, в вершине Д-4.)
– Что вы скажите о четности вершин в этом графе? ( Три вершины – четные, две – нечетные.)
– Как нужно совершить обход этого графа, согласно правилу Эйлера? (Начать обход в одной из нечетных вершин А или Е, а завершить в другой.)
6. Вычерчивание фигур одним росчерком
Итак, мы увидели, что на языке теории графов каждая решенная задача выглядит как задача изображения «одним росчерком» графа, представленного на рисунке.
Теперь нам нетрудно будет разобраться и показать, какую из любых данных фигур можно вычертить одним росчерком, без повторения линий, а какую нет. Каждую из задач подобного рода можно свести к разобранной уже нами Эйлеровой задаче о мостах.
Например, на рисунке изображена птица.
Взяв за вершины графа точки пересечения линии, получим 7 вершин, только две из которых имеют нечетную степень.
Поэтому в этом графе существует эйлеров путь, а значит, птицу можно нарисовать одним росчерком.
Нечетные вершины: две.
4. Итог урока
Учитель выясняет у детей, на все ли вопросы они получили интересующие их ответы, а также сообщает, что с остальными видами задач знакомство будет продолжено на следующем уроке.
- Белая шляпа – мыслим фактами, цифрами
- Желтая шляпа – позитивное мышление (что именно было полезно, хорошо и т.д., почему)
- Черная шляпа- противоположность желтой шляпе (что было трудно, неясно, негативно и т.д., почему)
- Красная шляпа – эмоциональное состояние (грусть, радость, интерес, удивление, агрессия, раздражение)
- Зеленая шляпа – творческое мышление (что можно изменить, применить, усовершенствовать и т.д.)
- Синяя шляпа – философская, обобщающая.
На сегодняшнем уроке мы познакомились с основными понятиями теории графов, примерами графов и их использованием в различных областях знаний, а также применением графов при решении различных задач.
5. Домашнее задание
- Изобразите свое генеалогическое дерево.
- Можно ли фигуру, изображенную на рисунке, нарисовать одним росчерком? (решить с помощью графа)
16.04.2014
urok.1sept.ru
Презентация к уроку математики в 5 классе по теме «Решение задач методом графов»

Математика 5 класс
Учитель математики Грязнова Т.Г.

План урока:
- Логический тренинг
- Решение логических задач
- Составь задачу
- Доклады
- Новый материал
- Самостоятельная работа
- Домашнее задание
- Итог урока

Что лишнее?
- килограмм
- километр
- центнер
- грамм
- тонна

Решите анаграмму
- МАПРЯЯ
- ЧУЛ
- РЕЗОТОК
- РИПЕТРЕМ

Что больше, произведение или сумма этих чисел:

Что здесь зашифровано?

Решение логических задач
Мама купила ягоды на варенье: ежевику, чернику, бруснику, малину и смородину. Ежевики было больше, чем черники, но меньше, чем брусники. А малины было меньше, чем смородины, но больше брусники. Сколько килограмм ягод каждого вида было, если известны массы: 1,3кг, 2,2кг, 3,7кг, 4,6кг, 5,8кг.?

Задача. Мама купила ягоды на варенье: ежевику, чернику, бруснику, малину и смородину. Ежевики было больше, чем черники, но меньше, чем брусники. А малины было меньше, чем смородины, но больше брусники. Сколько кг ягод каждого вида было, если известны массы: 1,3кг; 2,2кг; 3,7кг; 4,6кг; 5,8кг.?
Решение:
2,2 кг
Е
!—————
1,3 кг
Ч
!———
3,7 кг
!——————-
Б
4,6 кг
!————————
М
5,8 кг
С
!—————————
Ответ: Е-2,2кг;Ч-1,3кг.; Б- 3,7кг; М-4,6кг; См-5,8кг.

Решение логических задач
В группе 16 студентов, 9 человек изучают японский язык, 6 человек – китайский язык, а 3 человека говорят и на японском, и на китайском языках. Сколько студентов не знают ни одного из этих языков?

Решение:
1) Всего 16 студентов,
2) 9 студентов изучают японский язык,
3) 3 — знают оба языка,
4) 6 – говорят на китайском языке
* * * * * * * * * * * * * * * *
Ответ: 4 человека не говорят ни на
одном языке

Творческое задание
- Составьте задачу по рисунку:
* * *
* * *
* *
* *
*

Доклады
- Что такое комбинаторика
- Решение задач «Методом графов».

Новый материал Граф — дерево
Во время прогулки встретились друзья, все пожали друг другу руки, произошло 15 рукопожатий. Сколько мальчиков было.

Рассуждение:
- Если мальчиков ( ) :
1 *
1 – 0 рукопожатий ( ) ,
- 1 – 0 рукопожатий ( ) ,
2 — 1 (0+1=1р)
* 2
6 *
3 – 3 (1+2=3 р)
4 — 6 (3+3=6 р)
5 — 10 (6+4=10 р)
5 *
* 3
6 -15 (10+5=15 р)
* 4
Решение: 0+1+2+3+4+5=15
Ответ: 6 мальчиков.

Двудольные графы
- Задача 2. На школьный вечер отдыха пришли подружки: Белова, Чернова, и Краснова. Они были в платьях белого, чёрного и красного цвета. Но Белова не в белом, Чернова не в чёрном, а Краснова не в красном платье. Девочка в белом говорит: «Чернова, нам надо поменяться платьями». Кто и в каком платье пришёл?
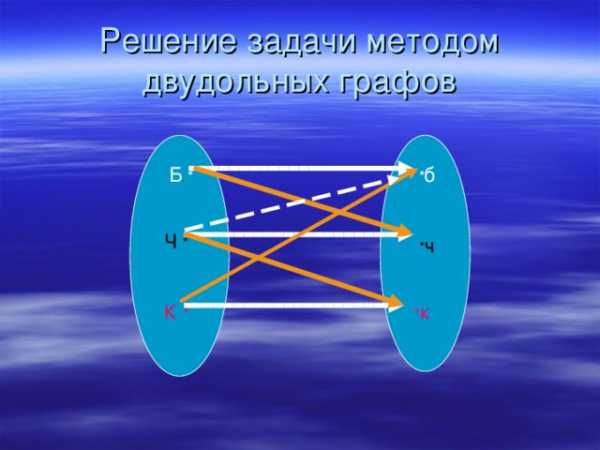
Решение задачи методом двудольных графов
Б *
* б
Ч *
* ч
К *
* к

Ответ:
- Белова в чёрном,
- Чернова в красном,
- Краснова в белом.


Верны ли следующие утверждения?
- 1, 2, 3 — натуральные числа.
- 5,7 – обыкновенная дробь.
- S=a 2 – площадь квадрата
- V=a*b*c – формула площади прямоугольника.
- 0 – натуральное число.
- 0,5 –десятичная дробь.
- 6 2 = 12 – это квадрат числа 6.
- 1% — это 10-я часть.

Самостоятельная работа
- Задача 1. Денис, Коля и Петя взяли с собой в поход: лимонад, сок и минеральную воду. Денис не любил минеральную воду и не пьёт лимонад. Коля не любит лимонад. Кто что взял с собой в поход?
- Задача 2. Первые четыре места по лыжным соревнованиям заняли: Коля, Боря, Вова, и Юра. На вопрос, какие места они заняли, трое из них ответили:
1. Коля: «Ни первое и ни четвёртое»;
2. Боря: «Второе»;
3. Вова: «Не был последним».
Какое место занял каждый из мальчиков?
- Задача 3. В редакцию журнала прислали рассказ, повесть, очерк, стихотворение, фельетон, которые написали Андреев, Борисов, Ветров, Гришин и Денисов. Каждый написал только одно произведение. Ветров думал, что стихотворение сочинил Борисов. Борисов предполагал, что Гришин написал фельетон, а Андреев — повесть. Гришин считал, что Денисов написал повесть, а Ветров – очерк. Андреев думал, что Борисов написал рассказ, а стихотворение сочинил Гришин. В результате оказалось, что они ошибались в своих предположениях.

Ответы для самостоятельной работы
Задача 1: Денис – сок,
Коля – минеральную воду,
Петя – лимонад.
Задача 2: Вова занял – 1 место,
Боря – второе,
Коля – третье,
Юра — четвертое.
Задача 3: Андреев – фельетон,
Борисов – очерк,
Ветров – повесть,
Гришин – рассказ,
Денисов – стихотворение.

Домашнее задание
- Карточки с заданиями
- Учебник: №1718 (1, 4, 7)
№ 1730

Итог урока
- Чем мы сегодня занимались на уроке?
- Какие новые слова вы сегодня узнали на уроке?
- Каким способом мы научились решать задачи?
- Что такое граф-дерево?
- Как выглядит двудольный граф?
- Каким у нас сегодня был урок?

Заключение
- На этом наш урок закончен
- Спасибо за работу!
kopilkaurokov.ru
План-конспект урока по алгебре (5 класс) по теме: Решение задач на движение с помощью графов
УРОК ПО МАТЕМАТИКЕ В 5 КЛАССЕ «РЕШЕНИЕ ЗАДАЧ НА ДВИЖЕНИЕ С ПОМОЩЬЮ ГРАФОВ» учителя математики Шершаковой Татьяны Александровны Энгельс 2012 |
Тема. Решение задач на движение с помощью графов.
Цели. 1. Познакомить учащихся с новым способом решения текстовых задач – «сетевым графом».
2. Работать над развитием математической речи; развивать внимание, наблюдательность.
3. Формировать умение работать в коллективе, помогать друг другу; воспитывать аккуратность при выполнении письменных заданий.
Оборудование: компьютер, проектор, индивидуальные карточки с алгоритмом составления графа.
ХОД УРОКА.
I. ОРГАНИЗАЦИОННЫЙ МОМОЕНТ.
II. СООБЩЕНИЕ ТЕМЫ И ЦЕЛЕЙ УРОКА.
— На уроках информатики мы с вами познакомились с такими понятиями как граф, вершины и ребра графа, граф с направленными ребрами. Сегодня на уроке мы научимся решать задачи на движение с помощью графов. Но вначале урока мы прогуляемся по одному городу.
III. УСТНЫЙ СЧЕТ.
- Сумма 500 и 130?
- Разность 998 и 63?
- Какое число в 5 раз меньше 60?
- Какое число больше 12 в 3 раза?
- Во сколько раз 480 больше 60?
- На машине турист проехал 36 км, что в 2 раза больше того расстояния, которое он прошел пешком. Сколько километров прошел турист пешком? Каким действием решали задачу? Почему?
IV. ОБЪЯСНЕНИЕ НОВОГО МАТЕРИАЛА.
1. Рассказ учителя.
— Есть такой город Калининград (слайд № 2), раньше он назывался Кенигсберг. Через город протекает река Преголя. Она делится на два рукава и огибает остров (слайд № 3). В XYIII веке в городе было семь мостов (рис. 1).
рис. 1
Рассказывают, что однажды житель города спросил у своего знакомого, сможет ли он пройти по всем мостам так, чтобы на каждом из них побывать только один раз и вернуться к тому месту, откуда началась прогулка. Многие горожане заинтересовались этой задачей, однако придумать решения никто не смог. Этот вопрос привлек внимание ученых разных стран. Разрешить проблему удалось известному математику (слайд №4) Леонарду Эйлеру в 1736 году (1707 – 1782, российский математик, швейцарец по происхождению, академик Петербургской и Берлинской академий наук). Причем, он не только решил эту конкретную задачу, но и придумал общий метод решения подобных задач. Эйлер поступил следующим образом: он «сжал» сушу в точки, а мосты «вытянул» в линии. В результате получился граф.
Определение графа. Пусть дано некоторое конечное множество точек и некоторые из них соединены линиями, не обязательно прямыми (рис. 2)
. .
. .
а) б) в) г) д)
рис. 2
Такие схемы или диаграммы называют графами. Схемы, изображенные на рисунке 2, могут представлять собой, например, состояния турнира четырех шахматистов. Участники турнира обозначены точками, которые можно пометить цифрами или буквами, а линии, соединяющие пары точек, обозначают соответствующие партии между шахматистами. Рисунок 2а – состояние перед началом турнира, т.е. жеребьевка; рисунки 2б – г – состоялось три тура; рисунок 2д – сыграны все шесть партий.
У вас на столах лежат рисунки (рис.3), на которых изображена схема, содержащая восемь точек и одиннадцать линий, которая может представлять сеть автомобильных или железнодорожных дорог или каких–нибудь других коммуникаций.
1 1
4 2 2 4 2
3
2 3 3
рис. 3
— Что могут обозначать цифры, обведенные кружочками? (это пункты — города, станции, перекрестки, или какие – либо другие объекты, между которыми существуют связи).
— Что могут обозначать линии, соединяющие пункты? (это могут быть дороги, улицы, провода и т.п.)
— А что могут обозначать цифры на линиях? (могут обозначать протяженность, время, пропускную способность, стоимость и др.)
— Граф – это математическое понятие, суть которого состоит в том, что задано конечное множество вершин и пар вершин. Вершины называют точками или узлами, а пары вершин ребрами или дугами, или линиями.
— Как называется вершина 1? (нечетная, потому что из нее выходит нечётное число ребер)
— Как называется вершина 5? (четная, потому что из нее выходит четное количество ребер)
2. Объяснение учителя.
— Составлять граф мы будем по определенному алгоритму (слайд № 5).
Алгоритм составления графа.
1. О каком процессе идет речь?
2. Какие величины характеризуют данный процесс?
3.Каким соотношением связаны эти величины?
4.Сколько процессов описывается в задаче?
5.Есть ли связь между элементами?
Ответы на эти вопросы записывать будем схематически. Эта схема и будет сетевым графом.
2. Практическая работа.
Задача 1. (слайд № 6)
Путь от станции Балаково до другой товарный поезд прошел за 9 ч, а пассажирский за 6 ч. Найдите скорость пассажирского поезда, если скорость товарного поезда равна 40 км/ч.
1. О каком процессе идет речь? (о движении)
2. Какими величинами он характеризуется? (слайд № 7) (скорость, время, расстояние) Каждую величину обозначим кружком.
S v t
3. Каким соотношением связаны эти три величины? (слайд №7)
S = v · t
S v t
4. Сколько различных процессов описывается? (слайд №7)
Sп vп tп
Sт vт tт
—
5. — Что известно в задаче? (слайд № 8)
— Что вы заметили в этой задаче? (одно и тоже расстояние проходят с различными скоростями два поезда)
В этом случае кружок S будет общий (слайд № 8).
В итоге рассуждений в тетрадях у учащихся должен получиться сетевой граф
S vп tп= 6 ч
vт =40 км/ч tт = 9 ч
Чтобы решить задачу, надо найти значение закрашенных кружков. Каждую линию, в нашем случае их три, будем называть ребром графа. По – какому же принципу мы будем заполнять кружки: имея (зная) два не закрашенных кружка на одном ребре, найти третий, закрашенный. Рассмотрим первое ребро графа. (слайд № 9) По условию задачи мы знаем: vт= 40 км/ч, tт = 9 ч, следовательно, можем найти S. По какой формуле? (слайд № 9) (S = v × t). Чему будет равно S. (S= 40×9 = 360 км) (слайд № 9)
S = 360 км vт= 40 км/ч tт = 9 ч
Рассмотрим второе ребро графа (слайд № 9). S у нас общее, его значение мы уже нашли, tп=6 ч, следовательно можем наитии vп. По какой формуле находим скорость? (v = S : t) (слайд № 9) Чему она будет равна? (v = 360 : 6 = 60 км/ч) (слайд № 9)
S = 360 км vп =60 км/ч tп = 6 ч
В итоге должен получиться вот такой граф (слайд 10):
S = 360 км vп= 60 км/ч tп= 6 ч
vт= 40 км/ч tт = 9 ч
1) 40 × 9 = 360 (км) – расстояние между станциями.
2) 360 : 6 = 60 (км/ч) – скорость пассажирского поезда.
Ответ: 60 км/ч.
Задача 2.
— (слайд № 11) Машина ехала 3 часа со скоростью 65 км/ч и 2 часа со скоростью 60 км/ч. Какой путь пройдет машина за эти 5 часов?
Все записи будем делать простым карандашом. Ученики чертят сетевой граф у себя в тетрадях, один ученик – на доске.
1. О каком процессе идет речь? (о движении)
2. Какими величинами он характеризуется? (скорость, время, расстояние) Каждую величину обозначим кружком.
3. Каким соотношением связаны эти три величины?
4. Сколько различных процессов описывается? (движение со скоростью 65 км/ч и движение со скоростью 60 км/ч)
1 1 1
2 2 2
5. Есть ли связь между одноименными элементами?
S1 v1= 65 км/ч t1= 3ч
S2 v2 = 60 км/ч t2 =2ч
S1 + S2
Элементами являются S1 и S2, V1 и V2, t1 и t2. Закрашиваем кружок величина, которого неизвестна, а кружок с известной величиной оставляем не закрашенным и подписываем его. ( три часа со скоростью 65 км/ч, два часа со скоростью 60 км/ч).
Как узнать, какое расстояние проехала машина за 5 часов? (для этого нужно найти весь путь, который проехала машина; через S1 и S2 проводим линию и завершаем её кружком S1+ S2).
Рассмотрим первое горизонтальное ребро графа. По условию задачи мы знаем: v1= 65 км/ч, t1= 3ч, следовательно, можем найти S1. По какой формуле? (S = v × t). Чему будет равно S1? (S1= 65×3 = 195 км)
S1 = 195 км v1= 65 км/ч t1= 3ч
Рассмотрим второе горизонтальное ребро графа. По условию задачи мы знаем: v2 = 60 км/ч, t2 = 2 ч, следовательно, можем найти S2. По какой формуле? (S = v × t). Чему будет равно S2? (S2 = 60×2 = 120 км)
S2 = 120 км v2 = 60 км/ч t2 = 2 ч
Рассмотрим вертикальное ребро, в котором уже найдены два кружка S1 и S2. Зная два закрашенных кружка на одном ребре, закрасить (найти) третий, т.е. можно найти S1+ S2.
S1 = 195 км
S2 = 120 км
S1+ S2 = 315 км
Находим S1+ S2 = 120 + 195 = 315 км.
— Я то же составила сетевой граф к этой задаче. Давайте сравним его с вашим (слайд № 12).
S1 = 195 км v1= 65 км/ч t1= 3ч
S2 = 120 км v2 = 60 км/ч t2 =2ч
S1 + S2 = 315 км
1) 65 × 3 = 195 (км) – прошла машина за 3 часа.
2) 60 × 2 = 120 (км) – прошла машина за 2 часа.
3) 195 + 120 = 315 (км) – прошла машина за 5 часов.
Ответ: 315 км.
V. ЗАКРЕПЛЕНИЕ.
— А теперь попробуйте самостоятельно решить следующую задачу.
Мотоциклист проехал расстояние от одного города до другого за 3 часа, двигаясь со скоростью 54 км/ч. Сколько времени потребуется мотоциклисту на обратный путь, но уже по другой дороге, если она длиннее первой на 22 км, а его скорость будет меньше прежней на 8 км/ч.
Сетевой граф будет выглядеть следующим образом:
S1=162 км v1=54 км/ч t1 =3 ч
S2 = 184 км v2 = 46 км/ч t2 = 4 ч
S1 2 на 22 км v1 >v2 на 8 км/ч
VI. ИТОГ УРОКА.
— С каким новым способом решения задач на движения мы познакомились сегодня на уроке?
— Что такое сетевой граф? (Граф – это математическое понятие, суть которого состоит в том, что задано конечное множество вершин и пар вершин. Вершины называют точками или узлами, а пары вершин ребрами или дугами, или линиями.)
— Кто впервые построил сетевой граф? (Леонард Эйлер).
nsportal.ru
Семинар ДООМ. Знакомство с графами (5 класс) — ТолВИКИ
Участник: Пенкина Любовь Ивановна
‘Тема: Графы’
Цель:
знакомство с новым способом решения задач повышенной трудности;
развитие логического мышления у учащихся;
воспитание интереса к предмету.
Оборудование:
карточки с задачами;
многогранники: куб, пирамида, додекаэдр;
школьная доска с готовыми рисунками графов.
Ход занятия.
I. Вводная беседа
Сегодня мы с вами познакомимся еще с одним способом решения логических задач. Рассмотрим сначала три задачи:
1. Кто играет Ляпкина-Тяпкина?
В школьном драмкружке решили ставить гоголевского «Ревизора». И тут разгорелся жаркий спор. Все началось с Ляпкина-Тяпкина. - Ляпкиным-Тяпкиным буду я! – решительно заявил Гена. - Нет, я буду Ляпкиным-Тяпкиным, - возразил Дима. – С раннего детства мечтал воплотить этот образ на сцене. - Ну, хорошо, согласен уступить эту роль, если мне дадут сыграть Хлестакова, - проявил великодушие Гена. - …А мне – Осипа – не уступил ему в великодушии Дима. - Хочу быть Земляникой или Городничим, - сказал Вова. - Нет, Городничим буду я, - хором закричали Алик и Боря. – Или Хлестаковым, - добавили они одновременно. Удастся ли распределить роли так, чтобы исполнители были довольны? (Мы не спрашиваем, будут ли довольны зрители.)
2. Сварливые соседи.
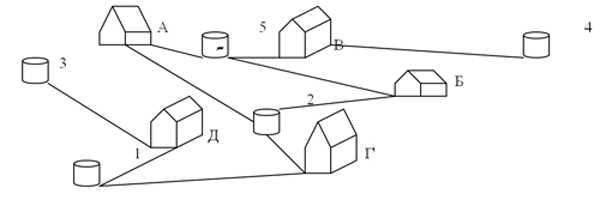
Житель пяти домов поссорились друг с другом и, чтобы не встречаться у колодцев, решили поделить их (колодцы) так,
чтобы хозяин каждого дома ходил к «своему» колодцу по «своей» тропинке. Удастся ли им это сделать?
3. Корзины, полные хлебцов.
В пяти корзинах лежат хлебцы пяти сортов. Хлебцы первого сорта лежат в корзинах Г и Д; хлебцы второго сорта – в корзинах А,
Б и Г; в корзинах А, Б и В имеются хлебцы пятого сорта, в корзине В имеются к тому же хлебцы четвертого сорта, а в корзине
Д – третьего. Требуется дать каждой корзине номер, но так, чтобы в корзине № 1 были хлебцы первого сорта (хотя бы один), в
корзине № 2 – второго и т.д.
II. Обсуждение.
Эти задачи довольно простые. Достойно удивления другое – хотя на первый взгляд эти задачи различны – в одной говорится о
распределении ролей, в другой – о тропинках от домов к колодцам, в третьей – о нумерации корзин с хлебцами, существует
единый подход к решению этих задач, связанный с так называемой теорией графов.
Переведя эти задачи на язык теории графов, вы увидите, что все три задачи превратятся в простенькую задачу «на графы».
Познакомимся с основными понятиями теории графов. Прежде всего, стоит сказать о том, что гра-фы, о которых идет речь, к
аристократам былых времен никакого отношения не имеют. Наши «графы» имеют корнем греческое слово «графо», что
значит «пишу». Тот же корень в словах «график», «биография», «голография»
Понятие графа проще всего выяснить на примере.
‘III. Разбор задач.
4. Первенство классов.
В первенстве класса по настольному теннису принимали участие 6 учеников: Андрей, Борис, Виктор, Галина, Дмитрий и
Елена. Первенство проводится по круговой системе – каждый из участников играет с каждым из остальных один раз. К
настоящему моменту некоторые игры уже проведены: Анд-рей сыграл с Борисом, Галиной и Еленой; Борис, как уже говорилось, с
Андреем и еще с Галиной; Виктор – с Галиной, Дмитрием и Еленой; Галина – с Андреем и Виктором. Сколько игр проведено к
настоящему моменту и сколько еще осталось?О б с у ж д е н и е.
Изобразим данные задачи в виде схемы. Участников будем изображать точками: Андрея –
точкой А, Бориса – точкой Б и т.д. Если двое участников уже сыграли между собой, то будем соединять изображающие их точки
отрезками. Получается схема, показанная на рисунке.
Такие схемы называются графами. Точки А, Б, В, Г, Д называются вершинами графа, соединяющие их отрезки – ребрами графа. Заметьте, что точки пересечения ребер графа не являются его вершинами. Во избежание путаницы вершины графа часто изображают не точками, а кружочками. Ребра зачастую оказывается удобнее изображать не прямолинейными отрезками, а криволинейными – «дугами». Решим нашу задачу. Число игр, проведенных к настоящему моменту, равно числу ребер, т.е. 7. Чтобы найти число игр, которые осталось провести, построим еще один граф с теми же вершинами, но ребрами будем соединять тех участников, которые еще не играли друг с другом. Ребер у этого графа оказалось 8, значит, осталось провести 8 игр.
Графами мы пользуемся довольно часто. Возьмите схему железных дорог: здесь станции – это вершины графа, перегоны (участки пути между станциями) – ребра графа. Вершины и ребра многогранни-ка (куба, пирамиды и т.д.) тоже образуют граф.
IV. Решение первых трех задач
А теперь решим первые три задачи с помощью графов.
Попробуем построить граф для ситуации, описанной в задаче 8.1:
«Кто играет Ляпкина-Тяпкина?» Изобразим юных актеров кружками верхнего ряда:
А — Алик,
Б — Боря,
В — Вова,
Г — Гена,
Д — Дима,
а роли, которые они собираются играть – кружками второго ряда:
1— Ляпкин-Тяпкин,
2 — Хлестаков,
3 — Осип,
4 — Земляника,
5 — Городничий.
Затем от каждого участника проведем отрезки, т. е. ребра, к ролям, которые он хотел бы сыграть.
У нас получится граф с десятью вершинами и десятью ребрами.
Чтобы решить задачу, нужно из десяти выбрать пять ребер, не имеющих общих вершин. Сделать это легко. Достаточно заметить, что в вершины 3 и 4 ведет по одному ребру, из вершин Д и В соответственно. Это означает, что Осипа (вершина 3) должен играть Дима (кто же еще?), а Землянику — Вова. Вершина 1 — Ляпкин-Тяпкин — соединена ребрами с Г и Д. Ребро 1 — Д отпадает, так как Дима уже занят, остается ребро 1 — Г, Ляпкина-Тяпкина должен играть Гена.
Остается соединить вершины А и Б с вершинами 2 и 5, соответствующими ролям Хлестакова и Городничего. Это можно сделать двумя способами: либо выбрать ребра А — 5 и Б — 2, либо ребра А—2 и Б — 5. В первом случае Алик будет играть Городничего, а Боря — Хлестакова, во втором случае наоборот. Как показывает наш граф, других решений задача не имеет.
Постройте теперь графы для второй и третьей задач.
У вас получились те же графы! Теперь вы видите, что вторая и третья
задачи по сути ничем не отличаются от первой. Отметив на этих графах по пять ребер,
не имеющих общих вершин, вы тем самым решите данные задачи.
Возникает вопрос: так ли уж нужны были графы в разобранных задачах?
Разве нельзя прийти к решению чисто логическим путем? Да, можно. Но графы придали условиям наглядность,
упростили решение и выявили сходство задач, превратив три задачи в одну, а это не так уж мало.
А теперь представьте себе задачи, графы которых имеют 100 или более вершин.
А ведь именно такие задачи приходится решать современным инженерам и экономистам. Тут уж без графов не обойтись.
Ceйчас почти в любой отрасли науки и техники встречаешься с графами: в электротехнике — при построении электрических схем,
в химии и биологии — при изучении молекул и их цепочек, в экономике — при решении задач о выборе оптимального пути
для потоков грузового транспорта и во многих других задачах.
О математике и говорить не приходится. С теорией графов связаны не только математические развлечения и головоломки,
но и такие серьезные науки, как теория отношений и теория групп.
И все же теория графов — наука сравнительно молодая: во времена Ньютона такой науки еще не было, хотя и были в
ходу «генеалогические деревья», представляющие собой разновидности графов. Первая работа по теории графов принадлежит
Леонарду Эйлеру, и появилась она в 1736 году в публикациях Петербургской Академии наук.
Начиналась эха работа с рассмотрения следующей задачи:
Задача о кенигсбергских мостах.
Город Кенигсберг (ныне Калининград) расположен на берегах и двух островах реки Прегель (Преголи). Различные части города были соединены семью моста¬ми, как пока-зано на рисунке В воскресные дни горожане совер¬шают прогулки по городу. Можно ли выбрать такой маршрут, чтобы пройти один и только один раз по каждому мосту и потом вернуться в начальную точку пути?
Обсуждение.
Обозначим различные части города буквами А, В, C ,D, а мосты — буквами a,b,c, d, e ,f, g. В этой задаче существенны лишь переходы через мосты: переходя через любой мост, мы всегда из одной части города попадаем в другую, — и, наоборот, переходя из одной части города в другую, мы непременно пройдем по мосту. Поэтому изобразим план города в виде графа, вершины которого А, В, С и D изображают отдельные части города, а ребра а, b9 с, d, e, f, g — мосты, соединяющие соответствующие части города.
Если бы существовал маршрут, удовлетворяющий условию задачи, то существовал бы замкнутый и непрерывный обход этого графа, проходящий один раз по каждому ребру. Иными словами, этот граф можно было бы вычертить, не отрывая карандаша от бумаги и не проходя дважды по одному и тому же ребру. Но это невозможно — какую бы вершину мы ни выбрали за исходную, нам придется проходить через остальные вершины, и при этом каждому «входящему» ребру (мосту, по которому мы вошли в эту часть города) будет соответствовать «выходящее» ребро (мост, которым мы воспользуемся затем, чтобы покинуть эту часть города): число ребер, входящих в каждую вершину, будет равно числу ребер, выходящих из нее, т. е. общее число ребер, сходящихся в каждой вершине, должно быть четным.
Наш граф этому условию не удовлетворяет, и поэтому требуемого маршрута не существует. Если в каждой вершине связного графа сходится четное число ребер, то такой граф называется «эйлеров». Можно доказать, что всякий эйлеров граф допускает непрерывный замкнутый обход (такой путь в теории графов называется ц и к л о м), проходящий по каждому ребру ровно один раз. Из предыдущих рассуждений следует, что граф, не являющийся эйлеровым, такого обхода не допускает.
V. Закрепление полученных навыков решения задач с помощью графов.
1. Сколькими способами можно пройти из А в В, двигаясь по линиям слева направо и сверху вниз?
2. В выходной день Миша решил навестить своих друзей: Алешу, Борю, Витю, Гену, Диму, Женю, Колю, Славу. Он начертил схему взаимного расположения домов, где живут мальчики, и дорог, соеди-няющих их. Посетил он их в следующем порядке: Алеша, Боря, Витя, Гена, Дима, Женя, Коля, Слава. Ус-тановите, какой дом кому принадлежит, если ни к одному из домов Миша не подходил более одного раза, Известно, что Миша живет в доме М, последним он посетил дом R.
3. Задача Леонарда Эйлера. Можно ли совершить прогулку по городу, план которого показан на рисунке, пройдя в точности один раз по каждому из пятнадцати мостов. Возвращаться в начальную точку пути не обязательно. Если такой обход существует, найти его, указав мосты в той последовательности, в которой вы их проходите. Если же такого обхода не может существовать, объясните, почему не может. Постройте граф — план города.
VI. Задание на дом.
1. Решение задач на разрезание
№ 1. Разрезать фигуру на четыре равные части (рис. 1):
№ 2. Пусть фигура состоит из трех равных квадратов, расположенных так, как показано на рис. 2. Вырезать из этой фигуры такую часть, чтобы приложив ее к оставшейся части, получить квадрат, внутри которого имеется квадратное отверстие.
№ 3. Квадрат с вырезанной «четвертушкой» легко разрезать на четыре равные части (см. рис. 1). А сможете ли вы разрезать сам квадрат на пять равных частей?
№ 4. На коврике изображено семь роз. Требуется тремя прямыми линиями разрезать коврик на семь частей, каждая из которых содержала бы по одной розе (рис. 3).
№ 5. Произвольный треугольник АВС разрезать на три части – такие, чтобы из них можно было со-ставить прямоугольник.
№ 6. Изображенную на рис. 4 фигуру требуется разделить на шесть частей, проведя всего лишь две прямые. Попытайтесь это сделать.
VII. Итог занятия.
Итак, сегодня мы познакомились еще с одним из способов решения задач. Таким образом, чтобы ответить на вопрос задачи, нужно найти наиболее оптимальный способ решения.
wiki.tgl.net.ru
