Задачи на множества круги эйлера: описание, примеры, для дошкольников, для школьников

Множества и операции над ними. Решение задач с помощью кругов Эйлера

1. Презентация «Множества и операции над ними. Решение задач с помощью кругов Эйлера»

Автор: учитель математики
МОУ ООШ с. Цепочкино
Саламатова А. Г.
Множества
Множество – совокупность объектов,
объединенных по какому – нибудь признаку.
Множества обозначают большими буквами
латинского алфавита: А, В, С, D и т. д.
Обозначения некоторых числовых множеств:
N – множество натуральных чисел;
Z – множество целых чисел;
Q – множество рациональных чисел;
I — множество иррациональных чисел;
R – множество действительных чисел.

4. Виды множеств

• Равные множества
{А, Е, Ё, И, О, У, Ы, Э, Ю, Я} = {Э, Е, А, Ё, Я, О, Ы, И, У, Ю}
• Конечные множества
А = {2; 3; 5; 7; 11; 13};
{х | 5< х <12}
• Бесконечные множества
{1; 4; 9; 16; 25; …}; {10; 20; 30; 40; 50; …};
• Пустое множество обозначается символом Ø
4

5. Множества

Задание 1
1) Задайте множество цифр, с помощью которых
записывается число:
а) 3254; б) 8797; в) 11000; г) 555555.
2) Задайте множество А описанием:
а) А = {1, 3, 5, 7, 9}; б) А = {- 2, — 1, 0, 1, 2};
в) А = {11, 22, 33, 44, 55, 66, 77, 88, 99};
г) А = {0,1; 0,01; 0,001; 0,0001; …};
д) А = {1/2, 2/3, 3/4, 4/5, … }.
3) Задание с выбором ответа. Даны множества: М = {5,4,6},
Р = {4,5,6}, Т = {5,6,7}, S = {4, 6}.
Какое из утверждений неверно?
а) М = Р. б) Р ≠ S. в) М ≠ Т. г) Р = Т.
5

6. Стандартные обозначения

х
А
— знак принадлежности.
«элемент х принадлежит множеству А»;
«х – элемент множества А».
5 N
«5 – число натуральное».
Наряду со знаком принадлежит используют и его
«отрицание» — знак
.
х
А
«элемент х не принадлежит множеству А».
0 N
«нуль не натуральное число»
6

7. Стандартные обозначения

Задание 2
1. Запишите на символическом языке следующее
утверждение:
а) число 10 – натуральное;
б) число – 7 не является натуральным;
в) число – 100 является целым;
г) число 2,5 – не целое.
2. Верно ли, что:
а) – 5 N; б) -5 Z; в) 2,(45) Q?
3. Верно ли, что:
а) 0,7 {х | х2 – 1 < 0}; б) – 7 {х | х2 + 16х ≤ — 64}?
7

8. Стандартные обозначения

А = {2; 4; 6} и В = {1; 2; 3; 4; 5; 6; 7}.
А
В
«множество А является подмножеством множества В».
Знак « » называют знаком включения.
Пустое множество считают подмножеством любого
множества.
8

9. Стандартные обозначения

Задание 3
1. Даны множества:
А = {10}, В = {10, 15}, С = {5, 10, 15}, D = {5, 10, 15, 20}.
Поставьте вместо … знак включения ( или ) так,
чтобы получилось верное утверждение:
а) А … D; б) А … В; в) С … А; г) С … В.
2. Даны три множества А = {1, 2, 3, …, 37}, В = {2, 4, 6, 8, …},
С = {4, 8, 12, 16, …, 36}.
Верно ли, что:
а) А В; б) В С; в) С
А; г) С В?
9

10. Операции над множествами

1) Пересечением множества А и В называют множество,
состоящие из всех общих элементов множеств А и В.
Пересечение множеств А и В обозначают так: А∩В.
Можно записать и так: А∩В = {х | х А и х В}.
Например,
если А = {3; 9; 12} и В = {1; 3; 5; 7; 9; 11}, то А∩В = {3; 9};
если А = {10; 20; …; 100} и В = {6; 12; 18;…}, то А∩В = {30; 60; 90}.
10

11. Операции над множествами

Задание 4
1. Даны множества: А = {2; 3; 8}, В = {2; 3; 8; 11},
С = {5; 11}.
Найдите: 1) А∩В; 2) А∩С; 3) С∩В.
2. Даны множества: А – множества всех натуральных
чисел, кратных 10, В = {1; 2; 3;…, 41}.
Найдите А∩В.
3. Даны множества: А = {a, b, c, d}, B = {c, d, e, f},
C = {c, e, g, k}. Найдите (А∩В)∩С.
11

12. Операции над множествами

2) Объединением множеств А и В называют множество,
состоящее из всех элементов, которые принадлежат хотя
бы одному из этих множеств.
Объединение множеств А и В обозначают так: АUВ.
Можно записать и так: АUВ = {х | х А или х В}.
Например,
если А = {3; 9; 12} и В = {1; 3; 5; 7; 9; 11},
то АUВ = {1; 3; 5; 7; 9; 11; 12}.
12

13.

Операции над множествамиЗадание 5
1. Даны множества: А = {2; 3; 8}, В = {2; 3; 8; 11}, С = {5; 11}.
Найдите: 1) АUВ; 2) АUС; 3) СUВ.
2. Даны множества: А = {a, b, c, d}, B = {c, d, e, f},
C = {c, e, g, k}.
Найдите (АUВ)UС.
13

14. Операции над множествами

3) Разность А и В это множество элементов А, не
принадлежащих В.
Разность А и В обозначают так: А\ В.
Например, если А = {2; 4; 6; 8; 10} и В = {5; 10; 15; 20},
то А\ В={2; 4; 6; 8}.
14

15. Операции над множествами

4) Дополнение множества А обозначают так: Ā.
Дополнение множества до множества К: Ā = К\А.
Например, если А = {3; 6; 9; 12} и К = {1; 2; 3; 4; 5; 6; …},
то Ā = {1; 2; 4; 5; 7; 8; 10; 11; 13; …}.
15

16. Решение задач с помощью кругов Эйлера

ЭЙЛЕР Леонард (1707-1783),
российский ученый — математик,
механик, физик и астроном.
16

17. Решение задач с помощью кругов Эйлера

Задача 1
Расположите 4 элемента в двух множествах так, чтобы в
каждом из них было по 3 элемента.
17

18. Решение задач с помощью кругов Эйлера

Задача 2
Множества А и В содержат соответственно 5 и 6 элементов,
а множество А ∩ В – 2 элемента. Сколько элементов в
множестве А U В?
18

19. Решение задач с помощью кругов Эйлера

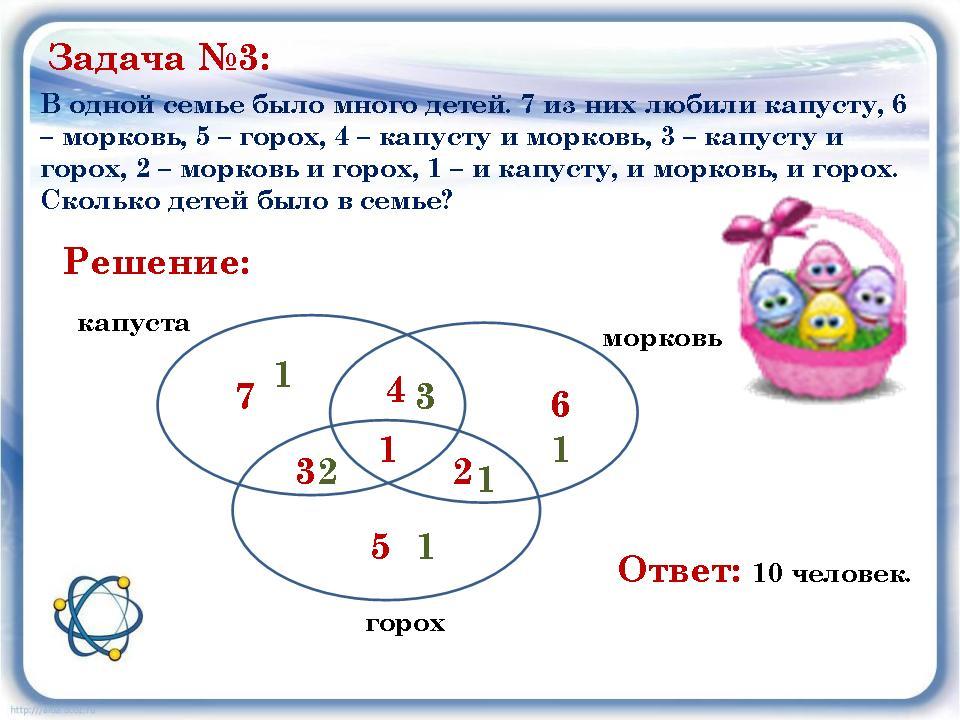
Задача 3
Каждая семья, живущая в нашем доме, выписывает или
газету, или журнал, или и то и другое вместе. 75 семей
выписывают газету, а 27 семей выписывают журнал и лишь
13 семей выписывают и журнал, и газету. Сколько
семей живет в нашем доме?
19

20. Решение задач с помощью кругов Эйлера

Задача 4
На школьной спартакиаде каждый из 25 учеников 9 –го
класса выполнил норматив или по бегу, или по прыжкам в
высоту. Оба норматива выполнили 7 человек, а 11 учеников
выполнили норматив по бегу, но не выполнили норматив
по прыжкам в высоту. Сколько учеников выполнили
норматив: а) по бегу; б) по прыжкам в высоту; в) по
прыжкам при условии, что не выполнен норматив по бегу?
20

21.

Решение задач с помощью кругов ЭйлераЗадача 5
Из 52 школьников 23 собирают значки, 35 собирают марки,
а 16 – и значки, и марки. Остальные не увлекаются
коллекционированием. Сколько школьников не
увлекаются коллекционированием?
21

22. Решение задач с помощью кругов Эйлера

Задача 6
Каждый из учеников 9-го класса в зимние каникулы ровно
два раза был в театре, посмотрев спектакли А, В или С. При
этом спектакли А, В, С видели соответственно 25, 12 и 23
ученика. Сколько учеников в классе?
22

23. Решение задач с помощью кругов Эйлера

Задача 7
В воскресенье 19 учеников нашего класса побывали в
планетарии, 10 – в цирке и 6 – на стадионе. Планетарий и
цирк посетили 5 учеников; планетарий и стадион-3; цирк и
стадион -1. Сколько учеников в нашем классе, если никто не
успел посетить все три места, а три ученика не посетили ни
одного места?
23

24. Решение задач с помощью кругов Эйлера

Задача 8
В одном классе 25 учеников. Из них 7 любят груши,
11 – черешню. Двое любят груши и черешню; 6 – груши и
яблоки; 5 – яблоки и черешню. Но есть в классе два ученика,
которые любят всё и четверо таких, что не любят фруктов
вообще. Сколько учеников этого класса любят яблоки?
24

25. Решение задач с помощью кругов Эйлера

Задача 9
На уроке литературы учитель решил узнать, кто из 40
учеников 9 –го класса читал книги А, В, С. Результаты
опроса выглядели так: книгу А прочитали 25 учеников,
книгу В – 22 ученика, книгу С – 22 ученика; одну из книг А
или В прочитали 33 ученика, одну из книг А или С
прочитали 32 ученика, одну из книг В или С – 31 ученик.
Все три книги прочитали 10 учеников.
Сколько учеников:
а) прочитали только по одной книге;
б) прочитали ровно две книги;
в) не прочили ни одной из указанных книг?
25

26. Решение задач с помощью кругов Эйлера

Задача 9. Решение:
а)
Ответ: 15 учеников
б)
в)
Ответ: 12 учеников
Ответ: 3 ученика
26

27.

Решение задач с помощью кругов ЭйлераЗадача 10
На зимних каникулах из 36 учащихся класса только двое
просидели дома, а 25 ребят ходили в кино, 15 – в театр,
17 – в цирк. Кино и театр посетили 11 человек, кино и
цирк – 10, театр и цирк – 4.
Сколько ребят побывало и в кино, и в театре, и в цирке?
27
Литература
[1] Алгебра, 9 класс. В 2 ч. Ч. 2. Задачник для учащихся
общеобразовательных учреждений
/ [А. Г. Мордкович, Л.А. Александрова и др.] -12-е изд.,
испр. — М.: Мнемозина, 2010.
[2] Занимательная математика. 5 – 11 классы. Авт.- сост.
Т.Д. Гаврилова. – Волгоград: Учитель, 2005. – 96 с.
[3] Математика 6 класс: учеб. для общеобразоват.
учреждений / Г.В. Дорофеев, И.Ф.
Шарыгин, С.Б. Суворова и др./; под ред. Г.В. Дорофеева,
И.Ф. Шарыгина; Рос. акад. наук, Рос. акад. образования,
изд-во «Просвещение». – 11 –е изд. — М.: Просвещение,
2010. – 303 с.: ил.
28

Как решать задачи на множества для 4-5 класса.

Задачи с решениями онлайн

Множество — это группа предметов (людей, понятий) с общими свойствами и собранных вместе. Предметы любого множества называют элементами множества.

Лучше всего знакомство со множествами начать с решения простых задач.

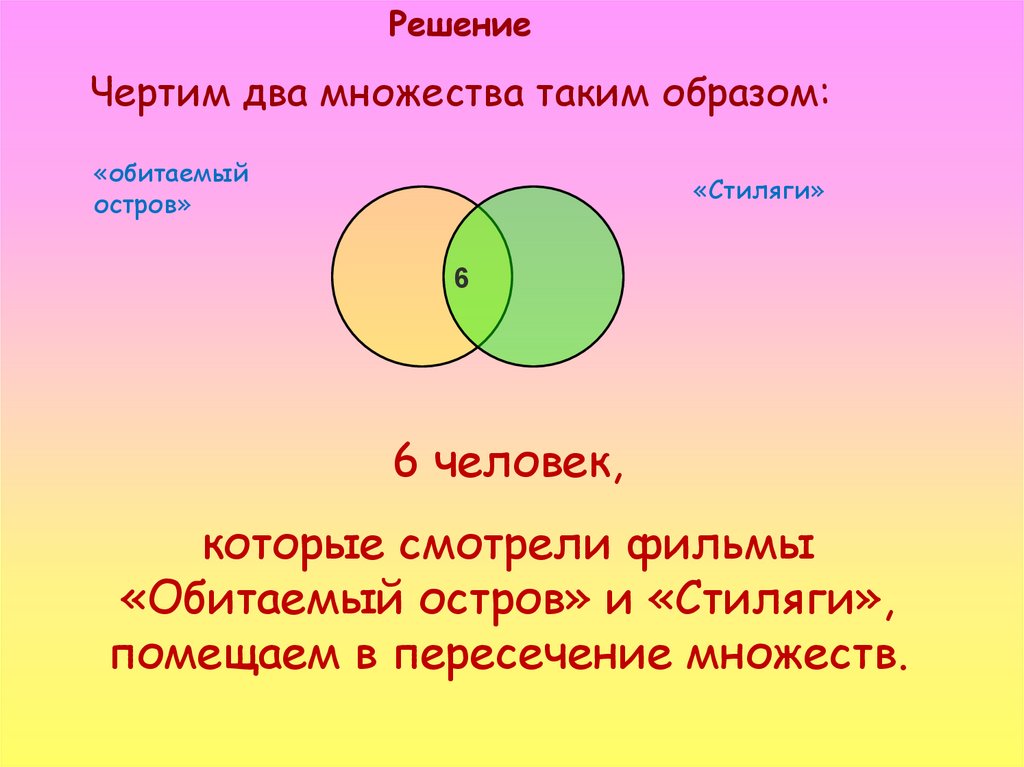
Задача 1. На выходных ученики ходили в кино. 20 из них посмотрели фильм «Завод», 13 смотрели фильм «Хеллбой» из них 8 посмотрели оба фильма. Сколько учеников посмотрело только фильм «Завод»?

Для решения этой задачи нам помогут круги Эйлера. С помощью этих кругов можно показать отношения между каким-либо множеством и его частью. Леонард Эйлер, в честь которого названы эти круги — это швейцарский, немецкий и российский математик и механик, внёсший фундаментальный вклад в развитие этих наук. Он родился в Швейцарии, но почти половину жизни провёл в России, поэтому он считается не только швейцарским математиком, но и российским.

Нарисуем схему:

Круг «Хеллбой» — те, кто посмотрели этот фильм.

Над ним число 13 — количество посмотревших.
Круг «Завод» — те, кто посмотрел фильм «Завод». Над ним число 20 — количество посмотревших.

Эти круги пересекаются и в месте пересечения число 8 — количество тех, кто посмотрел оба этих фильма. Это число 8 входит и в число 13 — посмотревших «Хеллбой», и в число 20 — посмотревших «Завод».

Из схемы хорошо видно, что посмотревшие только фильм «Завод», и не посмотревшие фильм «Хеллбой» — находятся в заштрихованной зоне круга «Завод». В эту зону не входят те 8 человек, которые посмотрели и «Хеллбой» и «Завод».

Таким образом, эта задача решается в одно действие: из 20 человек, посмотревших «Завод», надо вычесть 8 человек, которые посмотрели и «Завод» и «Хеллбой», и тем самым мы получим число тех, кто посмотрел только «Завод».

20 — 8 = 12 человек

Ответ: 12 человек

Хотите, чтобы ваш ребёнок обучался самостоятельно?
Вам поможет наш ВИДЕОКУРС

Задача 2. В овощной магазин за 1 час зашло 20 человек. Из них 12 купили картошку, 5 – лук, 7 не купили ничего. Сколько человек купили и картошку и лук?

Как вы уже наверное поняли из предыдущей задачи, такого рода задачи можно решить и без рисования кругов Эйлера.

Решение

1. Найдём общее число покупателей. Для этого из тех 20 человек, которые зашли в магазин, вычтем те 7 человек, которые ничего не купили.

20 – 7 = 13

2. Найдём число тех, кто купил только лук
Для этого из 13-ти купивших вычтем 12 человек, которые купили картошку. Останутся те люди, которые купили только лук и не купили картошку.

13 – 12 = 1

3. Найдём число тех, кто купил и картошку и лук

В множество тех людей, кто купил лук, входят те, кто купил и картошку и лук и те, кто купил только лук.

Число тех, кто купил только лук, мы нашли во втором действии — это 1 чеовек.

5 – 1 = 4 — число тех, кто купил и картошку и лук.

Ответ: 4

Задача 3. В классе 27 учеников. Из них 16 занимаются плаванием, 10 – футболом, а 5 не занимаются ни тем, ни другим. Сколько футболистов ходит ещё и на плавание?

Решение

Для решения этой задачи нарисуем круги Эйлера, хотя задачу можно решить и без них.

Буквой «П» обозначим множество тех, кто занимается плаванием, буквой «Ф» — тех, кто занимается футболом. П+Ф — те, кто занимаются и плаванием и футболом.

ВИДЕОКУРС 2plus2.online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов

в 5-й класс физматшколы.

Если мы вычтем из общего числа учеников (27) число тех, кто не занимается ни плаванием, ни футболом, то мы получим число тех, кто занимаются плаванием, футболом или и тем и другим.

1. Найдём число учеников, которые занимаются плаванием, футболом или и тем и другим
27 – 5 = 22

2. Найдём количество футболистов, которые не ходят на плавание

22 – 16 = 6

3. Найдём количество футболистов, которые ходят ещё и на плавание

В предыдущем действии мы наши число учеников, которые занимаются только футболом.
Таким образом, чтобы найти число учеников, которые занимаются и футболом, и плаванием, надо из общего числа футболистов вычесть тех, кто занимается только футболом (6).

10 – 6 = 4

Ответ: 4

Комбинаторика

— Почему нельзя построить диаграмму Венна для наборов $4+$ с помощью кругов?

спросил 12 лет, 8 месяцев назад

Изменено 2 года, 1 месяц назад

Просмотрено 82к раз

$\begingroup$

На этой странице приведены несколько примеров диаграмм Венна для наборов по $4$. Некоторые примеры:

Если немного подумать, то невозможно разбить плоскость на $16$ сегментов, необходимых для полной диаграммы Венна с $4$-множеством, используя только круги, как мы могли бы сделать для $<4$-множеств.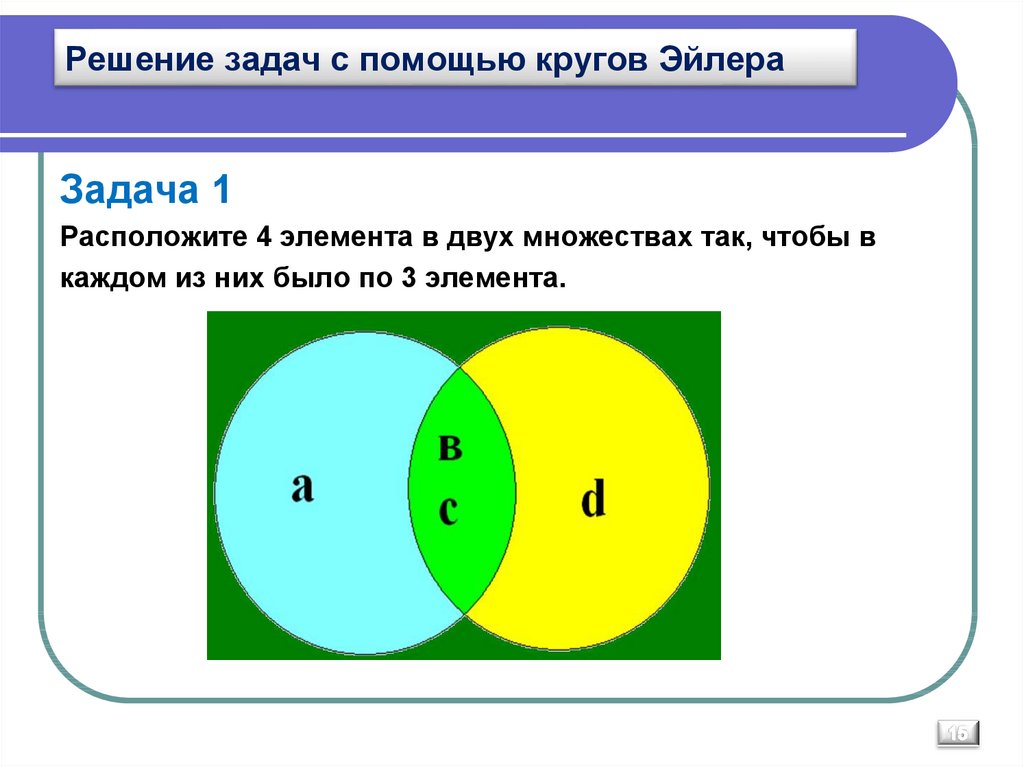 Тем не менее, это выполнимо с эллипсами или прямоугольниками, поэтому нам не нужны невыпуклые формы, как использует Эдвардс.

Итак, какие свойства формы определяют ее пригодность для диаграмм Венна с $n$-множеством? В частности, почему круги недостаточно хороши для случая $n=4$?

• комбинаторика
• геометрия
• логика
• круги

$\endgroup$

7

$\begingroup$

Краткий ответ из статьи Фрэнка Раски, Карлы Д. Сэвидж и Стэна Вагона выглядит следующим образом:

… невозможно нарисовать диаграмму Венна с кружками, которые будут представлять все возможные пересечения четырех (или более) множеств. Это простое следствие того факта, что окружности могут пересекаться не более чем в двух точках, и соотношения Эйлера F − E + V = 2 для количества граней, ребер и вершин плоского графа.

В той же статье довольно подробно описан процесс создания диаграмм Венна для более высоких значений

n , особенно для простых диаграмм с вращательной симметрией.

Для простого резюме лучший ответ, который я смог найти, был на WikiAnswers:

Две окружности пересекаются не более чем в двух точках, и каждое пересечение создает одну новую область. (Двигаясь по кругу по часовой стрелке, кривая от каждого пересечения до следующего делит существующий регион на два.) 94 = 16 регионов для представления всех возможных взаимосвязей между четырьмя наборами.

Но вы можете создать диаграмму Венна для четырех наборов с четырьмя эллипсами, потому что два эллипса могут пересекаться более чем в двух точках.

Оба этих источника указывают, что критическим свойством формы, которое делает ее подходящей или непригодной для диаграмм Венна более высокого порядка, является количество возможных пересечений (и, следовательно, подобластей), которые можно сделать, используя два одинаковых форма.

Чтобы проиллюстрировать далее, рассмотрим некоторые сложные формы, используемые для n =5, n =7 и n =11 (из Wolfram Mathworld):

Структура этих форм выбрана таким образом, что они могут пересекаться друг с другом столькими различными способами, сколько необходимо для создания количества уникальных областей, необходимых для данного n .

См. также: Диаграммы Венна ограничены тремя или меньшим числом наборов?

$\endgroup$

0

$\begingroup$

К нашему удивлению, мы обнаружили, что стандартное доказательство того, что вращательно-симметричная $n$-диаграмма Венна невозможна, когда $n$ не простое число, неверно. Итак, мы с Питером Уэббом нашли и опубликовали правильное доказательство, устраняющее ошибку. Все подробности обсуждаются в статье

Стэна Вагона и Питера Уэбба, Симметрия Венна и простые числа: новое соблазнительное доказательство, American Mathematical Monthly, август 2008 г. , стр. 645–648.

Все это мы обнаружили после длинной статьи с Savage et al. процитировано в другом ответе.

$\endgroup$

2

$\begingroup$

Теорема:

Диаграмма Венна из n множеств не может быть создана с кругами для $n \geq 4$.

Доказательство: Допустим, это возможно. Затем мы можем создать планарный граф $G$ из диаграммы Венна, разместив вершины на каждом пересечении, например:0005

$\small\text{(пример для 3-х множественной диаграммы Венна)}$

Покажем, что построенный таким образом граф из 4-х множественной диаграммы Венна не может быть плоским — противоречие.

Утверждение: Каждая пара окружностей пересекается в двух различных точках.

Предположим, что нет. Тогда есть пара окружностей, внутренности которых не пересекаются. Этого не может быть, поскольку мы требуем, чтобы граф диаграммы Венна имел грань для каждого попарного пересечения множеств. n \text{лиц.}$$ 9n- 2{n\выбрать 2}\leq2,$$ что приводит к явному противоречию при $n = 4$. Чтобы получить единицу для $n>4$, заметьте, что если бы существовала такая диаграмма Венна для некоторого $n > 4$, мы могли бы убрать из диаграммы кружки, чтобы получить диаграмму для $n=4$.

---

Следующее является хорошим ресурсом для более глубокого изучения комбинаторики диаграмм Венна: http://www.combinatorics.org/files/Surveys/ds5/VennEJC.html

$\endgroup$

5

$\begingroup$

Я сильно опоздал на вечеринку, но я хотел бы добавить очень простой, но гораздо менее строгий ответ для разнообразия.

Каждая область диаграммы Венна должна представлять некоторую комбинацию истинности или ложности для каждой категории. Например, диаграмма Венна с двумя кругами имеет 4 области: пересечение, внешнюю сторону и две последние части окружности. Пересечение содержит все, что верно для обеих категорий, вне ни одной из категорий, а последние две только для одной из двух категорий. (Вы можете перечислить их как TT, TF, FT, FF) 9n$ разделов. Каждая новая категория, которую мы добавляем, удваивает количество регионов, поскольку она должна разделить каждый существующий регион на 2 меньших региона. (Один для истинного случая новой категории, другой для ложного, поэтому область ТТ теперь разделена на ТТТ и ТТФ)

Мы видим, как третий круг пересекает все 4 региона, но нет возможности нарисовать 4-й круг, который пересекает все 8 новых регионов, что делает невозможным построение 4-х окружной диаграммы Венна.

$\endgroup$

0

Диаграммы типов Венна и Эйлера для векторных пространств и абелевых групп

Популярный способ визуализации взаимосвязей между некоторым конечным числом множеств — это диаграммы Венна или, в более общем случае, диаграммы Эйлера. На этих диаграммах множество изображается в виде двумерной формы, такой как диск или прямоугольник, и различные логические отношения между этими множествами (например, то, что одно множество содержится в другом, или что пересечение двух множеств равен трети) представлен булевой алгеброй этих форм; Диаграммы Венна соответствуют случаю, когда множества находятся в «общем положении» в том смысле, что все нетривиальные булевы комбинации множеств непусты. Например, чтобы изобразить общую ситуацию двух множеств вместе с их пересечением, можно использовать диаграмму Венна, такую ​​как

(где мы обозначили каждую область разным цветом и немного отодвинули края каждой области друг от друга, чтобы сделать их видимыми по отдельности), но если бы кто-то хотел вместо этого изобразить ситуацию, в которой пересечение было пустым , можно было бы использовать диаграмму Эйлера, такую ​​как

Можно использовать площадь различных областей на диаграмме Венна или Эйлера в качестве эвристического заместителя мощности (или меры) множества, соответствующего такой области.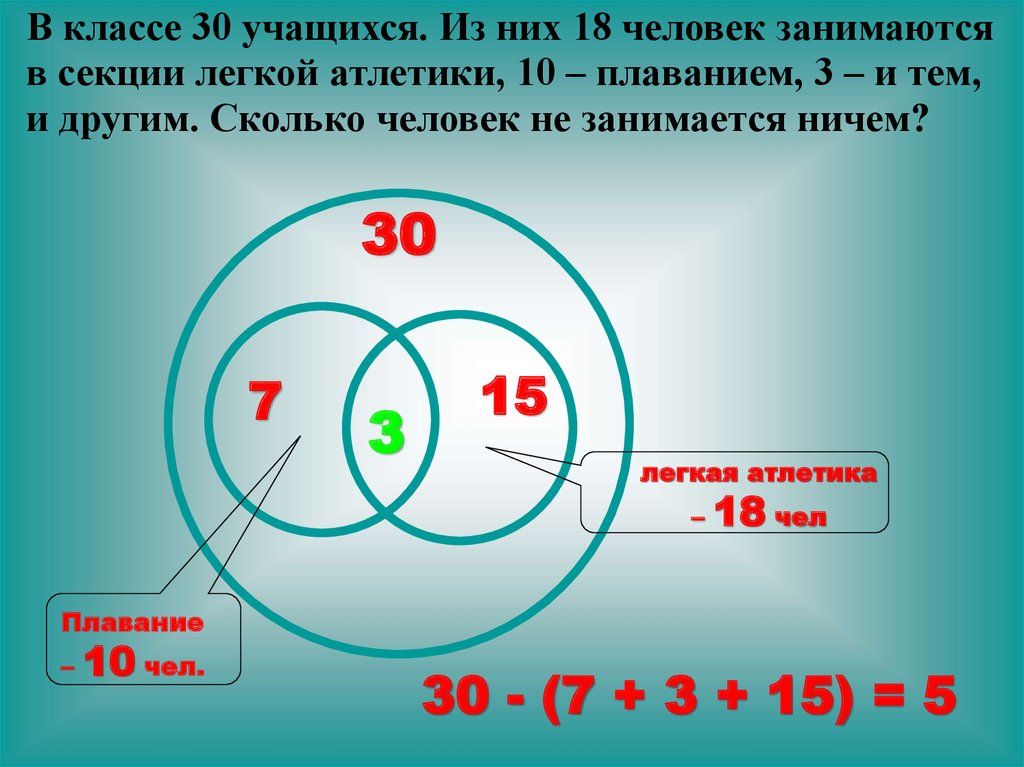 Например, приведенную выше диаграмму Венна можно использовать для интуитивного обоснования формулы включения-исключения 9.0005

для конечных множеств, в то время как приведенная выше диаграмма Эйлера аналогичным образом оправдывает частный случай

для конечных непересекающихся множеств.

Хотя диаграммы Венна и Эйлера традиционно двумерны по своей природе, ничто не мешает использовать одномерные диаграммы, такие как

или даже трехмерные диаграммы, такие как эта из Википедии:

Конечно, в таких случаях можно было бы использовать длину или объем в качестве эвристического показателя мощности или меры, а не площади.

С добавлением стрелок диаграммы Венна и Эйлера также могут вмещать (в некоторой степени) функции между наборами. Вот, например, изображение функции, изображение этой функции и изображение некоторого подмножества:

Здесь можно проиллюстрировать сюръективность, заполнив все ; аналогичным образом можно проиллюстрировать инъективность, задав точно такую ​​​​же форму (или, по крайней мере, ту же площадь), что и . Вот, например, как можно проиллюстрировать инъективную функцию:

Декартовы операции произведения могут быть включены в эти диаграммы с помощью соответствующих комбинаций одномерных и двумерных диаграмм. Вот, например, диаграмма, иллюстрирующая тождество:

В этом сообщении блога я хотел бы предложить аналогичное семейство диаграмм для иллюстрации отношений между векторными пространствами (над фиксированным базовым полем, таким как вещественные числа) или абелевыми группами , а не множествами. Категории (-)векторных пространств и абелевых групп во многом очень похожи; первая состоит из модулей над базовым полем, а вторая состоит из модулей над целыми числами; кроме того, обе категории являются основными примерами абелевых категорий. Понятие размерности векторного пространства во многом аналогично понятию мощности множества; см. этот предыдущий пост для примера этой аналогии (в контексте энтропии Шеннона). (ОБНОВЛЕНИЕ: я узнал, что по существу идентичная запись была также предложена в неопубликованной рукописи Рави Вакиля. )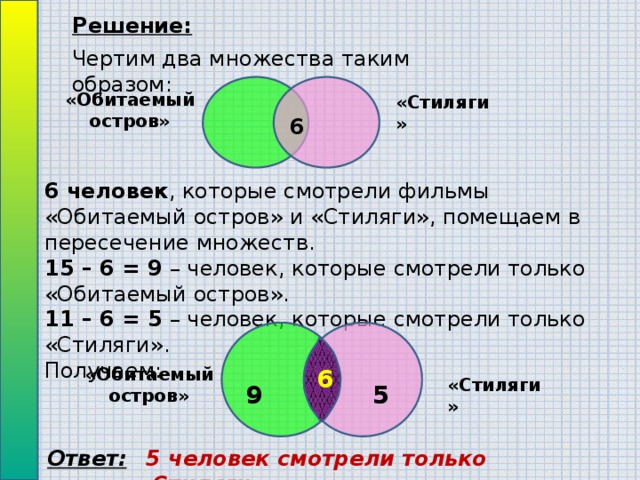

Как и в случае с диаграммами Венна и Эйлера, диаграммы, которые я предлагаю для векторных пространств (или абелевых групп), могут быть построены в любом измерении. Для простоты начнем с одного измерения и ограничимся векторными пространствами (ситуация для абелевых групп в основном идентична). В этой одномерной модели мы сможем изобразить следующие отношения и операции между векторными пространствами:

• Включение одного векторного пространства в другое (здесь я предпочитаю использовать для включения групповое обозначение, а не множество).
• Фактор векторного пространства по подпространству .
• Линейное преобразование между векторными пространствами, а также ядром, образом, коядром и кообразом.
• Одна короткая или длинная точная последовательность между векторными пространствами.
• (эвристический аналог) размерности векторного пространства.
• Прямая сумма двух пробелов.

Идея состоит в том, чтобы использовать полуоткрытые интервалы в реальной прямой для любого моделирования векторных пространств. Фактически мы можем сделать явное соответствие: отождествим каждый полуинтервал с (бесконечномерным) векторным пространством

то есть отождествляется с пространством непрерывных на отрезке функций, обращающихся в нуль на правом конце. Такие функции непрерывно продолжаются нулем до полупрямой.

Обратите внимание, что если тогда векторное пространство является подпространством , если мы продолжим функции в обоих пространствах нулем до полупрямой ; кроме того, частное естественно отождествляется с . Таким образом, включение , как и факторпространство , здесь можно смоделировать следующим образом:

Напротив, если , значительно менее «естественно» рассматривать его как подпространство ; это можно было бы сделать, расширив функции справа нулем и слева константами, но в этом соглашении об обозначениях следует рассматривать такое отождествление как «искусственное», и его следует избегать.

Все пространства бесконечномерны, но с моральной точки зрения размерность векторного пространства «пропорциональна» длине соответствующего интервала.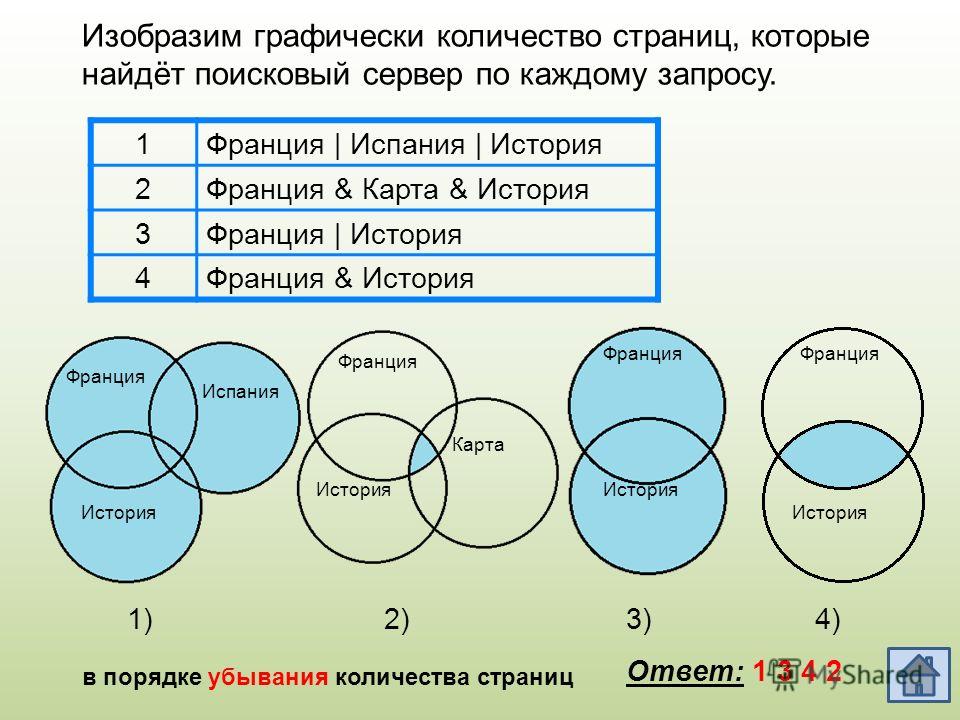 Интуитивно, если мы попытаемся дискретизировать это векторное пространство путем выборки в некоторой сетке интервалов , можно получить конечномерное векторное пространство размерностью примерно . Уже на приведенной выше диаграмме теперь изображена основная идентичность

между конечномерным векторным пространством, подпространством этого пространства и фактором этого пространства.

Обратите внимание, что если , то существует линейное преобразование из векторного пространства в векторное пространство, которое берет функцию в , ограничивает ее до , а затем расширяет ее нулем до . Ядро этого преобразования есть , образ (изоморфен) , коядро (изоморфно) , а кообраз (изоморфен) . Имея это в виду, теперь мы можем изобразить общее линейное преобразование и связанные с ним пространства с помощью следующей диаграммы:

Обратите внимание, как первая теорема об изоморфизме и теорема об отсутствии ранга эвристически иллюстрируются этой диаграммой. Можно специализироваться на случае инъективных, сюръективных или биективных преобразований, вырождая один или несколько полуоткрытых интервалов на приведенной выше диаграмме в пустой интервал. Сдвиг влево порождает нильпотентное линейное преобразование от самого себя:

В том же духе короткая точная последовательность векторных пространств (или абелевых групп) теперь может быть изображена диаграммой

и длинную точную последовательность можно аналогичным образом изобразить диаграммой

ОБНОВЛЕНИЕ: как я узнал из неопубликованной рукописи Рави Вакиля, это обозначение также может легко изображать группы когомологий коцепного комплекса с помощью диаграммы

и аналогичным образом изобразить группы гомологии цепного комплекса диаграммой

Можно связать несвязное объединение полуоткрытых интервалов с прямой суммой связанных векторных пространств, что дает возможность изображать прямые суммы с помощью этого обозначения:

Чтобы увеличить выразительность этой записи, мы теперь перейдем к двум измерениям, где мы также можем изобразить следующие дополнительные отношения и операции:

• Пересечение и сумма двух подпространств объемлющего пространства ;
• Несколько коротких или длинных точных последовательностей;
• Тензорное произведение двух векторных пространств.

Здесь мы заменяем полуоткрытые интервалы полуоткрытыми множествами: геометрическими фигурами, такими как многоугольники или диски, которые содержат часть границы (нарисованы сплошными линиями), но пропускают часть границы (нарисованы пунктирными линиями). . Каждая такая форма может быть связана с векторным пространством, а именно с непрерывными функциями, обращающимися в нуль на пропущенной части границы. Все отношения, которые раньше изображались с помощью одномерных диаграмм, теперь можно аналогичным образом изобразить с помощью двумерных диаграмм. Например, вот двумерное изображение векторного пространства, подпространства и его частного:

(В этом посте я попытаюсь последовательно сделать нижнюю и левую границы этих областей закрытыми, а верхнюю и правую — открытыми, хотя это не обязательно для применимости этого обозначения.)

Но теперь мы можем изобразить некоторые дополнительные отношения. Вот, например, один из способов изобразить пересечение и сумму двух подпространств:

Обратите внимание, как это иллюстрирует тождество

. между конечномерными векторными пространствами , а также некоторыми стандартными изоморфизмами, такими как .

Две конечные подгруппы абелевой группы называются соизмеримыми , если является подгруппой с конечным индексом группы . Это можно изобразить, сделав область между и маленькой и/или окрашенной в определенный цвет:

Здесь соизмеримость эквивалентна конечности групп и , которые соответствуют серым треугольникам на приведенной выше диаграмме. Теперь, например, становится интуитивно понятно, почему соизмеримость должна быть отношением эквивалентности.

Чтобы проиллюстрировать, как эта нотация может поддерживать несколько коротких точных последовательностей, я дал себе задание использовать эту нотацию для изображения леммы о змее, как показано на этой следующей диаграмме, взятой из только что связанной страницы Википедии:

Это оказалось чрезвычайно сложно выполнить без введения вырождений (например, исчезновение одного из ядер или коядер).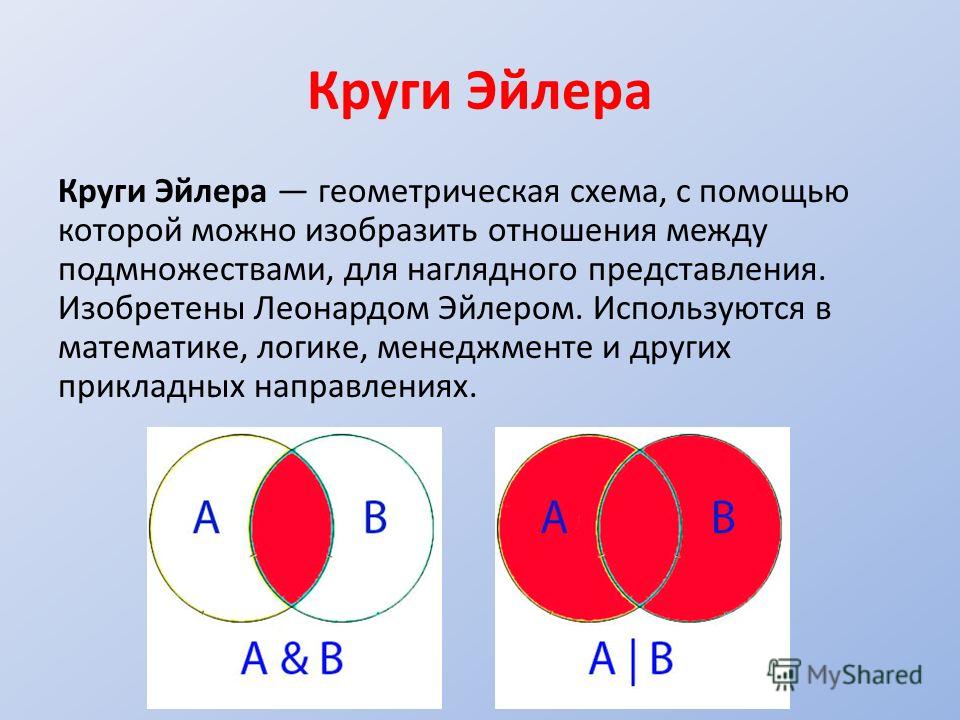 Вот одно решение, которое я придумал; возможно, есть более элегантные. В частности, должно быть изображение, которое более явно отражает двойственную симметрию диаграммы змеи.

Здесь карты между шестью пространствами являются очевидными картами ограничения (и можно визуально убедиться, что два квадрата на диаграмме змеи действительно коммутируют). Затем каждое из пространств ядра и коядра трех вертикальных карт ограничения связывается с объединением двух подобластей, как показано на диаграмме. Обратите внимание, как перекрытия между этими ядрами и коядрами создают длинную точную «змейку».

ОБНОВЛЕНИЕ: изменив аналогичную диаграмму в неопубликованной рукописи Рави Вакила, я теперь могу создать более симметричную версию приведенной выше диаграммы, опять же с очень заметной «змеей»:

В наших обозначениях (алгебраическое) тензорное произведение интервала и другого интервала не совсем , но это становится верным, если использовать -алгебраическую версию тензорного произведения благодаря теореме Стоуна-Вейерштрасса.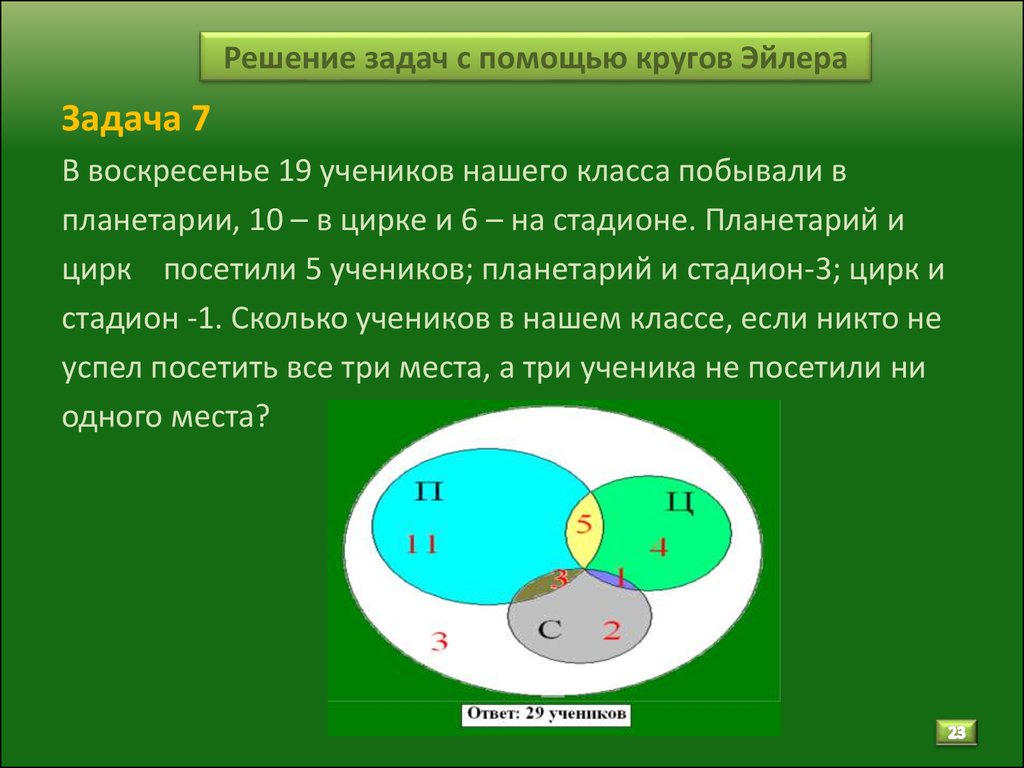 Таким образом, можно правдоподобно использовать декартовы произведения в качестве прокси для произведения тензора векторного пространства. Например, вот описание отношения когда является подпространством:

К сожалению, у этой записи есть некоторые ограничения: например, независимо от того, сколько измерений вы используете для своих диаграмм, эти диаграммы будут предлагать неверную идентичность.

(который, кстати, на данный момент является ответом, набравшим наибольшее количество голосов на вопрос MathOverflow «Примеры распространенных ложных убеждений в математике»). (См. также эту предыдущую запись в блоге о подобном явлении при использовании наборов или векторных пространств для моделирования энтропии информационных переменных.) Тем не менее, оно кажется достаточно точным, чтобы его можно было использовать для иллюстрации многих общих отношений между векторными пространствами и абелевыми группами. С соответствующей долей скептицизма ее можно было бы использовать и для других категорий помимо этих двух, хотя для неабелевых категорий следует действовать с осторожностью, поскольку диаграмма может указывать на отношения, которые на самом деле неверны в этой категории.