Урок математики «Решение задач на проценты», (5 класс)
Раздел долгосрочного плана: Раздел 5.4А Процент (12 ч) | Школа: | ||||
Дата: | ФИО учителя: | ||||
Класс: 5 | Количество присутствующих: | отсутствующих: | |||
Тема урока | Решение задач на проценты. Сложные проценты. | ||||
Тип урока | Закрепление знаний и формирование умений и навыков по пройденной теме | ||||
Цели обучения, которые достигаются на данном уроке (ссылка на учебную программу) | 5. | ||||
Цели урока | Закрепить понятия «простые проценты» и «сложные проценты»; Применять сложные проценты при решении задач. | ||||
Критерии оценивания | Понимает разницу между простыми и сложными процентами; Применяет сложные проценты при решении задач. | ||||
Языковые цели | Лексика и терминология, специфичная для предмета: процент, процентное отношение, процентное увеличение; процентное уменьшение; простые процентные начисления, сложные процентные начисления. Полезные выражения для диалогов и письма: Простые проценты используются ….. Формула вычисления сложных процентов удобна при вычислении …. Если проценты начисляют на изменяющуюся сумму, то говорят, что … | ||||
Привитие ценностей | Развитие навыков самостоятельного обучения, уважения к чужому мнению, ответственности за обучение через работу в парах и группах. Формирование критического практического взгляда на окружающую действительность в контексте решения задач на проценты. | ||||
Межпредметные связи | Решение задач экономики | ||||
Навыки использования ИКТ | Использование калькуляторов | ||||
Предварительные знания | процент, процентное отношение, процентное увеличение; процентное уменьшение; концентрация. | ||||
Ход урока | |||||
Запланированные этапы урока | Запланированная деятельность на уроке | Ресурсы | |||
Урок 1 Начало урока 5 мин | I. Организационный момент: — концентрация внимания учащихся; — совместно с учащимися определить цели урока/ЦО; — определить «зону ближайшего развития» учащихся, ожидания к концу урока; — проверка домашнего задания; — работа с терминологией на трех языках. | Презентация | |||
Середина урока 5 мин 5 мин 10 мин 15 мин | Устная работа. «Посчитай скорей!». Индивидуальная работа. Учащимся предлагается вспомнить и решить основные задачи по процентам: нахождение числа по процентам, процента от числа и процентное отношение двух чисел Виды заданий: Какое число является 30% от 150? 80 – это 75% какого числа? Какой процент от числа 60 составляет число 150? Работа происходит с проверкой ответов на слайде с последующим комментарием учащихся. Решение задач. Работа выполняется индивидуально или в составе малых групп. Учащимся предлагается решить задачу 1: дается 2-3 минуты на рассмотрение задачи и выбора метода решения, далее происходит обсуждение плана решения задачи. Учитель дает ещё несколько минут для того, чтобы учащиеся решили задачу полностью. Аналогично решаем задачу №2. Учителю при обсуждении задач необходимо акцентировать внимание учащихся на происходящие в задаче процессы для хорошего понимания использования процентов. Учащиеся должны объяснить, почему в первой задаче применяют простые проценты, а во второй задаче – сложные. IV. Тренировочные упражнения. Учащимся предлагаются различные задачи для закрепления. Задания решаются самостоятельно, с последующей взаимопроверкой. Дифференцированный подход осуществляет учитель (уровень А и Б). (Раздаточный материал содержит задачи с запасом на более способных учащихся с высокой скоростью решения). | Презентация Слайд 5 Презентация Слайд 6 Презентация Слайды 7-8 Раздаточный материал. Никольский С.М. и другие, Математика 6 класс, 2012г. с.166-167 | |||
Конец урока 5 мин | В конце урока учащиеся проводят рефлексию: Учащимся предлагается оценить свои знания по теме «Проценты», прикрепляя стикер со своим именем на процентной шкале слайда. Домашнее задание: уровень А: № 874, уровень Б: №878. | Презентация Слайд 10 Никольский С.М. и другие, Математика 6 класс, 2012г. с.166-167 | |||
Дифференциация Более способным учащимся предлагаются задания уровня Б. | Оценивание Формативное оценивание учителя в течение урока, в частности, «Большой палец». Самооценивание. | Здоровье и соблюдение техники безопасности Зарядка для глаз | |||
Рефлексия по уроку Были ли цели урока/цели обучения реалистичными? Все ли учащиеся справились с поставленными целями? Если нет, то почему? Правильно ли проведена дифференциация на уроке? Выдержаны ли были временные этапы урока? Какие отступления были от плана урока и почему? | |||||
Общая оценка Какие два аспекта урока прошли хорошо (подумайте как о преподавании, так и об обучении)? 1: 2: Что могло бы способствовать улучшению урока (подумайте как о преподавании, так и об обучении)? 1: 2: Что я выявил(а) за время урока о классе или достижениях/трудностях отдельных учеников, на что необходимо обратить внимание на последующих уроках? | |||||
Задачи на сплавы и смеси: подробный разбор
Как правило, ученики очень не любят задачи на сплавы и смеси. Для них они являются сложными и непонятными.
Для них они являются сложными и непонятными.
Поэтому многие даже время не тратят на попытки решения такой задачи в ЕГЭ, а просто пропускают ее. А зря!
Сейчас покажем, как можно решить такую задачу, выполнив всего три действия.
- Как решить задачу на смеси и сплавы: 3 действия
- Примеры решения задач на смеси: от простого к сложному
- Примеры решения задач на сплавы: от простого к сложному
Итак, решение любой задачи на смеси и сплавы сводится к выполнению трех действий:
- Необходимо составить таблицу, в которой указываем общую массу каждого вещества и чистую массу каждого вещества. Эти данные содержатся в условии задачи. Если какие-то данные в условии отсутствуют, то обозначаем их как неизвестные — х, у.

- Составляем систему уравнений, основываясь на том, что при соединении двух смесей (или сплавов) их массы складываются. Т.е. мы складываем как общую массу двух изначальных смесей (или сплавов), так и чистую массу каждого вещества, содержащихся в них. Решаем полученную систему уравнений.
- После решения системы уравнений и нахождения всех неизвестных обязательно возвращаемся к условию задачи и смотрим, что требовалось найти. Многие ученики, решив правильно систему уравнений, неправильно записывают ответ. Ведь решение системы – это еще не ответ к задаче! Вернитесь к условиям задачи, прочитайте, что именно требовалось найти, и запишите ответ.
А теперь разберем на примерах, как с помощью этих трех действий решать задачи на смеси и сплавы.
Задача 1Смешали 3 литра раствора, содержащего 20% кислоты, и 5 литров раствора, содержащего 40% той же кислоты. Какова концентрация кислоты в полученном растворе.
Какова концентрация кислоты в полученном растворе.
Решение:
Для решения задачи выполняем три действия, о которых мы говорили выше:
1. Составляем таблицу, в которой указываем общую массу раствора и массу чистого вещества, то есть в нашем случае – кислоты.
Из условий задачи имеем три раствора:
Раствор 1: 3 литра с 20% кислотой, т.е. общая масса = 3 литра, масса чистого вещества = 3 * 20% = 3 * 0,2 = 0,6
Раствор 2: 5 литров с 40% кислотой, т.е. общая масса = 5 литров, масса чистого вещества = 5 * 40% = 5 * 0,4 = 2
Раствор 3: какое-то количество раствора (обозначим его общую массу за х) с какой-то концентрацией кислоты (обозначим ее чистую массу за у), заносим эти данные в таблицу:Первое действие выполнено, переходим ко второму.
2. Составляем уравнения. Вспоминаем, что общая масса раствора 3 является суммой общих масс раствора 1 и раствора 2. А масса чистого вещества в растворе 3 является суммой массы чистового вещества в растворе 1 и массы чистового вещества в растворе 2. Таким образом, получаем:
Таким образом, получаем:
3 + 5 = х
0,6 + 2 = у
Решаем простейшее уравнение и получаем, что х = 8, а у = 2,6. Таким образом, раствор 3 получился 8 литров, из которых 2,6 литра – это кислота.
Но ответ к задаче записывать рано! Переходим к третьему действию решения нашей задачи.
3. Возвращаемся к условию задачи и вспоминаем, а что же требовалось найти. В нашей задаче требовалось определить концентрацию кислоты в растворе 3. Когда мы решили уравнения, мы нашли общую массу раствора 3 и массу чистого вещества (кислоты), содержащегося в нем.
Чтобы определить концентрацию вещества необходимо разделить массу чистого вещества на общую массу раствора.
Таким образом, концентрация кислоты в растворе 3 равна:
2,6 / 8 = 0,325
Переводим долю вещества в проценты. Для этого умножаем полученный результат на 100:
0,325 * 100 = 32,5%
Ответ: 32,5%
Задача 2Газ в сосуде А содержал 21% кислорода, а газ в сосуде В содержал 5% кислорода. Масса газа в сосуде А была больше массы газа в сосуде В на 300 г. Когда перегородку между сосудами убрали, газы перемешались, и получился третий газ, который содержит 14,6% кислорода. Найти массу третьего газа.
Масса газа в сосуде А была больше массы газа в сосуде В на 300 г. Когда перегородку между сосудами убрали, газы перемешались, и получился третий газ, который содержит 14,6% кислорода. Найти массу третьего газа.
Решение:
1. Составляем таблицу. Для этого обозначим массу газа в сосуде В – х. Остальные данные берем из условий задачи и формируем таблицу:2. Составляем уравнение. Известно, что третий газ имеет содержание кислорода 14,6%, соответственно мы можем приравнять массу чистого вещества газа 3 к 0,146 * (х + (х +300)). Получим уравнение:
(х +300) * 0,21 + х * 0,05 = 0,146 (х + (х +300))
0,21х + 63 + 0,05х = 0,292х + 43,8
0,26х + 63 = 0,292х + 43,8
0,032х = 19,2
х = 600
3. Возвращаемся к условиям задачи и вспоминаем, что нужно было найти. А найти нам нужно было массу третьего газа. Подставляем в уравнение общей массы газа 3 из таблицы и получаем:
600 + 600 + 300 = 1500 г
Ответ: масса третьего газа равна 1500 г.
Задача 3Смешали 40%ый и 15%ый растворы кислоты, затем добавили 3 кг чистой воды, в результате чего получили 20%ый раствор кислоты. Если бы вместо 3 кг воды добавили 3 кг 80% раствора той же кислоты, то получили бы 50%ый раствор кислоты. Сколько килограммов 40%го и 15%го растворов кислоты было смешано?
Если бы вместо 3 кг воды добавили 3 кг 80% раствора той же кислоты, то получили бы 50%ый раствор кислоты. Сколько килограммов 40%го и 15%го растворов кислоты было смешано?
Решение:
1. Составляем таблицу. По условиям задачи мы имеем пять растворов:
Раствор 1: 40%ая кислота. Обозначим ее массу за х, тогда масса чистого вещества = х * 40% = 0,4х
Раствор 2: 15%ая кислота. Обозначим ее массу за у, тогда масса чистого вещества = х * 15% = 0,15х
Вода: вода, масса которой равна 3 кг. Концентрация кислоты в воде равна 0. Таким образом, масса чистого вещества равна 3 * 0 = 0
Раствор 3: 80%ая кислота. Ее масса по условию задачи равна 3 кг, тогда масса чистого вещества равна 3 * 80% = 3 *0,8 = 2,4
Раствор 4: соединение раствора 1, раствора 2 и воды. Таким образом, общая масса полученного раствора равна х + у + 3. А масса чистого вещества в этом растворе равна 0,4х + 0,15у + 0
Раствор 5: соединение раствора 1, раствора 2 и раствора 3. Таким образом, общая масса полученного раствора равна х + у + 3. А масса чистого вещества в этом растворе равна 0,4х + 0,15у + 2,4.
А масса чистого вещества в этом растворе равна 0,4х + 0,15у + 2,4.
Сводим полученные результаты в таблицу:2. Составляем уравнение.
По условиям задачи раствор 5 имеет концентрацию 50%. Таким образом, чтобы получить массу чистого вещества в растворе 5 нужно его общую массу умножить на концентрацию. Получаем (х + у + 3) * 0,5. Теперь берем массу чистого вещества раствора 5, которую мы выразили в таблице и приравниваем два этих уравнения:
(х + у + 3) * 0,5 = 0,4х + 0,15у + 2,4
Аналогично поступаем с раствором 4. По условиям задачи его концентрация равна 20%. Тогда получаем следующее уравнение:
(х + у + 3) * 0,2 = 0,4х + 0,15у
Объединяем полученные уравнения в систему:Решаем систему и получаем х = 3,4, у = 1,6
3. Возвращаемся к условиям задачи.
По условиям задачи необходимо было найти, какое количество килограммов 40%го и 15%го растворов кислоты было смешано. Общая масса 40%й кислоты мы обозначали х, а общую массу 15%й кислоты мы обозначили у. Следовательно, масса 40%й кислоты = 3,4 кг, а масса15%й кислоты = 1,6 кг.
Следовательно, масса 40%й кислоты = 3,4 кг, а масса15%й кислоты = 1,6 кг.
Ответ: масса 40%й кислоты = 3,4 кг, а масса15%й кислоты = 1,6 кг.
Бронза является сплавом меди и олова (в разных пропорциях). Кусок бронзы, содержащий 1/12 часть олова, сплавляется с другим куском, содержащим 1/10 часть олова. Полученный сплав содержит 1/11 часть олова. Найдите вес второго куска, если вес первого равен 84 кг
Решение:
1. Составим таблицу. Обозначим массу второго куска – х.2. Составим уравнение. По условию задачи сплав 3 содержит 1/11 часть олова, тогда масса чистого вещества равна 1/11 * (84 + х). Таким образом, можно составить следующее уравнение:
1/12 * 84 + 1/10 * х = 1/11 * (84 + х)
7 + х/10 = 84/11 + х/11
х/10 – х/11 = 7/11
х/110 = 7/11
х/10 = 7
х = 70
3. Возвращаемся к условию задачи. Найти нужно было вес второго куска. Вес второго куска равен 70 кг.
Вес второго куска равен 70 кг.
Ответ: 70 кг.
Задача 2Имеются два сплава меди со свинцом. Один сплав содержит 15% меди, а другой 65%. Сколько нужно взять каждого сплава, чтобы получилось 200г сплава, содержащего 30% меди?
Решение.
1. Составим таблицу. Пусть масса первого сплава – х, масса второго сплава – у. Остальные данные берем из решения и составляем таблицу:2. По условиям задачи масса третьего сплава равна 200 г, значит:
х + у = 200
Содержание меди в третьем сплаве по условиям задачи равно 30%, т.е. масса чистого вещества равна 0,3(х + у). Следовательно, берем массу чистого вещества из таблицы и приравниваем:
0,15х + 0,65у = 0,3(х + у)
Получившиеся уравнения сводим в систему и решаем ее:х = 200 – у
0,15(200 – у) + 0,65у = 0,3 * 200
30 – 0,15у + 0,65у = 60
0,5у = 30
у = 60
х = 140
3. Возвращаемся к условиям задачи. Необходимо было найти массу первого и второго сплава. Масса первого сплава — 140 г, масса второго сплава -60 г.
Ответ: 140 г и 60 г.
Задача 3В первом сплаве содержание меди составляет 70%, а во втором – 40%. В каком отношении надо взять эти сплавы, чтобы получить из них новый сплав, который содержит 50% меди?
Решение:
1. Составим таблицу. Обозначим массу первого сплава – х, массу второго сплава – у. Тогда:2. По условиям задачи содержание меди в третьем сплаве равно 50%. Таким образом, масса чистого вещества равна 0,5 (х + у). Приравняем полученное уравнение к массе чистого вещества в составе третьего сплава из таблицы, получим:
0,7х + 0,4у = 0,5 (х + у)
0,7х + 0,4у = 0,5х + 0,5у
0,2х = 0,1у
х/у = ½
3. Возвращаемся к условию задачи. Необходимо было определить отношение первого и второго сплавов в третьем сплаве. Отношение сплавов равно ½.
Ответ: ½
Итак, решение задач на сплавы и смеси можно свести к трем действиям: составление таблицы, составление уравнения (или системы уравнений), возвращение к условиям задачи, чтобы дать ответ на поставленный вопрос. Задание 11 ЕГЭ по математике профильного уровня является одной из самых сложных задач, так как может содержать текстовую задачу любого типа. Это может быть как задача на сплавы и смеси, так и задача на движение, работу, проценты. Как решать все эти задачи вы можете узнать на нашем сайте или
Задание 11 ЕГЭ по математике профильного уровня является одной из самых сложных задач, так как может содержать текстовую задачу любого типа. Это может быть как задача на сплавы и смеси, так и задача на движение, работу, проценты. Как решать все эти задачи вы можете узнать на нашем сайте или
GMAT Math Help
Учащиеся, нуждающиеся в GMAT Math Help, получат большую пользу от нашей интерактивной программы. Мы разбираем все ключевые элементы, чтобы вы могли получить адекватную помощь по GMAT Math. Имея под рукой обязательные концепции обучения и актуальные практические вопросы, вы мгновенно получите много помощи по GMAT Math. Получите помощь сегодня с нашей обширной коллекцией необходимой информации GMAT по математике. Вступительный экзамен по менеджменту для выпускников — это препятствие, с которым приходится сталкиваться многим потенциальным студентам, изучающим бизнес. Часть «Количественное мышление», вероятно, является наиболее опасным разделом GMAT для большинства испытуемых. Многие испытуемые будут вспоминать математику в старших классах или бакалавриате и могут предвидеть сложные математические вопросы, сложные графики и пугающую геометрию. Нужен ли вам репетиторство по GMAT в Атланте, репетиторство по GMAT в Хьюстоне или репетиторство по GMAT в Сан-Франциско, работа один на один с экспертом может стать именно тем стимулом, в котором нуждается ваша учеба.
Многие испытуемые будут вспоминать математику в старших классах или бакалавриате и могут предвидеть сложные математические вопросы, сложные графики и пугающую геометрию. Нужен ли вам репетиторство по GMAT в Атланте, репетиторство по GMAT в Хьюстоне или репетиторство по GMAT в Сан-Франциско, работа один на один с экспертом может стать именно тем стимулом, в котором нуждается ваша учеба.
Экзамен GMAT Quantitative Reasoning на самом деле проверяет сложные математические понятия, с которыми вы, возможно, не сталкивались какое-то время. Тем не менее, при должной подготовке вы сможете с уверенностью ответить на вопросы. Раздел состоит из тридцати семи вопросов, на которые отводится семьдесят пять минут. Из них вы можете ожидать, что около двух третей будут довольно простыми вопросами, состоящими из проблемы, которую вам предлагается решить, выбрав правильный ответ из нескольких представленных вариантов.
Остальные вопросы относятся ко второму типу, немного более абстрактному. Это так называемые вопросы достаточности, которые просят вас сделать суждение. Вам предоставлено достаточно информации, чтобы решить вопрос, или вы не можете определить ответ, основываясь на том, что вам говорят? Рассмотрим следующий простой вопрос:
Это так называемые вопросы достаточности, которые просят вас сделать суждение. Вам предоставлено достаточно информации, чтобы решить вопрос, или вы не можете определить ответ, основываясь на том, что вам говорят? Рассмотрим следующий простой вопрос:
Если X и Y — положительные целые числа, какова их сумма?
1. Разница между X и Y составляет 50
2. X является произведением (Y/2) x 4
При ответе на этот вопрос ваша задача состоит в том, чтобы определить, можете ли вы вычислить сумму X и Y, используя только информацию из пункта 1 или пункта 2, если вам нужны оба пункта 1 и 2 вместе, чтобы иметь возможность решить проблему, или если вам нужно больше информации, чем предоставлено в пунктах 1 и 2 вместе взятых.
Большинство студентов считают, что дополнительное рассмотрение достаточности делает эти задачи намного более сложными, чем относительно простые вопросы решения проблем. Некоторые учащиеся могут считать эти вопросы достаточности самыми сложными вопросами, которые они пытаются решить в день экзамена.
Экзамен GMAT Quantitative Reasoning проверяет вашу способность критически мыслить и рассуждать. Развитие этих навыков посредством практики, сотрудничества и размышлений может быть намного лучше, чем любые короткие пути к более высокому баллу. Подумайте о работе с репетиторами, у которых есть собственная история успеха в тесте GMAT Quantitative Reasoning, поскольку они часто могут помочь вам существенно ускорить ваш первоначальный прогресс. Кроме того, изучите бесплатные ресурсы GMAT по математике от Varsity Tutors. Возможно, вы обнаружите, что наша страница справки GMAT по математике — отличное место, чтобы начать лучше понимать сложные математические понятия или типы вопросов, например, вопросы на достаточность. В нашей справке по математике GMAT представлены примеры задач, на которые даны ответы и даны подробные объяснения, что позволяет пройти через процесс решения сложного вопроса в качестве практического руководства.
Навыки, проверяемые в разделе Quantitative Reasoning теста GMAT, — это те же навыки, которые требуются в программах управления и в управленческой карьере. Вы можете дать себе большое преимущество в будущем, вкладывая время и усилия сейчас. Кроме того, учтите, что GMAT — это единственный объективный способ, с помощью которого сотрудники приемной комиссии оценивают различных кандидатов. Ваш колледж может сильно отличаться от колледжа другого абитуриента с точки зрения шкалы оценок или строгости оценок. Существенная разница в среднем балле может не свидетельствовать о разнице в способностях, а GMAT — лучший способ объективно и убедительно продемонстрировать свою способность к обучению и успеху. Вы можете рассматривать экзамен GMAT Quantitative Reasoning как возможность продемонстрировать свои способности, а не как еще одно препятствие, которое необходимо преодолеть. Воспользуйтесь этим шансом, чтобы продемонстрировать, почему вы принадлежите к одной из лучших бизнес-школ! 9{nt}\), где A представляет собой окончательный баланс после начисления процентов за время, t , в годах, на основную сумму, P , по годовой процентной ставке, r . Количество начислений процентов в году равно n .
Ваш колледж может сильно отличаться от колледжа другого абитуриента с точки зрения шкалы оценок или строгости оценок. Существенная разница в среднем балле может не свидетельствовать о разнице в способностях, а GMAT — лучший способ объективно и убедительно продемонстрировать свою способность к обучению и успеху. Вы можете рассматривать экзамен GMAT Quantitative Reasoning как возможность продемонстрировать свои способности, а не как еще одно препятствие, которое необходимо преодолеть. Воспользуйтесь этим шансом, чтобы продемонстрировать, почему вы принадлежите к одной из лучших бизнес-школ! 9{nt}\), где A представляет собой окончательный баланс после начисления процентов за время, t , в годах, на основную сумму, P , по годовой процентной ставке, r . Количество начислений процентов в году равно n .
Примеры вопросов по формуле сложных процентов
Пример 1:
Жасмин вносит 520 долларов на сберегательный счет, на который ежемесячно начисляется процентная ставка 3,5%. Каким будет остаток на сберегательном счете Жасмин через два года? 9{1(6)}\)
Каким будет остаток на сберегательном счете Жасмин через два года? 9{1(6)}\)
\(1{,}780,80=1,484P\)
\(1{,}200=P\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\) основная сумма, которую Лекс использовал для открытия счета 6 лет назад
Вопрос №1:
Учитель хочет инвестировать 30 000 долларов на счет, который ежегодно накапливается. Процентная ставка в этом банке составляет 1,8%. Сколько денег будет на счете через 6 лет?
43 389 долларов США6\)
\(A=$33{,}389,35\)
Скрыть ответ
Вопрос №2:
Инвестиции приносят 3% в год и начисляются ежемесячно. Рассчитайте общую стоимость через 6 лет при первоначальных инвестициях в размере 5000 долларов.
$ 5 114,74
$ 4 984,74
$ 5 984,74
$ 2 984,74
Показать ответ
Ответ:
Еще раз, используйте составной интерес для решения этой задачи.
\(A=5${,}984,74\)
Скрыть ответ
Вопрос №3:
Кристен хочет иметь 2 000 000 долларов на пенсию через 45 лет. Она инвестирует во взаимный фонд и платит 8,5% каждый год, ежеквартально начисляя сложные проценты. Какую сумму она должна первоначально внести во взаимный фонд?
$ 47 421,08
$ 35 421,08
$ 43 421,08
$ 45,421,08
Покажите ответ
Ответ:
Еще раз, используйте составной интерес. 9{180}\)
\(P=45${,}421,08\)
Скрыть ответ
Вопрос № 4:
Шон инвестирует 50 000 долларов США в индексный аннуитет, который в среднем составляет 6,5% в год, начисляемый каждые полгода. . Через 9 лет сколько будет на его счету?
$ 88 918,29
$ 89,918,29
$ 68 918,29
$ 81,918,29
Покажите ответ
Ответ:
Еще раз, используйте составной интерес.

 5.2.6. Решать текстовые задачи на проценты
5.2.6. Решать текстовые задачи на проценты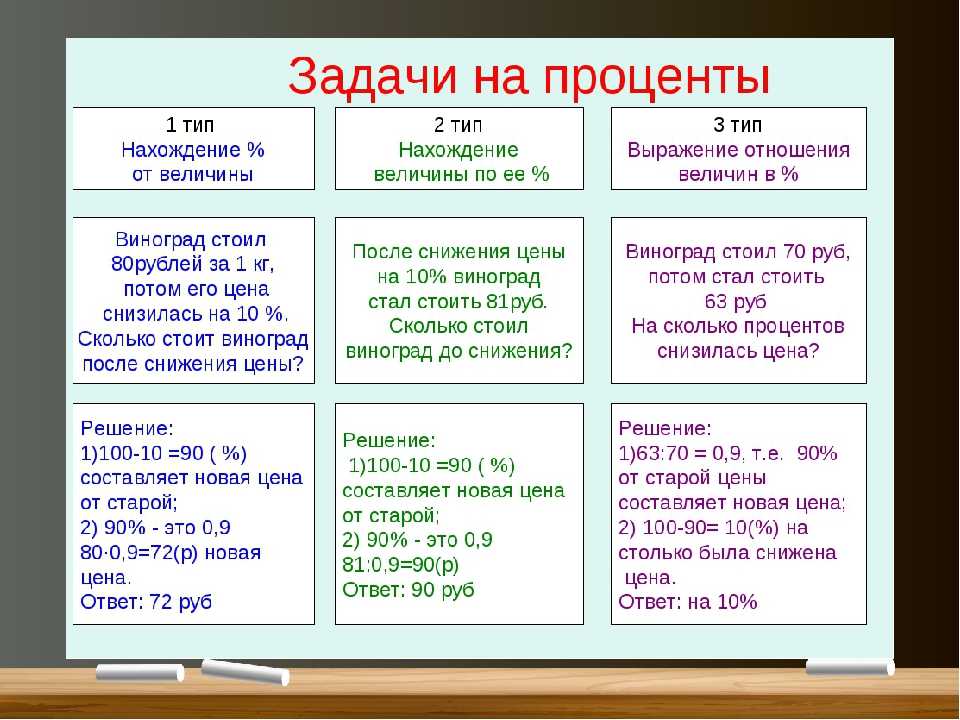 .
.
 Учащимся предлагается ответить на вопросы для повторения теоретических моментов темы «Проценты», а также придумать свои примеры на их использование.
Учащимся предлагается ответить на вопросы для повторения теоретических моментов темы «Проценты», а также придумать свои примеры на их использование. Ответ сверяется. В зависимости от результатов количества справившихся с задачей учащихся, задача разбирается у доски или в парах взаимопомощи.
Ответ сверяется. В зависимости от результатов количества справившихся с задачей учащихся, задача разбирается у доски или в парах взаимопомощи.

