Решение задач линейного программирования, теории игр и других экономико-математических методов и моделей. Методы оптимальных решений
В этом разделе разобраны типовые задачи методов оптимальных решений. Подробным образом рассматриваются задачи линейного программирования (графический и симплексный методы), транспортная задача. Перед примерами некоторых задач кратко изложены основные теоретические сведения. Данный материал может быть полезен студентам экономических специальностей.
О платной помощи студентам с учебой можно почитать на странице Как заказать решение задач по методам оптимальных решений…
- Линейное программирование
- Задачи линейного программирования
Подробно рассмотрено понятие линейного программирования, даны описания форм записи задач линейного программирования, приведены примеры задач линейного программирования.
Графический метод решения ЗЛПРассмотрен графический метод решения задачи линейного программирования (ЗЛП) с двумя переменными. На примере задачи приведено подробное описание построения чертежа и нахождения решения.
На примере задачи приведено подробное описание построения чертежа и нахождения решения.
Разобран метод искусственного базиса, применяемый для решения задач линейного программирования. Приведена краткая теория и, в качестве примеров, решены две задачи.
Двойственная задачаСодержит описание пары взаимно двойственных задач линейного программирования. Приведено правило построения двойственной задачи, сформулированы теоремы двойственности и на конкретных примерах рассмотрено их практическое применение при решении задач линейного программирования.
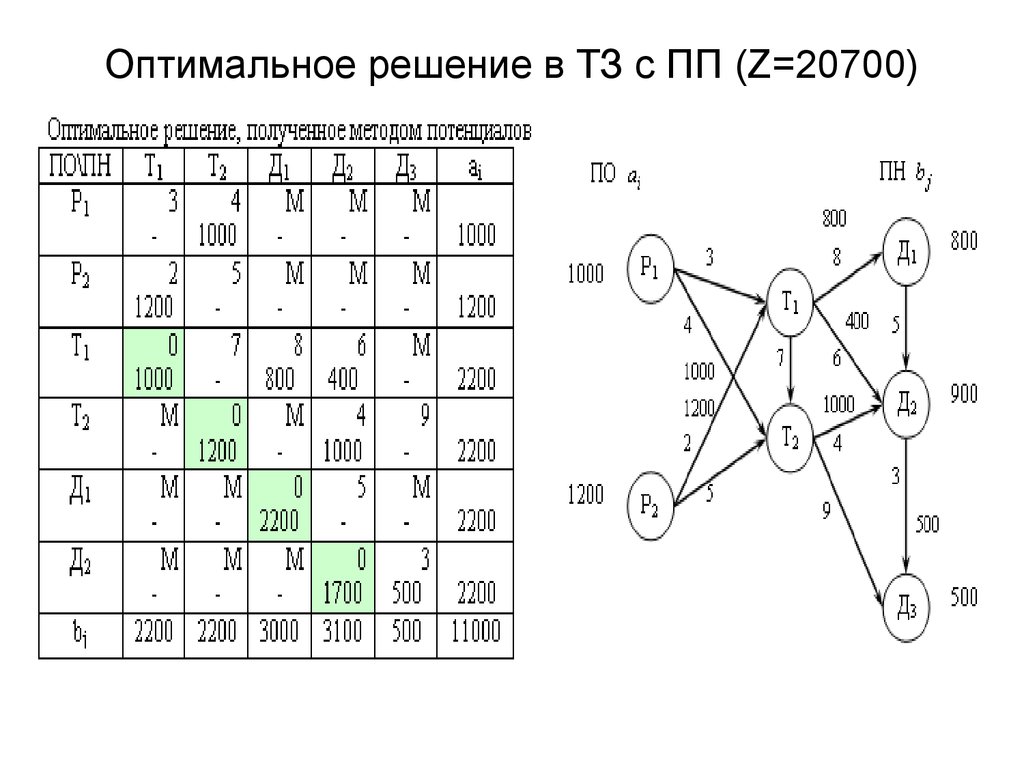
Транспортная задачаПодробно рассмотрена транспортная задача, ее математическая модель и методы решения — нахождение опорного плана методом минимального элемента и поиск оптимального решения методом потенциалов.
- Методы северо-западного угла, минимального элемента, Фогеля и двойного предпочтения
На конкретных примерах разобраны методы нахождения опорного плана транспортной задачи — северо-западного угла, минимального элемента, Фогеля и двойного предпочтения.
- Метод ветвей и границ
На примере решения задач целочисленного программирования иллюстрируется метод ветвей и границ. Наряду с разобранными задачами, на странице приведены краткие теоретические сведения по данной теме.
Метод ГомориНа примере решения задачи целочисленного программирования иллюстрируется метод Гомори. Приведены краткие теоретические сведения по данной теме.
- Матричные игры — основные понятия
На странице даются основные понятия теории игр — платежной матрицы, стратегии игроков, седловой точки, нижней и верхней цены игры. Приведена краткая теория и решены несколько простых задач на тему основных понятий матричных игр.
Содержит изложенные в краткой и доступной форме теоретические сведения о матричной игре без седловой точки и способе сведения такой задачи к задаче линейного программирования, для отыскания ее решения в смешанных стратегиях. Приведен пример решения задачи.
Статистические игрыРассмотрено решение статистической матричной игры в условиях неопределенности с помощью критериев Вальда, Сэвиджа, Гурвица, Лапласа, Байеса. На примере задачи подробно показано построение платежной матрицы и матрицы рисков.
- Метод множителей Лагранжа
На странице рассмотрено нахождение условного экстремума методом множителей Лагранжа. Показано построение функции Лагранжа на примере решения задачи нелинейного программирования. Решенную задачу предваряет краткая теория.
Графический метод решения задачи нелинейного программированияПриведен образец решения задачи квадратичного выпуклого программирования графическим методом.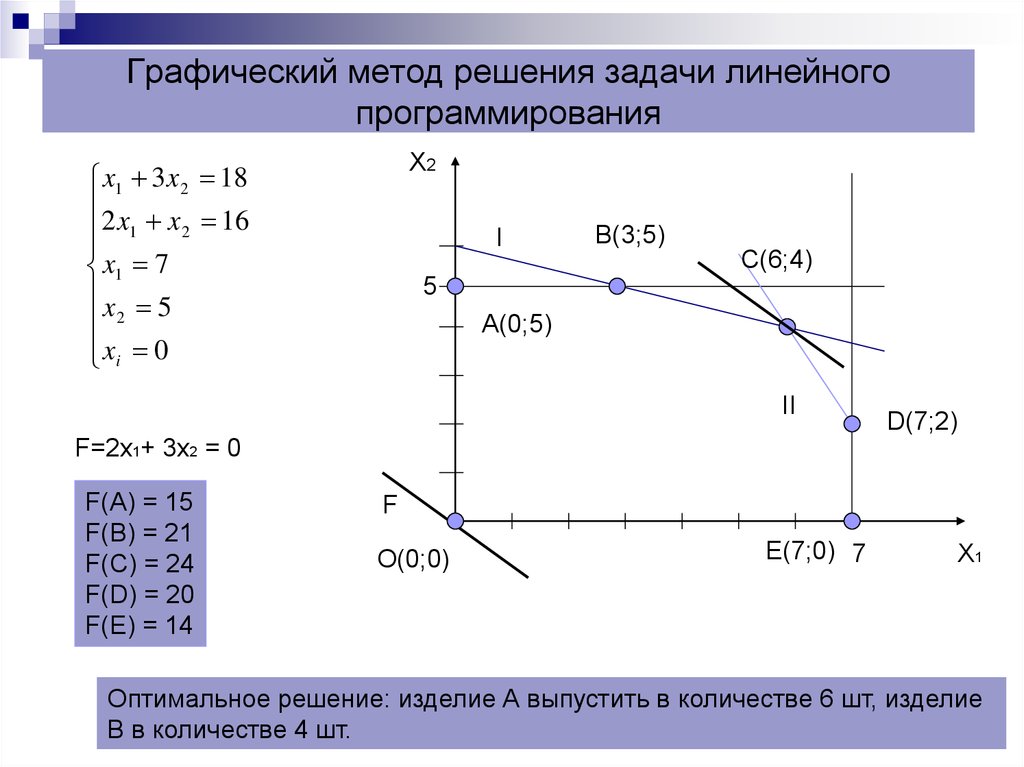
- Задача оптимального распределения ресурсов
Кратко изложены основные принципы динамического программирования (динамического планирования), рассмотрены уравнения Беллмана. Подробно решена задача оптимального распределения ресурсов между предприятиями.
- Многоканальная СМО с отказами
Приведены необходимые теоретические сведения, в частности формулы Эрланга, а также образец решения задачи по теме «Многоканальная система массового обслуживания с отказами». Подробно рассмотрены показатели многоканальной системы массового обслуживания (СМО) с отказами — вероятность отказа и вероятность обслуживания, абсолютная пропускная способность системы и среднее число каналов, занятых обслуживанием заявки.
Приведены необходимые теоретические сведения и образец решения задачи по теме «Многоканальная система массового обслуживания с неограниченной очередью», подробно рассмотрены показатели многоканальной системы массового обслуживания (СМО) с ожиданием обслуживания — среднее число каналов, занятых обслуживанием заявки, длина очереди, вероятность образования очереди, вероятность свободного состояния системы, среднее время ожидания в очереди.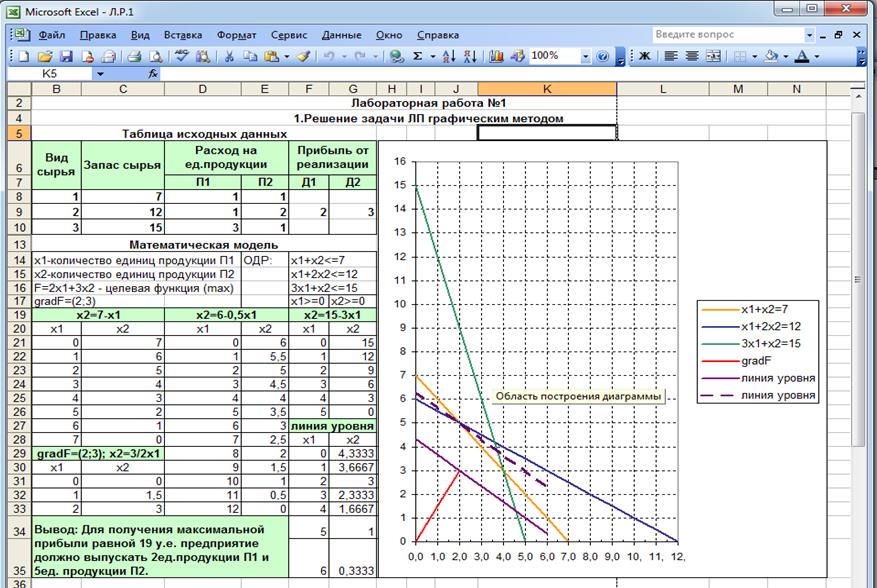
- Модель Уилсона
На примере решения задачи рассмотрена основная модель управления запасами (модель Уилсона). Вычислены такие показатели модели как оптимальный размер партии заказа, годовые затраты на хранение, интервал между поставками и точка размещения заказа.
- Модель Леонтьева
На примере решения задачи рассмотрена межотраслевая модель Леонтьева. Показано вычисление матрицы коэффициентов прямых материальных затрат, матрицы «затраты-выпуск», матрицы коэффициентов косвенных затрат, векторов конечного потребления и валового выпуска.
Научно-образовательный портал ТУСУР | Методы оптимальных решений. Часть 1. Линейное программирование: Курс лекций / Гендрина И. Ю. — 2018. 36 с.
Курс лекций
Теория методов оптимальных решений является одним из самых перспективных разделов современной прикладной математики. Теоретически обоснованные методы принятия оптимальных решений используются в самых различных областях науки и практики, включая исследование и управление экономическими процессами. Одним из самых разработанных разделов методов оптимальных решений является линейное программирование и, в частности, транспортные задачи. Курс лекций был разработан и прочитан студентам экономического факультета. Пособие может быть интересно также всем интересующимся методами принятия оптимальных управленческих решений.
Одним из самых разработанных разделов методов оптимальных решений является линейное программирование и, в частности, транспортные задачи. Курс лекций был разработан и прочитан студентам экономического факультета. Пособие может быть интересно также всем интересующимся методами принятия оптимальных управленческих решений.
Кафедра экономической математики, информатики и статистики
Автор: Гендрина И. Ю.
Год издания: 2018
Количество страниц: 36
Скачиваний: 29
Оглавление (содержание)
1. Элементы линейной алгебры 3
1.1 Системы линейных уравнений 3
1.2 Метод Гаусса 5
1.3 Решение линейных неравенств 7
1. 4 Решение систем линейных неравенств 8
4 Решение систем линейных неравенств 8
2. Задачи линейного программирования 9
2.1 Примеры задач, сводящихся к ЗЛП. Общая постановка ЗЛП 9
2.2 Графический метод решения ЗЛП 11
2.3 Свойства решений ЗЛП 13
2.4 Симплекс-метод решения ЗЛП 14
2.5 Симплекс-таблицы 14
2.6 Двойственные ЗЛП 15
2.7 Экономическая интерпретация взаимно-двойственных задач 17
2. 8 Анализ устойчивости двойственных оценок 20
8 Анализ устойчивости двойственных оценок 20
3. Транспортная задача 24
3.1 Постановка транспортной задачи 24
3.2 Способы построения первого опорного плана ТЗ 25
3.3 Метод потенциалов 27
3.4 Открытые транспортные задачи 28
4. Задачи для самостоятельного решения 30
4.1 Задачи линейного программирования 30
4.2 Транспортные задачи 33
5. Литература 36
Литература 36
смешанное целочисленное программирование — находит ли метод взвешенной суммы все парето-оптимальные решения в MILP
спросил
Изменено 2 года, 4 месяца назад
Просмотрено 701 раз
$\begingroup$
Я использую подход взвешенной суммы для задачи многокритериальной оптимизации, сформулированной как MILP. Это означает, что целевая функция является линейной. Я довольно часто читал, что метод взвешенной суммы не может найти определенные парето-оптимальные решения в случае невыпуклых целевых пространств (см., например, слайд 12 в этой презентации https://engineering.
Теперь, имея задачу MILP, могу ли я сделать вывод, что метод взвешенной суммы может найти все оптимальные по Парето решения, если я просто изменю веса? Конечно, количество парето-оптимальных решений может быть бесконечным, но я хотел бы знать, существует ли риск пропуска некоторых областей парето-фронта. Я интуитивно чувствую, что в MILP метод взвешенной суммы может фактически найти все парето-оптимальные решения.
Может ли кто-нибудь рассказать мне больше об этой проблеме? Буду очень признателен за каждый комментарий.
- смешанное целочисленное программирование
- многоцелевая оптимизация
$\endgroup$
3
$\begingroup$
Нет. Вы не можете быть уверены, что найдете все оптимальные по Парето решения MILP, используя подход взвешенной суммы. Вам даже не гарантируется, что вы найдете все недоминируемые исходы.
Гарантируется, что вы сможете генерировать только поддерживаемые недоминируемые решения. Все неподдерживаемые недоминируемые решения не могут быть найдены с использованием подхода взвешенной суммы (без добавления дополнительных ограничений). Это все связано с тем, что недостаточно, чтобы целевые функции были выпуклыми, также пространство решений должно быть выпуклым для подхода взвешенной суммы, чтобы гарантировать все недоминируемые результаты.
Вам даже не гарантируется, что вы найдете все недоминируемые исходы.
Гарантируется, что вы сможете генерировать только поддерживаемые недоминируемые решения. Все неподдерживаемые недоминируемые решения не могут быть найдены с использованием подхода взвешенной суммы (без добавления дополнительных ограничений). Это все связано с тем, что недостаточно, чтобы целевые функции были выпуклыми, также пространство решений должно быть выпуклым для подхода взвешенной суммы, чтобы гарантировать все недоминируемые результаты.
Рассмотрим следующий небольшой пример MILP с двумя целями: \начать{выравнивать} \мин\ & 4 + 2x_1+x_2+\frac{1}{2}y\\ \мин\ & 2+x_1+2x_2+3y\\ \mbox{s.t.:}\ & x_1+x_2+y\geq 2\\ \ & x_1,x_2\geq 0\\ \ & г\в\{0,1\} \end{выравнивание} Недоминирующие решения можно проиллюстрировать следующим образом:
Красная линия (сплошная и пунктирная) — эффективный фронт для $y=1$, а синяя сплошная линия — эффективный фронт для $y=0$. Следовательно, множество недоминируемых исходов задается объединением двух сплошных линий. Однако это только верхняя левая красная точка и все, что находится на синей линии, вы можете найти, используя скаляризацию взвешенной суммы. Вы можете найти верхнюю красную точку, используя веса $(0,9,0.1)$, средняя синяя точка с весами $(0.6,0.4)$ и правая нижняя синяя точка с весами $(0.1,0.9)$.
Однако это только верхняя левая красная точка и все, что находится на синей линии, вы можете найти, используя скаляризацию взвешенной суммы. Вы можете найти верхнюю красную точку, используя веса $(0,9,0.1)$, средняя синяя точка с весами $(0.6,0.4)$ и правая нижняя синяя точка с весами $(0.1,0.9)$.
Таким образом, вы не можете сгенерировать весь набор недоминируемых результатов для задач MILP в целом, используя скаляризацию взвешенной суммы.
$\endgroup$
13
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
[PDF] О поиске парето-оптимальных решений путем уменьшения размерности для некоторых многомерных многоцелевых задач оптимизации
- ID корпуса: 18774730
@inproceedings{DebOnFP,
title={О поиске парето-оптимальных решений посредством уменьшения размерности для некоторых многомерных многоцелевых задач оптимизации},
автор={Калянмой Деб и Диш Кумар Саксена}
} - К. Деб, Д. Саксена
- Информатика
Многие практические приложения многокритериальной оптимизации включают большое количество (10 и более) целей. Существующие методы эволюционной многокритериальной оптимизации (ЭМО) применяются только к задачам с меньшим числом целей (около пяти или около того) для задачи поиска репрезентативного набора парето-оптимальных решений за один запуск моделирования. Адекватно показав эту задачу, исследователи / практики EMO должны теперь выяснить, действительно ли эти методологии можно использовать для…
egr. msu.edu
msu.eduAn objective reduction algorithm using representative Pareto solution search for many-objective optimization problems
- Xiaofang Guo, Yuping Wang, Xiaoli Wang
Computer Science
Soft Computing
- 2015
A Предлагается быстрый алгоритм генерации неизбыточных целей, основанный на многокритериальном эволюционном алгоритме декомпозиции для генерации меньшего числа репрезентативных недоминируемых решений, широко распределенных на фронте Парето.
Уменьшение размерности в многокритериальной оптимизации с (частичным) сохранением структуры доминирования: обобщенные задачи минимального подмножества целей предложены три вопроса и соответствующие им алгоритмы, точный и эвристический, направленные на непосредственную интеграцию в процесс эволюционного поиска.
Многоцелевая оптимизация и поиск на основе гиперобъемов
- Д. Брокхофф
Информатика
- 2009
В этой диссертации рассматриваются такие классические проблемы многоцелевой оптимизации с точки зрения теоретических исследований для лучшего понимания МОЭ. многих целей и развивает методы сокращения целей, которые автоматически сокращают количество целей, в то время как отношение доминирования Парето сохраняется или изменяется лишь незначительно.
многих целей и развивает методы сокращения целей, которые автоматически сокращают количество целей, в то время как отношение доминирования Парето сохраняется или изменяется лишь незначительно.
Целевое сокращение на основе метода наименьших квадратов для многомерной многокритериальной задачи оптимизации
Предлагается новый алгоритм, а именно уменьшение большой размерности на основе метода наименьших квадратов, который увязывает каждую целевую функцию с линией и сравнивает различия наклона между каждыми двумя линиями и определяет, какая из них является избыточной, и дополнительно уменьшает эту.
Объективное сокращение многоцелевых задач оптимизации
- А. Гупта
Информатика
- 2019
Используются два подхода к объективному уменьшению: случайный и линейный коэффициенты, а также используется сумма рангов вместо Парето-ранжирования, которое превзошло многие другие оптимизации подходы применительно к многоцелевым задачам.
Интерактивная эволюционная многоцелевая процедура оптимизации и принятия решений
- С. Чаудхури, К. Деб
Информатика
Заявл. Мягкий компьютер.
- 2010
Эволюционная многообъективная оптимизация: обзор, алгоритмы и приложения
- R. Denysiuk
Компьютерная наука
- 2013
Применение Evolureation Algorithms alliz моделируются с использованием многокритериальных подходов, возникающих в результате математического моделирования передачи болезни денге и проектирования очистных сооружений.
Многокомъективные проблемы испытаний с дегенератными фронтами Pareto
- Liangli Zhen, M. Li, Ran Cheng, Dezhong Peng, X. Yao
Компьютерная наука
Arxiv
- 2018

Снижение размерности в многоцелевой оптимизации: минимальная задача объективного подмножества
- D. Brockhoff, E. Zitzler
Компьютерная наука
или
- 2006
Помимо общих определений. вводится задача вычисления минимального подмножества целей без потери информации (MOSS), а также алгоритм аппроксимации с оптимальным коэффициентом аппроксимации и точный алгоритм, который хорошо работает для небольших входных данных.
Многокритериальная оптимизация: избыточные и информативные цели
Основанный на статистическом методе анализа основных компонентов решается проблема сокращения числа целей, и предварительные результаты показывают, что этот статистический подход может быть ценным инструментом для принятия решений в многокритериальном анализе. оптимизация.
ПОКАЗАНЫ 1–10 ИЗ 25 ССЫЛОК
СОРТИРОВАТЬ ПОРелевантности Наиболее влиятельные документыНедавность
В поисках коленей в многоцелевой оптимизации
- Дж.
 Бранке, К. Деб, Хеннинг Дирольф, Матиас Освальд
Бранке, К. Деб, Хеннинг Дирольф, Матиас Освальд Информатика, экономика
PPSN
- 2004
Утверждается, что паретимальные наиболее интересные решения небольшое улучшение одной цели приведет к значительному ухудшению по крайней мере одной другой цели, иногда также называемой «коленами».
Поиск надежных парето-оптимальных решений в многокритериальной оптимизации
- K. Deb, Himanshu Gupta
Информатика
EMO
- 2005
глобальный Парето-оптимальный фронт.
Масштабируемые тестовые задачи для эволюционной многокритериальной оптимизации
Предлагаются три различных подхода к систематической разработке тестовых задач для систематической демонстрации эффективности многокритериальных эволюционных алгоритмов при решении задач, имеющих более двух целей.
Сравнение классических методов генерирования с эволюционным методом многообъективной оптимизации
- P.
 Shukla, K. Deb, Santosh Tiwari
Shukla, K. Deb, Santosh Tiwari Компьютерная наука
EMO
- 2005
- Дж. Бранке, К. Деб
Информатика
- 2005
- V. Khare, X. Yao, K. Deb
Компьютерная наука
EMO
- 2003
- К. Деб
Информатика
- 2009
- М. Фарина, П. Амато
Экономика, информатика
IEEE Trans. Сист. Человек Киберн. Часть А
- 2004
- T. Goel, R. Vaidyanathan, R. Haftka, W. Shyy, N. Queipo, K. Tucker
Информатика
- 2004 9004 9004
Три, разные класс. которые были предложены еще до появления методологий EMO, обсуждаются, и их оценка должна позволить исследователям разработать гибридный многокритериальный алгоритм оптимизации, который может быть лучше, чем каждый отдельный метод.
Интеграция пользовательских настроек в эволюционную многоцелевую оптимизацию
-объективных алгоритмов и показывает, что такие методы могут ускорить поиск и обеспечить более детальный выбор альтернатив в наиболее релевантных частях Парето-оптимального фронта.
масштабирование производительности многоцелевых эволюционных алгоритмов
Эти современные MOEA исследованы на предмет их масштабируемости по количеству целей и сравнены на основе их способности сходиться к фронту Парето, разнообразия полученных недоминируемых решений и времени их выполнения.
Многокритериальная оптимизация с использованием эволюционных алгоритмов
Этот текст представляет собой отличное введение в использование эволюционных алгоритмов в многоцелевой оптимизации, что позволяет использовать его в качестве учебника для выпускников или для самостоятельного изучения.
Нечеткое определение «оптимальности» для задач многокритериальной оптимизации
Различные нечеткие определения оптимальности и доминируемых решений, не основанные на предпочтениях, вводятся и проверяются на аналитических тестовых примерах, чтобы показать их достоверность и близость к принятию решений человеком.
Многокритериальная оптимизация и обработка множественных ограничений с помощью эволюционных алгоритмов.
 II. Пример применения
II. Пример примененияЭто исследование иллюстрирует, как может применяться такой метод, как многокритериальный генетический алгоритм, и показывает, как требования к дизайну могут быть уточнены по мере выполнения алгоритма, а также демонстрирует необходимость формулирования предпочтений в случаях, когда множество и сильно конкурирующих целей приводят к недоминируемое множество слишком велико для того, чтобы конечная совокупность могла эффективно выбираться.
Аппроксимация поверхности отклика оптимального по Парето фронта в многокритериальной оптимизации
Представлен систематический подход к аппроксимации оптимального по Парето фронта (POF) с помощью аппроксимации поверхности отклика, и аппроксимация POF может помочь визуализировать и количественно оценить компромиссы между целями для выбора компромиссных схем.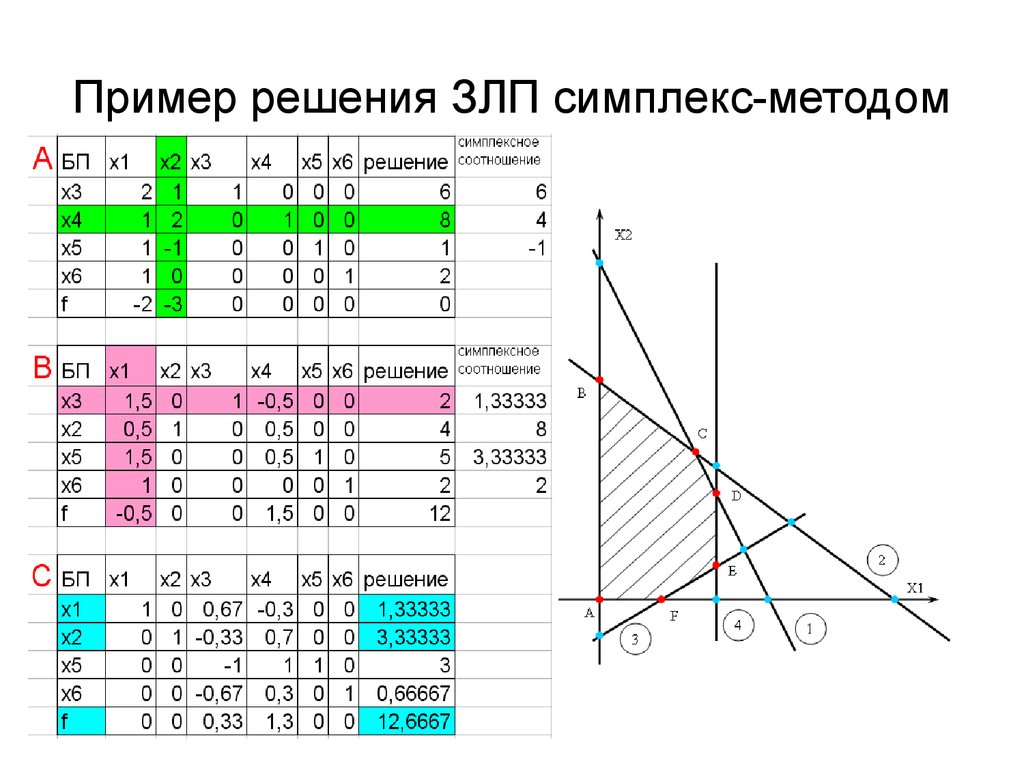

 Бранке, К. Деб, Хеннинг Дирольф, Матиас Освальд
Бранке, К. Деб, Хеннинг Дирольф, Матиас Освальд Shukla, K. Deb, Santosh Tiwari
Shukla, K. Deb, Santosh Tiwari