Задачи со степенями: Задачи со степенями

«Последняя цифра степени. Решение некоторых олимпиадных задач»

Муниципальное автономное общеобразовательное учреждение

Заревская средняя общеобразовательная школа

с углубленным изучением отдельных предметов

Домодедовского городского округа

Областной конкурс научно — исследовательской и проектной деятельности «Юный исследователь»

Секция: Точные науки.

Тема: «Последняя цифра степени. Решение некоторых олимпиадных задач»

Автор работы: Рагулин Владимир, 13 лет

                                                               

Научный руководитель: Шаповалова Вероника Николаевна

Черноголовка

2019

---

Оглавление

Введение ………………………………………………………………………….  3

Определение последней цифры натуральной степени натурального числа …. 4

Решение некоторых математических задач повышенной трудности ………… 7

Заключение ………………………………………………………………………. 9

Библиографический список …………………………………………………. … 10

---

Введение

В курсе алгебры 7 класса мы изучаем степени с натуральным показателем и их свойства. Меня заинтересовали эти задачи, так как степени чисел встречаются достаточно часто в заданиях работ разного уровня, в том числе олимпиадах и ОГЭ. Время на выполнение таких работ ограниченное, поэтому я задался вопросом: можно ли быстро определить последнюю цифру любой натуральной степени любого натурального числа при решении подобных задач?

Цель моей исследовательской работы – научиться быстро определять последнюю цифру любой натуральной степени любого натурального числа.

В ходе исследования решались следующие задачи:

• устанавливалось, есть ли закономерности получения последних цифр в степенях чисел;
• составлялась таблица последних цифр степеней;
• рассматривались примеры решений некоторых задач, опираясь на выведенные закономерности.

При работе над проектом я использовал материалы олимпиадных заданий для 7-9 классов из разных источников.

---

Определение последней цифры натуральной степени натурального числа

При решении задач на возведение в степень чисел я наблюдал, что последняя цифра степени любого натурального числа зависит только от последней цифры самого этого числа. Например, 1 в любой степени будет 1, значит, если число оканчивается на 1, то и любая степень этого числа – число, оканчивающееся на 1.

Попробуем выявить, а есть ли закономерности получения последней цифры для других случаев.

1. Легко убедиться, что любая степень числа, оканчивающегося на 5, и 6, будет оканчиваться на эти же цифры.
2. Рассмотрим степени числа 2: 21=2, 22=4, 23=8, 24=16, 25=32, 26=64, 27=128, 28=256, 29=512 и т.д. Как мы видим, через четыре шага, последняя цифра повторяется – это значит, что у нас есть закономерность определения последней цифры степени числа, оканчивающегося на 2.
3. Рассмотрим степени числа 3: 31=3, 32=9, 33=27, 34=81, 35=243, 36=729, 27=2187, 28=6561, 29=19683 и т.д. Как мы видим, через четыре шага, последняя цифра повторяется – это значит, что у нас снова есть закономерность определения последней цифры степени числа, оканчивающегося на 3.
4. Таким же образом, выявились закономерности повторения последних цифр степеней чисел, оканчивающихся на 7 и 8, также, через четыре шага: 71=7, 72=49, 73=343, 74=2401, 75=16807, 76=117649, 77=823543, 78=5764801, 79=40353607; 81=8, 82=64, 83=512, 84=4096, 85=32768, 86=262144, 87=2097152, 88=16777216, 89=134217728.
5. Рассмотрим степени числа 4: 41=4, 42=16, 43=64, 44=256, 45=1024, и т.д. Рассмотрим степени числа 9: 91=9, 92=81, 93=279, 94=6561, 95=59049, и т.д., здесь тоже есть закономерность – повторение последней цифры через два шага, то есть для нечетных и четных степеней.

Эти наблюдения позволили сделать вывод, что последние цифры степеней подчиняются закономерностям, и для наглядности я составил таблицу для быстрого определения этих цифр для всех случаев.

Последние цифры натуральных степеней натуральных чисел

1 степень	2 степень	3 степень	4 степень	5 степень
1	1	1	1	1
2	4	8	6	2
3	9	7	1	3
4	6	4	6	4
5	5	5	5	5
6	6	6	6	6
7	9	3	1	7
8	4	2	6	8
9	1	9	1	9

Рассмотрим на примерах, как пользоваться этой таблицей для решения конкретных заданий:

1. На какую цифру оканчивается число 127345?

Решение: число оканчивается на 7, через четыре шага цифры повторяются, значит, 345:4=86(ост. 1), значит 7345=71, оканчивается на 7.

2. Какая цифра будет последней в записи числа 2648569325?

Решение: число оканчивается на 9, при нечетных степенях – будет цифра 9, при четных — 1, значит, 2648569325, оканчивается на 9.

3. Какой цифрой оканчивается сумма чисел 21367+21878?

Решение: число 21367 оканчивается на 3, через четыре шага цифры повторяются, 67:4=16(ост. 3), значит, 367=33, оканчивается на 7; число 21878 оканчивается на 8, 78:4=19(ост. 2), значит, 878=82, оканчивается на 4. При сложении многозначных чисел сумма единиц 7+4=11, последняя цифра — 1.

4. Докажите, что

Решение: уменьшаемое оканчивается на цифру 1, любая степень единицы – число, оканчивающееся на 1, т.е. разность этих чисел оканчивается на 0, а это признак делимости числа на 10, что и требовалось доказать.

Таким образом, пользуясь выведенными закономерностями, достаточно легко выполнять такого типа задания.

---

Решение некоторых математических задач повышенной трудности

Рассмотрим решение некоторых типов задач, встречающихся на олимпиадах.

1. Докажите, что

Решение: выясним, какой цифрой оканчивается первое число: рассмотрим 77, 7:4=1(ост. 3), значит, 73 — оканчивается на 3, 37 – оканчивается на 7, так как, 7:4=1(ост. 3) и 37=33, опять 77 – оканчивается на 3, 37 – оканчивается на 7 и, очевидно, что и уменьшаемое оканчивается на цифру 3, и вычитаемое тоже оканчивается на цифру 3, т.е. разность этих чисел оканчивается на 0, а это признак делимости числа на 10, что и требовалось доказать.

2. Докажите, что число является составным.

Решение: натуральное число, имеющее больше двух делителей, называется составным;

 оканчивается на цифру 3, так как, основание степени оканчивается на 3, значит, последняя цифра меняется с шагом 4, показатель степени 589:4=148(ост. 1), 31=3. Рассмотрим второе слагаемое , где n – натуральное число, по таблице видим, что все возможные варианты степени числа 7 оканчиваются всегда на нечетную цифру, то есть Значит, будет оканчиваться на четную цифру, будет числом четным, а, значит, являться составным.

3. Докажите, что число 4545+5454 является составным.

Решение: выделив полный квадрат двучлена, разложим число на множители

4545+5454=(2545)2+(5452)2 + 2·2545·5452 — 2·2545·5452=(2545+5452)2 — 2546·5452=(2545+5452 — 545·2273)·(2545+5452 + 545·2273), так как 4545+5454 оканчивается на 9 (числа с 4 на конце в нечетной степени оканчиваются на 4, а числа с 5 на конце – в любой степени оканчиваются на 5), а каждая из скобок оканчивается на 7 (545:4=136(ост. 1), значит, 2545=21, оканчивается на 2, 5452=51, оканчивается на 5, и, произведение 545·2273 оканчивается на 0, т.к. 273:4=68(ост. 1), значит, 2273=21, 545·2=0, получаем 2+5-0=7 или 2+5+0=7), таким образом, множители в скобках отличные от 1 и от 4545+5454, значит, 4545+5454 является составным числом.

4. Докажите, что число n4+64  является составным.

Решение: по таблице видно, что четвертая степень любого натурального числа оканчивается либо на 1, либо на 6, кроме чисел, оканчивающихся на 5; значит, число n4+64 для всех натуральных n, кроме чисел, оканчивающихся на 5, будет составным, так как 1+4=5 — число кратно пяти, и, 6+4=10 – четное число;

рассмотрим случай – число n оканчивается на 5, значит n4+64 оканчивается на 9, выделив полный квадрат двучлена, разложим число на множители n4+64=(n2+8)2-16n2=(n2+8-4n)·(n2+8+4n), выясним, на какие цифры оканчиваются множители: n2 оканчивается на 5, 4n – на 0, значит 5+8-0=13 и 5+8+0=13, таким образом, множители в скобках отличные от 1 и от n4+64, значит, n4+64 является составным числом.

---

Заключение

Известный российский математик Василий Петрович Ермаков говорил: «В математике следует помнить не формулы, а процессы мышления». Я полностью согласен с ним. Работа над проектом помогла убедиться в том, что в математике много закономерностей, которые можно получить, правильно рассуждая и внимательно анализируя получаемые результаты.

Результаты данной работы помогут мне в дальнейшем расширять знания о степенях, а также применять полученные закономерности при решении олимпиадных задач, а также для подготовки к ОГЭ и ЕГЭ.

---

Библиографический список:

1. Московские математические олимпиады / Г.А. Гальперин, А.К. Толпыго. — М.: Просвещение, 1986г. — 303 с.
2. Пособие для учителей 5—8 классов / Под редакцией К. П. Сикорского. — М.: «Просвещение»,1967г. — 236 с.
3.  Сборник задач московских математических олимпиад / Болтянский В.Г. (ред.). – МГУ, 384 с.

Действия со степенью. ЕГЭ-2022. Решение задач

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. ЕГЭ-2022 Решение задач

Значение выражений
Школа
ЕГЭ
1

2. Свойства степени с рациональным показателем (для n ∈ Q, k ∈ Q)

1
a 0 1,
2
a1 a
1
3
a
4
a n
5
где a 0
6
1
, где a 0
a
1
n , где a 0
a
10
a
b
где a 0
7
a
8
a n b n ab
9
an a
,
n
b
b
n k
a nk
n
n
a n a k a n k
n
an
n k
a
,
k
a
n
b
,
a
где a 0 , b 0
где b 0

3.

1) Найдите значение выраженияРешение
Ответ : 30
© Рыжова С.А.
3

4. 2) Найдите значение выражения

Решение
Ответ : 100
© Рыжова С.А.
4

5. 3) Найдите значение выражения

Решение
Ответ : 32
© Рыжова С.А.
5

6. 4) Найдите значение выражения

Решение
Ответ : 3
© Рыжова С.А.
6

7. 5) Найдите значение выражения

Решение
Ответ : 0,2
© Рыжова С.А.
7

8. 6) Найдите значение выражения

Решение
Ответ : 4
© Рыжова С.А.
8

9. 7) Найдите значение выражения

Решение
Ответ : 2
© Рыжова С.А.
9

10. Свойства степени с рациональным показателем (для n ∈ Q, k ∈ Q)

1
a 0 1,
2
a1 a
1
3
a
4
a n
5
где a 0
6
1
, где a 0
a
1
n , где a 0
a
10
a
b
где a 0
7
a
8
a n b n ab
9
an a
,
n
b
b
n k
a nk
n
n
a n a k a n k
n
an
n k
a
,
k
a
n
b
,
a
где a 0 , b 0
где b 0
Задания открытого банка задач
1. Найдите значение выражения
652 562.
Решение.
652 562 (65 56)(65 56) 9 121 3 11 33.
2 7 .
2
2. Найдите значение выражения
Решение.
2 7
2
14
14
4 7 28
2.
14
14
3. Найдите значение выражения
Решение.
13 7 13 7
2
2
13 7 13
13 7 13 7 6.
7
.
Задания открытого банка задач
4. Найдите значение выражения 50,36 250,32 .
Решение.
50,36 250,32 50,36 52
0,32
50,36 50,64 50,36 0,64 51 5.
36,5
5. Найдите значение выражения 2,25 .
9
Решение.
36,5
36,5
36,5
6,5 4,5
2
3
3
9.
2,25
2,25
4,5
2
9
3
3
4
9
5
18
6. Найдите значение выражения 7 49 .
Решение.
4
9
5
18
7 49
4
9
5
2 18
7 7
4
9
5
9
7 7 7
4 5
9 9
9
9
7 71 7.
Задания открытого банка задач
23,5 35,5
7. Найдите значение выражения
.
64,5
Решение.
23,5 35,5 23,5 35,5 23,5 35,5
3
3,5 4,5
5,5 4,5
1
1
2
3
2
3
1,5.
4,5
4,5
4,5
4,5
6
2 3
2
2 3
8. Найдите значение выражения 35 4,7 75,7 : 5 3,7 .
Решение.
35 4,7 75,7 : 5 3,7 5 7
4,7
5 4,7 3,7 7 4,7 5,7
75,7 53,7 5 4,7 7 4,7 75,7 53,7
7
5 1 71 1,4.
5
2,8 4,2
9. Найдите значение выражения
Решение.
2,8 4,2
2,8 4,2
28 42
49 7.
0,24
24
0,24
0,24
.
Задания открытого банка задач
10. Найдите значение выражения
Решение.
6
5
3
3 1 :
.
7
7
28
27
27
6
5
3
12
3
12 28
3 1 :
:
7
7 28 7
7 28 7
7
3
27 28
12 28
27 28
12 28
9 4 4 4 6 4 2.
7
3
7
3
7 3
7 3
11. Найдите значение выражения
Решение.
9
9
7 18 7
.
6
7
7 18 7 18 72 18 7 18 72 7 18 73 18
1 1.
3
3
6
18 3
7
7
7
7
Задания открытого банка задач
12. 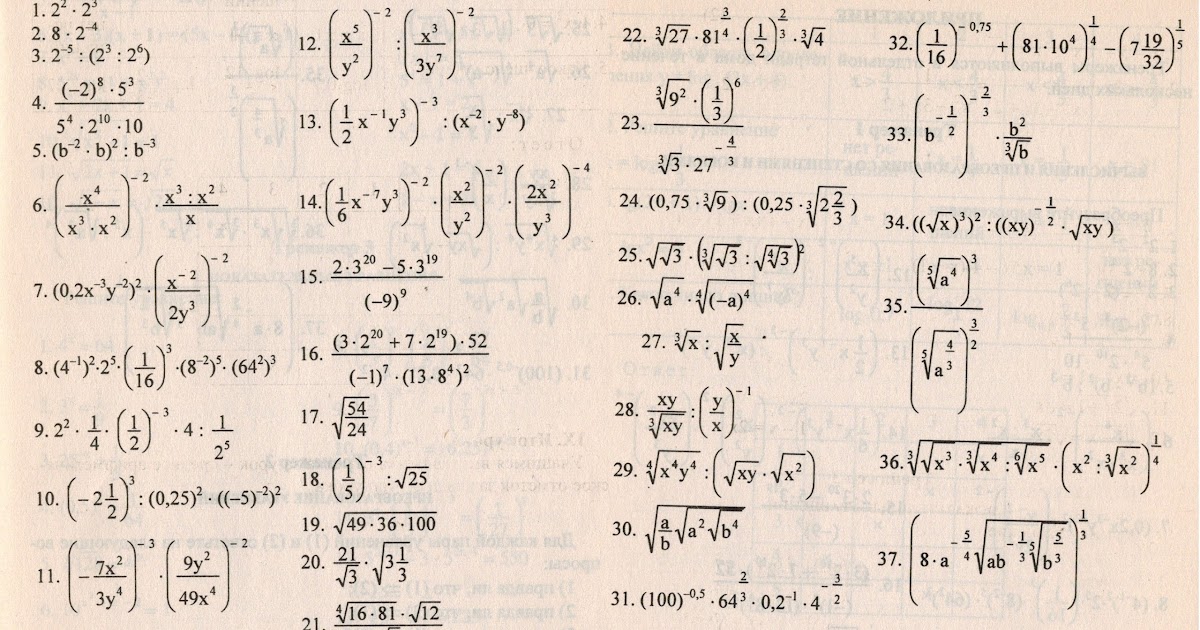Найдите значение выражения
Решение.
5
5
10 5 16
.
5
5
10 5 16 5 10 16 5
32 2.
5
5
5
13. Найдите значение выражения
Решение.
2 2
12
2
1
3
1
4
2
2 2
1
212
1
3
1
4
2
13 14
2 2
12
2
2
.
1 1 1 2
4 3 1 2
1 2
3 4 12
12
2
2 2.
2
2

English     Русский Правила

Полномочия и корни — короткие задачи

Это часть нашей коллекции коротких задач.

Вас также могут заинтересовать наши более длинные задачи о Силах и Корнях.

Рабочие листы для печати, содержащие выборку этих задач, доступны здесь.

Возраст Августа

Возраст от 11 до 14 Короткий

Уровень сложности

Английский математик Август де Морган определил свой возраст в алгебраических терминах. Можно узнать, когда он родился?

Десятая сила

Возраст от 11 до 14 лет Короткий

Уровень испытания

Эти силы выглядят странно. ..?

Квадратный процент

Возраст от 11 до 14 Короткий

Уровень сложности

Какой процент целых чисел от 1 до 10 000 составляют квадратные числа?

Квадрат моего возраста

Возраст от 11 до 14 Короткий

Уровень испытания

Лорен и Томас определяют свой возраст с помощью суммы квадратов. Можете ли вы определить, сколько им лет на самом деле?

Квадрат Треугольник

Возраст от 11 до 14 Короткий

Уровень сложности

Сколько треугольников имеют квадраты всех трех углов (в градусах)?

Mini Cross-number

Возраст от 11 до 14 Short

Challenge Level

Какая цифра заменяет x в этом crossnumber?

Чистые деньги

Возраст от 11 до 14 Короткий

Уровень испытания

Сколько денег раздала королева в пенсах в степени двойки?

у=1000$

Квадрат и корень

Возраст от 14 до 16 Короткий

Уровень сложности

Какой остаток получится, если квадрат из 49 разделить на квадратный корень из 49?

Пифагорейская четверка

Возраст от 14 до 16 Короткий

Уровень сложности

Сумма трех квадратных чисел равна $121$. Что это могут быть за числа…

Root 2017

Возраст от 14 до 16 Короткий

Уровень сложности

Между двумя целыми числами $\sqrt{2017}$ $?$

Полномочия четырех

Возраст от 14 до 16 лет Короткий

Уровень сложности

Сможете ли вы вычислить значение x в этом «мощном» уравнении?

Сила суммы

Возраст от 14 до 16 лет Короткий

Уровень сложности

Какова эта сумма, выраженная как степень двойки?

Мегабайты и килобайты

Возраст от 14 до 16 лет Короткий

Уровень сложности

Сколько байтов содержится в одном мегабайте?

Оценка корня

Возраст от 14 до 16 Короткий

Уровень сложности

Какое из этих значений является наилучшей аппроксимацией для этого квадратного корня?

Грубый корень

Возраст от 14 до 16 Короткий

Уровень сложности

Какой из этих вариантов ближе всего к этому квадратному корню?

Большой продукт

Возраст от 14 до 16 лет Короткий

Уровень сложности

Сколько цифр в этом продукте?

Мощный приказ

Возраст от 14 до 16 лет Короткий

Уровень испытания 98$?

Наибольшее выражение

Возраст от 14 до 16 лет Короткий

Уровень сложности

Какое из этих пяти алгебраических выражений является наибольшим, если $x$ находится между 0 и 1?

Корни около 9

Возраст от 14 до 16 Короткий

Уровень сложности

Для скольких целых чисел ð‘› разница между √𑛠и 9 меньше 1?

Какая Сила?

Возраст от 14 до 16 Короткий

Уровень сложности

Какая степень числа $16$ равна $64^6$? 99$ идеальные кубики?

Два на миллион

Возраст от 14 до 16 Короткий

Уровень сложности

Какова наибольшая степень числа 2, которая делится точно на 1000000?

Сколько квадратов?

Возраст от 14 до 16 Короткий

Уровень сложности

Сколько четырехзначных чисел являются полными квадратами?

Огромные силы

Возраст от 14 до 16 Короткий

Уровень сложности

Сможете ли вы расположить эти числа по порядку?

Мощные выражения 9{300}$?

Мощный 9

Возраст от 14 до 16 Низкий

Уровень сложности

Какая последняя цифра в этом расчете?

Степень 3

Возраст от 14 до 16 Короткий

Уровень сложности

Какая степень числа 27 нужна, чтобы получить правильную степень числа 3?

Power of Five

Возраст от 14 до 16 Short

Challenge Level

Степени со скобками, сложение и умножение

Знай свои силы

Возраст от 14 до 16 лет Короткий 9n$ является квадратным числом?

Решение десятичных задач со степенью десятка Скачать рабочий лист

Выберите другое занятие >

Один атта раз

Флэш-карты

Дистанционное обучение

Информация о листе >

Решение десятичных задач со степенью десятка

Каждый рабочий лист содержит 12 задач на умножение или деление десятичного числа в десятой степени.

Открыть PDF

Настроить предварительный просмотр

открыть в новом окне

Выберите рабочий лист
Уведомление : Неопределенный индекс: версия в /home/sabrep/public_html/page_files/download_worksheet/primary.php онлайн 209
Готовый 1
Уведомление : Неопределенный индекс: версия в public_html/page_files/download_worksheet/primary.php on line 209
Premade 2
Notice : Undefined index: version in /home/sabrep/public_html/page_files/download_worksheet/primary.php on line 209
Premade 3
Notice : Undefined index : версия в /home/sabrep/public_html/page_files/download_worksheet/primary.php в строке 209
Premade 4
Уведомление : Неопределенный индекс: версия в /home/sabrep/public_html/page_files/download_worksheet .php on line 209
Premade 5
Notice : Undefined index: version in /home/sabrep/public_html/page_files/download_worksheet/primary. php on line 209
Premade 6
Notice : Undefined index : версия в /home/sabrep/public_html/page_files/download_worksheet/primary.php в строке 209
Premade 7
Уведомление : Неопределенный индекс: версия в /home/sabrep/public_html/page_files/download_worksheet .php on line 209
Premade 8
Notice : Undefined index: version in /home/sabrep/public_html/page_files/download_worksheet/primary.php on line 209
Premade 9
Notice : Undefined index : версия в /home/sabrep/public_html/page_files/download_worksheet/primary.php в строке 209
Premade 10
Уведомление : Неопределенный индекс: версия в /home/sabrep/public_html/page_files/download_worksheets .php на линии 209
Все готовые
Уведомление : неопределенный индекс: версия в /home/sabrep/public_html/page_files/download_worksheet/primary.