Задачи теорема фалеса 8 класс: Задачи на теорему Фалеса — задачи с решениями

формула и примеры решения задач

Поможем решить контрольную, написать реферат, курсовую и диплом от 800р

Содержание:

• Формулировка теоремы Фалеса
• Примеры решения задач
• Историческая справка

Формулировка теоремы Фалеса

Теорема

Если на одной из двух прямых отложить последовательно несколько отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой пропорциональные отрезки (рис. 1).

В теореме нет ограничений на взаимное расположение секущих (она верна как для пересекающихся прямых, так и для параллельных). Также не важно, где находятся отрезки на секущих.

Теорема

Обобщённая теорема Фалеса

Параллельные прямые отсекают на секущих пропорциональные отрезки (рис. 1):

$$\frac{A_{1} A_{2}}{B_{1} B_{2}}=\frac{A_{2} A_{3}}{B_{2} B_{3}}=\frac{A_{1} A_{3}}{B_{1} B_{3}}$$

Теорема Фалеса является частным случаем обобщённой теоремы Фалеса, поскольку равные отрезки можно считать пропорциональными отрезками с коэффициентом пропорциональности, равным 1.

Теорема

Обратная теорема Фалеса

Если прямые, пересекающие две другие прямые (параллельные или нет), отсекают на обеих из них равные (или пропорциональные) между собой отрезки, начиная от вершины, то такие прямые параллельны (рис. 2).

Замечание. В обратной теореме Фалеса важно, что равные отрезки начинаются от вершины.

Примеры решения задач

Пример

Задание. Разделить данный отрезок на четыре равные части.

Решение. Пусть $AB$ — заданный отрезок (рис. 3), который необходимо разделить на четыре равные части.

Через точку $A$ проведем произвольную полупрямую $a$ и отложим на ней последовательно четыре равных между собой отрезка $AC, CD, DE, EK$ .

Соединим точки $B$ и $K$ отрезком и проведем через оставшиеся точки $C$, $D$ и $E$ прямые, параллельные прямой $BK$ так, чтобы они пересекли отрезок $AB$ .

Согласно теореме Фалеса отрезок $AB$ разделится на четыре равные части.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. На стороне $AB$ треугольника $ABC$ отмечена точка $K$. Отрезок $CK$ пересекает медиану $AM$ треугольника в точке $P$, причем $AK = AP$. Найти отношение $BK : PM$ .

Решение. Проведем через точку $M$ прямую, параллельную $CK$, которая пересечет $AB$ в точке $D$ (рис. 4).

По теореме Фалеса $BD = KD$ .

По теореме о пропорциональных отрезках имеем, что

$$P M=K D=\frac{B K}{2} \Rightarrow B K: P M=2: 1$$

Ответ. $B K: P M=2: 1$

Историческая справка

Теорема Фалеса (а также теоремы Чевы и Менелая) применяются в первую очередь тогда, когда в задаче даны соотношения между отрезками. Очень часто при этом приходится проводить дополнительный отрезок.

Аргентинская музыкальная группа представила песню, посвящённую теореме. В видеоклипе для этой песни приводится доказательство для прямой теоремы для пропорциональных отрезков.

Теорема Фалеса до сих пор используется в морской навигации в качестве правила о том, что столкновение судов, двигающихся с постоянной скоростью, неизбежно, если сохраняется курс судов друг на друга.

Вне русскоязычной литературы теоремой Фалеса иногда называют другую теорему планиметрии, а именно, утверждение о том, что вписанный угол, опирающийся на диаметр окружности, является прямым. Открытие этой теоремы действительно приписывается Фалесу, о чём есть свидетельство Прокла.

«Теорема Фалеса» 8 класс. Урок №9 по геометрии

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай».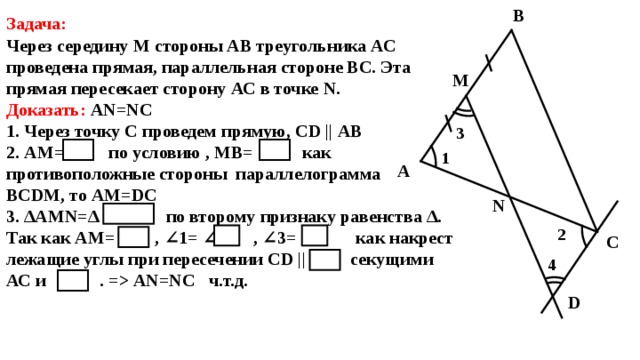 Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. Теорема Фалеса

Урок №9 по геометрии в 8
классе
Учитель: Федорова Т.Ф.
2009-2010 уч. год.
5klass.net

2. Цели урока:

• Рассмотреть теорему Фалеса и
закрепить ее в процессе решения
задач.
Совершенствовать навыки решения
задач на применение свойств
равнобедренной трапеции, ее
признаков, а также на применение
знаний по теме « Трапеция»

3. Задачи на готовых чертежах

В
В
С
С
75
40
А
D
Найти углы трапеции
В
А
BC║CD
Е
Найти углы трапеции
В
С
60
50
А
Найти С
D
А
5
D
С
60
Р
К
AD=7.Найти: СМ
D
В
С
х
Составим уравнение:
2х +х+90 = 180
3х = 180 — 90
х
х
3х = 90
2х
А
D
Х = 30
C = 30 + 90 = 120 .
Найти углы трапеции
Ответ:
А = D = 60 ,
C = B = 120 .

5. Ответы к задачам

1. A = D = 60 , B = C =120 .
2. A=40 , D=65 , C=115 , B=140 .
3. C = 100 .
4. CM =2.
Фалес Милетский
624-547г.г. до н.э.
Великий учёный Фалес
Милетский основал одну из
прекраснейших наукгеометрию. Известно, что
Фалес Милетский имел титул
одного из семи мудрецов
Греции, что он был поистине
первым философом, первым
математиком, астрономом и
вообще первым по всем наукам
в Греции. Короче: он был то
же для Греции, что Ломоносов
для России.
Карьеру он начинал как купец и ещё в
молодости попал в Египет. В Египте
Фалес застрял на много лет, изучая
науки в Фивах и Мемфисе.
Считается, что геометрию и
астрономию в Грецию привёз он.
Фалес- математик. Он измерил по
тени высоту пирамиды; установил,
что окружность диаметром
делится пополам, что углы при
основании равнобедренного
треугольника равны. Ему же
принадлежит теорема, что
вписанный угол, опирающийся на
диаметр окружности- прямой
До наших дней дошли изречения Фалеса, вот некоторые из них:
.
Фалес известен как геометр. Ему приписывают открытие и доказательство
ряда теорем: о делении круга диаметром пополам, о равенстве углов при
основании равнобедренного треугольника, о равенстве вертикальных
углов, один из признаков равенства прямоугольных треугольников и
другие. Он открыл любопытный способ определения расстояния от берега
до видимого корабля.
Столь же остроумно Фалес предложил измерять высоту предметов. Став недалеко
от предмета, надо дождаться пока тень человека не сделается равной его росту.
Измерив тогда длину тени предмета, можно заключить, что она равно длине
предмета. Говорят, что таким способом он измерял высоту египетских пирамид.

13. Задача № 384

В
1
М
3
Дано: тр-к АВС
АМ =МВ
N
4 D
МN || АС
Доказать: ВN =NC
2
А
С
Теорема: если параллельные прямые, пересекающие стороны
угла, отсекают на одной его стороне равные отрезки, то они
отсекают равные отрезки и на другой его стороне.
Дано: угол, параллельные прямые
пересекают стороны угла, А1А2=А2А3
В2
F
Доказать: В1В2=В2В3
В3
Доказательство.
E
1. Проведём через точку В2 прямую ЕF,
параллельную прямой А1А3.
В1
А1
А2
А3
2. По свойству параллелограмма
А1А2=FВ2, А2А3=В2Е.
3. Так как А1А2=А2А3, то FВ2=В2Е
4. Треугольники В2В1F и В2В3Е равны по
второму признаку ( у них В2F=В2Е по
доказанному. Углы при вершине В2
равны как вертикальные, а углы
В2FВ3равны как внутренние накрест
лежащие при параллельных А1В1 и А3В3
и секущей ЕF.)
5. Из равенства треугольников следует

16. Задача № 385

А1
А2
А3
А4
А1
А2
А3
А4
В1
В2
В3
В4
С
D
В1
В2
В3
В4
а
в
а
с
в
ЗАДАЧА: РАЗДЕЛИТЕ ДАННЫЙ ОТРЕЗОК НА n
РАВНЫХ ЧАСТЕЙ
Вn-1
В1
В2
В
2.Отложим на луче АО
равные отрезки:АА1,
А1А2, А2А3, …, Аn-1Аn.
В3
А
А1
А2
А3
1. Проведём из точки А
луч АО, не лежащий на
отрезке АВ.
Аn-1
Аn
О
3.Соединим отрезком
точку Аn с точкой В.
4.Через точки А1,А2, …
Аn-1проведём прямые,
параллельные АnВ.
5.По теореме Фалеса
отрезки АВ1, В1В2, …,Вn1В равны.

18. Задачи на готовых чертежах

B
Задачи на готовых чертежах
A
A1 A2 A3 A4
F
E
B1
5
4
12
A
C
EF║AC. Найти:РАВС
В
B3
B4
АВ4=20. Найти:В2В3.
С
10
В
С
М
N
М
B2
O
А
Доказать:АО = СО
D
А
К
Е
МК║ВЕ║СD, AD=16.
Найти:АК.
D

19. Задача №386

• Докажите, что отрезок, соединяющий середины
боковых сторон трапеции, параллелен
основаниям трапеции.
В
M
А
С
N
D

20. Задача № 393 б)

d1
d2
Дано:d1-диагональАС
d2- диагональ ВD
а- угол между диагоналями
a
Построить:
АВСD

21. Анализ

В
С
О
А
D
Допустим, что АВСD построен. СО = 0,5d1, ОD = 0,5d2,
значит, треугольник СОD можем построить по двум
сторонам и углу между ними, а затем достроим его до
параллелограмма.

22. Доказательство

В четырёхугольнике АВСD диагонали точкой
пересечения делятся пополам, значит АВСDпараллелограмм. АС=d1, ВD = d2 ,
угол СОD=a, значит АВСD – искомый
параллелограмм.

23. Исследование

Задача имеет одно решение и всегда возможна.

24. Домашнее задание

Задачи № 391, № 392
Дополнительная задача:
В равнобедренной трапеции острый
угол равен 60 . Докажите, что меньшее
основание равно разности большего
основания и боковой стороны.

English     Русский Правила

Теорема Фалеса – Объяснение и примеры

После того, как мы рассмотрели теорему о вписанном угле, пришло время изучить другую родственную теорему, которая является частным случаем теории вписанного угла m, , называемой теоремой Фалеса . Как и теорема о вписанном угле, ее определение также основано на диаметре и углах внутри круга.

Из этой статьи вы узнаете:

• Теорема Фалеса,
• Как решить теорему Фалеса; и
• Как решить теорему Фалеса только с одной стороной

 

Что такое теорема Фалеса?

Теорема Фалеса утверждает, что:

Если на окружности лежат три точки A, B и C, причем прямая AC является диаметром окружности, то угол ∠ ABC  – прямой угол (90°).

В качестве альтернативы мы можем сформулировать теорему Фалеса как:

Диаметр окружности всегда образует прямой угол с любой точкой окружности.

Вы заметили, что теорема Фалеса является частным случаем теоремы о вписанном угле (центральный угол равен удвоенному вписанному углу).

Теорема Фалеса приписывается Фалесу, греческому математику и философу, жившему в Милете. Фалес первым инициировал и сформулировал «Теоретическое изучение геометрии», чтобы сделать астрономию более точной наукой.

Существует способа доказать теорему Фалеса . Мы можем использовать методы геометрии и алгебры, чтобы доказать эту теорему. Поскольку это тема геометрии, давайте рассмотрим самый простой метод ниже.

Как решить теорему Фалеса?

• Чтобы доказать теорему Фалеса, проведите серединный перпендикуляр к ∠
• Пусть точка M будет серединой прямой AC.
• Пусть также ∠ MBA = ∠ BAM = β и ∠ MBC =∠ BCM =α
• Линия AM = MB = MC = радиус окружности.
• Δ AMB и Δ MCB равнобедренные треугольники.

По теореме суммы треугольника,

∠ BAC +∠ ACB +∠ CBA = 180°

β + β + α + α = 180° 90 уравнение.

2 β + 2 α = 180°

2 (β + α) = 180°

Разделить обе стороны на 2.

β + α = 90°.

Следовательно, ∠ ABC = 90°, следовательно, доказано

. Давайте решим несколько примеров задач, связанных с теоремой Фалеса.

Пример 1

Учитывая, что точка O является центром круга, показанного ниже, найдите значение x.

Решение

Учитывая, что прямая XY диаметр окружности, то по теореме Фалеса

∠ XYZ = 90°.

Сумма внутренних углов треугольника = 180°

90° + 50° + x =180°

Упростить.

140° + x =180°

Вычесть 140° с обеих сторон.

х = 180° – 140°

х = 40°.

Итак, значение x равно 40 градусам.

Пример 2

Если точка D является центром круга, показанного ниже, рассчитайте диаметр круга.

Решение

По теореме Фалеса, треугольник ABC — прямоугольный треугольник, где ∠ ACB = 90°.

Чтобы найти диаметр окружности, примените теорему Пифагора.

CB ² + AC ² =AB ²

8 ² + 6 ² = AB ²

64 + 36 = AB ²

100 = AB ²

AB = 10

Следовательно, диаметр круга равен 10 см

Пример 3

Найдите угол PQR в круге, показанном ниже.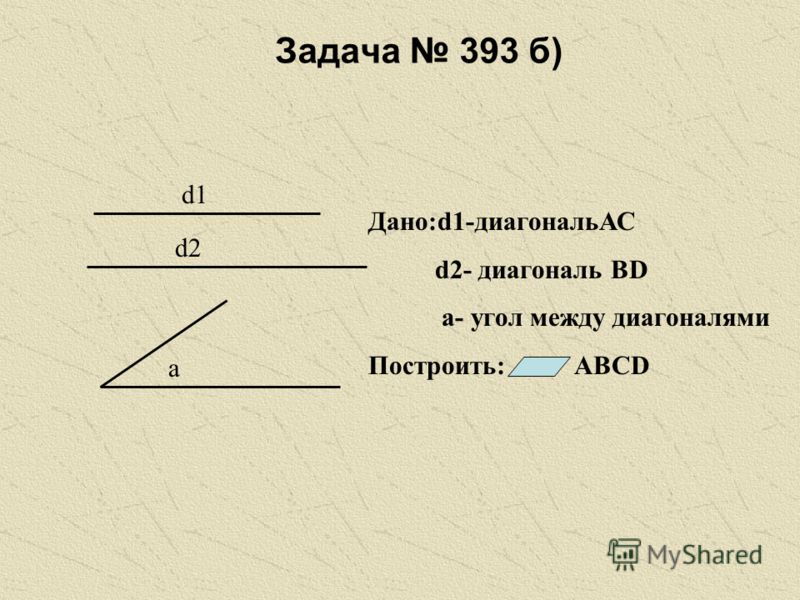 Предположим, что точка R является центром окружности.

Решение

Треугольник RQS и PQR равнобедренные треугольники.

тий RQS = ♂ RSQ = 64 °

Теорема Thales, тий PQS = 90 °

.0007

= 26°

Следовательно, угол PQR равен 26°.

Пример 4

Какое из следующих утверждений верно относительно определения теоремы Фалеса?

A. Центральный угол в два раза больше вписанного угла

B. Угол, вписанный в полуокружность, будет прямым.

C. Диаметр окружности — самая длинная хорда.

D. Диаметр круга в два раза больше длины радиуса.

Решение

Правильный ответ:

B. Угол, вписанный в полуокружность, будет прямым.

Пример 5

В показанном ниже круге линия AB представляет собой диаметр круга с центром C .

1. Найдите меру ∠ г. до н.э.
2. ∠ DCA
3. ∠ ACE
4. ∠ DCB

Решение

Данный треугольник ACE представляет собой треугольник Isocles,

тий CEA = ♂ CAE = 33 °

SO, T ACE = 180 ° — (33 ° + 33 °) Тий ACE = 114 °

, но углы на прямой = 180 °

Следовательно, ▲ BCE = 180 ° — 114 °

= 66 °

ТРИ -РАН ADC — это ISOSCELES Triangle, С. DAC =20°

По теореме суммы треугольников, ∠ DCA = 180 ° — (20 ° + 20 °)

тий DCA = 140 °

тий DCB = 180 ° — 140 °

= 40 °

Пример 6

Пример 6

Какова мера ∠ ABC ?

Раствор

Теорема Фалеса гласит, что BAC = 90 °

и по теореме SUM Triangle,

♂ ABC + 40 ° + 90 ° = 180 °

тром 9 ABC = 101010101010101010101010101010101010101010 100 ° = 180 °

тром 10 + ° + 90 ° = 180 °

тром 0 + 9010 ° = 90 ° = 180 °

тром

0 + 90 °. – 130°

= 50°

Пример 7

Найдите длину AB в круге, показанном ниже.

Решение

Треугольник ABC прямоугольный.

Примените теорему Пифагора, чтобы найти длину AB .

AB ² + 12 ² = 18 ²

AB ² + 144 = 324

AB ² + 144 = 324

AB ^{2 2924 — 324}

AB ² = 144 = 324

AB ² .0007

АВ ² = 180

АВ = 13,4

Следовательно, длина АВ равна 13,4 см.

Применение теоремы Фалеса

В геометрии ни одна из тем не используется в реальной жизни. Следовательно, теорема Фалеса также имеет некоторые приложения:

• Мы можем точно провести касательную к окружности, используя теорему Фалеса. Для этой цели можно использовать угольник.
• Мы можем точно найти центр круга, используя теорему Фалеса. Инструменты, используемые для этого приложения, представляют собой угольник и лист бумаги. Во-первых, вы должны поместить угол на окружность — пересечение двух точек с окружностью определяет диаметр. Вы можете повторить это, используя другую пару точек, что даст вам другой диаметр. Пересечение диаметров даст вам центр круга.

 

Евклидова геометрия | Определение, аксиомы и постулаты

конгруэнтные треугольники

Просмотреть все СМИ

Ключевые люди:

Евклид Дэвид Гилберт Марьям Мирзахани Адриан-Мари Лежандр

Связанные темы:

теорема Пифагора метод истощения квадратура постулат параллельности Принцип Кавальери

Просмотреть весь связанный контент →

Резюме

Прочтите краткий обзор этой темы

Евклидова геометрия , изучение плоских и объемных фигур на основе аксиом и теорем, используемых греческим математиком Евклидом (ок. 300 г. до н. э.). В общих чертах евклидова геометрия — это плоскостная и объемная геометрия, обычно изучаемая в средних школах. Действительно, до второй половины XIX века, когда неевклидовы геометрии привлекли внимание математиков,

геометрия означала евклидову геометрию. Это наиболее типичное выражение общего математического мышления. Вместо запоминания простых алгоритмов решения уравнений наизусть требуется глубокое понимание предмета, умные идеи для применения теорем в особых ситуациях, способность обобщать известные факты и настаивать на важности доказательства. В великом труде Евклида « элементов » единственными инструментами, используемыми для геометрических построений, были линейка и циркуль — ограничение, сохранившееся в элементарной евклидовой геометрии и по сей день.

В своей строгой дедуктивной организации Элементы оставались самой моделью научного изложения до конца 19 века, когда немецкий математик Давид Гильберт написал свои знаменитые Основ геометрии (1899).

Современная версия евклидовой геометрии — это теория евклидовых (координатных) многомерных пространств, где расстояние измеряется подходящим обобщением теоремы Пифагора. См. аналитическая геометрия и алгебраическая геометрия.

Евклид понял, что строгое развитие геометрии должно начинаться с основ. Следовательно, он начал « элементов » с некоторых неопределенных терминов, таких как «точка — это то, что не имеет частей» и «линия — это длина без ширины». Исходя из этих терминов, он определил дальнейшие понятия, такие как углы, окружности, треугольники и различные другие многоугольники и фигуры. Например, угол определялся как наклон двух прямых, а окружность — это плоская фигура, состоящая из всех точек, находящихся на фиксированном расстоянии (радиусе) от данного центра.

В качестве основы для дальнейших логических выводов Евклид предложил пять общих понятий, таких как «вещи, равные одной и той же вещи, равны», и пять недоказуемых, но интуитивных принципов, известных как постулаты или аксиомы.

В современных терминах аксиомы таковы:

Викторина по Британике

Дайте определение: математические термины

Вот ваша миссия, если вы решите ее принять: Дайте определение следующим математическим терминам до того, как истечет время.

• 1. Даны две точки, их соединяет прямая.

• 2. Прямой отрезок можно продолжать до бесконечности.

• 3. Окружность можно построить, если заданы точка для ее центра и расстояние для ее радиуса.

• 4. Все прямые углы равны.

• 5. Если прямая, падающая на две прямые, образует внутренние углы с одной и той же стороны меньше, чем два прямых угла, то две прямые, если их провести бесконечно, встретятся с той стороны, на которой углы меньше два прямых угла.

Гильберт усовершенствовал аксиомы (1) и (5) следующим образом:

• 1. Для любых двух различных точек (а) существует прямая, содержащая эти две точки, и (б) эта прямая единственна.

  No related posts.