|
1.Биномиальный закон распределения. 2.Геометрическое распределение. 3.Гипергеометрическое распределение. 4.Закон распределения Пуассона. 5.Равномерный закон распределения. 6.Нормальный закон распределения (закон Гаусса). 7.Показательный закон распределения. 8.Логарифмически-нормальное распределение. 9. χ ² распределение. 10.Распределение Стьюдента (t — распределение). 11.Распределение Фишера-Снедекора.
|
|||||||||||||||||||||||||||||
| 22 23 24 25 26 27 28 29 30 | |||||||||||||||||||||||||||||
1. Биномиальный закон распределения. Биномиальный закон распределения.
Биномиальный закон распределения описывает вероятность наступления события А m раз в n независимых испытаниях, при условии, что вероятность р наступления события А в каждом испытании постоянна.
|
|||||||||||||||||||||||||||||
Например, отдел продаж магазина бытовой техники в среднем получает один заказ на покупку телевизоров из 10 звонков. Составить закон распределения вероятностей на покупку m телевизоров. Построить полигон распределения вероятностей. |
|||||||||||||||||||||||||||||
Рис.1 |
|||||||||||||||||||||||||||||
|
В таблице m — число заказов, полученных компанией на покупку телевизора.
|
|||||||||||||||||||||||||||||
2.Геометрическое распределение. |
|||||||||||||||||||||||||||||
Геометрическое распределение случайной величины имеет следующий вид: где Pm — вероятность наступления события А в испытание под номером m. Пример. В компанию по ремонту бытовой техники поступила партия из 10 запасных блоков для стиральных машин. |
|||||||||||||||||||||||||||||
Рис.2 |
|||||||||||||||||||||||||||||
|
Из таблицы видно, что с увеличением числа m, вероятность того, что будет обнаружен бракованный блок, снижается. Последняя строчка (m=10) объединяет две вероятности: 1 — что десятый блок оказался неисправным — 0,038742049 , 2 — что все проверяемые блоки оказались исправными — 0,34867844. Так как вероятность того, что блок окажется неисправным относительно низкая (р=0,1), то вероятность последнего события Pm (10 проверенных блоков) относительно высокая.
|
|||||||||||||||||||||||||||||
3.Гипергеометрическое распределение. |
|||||||||||||||||||||||||||||
Гипергеометрическое распределение случайной величины имеет следующий вид: где Например, составить закон распределения 7-ми угаданных чисел из 49. В данном примере всего чисел N=49, изъяли n=7 чисел, M — всего чисел, которые обладают заданным свойством, т.е. правильно угаданных чисел, m — число правильно угаданных чисел среди изъятых. |
|||||||||||||||||||||||||||||
Рис.3 |
|||||||||||||||||||||||||||||
|
Из таблицы видно, что вероятность угадывания одного числа m=1 выше, чем при m=0.
|
|||||||||||||||||||||||||||||
4.Закон распределения Пуассона. |
|||||||||||||||||||||||||||||
Случайная величина Х имеет распределение Пуассона, если закон ее распределения имеет вид: где λ = np = const
Например, в среднем за день в компанию по продаже телевизоров поступает около 100 звонков. Вероятность заказа телевизора марки А равна 0,08; B — 0,06 и C — 0,04. Из условия имеем: m=100, λ1=8, λ2=6, λ3=4 ( ≤10 ) |
|||||||||||||||||||||||||||||
|
(таблица дана не полностью) |
Рис.4 |
||||||||||||||||||||||||||||
Если n достаточно большое и стремится к бесконечности, а значение p стремится к нулю, так что произведение np стремится к постоянному числу, то данный закон является приближением к биномиальному закону распределения. Из графика видно, что чем больше вероятность р, тем ближе кривая расположена к оси m, т.е. более пологая. (Рис.4) |
|||||||||||||||||||||||||||||
|
Необходимо отметить, что биномиальный, геометрический, гипергеометрический и закон распределения Пуассона выражают распределение вероятностей дискретной случайной величины.
|
|||||||||||||||||||||||||||||
5.Равномерный закон распределения. |
|||||||||||||||||||||||||||||
Если плотность вероятности ϕ(х) есть величина постоянная на определенном промежутке [a,b], то закон распределения называется равномерным. На рис.5 изображены графики функции распределения вероятностей и плотность вероятности равномерного закона распределения. |
|||||||||||||||||||||||||||||
|
|
Рис.5 |
||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||
6.Нормальный закон распределения (закон Гаусса). |
|||||||||||||||||||||||||||||
Среди законов распределения непрерывных случайных величин наиболее распрастраненным является нормальный закон распределения. Случайная величина распределена по нормальному закону распределения, если ее плотность вероятности имеет вид: где |
|||||||||||||||||||||||||||||
|
График плотности вероятности случайной величины, имеющей нормальный закон распределения, симметричен относительно прямой х=а, т. При изменении величины математического ожидания кривая будет смещаться вдоль оси Ох. На графике (Рис.6) видно, что при х=3 кривая имеет максимум, т.к. математическое ожидание равно 3. Если математическое ожидание примет другое значение, например а=6, то кривая будет иметь максимум при х=6. Говоря о среднем квадратическом отклонении, как можно увидеть из графика, чем больше среднее квадратическое отклонение, тем меньше максимальное значение плотности вероятности случайной величины. |
Рис.6 |
||||||||||||||||||||||||||||
Функция, которая выражает распределение случайной величины на интервале (-∞,х), и имеющая нормальный закон распределения, выражается через функцию Лапласа по следующей формуле: |
Рис. 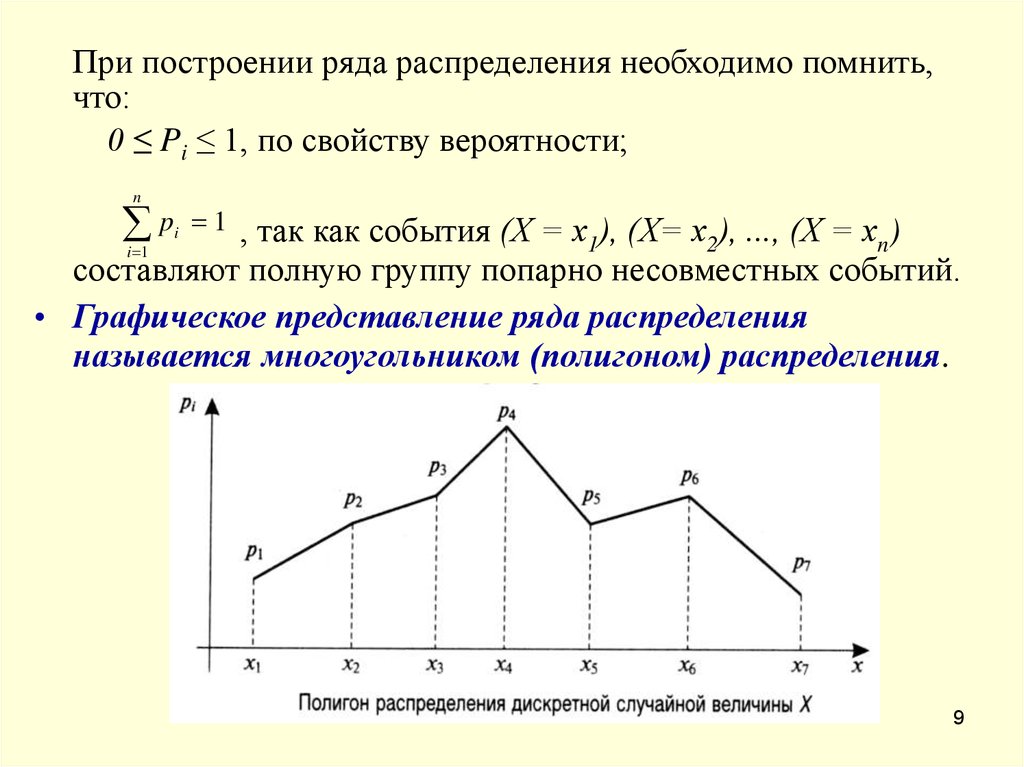 7 7 |
||||||||||||||||||||||||||||
Т.е. вероятность случайной величины Х состоит из двух частей: вероятности где x принимает значения от минус бесконечности до а, равная 0,5 и вторая часть — от а до х. (Рис.7)
|
|||||||||||||||||||||||||||||
7.Показательный закон распределения. |
|||||||||||||||||||||||||||||
Закон распределения случайной величины Х называется показательным (или экспоненциальным), если плотность вероятности имеет вид: где λ — параметр обратно-пропорциональный математическому ожиданию. График плотности вероятности с параметрами |
Рис.  8 8 |
||||||||||||||||||||||||||||
Функция распределения случайной величины Х, которая имеет показательное распределение, имеет вид: График функции изображен на рис.9 Если функцию распределения случайной величины выразить через плотность вероятности при х ≥ а, то она примет вид:
|
Рис.9 |
||||||||||||||||||||||||||||
8.Логарифмически-нормальное распределение. |
|||||||||||||||||||||||||||||
Если логарифм непрерывной случайной величины изменяется по нормальному закону, то случайная величина имеет логарифмически-нормальное распределение. Функция логаривмически-нормального распределения имеет вид. |
|||||||||||||||||||||||||||||
Рис.  10 10 |
|||||||||||||||||||||||||||||
|
Из графика видно, что чем меньше σ и больше математическое ожидание а, тем кривая становится более пологая и больше стремится к симметрии. Данный закон, чаще всего, используется для описания распределения поступления денежных средств (доходов), банковских вкладов, износа основных средств и т.д. (Рис.10)
|
|||||||||||||||||||||||||||||
9. χ ² распределение |
|||||||||||||||||||||||||||||
|
Сумма квадратов k независимых случайных величин, которые распределены по нормальному закону, называется χ ² распределением. χ ² распределение имеет вид: где Аi — i-ая случайная величина, распределенная по нормальному закону (i = 1,2,3,.
|
|||||||||||||||||||||||||||||
|
Плотность вероятности случайной величины, распределенной по распределению χ ² имеет вид:
|
Рис.11 |
||||||||||||||||||||||||||||
|
Из графика видно, что чем больше n=k, тем кривая стремиться к нормальному распределению. Рис.11.
|
|||||||||||||||||||||||||||||
10.Распределение Стьюдента (t — распределение) |
|||||||||||||||||||||||||||||
Распределение непрерывной случайной величины называется распределением Стьюдента, если оно имеет вид: где Z — случайная величина, распределенная по нормальному закону.
|
|||||||||||||||||||||||||||||
Плотность вероятности распределения Стьюдента имеет вид: |
Рис.12 |
||||||||||||||||||||||||||||
|
На рис.12 изображена плотность вероятности распределения Стьюдента. Из графика можно увидеть, что чем больше k, тем больше кривая приближается к нормальному распределению.
|
|||||||||||||||||||||||||||||
11. Распределение Фишера-Снедекора. |
|||||||||||||||||||||||||||||
|
Распределение случайной величины Фишера-Снедекора имеет вид: |
|||||||||||||||||||||||||||||
Плотность вероятности случайной величины имеет вид: |
Рис.  13 13 |
||||||||||||||||||||||||||||
|
При стремлении n к бесконечности распределение Фишера-Снедекора стремится к нормальному закону распределения.(Рис.13)
|
|||||||||||||||||||||||||||||
| 22 23 24 25 26 27 28 29 30 | |||||||||||||||||||||||||||||
Подбор закона распределения случайной величины по данным статистической выборки средствами Python / Хабр
О чём могут «рассказать» законы распределения случайных величин, если научиться их «слушать»
Законы распределения случайных величин наиболее «красноречивы» при статистической обработке результатов измерений. Адекватная оценка результатов измерений возможна лишь в том случае, когда известны правила, определяющие поведение погрешностей измерения. Основу этих правил и составляют законы распределения погрешностей, которые могут быть представлены представлены в дифференциальной (pdf) или интегральной (cdf) формах.
Адекватная оценка результатов измерений возможна лишь в том случае, когда известны правила, определяющие поведение погрешностей измерения. Основу этих правил и составляют законы распределения погрешностей, которые могут быть представлены представлены в дифференциальной (pdf) или интегральной (cdf) формах.
К основным характеристикам законов распределения относятся: наиболее вероятное значение измеряемой величины под названием математическое ожидание (mean); мера рассеивания случайной величины вокруг математического ожидания под названием среднеквадратическое отклонение (std).
Дополнительными характеристиками являются – мера скученности дифференциальной формы закона распределения относительно оси симметрии под названием асимметрия (skew) и мера крутости, огибающей дифференциальной формы под названием эксцесс (kurt). Читатель уже догадался, что приведенные сокращения взяты из библиотек scipy. stats, numpy, которые мы и будем использовать.
Рассказ о законах распределения погрешности измерений был бы неполным, если не упомянуть об связи между энтропийным и среднеквадратичным значением погрешности. Не утомляя читателей длинными выкладками из информационной теории измерений [1], сразу сформулирую результат.
С точки зрения информации, нормальное распределение приводит к получению точно такого же количества информации, как и равномерное. Запишем выражение для погрешности delta0 с использованием функций приведённых выше библиотек для распределения случайной величины x.
Это позволяет заменить любой закон распределения погрешности равномерным с тем же значением delta0.
Введём ещё один показатель – энтропийный коэффициент k, который для нормального распределения равен:
Следует отметить, что любое распределение отличное от нормального, будет иметь меньший энтропийный коэффициент.
Лучше один раз увидеть, чем семь раз прочитать. Для дальнейшего сравнительного анализа интегральных распределений: равномерного, нормального и логистического модернизируем примеры, приведённые в документации [2].
Программа для нормального распределения:
from scipy.stats import norm
import matplotlib.pyplot as plt
import numpy as np
fig, ax = plt.subplots(1, 1)
# Calculate a few first moments:
mean, var, skew, kurt = norm.stats(moments='mvsk')
# Display the probability density function (``pdf``):
x = np.linspace(norm.ppf(0.01), norm.ppf(0.99), 100)
ax.plot(x, norm.pdf(x),
'r-', lw=5, alpha=0.6, label='norm pdf')
ax.plot(x, norm.cdf(x),
'b-', lw=5, alpha=0.6, label='norm cdf')
# Check accuracy of ``cdf`` and ``ppf``:
vals = norm.ppf([0.001, 0.5, 0.999])
np.allclose([0.001, 0.5, 0.999], norm.cdf(vals))
# True
# Generate random numbers:
r = norm.rvs(size=1000)
# And compare the histogram:
ax.hist(r, normed=True, histtype='stepfilled', alpha=0.2)
ax.legend(loc='best', frameon=False)
plt.show()
Программа для равномерного распределения:
from scipy.stats import uniform import matplotlib.pyplot as plt import numpy as np fig, ax = plt.subplots(1, 1) # Calculate a few first moments: #mean, var, skew, kurt = uniform.stats(moments='mvsk') # Display the probability density function (``pdf``): x = np.linspace(uniform.ppf(0.01), uniform.ppf(0.99), 100) ax.plot(x, uniform.pdf(x),'r-', lw=5, alpha=0.6, label='uniform pdf') ax.plot(x, uniform.cdf(x),'b-', lw=5, alpha=0.6, label='uniform cdf') # Check accuracy of ``cdf`` and ``ppf``: vals = uniform.ppf([0.001, 0.5, 0.999]) np.allclose([0.001, 0.5, 0.999], uniform.cdf(vals)) # True # Generate random numbers: r = uniform.rvs(size=1000) # And compare the histogram: ax.hist(r, normed=True, histtype='stepfilled', alpha=0.2) ax.legend(loc='best', frameon=False) plt.show()
Программа для логистического распределения.
from scipy.stats import logistic import matplotlib.pyplot as plt import numpy as np fig, ax = plt.subplots(1, 1) # Calculate a few first moments: mean, var, skew, kurt = logistic.stats(moments='mvsk') # Display the probability density function (``pdf``): x = np.linspace(logistic.ppf(0.01), logistic.ppf(0.99), 100) ax.plot(x, logistic.pdf(x), 'g-', lw=5, alpha=0.6, label='logistic pdf') ax.plot(x, logistic.cdf(x), 'r-', lw=5, alpha=0.6, label='logistic cdf') vals = logistic.ppf([0.001, 0.5, 0.999]) np.allclose([0.001, 0.5, 0.999], logistic.cdf(vals)) # True # Generate random numbers: r = logistic.rvs(size=1000) # And compare the histogram: ax.hist(r, normed=True, histtype='stepfilled', alpha=0.2) ax.legend(loc='best', frameon=False) plt.show()
Теперь мы знаем, как выглядят интегральные формы нормального, равномерного и логистического законов и можем приступить к их сравнению с тестовым распределением поставив более общий вопрос — подбора закона распределения случайной величины по данным статистической выборки.
Как подобрать закон распределения, имея интегральное распределения вероятности тестовой выборки
Подготовим первую часть программы, которая будет осуществлять сравнение перечисленных интегральных распределений с тестовой выборкой. Для этого зададим общие для законов распределения основные параметры — математическое ожидание и среднеквадратичное отклонение, используя равномерное распределение.
Для этого зададим общие для законов распределения основные параметры — математическое ожидание и среднеквадратичное отклонение, используя равномерное распределение.
Первая часть программы предназначена для подготовки к сравнению трёх законов распределения в интегральной форме.
from scipy.stats import logistic,uniform,norm,pearsonr
from numpy import sqrt,pi,e
import numpy as np
import matplotlib.pyplot as plt
fig, ax = plt.subplots(1, 1)
n=1000# объём выборки
x=uniform.rvs(loc=0, scale=150, size=n)#равномерное распределение
x.sort()#сортировка
print("Математическое ожидание по выборке(общее для сравниваемых распределений) -%s"%str(round(np.mean(x),3)))
print("СКО по выборке(общее для сравниваемых распределений) -%s"%str(round(np.std(x),3)))
print("Энтропийное значение погрешности-%s"%str(round(np.std(x)*sqrt(np.pi*np.e*0.5),3)))
pu=uniform.cdf(x/(np.max(x)))#равномерное интегральное распределение
ax.plot(x,pu, lw=5, alpha=0.6, label='uniform cdf')
pn=norm. cdf(x, np.mean(x), np.std(x))#нормальное интегральное распределение
ax.plot(x,pn, lw=5, alpha=0.6, label='norm cdf')
pl=logistic.cdf(x, np.mean(x), np.std(x))# логистическое интегральное распределение
ax.plot(x,pl, lw=5, alpha=0.6, label='logistic cdf')
cdf(x, np.mean(x), np.std(x))#нормальное интегральное распределение
ax.plot(x,pn, lw=5, alpha=0.6, label='norm cdf')
pl=logistic.cdf(x, np.mean(x), np.std(x))# логистическое интегральное распределение
ax.plot(x,pl, lw=5, alpha=0.6, label='logistic cdf')
Здесь и далее результаты для сравнения введены в функцию print для контроля за ходом вычислений.
Тестовое интегральное распределение и результаты сравнения приведены во второй части программы. В ней определяются коэффициенты корреляции между тестовым и каждым из трёх интегральных законов распределения.
Поскольку коэффициенты корреляции могут отличатся незначительно, введено дополнительное определение возвещённых квадратов отклонения.
Вторая часть программы
p=np.arange(0,n,1)/n
ax.plot(x,p, lw=5, alpha=0.6, label='test')
ax.legend(loc='best', frameon=False)
plt.show()
print("Корреляция между нормальным распределением и тестовым - %s"%str(round(pearsonr(pn,p)[0],3)))
print("Корреляция между логистическим распределением и тестовым - %s"%str(round(pearsonr(pl,p)[0],3)))
print("Корреляция между равномерным распределением и тестовым - %s"%str(round(pearsonr(pu,p)[0],3)))
print('Взвешенная сумма квадратов отклонения нормального распределения от теста -%i'%round(n*sum(((pn-p)/pn)**2)))
print('Взвешенная сумма квадратов отклонения логистического распределения от теста -%i'%round(n*sum(((pl-p)/pl)**2)))
print('Взвешенная сумма квадратов отклонения равномерного распределения от теста -%i'%round(n*sum(((pu-p)/pu)**2))) Тестовая функция интегральной формы закона распределения построена в виде ступенчатого накопления –0+ 1/n +2/n+……+1
График и результат роботы программы.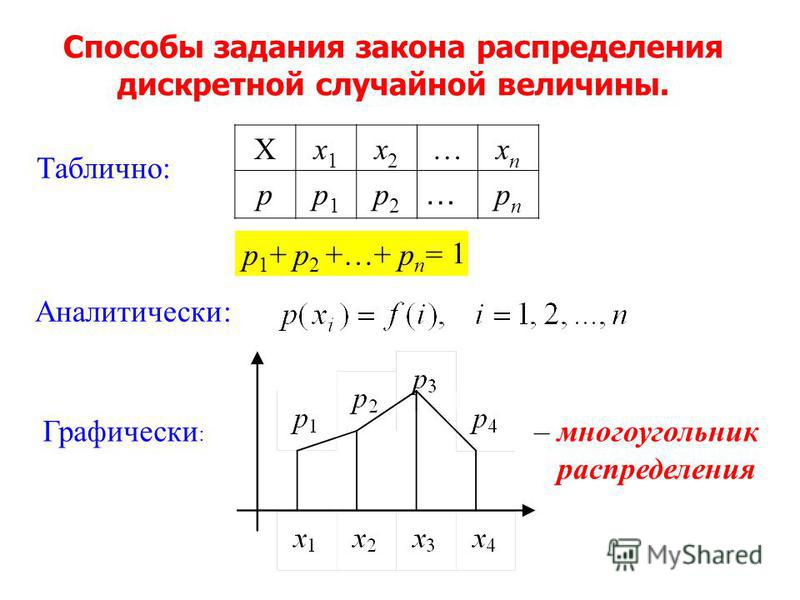
Математическое ожидание по выборке (общее для сравниваемых распределений) —77.3
СКО по выборке (общее для сравниваемых распределений) —43.318
Энтропийное значение погрешности-89.511
Корреляция между нормальным распределением и тестовым — 0.994
Корреляция между логистическим распределением и тестовым — 0.998
Корреляция между равномерным распределением и тестовым — 1.0
Взвешенная сумма квадратов отклонения нормального распределения от теста —37082
Взвешенная сумма квадратов отклонения логистического распределения от теста —75458
Взвешенная сумма квадратов отклонения равномерного распределения от теста —6622
Тестовое распределение вероятностей в интегральной форме является равномерным. При минимальном отличии по коэффициенту корреляции для равномерного распределения взвешенное отклонение от тестового в 5,6 раза меньше, чем у нормального и в 11 раз меньше, чем у логистического.
Вывод
Приведенная реализация подбора закона распределения случайной величины по данным статистической выборки возможно будет полезной при решении аналогичных задач.
1. Элементы информационной теории измерений.
2. Statistical functions.
Типы и использование в инвестировании
Что такое распределение вероятностей?
Распределение вероятностей — это статистическая функция, описывающая все возможные значения и вероятности, которые случайная величина может принимать в заданном диапазоне. Этот диапазон будет ограничен минимальным и максимальным возможными значениями, но именно то, где возможное значение, вероятно, будет нанесено на график распределения вероятностей, зависит от ряда факторов. Эти факторы включают среднее значение распределения (среднее), стандартное отклонение, асимметрию и эксцесс.
Как работает распределение вероятностей
Возможно, наиболее распространенным распределением вероятностей является нормальное распределение, или «колоколообразная кривая», хотя существует несколько широко используемых распределений. Как правило, процесс генерации данных о каком-либо явлении определяет его вероятностное распределение. Этот процесс называется функцией плотности вероятности.
Как правило, процесс генерации данных о каком-либо явлении определяет его вероятностное распределение. Этот процесс называется функцией плотности вероятности.
Распределения вероятностей также можно использовать для создания кумулятивных функций распределения (CDF), которые суммируют вероятность событий кумулятивно и всегда начинаются с нуля и заканчиваются на 100%.
Ученые, финансовые аналитики и управляющие фондами могут определить распределение вероятности конкретной акции, чтобы оценить возможную ожидаемую доходность, которую акция может принести в будущем. История доходности акции, которую можно измерить за любой временной интервал, вероятно, будет состоять только из части доходности акции, что приведет к ошибке выборки при анализе. Увеличивая размер выборки, эту ошибку можно значительно уменьшить.
Основные выводы
- Распределение вероятностей отображает ожидаемые результаты возможных значений для заданного процесса генерации данных.
- Распределения вероятностей бывают разных форм с различными характеристиками, определяемыми средним значением, стандартным отклонением, асимметрией и эксцессом.

- Инвесторы используют распределения вероятностей для прогнозирования доходности активов, таких как акции, с течением времени и для хеджирования своих рисков.
Типы вероятностных распределений
Существует множество различных классификаций вероятностных распределений. Некоторые из них включают нормальное распределение, распределение хи-квадрат, биномиальное распределение и распределение Пуассона. Различные распределения вероятностей служат разным целям и представляют разные процессы генерации данных. Биномиальное распределение, например, оценивает вероятность того, что событие произойдет несколько раз в течение заданного числа испытаний и с учетом вероятности события в каждом испытании. и может быть получен путем отслеживания того, сколько штрафных бросков делает баскетболист в игре, где 1 = попадание в корзину, а 0 = промах. Другим типичным примером может быть использование честной монеты и определение вероятности того, что эта монета выпадет орлом за 10 бросков подряд. Биномиальное распределение равно дискретный , в отличие от непрерывного, поскольку только 1 или 0 являются допустимым ответом.
Биномиальное распределение равно дискретный , в отличие от непрерывного, поскольку только 1 или 0 являются допустимым ответом.
Наиболее часто используемым распределением является нормальное распределение, которое часто используется в финансах, инвестициях, науке и технике. Нормальное распределение полностью характеризуется своим средним значением и стандартным отклонением, что означает, что распределение не является асимметричным и демонстрирует эксцесс. Это делает распределение симметричным, и на графике оно изображается в виде колоколообразной кривой. Нормальное распределение определяется средним (средним) значением, равным нулю, и стандартным отклонением, равным 1,0, с асимметрией, равной нулю, и эксцессом, равным 3. При нормальном распределении примерно 68% собранных данных будут находиться в пределах +/- одного стандарта. отклонение среднего; примерно 95% в пределах +/- двух стандартных отклонений; и 99,7% в пределах трех стандартных отклонений. В отличие от биномиального распределения, нормальное распределение является непрерывным, что означает, что представлены все возможные значения (в отличие от только 0 и 1 без промежуточных значений).
Распределения вероятностей, используемые в инвестировании
Часто предполагается, что доходность акций имеет нормальное распределение, но в действительности они демонстрируют эксцесс с большими отрицательными и положительными доходами, которые, кажется, возникают больше, чем можно было бы предсказать при нормальном распределении. Фактически, поскольку цены акций ограничены нулем, но предлагают потенциально неограниченный потенциал роста, распределение доходности акций было описано как логарифмически нормальное. Это видно на графике доходности акций, где хвосты распределения имеют большую толщину.
Распределения вероятностей часто используются в управлении рисками, а также для оценки вероятности и суммы убытков, которые может понести инвестиционный портфель, на основе распределения исторической доходности. Одним из популярных показателей управления рисками, используемых в инвестировании, является стоимость под риском (VaR). VaR дает минимальные убытки, которые могут возникнуть с учетом вероятности и временных рамок портфеля. В качестве альтернативы инвестор может получить вероятность убытка для суммы убытка и временных рамок, используя VaR. Злоупотребление и чрезмерная зависимость от VaR были названы одной из основных причин финансового кризиса 2008 года.
В качестве альтернативы инвестор может получить вероятность убытка для суммы убытка и временных рамок, используя VaR. Злоупотребление и чрезмерная зависимость от VaR были названы одной из основных причин финансового кризиса 2008 года.
Пример распределения вероятностей
В качестве простого примера распределения вероятностей рассмотрим число, наблюдаемое при броске двух стандартных шестигранных игральных костей. Каждая кость имеет вероятность 1/6 выпадения любого числа, от одного до шести, но сумма двух игральных костей сформирует распределение вероятностей, изображенное на изображении ниже. Семь — самый распространенный результат (1+6, 6+1, 5+2, 2+5, 3+4, 4+3). С другой стороны, два и двенадцать гораздо менее вероятны (1+1 и 6+6).
Изображение Сабрины Цзян © Investopedia 2020Объяснение концепций вероятностей: распределения вероятностей (введение, часть 3) | Джонни Брукс-Бартлетт
В своих первой и второй вводных статьях я рассказал об обозначениях, фундаментальных законах вероятности и аксиомах. Это то, что волнует математиков. Однако теория вероятностей часто оказывается полезной на практике, когда мы используем распределения вероятностей.
Это то, что волнует математиков. Однако теория вероятностей часто оказывается полезной на практике, когда мы используем распределения вероятностей.
Распределения вероятностей используются во многих областях, но мы редко объясняем, что они из себя представляют. Часто предполагается, что читатель уже знает (я предполагаю это больше, чем следовало бы). Поэтому я попытаюсь объяснить, что они из себя представляют, в этом посте.
Вспомним, что случайная переменная — это переменная, значение которой является результатом случайного события (см. первый вводный пост для напоминания, если это не имеет для вас никакого смысла). Например, случайной величиной может быть результат броска игральной кости или подбрасывания монеты.
A распределение вероятностей представляет собой список всех возможных исходов случайной величины вместе с соответствующими значениями вероятностей.
Чтобы привести конкретный пример, вот распределение вероятности правильного шестигранного кубика.
Для ясности, это пример дискретного одномерного распределения вероятностей с конечной поддержкой . Это немного многословно, поэтому давайте попробуем разобрать это утверждение и понять его.
Дискретный = Это означает, что если я выберу любые два последовательных исхода. Я не могу получить промежуточный результат. Например, если мы рассматриваем 1 и 2 как результаты броска шестигранного кубика, то у меня не может быть промежуточного результата (например, у меня может быть результат 1,5). В математике мы бы сказали, что список результатов исчисляем (но давайте не будем идти по пути определения и понимания счетных и несчетных множеств. Это становится странным). Вероятно, вы можете догадаться, что когда мы получаем непрерывные распределения вероятностей, это уже не так.
Одномерный = означает, что у нас есть только одна (случайная) переменная. В этом случае у нас есть только результат броска кубика. Напротив, если у нас есть более одной переменной, мы говорим, что имеем многомерное распределение . В конкретном случае, когда у нас есть 2 переменные, мы часто говорим, что это двумерное распределение .
В этом случае у нас есть только результат броска кубика. Напротив, если у нас есть более одной переменной, мы говорим, что имеем многомерное распределение . В конкретном случае, когда у нас есть 2 переменные, мы часто говорим, что это двумерное распределение .
конечная поддержка = Это означает, что существует ограниченное количество исходов. Поддержка — это, по существу, исходы, для которых определено распределение вероятностей. Так что опора в нашем примере есть. 1, 2, 3, 4, 5 и 6. А так как это не бесконечное число значений, значит, поддержка конечна.
Почему мы говорим о функциях?
В приведенном выше примере с броском шестигранного кубика было всего шесть возможных результатов, поэтому мы могли записать все распределение вероятностей в таблицу. Во многих сценариях количество результатов может быть намного больше, и поэтому записывать таблицу будет утомительно. Что еще хуже, количество возможных результатов может быть бесконечным, и в этом случае удачи в написании таблицы для этого.
Чтобы обойти проблему написания таблицы для каждого распределения, мы можем вместо этого определить функцию. Функция позволяет нам кратко определить распределение вероятностей .
Итак, давайте сначала определим, что такое функция в целом, а затем мы перейдем к функциям, используемым для распределения вероятностей.
Что такое функция?
На очень абстрактном уровне функция представляет собой коробку, которая принимает входные данные и возвращает выходные данные. В подавляющем большинстве случаев функция действительно должна что-то делать с входными данными, чтобы выходные данные были полезными.
Давайте определим нашу собственную функцию. Предположим, что эта функция принимает число в качестве входных данных, добавляет 2 к входному числу и возвращает новое число в качестве выходных данных. Графически наша функция (в виде блока) выглядит так:
Абстрактное изображение функции в виде блока, который принимает входные данные и возвращает выходные данные. В этом случае функция добавляет 2 ко входу.
В этом случае функция добавляет 2 ко входу.Таким образом, если бы на входе было 5, наша функция добавила бы к нему 2 и вернула бы результат 5+2 = 7.
Обозначение функций
Теперь было бы утомительно рисовать вышеприведенную диграмму для каждой функции, которую мы хотим создать. . Вместо этого мы используем символы/буквы для представления диаграммы, чтобы сделать ее более лаконичной. Вместо слова «вход» мы используем «x», вместо слова «функция» мы пишем «f», а вместо слова «выход» мы пишем «f(x)». Таким образом, приведенную выше диаграмму теперь можно записать как
Наша функция написана символами вместо слов, чтобы сделать ее более краткой. Это лучше, однако у нас все еще есть проблема, заключающаяся в том, что нам нужно нарисовать диаграмму, чтобы понять, что делает функция. Однако мы математики и не хотим тратить драгоценную энергию на рисование прямоугольника, поэтому мы придумали лучший способ написания функций, который означает, что нам не нужно ничего рисовать. Мы можем математически определить нашу функцию как
Мы можем математически определить нашу функцию как
Это эквивалентно диаграмме выше, потому что мы можем явно видеть, что входные данные для функции f равны x, мы вызвали нашу функцию f и знаем, что функция добавляет 2 к входным данным и возвращает x + 2 в качестве выходных данных.
Важно отметить, что выбор буквы для функции и ввода был произвольным. Я мог бы сказать, что «a» — это ввод, и я могу вызвать функцию «add_two», поэтому моя функция будет
. Другой способ написать ту же функцию, и это полностью эквивалентно функции выше.
Один из основных выводов из этого заключается в том, что с помощью функции мы можем увидеть, как мы будем преобразовывать любой ввод. С функцией f(x) = x+ 2 мы бы знали, что делать, если ввод был x=10 или если вход был x=10000. Поэтому нам не нужно записывать таблицу, как мы делали ранее в посте.
Последнее, что я хочу сделать здесь, это то, что функции, которые мы собираемся использовать, будут работать исключительно с числами как на входе, так и на выходе. Однако функции могут принимать в качестве входных данных все, что угодно, и выводить все, что угодно (даже ничего не выводить). Например, мы могли бы написать функцию на языке программирования, которая принимает строку текста в качестве входных данных и выводит первую букву этой строки. Вот пример этой функции на языке программирования Python
Однако функции могут принимать в качестве входных данных все, что угодно, и выводить все, что угодно (даже ничего не выводить). Например, мы могли бы написать функцию на языке программирования, которая принимает строку текста в качестве входных данных и выводит первую букву этой строки. Вот пример этой функции на языке программирования Python
Графическое представление функций
Учитывая, что одним из основных преимуществ функций является то, что они позволяют нам знать, как преобразовывать любые входные данные, мы также можем использовать это знание для явной визуализации функции. Давайте придерживаться нашего примера f(x) = x+2. Графически это выглядит так:
Графическое представление нашей функции f(x) = x + 2 Мы можем читать по горизонтальной оси внизу, поскольку наши входные числа и соответствующие числа на вертикальной оси слева являются выходными значениями f (х) = х + 2. Например, мы можем видеть, что синяя линия, представляющая функцию, пересекает точку, где вертикальная (белая) линия при x=1 пересекает горизонтальную (белую) линию f(x) = 3. Это графически показывает, что f(1) = 1 + 2 = 3,
Это графически показывает, что f(1) = 1 + 2 = 3,
Параметры функций
Одной из важнейших особенностей функций являются параметры. Параметры — это числа, которые вы найдете внутри функций, которые вы не обязательно вводите в качестве входных данных. В нашем примере f(x) = x + 2 число «2» является параметром, потому что оно нам нужно для определения функции, но мы не включаем его в качестве входных данных для функции.
Причина, по которой параметры важны, заключается в том, что они играют непосредственную роль в определении выходных данных. Например, давайте определим другую функцию h(x) = x+3. Единственная разница между функцией f(x) = x+2 и нашей новой функцией h(x) = x+3 заключается в значении параметра (теперь у нас есть «3» вместо «2»). Эта разница означает, что результаты, которые мы получаем, совершенно различны для одного и того же входа. Давайте посмотрим на это графически.
Разница между нашими функциями f(x) = x + 2 и h(x) = x + 3 Параметры, возможно, являются самой важной характеристикой функции вероятности (распределения), поскольку они определяют вывод функции, который сообщает нам вероятности определенных исходов в случайном процессе. Часто это параметры, которые мы пытаемся оценить в задачах, возникающих в науке о данных, и ранее я писал о двух методах, которые мы можем использовать для их оценки: оценка максимального правдоподобия и байесовский вывод.
Часто это параметры, которые мы пытаемся оценить в задачах, возникающих в науке о данных, и ранее я писал о двух методах, которые мы можем использовать для их оценки: оценка максимального правдоподобия и байесовский вывод.
Теперь мы готовы поговорить о распределениях вероятностей, используя язык функций.
Когда мы используем функцию вероятности для описания дискретного распределения вероятностей, мы называем ее функцией массы вероятности (обычно сокращенно pmf).
Помните из первого вводного поста о понятиях вероятности, что вероятность того, что случайная величина, которую мы обозначаем заглавной буквой X, примет значение, обозначенное строчной буквой x, записывается как P(X=x ). Итак, если мы используем бросок игральной кости в качестве нашего примера случайной величины, мы можем записать вероятность того, что игральная кость выпадет на числе 3, как P (X = 3) = 1/6.
Функция массы вероятности, которую мы назовем «f», возвращает вероятность исхода.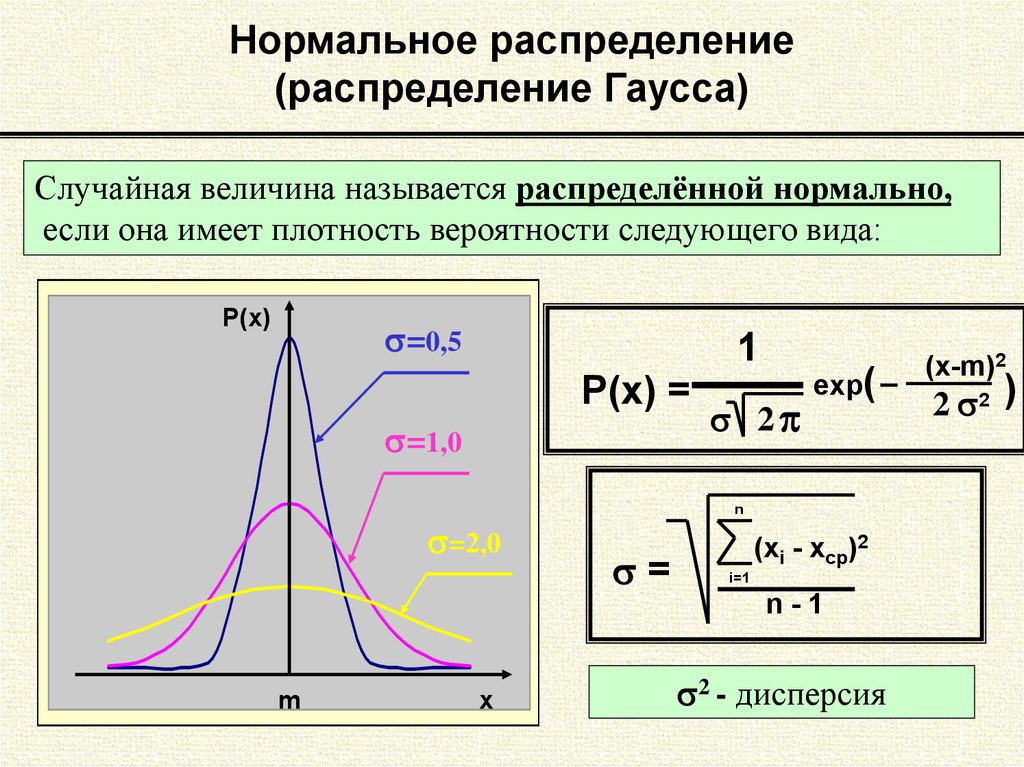 Следовательно, функция массы вероятности записывается как:
Следовательно, функция массы вероятности записывается как:
Я знаю, что это становится немного ужасным и математическим, но потерпите меня. Уравнение, которое мы видим выше, говорит, что функция массы вероятности «f» просто возвращает вероятность исхода x.
Итак, вернемся к примеру с честным шестигранным кубиком (вы, наверное, уже устали от этого примера). Функция массы вероятности f просто возвращает вероятность исхода. Следовательно, вероятность выпадения 3 равна f(3) = 1/6. Вот и все.
Поскольку функция массы вероятности возвращает вероятности, она должна подчиняться правилам вероятности (аксиомам), которые я описал в предыдущем посте. А именно, функция массы вероятности выводит значения от 0 до 1 включительно, а сумма функции массы вероятности (PMF) по всем результатам равна 1. Математически мы можем записать эти два условия как
Итак, мы видели, что мы можем записать дискретное распределение вероятностей в виде таблицы и функции. Мы также можем изобразить пример с броском кубика графически
Графическое представление распределения вероятностей результатов броска правильного шестигранного кубикаПример дискретного распределения вероятностей: Распределение Бернулли
Некоторые распределения вероятностей возникают так часто, что они были тщательно изучены и получили названия. Одно часто встречающееся дискретное распределение называется распределением Бернулли. Он описывает распределение вероятностей процесса, который имеет два возможных результата. Примером этого является подбрасывание монеты, когда выпадает орел или решка.
Одно часто встречающееся дискретное распределение называется распределением Бернулли. Он описывает распределение вероятностей процесса, который имеет два возможных результата. Примером этого является подбрасывание монеты, когда выпадает орел или решка.
Функция массы вероятности распределения Бернулли равна
Здесь x представляет результат и принимает значение 1 или 0. Таким образом, мы могли бы сказать, что решка = 1, а решка = 0. p — это параметр, который представляет вероятность результат равен 1. Таким образом, в случае честной монеты, где вероятность выпадения орла или решки равна 0,5, мы установили бы p = 0,5.
Часто мы хотим четко указать параметры, включаемые в функцию массы вероятности, поэтому мы пишем
Обратите внимание, что мы используем точку с запятой для отделения входных переменных от параметров.
Иногда нас интересуют вероятности случайных величин, которые имеют непрерывные результаты. Примеры включают рост взрослого человека, выбранного случайным образом из населения, или количество времени, которое водитель такси должен ждать до своей следующей работы. Для этих примеров случайная величина лучше описывается непрерывным распределением вероятностей.
Для этих примеров случайная величина лучше описывается непрерывным распределением вероятностей.
Когда мы используем функцию вероятности для описания непрерывного распределения вероятностей, мы называем ее функция плотности вероятности (обычно сокращенно pdf).
Функции плотности вероятности концептуально несколько сложнее, чем функции массы вероятности, но не волнуйтесь, мы доберемся до этого. Я думаю, проще всего будет начать с примера непрерывного распределения вероятностей, а затем обсудить его свойства.
Пример непрерывного распределения вероятностей: Нормальное распределение
Нормальное распределение, вероятно, является наиболее распространенным распределением во всей вероятности и статистике. Одна из основных причин, по которой она так часто всплывает, связана с центральной предельной теоремой. Мы не будем вдаваться в подробности в этом посте, но вот хорошая статья Карсона Фортера под названием «Единственная теорема, которую нужно знать ученым», в которой объясняется, что такое теорема и как она связана с нормальным распределением.
Функция плотности вероятности для нормального распределения определяется как
Где параметры (т. е. символы после точки с запятой) представляют среднее значение μ (точка, в которой находится центр распределения) и стандартное отклонение σ, (насколько распространено распределение) населения.
Если мы установим среднее значение равным нулю (μ=0) и стандартное отклонение равным 1 (σ=1), то получаемое нами распределение будет выглядеть следующим образом
Нормальное распределение со средним значением = 0 и стандартным отклонением, равным 1Нормальное распределение является примером непрерывного одномерного распределения вероятностей с бесконечной поддержкой . Под бесконечной поддержкой я подразумеваю, что мы можем вычислить значения функции плотности вероятности для всех результатов между минус бесконечностью и положительной бесконечностью. В математике мы иногда говорим, что он поддерживается на всей реальной линии .
Свойства непрерывного распределения вероятностей
Первое, на что следует обратить внимание, это то, что числа на вертикальной оси начинаются с нуля и идут вверх.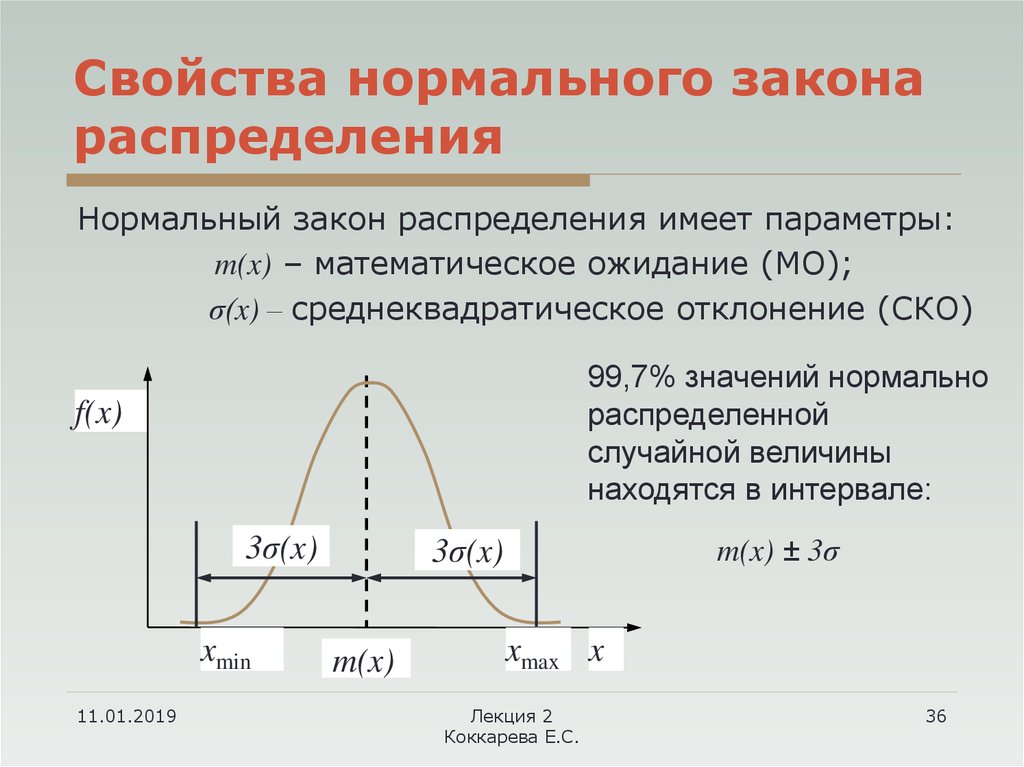 Это правило, которому должна подчиняться функция плотности вероятности. Любое выходное значение функции плотности вероятности больше или равно нулю. На математическом жаргоне мы бы сказали, что результат неотрицательный, или математически записали бы это как 9.0005
Это правило, которому должна подчиняться функция плотности вероятности. Любое выходное значение функции плотности вероятности больше или равно нулю. На математическом жаргоне мы бы сказали, что результат неотрицательный, или математически записали бы это как 9.0005
Однако, в отличие от функций массы вероятности, выход функции плотности вероятности не является значением вероятности. Это невероятно важное отличие, одно из которых я забыл.
Чтобы получить вероятность из функции плотности вероятности, нам нужно найти площадь под кривой. Итак, из нашего примера распределения со средним значением = 3 и стандартным отклонением = 1 мы можем найти вероятность того, что результат находится между 0 и 1, найдя область, показанную на изображении ниже 9.0005 Заштрихованная область — это вероятность того, что результат находится в диапазоне от 0 до 1.
Математически мы запишем это как
Мы можем прочитать это как « интеграл функции плотности вероятности между 0 и 1 (в левой части ) равна вероятности того, что результат случайной величины находится между нулем и 1 (в правой части) ».
Простите меня за то, что я не рассказал подробно об интегралах и о том, как они работают (у меня есть краткое концептуальное введение в интегралы в моем посте о маргинализации, но он не учит вас, как их вычислять). Если вы не знаете о них, то все, что вам нужно знать на данный момент, это то, что это математический метод нахождения площади под кривой, который в данном случае дает нам вероятности исходов. Возможно, мне нужно написать краткую серию статей, посвященных вводному исчислению.
Теперь мы рассмотрели еще одно свойство функций плотности вероятности. А именно, что вероятность между двумя исходами, скажем, «а» и «b», является интегралом функции плотности вероятности между этими двумя точками (это эквивалентно нахождению площади под кривой, полученной функцией плотности вероятности между точками «а» и «б»). Математически это
Помните, что мы по-прежнему должны следовать правилам распределения вероятностей, а именно правилу, которое гласит, что сумма всех возможных результатов равна 1.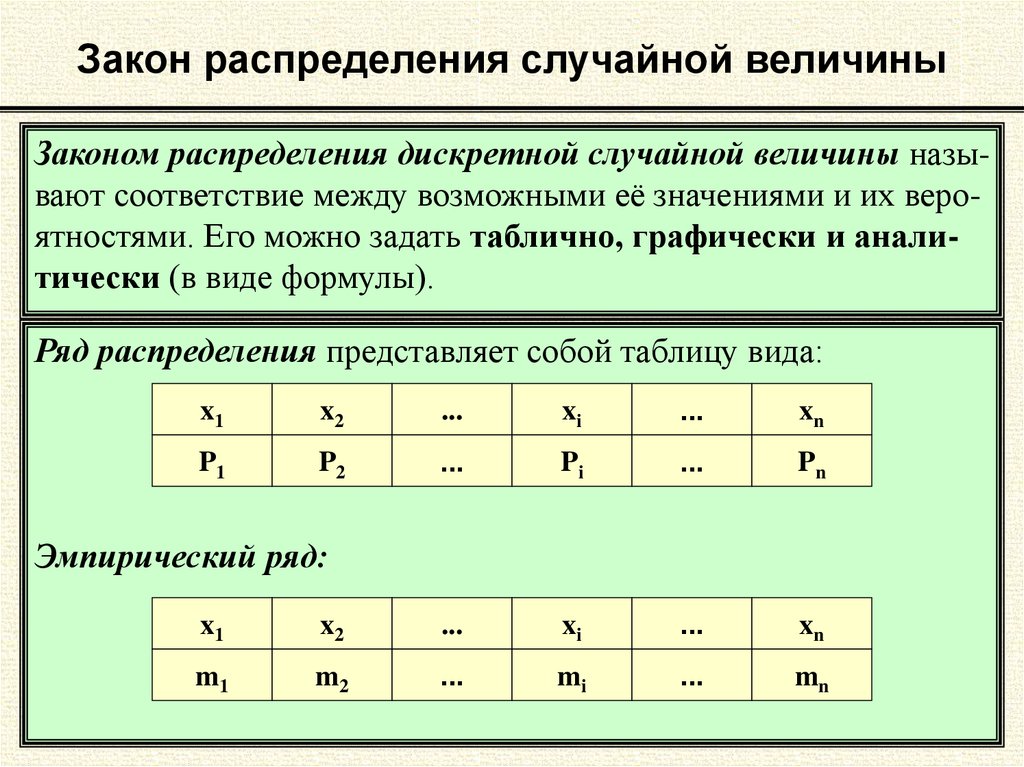 Мы можем охватить все возможные значения, если установим наш диапазон от минус бесконечности ‘ вплоть до ‘положительной бесконечности’. Поэтому для того, чтобы функция была функцией плотности вероятности, должно выполняться следующее
Мы можем охватить все возможные значения, если установим наш диапазон от минус бесконечности ‘ вплоть до ‘положительной бесконечности’. Поэтому для того, чтобы функция была функцией плотности вероятности, должно выполняться следующее
Это говорит о том, что площадь под кривой между минус бесконечностью и положительной бесконечностью равна 1.
Важно знать о непрерывных распределениях вероятностей (и то, что может быть действительно странным, чтобы смириться с этим концептуально) заключается в том, что вероятность того, что случайная величина равна определенному результату, равна 0. Например, если мы попытаемся получить вероятность того, что результат равен числу 2, мы получим
Это может показаться странным концептуально, но если вы понимаете исчисление, то это должно иметь немного больше смысла. В этом посте я не буду касаться исчисления. Вместо этого я хочу, чтобы вы усвоили из этого факта, что мы можем говорить только о вероятностях, возникающих между двумя значениями.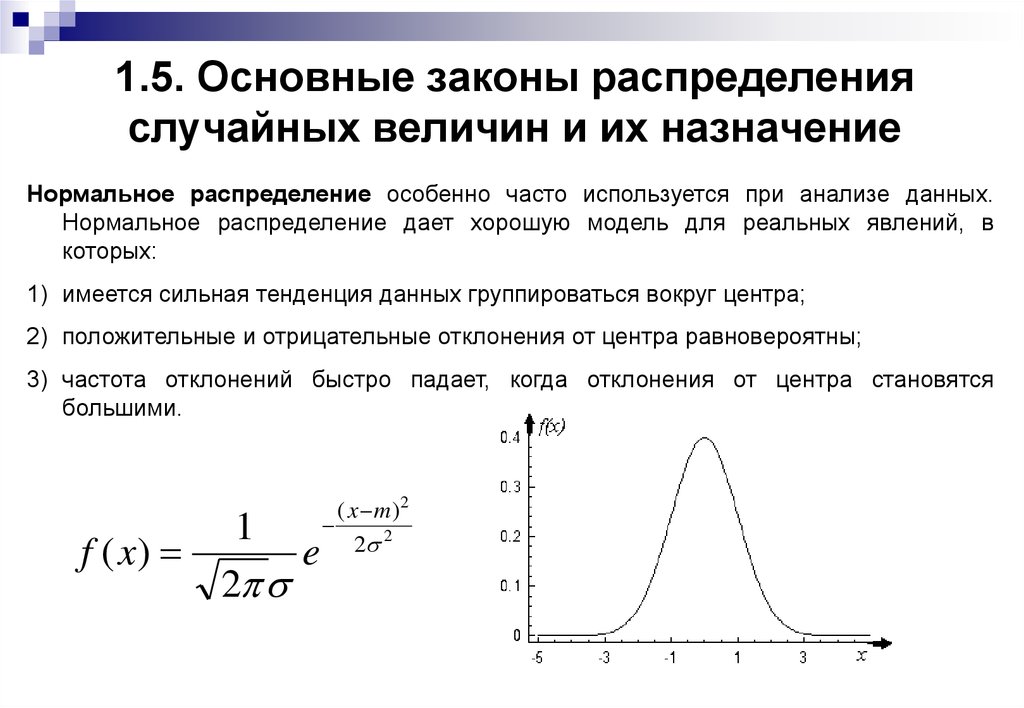 Или мы можем спросить о вероятности того, что результат будет больше или меньше определенного значения. Мы не может спрашивать о вероятности исхода, равного определенному значению.
Или мы можем спросить о вероятности того, что результат будет больше или меньше определенного значения. Мы не может спрашивать о вероятности исхода, равного определенному значению.
Внимательные читатели могли заметить, что я использовал символы «меньше (<)» и «больше (>)», а не «меньше или равно (≤)» и «больше или равно». (≥)». Для непрерывных распределений вероятностей это на самом деле не имеет значения, потому что они одинаковы. В явном виде я имею в виду
Таким образом, вероятность того, что случайная величина примет значение между a и b исключая, такая же, как вероятность того, что она примет значение между a и b включительно.
Важность параметров
Мы видели, что значения параметров могут изменить выходные значения функции, и это не отличается от распределения вероятностей.
Два нормальных распределения с разными параметрами дают совершенно разные вероятностные результаты. На рисунке выше мы построили функции плотности вероятности двух нормальных распределений.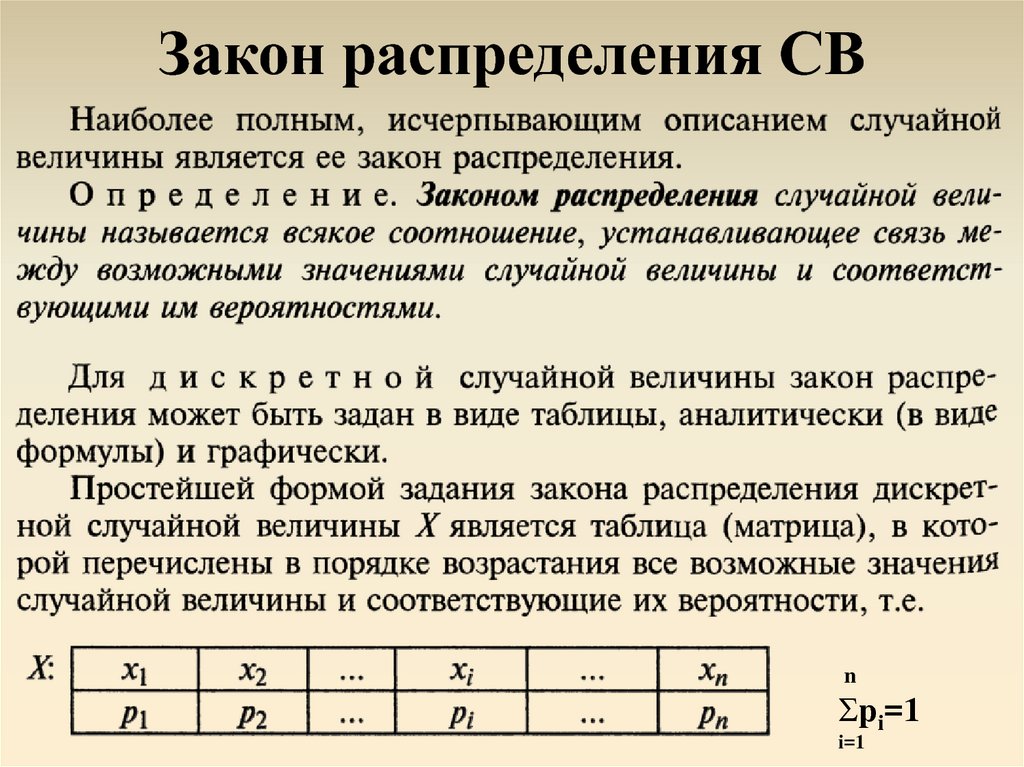 Синее распределение имеет значения параметров μ = 0 и σ = 1, тогда как красное распределение имеет значения параметров μ = 2 и σ = 0,5.
Синее распределение имеет значения параметров μ = 0 и σ = 1, тогда как красное распределение имеет значения параметров μ = 2 и σ = 0,5.
Теперь становится яснее, почему использование неверных значений параметров может привести к результатам, которые сильно отличаются от ожидаемых.
Вау! Это было намного дольше, чем я планировал. Подытожим основные моменты:
- Распределение вероятностей — это список исходов и связанных с ними вероятностей.
- Мы можем писать небольшие дистрибутивы с таблицами, но проще суммировать большие дистрибутивы с помощью функций.
- Функция, представляющая дискретное распределение вероятностей, называется функция массы вероятности .
- Функция, представляющая непрерывное распределение вероятностей, называется функцией плотности вероятности.
- Функции, представляющие распределения вероятностей, по-прежнему должны подчиняться правилам вероятности
- Результатом функции массы вероятности является вероятность , тогда как площадь под кривой, полученной функцией плотности вероятности, представляет вероятность .


 Сnm — число сочетаний m телевизоров по n, p — вероятность наступления события А, т.е. заказа телевизора, q — вероятность не наступления события А, т.е. не заказа телевизора, P m,n — вероятность заказа m телевизоров из n. На рисунке 1 изображен полигон распределения вероятностей.
Сnm — число сочетаний m телевизоров по n, p — вероятность наступления события А, т.е. заказа телевизора, q — вероятность не наступления события А, т.е. не заказа телевизора, P m,n — вероятность заказа m телевизоров из n. На рисунке 1 изображен полигон распределения вероятностей. Бывают случаи, что в партии оказывается 1 блок бракованный. Проводится проверка до обнаружения бракованного блока. Необходимо составить закон распределения числа проверенных блоков. Вероятность того, что блок может оказаться бракованным равна 0,1. Построить полигон распределения вероятностей.
Бывают случаи, что в партии оказывается 1 блок бракованный. Проводится проверка до обнаружения бракованного блока. Необходимо составить закон распределения числа проверенных блоков. Вероятность того, что блок может оказаться бракованным равна 0,1. Построить полигон распределения вероятностей. Рис.2.
Рис.2. Однако затем вероятность начинает быстро снижаться. Таким образом, вероятность угадывания 4-х чисел уже составляет менее 0,005, а 5-ти ничтожно мала.
Однако затем вероятность начинает быстро снижаться. Таким образом, вероятность угадывания 4-х чисел уже составляет менее 0,005, а 5-ти ничтожно мала. Составить закон распределения заказов на покупку телевизоров марок А,В и С. Построить полигон распределения вероятностей.
Составить закон распределения заказов на покупку телевизоров марок А,В и С. Построить полигон распределения вероятностей.


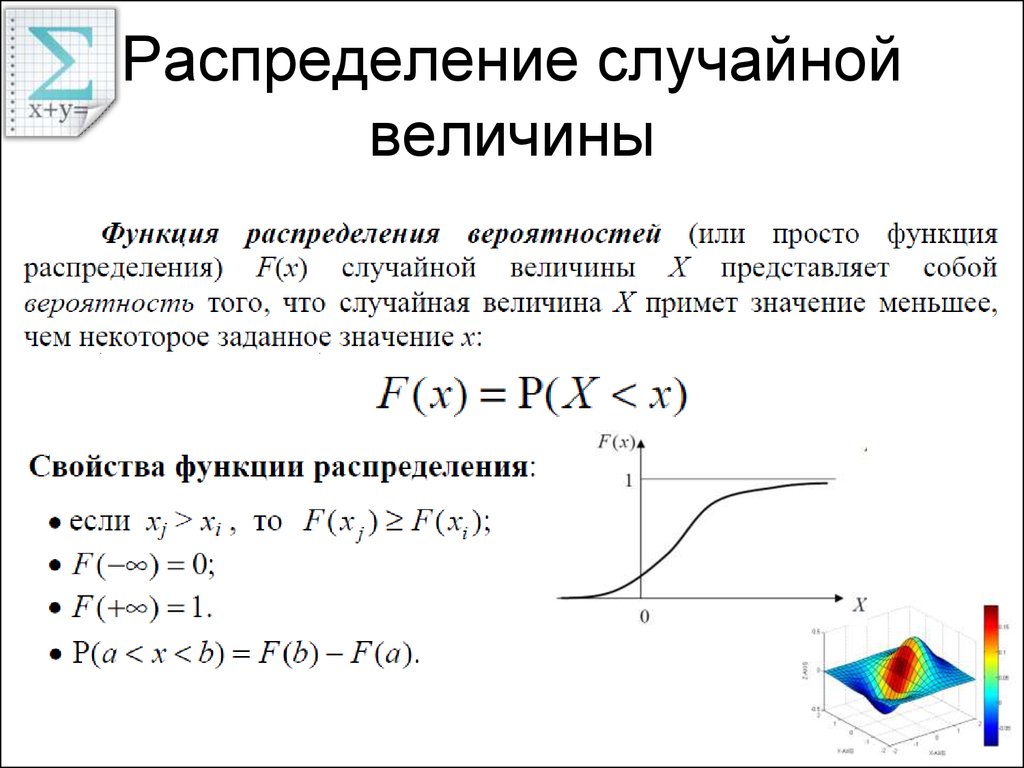 ..k).
..k).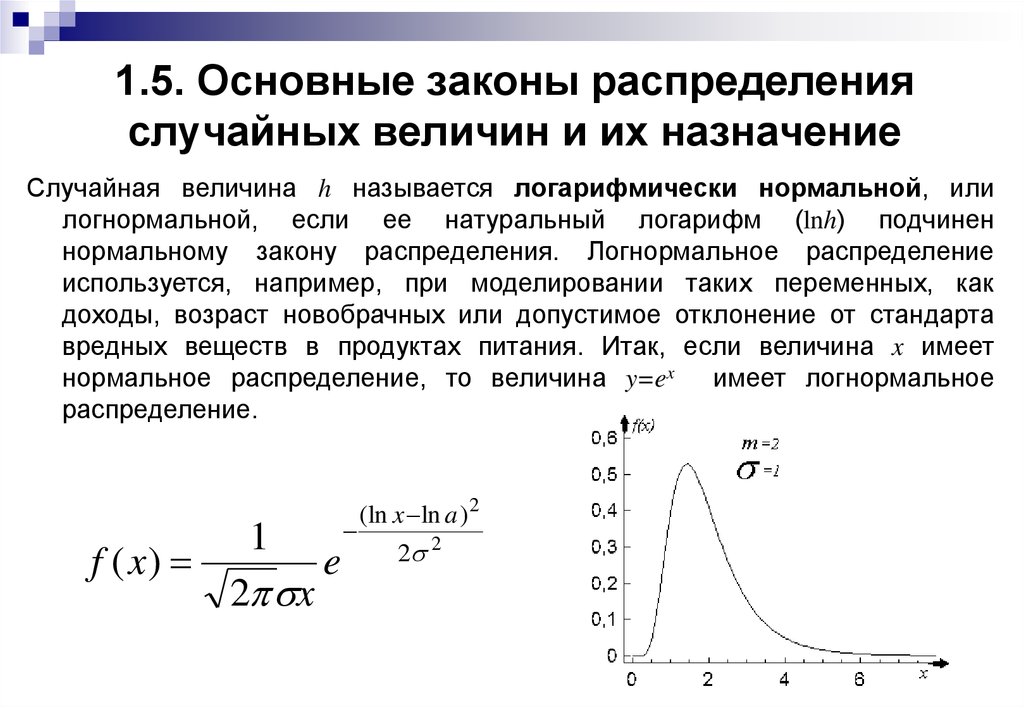
 pyplot as plt
import numpy as np
fig, ax = plt.subplots(1, 1)
# Calculate a few first moments:
#mean, var, skew, kurt = uniform.stats(moments='mvsk')
# Display the probability density function (``pdf``):
x = np.linspace(uniform.ppf(0.01), uniform.ppf(0.99), 100)
ax.plot(x, uniform.pdf(x),'r-', lw=5, alpha=0.6, label='uniform pdf')
ax.plot(x, uniform.cdf(x),'b-', lw=5, alpha=0.6, label='uniform cdf')
# Check accuracy of ``cdf`` and ``ppf``:
vals = uniform.ppf([0.001, 0.5, 0.999])
np.allclose([0.001, 0.5, 0.999], uniform.cdf(vals))
# True
# Generate random numbers:
r = uniform.rvs(size=1000)
# And compare the histogram:
ax.hist(r, normed=True, histtype='stepfilled', alpha=0.2)
ax.legend(loc='best', frameon=False)
plt.show()
pyplot as plt
import numpy as np
fig, ax = plt.subplots(1, 1)
# Calculate a few first moments:
#mean, var, skew, kurt = uniform.stats(moments='mvsk')
# Display the probability density function (``pdf``):
x = np.linspace(uniform.ppf(0.01), uniform.ppf(0.99), 100)
ax.plot(x, uniform.pdf(x),'r-', lw=5, alpha=0.6, label='uniform pdf')
ax.plot(x, uniform.cdf(x),'b-', lw=5, alpha=0.6, label='uniform cdf')
# Check accuracy of ``cdf`` and ``ppf``:
vals = uniform.ppf([0.001, 0.5, 0.999])
np.allclose([0.001, 0.5, 0.999], uniform.cdf(vals))
# True
# Generate random numbers:
r = uniform.rvs(size=1000)
# And compare the histogram:
ax.hist(r, normed=True, histtype='stepfilled', alpha=0.2)
ax.legend(loc='best', frameon=False)
plt.show()
 stats(moments='mvsk')
# Display the probability density function (``pdf``):
x = np.linspace(logistic.ppf(0.01),
logistic.ppf(0.99), 100)
ax.plot(x, logistic.pdf(x),
'g-', lw=5, alpha=0.6, label='logistic pdf')
ax.plot(x, logistic.cdf(x),
'r-', lw=5, alpha=0.6, label='logistic cdf')
vals = logistic.ppf([0.001, 0.5, 0.999])
np.allclose([0.001, 0.5, 0.999], logistic.cdf(vals))
# True
# Generate random numbers:
r = logistic.rvs(size=1000)
# And compare the histogram:
ax.hist(r, normed=True, histtype='stepfilled', alpha=0.2)
ax.legend(loc='best', frameon=False)
plt.show()
stats(moments='mvsk')
# Display the probability density function (``pdf``):
x = np.linspace(logistic.ppf(0.01),
logistic.ppf(0.99), 100)
ax.plot(x, logistic.pdf(x),
'g-', lw=5, alpha=0.6, label='logistic pdf')
ax.plot(x, logistic.cdf(x),
'r-', lw=5, alpha=0.6, label='logistic cdf')
vals = logistic.ppf([0.001, 0.5, 0.999])
np.allclose([0.001, 0.5, 0.999], logistic.cdf(vals))
# True
# Generate random numbers:
r = logistic.rvs(size=1000)
# And compare the histogram:
ax.hist(r, normed=True, histtype='stepfilled', alpha=0.2)
ax.legend(loc='best', frameon=False)
plt.show()
 cdf(x, np.mean(x), np.std(x))#нормальное интегральное распределение
ax.plot(x,pn, lw=5, alpha=0.6, label='norm cdf')
pl=logistic.cdf(x, np.mean(x), np.std(x))# логистическое интегральное распределение
ax.plot(x,pl, lw=5, alpha=0.6, label='logistic cdf')
cdf(x, np.mean(x), np.std(x))#нормальное интегральное распределение
ax.plot(x,pn, lw=5, alpha=0.6, label='norm cdf')
pl=logistic.cdf(x, np.mean(x), np.std(x))# логистическое интегральное распределение
ax.plot(x,pl, lw=5, alpha=0.6, label='logistic cdf')

