Закон вероятности: Закон вероятности

Теория вероятности сериал 2020 смотреть онлайн // Смотрим

Теория вероятности сериал 2020 смотреть онлайн // Смотрим

• Профиль

сериал

16+ драма Россия 2021

Чтобы спасти брата, молодой талантливый математик Никита Пирогов придумывает схему, с помощью которой можно обыграть казино.

Узнав о его неординарных способностях, боссы игорного бизнеса нанимают Никиту для вычисления шулеров. Сам того не подозревая, он вступает в мир, в котором кипят криминальные страсти, царит подпольная роскошь, а любовь и ненависть одинаково жестоки. Сможет ли молодой гений выйти победителем из игры, в которой не существует правил?

Режиссер: Юрий Мороз
В ролях: Максим Матвеев, Артем Ткаченко, Николай Козак, Игорь Миркурбанов, Роман Мадянов, Александра Ребенок

• Александра

  
  Ребенок

• Евгения

  
  Крегжде

• Юрий

  
  Мороз

• Кадры из сериала «Теория вероятности»

• Кадры из сериала «Теория вероятности»

• Кадры из сериала «Теория вероятности»

• Кадры из сериала «Теория вероятности»

• Кадры из сериала «Теория вероятности»

• Кадры из сериала «Теория вероятности»

• Кадры из сериала «Теория вероятности»

• Кадры из сериала «Теория вероятности»

• Кадры из сериала «Теория вероятности»

• Кадры из сериала «Теория вероятности»

• сериал
• драма
• Роман Мадянов
• Юрий Мороз
• Максим Матвеев
• российский
• Только у нас
• Артем Ткаченко
• Игорь Миркурбанов
• Александра Ребенок
• смотрим только у нас
• Топ сериалов-2021
• смотрим сериалы
• Фильмы с интригующим сюжетом
• сериалы-новинки

Авто-геолокация

Презентация — Теория Вероятности

Поделиться  

4,229
просмотров

Презентации / Математика / Теория Вероятности

Скачать презентацию Понравилось   |   2

Текст этой презентации

Слайд 1

Презентацию подготовилаАвотина Маргарита9ж
Теория вероятности

Слайд 2

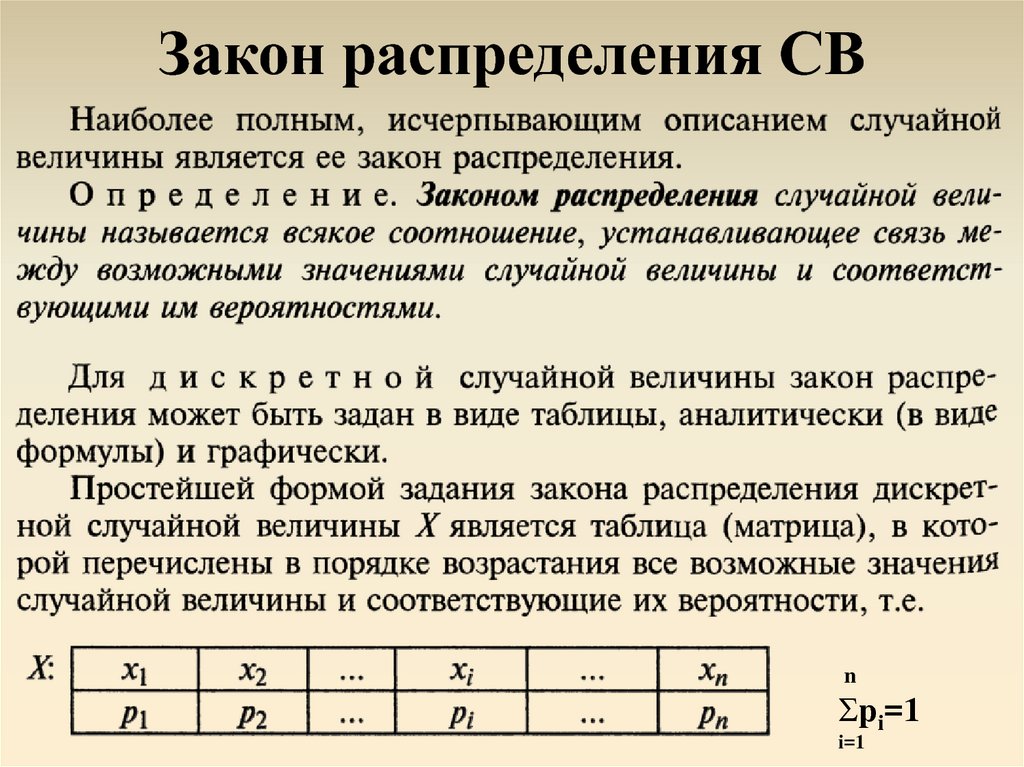
теория вероятности—
Тео́рия вероя́тностей — раздел математики, изучающий закономерности случайных явлений:случайные события, случайные величины, их свойства и операции над ними.

Слайд 3

Формула вероятности события
m — число благоприятствующих событию A исходовn — число всех элементарных исходов

Слайд 4

Формула вероятности противоположного события
P(Ā) — вероятность противоположного события AP(A) — вероятность события A

Слайд 5

Формула вероятности суммы несовместных событий
P(Ā) — вероятность противоположного события AP(A) — вероятность события A

Слайд 6

Формула вероятности суммы несовместных событий и — несовместные события. А и В не совместные события
  и  — несовместные события.
  и  — несовместные события.

Слайд 7

Формула для условной вероятности. А и В не совместные события

Слайд 8

Задачи на теорию вероятностей!

Слайд 9

Задача №1
Проводится жеребьёвка Лиги Чемпионов. На первом этапе жеребьёвки восемь команд, среди которых команда «Барселона», распределились случайным образом по восьми игровым группам — по одной команде в группу. Затем по этим же группам случайным образом распределяются еще восемь команд, среди которых команда «Зенит». Найдите вероятность того, что команды «Барселона» и «Зенит» окажутся в одной игровой группе.

Слайд 10

Ответ к задаче №1
После первого этапа жеребьевки команда «Барселона» попадет в некоторую группу, фиксируем ее номер. Теперь задача сводится к тому, чтобы определить вероятность того, что команда «Зенит» попадет в эту же группу.Всего групп 8. Попадание «Зенита» только в одну из них является благоприятным исходом. Следовательно, вероятность равна 1:8=0,125. 

Слайд 11

Задача №2
На столе лежат цветные ручки: синяя, красная, чёрная и зелёная. Петя случайно берёт со стола ручку. С какой вероятностью эта ручка окажется чёрной?

Слайд 12

Ответ к задаче №2
Петя может взять любую из четырех ручек. Только одна из ручек черного цвета. Вероятность того, что Петя возьмет черную ручку, равна: 1:4=0,25.

Слайд 13

Задача №3
В корзине лежат яблоки разных сортов: 20 красных, 35 жёлтых и 25 зелёных. С какой вероятностью случайно вынутое из корзины яблоко окажется красным?

Слайд 14

Ответ к задаче №3
Мальчик может взять любое из 20+25+35=80 яблок. Поскольку 20 из этих яблок красные, вероятность того, что он возьмет красное 20:80=0,25.

Слайд 15

Задача №4
Петя бросает игральный кубик. С какой вероятностью на верхней грани выпадет четное число?

Слайд 16

Ответ к задаче № 4
При броске кубика на верхней грани может выпасть любое из 6 чисел:1, 2, 3, 4, 5, 6. Из них четных три числа: 2, 4, 6. Вероятность того, что на верхней грани выпадет четное число, равна 36=0,5. 

Слайд 17

Задача№5
Биатлонист стреляет по мишеням. Вероятность попасть в мишень при одном выстреле равна 0,8. Найдите вероятность того, что биатлонист поразит все пять мишеней.

Слайд 18

Ответ к задаче №5
Всего 5 выстрелов, вероятность попадания при одном выстреле равна 0,8, поэтому вероятность попадания всех пяти равна (0,8)5=0,32768.

Слайд 19

Возникновение теории вероятностей как науки относят к средним векам и первым попыткам математического анализа азартных игр (орлянка, кости, рулетка). Первоначально её основные понятия не имели строго математического вида, к ним можно было относиться как к некоторым эмпирическим фактам, как к свойствам реальных событий, и они формулировались в наглядных представлениях. Самые ранние работы учёных в области теории вероятностей относятся к XVII веку. Исследуя прогнозирование выигрыша в азартных играх, Блез Паскаль и Пьер Ферма открыли первые вероятностные закономерности, возникающие при бросании костей[1]. Под влиянием поднятых и рассматриваемых ими вопросов решением тех же задач занимался и Христиан Гюйгенс. 
История возникновения

Слайд 20

Его работа, в которой вводятся основные понятия теории вероятностей (понятие вероятности как величины шанса; математическое ожидание для дискретных случаев, в виде цены шанса), а также используются теоремы сложения и умножения вероятностей (не сформулированные явно), вышла в печатном виде на двадцать лет раньше (1657 год) издания писем Паскаля и Ферма (1679 год)[

Слайд 21

Важный вклад в теорию вероятностей внёс Якоб Бернулли: он дал доказательство закона больших чисел в простейшем случае независимых испытаний. В первой половине XIX векатеория вероятностей начинает применяться к анализу ошибок наблюдений; Лаплас и Пуассон доказали первые предельные теоремы. Во второй половине XIX века основной вклад внесли русские учёные П. Л. Чебышёв, А. А. Марков и А. М. Ляпунов. В это время были доказаны закон больших чисел, центральная предельная теорема, а также разработана теория цепей Маркова. Современный вид теория вероятностей получила благодаря аксиоматизации, предложенной Андреем Николаевичем Колмогоровым. В результате теория вероятностей приобрела строгий математический вид и окончательно стала восприниматься как один из разделов математики.

Слайд 22

Спасибо за внимание.

Похожие презентации

Теория вероятности Сложение дробей с одинаковыми знаменателями Правильные и неправильные дроби Самостоятельные работы «Формулы сокращенного умножения» Танграм

2,$$ ты прав. c).$$ Мы можем сформулировать более общую версию этой формулы, применимую к общему разбиению выборочное пространство $S$.

Закон полной вероятности:
Если $B_1, B_2, B_3,\cdots$ является разбиением выборочного пространства $S$, то для любого события $A$ имеем $$P(A)=\sum_{i} P(A \cap B_i)=\sum_{i} P(A | B_i) P(B_i).$$

Используя диаграмму Венна, мы можем графически увидеть Идея закона полной вероятности. На рис. 1.24 мы имеем $$A_1=А\шапка B_1,$$ $$A_2=A \cap B_2,$$ $$A_3=A \cap B_3.$$ Как видно из рисунка, $A_1$, $A_2$ и $A_3$ образуют разбиение множества $A$, и, таким образом, по третьей аксиоме вероятности $$P(A)=P(A_1)+P(A_2)+P(A_3).$$

Рис.1.24 — Закон полной вероятности.

Вот доказательство закона полной вероятности с использованием аксиом вероятности:

Доказательство

Поскольку $B_1, B_2, B_3,\cdots$ является разбиением выборочного пространства $S$, мы можем записать

$S$	$=\bigcup_{i} B_i$
$А$	$= A\cap S$
	$=A \cap (\bigcup_{i} B_i)$
	$=\bigcup_{i} (A \cap B_i) \hspace{20pt} \hspace{20pt}$ по дистрибутивному закону (теорема 1. 2).

Теперь заметим, что множества $A \cap B_i$ не пересекаются (поскольку множества $B_i$ не пересекаются). Таким образом, по третьей аксиоме вероятности $$P(A)=P\bigg(\bigcup_i (A \cap B_i)\bigg)=\sum_{i} P(A \cap B_i)=\sum_{i} P(A | B_i) P(B_i ).$$

---

Вот типичный сценарий, в котором мы используем закон полной вероятности. Мы заинтересованы в нахождение вероятности события $A$, но мы не знаем, как найти $P(A)$ напрямую. Вместо, мы знаем условную вероятность $A$ при некоторых событиях $B_i$, где $B_i$ образуют разделение пространства выборки. Таким образом, мы сможем найти $P(A)$ по закону полной вероятности, $P(A)=\sum_{i} P(A | B_i) P(B_i)$.

---

Пример

У меня есть три сумки, каждая из которых содержит шарики по 100 долларов:

• Мешок 1 содержит красные шарики по 75$ и синие по 25$;
• В сумке 2 есть красные шарики по 60 долларов и синие по 40 долларов;
• В сумке 3 есть красные шарики по 45 долларов и синие по 55 долларов.

Я выбираю один из мешков наугад, а затем беру шарик из выбранных мешок, также наугад. Какова вероятность того, что выбранный шарик красный?

• Раствор

---

← предыдущая

следующая →

Печатная версия книги доступна на Amazon здесь.

Закон вероятности | Наука

••• Thinkstock/Comstock/Getty Images

Обновлено 25 апреля 2017 г.

Автор: Андреа Фаркас

Вероятность измеряет вероятность того, что событие произойдет. Выражаясь математически, вероятность равна числу возможных случаев возникновения определенного события, разделенному на общее количество всех возможных событий. Например, если у вас есть сумка с тремя шариками — одним синим и двумя зелеными — вероятность схватить невидимый голубой шарик равна 1/3. Существует один возможный исход, когда выбирается синий шарик, но всего три возможных исхода испытания — синий, зеленый и зеленый. Используя ту же математику, вероятность схватить зеленый шарик равна 2/3.

Закон больших чисел

Вы можете обнаружить неизвестную вероятность события с помощью экспериментов. Используя предыдущий пример, предположим, что вы не знаете вероятность того, что вытащите шарик определенного цвета, но знаете, что в мешке три шарика. Вы выполняете испытание и рисуете зеленый шарик. Вы выполняете еще одно испытание и вытягиваете еще один зеленый шарик. В этот момент вы можете заявить, что в мешке только зеленые шарики, но, основываясь на двух испытаниях, ваш прогноз ненадежен. Возможно, в мешке только зеленые шарики, а могут быть два других красных, а вы выбрали последовательно только один зеленый шарик. Если вы выполните одно и то же испытание 100 раз, вы, вероятно, обнаружите, что выбираете зеленый шарик примерно в 66% процентов случаев. Эта частота отражает правильную вероятность более точно, чем ваш первый эксперимент. Это закон больших чисел: чем больше число испытаний, тем точнее частота исхода события будет отражать его фактическую вероятность.

Закон вычитания

Вероятность может принимать значения только от 0 до 1. Вероятность 0 означает, что для этого события нет возможных исходов. В нашем предыдущем примере вероятность вытащить красный шарик равна нулю. Вероятность 1 означает, что событие произойдет в каждом испытании. Вероятность вытащить зеленый или синий шарик равна 1. Других возможных исходов нет. В мешке, содержащем один синий и два зеленых шарика, вероятность вытащить зеленый шарик равна 2/3. Это приемлемое число, потому что 2/3 больше 0, но меньше 1 — в диапазоне допустимых значений вероятности. Зная это, вы можете применить закон вычитания, который гласит, что если вы знаете вероятность события, вы можете точно определить вероятность того, что это событие не произойдет. Зная, что вероятность вытащить зеленый шарик равна 2/3, вы можете вычесть это значение из 1 и правильно определить вероятность того, что зеленый шарик не выпадет: 1/3.

Закон умножения

Если вы хотите найти вероятность того, что два события произойдут в последовательных испытаниях, используйте закон умножения. Например, вместо предыдущего мешка с тремя шариками скажем, есть мешок с пятью шариками. Есть один синий шарик, два зеленых шарика и два желтых шарика. Если вы хотите найти вероятность того, что вытащите синий и зеленый шарики в любом порядке (и не возвращая первый шарик в мешок), найдите вероятность вытащить синий и зеленый шарики. Вероятность вытащить синий шарик из мешка с пятью шариками равна 1/5. Вероятность вытащить зеленый шарик из оставшегося набора равна 2/4 или 1/2. Правильное применение закона умножения предполагает умножение двух вероятностей, 1/5 и 1/2, на вероятность 1/10. Это выражает вероятность того, что два события произойдут вместе.

Закон сложения

Применяя то, что вы знаете о законе умножения, вы можете определить вероятность того, что произойдет только одно из двух событий. Закон сложения гласит, что вероятность того, что произойдет одно из двух событий, равна сумме вероятностей того, что каждое событие произойдет по отдельности, минус вероятность того, что произойдут оба события. Допустим, в мешке с пятью шариками вы хотите узнать вероятность того, что вы вытащите либо синий, либо зеленый шарик. Прибавьте вероятность вытащить синий шарик (1/5) к вероятности вытащить зеленый шарик (2/5). Сумма 3/5. В предыдущем примере, выражающем закон умножения, мы обнаружили, что вероятность вытащить и синий, и зеленый шарик равна 1/10. Вычтите это из суммы 3/5 (или 6/10 для более легкого вычитания) для конечной вероятности 1/2.

Связанные статьи

Ссылки

• Вероятность; Математические вкусности; 2011
• Учебник по статистике; Базовая вероятность; СтатТрек; 2011
• Математический форум @ Drexel; Спросите доктора Математики: часто задаваемые вопросы; Введение в теорию вероятности

Об авторе

Андреа Фаркас пишет с 2005 года. Ее юридическая статья опубликована в журналах «Texas Tech Estate Planning» и «Community Property Law Journal». Фаркас окончила Техасский университет A&M и получила степень юриста в Школе права Техасского технологического университета.