Значение производной функции онлайн в точке: Значение производной в точке. Онлайн калькулятор с примерами

Определение производной функции в точке

Определение производной

Производная функции в точке

Пусть функция f(x) определена в некоторой окрестности точки x.
Производной f′(x) функции f(x) в точке x называется конечный предел отношения приращения функции к приращению ее аргумента, когда последний стремится к нулю:
(1)   .

Приращение аргумента функции

в точке x – это разность значений аргумента в некоторой точке и точке x:
.
Приращение аргумента является независимой переменной.

Приращение функции

в точке x – это разность значений функции в некоторой точке и точке x: .
Приращение функции является зависимой переменной. Оно зависит от и , или от и .

Дифференцирование

– это процесс вычисления производной.

В определении (1), приращение аргумента является одной переменной, хотя ее обозначение состоит из двух букв: и . Обычно переменную принято обозначать одной буквой или буквой с одним или несколькими индексами. Но приращение в математическом анализе настолько часто встречается, что его обозначают с небольшим нарушением правил. Приращение функции также является одной переменной.

В приведенных выше определениях, является независимой переменной, а – зависимой. зависит от двух переменных. Если использовать выражение , то приращение функции зависит от переменных x и . Если использовать , то зависит от x и . Но когда мы вычисляем производную в заданной точке x, то считаем, что x является постоянной. Тогда является функцией, зависящей только от одной переменной . Таким образом задача о нахождении производной в точке x сводится к задаче о вычислении предела от функции , зависящей от одной переменной при , или от функции , зависящей от одной переменной при .

В правой части (1) мы сделали замену, и перешли от переменной к переменной . Тогда . При ,
.

После того, как мы нашли производную в заданной точке, то x уже можно считать не фиксированным числом, а переменной. То есть предел (1) можно рассматривать как функцию от x.

Еще раз подчеркнем, что выражение является функцией от двух переменных: x и . А выражение , полученное после вычисления предела, зависит только от одной переменной x.

Ниже приводятся примеры вычислений производных ⇓, используя определение ⇑.

Обозначение производной

Обозначение Лагранжа

Наиболее популярным является обозначение Лагранжа. Производную функции обозначают как и саму функцию, добавляя штрих после ее характеристики: . Если функция задана алгебраическим выражением, то это выражение заключают в скобки, и ставят знак штриха справа за закрывающей скобкой: . При этом производная также является функцией от той же переменной x, что и . Правда область определения производной может не совпадать с областью определения функции, а является ее подмножеством.

Напомним, что в обозначении функции фигурируют три символа: независимая переменная, характеристика функции и зависимая переменная (см. «Определение функции»). Так, в выражении
(2)   ,
x является независимой переменной, или аргументом функции; f   – характеристикой функции; y   – зависимой переменной, или значением функции. Обозначение зависимой переменной может совпадать или не совпадать с обозначением характеристики. Производную функции (2) обозначают так:
.

Независимую переменную производной обозначают так же, как и независимую переменную функции. В нашем случае это x.

Характеристику производной обозначают тем же символом, что и характеристику функции, добавляя штрих справа: .

Зависимую переменную производной обозначают аналогично характеристике, добавляя штрих к обозначению зависимой переменной функции. Так, для примера (2), это будет : .

Если функция зависит от нескольких переменных, например
(3)   ,
но все кроме одной считают постоянными, то к характеристике производной добавляют нижний индекс, обозначающий ту переменную, по которой вычисляют производную. При этом знак штриха может быть опущен. Например, следующие два обозначения эквивалентны: . Здесь подразумевается, что переменные и мы считаем постоянными. Тогда в данном контексте, является функцией от одной переменной . К зависимой переменной производной также добавляют нижний индекс переменной, по которой выполняется дифференцирование:
.
Подобные производные функций от нескольких переменных называются частными производными. Детально они будут рассмотрены позже.

Нижний индекс добавляют и при вычислениях, связанных со сложными функциями. Пусть, например, функцию можно представить как сложную: , составленную из двух функций: и . При этом множества значений функций и совпадают. Поэтому их удобно обозначить одной переменной y. Тогда производную от y, выраженную через переменную x, обозначают как :
.
А производную от y, выраженную через переменную , обозначают как :
.

Обозначение производной по времени в физике

В механике и физике, производную по времени обозначают не штрихом, а точкой над зависимой переменной. Обычно время обозначают буквой t. Тогда
.

Обозначение Лейбница

В способе Лейбница, зависимую переменную обозначают в форме отношения дифференциалов:
.
Этот способ удобен, поскольку указывает, по какой переменной ведется дифференцирование. Такой способ применяется только для функций от одной переменной. Для функций от многих переменных используют обозначение частной производной: .

Иногда в форме дифференциалов обозначают характеристику производной, добавляя справа аргумент:
.
Однако этот способ скорее неудачен, и может привести к путанице.

Обозначение Коши

Также, для обозначения производной, используют обозначение Коши:
.
Но мы не будем им пользоваться.

Существование производной

Рассмотрим вопрос о существовании предела, который используется при вычислении производной, при заданном значении x:
(4)   .
Здесь могут возникнуть три случая:
1) в точке x существует конечный предел (4);
2) существует бесконечный предел или ;
3) предела (4) не существует.

1) Если существует конечный предел (4), то говорят, что функция имеет производную в точке x.

2) Если в некоторой точке x существует бесконечный предел (4), то говорят, что производной в этой точке не существует. Это согласуется с определением, ⇑ в котором указано, что производной называется конечный предел. Однако при этом говорят, что функция f имеет в точке x бесконечную производную, равную или . Здесь стоит обратить внимание на различие в определении предела и производной. Возможна ситуация, когда предел (4) существует (равный бесконечности), но при этом производная не существует (хотя существует ее значение, равное бесконечности).
См. пример ⇓.

3) Если предела (4) не существует, то функция не имеет производной в точке x.

Производные справа и слева

Определение

Правая (левая) производная функции f в точке x

Пусть функция f(x) определена в правой окрестности точки x. Тогда правой производной функции f в точке x называется правый предел
.
Соответственно, если функция определена в левой окрестности x, то левой производной функции f в точке x называется левый предел
.
Правую (левую) производную также называют производной справа (слева) в точке x, или правосторонней (левосторонней) производной в точке x.

Лемма об односторонних производных

Функция имеет в точке x производную тогда и только тогда, когда
она имеет в этой точке производные справа и слева, и они равны:
.
При этом
.

Доказательство

Для доказательства применим теорему об односторонних пределах.

Пусть существует производная функции в точке x. Это означает, что она определена в некоторой окрестности точки x, и существует конечный предел функции при :
.
Но тогда существуют правая и левая окрестности точки x, на которых определена. По теореме об односторонних пределах, существуют равные правый и левый пределы:
.
Отсюда следует, что в точке x существуют односторонние производные
.

Пусть теперь, в точке x, существуют равные односторонние производные:
.
Это означает, что существуют правая и левая окрестности точки x, в которой определена . И существуют односторонние равные пределы:
.
Отсюда следует, что существует двусторонняя окрестность точки x, на которой определена . И по теореме об односторонних пределах, существует двусторонний предел:
.
Это означает, что в точке x существует производная
.

Лемма доказана.

Следствие о неравных односторонних производных

Если функция имеет в точке x не равные односторонние производные:
,
то она не имеет производной в этой точке.

Действительно, допустим противное. Пусть функция имеет в точке x не равные односторонние производные, но при этом имеет производную в этой точке. Тогда, согласно лемме об односторонних производных, она имеет в этой точке равные производные слева и справа, что противоречит предположению.

См. пример ⇓.

Примеры вычисления производной, используя определение

Все примеры Здесь и далее мы приводим подробные решения примеров, в которых нужно вычислить производную функции , используя определение производной ⇑.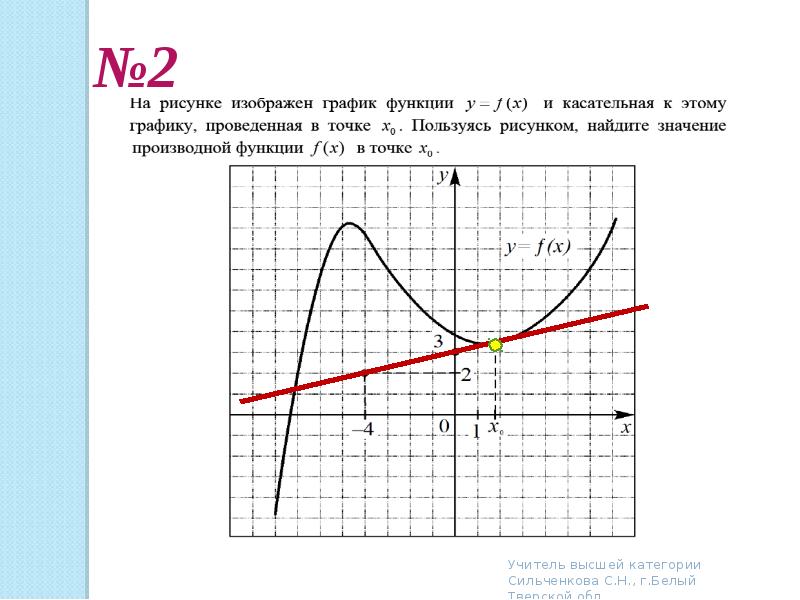
  решение ⇓ ;    ⇓ ;    ⇓ .

Пример

Все примеры ⇑ Найти производную функции , используя определение производной.

Решение

Функция определена для всех x. Поэтому она определена в любой окрестности любой точки x. Используем определение (1). Считаем, что x – фиксированное число, то есть что его значение задано. Найдем приращение функции в точке x:

.
Находим отношение приращения функции к приращению ее аргумента:
.
Находим предел функции , зависящей от переменной . При этом считаем, что x является фиксированным, заданным числом:
.

Итак, мы нашли производную:
.
Поскольку вычисленный нами предел существует, и является конечным числом для всех x, то функция имеет производную для всех значений аргумента x.

Ответ

.

Пример бесконечной производной +∞

Все примеры ⇑ Найдем производную функции .

Решение

Производная функции в точке x = 0 равна плюс бесконечности.

Функция определена для всех x. Найдем отношение приращения функции к приращению ее аргумента в точке x:
.
Применим формулу . Тогда
;
(5)   .
Считаем, что x является фиксированным числом. Тогда отношение является функцией от одной переменной : . При она определена для всех . При она определена для всех .

Пусть . Тогда:
.
Пусть . Подставим в (5) :
.
Поскольку , то
.

Ответ

Таким образом мы нашли, что функция имеет производную для всех . При функция не имеет производной, она равна .

Пример

Все примеры ⇑ Найдем производную функции . Покажем, что несмотря на то, что функция определена для всех x, ее производная в точке не существует.

Решение

Функция y = |x| не имеет производной в точке x = 0.

Функция определена для всех значений аргумента x. Поэтому она определена в любой окрестности произвольной точки x.

1. Пусть . Тогда ,
.

2. Пусть . Тогда ,

.

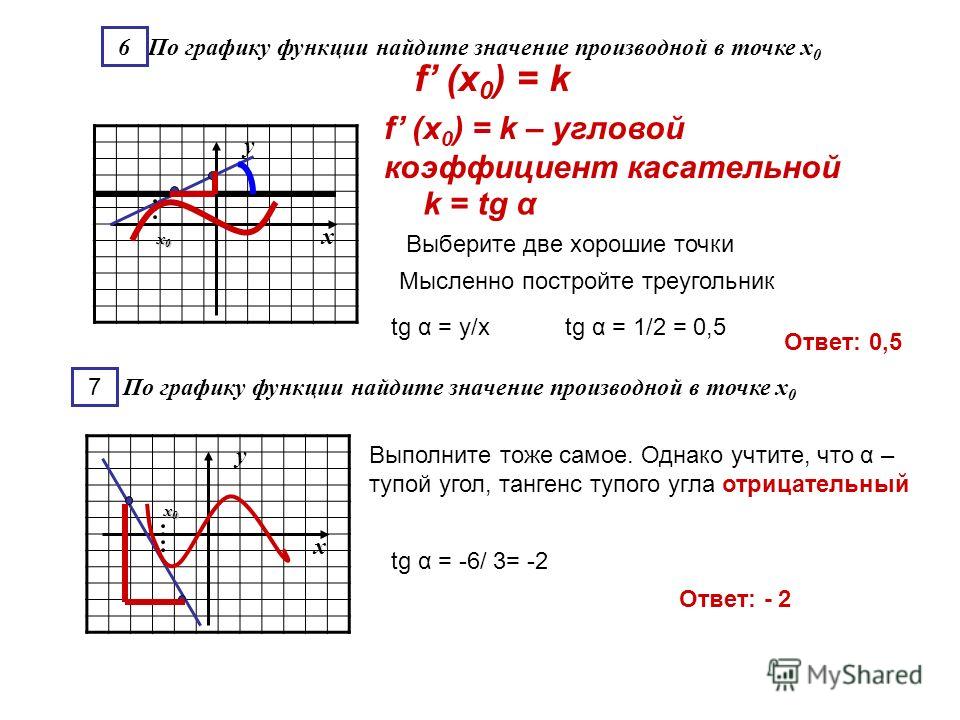
3. Рассмотрим точку . В ней
.
Найдем производную справа в точке . При этом ,
.
Теперь найдем производную слева в точке . В этом случае ,
.

Итак, мы нашли, что односторонние производные в точке существуют, но они не равны друг другу:
.
Согласно следствию леммы об односторонних производных, производной функции в точке не существует.

Ответ

;
;
.
В точке производная не существует.

Использованная литература:
Г.Е. Иванов. Лекции по математическому анализу. Часть 1. Москва, МФТИ, 2018.
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.

вычислить значение производной на каждом из участков графика

Вы искали вычислить значение производной на каждом из участков графика? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и вычислить значение производной функции в точке x0, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «вычислить значение производной на каждом из участков графика».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как вычислить значение производной на каждом из участков графика,вычислить значение производной функции в точке x0,геометрический смысл производной примеры решения задач,значение производной в точке,значение производной в точке как найти,значение производной функции f x в точке x,значение производной функции в точке,значение производной функции в точке как найти,как найти значение производной в точке,как найти значение производной в точке х0,как найти значение производной функции,как найти значение производной функции f x в точке x0,как найти значение производной функции f x в точке x0 по графику,как найти значение производной функции в точке,как найти значение производной функции в точке х0 по графику,как найти производную функции в точке x0,как по графику производной найти значение производной в точке,как по графику функции найти значение производной в точке х0,найдите значение производной,найдите значение производной в точке х0,найдите значение производной функции,найдите значение производной функции f x в точке y x0,найдите значение производной функции в точке,найдите значение производной функции в точке x0,найдите значение производной функции в точке х0,найти значение производной в точке x0,найти значение производной функции в точке,найти значение производной функции в точке х0.

На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и вычислить значение производной на каждом из участков графика. Просто введите задачу в окошко и нажмите «решить» здесь (например, геометрический смысл производной примеры решения задач).

Где можно решить любую задачу по математике, а так же вычислить значение производной на каждом из участков графика Онлайн?

Решить задачу вычислить значение производной на каждом из участков графика вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

Калькулятор производной в точке с шагами и решением

Введение в калькулятор производной в точке

Калькулятор производной — это онлайн-инструмент для вычисления производной функции в заданной точке. Это помогает вычислить среднюю скорость изменения функции в точке, следуя всем правилам производных; произведение, частное и цепь.

В исчислении производная функции в точке используется для аппроксимации ее в данной точке, чтобы найти соответствующую скорость изменения. Таким образом, это важное понятие исчисления. Мы представляем онлайн-инструмент, который поможет вам вычислить производную функции быстрее, чем вручную.

Связанный: Попробуйте второй калькулятор производной, чтобы вычислить удвоенную производную функции.

Как найти производную в точке с помощью калькулятора?

С помощью нашего инструмента очень легко вычислять производные, потому что он лучший во всех отношениях. Вам нужно дать ему входные значения, а затем он вычислит производную для вас.

Выполните следующие шаги, чтобы использовать этот инструмент:

1. Найдите калькуляторы в своем браузере и выберите калькулятор производной в точке из списка доступных инструментов.
2. Теперь на странице инструментов введите функцию в «Ввести функцию».
3. Или вы можете использовать «Загрузить примеры», чтобы выбрать случайную функцию.
4. Выберите порядок производных из «Вычислить».
5. Введите точку, в которой вы хотите найти производную в «Когда x=».
6. Нажмите на кнопку «Рассчитать».

Вы получите значение производной в заданной точке в течение минуты.

Производная в точке Формула

Когда мы хотим аппроксимировать функцию в точке, мы находим производную функции и затем подставляем в нее точку. Полученное решение называется производной в точке.

Пусть f — функция, а x=a — значение в области определения f, тогда производная в точке относительно точки x=a равна:

$$ f'(a) \;=\; \frac{f(a+h)-f(a)}{h} $$

Где

f’a = производная в точке a.

Приведенная выше формула используется калькулятором производной функции в точке для вычисления производной функции в заданной точке.

Зачем использовать онлайн-калькулятор производной в точке с шагами?

Производная функции в данной точке называется производной в точке. В исчислении эта концепция помогает найти наклон касательной к графику функции в точке. Поэтому она имеет большое значение в математике, полезной для решения многих задач, таких как нахождение скорости в определенной точке.

При расчете производной функции в точке вручную можно запутаться с формулой, поскольку она похожа на производную. Вот почему вам нужно использовать инструмент, который поможет вам без труда найти производную в точке. Если вы хотите понять, как найти производную функции в определенном направлении, калькулятор производной по направлению поможет вам решить нужные уравнения с помощью шагов.

Преимущества использования второй производной в калькуляторе без точек

Использование онлайн-инструмента для решения математических задач всегда более полезно и разумно. Это потому, что это может позволить вам улучшить свои навыки решения проблем за короткое время. Точно так же наш инструмент лучше всего поможет вам в расчете производных в точке. Есть и другие преимущества калькулятора формулы производной в точке. Это:

• Это поможет вам найти производные в точке, взяв только входные значения от вас.
• Калькулятор производной функции в точке поможет вам улучшить свои аналитические навыки, чтобы вы могли быстрее вычислять производные.
• Это бесплатный онлайн-инструмент, который ничего не требует для использования.
• Вам не нужно регистрировать учетную запись или подписываться на план, такой как инструменты премиум-класса.
• Быстро и точно вычисляет производные с шагом.

Хамза Харун

Последнее обновление 05 апреля 2022 г.

Я автор и создатель контента. Мне нравится писать контент на разные темы. Помимо писательства, я SEO-ASO-SMM специалист и любитель футбола.

Калькулятор производной в точке с пошаговыми инструкциями

Введение в калькулятор производной в точке

Калькулятор производной — это онлайн-инструмент, который позволяет вычислять производную в заданной точке функции без выполнения долгосрочных вычислений. Он использует значение функции в качестве входных данных и интервал, с которым вы хотите рассчитать скорость изменения этой функции.

В исчислении производная в точке является важным понятием, позволяющим найти скорость изменения любой функции. Он аппроксимирует заданную функцию в конце изменения. Мы представляем онлайн-инструмент, который поможет вам рассчитать производные в заданной точке на касательной.

Производная в точке Калькулятор с пошаговой формулой

Производная в точке относится к аппроксимации функции в точке. При этом дифференцировании мы сначала находим производную функции, а затем подставляем в нее точку.

Формула

Пусть f — функция, и в области определения f(x) есть точка x=a. Тогда производная f(x) по точке x=a равна

$$ f'(a) \;=\; \frac{f(a+h)-f(a)}{h} $$

Где,

f’a= Производная в a.

Калькулятор производной в точке использует эту формулу для аппроксимации заданной функции относительно точки.

Пример производной в точке

Вычислим производную sqrt x при x=4. Для этого предположим, что 9{-\frac{1}{2}}=\frac{1}{2\sqrt{x}}$$

При x=4,

$$f'(4)=\frac{1}{ 2\sqrt{4}}$$

Следовательно, производная sqrt x при x=4 равна

$$f'(4)=\frac{1}{2(2)}=\frac{1} {4}$$

Как найти производную в точке с помощью онлайн-калькулятора?

Этот инструмент нетрудно найти в Интернете. Вы можете выполнить поиск в своем браузере. Он доступен на сайте калькулятора. На этом сайте также есть множество различных математических инструментов.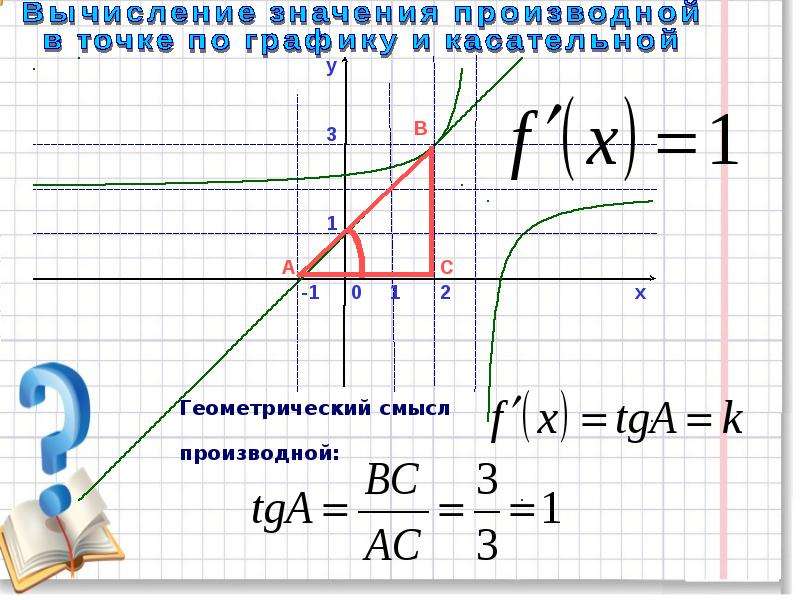 Вы также можете просто использовать URL-адрес нашего веб-сайта для доступа к веб-сайту.

Как работает калькулятор производной в точке?

Работа этого калькулятора зависит от функции ввода и точки, в которой должно быть вычислено значение функции. Он использует формулу фундаментального дифференциала для расчета скорости изменения функции в определенной точке. Он выполняется быстро и предоставляет вам пошаговое полное решение.

Когда вы вводите функцию в этот калькулятор, он анализирует функцию и переменную, по которой вы хотите найти скорость изменения. После этого он вычисляет производную функции и вводит в нее заданную точку, чтобы найти значение скорости изменения в этой точке.

Зачем использовать калькулятор формулы производной в точке?

Производная в точке и обычная Производная — два запутанных, но важных понятия для учащихся. Это понятие помогает найти наклон касательной к графику функции в точке. Поэтому он имеет множество приложений в математике и физике. Например, нахождение наклона в определенной точке выполняется путем нахождения производной в этой точке.

Можно запутаться в формуле при вычислении Производной в точке ручными вычислениями. Это потому, что обычная производная и производная в точке состоят почти из одних и тех же формул. Есть лишь небольшая разница, которая сбивает с толку студентов. Поэтому вам нужно использовать этот инструмент, чтобы избежать путаницы. Если вы хотите быстро найти производную от экстремума, вы также можете воспользоваться онлайн-калькулятором экстремумов.

Преимущества использования калькулятора второй производной в точке

Сегодня, в соответствии с последними технологическими обновлениями, нам необходимо обновить наши методы обучения с его помощью. Итак, следуя этому требованию, мы предлагаем вам калькулятор второй производной в баллах, который может дать вам много преимуществ не только в учебе, но и в улучшении ваших навыков решения задач. Некоторые из этих преимуществ выделены ниже.

• Это бесплатный онлайн-инструмент для вас. Для этого не требуется никакой учетной записи или платного плана подписки.
• Калькулятор производной в точке может сэкономить ваше время и энергию при выполнении сложных вычислений вручную.
• Он обеспечивает быстрые и 100% точные результаты.
• Вы можете найти производную в какой-то момент, не изучая никаких руководств, потому что она проста в использовании.
• Вы можете найти высокоточные производные в точке до 9-го порядка.

Как использовать пошаговый калькулятор производной в точке?

С помощью этого инструмента нетрудно найти производные в точке, потому что он обеспечивает простое и быстрое решение ваших математических задач. Есть несколько простых и легких шагов, чтобы использовать этот инструмент. Это:

• Запишите значение функции в поле «Введите функцию».
• Выберите порядок производных из «вычисляет с».
• Теперь выберите точку из «Когда x=».

  No related posts.