Как найти область определения и значения функции
Статьи › Находится › Как находится область определения функции заданной формулой
Областью определения функции являются все значения Х, на которых существует функция. Иными словами, те Х, которые можно подставить в уравнение функции и получить в результате Y. Область значения функции определяется значениями, которое принимает Y на всей своей области определения.
- Как найти область определения функции и значения
- Как найти область значения функции по формуле
- Как найти область определения выражения
- Что такое область определения и множество значений функции
- Как найти область определения функции y 3x 7
- Как найти область определения функции sin
- Как найти значение функции
- Чем отличается область определения и область значения
- Что такое область определения функции
- Что такое область значения функции 9 класс
- Как обозначается область значений функции
- Как найти множество значений функции
- Как найти область определения функции y sin2x
- Как найти область определения функции тангенс
- Как написать множество значений функции
- Что значит D от f
- Что такое д у
- Что такое область определения квадратичной функции
- Как найти область определения функции с двумя переменными
- Что такое область значений функции 7 класс
- Как найти наименьшее значение функции
- Как записывается область значения функции
Как найти область определения функции и значения
Если a — положительное целое число, то область определения функции есть множество действительных чисел: (−∞, +∞). Для нецелых действительных положительных показателей степени: D(f) = [0, +∞). Если a — отрицательное целое число, то область определения функции представляет собой множество (−∞, 0) ∪ (0, +∞).
Для нецелых действительных положительных показателей степени: D(f) = [0, +∞). Если a — отрицательное целое число, то область определения функции представляет собой множество (−∞, 0) ∪ (0, +∞).
Как найти область значения функции по формуле
Для того чтобы найти область значений на данном отрезке, необходимо: Найти вершину параболы по формуле: x = -b / (2 * a), подставить ее в формулу и найти y. Это значение y будет минимальным/максимальным в зависимости от того, куда направлены ветви параболы.
Как найти область определения выражения
Областью определения выражения с одной переменной называется множество значений переменной, при которых это выражение имеет смысл. Можно вычислить числовое значение алгебраического выражения при любом значении переменной из его области определения.
Что такое область определения и множество значений функции
Область значений (или множество значений) функции — множество, состоящее из всех значений, которые принимает функция.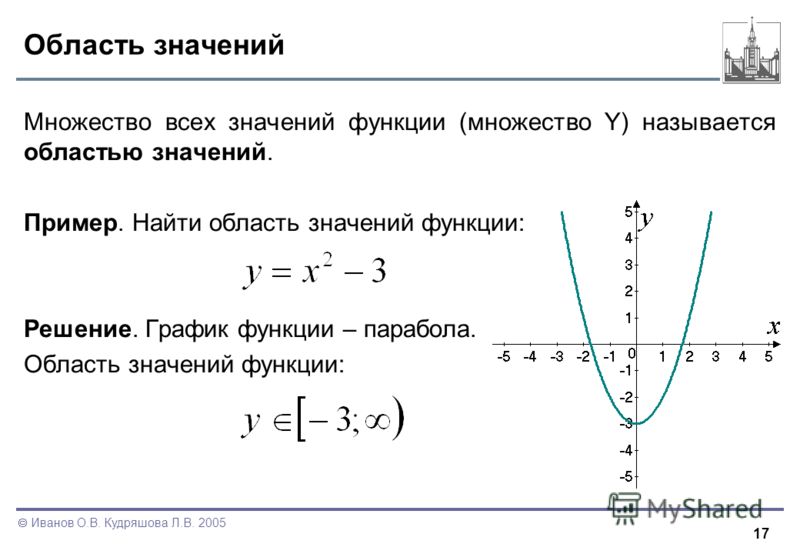
Как найти область определения функции y 3x 7
Функции y=3x-7 — является линейной функцией. Областью определения функции y=3x-7 является множество всех действительных чисел, то есть при любом значении х — функция будет существовать. Ответ: область определения функции y=3x-7 — множество всех действительных чисел.
Как найти область определения функции sin
Итак, Областью определения функций y = sin x и y = cos x является множество R всех действительных чисел.
Как найти значение функции
Чтобы найти значение функции при заданном значении аргумента, надо значение аргумента подставить в уравнение функции вместо x и вычислить ее значение.
Чем отличается область определения и область значения
Ответы1. Областью определения функции являются все значения Х, на которых существует функция. Иными словами, те Х, которые можно подставить в уравнение функции и получить в результате Y. Область значения функции определяется значениями, которое принимает Y на всей своей области определения.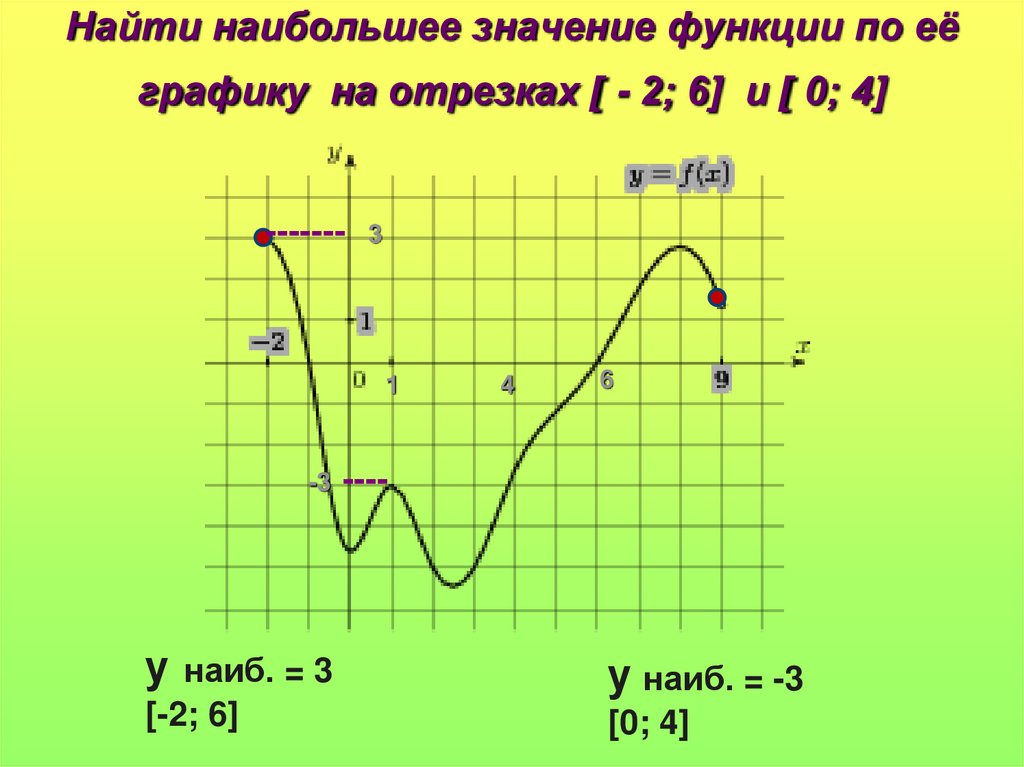
Что такое область определения функции
Область определения — множество, на котором задаётся функция. В каждой точке этого множества значение функции должно быть определено.
Что такое область значения функции 9 класс
Областью определения функции \(y = f(x)\) называют множество всех значений \(x\), для которых функция имеет смысл. Множество всех значений функции \(y = f(x)\), x ∈ X, называют областью значений функции.
Как обозначается область значений функции
Множество всех значений, которые может принять зависимая переменная, называется областью значения функции: E(f) т.
Как найти множество значений функции
Найти критические точки функции f(x) и выбрать те из них, которые принадлежат данному отрезку; вычислить значения функции на концах отрезка и в выбранных критических точках; среди найденных значений выбрать наименьшее и наибольшее значения; Множество значений функции заключить между этими значениями.
Как найти область определения функции y sin2x
Y = sin 2x. Синус — тригонометрическая функция, непрерывная, значит, область определения функции — любое число. Функция независимо от своего аргумента принимает значения, находящиеся в промежутке от -1 до 1.
Синус — тригонометрическая функция, непрерывная, значит, область определения функции — любое число. Функция независимо от своего аргумента принимает значения, находящиеся в промежутке от -1 до 1.
Как найти область определения функции тангенс
Область определения функции y = tgx — множество ℝ действительных чисел, кроме x = π 2 + π n, n ∈ ℤ. Множество значений функции y = tgx — все действительные числа.
Как написать множество значений функции
Множество чисел, пробегаемое функцией у, когда х принимает все возможные значения (т. е. при всех значениях), называется множеством значений функции, или областью значений функции, или областью изменения функции и обозначается через E(f).
Что значит D от f
Область определения функции — это множество всех значений переменной x, которые имеют соответствующие им значения функции. Обозначают: D(f). На графике область определения — это промежутки на оси ОX, над которыми (или под которыми) имеются части графика.
Что такое д у
Условный проход (обозначается DN, устаревшее обозначение Ду; другие названия: номинальный диаметр, диаметр условного прохода, номинальный размер, условный диаметр, номинальный проход) — номинальный параметр, применяемый при описании трубопроводных систем как характеризующий признак при монтаже и подгонке друг к другу
Что такое область определения квадратичной функции
Свойства квадратичной функции
Область определения функции — вся числовая прямая: D (f) = R = (− ∞; ∞). Область значений функции зависит от знака коэффициента.
Область значений функции зависит от знака коэффициента.
Как найти область определения функции с двумя переменными
Областью определения функции двух переменных называется множество всех пар, для которых существует значение. Графически область определения представляет собой всю плоскость либо её часть. Так, областью определения функции является вся координатная плоскость — по той причине, что для любой точки существует значение.
Что такое область значений функции 7 класс
Все значения, которые принимает независимая переменная x (аргумент), называют областью определения функции. Другими словами, множество всех допустимых значений аргумента х называется областью определения функции.
Как найти наименьшее значение функции
Чтобы найти наибольшее или наименьшее значение функции необходимо:
- Найти производную функции f ′ (х)
- Найти стационарные точки, решив уравнение f ′ (х) = 0.
- Проверить, какие стационарные точки входят в заданный отрезок.

- Вычислить значение функции на концах отрезка и в стационарных точках из п.
Как записывается область значения функции
Множество всех значений, которые может принять зависимая переменная, называется областью значения функции: E(f) т.
Понятие функции. Область определения функции. Множество значений функции
| Справочник по математике | Элементы математического анализа | Функции |
Содержание
| Понятие функции. Область определения функции. Множество значений функции |
| Примеры решения задач |
Понятие функции.
 Область определения функции. Множество значений функции
Область определения функции. Множество значений функцииОПРЕДЕЛЕНИЕ. Пусть X – некоторое множество чисел. Говорят, что на множестве X задана числовая функция, если указано правило, с помощью которого каждому числу x из множества X ставится в соответствие некоторое число.
Это принято обозначать так:
y = f (x),
причем в этой записи x называют аргументом функции или независимой переменной, а y называют значением функции, соответствующим аргументу x .
Множество X называют областью определения функции f и обозначают D ( f ) . Множество Y всех возможных значений функции y = f (x) называют множеством значений функции f и обозначают E ( f ) (рис. 1).
1).
Рис.1
Примеры решения задач
Часто в задачах известна формула, задающая функцию f , и требуется найти наиболее широкое множество чисел, к которым данную формулу можно применить. В этом случае указанная задача формулируется так: «Найти область определения функции y = f (x)». В некоторых задачах требуется найти не только область определения функции, но и множество ее значений.
ЗАДАЧА 1. Найти область определения функции
РЕШЕНИЕ. Указанная функцию представляет собой результат, полученный при делении числа x4 на число (3 + x) . Поскольку единственным ограничением является запрет деления на число 0 , то число (3 + x) не может равняться 0 , то есть .
ОТВЕТ. .
ЗАДАЧА 2. Найти область определения функции
Найти область определения функции
РЕШЕНИЕ. Поскольку квадратный корень можно извлекать только из неотрицательных чисел, то область определения данной функции задается неравенством
которое эквивалентно неравенству
и может быть записано в виде
.
Решая это неравенство с помощью метода интервалов, получим
ОТВЕТ. .
ЗАДАЧА 3. Найти область определения функции
РЕШЕНИЕ. Исходя из определений логарифма и квадратного корня, область определения данной функции задается следующей системой неравенств
| (1) |
Решая второе неравенство системы с помощью метода интервалов,
получим
Таким образом, система (1) эквивалентна системе
Решением этой системы является интервал
ОТВЕТ. .
.
ЗАДАЧА 4 . Найти множество значений функции
y = 3sin x + 4cos x
РЕШЕНИЕ. Воспользовавшись формулой дополнительного угла (вспомогательного аргумента), получим
y = 5 sin (x + φ) ,
где
Поскольку множеством значений функции y = sin (x + φ) является отрезок [–1, 1], то множеством значений функции y = 5 sin (x +φ) будет отрезок [–5, 5].
ОТВЕТ. .
ЗАДАЧА 5 . Найти множество значений функции
y = x2 + 6x + 8
РЕШЕНИЕ. Поскольку
и для каждого числа существуют решения уравнения
x2 + 6x + 8 = y ,
определяемые формулой
то множеством значений функции y = x2 + 6x + 8 будет множество .
ОТВЕТ. .
1.5 Поиск входных и выходных значений функции – математика 3080 Подготовка
Когда мы знаем входное значение и хотим определить соответствующее выходное значение для функции, мы оцениваем функцию. Вычисление всегда будет давать один результат, потому что каждое входное значение функции соответствует ровно одному выходному значению.
Когда мы знаем выходное значение и хотим определить входные значения, которые дадут это выходное значение, мы устанавливаем выход равным формуле функции и 9{2}+2p\text{}[/latex] решить для [латекс]\текст{}h\left(p\right)=3[/latex].
Раствор
Вычисление функций, выраженных в формулах
Некоторые функции определяются математическими правилами или процедурами, выраженными в форме уравнения. Если возможно выразить выход функции с помощью формулы, включающей входную величину, то мы можем определить функцию в алгебраической форме.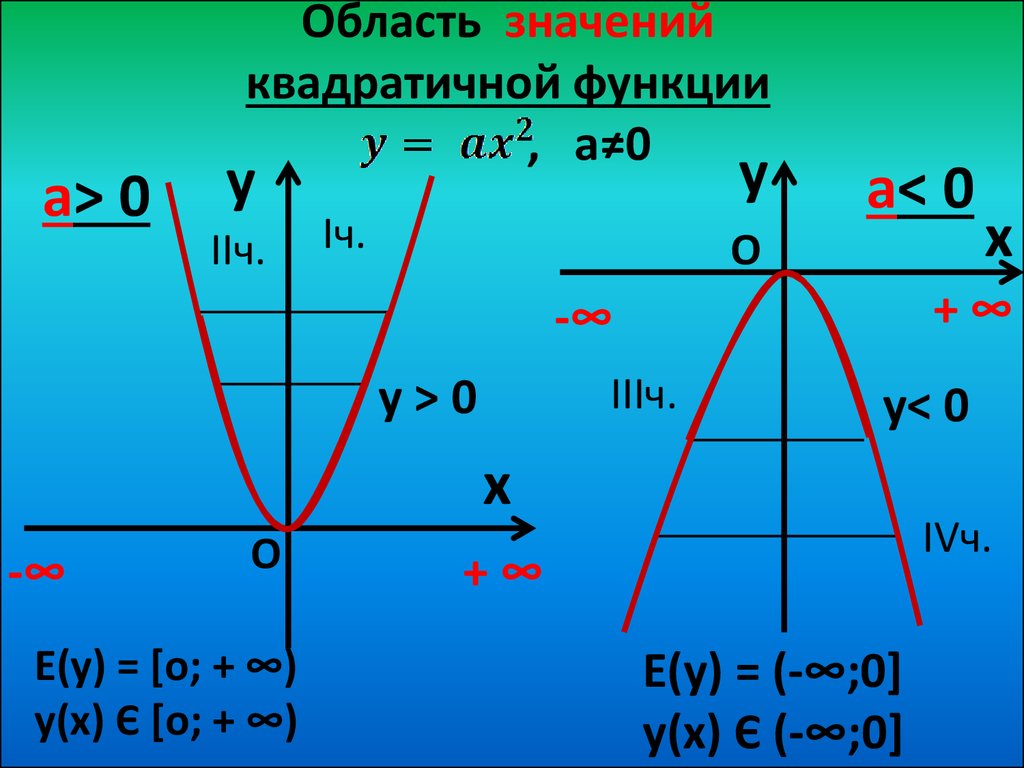
Дана функция в виде уравнения, напишите ее алгебраическую формулу.
- Решите уравнение, чтобы изолировать выходную переменную с одной стороны от знака равенства, с другой стороны как выражение, которое включает только входную переменную.
- Используйте все обычные алгебраические методы для решения уравнений, такие как прибавление или вычитание одной и той же величины из обеих частей или умножение или деление обеих частей уравнения на одну и ту же величину. 9{y},\text{}[/latex], если мы хотим выразить [latex]\text{}y\text{}[/latex] как функцию [latex]\text{}x,\text{} [/latex] не существует простой алгебраической формулы, включающей только [латекс]\текст{}х\текст{}[/латекс], равной [латекс]\текст{}у\текст{}[/латекс].
 Однако каждый [латекс]\текст{}х\текст{}[/латекс] определяет уникальное значение для [латекс]\текст{}у\текст{}[/латекс], и существуют математические процедуры, с помощью которых [ латекс]\текст{}у\текст{}[/латекс] можно найти с любой точностью. В этом случае мы говорим, что уравнение дает неявное (подразумеваемое) правило для [латекс]\текст{}у\текст{}[/латекс] как функцию от [латекс]\текст{}х\текст{}[ /latex], хотя формулу нельзя написать явно.
Однако каждый [латекс]\текст{}х\текст{}[/латекс] определяет уникальное значение для [латекс]\текст{}у\текст{}[/латекс], и существуют математические процедуры, с помощью которых [ латекс]\текст{}у\текст{}[/латекс] можно найти с любой точностью. В этом случае мы говорим, что уравнение дает неявное (подразумеваемое) правило для [латекс]\текст{}у\текст{}[/латекс] как функцию от [латекс]\текст{}х\текст{}[ /latex], хотя формулу нельзя написать явно. Вычисление функции, заданной в табличной форме
Как мы видели выше, мы можем представлять функции в виде таблиц. И наоборот, мы можем использовать информацию в таблицах для написания функций, и мы можем оценивать функции, используя таблицы. Например, насколько хорошо наши питомцы помнят приятные воспоминания, которыми мы делимся с ними? Существует городская легенда, что у золотой рыбки память 3 секунды, но это всего лишь миф. Золотая рыбка может помнить до 3 месяцев, а бета-рыбка имеет память до 5 месяцев. И если память щенка не превышает 30 секунд, то взрослая собака может помнить 5 минут.

Функцию, связывающую тип питомца с длительностью его памяти, легче визуализировать с помощью таблицы. См. Таблицу 1-10. [1]
Таблица 1-10 Домашнее животное Объем памяти в часах Щенок 0,008 Взрослая собака 0,083 Кат 16 Золотая рыбка 2160 Бета-рыба 3600 Иногда вычисление функции в виде таблицы может оказаться более полезным, чем использование уравнений.
 Здесь давайте вызовем функцию [latex]P[/latex]. Домен функции — это тип питомца, а диапазон — действительное число, представляющее количество часов, в течение которых сохраняется память питомца. Мы можем оценить функцию [latex]\text{}P\text{}[/latex] по входному значению «золотая рыбка». Мы бы написали [латекс]P\влево(\текст{золотая рыбка}\вправо)=2160[/латекс]. Обратите внимание, что для вычисления функции в форме таблицы мы идентифицируем входное значение и соответствующее выходное значение из соответствующей строки таблицы. Табличная форма для функции [latex]\text{}P\text{}[/latex] кажется идеально подходящей для этой функции, в большей степени, чем ее запись в форме абзаца или функции.
Здесь давайте вызовем функцию [latex]P[/latex]. Домен функции — это тип питомца, а диапазон — действительное число, представляющее количество часов, в течение которых сохраняется память питомца. Мы можем оценить функцию [latex]\text{}P\text{}[/latex] по входному значению «золотая рыбка». Мы бы написали [латекс]P\влево(\текст{золотая рыбка}\вправо)=2160[/латекс]. Обратите внимание, что для вычисления функции в форме таблицы мы идентифицируем входное значение и соответствующее выходное значение из соответствующей строки таблицы. Табличная форма для функции [latex]\text{}P\text{}[/latex] кажется идеально подходящей для этой функции, в большей степени, чем ее запись в форме абзаца или функции.Для функции, представленной в виде таблицы, определите конкретные выходные и входные значения.
- Найдите заданный вход в строке (или столбце) входных значений.
- Идентифицируйте соответствующее выходное значение в паре с этим входным значением.
- Найдите указанные выходные значения в строке (или столбце) выходных значений, отмечая каждый раз, когда появляется это выходное значение.

- Определите входное значение(я), соответствующее данному выходному значению.
Используя таблицу 1-11,
- Вычислить [латекс]\текст{}г\влево(3\вправо)[/латекс].
- Решить [латекс]\текст{}г\влево(п\вправо)=6[/латекс].
- Вычислить [латекс]\текст{}г\влево(1\вправо)[/латекс].
Таблица 1-11 [латекс]n[/латекс] 1 2 3 4 5 [латекс]г\влево(н\вправо)[/латекс] 8 6 7 6 8 Раствор
Поиск значений функции на графике
Вычисление функции с помощью графика также требует нахождения соответствующего выходного значения для заданного входного значения, только в этом случае мы находим выходное значение, глядя на график.
 Решение функционального уравнения с использованием графика требует нахождения всех экземпляров заданного выходного значения на графике и наблюдения за соответствующим входным значением (значениями).
Решение функционального уравнения с использованием графика требует нахождения всех экземпляров заданного выходного значения на графике и наблюдения за соответствующим входным значением (значениями).Учитывая график на рис. 1-4,
- Вычислить [latex](\text{}f\left(2\right)[/latex].
- Решите [латекс]\текст{}f\влево(х\вправо)=4[/латекс].
- Решите [латекс]\текст{}f\влево(х\вправо)=1[/латекс].
Решение
Бесплатный доступ на https://openstax.org/books/precalculus/pages/1-introduction-to-functions
- http://www.kgbanswers.com/how-long-is-a-dogs-memory-span/4221590. По состоянию на 24 марта 2014 г. ↵
Поиск значений функций по графикам
Пусть точка (x, y) находится на графике функции f. Тогда y — это значение функции для данного значения x.
Если (2, 5) находится на графике функции f(x), то 5 — это значение f(x) при x = 2. То есть
f(2) = 5
Найдите значение функции f(x) при x = a.

Шаг 1 :
Проведите вертикальную линию через значение ‘a’ по оси x.
Шаг 2 :
Отметьте точку пересечения линии x = a и графика f(x).
Шаг 3 :
Проведите горизонтальную линию от точки пересечения до оси Y.
Шаг 4 :
Пусть горизонтальная линия пересекает ось Y в точке «b».
Значение функции f(x) при x = a равно ‘b’.
То есть
f(a) = b
Пример 1:
Используйте график f(x), показанный ниже, чтобы найти f(6).
Решение:
Нам нужно найти значение функции f(x) при x = 6.
Шаг 1:
Проведите вертикальную линию через цифру 6 по оси x.
Шаг 2 :
Отметьте точку пересечения вертикальной линии x = 6 и графика f(x).
Шаг 3 :
Проведите горизонтальную линию от точки пересечения до оси Y.
Шаг 5:
Горизонтальная линия пересекает ось Y в точке 4.
Таким образом, значение функции f(x) при x = 6 равно 4.
То есть
f(6) = 4
Пример 2 :
Используйте график f(x), показанный ниже, чтобы найти f(9).

Решение:
Нам нужно найти значение функции f(x) при x = 9.
Шаг 1:
Проведите вертикальную линию через 9 по оси x.
Шаг 2 :
Отметьте точку пересечения вертикальной линии x = 9 и графика f(x).
Шаг 3 :
Проведите горизонтальную линию от точки пересечения до оси Y.
Шаг 5 :
Горизонтальная линия пересекает ось Y в точке 7.
Итак, значение функции f(x) при x = 9равно 7.
То есть
f(9) = 7
Пример 3:
Используйте график f(x), показанный ниже, чтобы найти f(4).
Решение :
Нам нужно найти значение функции f(x) при x = 4.
Шаг 1 :
Проведите вертикальную линию через 4 по оси x.
Шаг 2 :
Отметьте точку пересечения вертикальной линии x = 4 и графика f(x).
Шаг 3 :
Проведите горизонтальную линию от точки пересечения до оси Y.
Шаг 5:
Горизонтальная линия пересекает ось Y в точке 7.
Таким образом, значение функции f(x) при x = 4 равно 7.



 Однако каждый [латекс]\текст{}х\текст{}[/латекс] определяет уникальное значение для [латекс]\текст{}у\текст{}[/латекс], и существуют математические процедуры, с помощью которых [ латекс]\текст{}у\текст{}[/латекс] можно найти с любой точностью. В этом случае мы говорим, что уравнение дает неявное (подразумеваемое) правило для [латекс]\текст{}у\текст{}[/латекс] как функцию от [латекс]\текст{}х\текст{}[ /latex], хотя формулу нельзя написать явно.
Однако каждый [латекс]\текст{}х\текст{}[/латекс] определяет уникальное значение для [латекс]\текст{}у\текст{}[/латекс], и существуют математические процедуры, с помощью которых [ латекс]\текст{}у\текст{}[/латекс] можно найти с любой точностью. В этом случае мы говорим, что уравнение дает неявное (подразумеваемое) правило для [латекс]\текст{}у\текст{}[/латекс] как функцию от [латекс]\текст{}х\текст{}[ /latex], хотя формулу нельзя написать явно. 
 Здесь давайте вызовем функцию [latex]P[/latex]. Домен функции — это тип питомца, а диапазон — действительное число, представляющее количество часов, в течение которых сохраняется память питомца. Мы можем оценить функцию [latex]\text{}P\text{}[/latex] по входному значению «золотая рыбка». Мы бы написали [латекс]P\влево(\текст{золотая рыбка}\вправо)=2160[/латекс]. Обратите внимание, что для вычисления функции в форме таблицы мы идентифицируем входное значение и соответствующее выходное значение из соответствующей строки таблицы. Табличная форма для функции [latex]\text{}P\text{}[/latex] кажется идеально подходящей для этой функции, в большей степени, чем ее запись в форме абзаца или функции.
Здесь давайте вызовем функцию [latex]P[/latex]. Домен функции — это тип питомца, а диапазон — действительное число, представляющее количество часов, в течение которых сохраняется память питомца. Мы можем оценить функцию [latex]\text{}P\text{}[/latex] по входному значению «золотая рыбка». Мы бы написали [латекс]P\влево(\текст{золотая рыбка}\вправо)=2160[/латекс]. Обратите внимание, что для вычисления функции в форме таблицы мы идентифицируем входное значение и соответствующее выходное значение из соответствующей строки таблицы. Табличная форма для функции [latex]\text{}P\text{}[/latex] кажется идеально подходящей для этой функции, в большей степени, чем ее запись в форме абзаца или функции.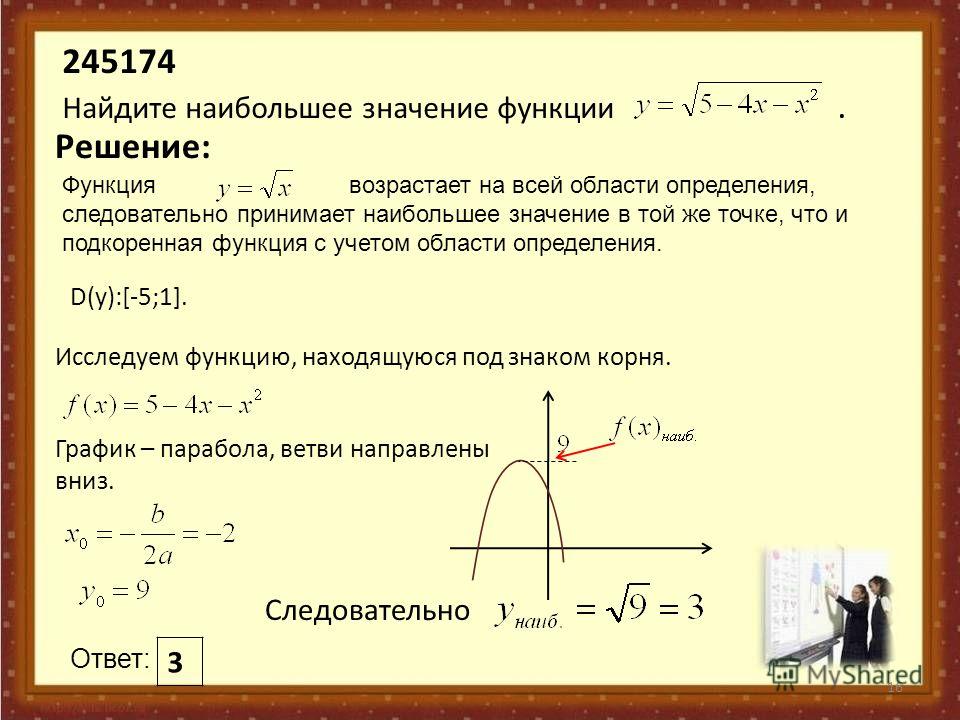
 Решение функционального уравнения с использованием графика требует нахождения всех экземпляров заданного выходного значения на графике и наблюдения за соответствующим входным значением (значениями).
Решение функционального уравнения с использованием графика требует нахождения всех экземпляров заданного выходного значения на графике и наблюдения за соответствующим входным значением (значениями).

