Производная — определение, физический и геометрический смысл, алгоритм поиска значения производной, примеры
- Приращение аргумента и приращение функции
- Определение производной
- Физический смысл производной
- Геометрический смысл производной
- Алгоритм поиска значения производной в заданной точке
- Алгоритм поиска уравнения производной
- Примеры
п.1. Приращение аргумента и приращение функции
Приращением аргумента называют разность $$ \triangle x=x-x_0 $$ где \(x\) — произвольное число, которое мало отличается от начальной точки \(x_0\). Приращение аргумента может быть как положительным, так и отрицательным.
Приращением функции называют соответствующую разность $$ \triangle y=f(x)-f(x_0 )=f(x_0+\triangle x)-f(x_0) $$ Приращение функции может быть как положительным, так и отрицательным.
Например:
\begin{gather*} y=2x-1\\ x_0=1,\ x=1,1 \end{gather*} Найдем приращение аргумента и функции. \begin{gather*} \triangle x= x-x_0=1,1-1=0,1\gt 0\\ \\ f(x)=f(1,1)=2\cdot 1,1-1=1,2\\ f(x_0 )=f(1)=2\cdot 1-1=1\\ \triangle y=f(x)-f(x_0 )=1,2-1=0,2\gt 0 \end{gather*} | |
| \begin{gather*} y=-x+2\\ x_0=1,\ x=1,1 \end{gather*} Найдем приращение аргумента и функции. \begin{gather*} \triangle x= x-x_0=1,1-1=0,1\gt 0\\ \\ f(x)=f(1,1)=-1,1+2=0,9\\ f(x_0 )=f(1)=-1+2=1\\ \triangle y=f(x)-f(x_0)=0,9-1=-0,1\lt 0 \end{gather*} |
Если функция возрастает, приращение аргумента и приращение функции имеют один и тот же знак: $$ \begin{cases} y=f(x) — \text{возрастает}\\ \triangle x\gt 0 \end{cases} \Rightarrow \triangle y\gt 0 $$ Если функция убывает, приращение аргумента и приращение функции имеют разные знаки: $$ \begin{cases} y=f(x) — \text{убывает}\\ \triangle x\gt 0 \end{cases} \Rightarrow \triangle y\lt 0 $$
п.2. Определение производной
Производной функции \(f(x)\) в точке \(x_0\) называют предел отношения приращения функции в точке \(x_0\) к приращению аргумента, если приращение аргумента стремится к нулю, а предел существует: $$ f'(x_0)=\lim_{\triangle x\rightarrow 0}\frac{\triangle y}{\triangle x} $$
Например:
Найдем производную функции \(f(x)=x^2-4\) в точке \(x_0=3\)
Значение функции в точке: \(f(x_0 )=3^2-4=5\)
Пусть \(\triangle x\) — некоторое приращение аргумента.
2=\triangle x(6+\triangle x) $$ Производная: $$ f'(x_0)=\lim_{\triangle x\rightarrow 0}\frac{\triangle x}{\triangle y}=\lim_{\triangle x\rightarrow 0}\frac{\triangle x(6+\triangle x)}{\triangle x}=\lim_{\triangle x\rightarrow 0}(6+\triangle x)=6+0=6 $$ Ответ: 6
п.3. Физический смысл производной
Рассмотрим прямолинейное движение.
Пусть расстояние по прямой между городами \(\triangle x=\) 300 км поезд преодолевает за \(\triangle t=\)4 часа. Мы легко можем найти его среднюю скорость: $$ v_{cp}=\frac{\triangle x}{\triangle t},\ \ v_{cp}=\frac{300}{4}=75\ (\text{км/ч}) $$ Но поезд не едет все время с одной и той же скоростью: где-то ускоряется, где-то замедляется, где-то и вовсе останавливается.
Если мы захотим определить скорость как можно точнее, нам понадобится уменьшать интервалы времени и измерять соответствующий путь. Уменьшив время до «мгновений», мы получим «мгновенную скорость» для каждой точки траектории в каждый момент времени.
Мгновенная скорость это скорость тела в данный момент времени \(t_0\): $$ v(t_0)=\lim_{\triangle t\rightarrow 0}\frac{\triangle x}{\triangle t}=x'(t_0) $$ где \(\triangle x=x-x_0\) — путь тела за время \(\triangle t=t-t_0,\ x(t)\) – уравнение движения.
Мгновенная скорость равна первой производной от уравнения движения при \(t=t_0\).
Сравнивая определения мгновенной скорости и производной функции, мы можем сформулировать физический смысл производной:
Производная функции \(y=f(x)\) в точке \(x_0\) равна скорости изменения функции в этой точке.
Или, ближе к физике/химии/биологии:
Производная уравнения процесса \(s=f(t)\) в момент времени \(t_0\) равна скорости протекания процесса в этот момент.
п.4. Геометрический смысл производной
Пусть на плоскости задана кривая \(y=f(x)\).
Выберем на кривой две точки \(A(x_0,y_0)\) и \(B(x,y)\). Прямая AB будет секущей для кривой \(y=f(x)\). Угол наклона прямой AB определяется угловым коэффициентом: $$ k_{AB}=tg\angle A=\frac{BC}{AC}=\frac{\triangle y}{\triangle x} $$ Начнем движение точки B вдоль кривой по направлению к точке A. Приращение аргумента при этом будет уменьшаться: \(\triangle x=AC\rightarrow 0\).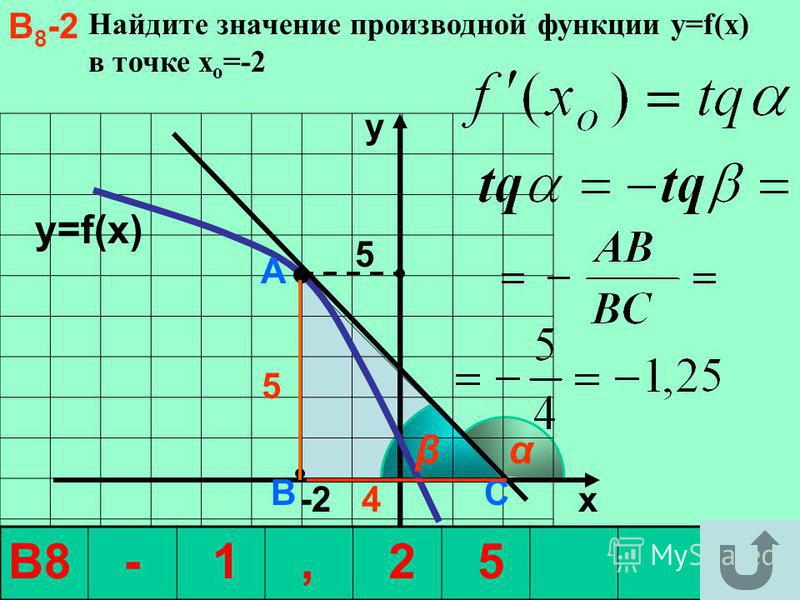
В тот момент, когда B совпадет с A, секущая AB превратится в касательную AD. Угловой коэффициент касательной: $$ k_{AD}=\lim_{\triangle x\rightarrow 0}\frac{\triangle y}{\triangle x}=y'(x_0) $$
Мы можем сформулировать геометрический смысл производной:
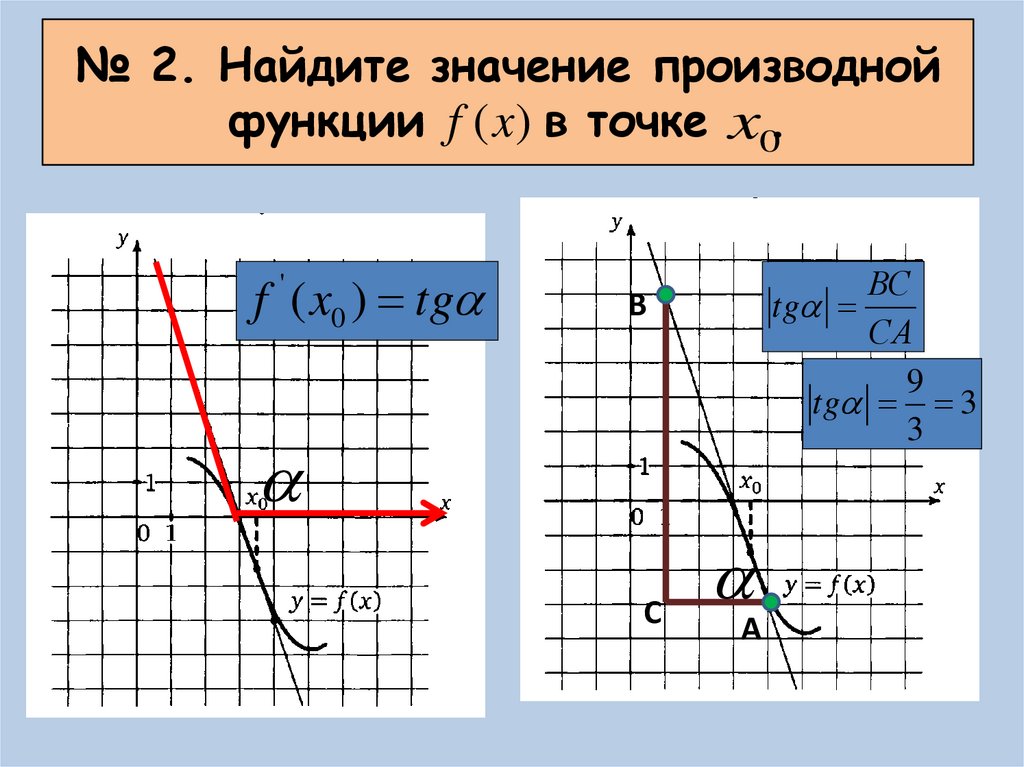
Производная функции \(y=f(x)\) в точке \(x_0\) равна угловому коэффициенту касательной к графику этой функции в этой точке.
п.5. Алгоритм поиска значения производной в заданной точке
На входе: уравнение функции \(y=f(x)\), точка \(x_0\)
Шаг 1. Найти значение функции в заданной точке \(y_0=f(x_0)\).
Шаг 2. Задать приращение аргумента \(\triangle x=x-x_0\), найти приращение функции \(\triangle y=f(x)-f(x_0)=f(x_0+\triangle x)-f(x_0)\).
Шаг 3. Найти предел \(\lim_{\triangle x\rightarrow 0}\frac{\triangle y}{\triangle x}=f'(x_0)\)
На выходе: значение производной в точке \(x_0\)
Например:
Найдем значение производной в точке \(x_0=1\) для функции \(y=x^2-3\).
2=(x+\triangle x-x)(x+\triangle x+x)=\triangle x(2x+\triangle x) \end{gather*} Ищем предел: \begin{gather*} \lim_{\triangle x\rightarrow 0}\frac{\triangle y}{\triangle x}=\lim_{\triangle x\rightarrow 0}\frac{\triangle x(2x+\triangle x)}{\triangle x}=\lim_{\triangle x\rightarrow 0}(2x+\triangle x)=2x+0=2x \end{gather*} Ответ: уравнение производной \(y\ ‘=2x\)
п.7. Примеры
Пример 1. Пользуясь алгоритмом поиска значения производной в заданной точке, найдите:
a) \( f'(1),\ \text{если}\ f(x)=2x \)
По условию \(x_0=1\)
Значение функции в заданной точке: \(f(x_0 )=2\cdot 1=2\)
Пусть \(\triangle x\) — некоторое приращение аргумента. Тогда приращение функции: \begin{gather*} \triangle y=f(x_0+\triangle x)-f(x_0)=2(1+\triangle x)-2=2+2\triangle x-2=2\triangle x \end{gather*} Ищем предел: \begin{gather*} \lim_{\triangle x\rightarrow 0}\frac{\triangle y}{\triangle x}=\lim_{\triangle x\rightarrow 0}\frac{2\triangle x}{\triangle x}=2 \end{gather*} Искомая производная в заданной точке: \(f'(1)=2\)
б) \( f'(3),\ \text{если}\ f(x)=3x^2 \)
По условию \(x_0=3\)
Значение функции в заданной точке: \(f(x_0 )=3\cdot 3^2=27\)
Пусть \(\triangle x\) — некоторое приращение аргумента.
2)=12+0+0=12 \end{gather*} Искомая производная в заданной точке: \(f'(2)=12\)
Ответ: а) 2; б) 18; в) 4; г) 12
Пример 2. Пользуясь алгоритмом поиска уравнения производной, найдите общее уравнение производной для функции \(y=f(x)\):
a) \( f(x)=C\), где C – постоянная величина
Пусть \(\triangle x\) — некоторое приращение аргумента. Тогда приращение функции: \begin{gather*} \triangle y=f(x+\triangle x)-f(x)=C-C=0 \end{gather*} Отношение \(\frac{\triangle y}{\triangle x}=\frac{0}{\triangle x}=0\)
Предел \(\lim_{\triangle x\rightarrow 0}\frac{\triangle y}{\triangle x}=\lim_{\triangle x\rightarrow 0}0=0\)
Производная \(y\ ‘=C’=0\)
Производная постоянной равна нулю: \(C ‘=0\)
б) \( f(x)=x\)
Пусть \(\triangle x\) — некоторое приращение аргумента. Тогда приращение функции: \begin{gather*} \triangle y=f(x+\triangle x)-f(x)=x+\triangle x-x=\triangle x \end{gather*} Ищем предел: \(\lim_{\triangle x\rightarrow 0}\frac{\triangle y}{\triangle x}=\lim_{\triangle x\rightarrow 0}\frac{\triangle x}{\triangle x}=\lim_{\triangle x\rightarrow 0}1=1\)
Производная \(x\ ‘=1\)
Производная аргумента равна единице: \(x ‘=1\)
в) \( f(x)=x^2\)
Пусть \(\triangle x\) — некоторое приращение аргумента.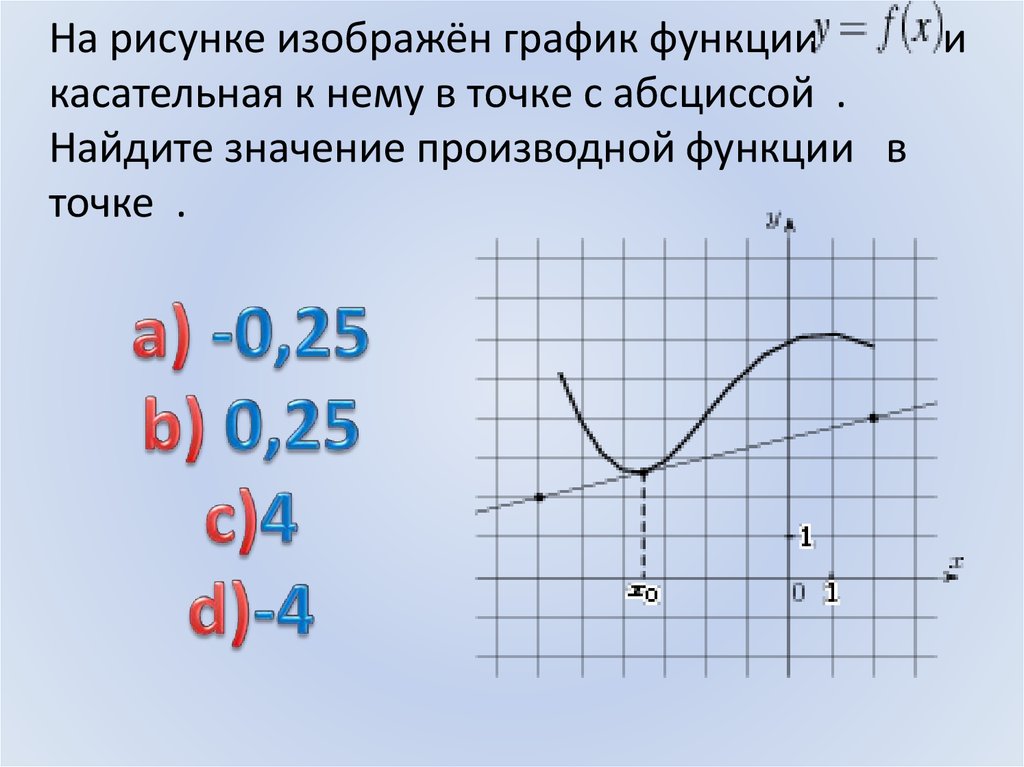
2}\)
e) \( f(x)=kx+b\)
Пусть \(\triangle x\) — некоторое приращение аргумента. Тогда приращение функции: \begin{gather*} \triangle y=f(x+\triangle x)-f(x)=k(x+\triangle x)+b-kx-b=k\triangle x \end{gather*} Ищем предел: \begin{gather*} \lim_{\triangle x\rightarrow 0}\frac{\triangle y}{\triangle x}=\lim_{\triangle x\rightarrow 0}\frac{k\triangle x}{\triangle x}=\lim_{\triangle x\rightarrow 0}k=k \end{gather*} Производная \((kx+b)\ ‘=k\)
ж) \( f(x)=\sqrt{x}\)
Пусть \(\triangle x\) — некоторое приращение аргумента. Тогда приращение функции: \begin{gather*} \triangle y=f(x+\triangle x)-f(x)=\sqrt{x+\triangle x}-\sqrt{x} \end{gather*} Ищем предел, умножив числитель и знаменатель на сопряженное выражение: \begin{gather*} \lim_{\triangle x\rightarrow 0}\frac{\triangle y}{\triangle x}=\lim_{\triangle x\rightarrow 0}\frac{\sqrt{x+\triangle x}-\sqrt{x}}{\triangle x}= \lim_{\triangle x\rightarrow 0}\frac{(\sqrt{x+\triangle x}-\sqrt{x})(\sqrt{x+\triangle x}+\sqrt{x})}{\triangle x(\sqrt{x+\triangle x}+\sqrt{x})}=\\ =\lim_{\triangle x\rightarrow 0}\frac{x+\triangle x-x}{\triangle x(\sqrt{x+\triangle x}+\sqrt{x})}=\lim_{\triangle x\rightarrow 0}\frac{1}{(\sqrt{x+\triangle x}+\sqrt{x})}=\frac{1}{\sqrt{x+0}+\sqrt{x}}=\frac{1}{2\sqrt{x}} \end{gather*} Производная \((\sqrt{x})\ ‘=\frac{1}{2\sqrt{x}}\)
Основы ценообразования и оценки производных финансовых инструментов
Повторное чтение
2022 Учебный план Программа CFA Уровень I Производные
Основы ценообразования и оценки деривативов
Загрузить полную версию (PDF)
Доступно для членов
Введение
w3.org/1999/xhtml»> Важно понимать, как определяются цены деривативов. Будь то покупатель или продавец, четкое понимание ценообразования финансовых продуктов имеет решающее значение для принятия эффективных инвестиционных решений. В конце концов, вряд ли можно определить, что предлагать или делать ставки на финансовый продукт или любой продукт, если на то пошло, если вы не знаете, как его характеристики объединяются для создания стоимости.
Важно понимать ценообразование финансовых активов. Методы и модели дисконтированных денежных потоков, такие как модель ценообразования капитальных активов и ее варианты, полезны для определения цен финансовых активов. Однако уникальные характеристики деривативов создают некоторые сложности, не связанные с активами, такими как акции и инструменты с фиксированным доходом. Несколько удивительно, однако, что производные также обладают некоторыми упрощающими характеристиками. Например, как мы увидим в этом чтении, на хорошо функционирующих рынках деривативов необходимость определения надбавок за риск устраняется возможностью построения безрискового хеджирования.
Соответственно, необходимость определять неприятие инвестором риска не имеет значения для ценообразования деривативов, хотя, безусловно, имеет значение для ценообразования базового актива.
Целью этого чтения является установление основ ценообразования деривативов на базовом концептуальном уровне. Рассматриваются следующие темы:
Как цена базового актива влияет на цену деривативов?
Как оцениваются деривативы с использованием принципа арбитража?
Как определяются цены и стоимость форвардных контрактов?
Чем отличаются цены фьючерсных контрактов от форвардных контрактов?
Как определяются цены и стоимость свопов?
Как определяются цены и стоимость европейских опционов?
Чем ценообразование американских опционов отличается от ценообразования европейских опционов?
w3.org/1999/xhtml»> Это чтение организовано следующим образом. В разделе 2 рассматриваются две взаимосвязанные темы: ценообразование базовых активов, на основе которых создаются производные инструменты, и принцип арбитража. Раздел 3 описывает ценообразование и оценку форвардов, фьючерсов и свопов. Раздел 4 знакомит с ценообразованием и оценкой опционов. Раздел 5 содержит резюме.
Результаты обучения
Участник должен уметь:
- объяснить, как концепции арбитража, репликации и нейтральности к риску используются при ценообразовании деривативов;
различать стоимость и цену форвардных и фьючерсных контрактов;
рассчитать форвардную цену актива с нулевой, положительной или отрицательной чистой стоимостью переноса;
w3.org/1999/xhtml» value=»4″>объясняют, как стоимость и цена форвардного контракта определяются при истечении срока действия контракта и в начале его действия;
описывают денежные и неденежные выгоды и затраты, связанные с владением базовым активом, и объясняют, как они влияют на стоимость и цену форвардного контракта;
определяют соглашение о форвардной процентной ставке и описывают его использование;
объяснить, почему форвардные и фьючерсные цены различаются;
объясняют, чем своп-контракты похожи, но отличаются от серии форвардных контрактов;
различать стоимость и цену свопов;
w3.org/1999/xhtml» value=»10″>объяснить стоимость исполнения, временную стоимость и денежность опциона;
определить факторы, определяющие стоимость опциона, и объяснить, как каждый фактор влияет на стоимость опциона;
объяснить паритет пут-колл для европейских опционов;
-
объяснить паритет пут-колл-форвард для европейских опционов;
объяснить, как определяется стоимость опциона с использованием однопериодной биномиальной модели;
- объясните, при каких обстоятельствах стоимость европейских и американских опционов различается.
Резюме
Это чтение о ценообразовании деривативов обеспечивает основу для понимания того, как деривативы оцениваются и торгуются.
Ключевые точки включают следующее:
Цена базового актива равна ожидаемой будущей цене, дисконтированной по безрисковой ставке, плюс премия за риск, плюс приведенная стоимость любых выгод, минус приведенная стоимость любых затрат, связанных с владением активом.
Арбитражная возможность возникает, когда два идентичных актива или комбинации активов продаются по разным ценам, что приводит к возможности покупки более дешевого актива и продажи более дорогого актива для получения безрискового дохода без каких-либо капиталовложений.
На хорошо функционирующих рынках возможности арбитража быстро используются, и, как следствие, увеличение покупок недооцененных активов и увеличение продаж активов по завышенным ценам возвращает цены к эквивалентности.
Цена деривативов определяется путем создания безрисковой комбинации базового актива и дериватива, что приводит к уникальной цене дериватива, исключающей любую возможность арбитража.
-
Арбитражное ценообразование деривативов исключает необходимость определения надбавок за риск или неприятие риска стороной, торгующей опционом, и называется ценообразованием, нейтральным к риску.
Стоимость форвардного контракта по истечении срока действия равна стоимости актива за вычетом форвардной цены.
Стоимость форвардного контракта до истечения срока представляет собой стоимость актива за вычетом приведенной стоимости форвардной цены.
Форвардная цена, установленная при заключении контракта, представляет собой цену, согласованную двумя сторонами, которая дает нулевую стоимость в начале.
Затраты и выгоды, полученные от владения базовым активом, влияют на форвардную цену, повышая и понижая ее соответственно.
Цены фьючерсов могут отличаться от форвардных цен из-за влияния процентных ставок на промежуточные денежные потоки от ежедневных расчетов.
Свопы могут быть оценены как неявная серия внерыночных форвардных контрактов, при этом каждый контракт имеет одинаковую цену, в результате чего некоторые контракты оцениваются положительно, а некоторые отрицательно, но их совокупная стоимость равна нулю.
По истечении срока опциона европейский колл или пут стоит стоимость исполнения, которая для коллов больше нуля или базовой цены минус цена исполнения, а для пут больше нуля и цены исполнения минус базовая цена.
Европейские коллы и путы зависят от стоимости базового актива, цены исполнения, безрисковой ставки, времени до экспирации, волатильности базового актива и любых понесенных затрат или выгод, полученных при удерживании базового актива.
Значения опционов испытывают падение стоимости во времени, что представляет собой потерю стоимости из-за течения времени и приближения истечения срока действия, а также денежности и волатильности.
Минимальная стоимость европейского колл-опциона равна максимуму, состоящему из нуля и базовой цены за вычетом текущей стоимости цены исполнения.
Минимальная стоимость европейского опциона пут равна максимуму нуля и приведенной стоимости цены исполнения за вычетом цены базового актива.
Европейские цены пут и колл связаны паритетом пут-колл, который указывает, что цена пут плюс цена базового актива равна цене колл плюс приведенная стоимость цены исполнения.
Европейские цены пут и колл связаны паритетом пут-колл-форвард, который показывает, что цена пут плюс стоимость безрисковой облигации с номинальной стоимостью, равной форвардной цене, равна цене колл плюс стоимость риск- свободная облигация с номинальной стоимостью, равной цене исполнения.
Значения европейских опционов можно получить с помощью биномиальной модели, которая определяет две возможные цены актива на один период позже и позволяет построить безрисковое хеджирование, состоящее из опциона и базового актива.
Американские цены колл могут отличаться от европейских цен колл только в том случае, если по базовому активу есть денежные потоки, такие как дивиденды или проценты; эти денежные потоки являются единственной причиной для досрочного исполнения колла.
Американские цены пут могут отличаться от европейских цен пут, потому что право на досрочное исполнение всегда имеет ценность для пут, что связано с более низким пределом стоимости базового актива.
Производная — Home Assistant
Интеграция производной (Википедия) создает датчик, который «сглаживает» другой датчик (исходный датчик ).
Производные указанного датчика будут усредняться в заданном временном окне с помощью алгоритма простого скользящего среднего, взвешенного по времени. Это полезно, например, для датчика, выдающего дискретные значения, или для фильтрации кратковременных шумов.
Производные датчики обновляются при изменении датчик источника .
Для датчиков, которые сбрасываются на ноль после отключения питания и нуждаются в «неотрицательной производной», таких как счетчики полосы пропускания в маршрутизаторах или датчики дождя, рассмотрите возможность использования вместо этого интеграции счетчика коммунальных услуг. В противном случае каждый сброс будет регистрировать значительное изменение в показаниях датчика производной.
Конфигурация
Добавление производного к вашему экземпляру Home Assistant может быть выполнено через пользователя интерфейс, используя эту кнопку My:
Имя
Имя, которое должен иметь датчик. Вы можете изменить его позже.
Входной датчик
Сущность, предоставляющая числовые показания для создания производной.
Точность
Округлить рассчитанное значение производной не более чем до N знаков после запятой.
Временное окно
Временное окно, в котором вычисляется производная. Производные в этом окне будут усреднены с помощью простого алгоритма скользящего среднего (SMA), взвешенного по времени. Это полезно, например, для датчика, который выводит дискретные значения, или для фильтрации кратковременных шумов. По умолчанию производная вычисляется между двумя последовательными обновлениями без какого-либо сглаживания.
Метрический префикс
Метрическая единица для префикса производного результата (Википедия).
Единица времени
СИ единица времени производной. Если этот параметр установлен, единица измерения будет установлена на x/y , где x — это единица датчика источника, а y — значение этого параметра.
Конфигурация YAML
Кроме того, эту интеграцию можно настроить и настроить вручную через YAML.
вместо. Чтобы включить производный датчик в вашей установке, добавьте
после вашего файл конфигурации.yaml :
# Пример записи в файле configuration.yaml
датчик:
- платформа: производная
источник: sensor.current_speed
Переменные конфигурации
Ищете файл конфигурации?
исходная строка Обязательно
Идентификатор объекта датчика, предоставляющего числовые показания
строка имени (необязательно)
Имя для использования во внешнем интерфейсе.
По умолчанию:
идентификатор исходного объекта производный
округление целого числа (необязательно, по умолчанию: 3)
Округление рассчитанного значения производной не более чем до N знаков после запятой.
unit_prefix строка (Необязательно, по умолчанию: Нет)
Метрическая единица для префикса производного результата (Википедия).
Доступные символы: «n» (1e-9), «µ» (1e-6), «m» (1e-3), «k» (1e3), «M» (1e6), «G» (1e9). , «Т» (1e12).
unit_time строка (Необязательно, по умолчанию: h)
СИ единица времени производной. Доступные единицы: с, мин, ч, д. Если этот параметр установлен, атрибут unit_of_measurement будет установлен как x/y, где x — это единица измерения датчика, заданная параметром source , а y — значение, указанное здесь.
строка единиц измерения (необязательно)
Единица измерения, используемая для производной. Это перезапишет автоматически установленный unit_of_measurement , как описано выше.
time_window time (Необязательно, по умолчанию: 0)
Временное окно, в котором вычисляется производная. По умолчанию производная вычисляется между двумя последовательными обновлениями без какого-либо сглаживания.
Пример температуры
Например, у вас есть датчик температуры sensor.temperature , который выводит значение каждые несколько секунд, но округляет до ближайшей половины числа.
Это означает, что два последовательных выходных значения могут быть одинаковыми (таким образом, производная равна Δy/Δx=0 , потому что Δy=0 !)
Тем не менее, температура может на самом деле меняться с течением времени.
Чтобы зафиксировать это, вы должны использовать time_window , чтобы немедленные скачки не приводили к высоким производным и чтобы после следующего обновления датчика производные не обращались в ноль.
Пример конфигурации YAML, в которой используется time_window это
:
- платформа: производная
источник: датчик.температура
название: Изменение температуры в час
раунд: 1
unit_time: h # результирующий "unit_of_measurement" будет °C/ч, если в sensor.temperate в качестве единицы измерения задан °C
time_window: "00:30:00" # смотрим изменение за последние полчаса
Помогите нам улучшить нашу документацию Предложите изменить эту страницу или оставьте/просмотрите отзыв об этой странице.