Значения тангенсов синусов косинусов: Таблицы значений основных тригонометрических функций: синуса, косинуса, тангенса, котангенса

Таблицы численных значений. (Таблица квадратов, кубов, синусов ….) + Таблицы Брадиса

Значения синусов, косинусов, тангенсов и котангенсов для «хороших» углов — Студопедия

2.3.10: Точные значения арксинуса, косинуса и тангенса

Кривые синусов, косинусов и тангенсов – БЛЕСТЯЩАЯ МАТЕМАТИКА

Обзор (ответы)

Словарь

Дополнительные ресурсы

Содержание

ГОСТы, СНиПы

Карта сайта TehTab.ru

Поиск по сайту TehTab.ru

Навигация по справочнику TehTab.ru: главная страница / / Техническая информация/ / Математический справочник / / Таблицы численных значений. (Таблица квадратов, кубов, синусов ….) + Таблицы Брадиса

Таблица умножения — традиционная 10×10, 12х12 и 20х20

Таблица деления — традиционная 10×10 и 12х12

Таблицы квадратов. Натуральных чисел от 1 до 30 и от 1 до 100. Удобная расчетная таблица 1,00 — 9,99.

Таблица квадратов натуральных чисел от 1 до 99 (от 1 до 9, от 10 до 99 ).

Таблицы кубов. Натуральных чисел от 1 до 20 и от 1 до 100. Удобная расчетная таблица 1,00 — 9,99.

Степени — квадрат и куб, корни — квадратный и кубический и обратные величины чисел от 1 до 100. Таблица степеней.

Таблица степеней натуральных чисел от 2 до 25 (включая от &quot2 до 10&quot и от &quot2 до 20&quot). Степени от 2 до 10. Таблица степеней.

Таблица 4-ой и 5-ой степени чисел от 1 до 100.

Точная и приблизительная таблицы факториалов (1-255)

Таблица. Длина окружности диаметра D.

Таблица соотношений между длинами дуг, стрелками, длинами хорд, площадями сегментов при радиусе, равном единице.

Длина хорды, центральный угол в ° (угловых градусах) и радианах при делении окружности единичного диаметра на равные сегменты.

Определение и численные соотношения между единицами измерения углов в РФ. Тысячные, угловые градусы, минуты, секунды, радианы, обороты.

Таблица соответствия угловых градусов, радиан, оборотов, тысячных (артиллерийских РФ). 0-360 градусов, 0-2π радиан.

Таблица синусов, она-же косинусов (см.

примечание внутри). Углы в угловых градусах. Таблица значений синусов.

Таблица синусов углов от 0° — 360°. Углы с шагом в 1°. Таблица значений синусов.

Таблица косинусов углов от 0° — 360°. Углы с шагом в 1°. Таблица значений косинусов.

Таблица тангенсов, она же котангенсов (см.примечание внутри). Углы в угловых градусах.

Таблица тангенсов углов углов от 0° — 360°. Углы с шагом в 1°. Таблица значений тангенса, tg

Таблица котангенсов углов углов от 0° — 360°. Углы с шагом в 1°. Таблица значений котангенса, ctg

Углы 0°,30°,45°,60°,90°,180°,270°,360°,(π/6,π/4,π/3,π/2,π,3π/2,2π). Синусы, косинусы, тангенсы и котангенсы. Таблица значений тригонометрических функций.

Знаки тригонометрических функций синус, косинус, тангенс и котангенс по четвертям в тригонометрическом круге.

Таблицы Брадиса. Значения тригонометрических, логарифмических функций. Прочее

Чиcло пи. π, 2π, 1/π, π/2, π/3, π/4, π/180, (π/180)

2, π², π³, π⁴ и др.

Численные значения числа e, 1/e, e², log₁₀ e и др.

Постоянная Эйлера γ, золотое сечение (золотая пропорция) φ, ln _{γ, e^γ, 1/φ и др.}

Таблица простых чисел от 1 до 10000. Таблица простых чисел от 1 до 1000

Таблица случайных чисел.

Таблицы : 100 случайных двузначных чисел и генератор случайных последовательностей.

Дополнительная информация от TehTab.ru:

Нашли ошибку? Есть дополнения? Напишите нам об этом, указав ссылку на страницу.

TehTab.ru

Реклама на сайте

Обращаем ваше внимание на то, что данный интернет-сайт носит исключительно информационный характер. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Все риски за использование информаци с сайта посетители берут на себя.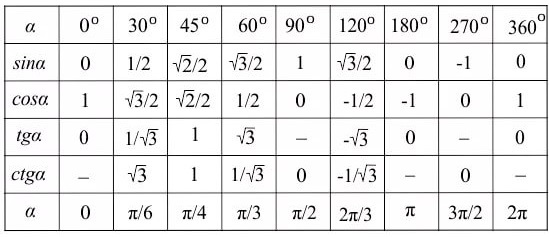

Проект TehTab.ru является некоммерческим, не поддерживается никакими политическими партиями и иностранными организациями.

Поделись с друзьями:

Радианы

Углы измеряются не в градусах, а в радианах, Радиан – это такой угол, что дуга единичной окружности равна радиусу (то есть 1). Это примерно 57 градусов. Половина окружности (180 °) – это π радиан. (π≈3.14159)

Пример 1: перевести в радианы 30 °
180° — π радиан 30° — х радиан,

Пример 2: перевести в градусы π/9 радиан

Как найти на единичной окружности угол в радианах

Пример: найти точку, соответствуюшую углу

Если число большое, то: 1) Делим нацело 2) Убираем полные обороты (четное количество «пи») 3) Если осталось «пи», приводим к общему знаменателю

= =

4) Подписываем точка на координатных осях, и приводим их к этому же знаменателю 5) И наконец находим нужную точку Внимание! Если есть «минус», откладываем углы в другую сторону!

Наша точка!

Синусы и косинусы, тангенсы и котангенсы

Синус угла — это ОРДИНАТА (кордината по У) соответств.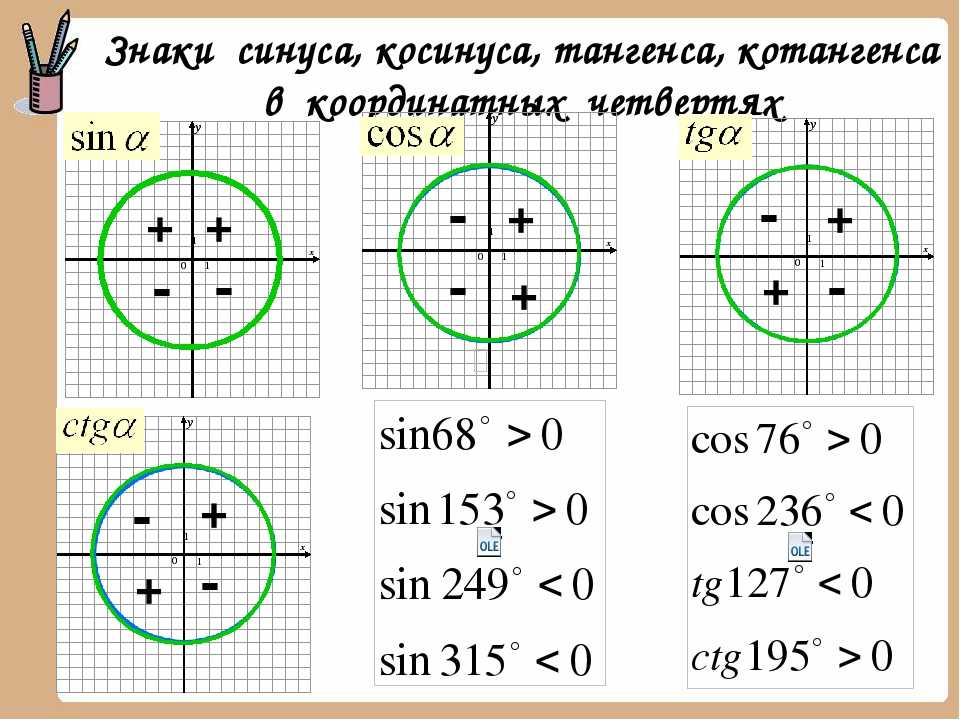

точки единичной окружности.

Косинус угла — это АБСЦИССА (коорд по Х) соответств. точки единичной окружности.

Тангенс – это синус, деленный на косинус:

Котангенс – это косинус, деленный на синус: ;

Если точка попадает на горизонтальную ось, то синус равен нулю, а котангенс не существует. Если на вертикальную ось, то косинус равен нулю, а тангенс не существует.

И еще надо знать ОСНОВНОЕ ТРИГОНОМЕТРИЧЕСКОЕ ТОЖДЕСТВО:

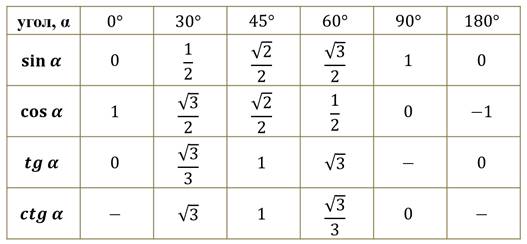
Значения синусов, косинусов, тангенсов и котангенсов для «хороших» углов

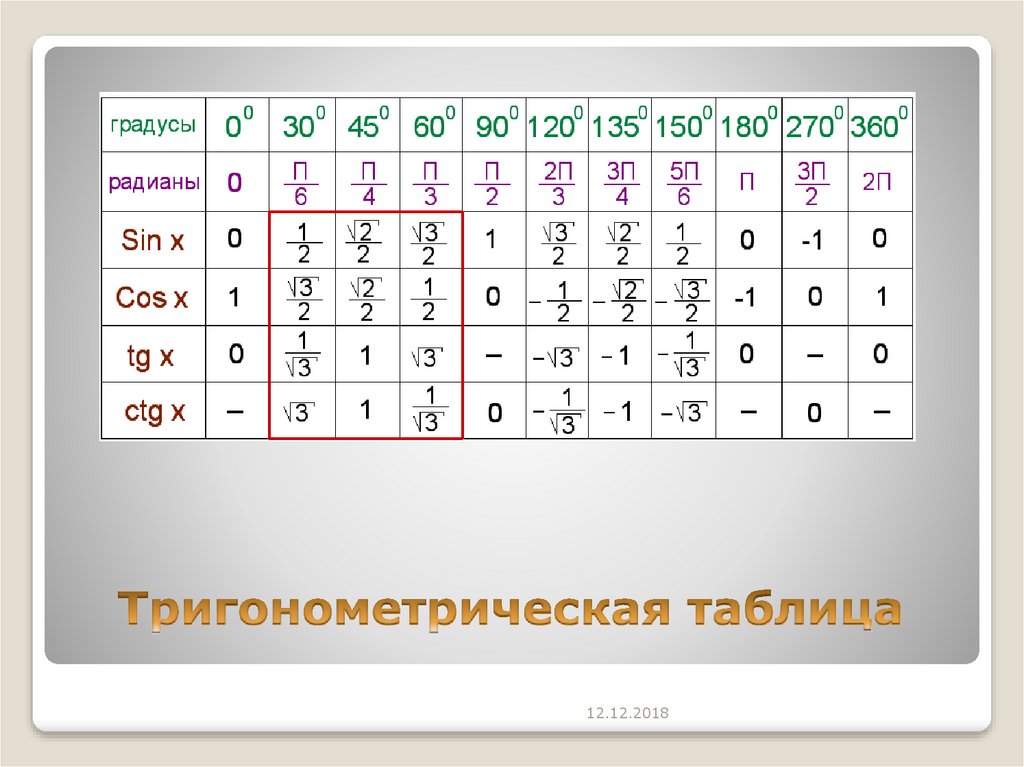Знаки синуса, косинуса, тангенса, котангенса

Знаки опеделяем так: из заданной точки рисуем вертикальную и горизонтальную стрелки наружу. Если направление стрелки совпадает с направлением оси координат, то соответствующая тригонометрическая функция (синус или косинус) имеет знак «плюс», иначе знак «минус». Знаки тангенса и котангенса (всегда одинаковые) определяются с учетом того, что надо синус делить на косинус.

Пример: Для точки, показанной на рисунке, синус положительный (стрелка вверх, совпадает с направлением оси игреков), косинус отрицательный (стрелка влево, противоположна направлению оси иксов), тангенс и котангенс отрицательные («плюс» делить на «минус»)

Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:

Последнее обновление
Сохранить как PDF

Идентификатор страницы: 14466

Найти все углы на единичной окружности, соответствующие точному триггерному соотношению

Вы работаете с треугольной скобой в мастерской. Скобка представляет собой прямоугольный треугольник, а длина одной стороны скобки равна \(\sqrt{3}\приблизительно 1,732\), и она соединена с другой стороной под прямым углом. Длина другой стороны равна 1. Вам нужно найти угол, который образует третья часть с первой частью, обозначенной ниже как «C»:

Рисунок \(\PageIndex{1}\)

Можете ли вы найти угол между ножками раскоса?

К тому времени, когда вы закончите читать этот урок, вы сможете ответить на этот вопрос. 9{\circ}\), значения триггерных функций часто запоминаются, поскольку они так часто используются.

Вспомните единичный круг и критические значения. С помощью обратных тригонометрических функций вы можете найти значение угла (в радианах или градусах), зная отношение и функцию. Убедитесь, что вы нашли все решения в пределах заданного интервала.

Давайте рассмотрим несколько примеров задач.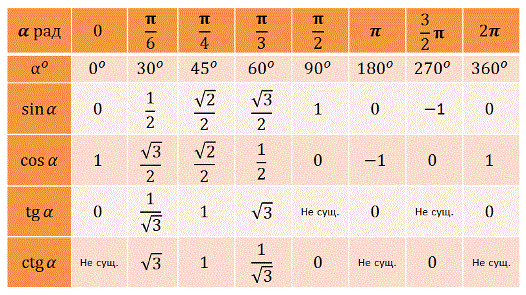 {\circ} \ конец {выровнено} \) 9{-1}(−1)\)

Чтобы просмотреть ответы на обзор, откройте этот PDF-файл и найдите раздел 4.2.

Срок	Определение
Тригонометрическая инверсия	Тригонометрическая обратная функция — это функция, которая отменяет тригонометрическую функцию, чтобы получить исходный аргумент функции. Его также можно использовать для нахождения недостающего угла треугольника по отношению двух сторон треугольника.

Срок

Определение

Тригонометрическая инверсия

Тригонометрическая обратная функция — это функция, которая отменяет тригонометрическую функцию, чтобы получить исходный аргумент функции. Его также можно использовать для нахождения недостающего угла треугольника по отношению двух сторон треугольника.

Видео: Примеры: Определение значений триггерной функции с помощью эталонных треугольников

Практика: Точные значения арксинуса, косинуса и тангенса

Эта страница под названием 2.3.10: Точные значения для арксинуса, косинуса и тангенса распространяется под лицензией CK-12 и была создана, изменена и/или курирована Фондом CK-12 через исходный контент, который был отредактирован для стиль и стандарты платформы LibreTexts; подробная история редактирования доступна по запросу.

ПОД ЛИЦЕНЗИЕЙ

Наверх

Была ли эта статья полезной?

Тип изделия
Раздел или Страница
Автор
СК12
Лицензия
СК-12
Программа OER или Publisher
СК-12
Теги
1. источник@https://www.ck12.org/c/trigonometry

Угол в град

Запоминать надо только значения синусов. Значения косинусов пишутся «наоборот» — справа налево. Значения тангенса можно получить, если синус разделить на косинус; котангенса – если косинус разделить на синус.

Если значения синусов не запомнить, можно поступить так: во всех клетках таблицы нарисовать дроби со знаменателем 2, а в числителе – корни из чисел 0,1,2,3,4:

Дальще надо сосчитать те корни, которые можно, и получится строчка для синусов

Угол в радианах

Не сущес-твует

Не сущес-твует

Цели

В конце урока учащиеся должны уметь;

Продемонстрировать четкое понимание синусоиды, косинуса и касательной.
Найдите максимальную и минимальную точки синусоиды, косинуса и касательной.

График тригонометрических функций

Графики трех основных круговых функций особенно важны, и они будут рассмотрены, чтобы показать поведение каждой функции при изменении. Нарисуем графики функций синуса, косинуса и тангенса.

Синусоидальная кривая

Синусоидальная кривая (или форма синусоидального сигнала) получается при построении графика sin θ по вертикали против θ по горизонтали. Значения sin θ

θ можно получить с помощью научного калькулятора.

Сначала нарисуем график y = sin θ для диапазона 0 < θ < 360

Заполните следующую таблицу значений sin , взяв область значений от 0 ⁰ до 360 ⁰ на 30 ⁰ шагов:

sinθ имеет значения от -1 до 1 включительно

Следует отметить следующие особенности.

В первом квадранте при увеличении θ от 0 до 90 sin θ увеличивается от 0 до 1.
Во втором квадранте при увеличении θ с 90 до 180 sin θ уменьшается с 1 до 0.
В третьем квадранте при увеличении θ от 180 до 270 sin θ уменьшается от 0 до -1.
В четвертом квадранте при увеличении θ с 270 до 360 sin θ увеличивается с -1 до 0,

Косинусоидальная кривая

Косинусоидальная кривая также может быть построена, как показано на диаграмме, но обычно она рисуется с основанием угла горизонтально. Это позволяет сравнивать ее с другими тригонометрическими кривыми.

Заполните следующую таблицу значений cosθ, взяв область значений от 0 ⁰ до 360 ⁰ на шагах 30 ⁰:0071

Следует отметить следующие особенности.

В первом квадранте при увеличении θ от 0 до 90 cos θ уменьшается от 1 до 0.
Во втором квадранте при увеличении θ от 90 до 180 cos θ уменьшается от 0 до – 1.
В третьем квадранте при увеличении θ от 180 до 270 cos θ увеличивается от -1 до 0.
В четвертом квадранте при увеличении θ от 270 до 360 cos θ увеличивается от 0 до 1.

График cos θ и sin θ

На графике показан один цикл каждой функции.

Вы можете проверить формы графиков, используя графические калькуляторы. Синусоида имеет максимум 1, когда θ = 90 ⁰, и минимум -1, когда θ = 270 ⁰. Косинусоидальная кривая идентична синусоидальной кривой, но сдвинута на 90 ⁰ влево. Разность называется разностью фаз между двумя функциями.

Для углов больше 360 ⁰ или менее 0 ⁰ кривые повторяются в последовательных циклах. Повторяющиеся таким образом функции называются периодическими функциями . Каждая функция синуса и косинуса имеет период 360 ⁰ .

Касательная кривая

Касательная кривая может быть построена путем построения графика зависимости тангенса θ (полученного из калькулятора) от θ.

Заполните следующую таблицу значений tanθ, взяв область значений 0 ⁰ до 360 ⁰ в 30 ⁰ шагов:

Следует отметить следующие особенности.

Кривая состоит из трех ветвей.
В первом квадранте при увеличении θ от 0 до 90 тангенс θ увеличивается от 0 до бесконечности.
Во втором квадранте при увеличении θ от 90 до 180 тангенс θ увеличивается от минус бесконечности до 0,
В третьем квадранте при увеличении θ от 180 до 270 тангенс θ увеличивается от 0 до бесконечности.
В четвертом квадранте при увеличении θ с 270 до 360 тангенс θ увеличивается от минус бесконечности до 0.

Пример 1

Нарисуйте график зависимости y = sinx + cosx для значений x от 0 ⁰ до 360 ⁰, используя интервалы 7,92 20 40 30 Используйте свой график, чтобы найти:

a) Значения x верны в ближайшей степени, для которой sin x + cos x = 0,75;

b) Минимальное и максимальное значения y с указанием значений x, для которых они встречаются.