Раздел недели: Скоропись физического, математического, химического и, в целом, научного текста, математические обозначения. Математический, Физический алфавит, Научный алфавит. | |||||||||||||||||||||||||||||||||||||
| Поиск на сайте DPVA Поставщики оборудования Полезные ссылки О проекте Обратная связь Ответы на вопросы. Оглавление Таблицы DPVA.ru — Инженерный Справочник | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация/ / Математический справочник / / Таблицы численных значений. (Таблица квадратов, кубов, синусов . Поделиться:
| ||||||||||||||||||||||||||||||||||||
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. | |||||||||||||||||||||||||||||||||||||
Коды баннеров проекта DPVA.ru Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator Free xml sitemap generator | ||||||||||||||||||||||||||||||||||||
Свойства синуса, косинуса, тангенса и котангенса
В этой статье будут рассмотрены три основных свойства тригонометрических функций: синуса, косинуса, тангенса и котангенса.
Первое свойство — знак функции в зависимости от того, какой четверти единичной окружности приналдежит угол α. Второе свойство — периодичность. Согласно этому свойству, тигонометрическая функция не меняет значения при изменении угла на целое число оборотов. Третье свойсто определяет, как меняются значения функций sin, cos, tg, ctg при противоположных углах α и -α.
Знаки тригонометрических функций по четвертям
Часто в математическом тексте или в контексте задачи можно встретить фразу: «угол первой, второй, третьей или четвертой координатной четверти». Что это такое?
Обратимся к единичной окружности. Она разделена на четыре четверти. Отметим на окружности начальную точку A0(1, 0) и, поворачивая ее вокруг точки O на угол α, попадем в точку A1(x, y).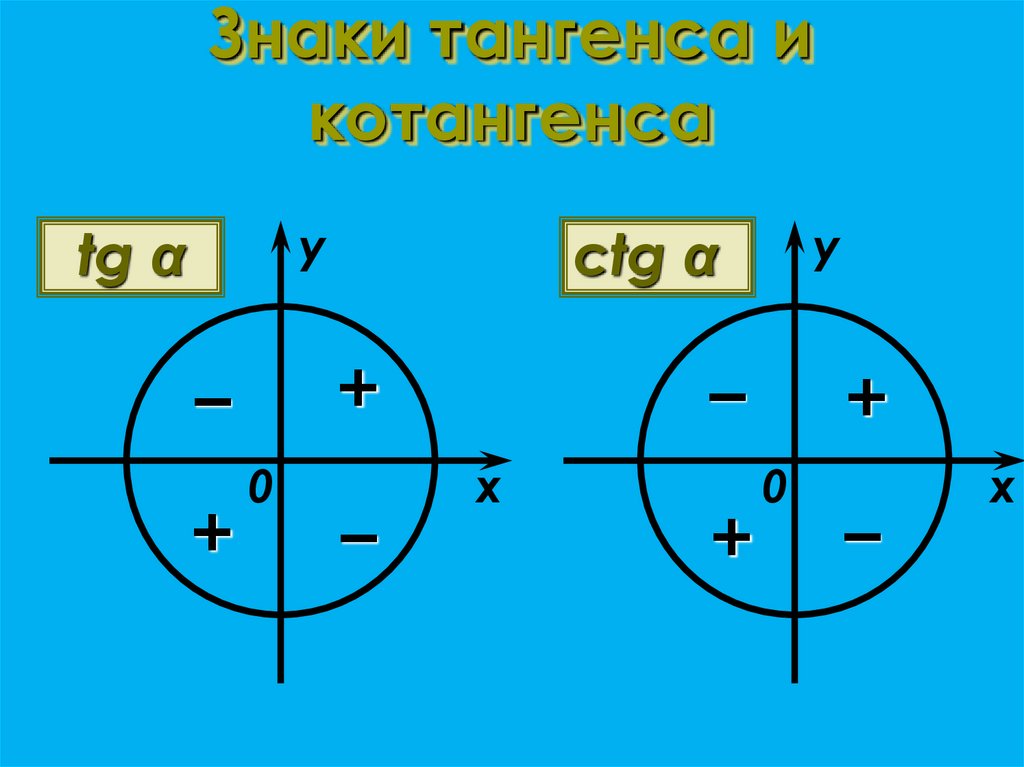 В зависимости от того, в какой четверти будет лежать точка A1(x, y), угол α будет называться углом первой, второй, третьей и четвертой четвети соответственно.
В зависимости от того, в какой четверти будет лежать точка A1(x, y), угол α будет называться углом первой, второй, третьей и четвертой четвети соответственно.
Для наглядности приведем иллюстрацию.
Угол α=30° лежит в первой четверти. Угол -210° является углом второй четверти. Угол 585° — угол третьей четверти. Угол -45° — это угол четвертой четверти.
При этом углы ±90°, ±180°, ±270°, ±360° не принадлежат ни одной четверти, так как лежат на координатных осях.
Теперь рассмотрим знаки, которые принимают синус, косинус, тангенс и котангенс в зависимости от того, в какой четверти лежит угол.
Чтобы определить знаки синуса по четвертям, вспомним опредение. Синус — это ордината точки A1(x, y). Из рисунка видно, что в первой и второй четвертях она положительна, а в третьей и четверной — отрицательна.
Косинус — это абсцисса точки A1(x, y). В соответсии с этим, определяем знаки косинуса на окружности. Косинус положителен в первой и четвертой четвертях, а отрицателен во второй и третьей четверти.
Для определения знаков тангенса и котангенса по четвертям также вспоминаем определения этих тригонометрических функций. Тангенс — отношение ординаты точки к абсциссе. Значит, по правилу деления чисел с разными знаками, когда ордината и абсцисса имеют одинаковые знаки, знак тангенса на окружности будет положительным, а когда ордината и абсцисса имеют разные знаки — отрицательным. Аналогично определяются знаки котангенса по четвертям.
Важно помнить!
- Синус угла α имеет знак плюс в 1 и 2 четвертях, знак минус — в 3 и 4 четвертях.
- Косинус угла α имеет знак плюс в 1 и 4 четвертях, знак минус — в 2 и 3 четвертях.
- Тангенс угла α имеет знак плюс в 1 и 3 четвертях, знак минус — в 2 и 4 четвертях.
- Котангенс угла α имеет знак плюс в 1 и 3 четвертях, знак минус — в 2 и 4 четвертях.
Свойство периодичности
Свойство периодичности — одно из самых очевидных свойств тригонометрических функций.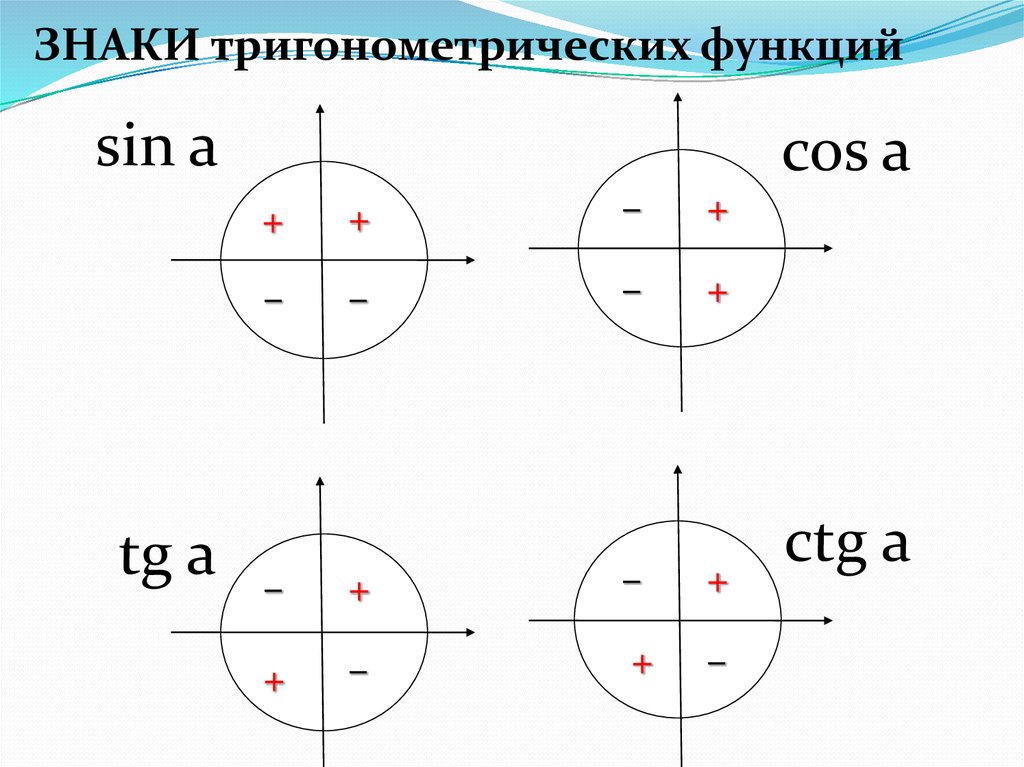
При изменении угла на целое число полных оборотов значения синуса, косинуса, тангенса и котангенса данного угла остаются неизменными.
Действительно, при изменении угла на целое число оборотов мы всегда будем попадать из начальной точки A на единичной окружности в точку A1 с одними и теми же координатами. Соответственно, не будут меняться и значения синуса, косинуса, тангенса и котангенса.
Математически данное свойство записывается так:
sinα+2π·z=sin αcosα+2π·z=cos αtgα+2π·z=tg αctgα+2π·z=ctg α
Какое применение на практике находит это свойство? Свойство периодичности, как и формулы приведения, часто используется для вычисления значений синусов, косинусов, тангенсов и котангенсов больших углов.
Приведем примеры.
sin13π5=sin3π5+2π=sin3π5
tg(-689°)=tg(31°+360°·(-2))=tg31°tg(-689°)=tg(-329°+360°·(-1))=tg(-329°)
Свойства синусов, косинусов, тангенсов и котангенсов противоположных углов
Вновь обратимся к единичной окружности.
Точка A1(x, y) — результат поворота начальной точки A0(1, 0) вокруг центра окружности на угол α. Точка A2(x, -y) — результат поворота начальной точки на угол -α.
Точки A1и A2 симметричны относительно оси абсцисс. В случае, когда α=0°, ±180°, ±360° точки A1и A2 совпадают. Пусть одна точка имеет координаты (x, y), а вторая — (x, -y). Вспомним определения синуса, косинуса, тангенса, котангенса и запишем:
sin α=y, cos α=x, tg α=yx, ctg α=xysin-α=-y, cos-α=x, tg-α=-yx, ctg-α=x-y
Отсюда следует свойство синусов, косинусов, тангенсов и котангенсов противоположных углов.
Свойство синусов, косинусов, тангенсов и котангенсов противоположных угловsin-α=-sin αcos-α=cos αtg-α=-tg αctg-α=-ctg α
Согласно этому свойству, справедливы равенства
Рассмотренное свойство часто используется при решении практических задач в случаях, когда нужно избавиться от отрицательных знаков углов в агрументах тригонометрических функций.
1.2: Функции косинуса и синуса
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 7098
- Тед Сандстром и Стивен Шликер
- Государственный университет Гранд-Вэлли через ScholarWorks @Grand Valley State University
Основные вопросы
Следующие вопросы предназначены для того, чтобы направлять наше изучение материала в этом разделе. Изучив этот раздел, мы должны понять концепции, мотивированные этими вопросами, и быть в состоянии написать точные, связные ответы на эти вопросы.
- Если действительное число \(t\) представляет (со знаком) длину дуги, как мы определяем \(\cos(t)\) и \(\sin(t)\)?
- В каких квадрантах (конечной точки дуги t на единичной окружности) \(\cos(t)\) положительно (отрицательно)? В каких квадрантах (конечной точки дуги \(t\) на единичной окружности) \(\sin(t)\) положительна (отрицательна)?
- Что такое пифагорейская идентичность? Как это тождество выводится из уравнения для единичного круга?
Начало деятельности
- Что такое единичный круг? Что такое уравнение единичной окружности?
- Просмотрите упражнение 1.
 4 на стр. 9.
4 на стр. 9. - Просмотрите завершенную версию рисунка 1.4, которая содержится в ответах к упражнению 1.2 на странице 6.
- Какова конечная точка дуги на единичной окружности, соответствующей интервалу \([0, \dfrac{\pi}{2}]\)?
- Какова конечная точка дуги на единичной окружности, соответствующей интервалу \([0, \pi]\)?
- Какова конечная точка дуги на единичной окружности, соответствующей интервалу \([0, \dfrac{3\pi}{2}]\)?
- Какова конечная точка дуги на единичной окружности, соответствующей интервалу \([0, -\dfrac{\pi}{2}]\)?
Мы начали изучение тригонометрии с изучения единичной окружности, того, как обернуть числовую прямую вокруг единичной окружности и как построить дуги на единичной окружности. Теперь мы можем использовать эти идеи для определения двух основных круговых, или тригонометрических, функций. Эти круговые функции позволят нам моделировать периодические явления, такие как приливы, количество солнечного света в течение дней года, орбиты планет и многие другие.
Рисунок \(\PageIndex{1}\): круговые функции
Может показаться, что единичный круг — довольно простой объект и не представляет большого интереса, но математики почти всегда могут найти что-то интересное даже в таких простых объектах. . Например, мы определяем две основные круговые функции, косинус и синус в терминах единичного круга следующим образом. На рисунке \(\PageIndex{1}\) показана дуга длины \(t\) на единичной окружности. Эта дуга начинается в точке \((1, 0)\) и заканчивается в ее конечной точке \(P(t)\). Затем мы определяем косинус и синус дуги \(t\) как \(x\) и \(y\) координаты точки \(P\), так что \(P(t) = (\cos (t), sin(t))\) (косинус обозначается как \(\cos\), а синус — как \(\sin\)). Таким образом, значения косинуса и синуса определяются дугой \(t\), а косинус и синус равны функции дуги \(t\). Поскольку дуга лежит на единичной окружности, мы называем косинус и синус круговыми функциями . Важной частью тригонометрии является изучение косинуса и синуса и периодических явлений, которые эти функции могут моделировать. Это одна из причин, по которой круговые функции также называют тригонометрическими функциями .
Это одна из причин, по которой круговые функции также называют тригонометрическими функциями .
Примечание
Согласно веб-сайту «Самые ранние известные случаи использования некоторых математических слов» jeff560.tripod.com/mathword.html, слово «синус» произошло от санскрита через арабский и латинский языки. Хотя сведения о фактическом происхождении различаются, похоже, что санскритское произведение «jya» (аккорд) было переведено на арабский язык как «jiba», но затем было переведено на латынь как «jaib» (залив), которое стало «sinus» (залив). или кривая). Затем это слово было англизировано и стало нашим «синусом». Слово косинус началось с Платона из Тиволи, который использовал выражение «chorda residui». В то время как латинское слово хорда был лучшим переводом санскритско-арабского слова для синуса, чем слово синус, это слово уже использовалось. Таким образом, «остаточная хорда» стала «косинусом».
Примечание
В математике мы всегда создаем формальные определения для объектов, которые обычно используем.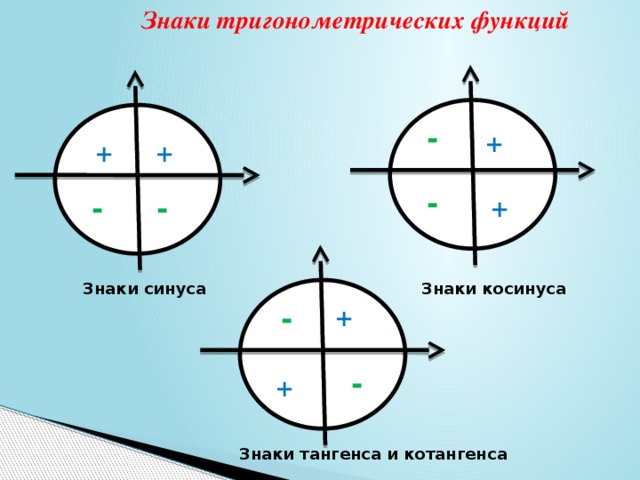 Определения критически важны, потому что с согласованными определениями у всех будет общее понимание того, что означают эти термины. Без такого общего понимания было бы много путаницы, поскольку разные люди имеют разные значения для разных терминов. Поэтому необходимы тщательные и точные определения, чтобы развить математические свойства этих объектов. Чтобы изучить и понять тригонометрию, человек должен уметь объяснить, как определяются круговые функции. Так что сейчас самое время начать работать над пониманием этих определений. 92 = 1\) (с положительным направлением против часовой стрелки) с начальной точкой \((1, 0)\) и конечной точкой \((x, y)\), то косинус функции \(t\), обозначенный \(\cos(t)\), и синус t, обозначенный \(\sin(t)\), определяются как \[\cos (t) = x\] и \[\sin ( t) = y.\]
Определения критически важны, потому что с согласованными определениями у всех будет общее понимание того, что означают эти термины. Без такого общего понимания было бы много путаницы, поскольку разные люди имеют разные значения для разных терминов. Поэтому необходимы тщательные и точные определения, чтобы развить математические свойства этих объектов. Чтобы изучить и понять тригонометрию, человек должен уметь объяснить, как определяются круговые функции. Так что сейчас самое время начать работать над пониманием этих определений. 92 = 1\) (с положительным направлением против часовой стрелки) с начальной точкой \((1, 0)\) и конечной точкой \((x, y)\), то косинус функции \(t\), обозначенный \(\cos(t)\), и синус t, обозначенный \(\sin(t)\), определяются как \[\cos (t) = x\] и \[\sin ( t) = y.\]
На рис. 1.6 показаны эти определения для дуги, конечная точка которой находится в первом квадранте.
В настоящее время невозможно определить точные значения функций косинуса и синуса для определенных значений \(t\). Однако это можно сделать, если конечная точка дуги длины \(t\) лежит на оси \(х\) или оси \(у\). Например, поскольку длина окружности единичного круга равна \(2\pi\), дуга длины \(t = \pi\) будет иметь конечную точку на полпути вокруг окружности от точки \((1, 0)\). То есть конечная точка находится в \((1, 0)\). Следовательно, \[\cos (\pi) = -1\] и \[\sin (\pi) = 0.\]
Однако это можно сделать, если конечная точка дуги длины \(t\) лежит на оси \(х\) или оси \(у\). Например, поскольку длина окружности единичного круга равна \(2\pi\), дуга длины \(t = \pi\) будет иметь конечную точку на полпути вокруг окружности от точки \((1, 0)\). То есть конечная точка находится в \((1, 0)\). Следовательно, \[\cos (\pi) = -1\] и \[\sin (\pi) = 0.\]
Упражнение \(\PageIndex{1}\)
Определите точные значения каждого из следующих параметров:
- \(\cos(\dfrac{\pi}{2})\) и \(\sin( \dfrac{\pi}{2})\).
- \(\cos(\dfrac{3\pi}{2})\) и \(\sin(\dfrac{3\pi}{2})\).
- \(\cos(0)\) и \(sin(0)\).
- \(\cos(-\dfrac{\pi}{2})\) и \(\sin(-\dfrac{\pi}{2})\).
- \(\cos(2\pi)\) и \(\sin(2\pi)\).
- \(cos(-\pi)\) и \(\sin(-\pi)\).
Важное примечание. Поскольку косинус и синус являются функциями дуги, длина которой равна действительному числу t, ввод t определяет вывод косинуса и синуса.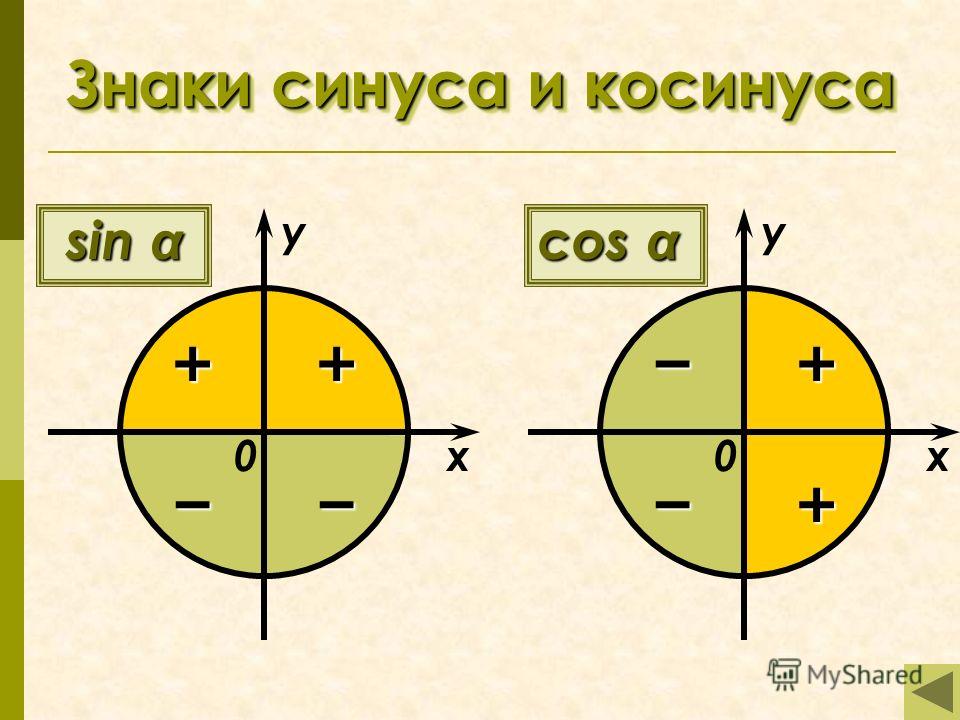 В результате необходимо указывать входное значение при работе с косинусом и синусом. Другими словами, мы ВСЕГДА пишем \(\cos(t)\), где \(t\) — ввод вещественного числа, и НИКОГДА просто \(\cos\). Повторим еще раз: косинус и синус — это функции, поэтому мы ДОЛЖНЫ указывать входные данные для этих функций.
В результате необходимо указывать входное значение при работе с косинусом и синусом. Другими словами, мы ВСЕГДА пишем \(\cos(t)\), где \(t\) — ввод вещественного числа, и НИКОГДА просто \(\cos\). Повторим еще раз: косинус и синус — это функции, поэтому мы ДОЛЖНЫ указывать входные данные для этих функций.
- Ответить
- \[\cos(\dfrac{\pi}{2}) = 0\] \[\sin(\dfrac{\pi}{2}) = 1\]
- \[\cos(\dfrac{3\pi}{2}) = 0\] \[\sin(\dfrac{3\pi}{2}) = -1\]
- \[\cos(0) = 1\] \[\sin(0) = 1\]
- \[\cos(-\dfrac{\pi}{2}) = 0\] \[\sin(-\dfrac{\pi}{2}) = -1\]
- \[\cos(2\pi) = 0\] \[\sin(2\pi) = 1\]
- \[\cos(-\pi) = -1\] \[\sin(-\pi) = 0\]
Упражнение \(\PageIndex{2}\)
В этом упражнении мы будем использовать апплет Geogebra под названием «Конечные точки дуг на единичной окружности». Веб-адрес этого апплета:
http://gvsu. edu/s/JY
edu/s/JY
Для этого апплета мы контролируем значение ввода \(t\) с помощью ползунка для \(t\). Значения \(t\) варьируются от \(-20\) до \(20\) с шагом \(0,5\). Для заданного значения \(t\) рисуется дуга длины \(t\) и отображаются координаты конечной точки этой дуги. Используйте этот апплет, чтобы найти приблизительные значения для каждого из следующих параметров:
- \(\cos(1)\) и \(\sin(1)\)
- \(\cos(2)\) и \(\sin(2)\)
- \(\cos(-4)\) и \(\sin(-4)\)
- \(\cos(5.5)\) и \(\sin(5.5)\)
- \(\cos(15)\) и \(\sin(15)\)
- \(\cos(-15)\) и \(\sin(-15)\)
- Ответить
- \[\cos(1) \приблизительно 0,5403, \sin(1) \приблизительно 0,8415\]
- \[\cos(2) \приблизительно -0,4161, \sin(2) \приблизительно 0,9093\]
- \[\cos(-4) \приблизительно -0,6536, \sin(-4) \приблизительно 0,7568\]
- \[\cos(5.
 5) \приблизительно 0,7807, \sin(5.5) \приблизительно -0,7055\]
5) \приблизительно 0,7807, \sin(5.5) \приблизительно -0,7055\] - \[\cos(15) \приблизительно -0,7597, \sin(15) \приблизительно 0,6503\]
- \[\cos(-15) \приблизительно -0,7597, \sin(-15) \приблизительно 0,6503\]
Некоторые свойства функций косинуса и синуса
Функции косинуса и синуса называются круговыми функциями , поскольку их значения определяются координатами точек на единичной окружности. Для каждого действительного числа \(t\) существует соответствующая дуга, начинающаяся в точке \((1, 0)\) (направленной) длины \(t\), которая лежит на единичной окружности. Координаты конечной точки этой дуги определяют значения \(\cos(t\) и \(\sin(t\).
На предыдущих курсах математики мы узнали, что область определения функции — это набор всех входных данных, которые дают определенный результат. Мы также узнали, что диапазон функции — это набор всех возможных выходов функции.
Упражнение \(\PageIndex{3}\)
- Какова область определения функции косинуса? Почему?
- Какова область определения синуса? Почему?
- Какова наибольшая координата \(x\), которую может иметь точка на единичной окружности? Какова наименьшая координата \(x\), которую может иметь точка на единичной окружности? Что это говорит нам о диапазоне функции косинуса? Почему?
- Какова наибольшая координата \(y\), которую может иметь точка на единичной окружности? Какова наименьшая координата \(y\), которую может иметь точка на единичной окружности? Что это говорит нам о диапазоне функции синуса? Почему?
- Ответить
- Поскольку мы можем обернуть любое число на единичную окружность, мы всегда можем найти конечную точку дуги, соответствующую любому числу.
 Таким образом, косинус любого действительного числа определен, а область определения функции косинуса — это набор всех действительных чисел.
Таким образом, косинус любого действительного числа определен, а область определения функции косинуса — это набор всех действительных чисел. - По той же причине, что и для функции косинуса, областью определения функции синуса является множество всех действительных чисел.
- На единичном круге наибольшая координата x, которую может иметь точка, равна 1, а наименьшая координата x, которую может иметь точка, равна 1. Поскольку выход функции косинуса представляет собой координату x точки на единичном круге, диапазон функции косинуса — это закрытый интервал \([-1, 1]\). Это означает \(-1 \leq \cos(t) \leq 1\) для любого действительного числа \(t\).
- На единичной окружности наибольшая координата y, которую может иметь точка, равна 1, а наименьшая координата y, которую может иметь точка, равна 1. Поскольку выходным сигналом функции синуса является координата y точки на единичной окружности, диапазон функции синуса — это замкнутый интервал \([-1, 1]\).
 Это означает \(-1 \leq \sin(t) \leq 1\) для любого действительного числа \(t\).
Это означает \(-1 \leq \sin(t) \leq 1\) для любого действительного числа \(t\).
- Поскольку мы можем обернуть любое число на единичную окружность, мы всегда можем найти конечную точку дуги, соответствующую любому числу.
Хотя мы не можем вычислить точные значения для многих входных значений функций косинуса и синуса, мы можем использовать наши знания о системе координат и ее квадрантах, чтобы определить, являются ли определенные значения косинуса и синуса положительными или отрицательными. Идея состоит в том, что знаки координат точки \(P(x, y)\), нанесенной на координатный план, определяются квадрантом, в котором лежит точка (если только она не лежит на одной из осей). Рисунок \(\PageIndex{2}\) суммирует эти результаты для знаков значений функций косинуса и синуса. Левая колонка в таблице предназначена для положения конечной точки дуги, определяемой действительным числом \(t\).
| Квадрант | \(\cos(t)\) | \(\sin(t)\) |
|---|---|---|
| QI | положительный | положительный |
| II квартал | отрицательный | положительный |
| QIII | отрицательный | отрицательный |
| IV квартал | положительный | отрицательный |
Теперь нам нужно определить, в каком квадранте лежит конечная точка дуги, определяемой вещественным числом t.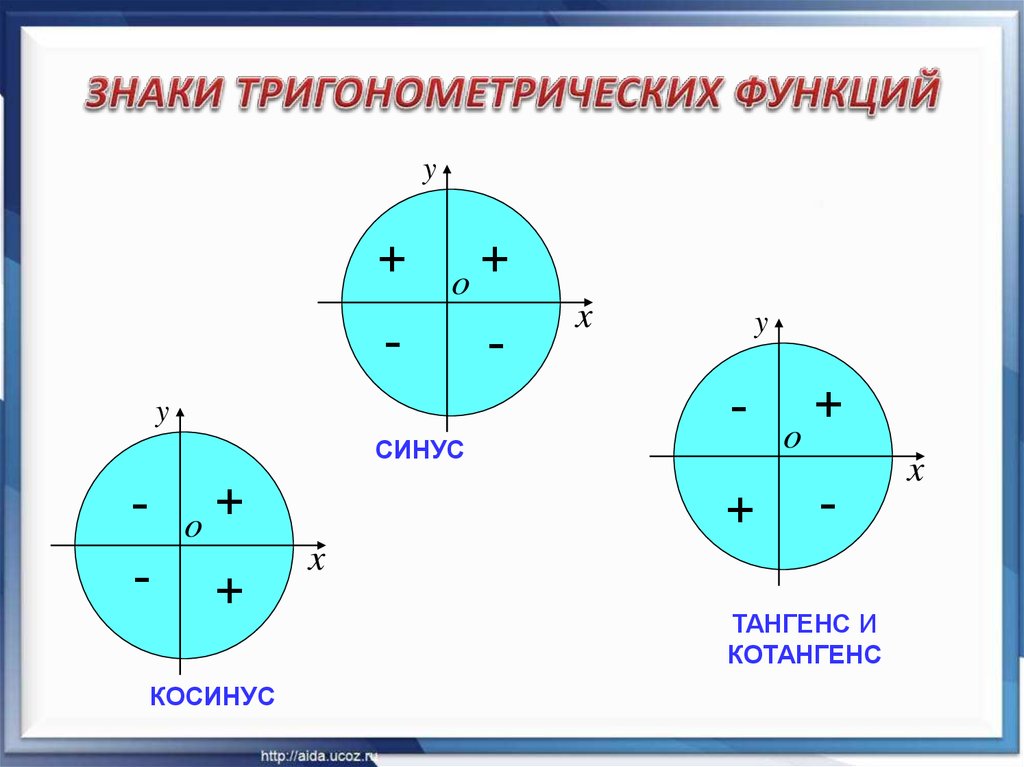 Мы можем сделать это, еще раз используя тот факт, что длина окружности единичного круга равна \(2\pi\), и когда мы движемся по единичному кругу из точки .1; 0/ в положительном (против часовой стрелки) направлении мы будем пересекать одну из осей координат каждую четверть оборота. Например, если \(0 < t < \dfrac{\pi}{2}\), конечная точка дуги, определяемой \(t\), находится в первом квадранте и \(\cos(t) > 0 \) и \(\sin(t) > 0\).
Мы можем сделать это, еще раз используя тот факт, что длина окружности единичного круга равна \(2\pi\), и когда мы движемся по единичному кругу из точки .1; 0/ в положительном (против часовой стрелки) направлении мы будем пересекать одну из осей координат каждую четверть оборота. Например, если \(0 < t < \dfrac{\pi}{2}\), конечная точка дуги, определяемой \(t\), находится в первом квадранте и \(\cos(t) > 0 \) и \(\sin(t) > 0\).
Упражнение \(\PageIndex{4}\)
- Если \( \dfrac{\pi}{2} < t < \pi\), то каковы знаки \(\cos(t)\) и \(\sin(t)\)?
- Если \( \pi < t < \dfrac{3\pi}{2}\), то какие знаки у \(\cos(t)\) и \(\sin(t)\)?
- Если \(\dfrac{3\pi}{2} < t < 2\pi\), то какие знаки у \(\cos(t)\) и \(\sin(t)\)?
- Если \(\dfrac{5\pi}{2} < t < 3\pi\), то какие знаки у \(\cos(t)\) и \(\sin(t)\)?
- Для каких значений \(t\) (между \(0\) и \(2\pi\)) является положительным значением \(\cos(t)\)? Почему?
- Для каких значений \(t\) (между \(0\) и \(2\pi\)) является положительным значением \(\sin(t)\)? Почему?
- Для каких значений \(t\) (между \(0\) и \(2\pi\)) является отрицательным значением \(\cos(t)\)? Почему?
- Для каких значений \(t\) (между \(0\) и \(2\pi\)) является отрицательным значением \(\sin(t)\)? Почему?
- Ответить
- Если \(\dfrac{\pi}{2} < t < \pi\), то конечная точка дуги \(t\) находится во втором квадранте, поэтому \(\cos(t) < 0 \) и \(\sin(t) > 0\).

- Если \(\pi < t < \dfrac{3\pi}{2}\), то конечная точка дуги t находится в третьем квадранте, поэтому \(\cos(t) < 0\) и \ (\sin(t) < 0\).
- Если \(\dfrac{3\pi}{2} < t < 2\pi\), то конечная точка дуги t находится в четвертом квадранте, поэтому \(\cos(t) > 0\) и \(\sin(t) < 0\).
- Если \(\dfrac{5\pi}{2} < t < 3\pi\), то конечная точка дуги t находится во втором квадранте, поэтому \(\cos(t) > 0\) и \(\sin(t) > 0\).
- Обратите внимание, что \(\cos(t) = 0\) при \(t = \dfrac{\pi}{2}\) и \(t = \dfrac{3\pi}{2}\). Поскольку \(\cos(t)\) является координатой x конечной точки дуги \(t\), предыдущий ответ показывает, что \(\cos(t)\) положительно, когда \(t\) находится в одном из интервалов \([0, \dfrac{\pi}{2})\) или \((\dfrac{3\pi}{2}, 2\pi]\).
- Обратите внимание, что \(\sin(t) = 0\) при \(t = 0\) и \(t = \pi\). Поскольку \(\sin(t)\) является координатой x конечной точки дуги \(t\), предыдущий ответ показывает, что \(\sin(t)\) положительно, когда \(t\) находится в одном из интервалов \((0, \pi)\).

- Обратите внимание, что \(\cos(t) = 0\) при \(t = \dfrac{\pi}{2}\) и \(t = \dfrac{3\pi}{2}\). Поскольку \(\cos(t)\) является координатой x конечной точки дуги \(t\), предыдущий ответ показывает, что \(\cos(t)\) положительно, когда \(t\) находится в интервале \((\dfrac{\pi}{2}, \dfrac{3\pi}{2})\).
- Обратите внимание, что \(\sin(t) = 0\) при \(t = \pi\) и \(t = 2\pi\). Поскольку \(\sin(t)\) является координатой x конечной точки дуги \(t\), предыдущий ответ показывает, что \(\sin(t)\) положительно, когда \(t\) находится в одном из интервалов \([0, \dfrac{\pi}{2})\) или \((\pi, 2\pi)\).
- Если \(\dfrac{\pi}{2} < t < \pi\), то конечная точка дуги \(t\) находится во втором квадранте, поэтому \(\cos(t) < 0 \) и \(\sin(t) > 0\).
Упражнение \(\PageIndex{5}\)
Используйте результаты, представленные на рисунке \(\PageIndex{2}\), чтобы определить, являются ли следующие величины положительными, отрицательными или нулевыми. (Не используйте калькулятор.)
- \(\cos(\dfrac{\pi}{5})\)
- \(\sin(\dfrac{\pi}{5})\)
- \(\cos(\dfrac{5\pi}{8})\)
- \(\sin(\dfrac{5\pi}{8})\)
- \(\cos(\dfrac{-9\pi}{16})\)
- \(\sin(\dfrac{-9\pi}{16})\)
- \(\cos(\dfrac{-25\pi}{12})\)
- \(\sin(\dfrac{-25\pi}{12})\)
- Ответить
- Так как \(0 < \dfrac{\pi}{5} < \dfrac{\pi}{2}\), конечная точка дуги \(\dfrac{\pi}{5}\) находится в первый квадрант.
 Следовательно, \(\cos(\dfrac{\pi}{5})\) положителен.
Следовательно, \(\cos(\dfrac{\pi}{5})\) положителен. - Используя информацию о \(t\) в (1), \(\sin(\dfrac{\pi}{5})\) положительно.
- Мы можем записать \(\dfrac{\pi}{2}\) как \(\dfrac{4\pi}{8}\) и \(\pi\) как \(\dfrac{8\pi}{ 8}\), поэтому \(\dfrac{\pi}{2}\ < \dfrac{5\pi}{8} < \pi\). Это помещает конечную точку дуги \(\dfrac{5\pi}{8}\) во второй квадрант. Следовательно, \(\cos(\dfrac{5\pi}{8})\) отрицательно.
- Используя информацию о \(t\) в (3), \(\sin(\dfrac{5\pi}{8})\) отрицательно.
- Мы можем записать \(-\dfrac{\pi}{2}\) как \(\dfrac{-8\pi}{16}\) и \(-\pi\) как \(\dfrac{-16 \pi}{16}\), поэтому \(-\pi < \dfrac{-9\pi}{16} < -\dfrac{\pi}{2}\). Это помещает конечную точку дуги \(\dfrac{-9\pi}{16}\) в третий квадрант. Следовательно, (\cos(\dfrac{-9\pi}{16})\) отрицательно.
- Используя информацию о \(t\) в (5), (\sin(\dfrac{-9\pi}{16})\) отрицательно.
- Мы можем записать \(-2\pi\) как \(\dfrac{-24\pi}{12}\) и \(-\dfrac{5\pi}{2}\) как \(\dfrac{ -30\pi}{12}\), поэтому \(\dfrac{-5\pi}{2} < \dfrac{-25\pi}{12} < 2\pi\).
 Это помещает конечную точку дуги \(\cos(\dfrac{-25\pi}{12})\) в четвертый квадрант.
Это помещает конечную точку дуги \(\cos(\dfrac{-25\pi}{12})\) в четвертый квадрант. - Используя информацию о дуге \(t\) в (7), \(\sin(\dfrac{-25\pi}{12})\) отрицательно.
- Так как \(0 < \dfrac{\pi}{5} < \dfrac{\pi}{2}\), конечная точка дуги \(\dfrac{\pi}{5}\) находится в первый квадрант.
Пифагорейское тождество
В математике тождество 92)\).
Тождество Пифагора позволяет нам определить значение \(\cos(t)\) или \(\sin(t)\), если мы знаем значение другого и квадрант, в котором конечная точка дуги \(t\) лежит. Это показано в следующем примере.
Пример \(\PageIndex{1}\)
Предположим, что \(\cos(t) = \dfrac{2}{5}\) и конечная точка дуги\((t)\) лежит в четвертый квадрант.5 Используйте эту информацию для определения значения \(\sin(t)\).
Раствор 2(t) = \dfrac{21}{25} \]
Это означает, что \(\sin(t) = \pm\sqrt{\dfrac{21}{25}}\), и поскольку конечная точка дуги \((t)\) находится в четвертом квадранте, мы знаем, что \(\sin(t) < 0\). Следовательно, \(\sin(t) = -\sqrt{\dfrac{21}{25}}\).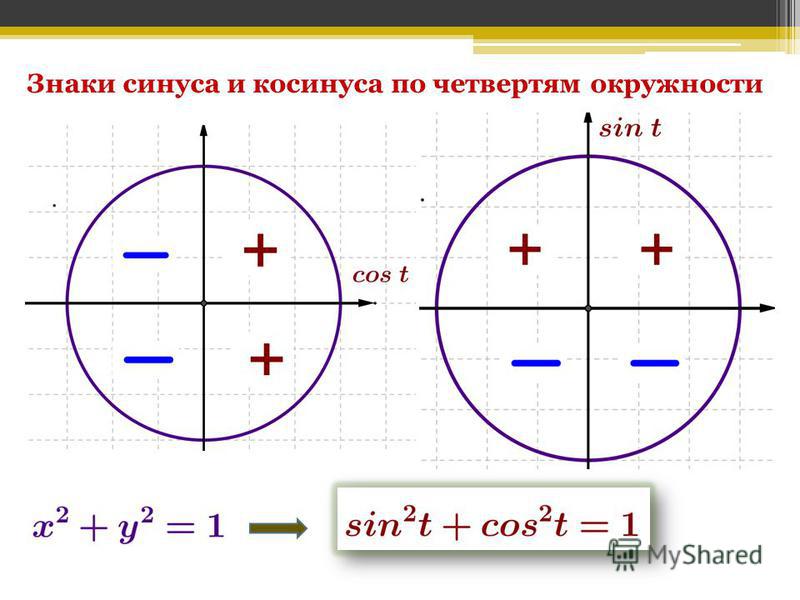 Поскольку \(\sqrt{25} = 5\), мы можем записать
Поскольку \(\sqrt{25} = 5\), мы можем записать
\[\sin(t) = -\sqrt{\dfrac{21}{25}} = -\dfrac{\sqrt{21}} {5}.\]
Упражнение \(\PageIndex{7}\)
- Если \(\cos(t) = \dfrac{1}{2}\) и конечная точка дуги \(t \) находится в четвертом квадранте, определите значение \(\sin(t)\). 9{2}(t) = \dfrac{3}{4}\]
\[\sin(t) = \pm\dfrac{\sqrt{3}}{4}\]
Обратите внимание, что мы не можем определить знак \(\sin(t)\), используя только тождество Пифагора. Нам потребуется дополнительная информация о дуге \(t\). В этом случае нам дано, что конечная точка дуги \(t\) находится в четвертом квадранте, а значит, \(\sin(t) < 0\). Следовательно,
\[\sin(t) = -\sqrt{\dfrac{3}{4}} = -\dfrac{\sqrt{3}}{2}\]
2. Поскольку \(\sin(t) = -\dfrac{2}{3}\), мы можем использовать тождество Пифагора, чтобы получить 9{2}(t) = \dfrac{5}{9}\]
\[\sin(t) = \pm\dfrac{\sqrt{5}}{9}\]
И снова нам нужна информация о дуге \(t\), чтобы определить знак \(\cos(t)\).
 В этом случае нам дано, что \(\pi < t < \dfrac{3\pi}{2}\). Следовательно, конечная точка дуги t находится в третьем квадранте и, следовательно, \(\sin(t) < 0\). Следовательно,
В этом случае нам дано, что \(\pi < t < \dfrac{3\pi}{2}\). Следовательно, конечная точка дуги t находится в третьем квадранте и, следовательно, \(\sin(t) < 0\). Следовательно,\[\cos(t) = -\sqrt{\dfrac{5}{9}} = \dfrac{\sqrt{5}}{3}.\]
Резюме
В этом разделе мы изучили следующие важные концепции и идеи: 92 = 1\) (с положительным направлением против часовой стрелки) с начальной точкой \((1, 0)\) и конечной точкой \((x, y)\), тогда \(\cos(t) = x\) и \(\sin(t) = y\).
- Знаки \(\cos(t)\) и \(\sin(t)\) определяются квадрантом, в котором лежит конечная точка дуги \(t\).
- Одно из наиболее важных тождеств в тригонометрии, называемое тождеством Пифагора, выводится из уравнения для единичного круга и утверждает: 92(t) = 1.
 \номер\]
\номер\]Эта страница под названием 1.2: Функции косинуса и синуса распространяется по лицензии CC BY-NC-SA 3.0, автором, ремиксом и/или куратором являются Тед Сандстром и Стивен Шликер (ScholarWorks @Grand Valley State University) через источник контент, отредактированный в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Тед Сандстром и Стивен Шликер
- Лицензия
- CC BY-NC-SA
- Версия лицензии
- 3,0
- Показать страницу TOC
- нет
- Теги
- Круговые функции
- Функция косинуса
- Пифагорейское тождество
- Синусоидальная функция
- источник@https://scholarworks.
 gvsu.edu/books/12
gvsu.edu/books/12
Тригонометрические функции
Тригонометрические функцииПроизвольные углы и единичная окружность
До сих пор мы использовали единичный круг для определения тригонометрических функций для острых углов. В следующем разделе, где мы рассмотрим косые треугольники, нам понадобятся не только острые углы. Некоторые косые треугольники тупые, и нам нужно знать синус и косинус тупых углов. Пока мы это делаем, мы также должны определить триггерные функции для углов, превышающих 180°, и для отрицательных углов. Во-первых, нам нужно понять, что такое такие углы.Древнегреческие геометры рассматривали только углы между 0° и 180°, и они не считали ни прямой угол 180°, ни вырожденный угол 0° углами. Полезно не только считать эти частные случаи углами, но также включать углы от 180° до 360°, иногда называемые «рефлекторными углами». С применением тригонометрии к предметам исчисления и дифференциальных уравнений также стали приняты углы за пределами 360 ° и отрицательные углы.

Рассмотрим единичный круг. Обозначим его центр (0,0) как O, , а точку (1,0) на нем как A. В качестве движущейся точки B движется по единичной окружности, начиная с против часовой стрелки, угол AOB как угол 0° и увеличивается. Когда B пройдет весь круг и вернется к A, , тогда угол AOB будет равен 360°. Конечно, это тот же угол, что и угол 0°, поэтому мы можем идентифицировать эти два угла. Как B продолжается второй раз по кругу, мы получаем углы от 360° до 720°. Это те же ракурсы, которые мы видели в первый раз, но у нас для них разные названия. Например, прямой угол называется либо 90°, либо 450°. Каждый раз по кругу мы получаем другое название угла. Таким образом, 90°, 450°, 810° и 1170° обозначают один и тот же угол.
Если B начинается в той же точке A и движется по часовой стрелке, то мы получим отрицательные углы, а точнее имена в отрицательных градусах для тех же углов.
 Например, если вы пройдете четверть круга по часовой стрелке, угол AOB обозначен как –90°. Конечно, это то же самое, что угол 270°.
Например, если вы пройдете четверть круга по часовой стрелке, угол AOB обозначен как –90°. Конечно, это то же самое, что угол 270°.Таким образом, любой угол имеет бесконечное множество имен, но все они отличаются друг от друга на кратное 360°.
Синусы и косинусы произвольных углов
Теперь, когда мы задали произвольные углы, мы можем определить их синусы и косинусы. Пусть угол расположен так, что его вершина находится в центре единичной окружности O = (0,0), а первая сторона угла расположена вдоль x — ось. Пусть вторая сторона угла пересекает единичную окружность в точке B. Тогда угол равен углу AOB , где A равно (1,0). Мы используем координаты B для определения косинуса угла и синуса угла. В частности, координата x координаты B является косинусом угла, а координата y координатой B является синусом угла.Это определение расширяет определения синуса и косинуса, данные ранее для острых углов. 
Свойства синусов и косинусов, вытекающие из этого определения
Есть несколько свойств, которые мы можем легко вывести из этого определения. Некоторые из них обобщают тождества, которые мы уже видели для острых углов.- Синус и косинус являются периодическими функциями периода 360°, то есть периода 2 π . Это потому, что синусы и косинусы определяются в терминах углов, и вы можете добавить числа, кратные 360°, или 2 π , и это не изменит угол. Таким образом, для любого угла θ ,
sin ( θ + 360°) = sin θ, и cos ( θ + 360°) = cos θ.
Многие из современных приложений тригонометрии вытекают из использования тригонометрического исчисления, особенно те приложения, которые имеют дело непосредственно с тригонометрическими функциями. Таким образом, мы должны использовать радианную меру, когда думаем о триггере с точки зрения триггерных функций. В радианах последняя пара уравнений читается как
sin ( θ + 2 π ) = sin θ, и cos ( θ + 2 π ) = 5 cos 90,6 6 θ
- Синус и косинус дополняют друг друга:
cos θ = sin ( π / 2 – θ ) sin θ = cos ( π / 2 – θ )
Мы видели это раньше, но теперь у нас есть это для любого угла θ.
 Это правда, потому что, когда вы отражаете плоскость через диагональную линию y = x, угол обменивается на его дополнение.
Это правда, потому что, когда вы отражаете плоскость через диагональную линию y = x, угол обменивается на его дополнение. - Тождество Пифагора для синусов и косинусов следует непосредственно из определения. Поскольку точка B лежит на единичной окружности, ее координаты x и y удовлетворяют уравнению x 2 + y 2 =1. Но координаты косинус и синус, так что делаем вывод
sin 2 θ + cos 2 θ = 1, Теперь мы готовы рассмотреть синус и косинус как функции.
- Синус — нечетная функция, а косинус — четная функция. Возможно, вы не встречали этих прилагательных «нечетный» и «четный» применительно к функциям, но знать их важно. Функция f называется нечетной функцией , если для любого числа x, f (– x ) = – f ( x ). Функция f называется функцией даже , если для любого числа x, f (– x ) = f ( x ).
 Большинство функций не являются ни нечетными, ни четными функциями, но некоторые из наиболее важных функций являются либо теми, либо другими. Любой многочлен только с нечетными степенями является нечетной функцией, например, f ( x ) = x 5 + 8 x 3 – 2 x. (Обратите внимание, что все степени числа x — нечетные числа.) Точно так же любой полином только с четными степенями является четной функцией. Например, f ( x ) = x 4 – 3 x 2 – 5. )
Большинство функций не являются ни нечетными, ни четными функциями, но некоторые из наиболее важных функций являются либо теми, либо другими. Любой многочлен только с нечетными степенями является нечетной функцией, например, f ( x ) = x 5 + 8 x 3 – 2 x. (Обратите внимание, что все степени числа x — нечетные числа.) Точно так же любой полином только с четными степенями является четной функцией. Например, f ( x ) = x 4 – 3 x 2 – 5. )Синус — нечетная функция, а косинус — четная
sin (– θ ) = –sin θ, и cos (– θ ) = cos θ.
Эти факты следуют из симметрии единичного круга относительно оси x . Угол — х — это тот же угол, что и х , за исключением того, что он находится по другую сторону оси х . Переворот точки ( x,y ) на другую сторону оси x превращает ее в ( x,–y ), поэтому координата y инвертируется, то есть синус инвертируется , но x -координата остается прежней, то есть косинус не меняется.

- Очевидным свойством синусов и косинусов является то, что их значения лежат в диапазоне от –1 до 1. Каждая точка на единичной окружности находится на расстоянии 1 единицы от начала координат, поэтому координаты любой точки также находятся в пределах 1 от 0.
Графики функций синуса и косинуса
Возьмем t в качестве переменного угла. Вы можете думать о t и как об угле, и как о времени. Хороший способ для человека понять функцию — посмотреть на ее график. Начнем с графика sin т.р. Возьмите горизонтальную ось за ось t (а не ось x , как обычно), возьмите вертикальную ось за ось y и постройте уравнение y = sin t . Выглядит так.Во-первых, обратите внимание, что это периодический период 2 π . Геометрически это означает, что если вы возьмете кривую и сдвинете ее 2 π влево или вправо, то кривая вернется сама на себя. Во-вторых, обратите внимание, что график находится в пределах одной единицы т -ось.
 Мало что еще очевидно, за исключением того, где оно увеличивается и уменьшается. Например, sin t растет от 0 до π /2, поскольку координата y точки B увеличивается с увеличением угла AOB от 0 до π /2.
Мало что еще очевидно, за исключением того, где оно увеличивается и уменьшается. Например, sin t растет от 0 до π /2, поскольку координата y точки B увеличивается с увеличением угла AOB от 0 до π /2.Далее давайте посмотрим на график косинуса. Снова возьмем горизонтальную ось за ось t , но теперь возьмем вертикальную ось за ось x и нарисуем уравнение 9.0656 x 90 657 = cos 90 656 t.
Обратите внимание, что он выглядит точно так же, как график sin t , за исключением того, что он сдвинут влево на π /2. Это из-за тождества cos t = sin ( π /2 + t ). Хотя мы раньше не встречались с этим тождеством, оно легко следует из уже виденных: π /2 + t ).
Графики функций тангенса и котангенса
График функции тангенса имеет вертикальную асимптоту при x = π /2. Это происходит потому, что тангенс стремится к бесконечности, когда t приближается к π /2.
| Квадрант | \(\cos(t)\) | \(\sin(t)\) |
|---|---|---|
| QI | положительный | положительный |
| II квартал | отрицательный | положительный |
| QIII | отрицательный | отрицательный |
| IV квартал | положительный | отрицательный |

 …) + Таблицы Брадиса / / Знаки тригонометрических функций синус, косинус, тангенс и котангенс по четвертям в тригонометрическом круге.
…) + Таблицы Брадиса / / Знаки тригонометрических функций синус, косинус, тангенс и котангенс по четвертям в тригонометрическом круге.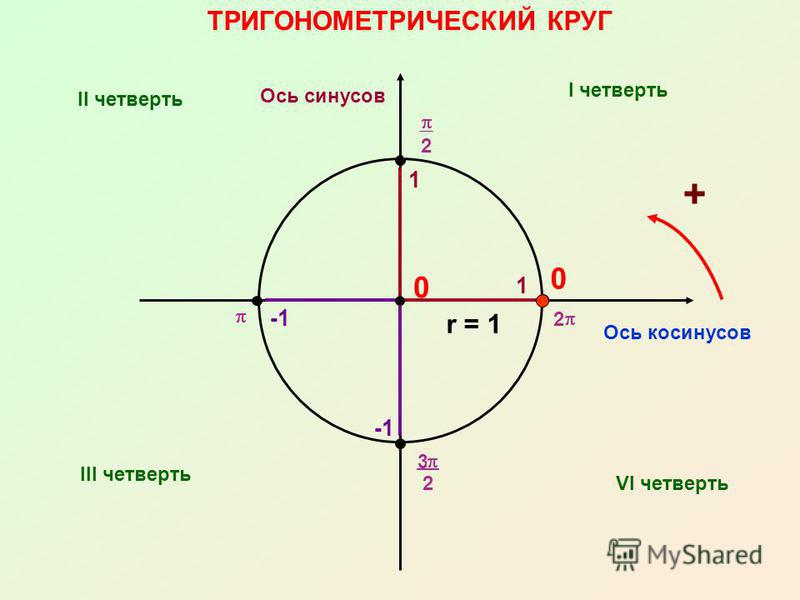 Введите свой запрос:
Введите свой запрос: 4 на стр. 9.
4 на стр. 9.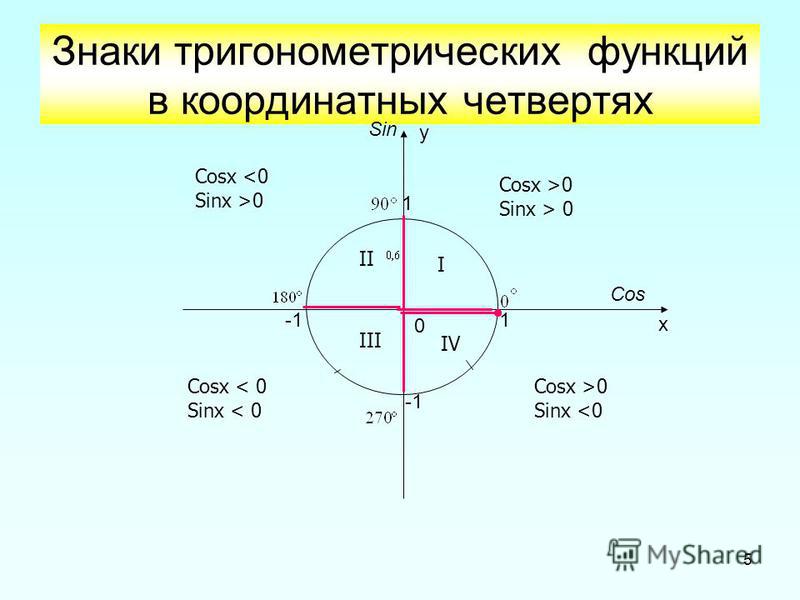 5) \приблизительно 0,7807, \sin(5.5) \приблизительно -0,7055\]
5) \приблизительно 0,7807, \sin(5.5) \приблизительно -0,7055\] Таким образом, косинус любого действительного числа определен, а область определения функции косинуса — это набор всех действительных чисел.
Таким образом, косинус любого действительного числа определен, а область определения функции косинуса — это набор всех действительных чисел.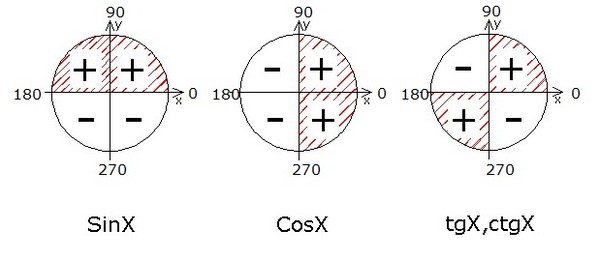 Это означает \(-1 \leq \sin(t) \leq 1\) для любого действительного числа \(t\).
Это означает \(-1 \leq \sin(t) \leq 1\) для любого действительного числа \(t\).
 Следовательно, \(\cos(\dfrac{\pi}{5})\) положителен.
Следовательно, \(\cos(\dfrac{\pi}{5})\) положителен.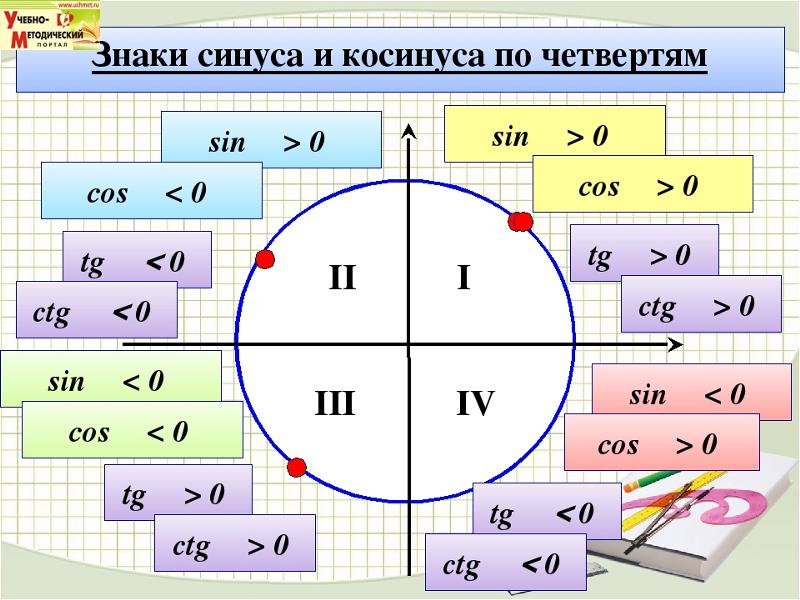 Это помещает конечную точку дуги \(\cos(\dfrac{-25\pi}{12})\) в четвертый квадрант.
Это помещает конечную точку дуги \(\cos(\dfrac{-25\pi}{12})\) в четвертый квадрант. В этом случае нам дано, что \(\pi < t < \dfrac{3\pi}{2}\). Следовательно, конечная точка дуги t находится в третьем квадранте и, следовательно, \(\sin(t) < 0\). Следовательно,
В этом случае нам дано, что \(\pi < t < \dfrac{3\pi}{2}\). Следовательно, конечная точка дуги t находится в третьем квадранте и, следовательно, \(\sin(t) < 0\). Следовательно, \номер\]
\номер\]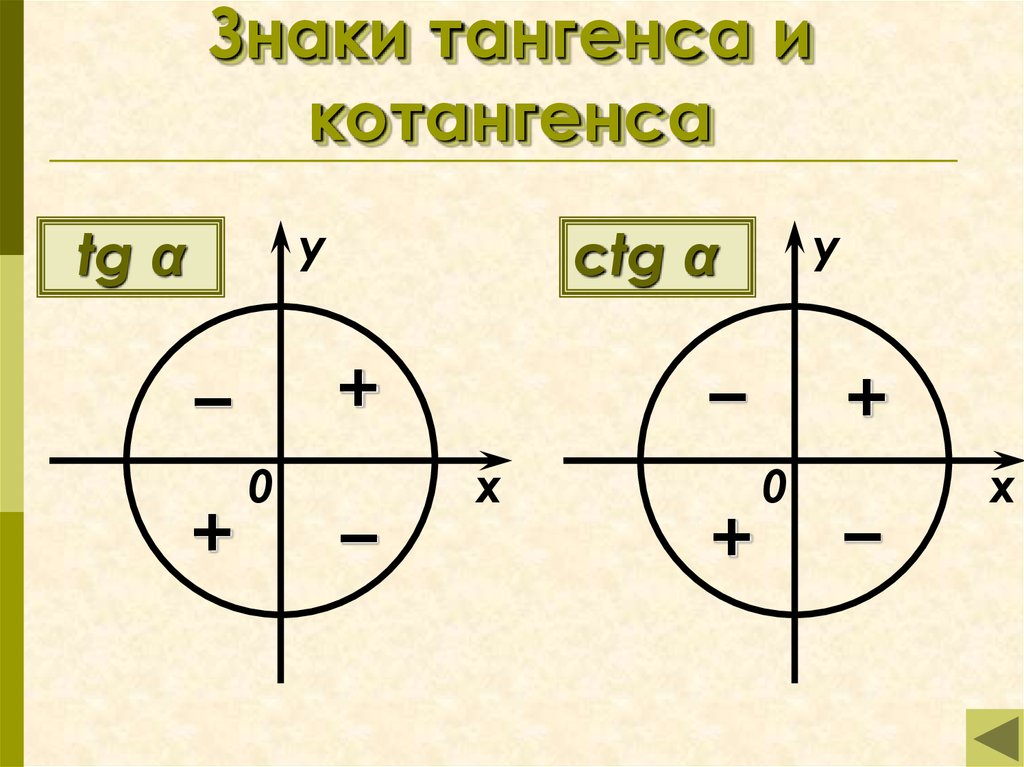 gvsu.edu/books/12
gvsu.edu/books/12
 Например, если вы пройдете четверть круга по часовой стрелке, угол AOB обозначен как –90°. Конечно, это то же самое, что угол 270°.
Например, если вы пройдете четверть круга по часовой стрелке, угол AOB обозначен как –90°. Конечно, это то же самое, что угол 270°.
 Это правда, потому что, когда вы отражаете плоскость через диагональную линию y = x, угол обменивается на его дополнение.
Это правда, потому что, когда вы отражаете плоскость через диагональную линию y = x, угол обменивается на его дополнение. Большинство функций не являются ни нечетными, ни четными функциями, но некоторые из наиболее важных функций являются либо теми, либо другими. Любой многочлен только с нечетными степенями является нечетной функцией, например, f ( x ) = x 5 + 8 x 3 – 2 x. (Обратите внимание, что все степени числа x — нечетные числа.) Точно так же любой полином только с четными степенями является четной функцией. Например, f ( x ) = x 4 – 3 x 2 – 5. )
Большинство функций не являются ни нечетными, ни четными функциями, но некоторые из наиболее важных функций являются либо теми, либо другими. Любой многочлен только с нечетными степенями является нечетной функцией, например, f ( x ) = x 5 + 8 x 3 – 2 x. (Обратите внимание, что все степени числа x — нечетные числа.) Точно так же любой полином только с четными степенями является четной функцией. Например, f ( x ) = x 4 – 3 x 2 – 5. )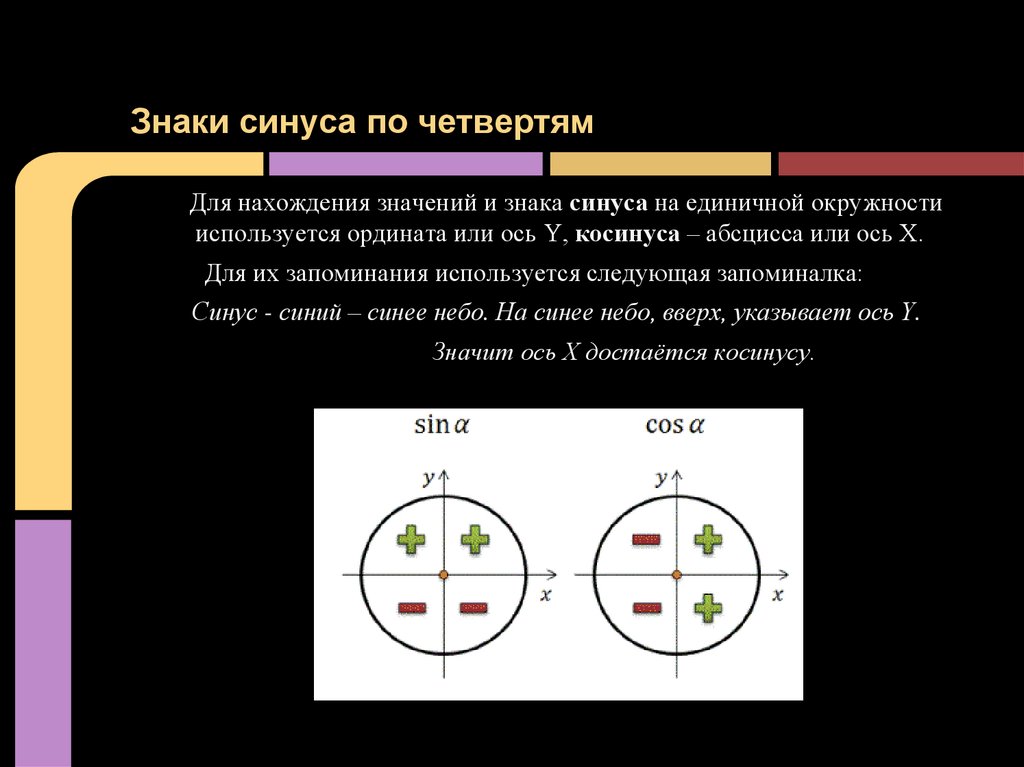
 Мало что еще очевидно, за исключением того, где оно увеличивается и уменьшается. Например, sin t растет от 0 до π /2, поскольку координата y точки B увеличивается с увеличением угла AOB от 0 до π /2.
Мало что еще очевидно, за исключением того, где оно увеличивается и уменьшается. Например, sin t растет от 0 до π /2, поскольку координата y точки B увеличивается с увеличением угла AOB от 0 до π /2.