как найти длину окружности зная диаметр. Способы нахождения длины окружности
Таблица Брадиса 6 служит для определения длины окружности (С) по данному её диаметру (d), а также для решения обратной задачи. Устройство и употребление этой таблицы одинаковы с устройством и употреблением таблицы квадратов .
Примеры:
♦ Найти С, если d равно: 1) 2,85 м, 2) 3,664 см, 3) 8,069 км.
Ответы:
1) 8,954 м (двадцать восьмая строка, пятый столбец).
2) 11,511 см (тридцать шестая строка, шестой столбец, поправка на 4).
3) 25,350 км (восьмидесятая строка, седьмой столбец, вычитается поправка на 1).
♦ Найти d, если С равно 1) 7,740 см, 2) 22,861 м.
Ответы:
1) 2,464 см (ближайшее табличное число 7,728, поправка 12),
2) 7,277 м (ближайшее табличное число 22,871. поправка 10).
Если данный диаметр меньше 1 или больше 10, переносим в нём знак дробности так. чтобы получилось число, заключённое между 1 и 10, и находим из таблицы изменённую длину окружности. Замечая, что длина окружности пропорциональна диаметру, заключаем, что найденную изменённую длину надо исправить, перенося в ней знак дробности в обратном направлении на столько же мест. Аналогично поступаем при решении обратной задачи, если данная длина окружности меньше 3,142 или больше 31,416.
Замечая, что длина окружности пропорциональна диаметру, заключаем, что найденную изменённую длину надо исправить, перенося в ней знак дробности в обратном направлении на столько же мест. Аналогично поступаем при решении обратной задачи, если данная длина окружности меньше 3,142 или больше 31,416.
Примеры:
◊ Найти С, если d равно 0,0835 см. Диаметру 8,35 см соответствует длина окружности 26,232 см. Следовательно, искомое С равно 0,26232 см.
◊ Найти d, если С равно 40 000 км. Длине окружности в 4,000 соответствует диаметр 1,273. Следовательно, искомое d равно 12 730 км.
| d | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 1 | 2 | 3 | 4 | 5 |
| 1,0 | 3,142 | 3,173 | 3,204 | 3,236 | 3,267 | 3,299 | 3,330 | 3,362 | 3,393 | 3,424 | 3 | 6 | 9 | 13 | 16 |
| 1,1 | 3,456 | 3,487 | 3,519 | 3,550 | 3,581 | 3,613 | 3,644 | 3,676 | 3,707 | 3,738 | 3 | 6 | 9 | 13 | 16 |
| 1,2 | 3,770 | 3,801 | 3,833 | 3,864 | 3,896 | 3,927 | 3,958 | 3,990 | 4,021 | 4,053 | 3 | 6 | 9 | 13 | 16 |
| 1,3 | 4,084 | 4,115 | 4,147 | 4,178 | 4,210 | 4,241 | 4,273 | 4,304 | 4,335 | 4,367 | 3 | 6 | 9 | 13 | 16 |
1. 4 4 | 4,398 | 4,430 | 4,461 | 4,492 | 4,524 | 4,555 | 4,587 | 4,618 | 4,650 | 4,681 | 3 | 6 | 9 | 13 | 16 |
| 1,5 | 4,712 | 4,744 | 4,775 | 4,807 | 4,838 | 4,8f9 | 4,901 | 4,932 | 4,964 | 4,995 | 3 | 6 | 9 | 13 | 16 |
| 1,6 | 5,027 | 5,058 | 5,089 | 5,121 | 5,152 | 5,184 | 5,215 | 5,246 | 5,278 | 5,309 | 3 | 6 | 9 | 13 | 16 |
| 1,7 | 5,341 | 5,372 | 5,404 | 5,435 | 5,466 | 5,498 | 5,529 | 5,561 | 5,592 | 5,623 | 3 | 6 | 9 | 13 | 16 |
| 1,8 | 5,655 | 5,686 | 5,718 | 5,749 | 5,781 | 5,812 | 5,843 | 5,875 | 5,906 | 5,938 | 3 | 6 | 9 | 13 | 16 |
| 1,9 | 5,969 | 6,000 | 6,032 | 6,063 | 6,095 | 6,126 | 6,158 | 6,189 | 6,220 | 6,252 | 3 | 6 | 9 | 13 | 16 |
| 2,0 | 6,283 | 6,315 | 6,346 | 6,377 | 6,409 | 6,440 | 6,472 | 6,503 | 6,535 | 6,566 | 3 | 6 | 9 | 13 | 16 |
| 2,1 | 6,597 | 6,629 | 6,660 | 6,692 | 6,723 | 6,754 | 6,786 | 6,817 | 6,849 | 6. 88С 88С | 3 | 6 | 9 | 13 | 16 |
| 2,2 | 6,912 | 6,943 | 6,974 | 7,006 | 7,037 | 7,069 | 7,100 | 7,131 | 7,163 | 7,194 | 3 | 6 | 9 | 13 | 16 |
| 2,3 | 7,226 | 7,257 | 7,288 | 7,320 | 7,351 | 7,383 | 7,414 | 7,446 | 7,477 | 7,508 | 3 | в | 9 | 13 | 16 |
| 2,4 | 7,540 | 7,571 | 7,603 | 7,634 | 7,665 | 7,697 | 7,728 | 7,760 | 7,791 | 7,823 | 3 | 6 | 9 | 13 | 16 |
| 2,5 | 7,854 | 7,885 | 7,917 | 7,948 | 7,980 | 8,011 | 8,042 | 8,074 | 8,105 | 8,137 | 3 | 6 | 9 | 13 | 16 |
| 2,6 | 8,168 | 8,200 | 8,231 | 8,262 | 8,294 | 8,325 | 8,357 | 8,388 | 8,419 | 8,451 | 3 | 6 | 9 | 13 | 16 |
| 2,7 | 8,482 | 8,514 | 8,545 | 8,577 | 8,608 | 8,639 | 8,671 | 8,702 | 8,734 | 8,765 | 3 | 6 | 9 | 13 | 16 |
| 2,8 | 8,796 | 8,828 | 8,859 | 8,891 | 8,922 | 8,954 | 8,985 | 9,016 | 9,048 | 9,079 | 3 | 6 | 9 | 13 | 16 |
| 2,9 | 9,111 | 9,142 | 9,173 | 9,205 | 9,236 | 9,268 | 9,299 | 9,331 | 9,362 | 9,393 | 3 | 6 | 9 | 13 | 16 |
| 9,425 | 9,456 | 9,488 | 9,519 | 9,550 | 9,582 | 9,613 | 9,645 | 9,676 | 9,708 | 3 | 6 | 9 | 13 | 16 | |
| 3,1 | 9,739 | 9,770 | 9,802 | 9,833 | 9,865 | 9,896 | 9,927 | 9,959 | 9,990 | 10,022 | 3 | 6 | 9 | 13 | 16 |
| 3,2 | 10,053 | 10,085 | 10,116 | 10,147 | 10,179 | 10,210 | 10,242 | 10,273 | 10,304 | 10,336 | 3 | 6 | 9 | 13 | 16 |
| 3,3 | 10,367 | 10,399 | 10,430 | 10,462 | 10,493 | 10,524 | 10,556 | 10,587 | 10,619 | 10,650 | 3 | 6 | 9 | 13 | 16 |
| 3,4 | 10,681 | 10,713 | 10,744 | 10,776 | 10,807 | 10,838 | 10,870 | 10,901 | 10,933 | 10,964 | 3 | 6 | 9 | 13 | 16 |
| 3,5 | 10,996 | 11,027 | 11,058 | 11,090 | 11,121 | 11,153 | 11,184 | 11,215 | 11,247 | 11,278 | 3 | в | 9 | 13 | 16 |
| 3,6 | 11,310 | 11,341 | 11,373 | 11,404 | 11,435 | 11,467 | 11,498 | 11,530 | 11,561 | 11,592 | 3 | 6 | 9 | 13 | 16 |
| 3,7 | 11,624 | 11,655 | 11,687 | 11,718 | 11,750 | 11,781 | 11,812 | 11,844 | 11,875 | 11,907 | 3 | 6 | 9 | 13 | 16 |
| 3,8 | 11,938 | 11,969 | 12,001 | 12,032 | 12,064 | 12,095 | 12,127 | 12,158 | 12,189 | 12,221 | 3 | 6 | 9 | 13 | 16 |
| 3,9 | 12,252 | 12,284 | 12,315 | 12,346 | 12,378 | 12,409 | 12,441 | 12,472 | 12,504 | 12,535 | 3 | 6 | 9 | 13 | 16 |
| 4,0 | 12,566 | 12,598 | 12,629 | 12,661 | 12,692 | 12,723 | 12,755 | 12,786 | 12,818 | 12,849 | 3 | 6 | 9 | 13 | 16 |
| 4,1 | 12,881 | 12,912 | 12,943 | 12,975 | 13,006 | 13,038 | 13,069 | 13,100 | 13,132 | 13,163 | 3 | 6 | 9 | 13 | 16 |
| 4,2 | 13,195 | 13,226 | 13,258 | 13,289 | 13,320 | 13,352 | 13,383 | 13,415 | 13,446 | 13,477 | 3 | 6 | 9 | 13 | 16 |
| 4,3 | 13,509 | 13,540 | 13,572 | 13,603 | 13,635 | 13,666 | 13,697 | 13,729 | 13,760 | 13,792 | 3 | 6 | 9 | 13 | 16 |
| 4,4 | 13,823 | 13,854 | 13,886 | 13,917 | 13,949 | 13,980 | 14,012 | 14,043 | 14,074 | 14,106 | 3 | 6 | 9 | 13 | 16 |
| d | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 1 | 2 | 3 | 4 | 5 |
Если диаметр увеличить (уменьшить) в 10, 100, 1000 и т.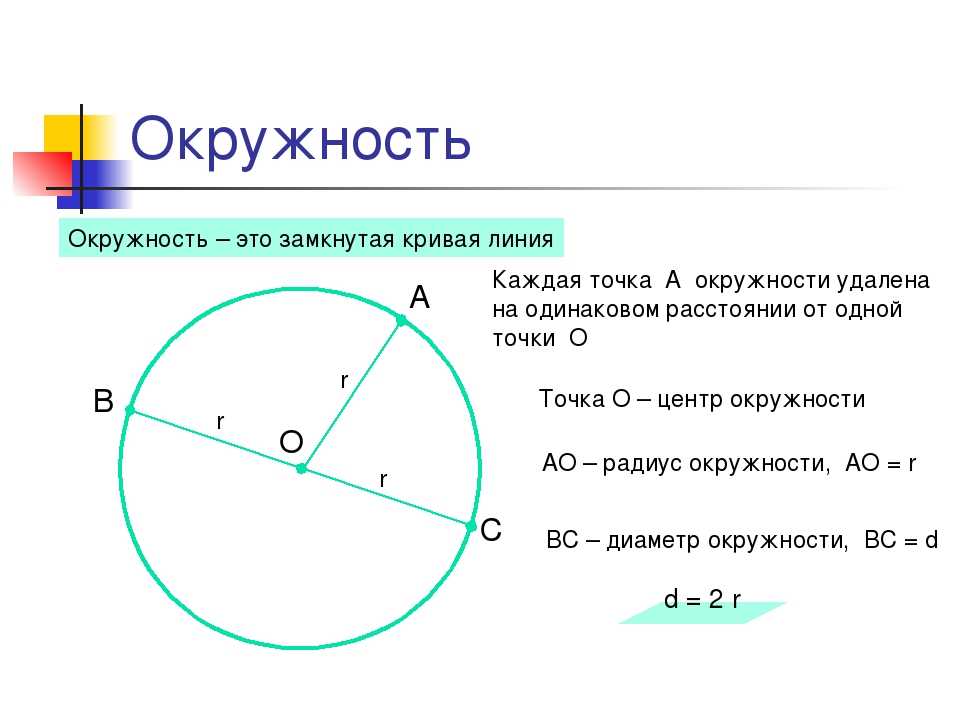 д. раз, то длина окружности увеличится (уменьшится) во столько же раз.
д. раз, то длина окружности увеличится (уменьшится) во столько же раз.
Сначала разберемся в отличии между кругом и окружностью. Чтобы увидеть эту разницу, достаточно рассмотреть, чем являются обе фигуры. Это бесчисленное количество точек плоскости, располагающиеся на равном расстоянии от единственной центральной точки. Но, если круг состоит и из внутреннего пространства, то окружности оно не принадлежит. Получается, что круг это и окружность, ограничивающая его (о-кру(г)жность), и бесчисленное число точек, что внутри окружности.
Для любой точки L , лежащей на окружности, действует равенство OL=R . (Длина отрезка OL равняется радиусу окружности).
Отрезок, который соединяет две точки окружности, является ее хордой .
Хорда, проходящая прямо через центр окружности, является диаметром этой окружности (D) . Диаметр можно вычислить по формуле: D=2R
Длина окружности вычисляется по формуле: C=2\pi R
Площадь круга : S=\pi R^{2}
Дугой окружности называется та ее часть, которая располагается между двух ее точек. {\circ}}
{\circ}}
Диаметр, что перпендикулярен хорде, делит хорду и стянутые ею дуги пополам.
В случае, если хорды AB и CD окружности имеют пересечение в точке N , то произведения отрезков хорд, разделенные точкой N , равны между собой.
AN\cdot NB = CN \cdot ND
Касательная к окружности
Касательной к окружности принято называть прямую, у которой имеется одна общая точка с окружностью.
Если же у прямой есть две общие точки, ее называют секущей .
Если провести радиус в точку касания, он будет перпендикулярен касательной к окружности.
Проведем две касательные из этой точки к нашей окружности. Получится, что отрезки касательных сравняются один с другим, а центр окружности расположится на биссектрисе угла с вершиной в этой точке.
AC = CB
Теперь к окружности из нашей точки проведем касательную и секущую. Получим, что квадрат длины отрезка касательной будет равен произведению всего отрезка секущей на его внешнюю часть. {\circ}
{\circ}
\angle ADB = \angle AEB = \angle AFB
На одной окружности находятся вершины треугольников с тождественными углами и заданным основанием.
Угол с вершиной внутри окружности и расположенный между двумя хордами тождественен половине суммы угловых величин дуг окружности, которые заключаются внутри данного и вертикального углов.
\angle DMC = \angle ADM + \angle DAM = \frac{1}{2} \left (\cup DmC + \cup AlB \right)
Угол с вершиной вне окружности и расположенный между двумя секущими тождественен половине разности угловых величин дуг окружности, которые заключаются внутри угла.
\angle M = \angle CBD — \angle ACB = \frac{1}{2} \left (\cup DmC — \cup AlB \right)
Вписанная окружность
Вписанная окружность — это окружность, касающаяся сторон многоугольника.
В точке, где пересекаются биссектрисы углов многоугольника, располагается ее центр.
Окружность может быть вписанной не в каждый многоугольник.
Площадь многоугольника с вписанной окружностью находится по формуле:
S = pr ,
p — полупериметр многоугольника,
r — радиус вписанной окружности.
Отсюда следует, что радиус вписанной окружности равен:
r = \frac{S}{p}
Суммы длин противоположных сторон будут тождественны, если окружность вписана в выпуклый четырехугольник. И наоборот: в выпуклый четырехугольник вписывается окружность, если в нем суммы длин противоположных сторон тождественны.
AB + DC = AD + BC
В любой из треугольников возможно вписать окружность. Только одну единственную. В точке, где пересекаются биссектрисы внутренних углов фигуры, будет лежать центр этой вписанной окружности.
Радиус вписанной окружности вычисляется по формуле:
r = \frac{S}{p} ,
где p = \frac{a + b + c}{2}
Описанная окружность
Если окружность проходит через каждую вершину многоугольника, то такую окружность принято называть описанной около многоугольника . {\circ}
{\circ}
Около любого треугольника можно описать окружность, причем одну-единственную. Центр такой окружности будет расположен в точке, где пересекаются серединные перпендикуляры сторон треугольника.
Радиус описанной окружности можно вычислить по формулам:
R = \frac{a}{2 \sin A} = \frac{b}{2 \sin B} = \frac{c}{2 \sin C}
R = \frac{abc}{4 S}
a , b , c — длины сторон треугольника,
S — площадь треугольника.
Теорема Птолемея
Под конец, рассмотрим теорему Птолемея.
Теорема Птолемея гласит, что произведение диагоналей тождественно сумме произведений противоположных сторон вписанного четырехугольника.
AC \cdot BD = AB \cdot CD + BC \cdot AD
Окружностью называется ряд равноудалённых точек от одной точки, которая, в свою очередь, является центром этой окружности. Окружность имеет также свой радиус, равный расстоянию этих точек от центра.
Отношение длины, какой либо окружности к её диаметру, для всех окружностей одинаково. Это отношение есть число, являющееся математической константой, которое обозначается греческой буквой π .
Это отношение есть число, являющееся математической константой, которое обозначается греческой буквой π .
Определение длины окружности
Произвести расчёт окружности можно по следующей формуле:
L = π D = 2 π r
r — радиус окружности
D — диаметр окружности
L — длина окружности
π — 3.14
Задача:
Вычислить длину окружности , имеющей радиус 10 сантиметров.
Решение:
Формула для вычисления дины окружности имеет вид:
L = π D = 2 π r
где L – длина окружности, π – 3,14 , r – радиус окружности, D – диаметр окружности.
Таким образом, длина окружности, имеющей радиус 10 сантиметров равна:
L = 2 × 3,14 × 5 = 31,4 сантиметра
Окружность представляет собой геометрическую фигуру, являющуюся совокупностью всех точек на плоскости, удаленных от заданной точки, которая называется ее центром, на некоторое расстояние, не равное нулю и именуемое радиусом. Определять ее длину с различной степенью точности ученые умели уже в глубокой древности: историки науки считают, что первая формула для вычисления длины окружности была составлена примерно в 1900 году до нашей эры в древнем Вавилоне.
Определять ее длину с различной степенью точности ученые умели уже в глубокой древности: историки науки считают, что первая формула для вычисления длины окружности была составлена примерно в 1900 году до нашей эры в древнем Вавилоне.
С такими геометрическими фигурами, как окружности, мы сталкиваемся ежедневно и повсеместно. Именно ее форму имеет внешняя поверхность колес, которыми оснащаются различные транспортные средства. Эта деталь, несмотря на свою внешнюю простоту и незатейливость, считаются одним из величайших изобретений человечества, причем интересно, что аборигены Австралии и американские индейцы вплоть до прихода европейцев совершенно не имели понятия о том, что это такое.
По всей вероятности, самые первые колеса представляли собой отрезки бревен, которые насаживались на ось. Постепенно конструкция колеса совершенствовалась, их конструкция становилась все более и более сложной, а для их изготовления требовалось использовать массу различных инструментов. Сначала появились колеса, состоящие из деревянного обода и спиц, а затем, для того, чтобы уменьшить износ их внешней поверхности, ее стали обивать металлическими полосами. Для того чтобы определить длины этих элементов, и требуется использовать формулу расчета длины окружности (хотя на практике, вероятнее всего, мастера это делали «на глаз» или просто опоясывая колесо полосой и отрезая требуемый ее участок).
Для того чтобы определить длины этих элементов, и требуется использовать формулу расчета длины окружности (хотя на практике, вероятнее всего, мастера это делали «на глаз» или просто опоясывая колесо полосой и отрезая требуемый ее участок).
Следует заметить, что колесо используется отнюдь не только в транспортных средствах. Например, его форму имеет гончарный круг, а также элементы шестеренок зубчатых передач, широко применяемых в технике. Издавна колеса использовались в конструкциях водяных мельниц (самые древние из известных ученым сооружений такого рода строились в Месопотамии), а также прялок, применявшихся для изготовления нитей из шерсти животных и растительных волокон.
Окружности нередко можно встретить и в строительстве. Их форму имеют достаточно широко распространенные круглые окна, очень характерные для романского архитектурного стиля. Изготовление этих конструкций – дело весьма непростое и требует высокого мастерства, а также наличия специального инструмента. Одной из разновидностей круглых окон являются иллюминаторы, устанавливаемые в морских и воздушных судах.
Одной из разновидностей круглых окон являются иллюминаторы, устанавливаемые в морских и воздушных судах.
Таким образом, решать задачу определения длины окружности часто приходится инженерам-конструкторам, разрабатывающим различные машины, механизмы и агрегаты, а также архитекторам и проектировщикам. Поскольку число π , необходимое для этого, является бесконечным, то с абсолютной точностью определить этот параметр не представляется возможным, и поэтому при вычислениях учитывается та ее степень, которая в том или ином конкретном случае является необходимой и достаточной.
Определение окружности в статье Окружность .
Длина окружности вычисляется из диаметра по формуле::
где r — это радиус, d — диаметр круга, а π (греческая буква пи), которая является математической постоянной, отношением длины окружности к ее диаметру (значение пи, первые цифры: 3.141 592 653 589 793).
Wikimedia Foundation . 2010 .
Смотреть что такое «Длина окружности» в других словарях:
длина окружности резервуара — — Тематики нефтегазовая промышленность EN tank circumference …
длина окружности совокупность известных операций — — [А. С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN circuit … Справочник технического переводчика
С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN circuit … Справочник технического переводчика
ДЛИНА, длины, мн. нет, жен. Протяжение линии, плоскости, тела в том направлении, в котором две крайние точки (линии, плоскости, тела) лежат на наибольшем расстоянии одна от другой. Предметы измеряются в длину, ширину и высоту. Длина стола. Меры… … Толковый словарь Ушакова
длина — ы/, только ед., ж. 1) Протяжение в том направлении, в котором две крайние точки линии, плоскости, тела лежат на наибольшем расстоянии друг от друга. Мера длины. Лыжи длиной в два метра. Измерить площадку в длину и в ширину. Синонимы: расстоя/ние… … Популярный словарь русского языка
— (или, что то же, длина дуги кривой) в метрическом пространстве числовая характеристика протяжённости этой кривой. Исторически вычисление длины кривой называлось спрямлением кривой (от лат. rectificatio, спрямление). Если длина кривой… … Википедия
Длина шкалы — Расстояние между крайними отметками шкалы, отсчитанное по дуге окружности или по прямой линии, проходящей через середины наименьших отметок
Окружностью называют кривую линию, которая ограничивает собой круг. В геометрии фигуры плоские, поэтому определение относится к двухмерному изображению. Предполагается, что все точки этой кривой удалены от центра круга на равное расстояние.
В геометрии фигуры плоские, поэтому определение относится к двухмерному изображению. Предполагается, что все точки этой кривой удалены от центра круга на равное расстояние.
У окружности есть несколько характеристик, на основе которых производят расчеты, связанные с этой геометрической фигурой. В их число входит: диаметр, радиус, площадь и длина окружности. Эти характеристики взаимосвязаны, то есть для их вычисления достаточно информации хотя бы об одной из составляющих. Например, зная только радиус геометрической фигуры по формуле можно найти длину окружности, диаметр, и ее площадь.
- Радиус окружности – это отрезок внутри окружности, соединённый с ее центром.
- Диаметр – это отрезок внутри окружности, соединяющий ее точки и проходящий через центр. По сути, диаметр – это два радиуса. Именно так выглядит формула для его вычисления: D=2r.
- Есть еще одна составляющая окружности – хорда. Эта прямая, которая соединяет две точки окружности, но не всегда проходит через центр.
 Так вот ту хорду, которая через него проходит, тоже называют диаметром.
Так вот ту хорду, которая через него проходит, тоже называют диаметром.
Как узнать длину окружности? Сейчас выясним.
Длина окружности: формула
Для обозначения этой характеристики выбрана латинская буква p. Еще Архимед доказал, что отношение длины окружности к ее диаметру является одним и тем же числом для всех окружностей: это число π, которое приблизительно равно 3,14159. Формула для вычисления π выглядит так: π = p/d. Согласно этой формуле, величина p равна πd, то есть длина окружности: p= πd. Поскольку d (диаметр) равен двум радиусам, то эту же формулу длины окружности можно записать как p=2πr.Рассмотрим применение формулы на примере простых задач:
Задача 1
У основания царь-колокола диаметр равен 6,6 метров. Какова длина окружности основания колокола?
- Итак, формула для вычисления окружности — p= πd
- Подставляем имеющееся значение в формулу: p=3,14*6,6= 20,724
Ответ: длина окружности основания колокола 20,7 метра.
Задача 2
Искусственный спутник Земли вращается на расстоянии 320 км от планеты. Радиус Земли – 6370 км. Какова длина круговой орбиты спутника?
- 1.Вычислим радиус круговой орбиты спутника Земли: 6370+320=6690 (км)
- 2.Вычислим длину круговой орбиты спутника по формуле: P=2πr
- 3.P=2*3,14*6690=42013,2
Ответ: длина круговой орбиты спутника Земли 42013,2 км.
Способы измерения длины окружности
Вычисление длины окружности на практике используется не часто. Причиной тому приблизительное значение числа π. В быту для поиска длины круга используют специальный прибор – курвиметр. На окружности отмечают произвольную точку отсчета и ведут от нее прибор строго по линии, пока опять не дойдут до этой точки.
Как найти длину окружности? Нужно просто держать в голове незамысловатые формуля для вычислений.
Решение варианта СтатГрад 31.01.23 ОГЭ 2023 Математика
Решение и ответы заданий варианта МА2290301 СтатГрад 31 января ОГЭ 2023 по математике. ГДЗ профиль для 9 класса. Решебник для 9 класса. Ответы с решением. Полный разбор всех заданий.
ГДЗ профиль для 9 класса. Решебник для 9 класса. Ответы с решением. Полный разбор всех заданий.
Все материалы получены из открытых источников и публикуются после окончания тренировочного экзамена в ознакомительных целях.
ЧАСТЬ 1
Задание 1-5.
Автомобильное колесо, как правило, представляет из себя металлический диск с установленной на него резиновой шиной. Диаметр диска совпадает с диаметром внутреннего отверстия в шине.
Для маркировки автомобильных шин применяется единая система обозначений. Например, 195/65 R15 (рис. 1). Первое число (число 195 в приведённом примере) обозначает ширину шины в миллиметрах (параметр B на рис. 2). Второе число (число 65 в приведённом примере) – процентное отношение высоты боковины (параметр H на рис. 2) к ширине шины, то есть 100·\frac{H}{B}.
Последующая буква обозначает тип конструкции шины. В данном примере буква R означает, что шина радиальная, то есть нити каркаса в боковине шины расположены вдоль радиусов колеса. {6}}.
{6}}.
Задание 9.
Решите уравнение 6x2 = 36x.
Если уравнение имеет больше одного корня, в ответе запишите меньший из корней.
Задание 10.
В магазине канцтоваров продаётся 100 ручек: 37 красных, 8 зелёных, 17 фиолетовых, остальные синие и чёрные, их поровну. Найдите вероятность того, что случайно выбранная в этом магазине ручка будет красной или чёрной.
Задание 11.
Установите соответствие между графиками функций и формулами, которые их задают.
ГРАФИКИ
ФОРМУЛЫ
1)y=-\frac{4}{x}
2)y=\frac{4}{x}
3)y=\frac{1}{4x}
В таблице под каждой буквой укажите соответствующий номер.
Задание 12.
Центростремительное ускорение при движении по окружности (в м/с2) вычисляется по формуле a = ω2R, где ω – угловая скорость (в с–1), R – радиус окружности (в метрах). Пользуясь этой формулой, найдите радиус R, если угловая скорость равна 10 с–1, а центростремительное ускорение равно 54 м/с2. Ответ дайте в метрах.
Ответ дайте в метрах.
Задание 13.
Укажите решение системы неравенств
\begin{cases} x-5,2\ge 0, \\ x+4\le 10. \end{cases}
1) (–∞; 5,2] ∪ [6; +∞)
2) [5,2; +∞)
3) [6; +∞)
4) [5,2; 6]
Задание 14.
В ходе распада радиоактивного изотопа его масса уменьшается вдвое каждые 9 минут. В начальный момент масса изотопа составляла 400 мг. Найдите массу изотопа через 36 минут. Ответ дайте в миллиграммах.
Задание 15.
В треугольнике ABC известно, что AB = 7, BC = 8, AC = 13. Найдите cos∠ABC.
Задание 16.
Хорды AC и BD окружности пересекаются в точке P, BP = 10, CP = 8, DP = 12. Найдите длину отрезка AP.
Задание 17.
Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 25° и 30°. Найдите больший угол этого параллелограмма. Ответ дайте в градусах.
Ответ дайте в градусах.
Задание 18.
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.
Задание 19.
Какое из следующих утверждений верно?
1) Средняя линия трапеции равна полусумме её оснований.
2) Диагонали любого прямоугольника делят его на четыре равных треугольника.
3) Косинус острого угла прямоугольного треугольника равен отношению гипотенузы к прилежащему к этому углу катету.
В ответе запишите номер выбранного утверждения.
ЧАСТЬ 2
Задание 20.
Решите неравенство (x – 6)2 < √10(x – 6).
Задание 21.
Моторная лодка прошла против течения реки 77 км и вернулась в пункт отправления, затратив на обратный путь на 2 часа меньше, чем на путь против течения. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 4 км/ч. {2}-8x+14 \:\:при \:\:x\ge 3,\\ x-2 \:\:при \:\:x\lt 3.\end{cases}
{2}-8x+14 \:\:при \:\:x\ge 3,\\ x-2 \:\:при \:\:x\lt 3.\end{cases}
Определите, при каких значениях m прямая y = m имеет с графиком ровно две общие точки.
Задание 23.
Отрезки AB и CD являются хордами окружности. Найдите расстояние от центра окружности до хорды CD, если AB = 40, CD = 42, а расстояние от центра окружности до хорды AB равно 21.
Задание 24.
Известно, что около четырёхугольника ABCD можно описать окружность и что продолжения сторон AD и BC четырёхугольника пересекаются в точке K. Докажите, что треугольники KAB и KCD подобны.
Задание 25.
На стороне BC остроугольного треугольника ABC как на диаметре построена полуокружность, пересекающая высоту AD в точке M, AD = 15, MD = 12, H – точка пересечения высот треугольника ABC. Найдите AH.
Источник варианта: СтатГрад/statgrad.org.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 2
Количество оценок: 2
Оценок пока нет. Поставь оценку первым.
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
- Запись опубликована:31.01.2023
- Рубрика записи+ Типовые экзаменационные варианты ОГЭ
- Автор записи:Andrei Maniakin
Длина окружности — определение, формула, примеры, факты
Что такое длина окружности?
Ежедневно мы видим множество круглых объектов, таких как монеты, пуговицы, настенные часы, колеса и т. д. Граница любого круглого объекта имеет большое значение в математике.
Давайте узнаем значение длины окружности на примере из жизни. Предположим, мальчик гуляет по круглому парку и завершает один круг. Расстояние, пройденное им, равно окружности круглого парка.
Родственные игры
Окружность круга: Определение
Окружность — это длина границы круга. Он также известен как «периметр» круга. Поскольку он представляет собой длину, он измеряется в таких единицах длины, как футы, дюймы, сантиметры, метры, мили или километры.
Он также известен как «периметр» круга. Поскольку он представляет собой длину, он измеряется в таких единицах длины, как футы, дюймы, сантиметры, метры, мили или километры.
Если мы разрежем круг и проведем прямую линию, длина этой линии даст нам длину окружности.
Давайте повторим несколько важных терминов, связанных с окружностями, чтобы понять, как рассчитать длину окружности.
Связанные листы
Диаметр окружности
Диаметр — это прямая линия, проходящая через центр и делящая окружность пополам. Обе его конечные точки лежат на окружности окружности.
Радиус окружности
Все точки на границе окружности находятся на одинаковом расстоянии от ее центра. Радиус — это расстояние от центра круга до любой точки на окружности круга . Это половина длины диаметра.
Как найти длину окружности с помощью нити?
Как правило, внешнюю длину многоугольников (квадратных, треугольных, прямоугольных и т. д.) можно рассчитать с помощью масштаба или линейки, но этого нельзя сделать для кругов из-за их изогнутой формы.
д.) можно рассчитать с помощью масштаба или линейки, но этого нельзя сделать для кругов из-за их изогнутой формы.
Тогда как мы можем найти длину окружности или как найти периметр окружности ? Один из способов — использовать нить. Обратите внимание, что вычисление периметра круга такое же, как вычисление его окружности.
Шаг 1: Возьмите нить и оберните ее вокруг круглого объекта, который вы хотите измерить.
Шаг 2: Отметьте начальную и конечную точки резьбы.
Шаг 3: С помощью линейки измерьте длину нити от начальной до конечной точки. Это даст вам длину окружности.
Хотя этот метод дает нам только оценку, нам нужно использовать формулу длины окружности для получения более точных результатов. То же самое обсуждается в следующем разделе.
Какое отношение длины окружности к диаметру?
Отношение длины окружности к диаметру любого круга является константой. Постоянное значение называется пи (обозначается π). Пусть С — длина окружности, а d — ее диаметр. Тогда
Постоянное значение называется пи (обозначается π). Пусть С — длина окружности, а d — ее диаметр. Тогда
C/d $=$ π
Для всех кругов, независимо от того, малы они или велики, это отношение остается постоянным. Приблизительное значение π равно 3,14 или 227.
Формула длины окружности
Мы только что узнали, что:
Окружность (C) / Диаметр (d) $= 3,14159$
Или,
C/d $=$ π
$ πd … длина окружности с использованием диаметра
Это дает нам формулу для длины окружности , когда задан диаметр.
Также мы знаем, что диаметр окружности в два раза больше радиуса
или, d $= 2$r
Таким образом, заменив значение d в приведенной выше формуле, мы получим:
C $=$ π(2r)
или C $= 2$ πr … длина окружности с использованием радиуса
Следовательно, $=0 окружности окружности24 уравнение 90 πр.
Пример 1: Если радиус окружности равен 7 единицам, то длина окружности будет равна
$2 \times$ π $\times 7 = 2 \times 3,14159 \times 7$ $ единиц
Пример 2: Предположим, что диаметр круга равен 12 футам. Затем мы можем использовать формулу πd для вычисления длины окружности.
Окружность $=$ πd $= 3.14159 \times 12 = 37.69$ футов
Вывод
Теперь вы знаете как вычислить длину окружности если вы знаете ее радиус или диаметр!
Поскольку длина окружности определяет длину границы круга, она служит многим практическим целям. Решение приведенных практических задач поможет вам лучше усвоить понятие длины окружности. Удачи!
Решенные примеры
1. Какова длина окружности диаметром 14 футов? Используйте № $ = 3,14 $ .
Решение:
Дано, диаметр (D) = 14 футов
Окружность круга = πd
= 3,14 × 14 футов
= 43,96 футов
2. Радиус из круга. составляет 6 дюймов. Какова окружность круга? Используйте π = 3,14.
Радиус из круга. составляет 6 дюймов. Какова окружность круга? Используйте π = 3,14.
Решение
Дано, радиус (r)$= 6$ дюймов
Длина окружности (c)$= 2$πr
$= 2 \times 3.14 \times 6$ дюймов
$= 37,68$ дюймов
3. Длина окружности 100 футов. Найдите его диаметр . Используйте π $= 3,14$ .
Решение:
Применение формулы:
Окружность (C) $ = $ πd
100 футов $ = 3,14 \ Times $ D
D $ = 100 $ FEET / 3,14
D $ = 31,85 $ футов
Следовательно, d $= 31,85$ футов
4. Длина окружности равна 120 м. Найдите его радиус. Используйте № $ = 3,14 $ .
Решение:
. $= 603,14$
Следовательно, r $= 19,11$ м
5. Если диаметр круга равен 15 милям, какова будет длина его границы?
Решение:
Длина границы круга равна длине окружности.
Итак, давайте сначала найдем длину окружности.
Дано, диаметр (d) $= 15$ см
Окружность (C) $=$ πd $= 3,14 \times 15$ см $= 47,1$ см
Практические задачи
1
Периметр квадрата провод 25 дюймов. Та же проволока сгибается, образуя круг. Найдите радиус образовавшейся окружности.
2,55 дюйма
3,98 дюйма
4,51 дюйма
5,25 дюйма
Правильный ответ: 3,98 дюйма
Периметр квадрата = общая длина провода $=$ длина окружности круга.
Следовательно, длина окружности (C) $=$ 25 дюймов.
Применение формулы:
C $=$ $2πr$
25 дюймов $= 2 \times 3,14 \times$ r
25 дюймов $= 6,28 \times$ r
r $= 25/6,28$
r $= 3,98$ дюймы
2
Диаметр велосипедного колеса 7 дюймов. Сколько раз должно повернуться колесо, чтобы пройти расстояние 110 футов? Возьмем π $=\frac{22}{7}$
500 раз
600 раз
5 раз
60 раз
Правильный ответ: 60 раз
Окружность колеса даст нам расстояние, пройденное колесом за один оборот. Итак, сначала вычислим длину окружности.
Итак, сначала вычислим длину окружности.
Дано, диаметр (d) $=$ 7 дюймов
Окружность $=$ πd
$= 22/7 \times 7$
$= 22$ дюймов
Значит, расстояние, пройденное колесом за один оборот $= 22$ дюймы
Общее расстояние, которое необходимо преодолеть $= 110$ футов $= (110 х 12)$ дюймов $= 1320$ дюймов
Следовательно, нет. необходимое количество оборотов$= 1320/22 = 60$
3
Круглая клумба имеет диаметр 20 футов. Найдите стоимость ограждения клумбы из расчета $10$ за фут. Возьмем $\pi$ = 3,14.
$\$$228
$\$$528
$\$$628
$\$$728
Правильный ответ: $\$$628
Диаметр клумбы (d) $=$ 20 футов F
Круглая клумба относится к границе круга, т. е. окружности круга.
Окружность клумбы $=$ πd
$= 3,14 \times 20$ м $= 62,8$ футов
Теперь стоимость ограждения $=$ $\$$10 за м
Итак, стоимость ограждения $62,8$ футов $ = 62,8 \times$ $\$$10 $=$ $\$$628
4
Разница между длиной окружности и диаметром составляет 10 футов.
 Найдите его радиус. Возьмем π $= 3,14$.
Найдите его радиус. Возьмем π $= 3,14$.1,33 фута
2,33 фута
3,33 фута
4,33 фута
Правильный ответ: 2,33 фута
Дано: длина окружности – диаметр $=$ 10 футов
Мы знаем, что:
Окружность $= 2$πr
Диаметр $= 2$r
Итак, $2$πr $-$ $2$r $= 10$ футов
$2$r$(\text{π}$ $- $ $1) = 10$ футов
$2$r $(3,14$ $-$ $1) = 10$ футов
$2$r $\times 2,14 = 10$ футов
r = 10 / 4,28
r = 2,33 фута
5
Соотношение длин двух окружностей 4:5. Найдите отношение их радиусов.
4:5
5:4
2:3
3:2
Правильный ответ: 4:5
Мы знаем, что длина окружности равна $2$πr.
Предположим, что радиус первого круга равен R₁, а радиус второго круга равен R₂.
Итак,
Окружность 1-го круга $= 2$πR₁
Окружность 1-го круга $= 2$πR₂
Отношение $= \frac{2πR_1}{2πR_2} = \frac{4}{5}$
Отмена $2$π из обоих отношения,
$\frac{R_1}{R_2}= \frac{4}{5}$
Следовательно, отношение двух радиусов равно 4:5.
Часто задаваемые вопросы
В чем разница между сферой и кругом?
Круг — это двухмерная фигура, тогда как сфера — трехмерный твердый объект. Следовательно, у круга нет объема, а у шара есть.
Какова окружность Земли?
Окружность Земли составляет около 24 901 мили.
Какова площадь круга?
Площадь круга – это пространство, занимаемое границей круга. Это
По какой формуле вычисляется длина окружности полукруга?
Длина окружности полукруга может быть вычислена как C $=$ πr $+$ d.
В чем разница между длиной окружности и площадью круга?
Окружность — это длина внешней границы круга, а площадь — это общее пространство, ограниченное этой границей.
Статьи по теме Ссылка
Окружность
Сфера
Периметр
Легко узнать, как найти окружность
Главная / 7 класс / Легко Научитесь находить длину окружности
Вот как можно измерить длину окружности Длина окружности — это общий периметр или ребро окружности. Вы можете измерить окружность окружности, используя либо радиус, либо диаметр. Диаметр в два раза больше радиуса, или радиус равен половине диаметра. Формула, которую вы используете для нахождения окружности круга, зависит от того, знаете ли вы радиус или диаметр. Если вы знаете радиус, вы будете использовать формулу, умноженную на два числа пи, умноженное на радиус. Если вы знаете диаметр, вы будете использовать пи, умноженное на диаметр. При упрощении нужно соблюдать порядок действий.
Вы можете измерить окружность окружности, используя либо радиус, либо диаметр. Диаметр в два раза больше радиуса, или радиус равен половине диаметра. Формула, которую вы используете для нахождения окружности круга, зависит от того, знаете ли вы радиус или диаметр. Если вы знаете радиус, вы будете использовать формулу, умноженную на два числа пи, умноженное на радиус. Если вы знаете диаметр, вы будете использовать пи, умноженное на диаметр. При упрощении нужно соблюдать порядок действий.
Общий базовый стандарт: 7.G.5
Связанные темы: Площадь круга, площадь полуокружности, длина окружности полукруга, дополнительные углы, дополнительные углы, вертикальные углы : Дом, 7 класс
Что такое формула длины окружности?
Первая формула для длины окружности C=(pi)(диаметр). Вторая формула для окружности круга: C=2(pi)(r). Окружность круга – это вся внешняя граница или край круга. Вы можете определить окружность круга, используя либо радиус, либо диаметр. Диаметр в два раза больше радиуса пролета. Уравнение, которое вы используете для определения длины окружности, зависит от того, знаете ли вы радиус или диаметр. Если вы знаете радиус, вы будете использовать уравнение, умноженное на два числа пи, умноженное на радиус. Если вы знаете диаметр, вы будете использовать пи, умноженное на диаметр.
Вы можете определить окружность круга, используя либо радиус, либо диаметр. Диаметр в два раза больше радиуса пролета. Уравнение, которое вы используете для определения длины окружности, зависит от того, знаете ли вы радиус или диаметр. Если вы знаете радиус, вы будете использовать уравнение, умноженное на два числа пи, умноженное на радиус. Если вы знаете диаметр, вы будете использовать пи, умноженное на диаметр.
- Если вы знаете радиус, вы умножите его на пи, умноженное на два.
- Если вы знаете диаметр, вы умножите диаметр на число пи.
- Дважды проверьте свое решение и убедитесь, что оно имеет правильные единицы измерения.
Тест на определение длины окружности Посмотрите видеообъяснение нашего рабочего листа 9 для определения длины окружности.0249
Посмотрите наше бесплатное видео о том, как найти длину окружности .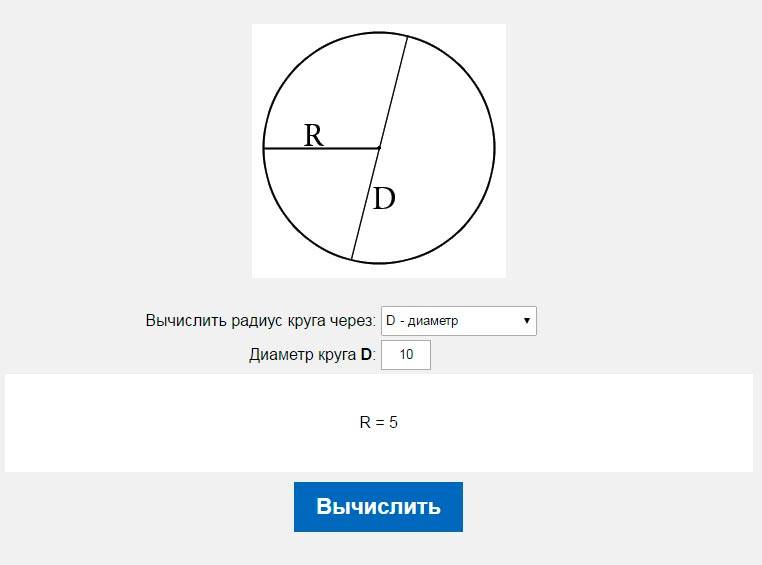 В этом видео показано, как решать задачи из нашего бесплатного рабочего листа «Окружность круга», который вы можете получить, отправив свое электронное письмо выше.
В этом видео показано, как решать задачи из нашего бесплатного рабочего листа «Окружность круга», который вы можете получить, отправив свое электронное письмо выше.
Посмотрите бесплатное видео об окружности на YouTube здесь: Видео о окружности
Расшифровка видео:
Это видео о том, как найти длину окружности. Вы можете получить рабочий лист, использованный в этом видео, бесплатно, нажав на ссылку в описании ниже.
При нахождении длины окружности обычно есть две формулы, которые вы должны использовать на основе информации, предоставленной вам в задаче. Определение того, какую формулу окружности вы используете, зависит от того, дан ли вам радиус или диаметр. Теперь радиус — это просто расстояние от середины круга до внешнего края круга, а диаметр — это расстояние от одного края до круга через середину круга до другого края. Если вам дан радиус, формула для длины окружности будет выглядеть так: c равно 2 пи, умноженным на радиус, где r — радиус.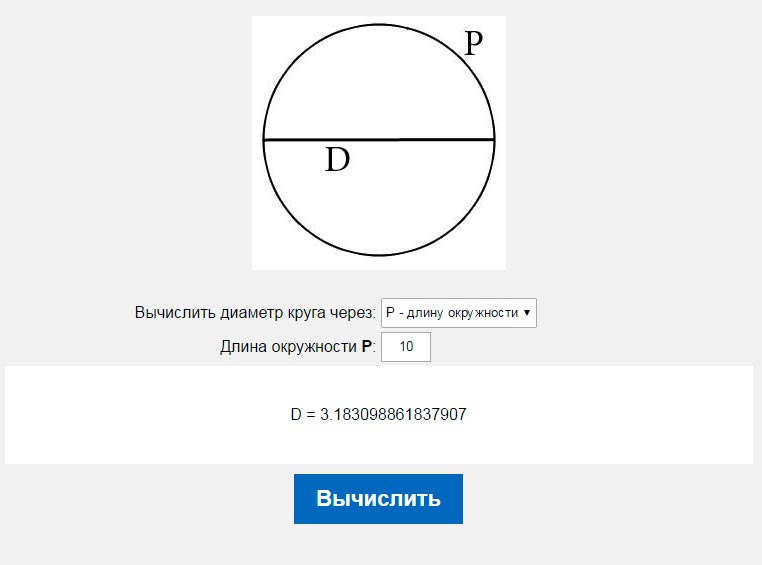 И если вам дан диаметр для окружности круга, вы собираетесь сделать длину окружности равной пи, умноженной на диаметр. В случае этого примера, который дает нам радиус, мы возьмем 15, потому что 15 сантиметров — это радиус, и мы подставим его вместо r. Ваша формула теперь будет 2 пи умножить на 15, потому что 15 — это радиус. Затем вы берете свою формулу окружности и умножаете 2 на 15, и вы получаете 417,12 сантиметра для длины окружности.
И если вам дан диаметр для окружности круга, вы собираетесь сделать длину окружности равной пи, умноженной на диаметр. В случае этого примера, который дает нам радиус, мы возьмем 15, потому что 15 сантиметров — это радиус, и мы подставим его вместо r. Ваша формула теперь будет 2 пи умножить на 15, потому что 15 — это радиус. Затем вы берете свою формулу окружности и умножаете 2 на 15, и вы получаете 417,12 сантиметра для длины окружности.
Наш второй пример дает нам диаметр. Диаметр в данном случае равен 3 футам, поэтому мы берем 3 и подставляем вместо d. Мы умножим число пи на 3, а затем возьмем формулу длины окружности и решим число пи, умноженное на 3, что даст вам 9,42 фута. Основное различие в решении того, что является окружностью круга, заключается в использовании либо формулы, включающей радиус, либо формулы, включающей диаметр, в зависимости от различий, которые могут дать вам задачи.
Давайте решим пару практических задач на листе окружности круга. Первая задача на нашем рабочем листе окружности круга дает нам 5 дюймов для радиуса.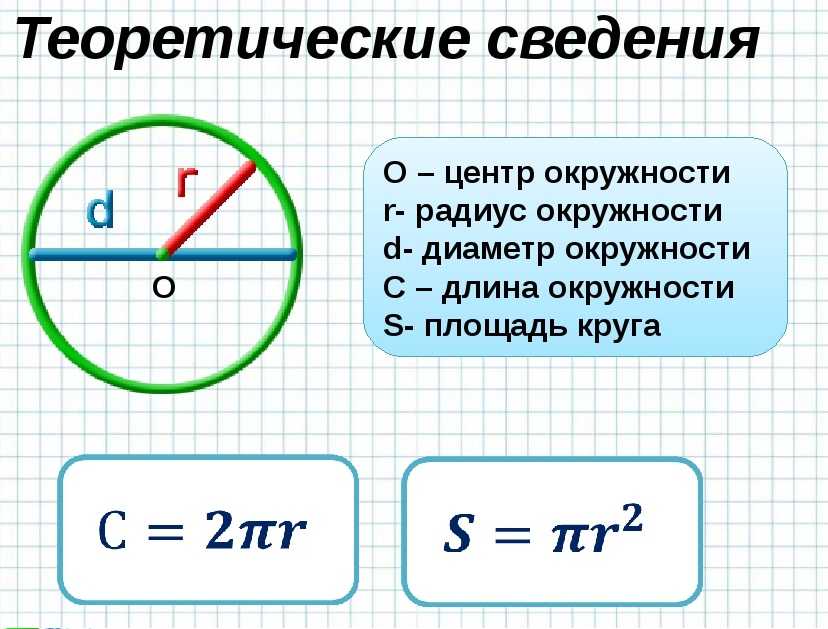 Я знаю, что это радиус, потому что он проходит от центральной точки круга до внешнего края. Формула, которую мы собираемся использовать, такова: длина окружности равна 2 пи, умноженным на радиус. В случае этой проблемы я знаю, что радиус составляет 5 дюймов. Мы знаем, что r равно 5. Возьмем радиус 5 и подставим его вместо r. Теперь наша формула: длина окружности равна 2 пи умножить на 5, потому что радиус был равен 5, а затем, когда вы вычисляете длину окружности, умноженную на 2 пи умножить на 5, вы получите 31,42 дюйма для длины окружности.
Я знаю, что это радиус, потому что он проходит от центральной точки круга до внешнего края. Формула, которую мы собираемся использовать, такова: длина окружности равна 2 пи, умноженным на радиус. В случае этой проблемы я знаю, что радиус составляет 5 дюймов. Мы знаем, что r равно 5. Возьмем радиус 5 и подставим его вместо r. Теперь наша формула: длина окружности равна 2 пи умножить на 5, потому что радиус был равен 5, а затем, когда вы вычисляете длину окружности, умноженную на 2 пи умножить на 5, вы получите 31,42 дюйма для длины окружности.
Вторая задача, которую мы собираемся решить на нашем рабочем листе окружности круга, номер четыре, на этот раз задача дает нам диаметр. Я знаю, что это диаметр, потому что он проходит от одной стороны круга до другой через середину, так что это вся длина. Это будет диаметр, потому что я знаю, что это диаметр. Я знаю, что формула окружности равна пи, умноженному на диаметр. В данном случае диаметр равен 22 сантиметрам, поэтому мы берем 22 и подставляем вместо диаметра.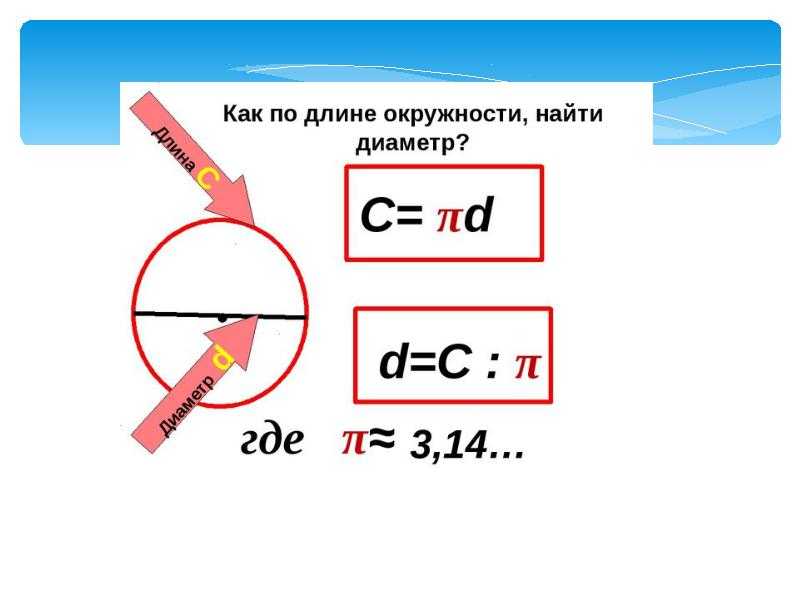

 Так вот ту хорду, которая через него проходит, тоже называют диаметром.
Так вот ту хорду, которая через него проходит, тоже называют диаметром.