Решение уравнений вида х+15 = 68:2. Видеоурок. Математика 4 Класс
С помощью данного урока вы научитесь решать усложненные уравнения. Сможете без труда понять, как упростить уравнение перед непосредственным поиском корня. Также повторите и вспомните, что такое уравнения. Узнаете, что такое корень уравнения, как его искать. Научитесь решать и, главное, проверять свои вычисления. На уроке вы подробно познакомитесь с пошаговой инструкцией решения усложненных уравнений. Решите много интересных заданий и выучите важные определения.
Уравнение – это равенство с неизвестным числом. Неизвестное число обозначают латинской буквой.
Рассмотрите записи (рис. 1) и укажите, сколько на рисунке уравнений.
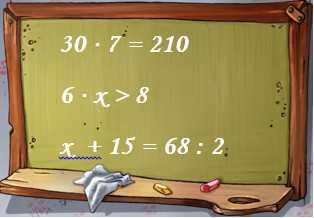
Рис. 1. Записи (Источник)
Решение: 1. Проанализируем каждую запись на доске (рис. 1). Первая строка – это равенство без неизвестных – пример. Вторая строка – неравенство. Именно в третьей строке есть уравнение, потому что только в этой записи есть равенство с неизвестным числом и данное число обозначено латинской буквой. Можно сделать вывод о том, что на рисунке 1 только одно уравнение.
Решить уравнение – это найти значение неизвестного, при котором равенство будет верным (или доказать, что таких значений не существует).
Решите уравнение (рис. 1).
Решение: 1. Сумма неизвестного числа и пятнадцати равна частному чисел шестьдесят восемь и два. Так как в этом уравнении сумма представлена числовым выражением, вначале упростим выражение и найдем значение частного. Теперь для того, чтобы найти неизвестное слагаемое, необходимо от суммы отнять известное слагаемое. После того как найдем значение неизвестного – корня уравнения, необходимо выполнить проверку – подставить значение корня в уравнение и вычислить значение, полученные результаты сравнить. Если результаты совпадают, уравнение решено верно. Если результаты не совпадают, необходимо решить уравнение сначала.
Решите уравнения (рис. 2).

Рис. 2. Уравнения (Источник)
Решение: 1. В первом уравнении вначале можно упростить его правую часть – найти разность. Потом найти неизвестное слагаемое и выполнить проверку.
2. Для того чтобы решить второе уравнение, необходимо найти сумму в правой части. Потом определить неизвестное слагаемое и выполнить проверку.
Список литературы
- Математика. 4 класс. Учеб. для общеобразоват. учреждений. В 2 ч. Ч. 1 / [М.И. Моро, М.А. Бантова, Г.В. Бельтюкова и др.] – 8-е изд. – М.: Просвещение, 2011. – 112 с. : ил. – (Школа России). Истомина Н.Б. Математика. 4 класс. – М.: Ассоциация ХХІ век.
- Петерсон Л.Г. Математика, 4 класс. – М.: Ювента.
Домашнее задание
- Математика. 4 класс. Учеб. для общеобразоват. учреждений. В 2 ч. Ч. 1 / [М.И. Моро, М.А. Бантова, Г.В. Бельтюкова и др.] – 8-е изд. – М.: Просвещение, 2011, ст. 64 № 310.
- Что такое уравнение?
- Что значит решить уравнение? Что такое корень уравнения?
- * Решите такие уравнения.
а) б) в)
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал Festival.1september.ru (Источник).
- Интернет-портал School-172.my1.ru (Источник).
- Интернет-портал Mathematics-tests.com (Источник).
interneturok.ru
9 х (7512 – а) = 34722 | ||
1 этап | ||
1 | Пронумеровать порядок действий | 2 1 9 х (7512 – а) = 34722 |
2 | Назвать компоненты 2 действия данного уравнения | 9 х (7512 – а) = 34722 1 множитель 2 множитель произведение |
3 | Определить компонент с неизвестным | Компонент с неизвестным – 2 множитель. |
4 | Вспомнить правило нахождения неизвестного компонента | Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель. |
5 | Применить правило и найти неизвестный компонент | 7512 – а = 34722 : 9 |
6 | Сделать вычисление, записать ответ. | 7512 – а = 3858 |
2 этап | ||
7 | Назвать компоненты действия данного уравнения | 7512 – а = 3858 Уменьшаемое вычитаемое разность |
8 | Определить неизвестный компонент | Неизвестный компонент – вычитаемое. |
9 | Вспомнить правило нахождения неизвестного компонента | Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность |
10 | Применить правило и найти неизвестный компонент | а = 7512 — 3858 |
11 | Сделать вычисление Записать корень уравнения | а = 3654 |
12 | Сделать подстановку и проверку | 9 х (7512 – 3654) = 34722 34722 = 34722 |
nsportal.ru
Урок математики по теме «Решение уравнений» (4-й класс)
Разделы: Начальная школа
Цель
: Рассмотреть практические способы решения уравнений, требующих выполнения более одного арифметического действия.Оборудование урока: компьютерная презентация устного счета, карточки с уравнениями, карточки трех ступеней для самостоятельной работы над задачами, кубик обратной связи
Ход урока
1. Оргмомент
Проверка готовности к уроку. В тетрадях записывается число, классная работа.
2. Устный счет (компьютерная презентация, слайд №1)
Игра «Соревнование улиток»
Ваш любимый пес Алик на соревновании улиток. Две улитки должны подняться до вершины горы. Кто же из них окажется первой? Наша с вами улитка под №1 слева. Улитка делает шаг, только если мы правильно найдем значение выражения.
Вы готовы?
Сигнал к старту уже прозвучал. Повторяем порядок действий и называем правильные значения выражений.
(122 + 18) : 70 = 2
(64 : 8 + 20) : 7 = 4
20 · (26 + 14) : 100 = 8
1 · (30 + 2) – 4 · 4 = 16
5 · 4 + 12 = 32
(400 – 300) – 36 = 64
У нас получился ряд чисел.
2, 4, 8, 16, 32, 64
Какую закономерность в составлении этого ряда заметили? (каждое следующее число увеличено в два раза)
Продолжите этот ряд чисел и назовите не менее трех следующих чисел. (128, 256, 512…)
Молодцы! Мы решали все правильно, поэтому наша улитка на вершине горы.
За каждым числом зашифрована буква. Перевернем их и прочитаем тему сегодняшнего урока.
2 4 8 16 32 64 128 256 512
У Р А В Н Е Н И Е
Что называется уравнением?
Что называется корнем уравнения?
Что значит решить уравнение?
3. Решение простых уравнений. Подготовка к введению нового материала.
На магнитной доске в произвольном порядке карточки с уравнениями.
На какие группы можно разделить все эти уравнения? (уравнения распределяются в 3 столбика)
1) 7000 – х = 2489
7000 – х = 3489
7000 – х = 1689
Почему мы выделили эти уравнения в первую группу? (простые уравнения с одинаковым уменьшаемым) Можем мы их решить ?
Найдите среди них уравнение с наибольшим корнем и решите его (один ученик у доски)
2) 71 : х = 20 + 7
х : 3 = 16 + 11 ( это уравнения, в правой части которых выражение)
Можем ли мы решить уравнения второго столбика?
Решите любое из уравнений, но замените в правой части сумму на разность. Корень уравнения при этом должен остаться прежним. (два ученика у доски)
3) ( 490 – х ) – 250 = 70
Посмотрите на оставшееся уравнение. Легко ли нам его решить? Почему?
4. Работа над новым материалом. (фронтальная беседа с классом, в ходе которой рассматривается решение уравнения)
( 490 – х ) – 250 = 70
490 – х = 70 + 250
490 – х = 320
х = 490 – 320
х = 170
( 490 – 170 ) – 250 = 70
70 = 70
Ответ: 70
5. Закрепление.
1) Решение уравнения (один из сильных учеников у доски)
5 · а + 500 = 4500 : 5
5 · а + 500 = 900
5 · а = 900 – 500
5 · а = 400
а = 400 : 5
а = 80
5 · 80 + 500 = 900
900 = 900
Ответ: 80
2) № 399
Решите уравнения.
а + 156 = 17 ∙ 20 (1604 – у) – 108 = 800
252 : 36 ∙ х = 560 103300 : (х + 297) = 25 ∙2
Мы решили два новых сложных уравнения. Посмотрите на уравнения, которые перед вами. Все ли они сложные? Какое уравнение лишнее? Почему? Остальные – в левой части выражение в несколько действий. Найдите среди них с таким порядком действий, которое уже встречалось сегодня.
(1604 – у) – 108 = 800
1604 – у = 800 + 108
1604 – у = 908
у = 1604 – 908
у = 696
(1604 – 696) – 108 = 800
800 = 800
Ответ: 696
Уравнение решают в парах. Один ученик на развороте доски для последующей проверки.
6. Решение задачи
Самостоятельная работа по карточкам 3 ступеней. Выполнив задание первой ступени, ученик переходит к выполнению задания второй ступени, затем третьей.( различные способы дифференцированной работы)
| 1 ступень | 2 ступень | 3 ступень |
| Школьники должны были высадить 25700 саженцев деревьев. После того, как они высадили часть саженцев, им осталось посадить еще12350 деревьев. Сколько деревьев они уже высадили? Реши задачу, составив уравнение |
Измени задачу так, чтобы она решалась уравнением, в правой части которого было бы выражение. Запиши это уравнение и реши его. |
Школьники должны были высадить 25700 саженцев деревьев. После того, как они высадили несколько саженцев липы и 8580 кленов, им осталось высадить 12350саженцев. Сколько лип они уже посадили? |
Проверка фронтальная
1) 25700 – х = 12350
х = 25700 – 12350
25700 – 13350 = 12350
12350 = 12350
Ответ: 13350 саженцев.
2) 25700 – х = 12000 + 350
3) 25700 – (х + 8580) = 12350
х + 8580 = 25700 – 12350
х + 8580 = 13350
х = 13350 – 8580
х = 4770
25700 – (4770 + 8580) =12350
12350 = 12350
Ответ: 4770 лип.
4) А какое еще уравнение можно было составить?
(25700 – х) – 8580 = 12350
Мы решили три задачи, составив три уравнения. Какое уравнение отнесем к сложным? Почему?
7. Домашнее задание.
Рассмотреть, как решались уравнения в учебнике на стр. 106 и решить уравнение в тетради на печатной основе № 44 (а).
Решить задачу № 47. Дополнительное задание: какие еще вопросы можно поставить к этой задаче?
8. Итог урока.
Какие уравнения учились решать на уроке?
Трудно было?
24.02.2009
Поделиться страницей:urok.1sept.ru
4 класс. Математика. Решение уравнений. — Уравнение с неизвестным слагаемым.
Комментарии преподавателя
Равенство, содержащее неизвестное число, называется уравнением. Неизвестное число обозначено латинской буквой. Например:
Решить уравнение – это значит найти такое значение буквы, чтобы равенство стало верным (или доказать, что таких значений не существует).
В уравнении решением является , так как сумма чисел , то есть получилось верное равенство.
Число называют корнем уравнения.
Чтобы найти корень уравнения, надо знать, как связаны компоненты действия между собой.
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
С помощью данного урока вы научитесь решать усложненные уравнения. Сможете без труда понять, как упростить уравнение перед непосредственным поиском корня. Также повторите и вспомните, что такое уравнения. Узнаете, что такое корень уравнения, как его искать. Научитесь решать и, главное, проверять свои вычисления. На уроке вы подробно познакомитесь с пошаговой инструкцией решения усложненных уравнений. Решите много интересных заданий и выучите важные определения.
Рассмотрите записи (рис. 1) и укажите, сколько на рисунке уравнений.
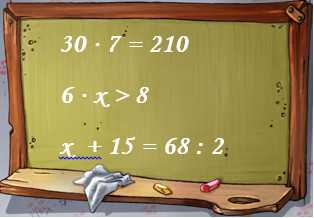
Рис. 1. Записи (Источник)
Решение: 1. Проанализируем каждую запись на доске (рис. 1). Первая строка – это равенство без неизвестных – пример. Вторая строка – неравенство. Именно в третьей строке есть уравнение, потому что только в этой записи есть равенство с неизвестным числом и данное число обозначено латинской буквой. Можно сделать вывод о том, что на рисунке 1 только одно уравнение.
Решить уравнение – это найти значение неизвестного, при котором равенство будет верным (или доказать, что таких значений не существует).
Решите уравнение (рис. 1).
Решение: 1. Сумма неизвестного числа и пятнадцати равна частному чисел шестьдесят восемь и два. Так как в этом уравнении сумма представлена числовым выражением, вначале упростим выражение и найдем значение частного. Теперь для того, чтобы найти неизвестное слагаемое, необходимо от суммы отнять известное слагаемое. После того как найдем значение неизвестного – корня уравнения, необходимо выполнить проверку – подставить значение корня в уравнение и вычислить значение, полученные результаты сравнить. Если результаты совпадают, уравнение решено верно. Если результаты не совпадают, необходимо решить уравнение сначала.
Решите уравнения (рис. 2).

Рис. 2. Уравнения (Источник)
Решение: 1. В первом уравне&
www.kursoteka.ru
«Решение уравнений, содержащих несколько действий» (4 класс)
Решение уравнений, содержащих несколько действий
Уравнение – это равенство с переменной.
Для решения уравнения необходимо:
1. Определить порядок действий в уравнении
2 1 3 5 4
( 22 – У ∙ 2) : 5 + 30 : 6 = 7
2. Найти последнее действие. В нашем уравнении это сложение.
3. Определить название компонентов и результата действия как в простом уравнении
2 1 3 5 4
( 22 – У ∙ 2) : 5 30 : 6 = 7
Это 1 слагаемое 2 слаг. сумма
4. Определить место переменной. У – стоит на месте 1 слагаемого.
5. Вспомнить правило:
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое. Получается запись:
( 22 – У ∙ 2) : 5 = 7 — 30 : 6
(Находим значение выражения правой части)
( 22 – У ∙ 2) : 5 = 2
6. Теперь опять необходимо определить порядок действий.
2 1 3
( 22 – У ∙ 2) 5 = 2
Последнее действие – деление. (Игрик) У стоит перед знаком деления, значит,
( 22 – У ∙ 2) 5 = 2 — частное
делимое делитель
7. Вспомнить правило:
Чтобы найти неизвестное делимое, нужно частное умножить на делитель
22 – У ∙ 2 = 2 ∙ 5
22 – У ∙ 2 = 10
8. Опять расставить порядок действий.
2 1
22 – У ∙ 2 = 10 Последнее действие – вычитание.
уменьш. вычит. разность
Вспомнить правило…
У ∙ 2 = 22 — 10
У ∙ 2 = 12
9. Уравнение далее решать как простое.
Определить место переменной. Вспомнить правило
У = 12 : 2
У = 6 – Это корень уравнения.
Далее нужно проверить уравнение.
( 22 – 6 ∙ 2) : 5 + 30 : 6 = 7
7 = 7
Ответ: х = 6.
infourok.ru
Урок математики «Решение сложных уравнений» ( 4 класс)
Тема: Решение сложных уравнений.
Урок открытия нового знания.
Цель: актуализировать знания алгоритма решения сложных уравнений, познакомиться с алгоритмом решения сложных уравнений нового вида.
Задачи: 1) актуализировать знание порядка выполнения действий в выражениях, умение решать задачи при помощи уравнений; добиться усвоения алгоритма решения сложных уравнений;
2) УУД: — Познавательные: овладение основами логического и алгоритмического мышления;
Регулятивные: развитие умения читать и записывать информацию в виде различных математических моделей, планировать действия в соответствии с поставленной задачей;
Коммуникативные: сроить высказывания, аргументировано доказывать свою точку зрения;
Личностные: развитие навыков сотрудничества со сверстниками,
3) — воспитывать чувство товарищества.
Оборудование: презентация, конспект урока, компьютер, проектор.
Ход урока:
Мотивация (самоопределение) к учебной деятельности.
Труд и вера — вот твои доспехи,
И не бойся никаких задач.
Самый же надежный путь к успеху —
Сложный путь падений и удач.
На доске эпиграф: «С малой удачи начинается успех»
— Какое ключевое слово в этом высказывании? (УСПЕХ)
— Что необходимо для успешной работы на уроке?
-Я желаю Вам успешно поработать на уроке. Пожмите друг другу руки и пожелайте успеха.
Смело иди вперёд, не стой на месте.
Что не сделаешь один, сделаем вместе.
— Работать сегодня мы будем в парах. Вспомните правила работы в парах. (Прислушиваться к мнению соседа, работать дружно, помогать друг другу)
В конце урока каждый из вас оценит свою работу и работу партнёра по шкале достижений.
Комментарии:
На данном этапе урока происходит вовлечение учащихся в деятельность на личностно-значимом уровне. Формируются личностные УУД.
Перейдём к следующему этапу урока.
Актуализация и фиксирование индивидуального затруднения в пробном действии.
Приступим к работе. Посмотрите на доску и подумайте, почему так сгруппированы записи?
b – 45:5 500 • х=1500:3
a • (56 • 40) y • 10=1500:30
k: (1800:900) х+500 • 3=2000
(выражения с переменной) (уравнения)
— Какое задание можно дать к выражениям с переменной? (назвать порядок действий)
— Какое задание можно дать к уравнениям? (решить уравнения). Решите.
Комментарии:
На этапе актуализации идёт повторение изученного материала, необходимого для «открытия нового знания», и выявление затруднений в индивидуальной деятельности каждого учащегося. Формируются регулятивные УУД.
Выявление места и причины.
— Решение, какого уравнения вызвало затруднение? Почему?
— Какую учебную задачу поставите перед собой? (Научиться решать сложные уравнения нового вида)
Учитель использует побуждающий от проблемной ситуации диалог, происходит обсуждение затруднений. Дети учатся обнаруживать и формулировать учебную проблему, задачу совместно с учителем. Формируются регулятивные УУД.
Построение проекта выхода из затруднения (тема, цель, задачи, план, способ, средство)
— На какой вопрос предстоит ответить? (Как решать сложные уравнения нового вида?)
— Какова тема урока? (Решение сложных уравнений).
Составим план работы для выполнения задач:
— вспомнить, алгоритм решения сложного уравнения;
— определить способ решения сложных уравнений нового вида
-научиться решать сложные уравнения
— научиться применять умение решать сложные уравнения при решении задач
Комментарии:
Дети учатся определять цель учебной деятельности с помощью учителя и самостоятельно, искать средства её осуществления; составлять план выполнения задач, решения проблем поискового характера, выполнения проекта совместно с учителем. Формируются регулятивные УУД.
Реализация построенного проекта.
— Давайте решим сложное уравнение: х+500 • 3=2000
— Что нового в записи этого уравнения? (Левая часть уравнения записана в виде выражения).
— Какие есть предположения, как решить уравнение? (нужен алгоритм решения такого уравнения)
— Вы можете сразу его предложить? (Нет, не можем).
— Какая из схем может помочь решить уравнение?
•
__________________ ______________
• х х
— Какие есть предположения? (Дети выдвигают предположения, решают уравнение, затем делается общий вывод)
— Как проверить, правильно ли решено уравнение? (Посмотреть в учебнике, какой алгоритм решения такого вида сложных уравнений предлагают учёные-математики)
(Дети читают текст учебника, делают выводы)
Комментарии:
На данном этапе дети учатся добывать информацию различными способами: наблюдение, чтение, слушание .Происходит открытие нового знания. Формируются познавательные УУД.
Учатся доносить свою позицию до других (строить высказывания, пользуясь математической терминологией), слушать других, пытаться принимать другую точку зрения, быть готовым изменить свою точку зрения, при необходимости отстаивать свою точку зрения, аргументировать её.. Формируются коммуникативные УУД,
Первичное закрепление с проговариванием во внешней речи
(- Проговаривание нового знания)
— Сколько шагов должны выполнить, решая уравнение? (5 шагов)
Алгоритм:
1. Разбить выражения, записанные в одной или обеих частях уравнения, на части (расставить порядок действий). Определить неизвестный компонент.
2. Упростить выражение (если необходимо).
3. Решить простое уравнение, содержащее одно действие.
4. Выполнить проверку правильности решения.
5. Записать ответ.
(Решение уравнения с проговариванием) Цель: учиться применять новый алгоритм решения уравнений
Х – (560:4)=1880 y • (80:20)= 1800
Комментарии:
На данном этапе формируются познавательные УУД: использовать полученную информацию в деятельности, развитие мыслительных операций, решать задания по аналогии, используя алгоритм действий.
Физминутка
Самостоятельная работа в парах с самопроверкой по эталону.
— Запишите уравнения парами с равными корнями
Х+1800:3=2039 х • 40=800 х • (5 • 8)=800
Х-800 • 4=40 х+600=2 039 х -200=40
— Проверьте правильность выполнение задания (сверка по эталону).
— Можно ли выполнить это задание, не решая уравнений?
Комментарии:
На данном этапе дети учатся самостоятельно применять знания в новой ситуации. Формируются регулятивные УУД.
Каждый делает для себя вывод, что он уже умеет. Формируются личностные УУД (самоконтроль, самооценка, саморефлексия, способность к саморазвитию)
Включение в систему знаний повторение.
А) Решение уравнений изученного вида с.63 №6
Цель: учиться применять алгоритм при решении уравнений нового вида.
— При выполнении, каких заданий мы можем применять умение решать уравнения? (Решение задач). Потренируемся в решении задач при помощи уравнения.
С. 63 №7(б) учебник. Решение задачи при помощи уравнения. Проверка по образцу.
Цель: научиться решать задачи при помощи уравнения .
Комментарии:
На данном этапе предлагаются не только задания, при решении которых используется новый алгоритм, но и выполняются задания, в которых новое знание используется вместе с ранее изученным. Выполняются универсальные логические действия: анализ, синтез.
Дети учатся находить информацию в тексте задачи, выделять главное, применять новые знания в другой ситуации. Формируются познавательные УУД.
Рефлексия УД на уроке.
— Итак, над какой темой мы работали? Удалось ли решить поставленную задачу? Каким способом? Какие получили результаты? Что нужно сделать ещё?
— В чём испытывали трудности?
— Где можем применить новые знания? (При решении задач)
— Оцените работу вашего партнёра и себя на шкале достижений. Покажите друг другу результаты ваших оценок и поздравьте своих друзей с успешным окончанием работы.
— Я поздравляю Вас, вы поднялись ещё на одну ступеньку знаний вверх Молодцы. Спасибо за урок.
В диалоге с учителем дети учатся определять степень успешности выполнения своей работы и работы все, осознание своей УД. Понимать причины своего неуспеха и находить способы выхода из этой ситуации. Регулятивные УУД.
Домашнее задание (по выбору).
А) Решить задачу №7(в) с. 63 при помощи уравнения
Б) — Составить для партнёра в паре 2 два сложных уравнения
Комментарии:
Д/з включает в себя как репродуктивное задание, так и творческое, что позволяет вызвать у детей познавательный интерес. Формируются познавательные УУД,
infourok.ru
