Тренинг по теме «Сокращение дробей» (6 класс)
Макарова Т.П., ГБОУ СОШ № 618
Макарова Татьяна Павловна,
Учитель ГБОУ СОШ №618 г. Москвы
Контингент: 6 класс
Тема: Сокращение дробей.
Вид работы: Тренинг
Тренинг направлен на проверку знаний и умений учеников по теме «Сокращение дробей». Тренинг предназначен для учащихся 6 класса к учебнику Н.Я. Виленкин, В.И. Жохова и др. Учебник для 6 класса. – М.: Мнемозина, 2013. – 288с.
Цели: отработать умения и навыки по применению сокращения дробей для решения задач; развивать воображение, логическое мышление, внимание, навыки умственной и практической деятельности, самоконтроля, содействовать воспитанию интереса к предмету.
Тренинг содержит четыре варианта по восемь заданий в каждом. Полностью соответствует программным требованиям, может быть использован при проведении классно-урочного контроля.
Вариант 1
Вариант 2
1.Выберете те из дробей , которые являются несократимыми
1.Выберете те из дробей , которые являются несократимыми.
2. Сократите дробь:
а)
б)
в)
г)
2. Сократите дробь:
а)
б)
в)
г)
3. Выполните действия, сократив, полученную дробь:
а)
б)
3. Выполните действия, сократив, полученную дробь:
а)
б)
4. Сократите дробь и исключите из каждой из них целую часть:
4. Сократите дробь и исключите из каждой из них целую часть: .
5.Какую часть развернутого угла составляет угол, градусная мера которого равна 840.
5. Какую часть прямого угла составляет угол, градусная мера которого равна 48 0
6. Сократите:
6. Сократите:
7. Какую часть часа составляют 50 минут ?
7. Какую часть минуты составляют 48 секунд ?
8. Запишите десятичную дробь в виде обыкновенной дроби и результат сократите 0,456.
8. Запишите десятичную дробь в виде обыкновенной дроби и результат сократите 0,425.
Вариант 3
Вариант 4
1.Выберете те из дробей , которые являются несократимыми
1.Выберете те из дробей , которые являются несократимыми.
2. Сократите дробь:
а)
б)
в)
г) .
2. Сократите дробь:
а)
б)
в)
г) .
3. Выполните действия, сократив, полученную дробь:
а)
б)
3. Выполните действия, сократив, полученную дробь:
а)
б)
4. Сократите дробь и исключите из каждой из них целую часть:
4. Сократите дробь и исключите из каждой из них целую часть:
5.Какую часть развернутого угла составляет угол, градусная мера которого равна 270.
5. Какую часть прямого угла составляет угол, градусная мера которого равна 720
6. Сократите:
6. Сократите:
7. Какую часть часа составляют 45 минут ?
7. Какую часть минуты составляют 28 секунд ?
8. Запишите десятичную дробь в виде обыкновенной дроби и результат сократите 0,256.
8. Запишите десятичную дробь в виде обыкновенной дроби и результат сократите 0,632.
infourok.ru
Тест по математике для 6 класса «Сокращение дробей»
Вариант 11. Сократите дробь на НОД числителя и знаменателя.
а) б) в) г) дробь несократимая.
2. Какие из дробей равны дроби ?
а) только б) только в) только г) .
3. Запишите частное 50:175 в виде дроби и сократите её.
а) б) в)
4. Найдите значение m в равенстве
а) 288; б) 2; в) 144; г) 72.
5. Сократите дробь
а) б) в) г)
6. Какую дробь можно привести к знаменателю 50?
а) б) в) г)
7. Приведите дробь к знаменателю 49:
а) б) в) г)
8. Наименьшим общим знаменателем дробей и является число:
а) 150 б) 30 в) 25 г) 60
Вариант II
1. Сократите дробь на НОД числителя и знаменателя.
а) б) в) г) дробь несократимая.
2. Какие из дробей равны дроби ?
а) только б) только в) только г) .
3. Запишите частное 75:200 в виде дроби и сократите её.
а) б) в)
4. Найдите значение n в равенстве
а) 45; б) 3; в) 5; г) 15.
5. Сократите дробь
а) б) в) г)
6. Какую дробь можно привести к знаменателю 60?
а) б) в) г)
7. Приведите дробь к знаменателю 35:
а) б) в) г)
8. Наименьшим общим знаменателем дробей и является число:
а) 48 б) 70 в) 28 г) 460
infourok.ru
Самостоятельная работа по математике Сокращение дробей 6 класс
Самостоятельная работа по математике Сокращение дробей 6 класс с ответами. Самостоятельная работа включает 2 варианта, в каждом по 6 заданий.
Вариант 1
1. Сократите дроби:
3/6; 8/16; 8
/12; 42n/49n.2. Представьте числа в виде обыкновенной несократимой дроби:
а) 0,36
б) 0,7
в) 0,625
3. Андрей красит за 2 часа 7 м2 забора, а Иван 15 м2 забора за 6 ч. Кто из них красит 1 м2 забора быстрее и на сколько?
4. Выполните действия:
32/8 − 14/8 + 16/8.
5. Сократите дробь
1554/3465
6. Сколько трехзначных чисел можно составить из четных цифр, если цифры в записи числа не повторяются?
Вариант 2
1. Сократите дроби:
4/8; 6/8; 7/14; 22n/33n.
2. Представьте числа в виде обыкновенной несократимой дроби:
а) 0,24
б) 0,3
в) 0,875
3. Маша выпекает 6 пирожных за час, а Аня — 12 пирожных за 3 часа. Кто из них выпекает 1 пирожное быстрее и насколько?
4. Выполните действия:
42/6 − 13/6 − 4/6
5. Сократите дробь
1887/2664
6. Сколько трехзначных чисел можно составить из нечетных цифр, если цифры в записи числа не повторяются?
Ответы на самостоятельную работу по математике Сокращение дробей 6 класс
Вариант 1
1. 1/2; 1/2; 2/3; 6/7
2.
а) 9/25
б) 7/10
в) 5/8
3. Андрей, на 4/35 часа
4. 31/2
5. 74/165
6. 48
Вариант 2
1. 1/2; 3/4; 1/2; 2/3
2.
а) 6/25
б) 3/10
в) 7/8
3. Маша, на 1/12 часа
4. 3/2
5. 17/24
6. 60
testytut.ru
Тест. Сокращение дробей
© 2018, ООО КОМПЭДУ, http://compedu.ru При поддержке проекта http://videouroki.net
Будьте внимательны! У Вас есть 10 минут на прохождение теста. Система оценивания — 5 балльная. Разбалловка теста — 3,4,5 баллов, в зависимости от сложности вопроса. Порядок заданий и вариантов ответов в тесте случайный. С допущенными ошибками и верными ответами можно будет ознакомиться после прохождения теста. Удачи!Список вопросов теста
Вопрос 1
Варианты ответов
Вопрос 2
Какой несократимой дроби равна дробь 2864?Варианты ответов
Вопрос 3
Варианты ответов
Вопрос 4
Дробь, числитель и знаменатель которой — взаимно простые числа, называют … .
Вопрос 5
Деление числителя и знаменателя на их общий делитель, отличный от одного, называют … дроби.
Вопрос 6
При каких натуральных значениях дробь n6 будет правильной несократимой?
Варианты ответов
Вопрос 7
Сократите дробь 243·3434·49·81. Укажите чему будет равен числитель и знаменатель несократимой дроби.
Варианты ответов
- числитель равен 21
- числитель равен 4
- знаменатель равен 21
- знаменатель равен 4
Вопрос 8
Укажите дроби, которые являются различными записями числа 45.
Варианты ответов
810
215
2030
3240
210
2835
Вопрос 9
Сократите дроби и сопоставьте их значения с сокращенными.
Варианты ответов
Вопрос 10
Какое натуральное число является числителем дроби в равенстве 327=x9?
videouroki.net
6 класс. Математика. Сокращение дробей — Сокращение дробей
Комментарии преподавателя
Представьте себе такую ситуацию.
За столом 3 человека и 5 яблок. Делятся 5 яблок на троих. Каждому достается по яблока.
А за соседним столом еще 3 человека и тоже 5 яблок. Каждому опять по .
При этом всего 10 яблок и 6 человек. Каждому по .
Но это одно и то же.
. Эти дроби эквивалентны.
Можно увеличить в два раза количество людей и в два раза количество яблок. Результат будет тем же самым.
В математике это формулируется так:
Если числитель и знаменатель дроби умножить или разделить на одно и то же число (не равное 0), то новая дробь будет равна исходной.
Это свойство иногда называют «основным свойством дроби».
Примеры эквивалентных дробей
1. Путь от города до деревни – 7 км.
Мы идем по дороге и определяем пройденный путь по километровым столбикам. Пройдя три столбика, три километра, мы понимаем, что прошли пути.
Но если мы не видим столбиков (может, их не установили), можно путь считать по электрическим столбам вдоль дороги. Их 20 штук на каждый километр. То есть всего 140 на всем пути. Три километра – столбов. То есть мы прошли 60 из 140 столбов, .
2. Дробь на координатной плоскости можно отмечать точкой. Чтобы изобразить дробь отметим точку с координатой 3 по оси и 4 по оси . Проведем прямую из начала координат через нашу точку.
На этой же прямой будет лежать и точка, соответствующая дроби .
Они являются эквивалентными: (см. Рис. 1)
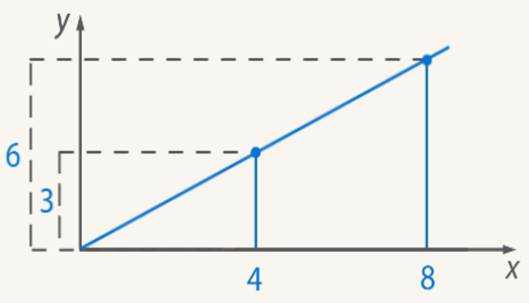
Рис. 1. Иллюстрация к приме&
www.kursoteka.ru
Контрольная работа по математике Основное свойство дроби 6 класс
Контрольная работа по математике Основное свойство дроби. Сокращение дробей. Приведение дробей к общему знаменателю. Сравнение, сложение и вычитание дробей с разными знаменателями. Сложение и вычитание смешанных чисел 6 класс с ответами. Контрольная работа включает 4 варианта, в каждом по 6 заданий.
Вариант 1
1. Сократите дроби:
2/4; 5/15; 6/10; 8n/14n
2. Приведите к наименьшему общему знаменателю дроби.
2/7 и 5/8
3. Сравните дроби:
а) 5/7 и 2/3
б) 3/11 и 2/9
4. Найдите значение выражения:
(23/5 − 17/10) + (11/2 − 7/20)
5. Решите уравнение:
х + 21/3 + 31/9 − 11/12 = 57/12
6. Сколькими способами могут разместиться 3 пассажира в 6-местной лодке?
Вариант 2
1. Сократите дроби:
3/6; 4/12; 5/20; 6n/18n
2. Приведите к наименьшему общему знаменателю дроби.
4/9 и 5/12
3. Сравните дроби:
а) 2/11 и 3/14
б) 1/15 и 2/29
4. Найдите значение выражения:
(31/7 − 23/14) + (23/42 − 11/17)
5. Решите уравнение:
31/5 + 22/5 − х = 31/10 − 11/5
6. Сколькими способами могут разместиться 4 пассажира в 6-местной лодке?
Вариант 3
1. Сократите дроби:
14/21; 13/39; 24/36; 17n/51n
2. Приведите к наименьшему общему знаменателю дроби.
3/14 и 5/21
3. Сравните дроби:
а) 3/8 и 2/5
б) 4/13 и 2/7
4. Найдите значение выражения:
(42/7 − 31/14) + (11/28 − 3/14)
5. Решите уравнение:
32/5 − х − 11/4 = 11/12
6. Сколькими способами могут разместиться 3 пассажира в 5-местной лодке?
Вариант 4
1. Сократите дроби:
3/18; 4/16; 18/54; 13n/52n
2. Приведите к наименьшему общему знаменателю дроби.
5/11 и 1/6
3. Сравните дроби:
а) 3/7 и 1/3
б) 4/19 и 2/11
4. Найдите значение выражения:
(51/8 − 21/4) + (37/16 − 9/8)
5. Решите уравнение:
х + 26/13 − 11/39 = 23/13 + 32/13
6. Сколькими способами могут разместиться 4 пассажира в 5-местной лодке?
Ответы на контрольную работу по математике Основное свойство дроби. Сокращение дробей. Приведение дробей к общему знаменателю. Сравнение, сложение и вычитание дробей с разными знаменателями. Сложение и вычитание смешанных чисел 6 класс
Вариант 1
1. 1/2; 1/3; 3/5; 4/7
2.
2/7 = 16/56
5/8 = 35/56
3.
а) 5/7 > 2/3
б) 3/11 > 2/9
4. 21/20
5. 12/9
6. 120
Вариант 2
1. 1/2; 1/3; 2/3; 1/3
2.
4/9 = 16/36
5/12 = 15/36
3.
а) 2/11 < 3/14
б) 1/15 < 2/29
4. 16/7
5. 37/10
6. 360
Вариант 3
1. 2/3; 1/3; 2/3; 1/3
2.
3/14 = 9/42
5/21 = 10/42
3.
а) 3/8 < 2/5
б) 4/13 > 2/7
4. 21/28
5. 11/15
6. 60
Вариант 4
1. 1/6; 1/4; 1/3; 1/4
2.
5/11 = 30/66
1/6 = 11/66
3.
а) 3/7 > 1/3
б) 4/19 > 2/11
4. 53/16
5. 337/39
6. 120
testytut.ru
Сокращение дробей 6 класс — К уроку — Математика, алгебра, геометрия
Автор: Тазетдинова Анастасия Николаевна, учитель математики
МОУ лицей №6 Октябрьского района городского округа город Уфа Республики Башкортостан, licey6@ufanet.ru
Тема: Сокращение дробей
Тип урока: урок совершенствования и контроля ЗУН.
Цели:
Знать основное свойство дроби и уметь применять его при сокращении дробей.
Развивать интерес к предмету.
Рассказать учащимся о картине Н. П. Богданова-Бельского «Устный счёт», обращая внимание на задачу, условие которой написано на классной доске.
Учить работать учащихся как индивидуально, так и в группах, воспитывая критическое отношение к своим знаниям, умение прислушиваться к чужому мнению.
Проверить усвояемость пройденного материала.
Оборудование:
Интерактивная доска.
Проектор.
ПК (с таким расчетом, чтобы за одним ПК работало не более 2 учащихся) с установленным тестом по теме «Сокращение дробей».
Репродукция картины Н. П. Богданова-Бельского «Устный счёт».
Литература:
Виленкин Я. Н. и др. Математика 6: Учебное пособие. М.: Мнемозина, 2004.
Фаермарк Д. С. Задача пришла с картины. – М.: Наука, 1974 г.
Ход урока
Сообщение задачи урока.
Здравствуйте, ребята! Сегодня мы будем применять на практике те знания, которые вы получили на предыдущих уроках по теме «Сокращение дробей». Вы увидите, что умение сокращать дроби очень помогает при решении примеров на вычисление. А в конце урока с помощью тестирования вы узнаете, хорошо ли вы усвоили пройденный материал.
Для начала – устная разминка:
Вопросы:
В чём заключается основное свойство дроби?
Изменится ли значение дроби, если её числитель уменьшить в 2 раза, а знаменатель увеличить в 2 раза?
Изменится ли значение дроби, если к числителю и знаменателю прибавить 2?
Изменится ли значение дроби, если её числитель умножить на 2, а знаменатель разделить на ?
Сократите дроби:
Многие люди бодрствуют 16 часов в сутки. Какую часть суток люди спят? Ответ дайте в виде несократимой дроби.
Ну что ж, разминка показала, что вы усвоили тему, и мы можем приступать к решению примеров. Запишите в тетрадях число, тему «Сокращение дробей».
Далее решаются №236, 277, 282 из учебника. Учащиеся по одному выходят к доске и комментируют своё решение. Так как учащиеся уже знают, как работать с интерактивной доской, им разрешается самим выбрать цвет ручки. Если одним учащимся на доске допущена ошибка, другой учащийся своим цветом исправляет её.
А теперь перейдём к решению более интересного примера.
Демонстрируется репродукция картины «Устный счёт» Николая Петровича Богданова-Бельского (1868-1945), написанная в 1895-96 г.
Как правило, в каждом классе находятся учащиеся, чем-то напоминающие героев картины, поэтому ученики с интересом обсуждают, что они видят. Итак, класс сельской школы. Идёт урок арифметики. Учитель написал на доске задачу, и ребятишки решают её в уме. На переднем плане – мальчик в длинной холщовой рубахе, подпоясанной бечёвкой. Из рваного рукава виден голый локоть.(Сирота, наверное, некому присмотреть). единственное, что на нём целое и ладное, — этот новенькие лапти, сплетённые, должно быть, собственными руками. Высокий лоб, большие умные глаза. Во всём облике угадывается большое упорство и внутренняя сила. Он, может быть, не всегда быстро, но всегда самостоятельно доходит до сути вещей. Как знать, может в этом маленьком оборвыше художник изобразил самого себя, своё безрадостное детство. Рядом другой подросток в вышитой рубахе и синих портках. Одну руку он заложил за голову, он думает. Широко раскрыты голубые глаза, как будто они стараются где-то вдалеке разглядеть решение. Один из мальчиков наклонился к уху учителя и, прикрыв рот ладошкой, шепчет с видом заговорщика, ответ. Справа от него другой мальчик скосил глаза: ему хочется подслушать ответ. Слева от учителя – мальчик в сиреневой рубашке и добротных сапогах, видно, из зажиточных, старательно считает на пальцах, и губы его что-то шепчут. Мальчик, стоящий слева от доски, кажется, вот-вот решит задачу. Два мальчика – один в розовой рубашке, второй — в белой, справа от доски, решают задачу совместно. Вместе – легче, они ведь маленькие. Учитель, сидя в спокойной позе, внимательно, с интересом наблюдает за учениками. Художник изобразил на этой картине невыдуманных учеников и учителя. С 1833 по 1902 г. жил известный русский педагог Сергей Александрович Рачинский, замечательный представитель русских образованных людей девятнадцатого века. Он был доктором естественных наук и профессором ботаники Московского Университета. В 1868 г. С. А. Рачинский оставляет должность профессора, открывает школу для крестьянских детей в селе Татево, Смоленской области, и становится в ней учителем. Его ученики так хорошо считали устно, что этому удивлялись все посетители школы: другие учителя, инспектора. Сам Николай Петрович был учеником С. А. Рачинского. Рачинский учил детей не только устному счёту, он учил их думать и рассуждать, подбирая соответствующие примеры и задачи. Что же за пример решают ученики трёхклассной сельской школы?
Когда я предлагаю ученикам решить этот пример, многие берут в руки карандаши или ручки. Останавливаю их: «Ведь ребята с картины решают этот пример устно!» Через какое-то время некоторые учащиеся, вспомнив устную разминку в начале урока, догадываются что , т.е. ответ задачи 2. для них решение этого примера – подлинная радость, открытие. Называю время, потраченное ими на решение примера, и сообщаю, что с помощью компьютера эта задача решается мгновенно, разумеется, если правильно составить программу для вычисления. Но составлять программы учащиеся будут на уроках информатики, а пока предлагаю им с помощью ПК проверить свои знания в области сокращения дробей.
На доске показывается демонстрационная версия теста по данной теме, а затем учащиеся рассаживаются за компьютеры с таким расчётом, чтобы за одним компьютером находилось не более двух человек, и решают тест по теме «Сокращение дробей».
На какое наибольшее число можно сократить дробь:
на числитель;
на знаменатель;
на наибольший общий делитель числителя и знаменателя;
на наименьшее общее кратное числителя и знаменателя.
Какую цифру вместо звёздочки нужно вписать, чтобы дробь стала несократимой?
Дробь называется несократимой, если её числитель и знаменатель:
взаимно простые числа;
взаимно обратные числа;
противоположные числа;
натуральные числа.
Сократите дробь .
Какую часть суток составляют 8 часов? Ответ дайте в виде несократимой дроби.
Сократите дробь .
Какую из дробей можно сократить?
Вначале дробь сократили на 2, потом на 3, потом на 5. На какое число можно было сразу сократить дробь?
Сократите дробь .
На сколько можно сократить дробь
на 6;
на 8;
на 20;
на 30.
Тест составлен таким образом, что учащийся после выполнения задания видит не только свою оценку, но и вопросы, в которых он допустил ошибку, что позволяет учащимся скорректировать свои знания. Оценка, полученная за тест, и является оценкой за урок, кроме того, учитывается и активность учащегося во время урока.
В оставшееся время подводится итог урока: учащиеся обсуждают, что нового они узнали, сумели ли применить полученные знания на практике и уровень своей подготовки по теме «Сокращение дробей».
pedsovet.su
