Основные понятия, решение систем линейных неравенств. Видеоурок. Алгебра 9 Класс
На этом уроке мы начнем изучение систем неравенств. Вначале будем рассматривать системы линейных неравенств. В начале урока рассмотрим, откуда и зачем возникают системы неравенств. Далее изучим, что значит решить систему, и вспомним объединение и пересечение множеств. В конце будем решать конкретные примеры на системы линейных неравенств.
Тема: Рациональные неравенства и их системы
Урок: Основные понятия, решение систем линейных неравенств
До сих пор мы решали отдельные неравенства и применяли к ним метод интервалов, это могли быть и линейные неравенства, и квадратные и рациональные. Теперь перейдем к решению систем неравенств – сначала линейных систем. Посмотрим на примере, откуда берется необходимость рассматривать системы неравенств.
Найти область определения функции
Найти область определения функции
Найти область определения функции
Функция существует, когда существуют оба квадратних корня, т.е.
Как решать такую систему? Необходимо найти все x, удовлетворяющие и первому и второму неравенству.
Изобразим на оси ox множество решений первого и второго неравенства.
Промежуток пересечения двух лучей и есть наше решение.
Ответ:
Такой метод изображения решения системы неравенств иногда называют методом крыш.
Решением системы является пересечение двух множеств.
Изобразим это графически. Имеем множество А произвольной природы и множество В произвольной природы, которые пересекаются.
Определение: Пересечением двух множеств А и В называется такое третье множество, которое состоит из всех элементов, входящих и в А и в В.
Рассмотрим на конкретных примерах решения линейных систем неравенств, как находить пересечения множеств решений отдельных неравенств, входящих в систему.
Решить систему неравенств:
1.
Ответ:
2.
Ответ: (7; 10].
3.
Ответ:
4. Решить систему
Откуда может взяться второе неравенство системы? Например, из неравенства
Графически обозначим решения каждого неравенства и найдем промежуток их пересечения.
Ответ:
Таким образом, если мы имеем систему, в которой одно из неравенств удовлетворяет любому значению x, то его можно исключить.
5.
Ответ: система противоречива.
6.
Ответ:
Мы рассмотрели типовые опорные задачи, к которым сводится решение любой линейной системы неравенств.
Рассмотрим следующую систему.
7.
Ответ:
Иногда линейная система задается двойным неравенством, рассмотрим такой случай.
8.
Ответ:
Мы рассмотрели системы линейных неравенств, поняли, откуда они появляются, рассмотрели типовые системы, к которым сводятся все линейные системы, и решили некоторые из них.
Список рекомендованной литературы
1. Мордкович А.Г. и др. Алгебра 9 кл.: Учеб. Для общеобразоват. Учреждений.- 4-е изд. – М.: Мнемозина, 2002.-192 с.: ил.
2. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М.: Мнемозина, 2002.-143 с.: ил.
3. Макарычев Ю. Н. Алгебра. 9 класс : учеб. для учащихся общеобразоват. учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, И. Е. Феоктистов. — 7-е изд., испр. и доп. — М.: Мнемозина, 2008.
4. Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. Алгебра. 9 класс. 16-е изд. — М., 2011. — 287 с.
5. Мордкович А. Г. Алгебра. 9 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, П. В. Семенов. — 12-е изд., стер. — М.: 2010. — 224 с.: ил.
6. Алгебра. 9 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Л. А. Александрова, Т. Н. Мишустина и др.; Под ред. А. Г. Мордковича. — 12-е изд., испр. — М.: 2010.-223 с.: ил.
Рекомендованные ссылки на интернет-ресурсы
1. Портал Естественных Наук (Источник).
2. Электронный учебно-методический комплекс для подготовки 10-11 классов к вступительным экзаменам по информатике, математике, русскому языку (Источник).
3. Виртуальный репетитор (Источник).
4. Центр образования «Технология обучения» (Источник).
5. Раздел College.ru по математике (Источник).
Рекомендованное домашнее задание
1. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М. : Мнемозина, 2002.-143 с.: ил. №№ 53; 54; 56; 57.
interneturok.ru
Решение систем неравенств
Вопросы занятия:
· повторить основные свойства систем неравенств;
· повторить алгоритм решения систем неравенств.
Материал урока
Как решаются системы линейных неравенств с одной переменной, мы уже вспоминали.
Сегодня на уроке мы рассмотрим системы не линейных неравенств.
Определение.
Говорят, что задана система двух неравенств с одной переменной, если требуется найти все значения переменной, при которых оба неравенства системы обращаются в верные числовые неравенства.
Определение.
Решением системы неравенств называют такое значение переменной, при котором неравенства системы преобразуются в верные числовые неравенства.
Определение.
Решить систему неравенств – это значит найти все её решения или доказать, что решений нет.
Определение.
Два неравенства называются равносильными, если каждое решение одного неравенства является решением другого, и наоборот, то есть они имеют одни и те же решения. Равносильными называются и неравенства, которые не имеют решений.
Теперь давайте вспомним основные свойства неравенств.
1. Если в неравенстве перенести слагаемое из одной части в другую с противоположным знаком, то получится неравенство, равносильное данному.
2. Если обе части неравенства умножить или разделить на одно и то же положительное число, то получится неравенство, равносильное данному.
3. Если обе части неравенства умножить или разделить на одно и то же отрицательное число и изменить знак неравенства на противоположный, то получится неравенство, равносильное данному.
Давайте повторим алгоритм решения систем линейных неравенств.
1. Решить каждое из неравенств системы отдельно.
2. Изобразить полученные решения на числовой прямой.
3. Найти пересечение этих решений.
По такому же алгоритму будут решаться и системы, которые мы рассмотрим на этом уроке.
Пример.
Рассмотрим ещё один пример.
Пример.
Рассмотрим ещё один пример.
Пример.
Итоги урока
Сегодня на уроке, мы вспомнили что такое системы неравенств, вспомнили основные свойства неравенств, повторили алгоритм решения систем неравенств, рассмотрели несколько примеров.
videouroki.net
Готовимся к экзамену по математике за период обучения на II ступени общего среднего образования: 13. Системы неравенств
МАТЕРИАЛ ДЛЯ ПОВТОРЕНИЯ
Если ставится задача найти множество общих решений двух или более неравенств, то говорят, что надо решить систему неравенств.Неравенства, входящие в систему, объединяются фигурной скобкой. Иногда системы неравенств записывают в виде двойного неравенства:
-5<x<12 илиРешением системы неравенств называется число, которое при его подстановке в систему обращает каждое неравенство в верное числовое неравенство.
Решить систему неравенств – значит найти решения для всей системы, либо доказать, что у данной системы решений нет.
Чтобы решить систему неравенств с одной переменной, надо:
1) отдельно решить каждое неравенство;
2) найти пересечение найденных решений, отметив решение каждого неравенства на числовой прямой.
Это пересечение и является множеством решений системы неравенств.
Пример:Решить систему неравенств:
Решим каждое неравенство в отдельности
5x-x2=0,
x(5-x)=0,
x=0 или 5-x=0,
-x=-5,
x=5.
Находим решение с помощью метода интервалов:
2) 6-2x<-2,
-2x<-2-6,
-2x<-8,
x>-8:(-2),
x>4.
Объединим оба решения:
Ответ: (4; 5].Говорят, что несколько неравенств с одной переменной образуют совокупность, если необходимо найти все такие значения переменной, каждое из которых является решением хотя бы одного из данных неравенств. Совокупность неравенств обозначается квадратной скобкой.
Решением совокупности неравенств называют такие значения переменной, которые являются верными хотя бы для одного из этих неравенств.
Чтобы решить совокупность неравенств с одной переменной, надо:
1) отдельно решить каждое неравенство;
2) найти объединение найденных решений, отметив решение каждого неравенства на числовой прямой.
Это объединение и является решением совокупности неравенств.
Пример:
Решить совокупность неравенств:
Решим каждое неравенство в отдельности
1) 5х+6≤1,
5х≤ -5,
х≤ -1.
2) 2х+1≥3,
2х≥2,
х≥1.
Объединим оба решения:
Ответ: (-∞; -1]U[1;+∞).
УПРАЖНЕНИЯ
1. Решите систему неравенств:Решение:
а)
Ответ: (5; 7]
2. Решите систему неравенств:
Решение:
Ответ: (1; 10].
3. Найдите целые решения системы неравенств:
Решение:
а)
Ответом являются все целые числа, которые принадлежат промежутку (-15; 5).
Ответ: -14; -13; -12; -11; -10; -9; -8; -7; -6.
Решение:
Ответ: (-1; 3).
5. Решите систему неравенств:
Решение:
Ответ: (-1;2).
6. Решите систему неравенств:
Решение:
Ответ: нет решений.
7. Решите систему неравенств:
Решение:
Ответ: (0; +∞).
8. Решите неравенство:
а) -2<3x+5≤10; б) 2<4x+6≤12.
Решение:Ответ: (-2 1/3; 1 2/3].
9. Решите систему неравенств:
Решение:
Ответ: [0,4; 0,5).10. Решите систему неравенств (№ 3.4.52 [7]):
Решение:
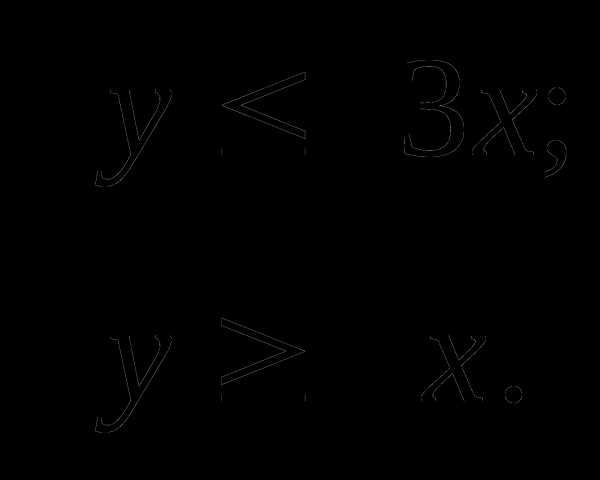Ответ: (-1; 2).11. Решите систему неравенств:
Решение:
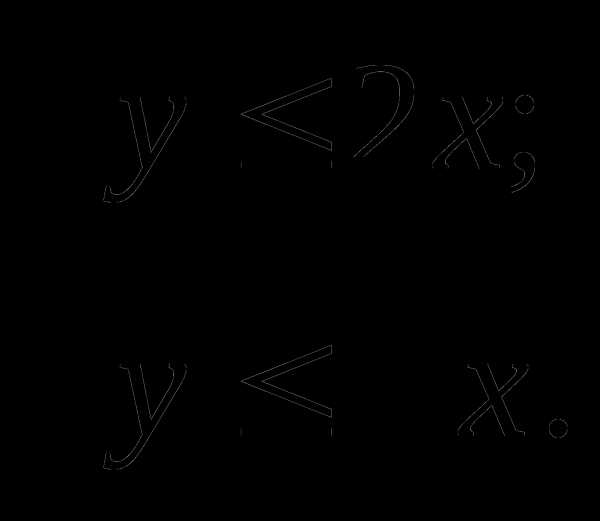Ответ: [-9; 3)U(3; 9].12. Решите систему неравенств:
Решение:
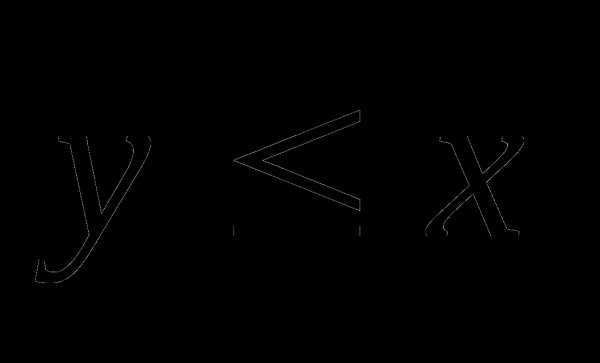
Ответ: (-7; -6)U(1;7).
13. Решите систему неравенств:
Решение:
Ответ: (2; 4).14. Решите систему неравенств:
Решение:
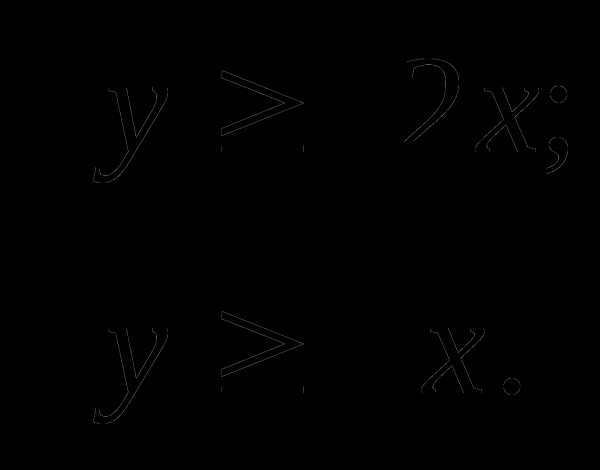Ответ: (-7; -2)U(0; 2).ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Решите систему неравенств:
2. Решите систему неравенств:
3. Решите систему неравенств:
4. Решите систему неравенств:
5. Решите систему неравенств:
6. Решите систему неравенств:
7. Решите систему неравенств:
8. Решите систему неравенств:
9. Решите систему неравенств:
10. Решите систему неравенств:
Проверь себя
mathembs.blogspot.com
Урок алгебры в 9 классе на тему «Решение систем неравенств».
Открытый урок по алгебре в 9А классе КГУ «Школа-лицей №20 г. Темиртау».
от 08.11.14
учитель: СемакинаВ.Н.
Тема: Решение систем неравенств.
Карта «Биоинтернет»
Правило «РЕШИЛ+ ОБЪЯСНИЛ=УСВОИЛ»
Цель урока: Закрепление знаний, полученных в ТК «Алгоритм» в умении объяснять и комментировать терминологически свои действия.
Задачи:
Развивающие:
-развитие коммуникативных компетенций;
-формирование умений работать в группе;
-формирование навыков самоорганизации, взаимообучения, взаимоконтроля.
Воспитательные:
-формирование коллективного разума (синергетический принцип).
Учащиеся должны знать:
-определение понятий: линейное неравенство, общий вид линейного неравенства, квадратное неравенство, нули функции, область определения функции.
-алгоритм решения линейных неравенств, алгоритм решения неравенств методом интервалов, алгоритм решения систем неравенств.
Уметь:
-приводить линейные и квадратные неравенства к общему виду;
-находить нули функции;
-определять знаки на интервалах;
-изображать решение каждого неравенства на числовой прямой;
-находить пересечение решений.
1 этап
Упражнения для развития памяти ТЕМАТИЧЕСКИЙ СЛОВАРНЫЙ ЗАПАС
Учащиеся 120 секунд запоминают слова и словосочетания записанные на доске. Затем учащиеся в течении120 секунд пишут то, что запомнили.
1-2 линейное неравенство
3 квадратное
4 система
5 больше
6 меньше
7-8 числовая прямая
9-10 метод интервалов
11-12 знаки промежутков
13-14 пересечение решений
Проверка и подсчет
2 этап
Правила работы по карте:
Обобщение материала
Расстановка коэффициентов в ОВР: кто первый выполняет, сдаёт учителю и выбирает себе «ученика», делая себе пометку в сайте «ученика». Если ученик не справился с заданием, то «учитель» объясняет ему сам, затем «ученик» терминологически комментирует каждый шаг по ОСУДу. Если «учителя» удовлетворил ответ «ученика», ставится в ячейке «+», если нет «-«.
«Учитель несет ответственность за то, как он научил своего ученика!».
Когда все проговорят, проводится экспресс контрольная работа для разбивки на уровни по ТК «Тренажер».
Оценки получают «учителя» с учетом наблюдения учителя. Учитель оставляет за собой право проверить любого обученного, наблюдает за процессом, задает вопросы по ходу работы.
3 этап
В ходе работы по карте «Алгоритм» мы вышли на промежуточный порог сложности, достигли 65% выполнения задания.
Проблемы предыдущего урока? (озвучивают учащиеся)
Выбор решения в зависимости от вида неравенства. (1 шаг)
Изображение решения каждого неравенства на числовой прямой.
Пересечение решений на чертеже.
Разбор задания у доски:
2Х
Возможные вопросы учащихся:
1.Как определить знак на интервалах?
2.Почему точки 3 и -2 не закрашены?
3.Почему промежуток от (8;
4 этап
Работа по выполнению задания.
≤0
3х+4≤10
Когда у всех будут пометки по МПМ, работа на этом этапе завершается.
5 этап
Синхронопись. (Учащиеся одновременно правой и левой рукой чертят знак∞, затем левой рукой 5 треугольников, а правой 5 квадратов.
6 этап Экспресс контрольная работа.
γ
(х-3)(х+1)<0
2х-3>1
(2;3)
β
Х2-3х-4<0
3х-12>0
Нет решения
α
≤0
-2х+3<13
(-5;-4]υ[-2;2)
6 этап Рефлексия урока.
Сегодня я узнал…….
Было интересно…….
Теперь я могу……….
Мне было трудно……
Готовность к «Тренажеру»
Выставление оценок.
Домашнее задание стр 29 №145(1), №146(1).
infourok.ru
План-конспект урока по алгебре (9 класс) на тему: Решение неравенств
По теме: методические разработки, презентации и конспекты
Контрольно-обобщающий урок «Решение неравенств и систем неравенств с одной переменной»Контрольно-обобщающий урок «Решение неравенств и систем неравенств с одной переменной». Цель урока: обобщение, систематизация и проверка знаний, умений и навыков в…
Обобщающий урок по теме «Решение неравенств с одной переменной и решение систем неравенств»Данный урок является закрепляющим уроком по теме «Решение неравенств и систем неравенств» в 8 классе. В помощь учителю создана презентация….
Решение неравенств и систем неравенств с двумя переменнымиАлгебра.Повторение. Подготовка к ГИА. 9 класс….
Урок алгебры в 9ом классе «Решение неравенств и системы неравенств»Комбинированый урок алгебры в 9ом классе, завершающий изучени по теме: «Решение неравенств и системы неравенств»…
Презентация. «Решение неравенств, систем неравенств.»Презентация может быть использована на уроках повторения и обобщения, или как изучение нового материала….
Решение неравенств и систем неравенств с одной переменной.Цели:Совершенствовать умения решать неравенства и системы неравенств, графически изображать множество их решений, а также записывать решения в виде числового промежутка…
Тест по темам « Решение уравнений и их систем», «Решение неравенств и их систем» и «Решение уравнений, неравенств, систем неравенств с модулем».Задания теста соответствуют содержанию учебника «Алгебра. 9 класс : учеб. для учащихся общеобразовательных учреждений / Ю. Н. Макарычев , Н. Г. Миндюк , К. И. Нешков , И. Е. Феоктист…
nsportal.ru
Презентация решение систем неравенств 9 класс
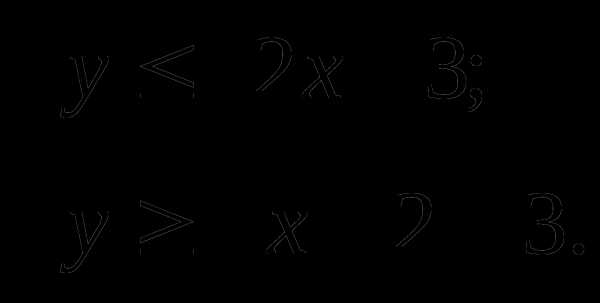
(9 класс)
А. Нивен
Запомним
Решить систему неравенств – это значит найти значение переменной , при котором верно каждое из неравенств системы.
Запомним
Если надо решить систему неравенств, то :
- решаем каждое неравенство системы отдельно
- изображаем полученные решения на числовой прямой и смотрим пересечения этих решений.
Эта общая часть и является решением данной системы неравенств.
Содержание
- Решение систем линейных неравенств
- Решение двойных неравенств
- Решение систем, содержащих квадратные неравенства
6 2х – 4 Решение: решим каждое неравенство отдельно 5х + 1 6 2х – 4 5х 6 -1 2х 5х 5 2х х 1 х 1 3,5 х Ответ: (1; 3,5)»
Решим систему неравенств (состоящую из линейных неравенств)
5х + 1 6
2х – 4
Решение: решим каждое неравенство отдельно
5х + 1 6 2х – 4
5х 6 -1 2х
5х 5 2х
х 1 х
1 3,5 х
Ответ: (1; 3,5)
— 3 х ≥ -3,5 Изобразим на числовой прямой: -3,5 -3 4 Ответ: ( -3; 4]»
Решим систему неравенств
5х + 12 ≤ 3х+ 20
х
2х + 7 ≥ 0
Решение: решим каждое неравенство отдельно
5х + 12 ≤ 3х+ 20 х 2х + 7 ≥ 0
5х – 3х ≤ — 12 + 20 х – 2х
2х ≤ 8 -х
х ≤ 4 х — 3 х ≥ -3,5
Изобразим на числовой прямой:
-3,5 -3 4
Ответ: ( -3; 4]
12 + 11х 5х – 1 ≥ 0 Проверим ответы: 1) [2; +∞) 2) Нет решения»
Работа в парах:
Решить систему
неравенств:
1) 3х – 2 ≥ х + 1
4 – 2х ≤ х – 2
2) 3х 12 + 11х
5х – 1 ≥ 0
Проверим ответы:
1) [2; +∞)
2) Нет решения
Примеры двойных неравенств
Прочитайте неравенства :
-6 х 0
-1,2 ≤ х 3,5
0 х ≤ 5,9
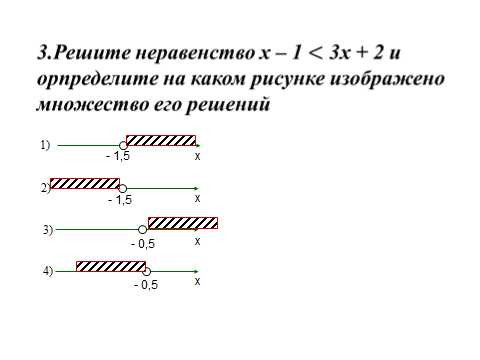0 4х + 2 ≤ 6 Решим каждое неравенство системы отдельно: 1) 4х + 2 0 2) 4х + 2 ≤ 6 х — 0,5 х ≤ 1 Полученные результаты изобразим на числовой прямой: -0,5 1 х Ответ: -0,5 или (-0,5; 1]»
Решение двойных неравенств
Решить неравенство: 0 4х +2 ≤ 6
Решение: составим систему: 4х + 2 0
4х + 2 ≤ 6
Решим каждое неравенство системы отдельно:
1) 4х + 2 0 2) 4х + 2 ≤ 6
х — 0,5 х ≤ 1
Полученные результаты изобразим на числовой прямой:
-0,5 1 х
Ответ: -0,5 или (-0,5; 1]
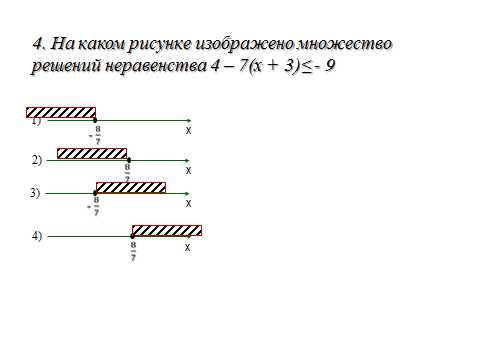
Решите неравенства, работая в парах
Решить неравенства:
Проверим
ответы:
1) [-1; 2]
2) (2,5; 7 ]
3) [- 1,5; — 1)
4) (-2; 1)
5) (-4; 0)
- -6 ≤ — 3х ≤ 3
- 4 ≤ 13
- -2 ≤ 6х + 7 1
- 0,3
9/4=2,25 Полученные результаты изобразим на числовой прямой: 1 2,25 4 х Ответ: [ 4; +∞)»
Решим систему неравенств (в которую входит квадратное неравенство)
Решить систему неравенств: х ² — 5х + 4 ≤ 0
9 — 4х
Решение: решим каждое неравенство системы отдельно
1) х ² — 5х + 4 ≤ 0 2) 9 — 4х
х ² — 5х + 4 = 0 — 4х
т.к. а+в+с=0, то х 1 =1; х 2 =4 х 9/4=2,25
Полученные результаты изобразим на числовой прямой:
1 2,25 4 х
Ответ: [ 4; +∞)
0 Решение: решим каждое неравенство отдельно х ² — 3х + 2 2х² — 3х – 5 0 Найдем корни соответствующих квадратных уравнений х ² — 3х + 2 = 0 2х² — 3х – 5 = 0 По свойствам коэффициентов имеем: х 1 = 1 х 2 = 2 х 1 = -1 х 2 = 5/2= 2,5 Изобразим метод интервала на числовой оси: -1 1 2 2,5 х Ответ: (- ∞; -1) υ (2,5; +∞)»
Решим систему неравенств (в которую входит квадратное неравенство)
Решить систему неравенств:
х ² — 3х + 2
2х² — 3х – 5 0
Решение: решим каждое неравенство отдельно
х ² — 3х + 2 2х² — 3х – 5 0
Найдем корни соответствующих квадратных уравнений
х ² — 3х + 2 = 0 2х² — 3х – 5 = 0
По свойствам коэффициентов имеем:
х 1 = 1 х 2 = 2 х 1 = -1 х 2 = 5/2= 2,5
Изобразим метод интервала на числовой оси:
-1 1 2 2,5 х
Ответ: (- ∞; -1) υ (2,5; +∞)
0 4х – 1 ≥ 0 2) 4х² — 1 ≤ 0 х² 1 3х² — 2х – 1 х² — х – 6 0″
Решим системы неравенств, работая вместе
1) 6х² — 5х + 1 0
4х – 1 ≥ 0
2) 4х² — 1 ≤ 0
х² 1
х² — х – 6 0
0 4х – 1 ≥ 3 3) 2х² — 7х + 5 2 – х ≥ 0 Проверим ответы: 1) (4; 9 ] 2) [1; 2) 3) (- ∞ ; 1 )»
Решите системы неравенств, работая самостоятельно
1) х² — 10х + 9 ≥ 0
12 – 3х
2) 2х²- 5х + 2 0
4х – 1 ≥ 3
3) 2х² — 7х + 5
2 – х ≥ 0
Проверим ответы:
1) (4; 9 ]
2) [1; 2)
3) (- ∞ ; 1 )
kopilkaurokov.ru
Решение систем неравенств (9 класс)
Обратная связь
Если не удалось найти и скачать доклад-презентацию, Вы можете заказать её на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:
Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:
Email: [email protected]
Мы в социальных сетях
Социальные сети давно стали неотъемлемой частью нашей жизни. Мы узнаем из них новости, общаемся с друзьями, участвуем в интерактивных клубах по интересам
ВКонтакте >
Что такое Myslide.ru?
Myslide.ru — это сайт презентаций, докладов, проектов в формате PowerPoint. Мы помогаем учителям, школьникам, студентам, преподавателям хранить и обмениваться своими учебными материалами с другими пользователями.
Для правообладателей >
myslide.ru