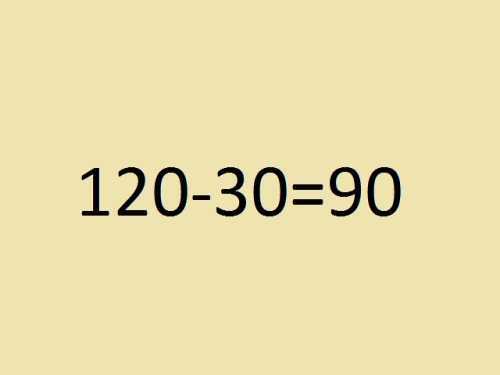Найдите значение числового выражения – .

Как найти значение выражения 🚩 вычислите значение выражения 🚩 Математика

Отличительной особенностью выражения является наличие математических действий. Оно обозначаются определенными знаками (умножения, деления, вычитания или сложения). Последовательность выполнения математических действий при необходимости корректируется скобками. Выполнить математические действия – значит найти значение выражения.

Не всякую математическую запись можно отнести к числу выражений.

Равенства не являются выражениями. Присутствуют при этом в равенстве математические действия или нет, не имеет значения. Например, a=5 – это равенство, а не выражение, но и 8+6*2=20 тоже нельзя считать выражением, хотя в нем и присутствуют умножение и сложение. Этот пример тоже принадлежит к категории равенств.

Понятия выражения и равенства не являются взаимоисключающими, первое входят в состав второго. Знак равенства соединяет два выражения:
5+7=24:2

Можно это равенство упростить:
5+7=12

Выражение всегда предполагает, что представленные в нем математические действия могут быть выполнены. 9+:-7 – это не выражение, хотя здесь есть знаки математических действий, ведь выполнить эти действия невозможно.

Существуют и такие математические примеры, которые формально являются выражениями, но не имеют смысла. Пример такого выражения:
46:(5-2-3)

Число 46 необходимо разделить на результат действий в скобках, а он равен нулю. На нуль же делить нельзя, такое действие в математике считается запретным.

Существует два вида математических выражений.

Если выражение содержит только числа и знаки математических действий, такое выражение называется числовым. Если же в выражении наряду с числами присутствуют переменные, обозначаемые буквами, или чисел нет вообще, выражение состоит только из переменных и знаков математических действий, оно называется алгебраическим.

Принципиальное отличие числового значения от алгебраического состоит в том, что у числового выражения значение только одно. Например, значение числового выражения 56–2*3 всегда будет равно 50, ничего изменить нельзя. У алгебраического же выражения значений может быть много, ведь вместо буквы можно подставить любое число. Так, если в выражении b–7 вместо b подставить 9, значение выражения будет равно 2, а если 200 – оно будет составлять 193.

www.kakprosto.ru

Числовые выражения

Числовые выражения.

Числовое выражение – это любая запись из чисел, знаков арифметических действий и скобок. Числовое выражение может состоять и просто из одного числа. Напомним, что основными арифметическими действиями являются «сложение», «вычитание», «умножение» и «деление». Этим действиям соответствуют знаки «+», «-», «∙», «:».

Конечно же, чтобы у нас получилось числовое выражение, запись из чисел и арифметических знаков должна быть осмысленной. Так, например, такую запись 5 : + ∙  нельзя назвать числовым выражением, так как это случайный набор символов, не имеющий смысла. Напротив, 5 + 8 ∙ 9 — уже настоящее числовое выражение.

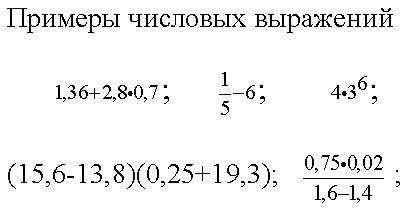
Значение числового выражения.

Сразу скажем, что если мы выполним действия указанные в числовом выражении, то в результате мы получим число. Это число называется значением числового выражения

.

Попробуем вычислить, что у нас получится в результате выполнения действий нашего примера. Согласно порядку выполнения арифметических действий, сначала выполним операцию умножения. Умножим 8 на 9. Получим 72. Теперь сложим 72 и 5. Получим 77.
Итак, 77 – значение числового выражения 5 + 8 ∙ 9.

Числовое равенство.

Можно это записать таким образом: 5 + 8 ∙ 9 = 77. Здесь мы впервые использовали знак «=» («Равно»). Такая запись, при которой два числовых выражения разделены знаком «=», называется числовым равенством. При этом, если значения левой и правой части равенства совпадают, то равенство называют верным. 5 + 8 ∙ 9 = 77 – верное равенство.
Если же мы напишем 5 + 8 ∙ 9 = 100, то это уже будет неверное равенство, так как значения левой и правой части данного равенства уже не совпадают.

Следует отметить, что в числовом выражении мы также можем использовать скобки. Скобки влияют на порядок выполнения действий. Так, например, видоизменим наш пример, добавив скобки: (5 + 8) ∙ 9. Теперь сначала нужно сложить 5 и 8. Получим 13. А затем умножить 13 на 9. Получим 117. Таким образом, (5 + 8) ∙ 9 = 117.

117 – значение числового выражения (5 + 8 ) ∙ 9.

Как прочитать числовое выражение?

Чтобы правильно прочитать выражение, нужно определить какое именно действие выполняется последним для вычисления значения данного числового выражения. Так, если последнее действие вычитание, то выражение называют «разностью». Соответственно, если последнее действие сумма — «суммой», деление – «частным», умножение – «произведением», возведение в степень – «степенью».

Например, числовое выражение (1+5)(10-3) читается так: «произведение суммы чисел 1 и 5 на разность чисел 10 и 3».

Примеры числовых выражений.

Приведем пример более сложного числового выражения:

\[\left( \frac{1}{4}+3,75 \right):\frac{1,25+3,47+4,75-1,47}{4\centerdot 0,5}\]

В данном числовом выражении используются простые числа, обыкновенные и десятичные дроби. Также используются знаки сложения, вычитания, умножения и деления. Черта дроби также заменяет знак деления. При кажущейся сложности, найти значение данного числового выражения довольно просто. Главное уметь выполнять операции с дробями, а также внимательно и аккуратно делать вычисления, соблюдая порядок выполнения действий.

В скобках у нас выражение $\frac{1}{4}+3,75$. Преобразуем десятичную дробь 3,75 в обыкновенную.

$3,75=3\frac{75}{100}=3\frac{3}{4}$

Итак, $\frac{1}{4}+3,75=\frac{1}{4}+3\frac{3}{4}=4$

Далее, в числителе дроби \[\frac{1,25+3,47+4,75-1,47}{4\centerdot 0,5}\] у нас выражение 1,25+3,47+4,75-1,47. Для упрощения данного выражения применим переместительный закон сложения, который гласит: «От перемены мест слагаемых сумма не изменяется». То есть, 1,25+3,47+4,75-1,47=1,25+4,75+3,47-1,47=6+2=8.

В знаменателе дроби выражение $4\centerdot 0,5=4\centerdot \frac{1}{2}=4:2=2$

Получаем $\left( \frac{1}{4}+3,75 \right):\frac{1,25+3,47+4,75-1,47}{4\centerdot 0,5}=4:\frac{8}{2}=4:4=1$

Когда числовые выражения не имеют смысла?

Рассмотрим еще один пример. В знаменателе дроби $\frac{5+5}{3\centerdot 3-9}$ значением выражения $3\centerdot 3-9$ является 0. А, как мы знаем, деление на нуль невозможно. Следовательно, у дроби $\frac{5+5}{3\centerdot 3-9}$ нет значения. Про числовые выражения, у которых нет значения, говорят, что они «не имеют смысла».

Если мы в числовом выражении помимо чисел будем использовать буквы, то у нас получится уже алгебраическое выражение.

Дата публикации: 30.08.2014 10:58 UTC

Теги: числовые выражения :: 7 класс

---

Смотрите также учебники, книги и учебные материалы:

Следующие учебники и книги:

Предыдущие статьи:

• Уроки математики, Пособие для учителей, 2 класс, Дорофеев Г.В., Миракова Т.Н., 2009
• Математика, 6 класс, Методические рекомендации, Суворова С.Б., Кузнецова Л.В., Минаева С.С., Рослова Л.О., 2013
• Математика, 6 класс, Методические рекомендации, Потапов М.К., Шевкин А.В., 2013
• Математика, 5 класс, Методические рекомендации, Суворова С.Б., Кузнецова Л.В., Минаева С.С., Рослова Л.О., 2013

---

nashol.com

Как найти значение числового выражения.

Как правило, дети начинают изучать алгебру уже в младших классах. После освоения основных принципов работы с числами, они решают примеры с одной или несколькими неизвестными переменными. Найти значение выражения подобного плана может быть довольно трудно, однако если упростить его, используя знания начальной школы, все получится легко и быстро.

 

Что такое значение выражения

Реклама

 
Числовым выражением называют алгебраическую запись, состоящую из чисел, скобок и знаков в том случае, если она имеет смысл.

Иными словами, если есть возможность найти значение выражения, значит запись не лишена смысла, и наоборот.

Примеры следующих записей являются правильными числовыми конструкциями:

• 3*8-2;
• 18;
• 15/3+6;
• 0,3*8-4/2;
• 3/1+15/5;

Отдельное число также будет представлять собой числовое выражение, как число 18 из вышеуказанного примера.
Примеры неправильных числовых конструкций, которые не имеют смысла:

Неправильные числовые примеры представляют собой лишь набор математических знаков и не имеют никакого смысла.

 

Как находить значение выражения

 
Поскольку в подобных примерах присутствуют арифметические знаки, можно сделать вывод, что они позволяют произвести арифметические вычисления. Чтобы просчитать знаки или, говоря иначе, найти значение выражения, необходимо выполнить соответствующие арифметические манипуляции.
 
В качестве примера можно рассмотреть следующую конструкцию: (120-30)/3=30. Число 30 будет являться значением числового выражения (120-30)/3.
 
Инструкция:

1. Необходимо выполнить действие в скобках, то есть из 120 вычесть 30.
2. В результате получается число 90, которое, в свою очередь, следует разделить на 3.
3. Выполнив все расчеты в правильном порядке, мы получим результат равный тридцати.

 

Понятие числового равенства

 
Числовым равенством называется ситуация, когда две части примера разделены знаком «=». То есть одна часть полностью равна (идентична) другой, пусть даже отображенной в виде других сочетаний символов и цифр.
Например, любую конструкцию типа 2+2=4 можно назвать числовым равенством, поскольку, даже поменяв части местами, смысл не изменится: 4=2+2. То же самое касается более сложных конструкций, включающих скобки, деление, умножение, действие с дробями и так далее.
 

Как находить значение выражения правильно

 
Чтобы верно найти значение выражения необходимо выполнять вычисления согласно определенному порядку действий. Этот порядок преподается еще на уроках математики, а позже – на занятиях алгебры в начальной школе. Он также известен как ступени арифметических действий.
 
Ступени арифметических действий:

1. Первая ступень – выполняется сложение и вычитание чисел.
2. Вторая ступень – выполняется деление и умножение.
3. Третья ступень – числа возводятся в квадрат или куб.

Соблюдая следующие правила, вы всегда сможете верно определить значение выражения:

1. Выполняйте действия, начиная с третьей ступени, заканчивая первой, если в примере нет скобок. То есть сперва возводите в квадрат или куб, затем делите или умножайте и только потом – складывайте и вычитайте.
2. В конструкциях со скобками сперва выполняйте действия в скобках, а затем руководствуйтесь вышеописанным порядком. Если скобок несколько, также используйте порядок действий из первого пункта.
3. В примерах в виде дроби сначала узнайте результат в числителе, затем – в знаменателе, после чего первый поделите на второй.

Найти значение выражения не составит труда, если усвоить элементарные знания начальных курсов алгебры и математики. Руководствуясь вышеописанной информацией, вы сможете решить любую задачу, даже повышенной сложности.

otvetkak.ru

Найдите значение числового логарифмического выражения – как решать

Формулировка задачи: Найдите значение числового логарифмического выражения.

Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 5 (Вычисления и преобразования).

Рассмотрим, как решаются подобные задачи на логарифмы на примерах.

Пример задачи 1:

Найдите значение выражения log_0,310 – log_0,33

Решение:

Разность логарифмов с одинаковым основанием равна логарифму частного:

log_0,310 – log_0,33 = log_0,3(10/3)

Возведем 10/3 в степень -1, вынесем степень из под логарифма (логарифм степени):

log_0,3

(10/3) = -log_0,3(3/10) = -1

Ответ: -1

Пример задачи 2:

Найдите значение выражения log₇13 / log₄₉13

Решение:

Преобразуем знаменатель: для этого вынесем степень основания из под логарифма:

log₄₉13 = log_(7)²13 = 1/2 ⋅ log₇13

Тогда значение выражения равно:

log₇13 / log₄₉13 = 2 ⋅ log₇13 / log₇13 = 2

Ответ: 2

Пример задачи 3:

Найдите значение выражения 9^log₅50 / 9^log₅2

Решение:

Преобразуем выражение:

9^log₅50 / 9^log₅2 = 9^{log₅50 – log₅2}

Разность логарифмов с одинаковыми основаниями равна логарифму частного:

log₅50 – log₅2 = log₅(50/2) = log₅25 = 2

Тогда значение выражения равно:

Ответ: 81

Пример задачи 4:

Найдите значение выражения 6log₇∛7

Решение:

Вынесем корень за пределы логарифма:

6log₇∛7 = 6 ⋅ 1/3 ⋅ log₇7 = 2

Ответ: 2

Пример задачи 5:

Найдите значение выражения log₃5 / log₃7 + log₇0,2

Решение:

Преобразуем частное с помощью формулы перехода от логарифма в одном основании к логарифму при другом основании:

Сумма логарифмов с одним основанием равна логарифму произведения:

log₇5 + log₇0,2 = log₇1 = 0

Ответ: 0

Пример задачи 6:

Найдите значение выражения log_0,83 ⋅ log₃1,25

Решение:

Преобразуем второй множитель и приведем его к тому же основанию:

log₃1,25 = log₃(5/4) = -log₃(4/5) = -log₃0,8 = -1 / log_0,83

И найдем значение выражения:

log_0,83 ⋅ log₃1,25 = -log_0,83 / log_0,83 = -1

Ответ: -1

Пример задачи 7:

Найдите значение выражения 5^log₂₅49

Решение:

Вынесем степень основания логарифма за его пределы:

Внесем ее обратно как логарифм корня:

1/2 ⋅ log₅49 = log₅(49)^1/2 = log₅7

И воспользуемся основным логарифмическим тождеством:

Ответ: 7

Пример задачи 8:

Найдите значение выражения log₄(log₂16)

Решение:

Вычислим значение выражения в скобках:

Тогда значение выражения равно:

Ответ: 1

Пример задачи 9:

Найдите значение выражения log₄2 + log_0,258

Решение:

Найдем значения каждой части выражения и получим результат:

log₄2 =1/2 ⋅ log₂2 = 1/2 ⋅ 1 = 0,5

log_0,258 = log_1/48 = 1/2 ⋅ log_1/28 = 1/2 ⋅ log_1/22³ = 1/2 ⋅ (-3) = -1,5

Тогда значение выражения равно:

log₄2 + log_0,258 = 0,5 – 1,5 = -1

Ответ: -1

Пример задачи 10:

Найдите значение выражения 2^{log₂6 – 3}

Решение:

Разложим число на множители:

2^{log₂6 – 3} = 2^log₂6 ⋅ 2^–3

Применим основное логарифмическое тождество к первому множителю и выполним оставшиеся вычисления:

2^log₂6 ⋅ 2^-3 = 6 ⋅ 1/8 = 0,75

Ответ: 0,75

Пример задачи 11:

Найдите значение выражения 7^–2log₇2

Решение:

Вынесем множитель перед логарифмом в степень, чтобы избавиться от него:

–2log₇2 = log₇2^–2 = log₇0,25

И применим основное логарифмическое тождество:

7^–2log₇2 = 7^log₇0,25 = 0,25

Ответ: 0,25

Пример задачи 12:

Найдите значение выражения (3^log₂3)^log₃2

Решение:

Если мы возведем число сначала в степень log₃2, а потом уже в степень log₂3, то сможем применить основное логарифмическое тождество:

(3^log₂3)^log₃2 = (3^log₃2)^log₂3 = 2^log₂3 = 3

Ответ: 3

Пример задачи 13:

Найдите значение выражения (1 – log₂12) ⋅ (1 – log₆12)

Решение:

Преобразуем логарифмы:

log₂12 = log₂(2 ⋅ 6) = log₂2 + log₂6 = 1 + log₂6

log₆12 = log₆(2 ⋅ 6) = log₆2 + log₆6 = log₆2 + 1

Подставим полученные значения в выражение:

(1 – (1 + log₂6)) ⋅ (1 – (log₆2 + 1)) = (1 – 1 – log₂6) ⋅ (1 – log₆2 – 1) = – log₂6 ⋅ (– log₆2) = log₂6 ⋅ log₆2

Преобразуем второй множитель, чтобы логарифмы имели одинаковые основания, и выполним остальные действия:

log₂6 ⋅ log₆2 = log₂6 ⋅ 1/log₂6 = 1

Ответ: 1

Пример задачи 14:

Найдите значение выражения log₃18 / (2 + log₃2)

Решение:

Преобразуем 2 в знаменателе в логарифм с основанием 3 (возведем 3 в степень 2 и получим число под логарифмом):

Сумма логарифмов с одним основанием в знаменателе равна логарифму произведения:

2 + log₃2 = log₃9 + log₃2 = log₃(9 ⋅ 2) = log₃18

Осталось сократить числитель и знаменатель:

Ответ: 1

worksbase.ru

Числовые выражения, преобразование числовых выражений

   Числовые выражения, преобразование числовых выражений (рациональных и иррациональных). Друзья! В этой статье для вас представлено решение числовых рациональных и иррациональных выражений. Это несложные задания на ЕГЭ по математике, достаточно знать свойства степеней и корней. Ещё необходимо уметь работать с дробями (находить их сумму, разность, произведение, частное). Процесс решения такого задания занимает минуты две, не более. Не много теории:

Говоря простым (не математическим) языком рациональные выражения — это целые и дробные выражения. Ниже рассматриваются дробные выражения.

Алгебраическое выражение называется иррациональным, если в выражении, наряду с операциями сложения, вычитания, умножения и деления производится операция возведения в рациональную (не целую) степень.

Обыкновенная дробь – это отношение, вида:

*ОТНОШЕНИЕ это есть действие — ДЕЛЕНИЕ (в данном случае «a» делим на «b»).

Также может быть записано в виде: a/b или a:b (косая черта и знак «:» означает — деление). Примеры обыкновенных дробей:

Как видно, число 4 можно записать в виде дроби 4/1. Есть дроби которые можно сократить, например, 48/8 = 6. Некоторые можно представить как конечные десятичные дроби:  ½ = 0,5    ¼ = 0,25.

Если имеем целое число с дробной частью (смешанная дробь) и нам необходимо выполнить действие, то её нужно представить в виде простой дроби. Как?

Имеем число вида:

Чтобы получить дробное равное ему число, целую часть умножаем на знаменатель и прибавляем числитель, результат записываем в числитель, знаменатель остаётся прежний:

Например:

Если нужно вычислить сумму (разность) двух дробей с разными знаменателями, необходимо дроби привести к такому виду, чтобы их знаменатели были равны:

*То есть мы получили общий знаменатель путём умножения числителя и знаменателя первой дроби на знаменатель второй и умножением числителя и знаменателя второй дроби на знаменатель первой. Я намеренно не упоминаю здесь наименьшее общее кратное, так как для некоторых, закончивших школу «давно», возможна перегрузка информацией.

Весь смысл действия в том, чтобы привести дроби к общему знаменателю, так как с разными знаменателями дроби складывать нельзя. Если же дроби имеют общий знаменатель, то результатом суммы дробей будет дробь с тем же знаменателем, а числители складывают.

Если нужно вычислить произведение двух дробей, то результатом будет дробь, числитель которой равен произведению числителей этих дробей, а знаменатель равен произведению знаменателей:

Если одну дробь необходимо разделить на другую, то данное действие сводится к произведению делимого и дроби обратной делителю:

*То есть, говоря простым языком, мы «переворачиваем» ту дробь на которую делим и деление заменяем умножением.

Свойства степени и корня можно посмотреть здесь.

Рассмотрим задания:

77387. Найдите значение выражения

Ответ: 8

77389. Найдите значение выражения

Ответ: 5

77391. Найдите значение выражения

Ответ: 10

77392. Найдите значение выражения

*В данной задаче не нужно вычислять произведения и затем отношение. Глядя на числа видно, что они прекрасно сокращаются. Достаточно произвести несложные преобразования и пример вычисляется устно.

Ответ: 10

86983. Найдите значение выражения

Упрощаем, используя формулу разности квадратов

и вычисляем:

Ответ: 702

61513. Найдите значение выражения

Ответ: 24

62385. Найдите значение выражения

Ответ: 2

62647.  Найдите значение выражения

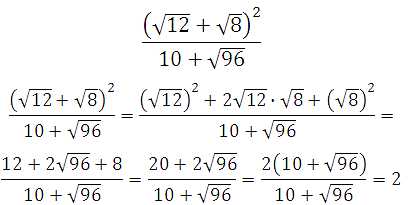
Ответ: 2

68141. Найдите

Определим числитель и знаменатель:

Числитель равен знаменателю. Это означает, что отношение равно единице:

Ответ: 1

26745. Найдите значение выражения

*Если корни имеют разные степени, то преобразования с внесением выражений под один корень выполнять нельзя. Требуется привести все корни к равной степени. Используем свойство:

Ответ: 1

77405. Найдите значение выражения

*На заключительном этапе использовали: 

Ответ: 7

Полезным будет посмотреть статью с показательными выражениями.

26900. Найдите значение выражения

Посмотреть решение

77390. Найдите значение выражения

Посмотреть решение

26735.  Найдите значение выражения

Посмотреть решение

26736. Найдите значение выражения

Посмотреть решение

26737. Найдите значение выражения

Посмотреть решение

26743. Найдите значение выражения

Посмотреть решение

26744. Найдите значение выражения

Посмотреть решение

26746. Найдите значение выражения

Посмотреть решение

26750. Найдите значение выражения

Посмотреть решение

26752. Найдите значение выражения

Посмотреть решение

На этом всё. Посмотрите, какие чудеса можно нарисовать простым карандашом.

Успеха вам!

С уважением, Александр Крутицких.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

matematikalegko.ru

Найдите значение алгебраического выражения – как решать

Формулировка задачи: Найдите значение алгебраического выражения.

Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 5 (Вычисления и преобразования).

Рассмотрим, как решаются подобные задачи на примерах.

Пример задачи 1:

Найдите значение выражения:

Решение:

Приведем разность в скобках к общему знаменателю:

Преобразуем первый множитель по формуле разности квадратов и сократим получившуюся дробь:

Ответ: 6

Пример задачи 2:

Найдите значение выражения

Решение:

Преобразуем числитель по формуле разности квадратов, приведем подобные и сократим дробь:

Ответ: -12

Пример задачи 3:

Найдите значение выражения 2x + y + 6z, если 4x + y = 5, а 12z + y = 7.

Решение:

Легко заметить, что если мы сложим 2 приведенных равенства, то получим удвоенное значение выражения, которое нужно найти:

4x + y + 12z + y = 4x + 2y + 12z = 5 + 7 = 12

Поэтому нам достаточно разделить получившееся значение пополам:

4x + 2y + 12z = 12

2x + y + 6z = 6

Ответ: 6

Пример задачи 4:

Найдите значение выражения 5(p(2x) – 2p(x + 5)), если p(x) = x – 10.

Решение:

Найдем, чему равно p(2x), для этого в функцию p(x) подставим в качестве аргумента 2x:

Найдем, чему равно p(x + 5), для этого в функцию p(x) подставим в качестве аргумента x + 5:

p(x + 5) = x + 5 – 10 = x – 5

Подставим полученные значения в выражение и вычислим его значение:

5(p(2x) – 2p(x + 5)) = 5 ⋅ (2x – 10 – 2 ⋅ (x – 5)) = 5 ⋅ (2x – 10 – 2x + 10) = 5 ⋅ 0 = 0

Ответ: 0

Пример задачи 5:

Найдите значение выражения (√10 – 2√3)(√10 + 2√3)

Решение:

Преобразуем выражение по формуле разности квадратов, чтобы избавиться от корней, и вычислим значение выражения:

(√10 – 2√3)(√10 + 2√3) = (√10)² – (2√3)² = 10 – 4 ⋅ 3 = 10 – 12 = -2

Ответ: -2

Пример задачи 6:

Найдите значение выражения

при b = 345

Решение:

Приведем разность в скобках к общему знаменателю и упростим числитель:

Преобразуем первый множитель по формуле разности квадратов и заменим упрощенную разность:

Осталось подставить значение b и вычислить результат:

Ответ: 346

Пример задачи 7:

Найдите

если

при b ≠ 0

Решение:

Найдем значение p(1/b), для этого в функцию p(b) подставим в качестве аргумента 1/b:

Поскольку p(1/b) равно p(b), частное от их деления будет равно 1:

Ответ: 1

Пример задачи 8:

Найдите p(x) + p(6 – x), если

при x ≠ 3

Решение:

Найдем значение p(6 – x), для этого в функцию p(x) подставим в качестве аргумента 6 – x:

Тогда значение выражения равно:

p(x) + p(6 – x) = p(x) – p(x) = 0

Ответ: 0

Пример задачи 9:

Найдите a/b, если

Решение:

Разделим и числитель и знаменатель на b:

Таким образом среди неизвестных осталась только дробь a/b, которую и нужно найти. Вычислим ее значение из равенства:

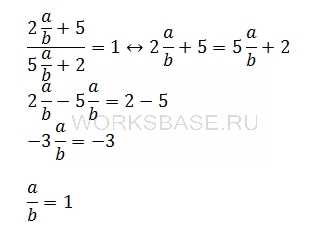
Ответ: 1

Пример задачи 10:

Найдите

если a/b = 3.

Решение:

Разделим числитель и знаменатель на b и заменим a/b на 3, после чего упростим выражение:

Ответ: 2

worksbase.ru

Репетитор по математике.Найти значение выражения. Задание 1 ГИА (ОГЭ)

---

Найти значение выражения обычно предлагают школьникам в первой части ОГЭ (ГИА) и они достаточно просты. Для решения такого задания нужно уметь вычислять, то есть знать таблицу умножения, уметь умножать десятичные числа, понимать смысл дроби и уметь работать со степенями. Таким образом, первое задание проверяет сразу несколько умений школьника. Найти значение выражения, не умея работать с числами и степенями, невозможно.

Найти значение выражения

Решение: Перемножим 6,8 на 2, получим 13,6. Теперь умножим на основания степеней одинаковые, значит, складываем показатели степеней.
Получим В итоге получим
Ответ:

Найти значение выражения

Решение: тогда
Ответ: -30.

Найти значение выражения

Решение: перепишем данное выражение в следующем виде
Почему мы смогли так записать? Потому что мы использовали свойство степени:
Тогда в нашем задании мы получаем или
или
или
Итак, имеем:
Ответ: 0,3054.

Найти значение выражения

Решение: Можно просто перемножить 6,8 на 7,5, а затем, полученное число разделить столбиком на 8,5. А можно перевести десятичные дроби в обыкновенные и попробовать упростить.

68 и 10 сократим на 2, а 75 и 85 на 5, тогда получим:
Ответ: 6.

Найти значение выражения

 

Решение:
Ответ:

 

Следующая запись »

---

repetitor-mathematics.ru