абсолютное значение числа — это… Что такое абсолютное значение числа?
- абсолютное значение числа
абсолютное значение числа
модуль числа
абсолютная величина числа
—
[Л.Г.Суменко. Англо-русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.]абсолютное значение
Величина числа без учета его знака.
Так, числа +18 и -18 имеют одно и то же абсолютное значение: 18.
[http://www.morepc.ru/dict/]Тематики
- информационные технологии в целом
Синонимы
- модуль числа
- абсолютная величина числа
Справочник технического переводчика. – Интент. 2009-2013.
- абсолютное значение погрешности
- абсолютное измерение
Смотреть что такое «абсолютное значение числа» в других словарях:
АБСОЛЮТНОЕ ЗНАЧЕНИЕ — на теле отображение тела Кв множество действительных чисел, удовлетворяющее условиям: А. з. часто обозначается вместо . А. з. наз. также нормой, мультипликативным нормированием. А. з. могут рассматриваться на любом кольце со значениями в линейно… … Математическая энциклопедия
Значение (значения) — Значение: Значение смысловое содержание слова, фразы или знака. Значение функции результат вычисления функции. Абсолютное значение модуль числа. Значение величины отношение измеренной физической величины к единице… … Википедия
Числа — Во многих культурах, особенно в вавилонской, индуистской и пифагорейской, число есть фундаментальный принцип, лежащий в основе мира вещей. Оно начало всех вещей и той гармонии вселенной, стоящей за их внешней связью. Число это основной принцип… … Словарь символов
ГОСТ 31369-2008: Газ природный. Вычисление теплоты сгорания, плотности, относительной плотности и числа Воббе на основе компонентного состава
— Терминология ГОСТ 31369 2008: Газ природный. Вычисление теплоты сгорания, плотности, относительной плотности и числа Воббе на основе компонентного состава оригинал документа: 2.1 высшая теплота сгорания (superior calorific value): Количество… … Словарь-справочник терминов нормативно-технической документацииМОЛЕКУЛЯРНЫЙ ВЕС — есть относительный вес молекулы вещества. Кроме возможности находиться в трех различных фазах (см. Аггрвгатное состояние) вещества обладают способностью распределяться одно в другом, образуя так наз. растворы. Согласно вант Гоффу (van t Hoff)… … Большая медицинская энциклопедия
Московский химический лицей № 1303 — Лицей № 1303 … Википедия
Коэффициент корреляции — (Correlation coefficient) Коэффициент корреляции это статистический показатель зависимости двух случайных величин Определение коэффициента корреляции, виды коэффициентов корреляции, свойства коэффициента корреляции, вычисление и применение… … Энциклопедия инвестора
Корреляция — (Correlation) Корреляция это статистическая взаимосвязь двух или нескольких случайных величин Понятие корреляции, виды корреляции, коэффициент корреляции, корреляционный анализ, корреляция цен, корреляция валютных пар на Форекс Содержание… … Энциклопедия инвестора
ВРЕМЯ — обозначает течение, длительность и последовательность событий. Оно есть условие существования конечных вещей и существ тварного мира. Согласно христ. учению, В. как творение Божие подчинено домостроительству спасения и своими границами имеет… … Православная энциклопедия
предел повторяемости — 3.7 предел повторяемости: Абсолютная разность результатов максимального и минимального значений из указанного числа измерений, выполненных в условиях повторяемости по ГОСТ Р ИСО 5725 1. Источник … Словарь-справочник терминов нормативно-технической документации
technical_translator_dictionary.academic.ru
Абсолютное значение — это… Что такое Абсолютное значение?
1) Нормирование — от глагола «Нормировать» в первом значении : НОРМИРОВАТЬ, нормирую, нормируешь, сов. и несов., что. Регулировать что-н., установить (устанавливать) законные пределы чему-н., ввести (вводить) в норму. Нормировать зарплату. Нормировать работу. (Толковаый словарь русского языка под редакцией Ушакова.)
2) Норми́рование(мат.) — отображение элементов поля F в некоторое упорядоченное поле P x→|x|, обладающее следующими свойствами:
1)|x|≥0 и |x|=0 только при x=0
2)|xy| ≤ |x||y|
3)|x+y| ≤ |x|+|y|
Если вместо 3) выполняется более сильное условие:
3a)|x+y| ≤ max(|x|,|y|), то нормирование называется неархимедовым.
Значение | x | (иногда обозначаемое ) называется нормой элемента x. Если упорядоченное поле P является полем действительных чисел R, то нормирование часто называют абсолютным значением.
Примеры нормирований
- Нормирование, при котором |0|=0, |x|=1 для остальных x. Такое нормирование называется тривиальным.
- Обычная абсолютная величина в поле действительных чисел R или модуль в поле комплексных чисел C является нормированием.
- Пусть Q — поле рациональных чисел, а p — некоторое простое число. Любое рациональное число можно представить в виде дроби x=apn/b, где a и b не кратны p. Можно определить следующее нормирование |x|p=p-n. Это нормирование является неархимедовым и называется p-адическим нормированием.
Свойства нормы
- |1|=|-1|=1
- | |x|-|y| |≤|x-y| (в этом случае абсолютная величина в упорядоченном поле P берётся от разности двух норм |x|-|y| элементов поля F)
- Действительнозначное нормирование является неархимедовым тогда и только тогда, когда существует положительное число A, такое, что для любой суммы единичных элементов поля F :
3b) |1+1+…+1|≤A
Пусть данное условие выполнено. Тогда для любых элементов x и y из поля F имеем:
|(x+y)n|=|xn+…Cnixnyi+…yn|≤(n+1)A(max(|x|,|y|)n
Извлекая из обеих частей корень и переходя к пределу при n→∞
Нормированное поле как метрическое пространство
Из свойств 1-3 немедленно следует, что определяя расстояние между двумя элементами действительнозначного нормированного поля F как норму разности |x-y| мы превращеем его в метрическое пространство, в случае неархимедовой нормы — в ультраметрическое пространство. Разные нормы определяют разные метрики. Если при этом они определяют одинаковую топологию в F, то такие нормы называются зависимыми.
Пополнение
Как и для любого метрического пространства можно ввести понятие полноты и доказать, что любое нормированное поле F изоморфно вкладывается в полное нормированное поле F*, то есть существует изоморфизм . Норма в F* продолжает норму в F, то есть для каждого x из F: , причём F плотно в F* относительно этой нормы. Любое такое поле F* определено однозначно с точностью до изоморфизма, сохраняющего нормы (изометрии) и тождественного на F; оно называется пополнением поля F.
Пример. Пополнением поля рациональных чисел Q с p-адической метрикой является поле p-адических чисел Qp.
Литература
- Ван дер Варден Б. Л. Алгебра — М: Наука. 1975.
- Зарисский О., Самюэль П. Коммутативная алгебра т.2 — М: ИЛ. 1963.
- Ленг С. Алгебра — М: Мир. 1967.
См. также
- Теорема Островского
- Аппроксимационная теорема
Wikimedia Foundation. 2010.
dic.academic.ru
Определение абсолютное значение общее значение и понятие. Что это такое абсолютное значение
Понятие абсолютного значения используется в области математики для обозначения значения, число которого выходит за его знак. Это означает, что абсолютное значение, также известное как модуль, является

Возьмите случай абсолютного значения 5 . Это абсолютное значение как +5 (5 положительных) и -5 (5 отрицательных). Короче говоря, абсолютное значение одинаково для положительного и отрицательного числа: в данном случае 5 . Следует отметить, что абсолютное значение записывается между двумя параллельными вертикальными полосами; следовательно, правильное обозначение | 5 |,
Определение понятия указывает, что абсолютное значение всегда равно или больше 0 и никогда не бывает отрицательным . Из вышесказанного можно добавить, что абсолютное значение противоположных чисел одинаково; 8 и -8, таким образом, имеют одинаковое абсолютное значение: | 8 |,
Вы также можете понимать абсолютное значение как расстояние между числом и 0 . Число 563 и число -563 находятся на числовой линии на одинаковом расстоянии от 0 . Таким образом, это абсолютная величина обоих: | 563 |,
Расстояние между двумя действительными числами, с другой стороны, является абсолютной величиной их разности. Например, между 8 и 5 существует расстояние 3 . Эта разница имеет абсолютное значение | 3 |,
Понятие абсолютной стоимости присутствует в нескольких предметах математики, и вектор является одним из них; точнее, именно в векторной норме
Под евклидовым пространством мы понимаем некое геометрическое пространство, в котором выполняются аксиомы Евклида . Аксиома — это суждение, чья ясность такова, что не требует подтверждения; в частности, в области математики он называется так фундаментальными и недоказуемыми принципами, на которых строятся теории .
Евклид, с другой стороны, родился в Греции примерно в 325 году. C., а его преданность числам сделала его достойным звания «Отец геометрии». Его самая важная работа представляет собой сборник из тринадцати книг, сгруппированных под названием « Элементы », в котором представлены вышеупомянутые аксиомы (также известные как постулаты Евклида ), и мы кратко рассмотрим ниже:
 1) если мы возьмем любые две точки, их можно соединить с помощью линии;
1) если мы возьмем любые две точки, их можно соединить с помощью линии;
2) можно непрерывно расширять все сегменты независимо от направления;
3) Окружности могут исходить из любой точки, которая будет считаться ее центром, а ее радиус может принимать любое значение;
4) любая пара прямых углов конгруэнтна;
5) Можно провести одну прямую параллельно другой из точки за пределами последней.
Обнажив основы евклидовых пространств, можно сказать, что векторы в них могут быть представлены в виде отрезков, ориентированных между любыми двумя точками. Если мы возьмем вектор, мы можем определить его норму как расстояние между двумя точками, которые служат пределом; настолько, что в евклидовом пространстве эта норма соответствует модулю, то есть длине указанного вектора.
Как и абсолютное значение, модуль вектора всегда является положительным числом или нулем, поскольку он представляет
ru.tax-definition.org
Абсолютная величина — это… Что такое Абсолютная величина?
График вещественной функции Модуль и другие характеристики комплексного числаАбсолю́тная величина́ или мо́дуль числа — неотрицательное число, определение которого зависит от типа числа . Обозначается: .
В случае вещественного абсолютная величина есть непрерывная кусочно-линейная функция, определённая следующим образом:
Обобщением этого понятия является модуль комплексного числа , также иногда называемый абсолютной величиной[1]. Он определяется по формуле:
Основные свойства
С геометрической точки зрения, модуль вещественного или комплексного числа есть расстояние между числом и началом координат. В математике широко используется тот факт, что геометрически величина означает расстояние между точками и и, таким образом, может быть использована как мера близости одной (вещественной или комплексной) величины к другой.
Вещественные числа
Комплексные числа
Алгебраические свойства
Для любых имеют место следующие соотношения:
Как для вещественных, так и для комплексных имеют место соотношения:
История
Считают, что термин предложил использовать Котс, ученик Ньютона. Лейбниц тоже использовал эту функцию, которую называл модулем и обозначал: mol x. Общепринятое обозначение абсолютной величины введено в 1841 году Вейерштрассом. Для комплексных чисел это понятие ввели Коши и Арган в начале XIX века.
В языках программирования
Поскольку эта функция вычисляется достаточно просто (только сравнениями и присваиванием), то обычно она входит в стандартный список функций во все языки программирования. Например, в Pascal есть функция abs(x), а в C fabs(x) для вещественного типа.
Обобщение
Обобщением понятия модуля можно считать норму элемента многомерного векторного пространства, обозначаемую . Норма вектора в евклидовом пространстве иногда тоже называется модулем. По аналогии с модулем разности чисел, норма разности двух векторов является мерой близости между ними. В отличие от модуля числа, норма вектора может определяться различными способами, однако в случае одномерного пространства норма вектора пропорциональна (часто и равна) модулю его единственной координаты.
См. также
Примечания
dic.academic.ru
АБСОЛЮТНОЕ ЗНАЧЕНИЕ — это… Что такое АБСОЛЮТНОЕ ЗНАЧЕНИЕ?
- АБСОЛЮТНОЕ ЗНАЧЕНИЕ
- АБСОЛЮТНОЕ ЗНАЧЕНИЕ
-
Экономика. Толковый словарь. — М.: «ИНФРА-М», Издательство «Весь Мир». Дж. Блэк. Общая редакция: д.э.н. Осадчая И.М.. 2000.
Экономический словарь. 2000.
- «ЯЩИК»
- АБСОЛЮТНЫЙ МАКСИМУМ
Смотреть что такое «АБСОЛЮТНОЕ ЗНАЧЕНИЕ» в других словарях:
абсолютное значение — [Интент] Параллельные тексты EN RU The measured voltage value is displayed both as a per unit quantity referred to the nominal voltage of the P63x and as a primary quantity. [Schneider Electric] Измеренное значение напряжения отображается как в… … Справочник технического переводчика
абсолютное значение — absoliučioji vertė statusas T sritis fizika atitikmenys: angl. absolute value vok. Absolutwert, m rus. абсолютное значение, n pranc. valeur absolue, f … Fizikos terminų žodynas
АБСОЛЮТНОЕ ЗНАЧЕНИЕ — См. значение абсолютное … Толковый словарь по психологии
Абсолютное значение — 1) Нормирование от глагола Нормировать в первом значении : НОРМИРОВАТЬ, нормирую, нормируешь, сов. и несов., что. Регулировать что н., установить (устанавливать) законные пределы чему н., ввести (вводить) в норму. Нормировать зарплату.… … Википедия
АБСОЛЮТНОЕ ЗНАЧЕНИЕ — на теле отображение тела Кв множество действительных чисел, удовлетворяющее условиям: А. з. часто обозначается вместо . А. з. наз. также нормой, мультипликативным нормированием. А. з. могут рассматриваться на любом кольце со значениями в линейно… … Математическая энциклопедия
абсолютное значение числа — модуль числа абсолютная величина числа — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] абсолютное значение Величина числа без учета его знака. Так, числа +18 и 18 имеют одно и то же абсолютное… … Справочник технического переводчика
абсолютное значение погрешности — Значение погрешности без учета ее знака (модуль погрешности). Примечание. Необходимо различать термины абсолютная погрешность и абсолютное значение погрешности. [РМГ 29 99] Тематики метрология, основные понятия EN absolute value of an error FR… … Справочник технического переводчика
Абсолютное значение мощности побочных излучений — Значение уровня побочных излучений, выраженное в единицах мощности (мВт, мкВт), подаваемой в фидер антенны на частоте побочного излучения Источник … Словарь-справочник терминов нормативно-технической документации
Абсолютное значение мощности побочных колебаний — Значение уровня побочных колебаний, выраженное в единицах мощности (мВт, мкВт) Источник … Словарь-справочник терминов нормативно-технической документации
абсолютное значение ошибки — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва] Тематики электротехника, основные понятия EN absolute error … Справочник технического переводчика
Книги
- Кинетостатика плоских механизмов, Юдин В. А., Кинетостатика механизмов, разбирая вопросы динамики заданного движения, обычно содержит решение двух основных задач, в соответствии с которыми настоящая работа подразделяется на две следующие… Издатель: ЁЁ Медиа, Производитель: ЁЁ Медиа, Подробнее Купить за 2591 грн (только Украина)
- Кинетостатика плоских механизмов, Юдин В. А., Кинетостатика механизмов, разбирая вопросы динамики заданного движения, обычносодержит решение двух основных задач, в соответствии с которыми настоящая работа подразделяется на две следующие… Серия: — Издатель: ЁЁ Медиа, Подробнее Купить за 2003 руб
- Конец власти. От залов заседаний до полей сражений, от церкви до государства. Почему управлять сегодня нужно иначе, Мойзес Наим, Мойзес Наим был главным редактором журнала Foreign Policy и исполнительным директором Всемирного банка, он лучше многих представляет, что такое власть в мировом масштабе. Его книга предлагает… Издатель: Культур-Мультур, Подробнее Купить за 379 руб аудиокнига
dic.academic.ru
абсолютное значение числа — это… Что такое абсолютное значение числа?
- абсолютное значение числа
- absolute value
абсолютное значение числа
модуль числа
абсолютная величина числа
—
[Л.Г.Суменко. Англо-русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.]абсолютное значение
Величина числа без учета его знака.
Так, числа +18 и -18 имеют одно и то же абсолютное значение: 18.
[http://www.morepc.ru/dict/]Тематики
- информационные технологии в целом
Синонимы
- модуль числа
- абсолютная величина числа
EN
Русско-английский словарь нормативно-технической терминологии. academic.ru. 2015.
- абсолютное значение погрешности
- абсолютное измерение
Смотреть что такое «абсолютное значение числа» в других словарях:
абсолютное значение числа — модуль числа абсолютная величина числа — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] абсолютное значение Величина числа без учета его знака. Так, числа +18 и 18 имеют одно и то же абсолютное… … Справочник технического переводчика
АБСОЛЮТНОЕ ЗНАЧЕНИЕ — на теле отображение тела Кв множество действительных чисел, удовлетворяющее условиям: А. з. часто обозначается вместо . А. з. наз. также нормой, мультипликативным нормированием. А. з. могут рассматриваться на любом кольце со значениями в линейно… … Математическая энциклопедия
Значение (значения) — Значение: Значение смысловое содержание слова, фразы или знака. Значение функции результат вычисления функции. Абсолютное значение модуль числа. Значение величины отношение измеренной физической величины к единице… … Википедия
Числа — Во многих культурах, особенно в вавилонской, индуистской и пифагорейской, число есть фундаментальный принцип, лежащий в основе мира вещей. Оно начало всех вещей и той гармонии вселенной, стоящей за их внешней связью. Число это основной принцип… … Словарь символов
ГОСТ 31369-2008: Газ природный. Вычисление теплоты сгорания, плотности, относительной плотности и числа Воббе на основе компонентного состава — Терминология ГОСТ 31369 2008: Газ природный. Вычисление теплоты сгорания, плотности, относительной плотности и числа Воббе на основе компонентного состава оригинал документа: 2.1 высшая теплота сгорания (superior calorific value): Количество… … Словарь-справочник терминов нормативно-технической документации
МОЛЕКУЛЯРНЫЙ ВЕС — есть относительный вес молекулы вещества. Кроме возможности находиться в трех различных фазах (см. Аггрвгатное состояние) вещества обладают способностью распределяться одно в другом, образуя так наз. растворы. Согласно вант Гоффу (van t Hoff)… … Большая медицинская энциклопедия
Московский химический лицей № 1303 — Лицей № 1303 … Википедия
Коэффициент корреляции — (Correlation coefficient) Коэффициент корреляции это статистический показатель зависимости двух случайных величин Определение коэффициента корреляции, виды коэффициентов корреляции, свойства коэффициента корреляции, вычисление и применение… … Энциклопедия инвестора
Корреляция — (Correlation) Корреляция это статистическая взаимосвязь двух или нескольких случайных величин Понятие корреляции, виды корреляции, коэффициент корреляции, корреляционный анализ, корреляция цен, корреляция валютных пар на Форекс Содержание… … Энциклопедия инвестора
ВРЕМЯ — обозначает течение, длительность и последовательность событий. Оно есть условие существования конечных вещей и существ тварного мира. Согласно христ. учению, В. как творение Божие подчинено домостроительству спасения и своими границами имеет… … Православная энциклопедия
предел повторяемости — 3.7 предел повторяемости: Абсолютная разность результатов максимального и минимального значений из указанного числа измерений, выполненных в условиях повторяемости по ГОСТ Р ИСО 5725 1. Источник … Словарь-справочник терминов нормативно-технической документации
normative_ru_en.academic.ru
1.3. Абсолютная величина числа
Определение. Абсолютной
величиной (или модулем) числа х называется само число  ,
если
,
если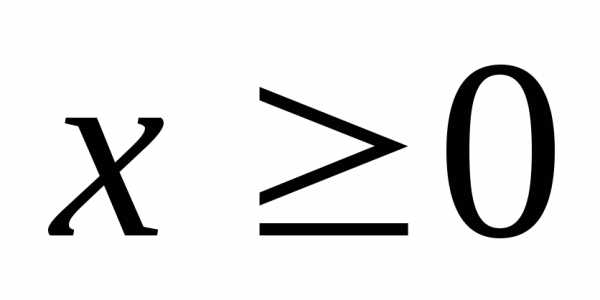 ,
число (
,
число (  ),
если
),
если .
.
Абсолютная величина
числа  обозначается
обозначается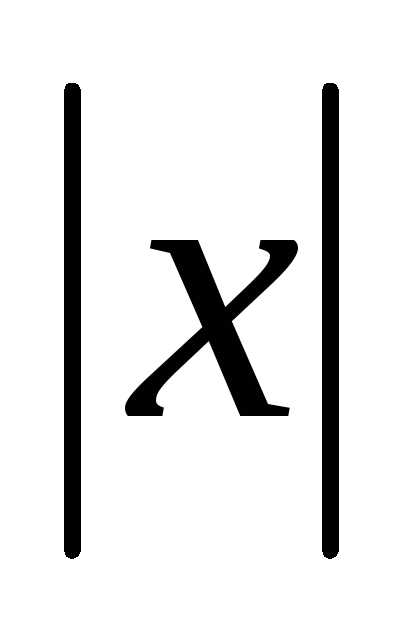 .
Таким образом,
.
Таким образом,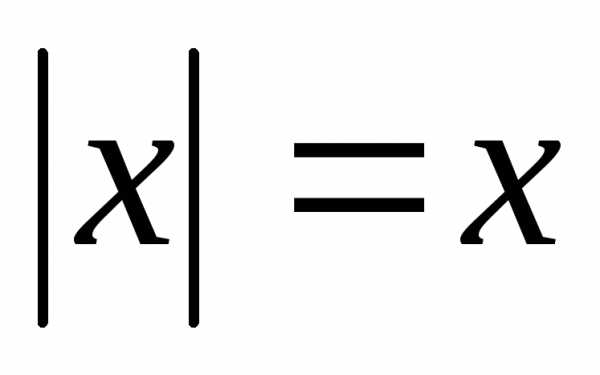 ,
если
,
если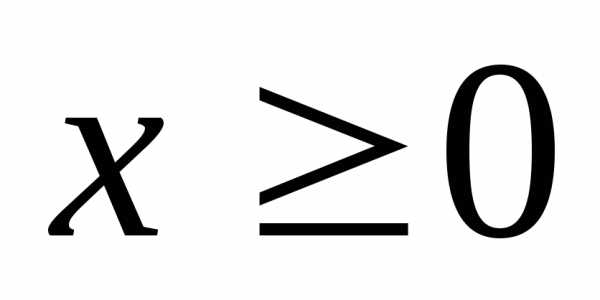 ,
и
,
и ,
если
,
если .
.
Из определения абсолютной величины числа вытекает ряд ее свойств.
 . Доказательство. Если
. Доказательство. Если  ,
то
,
то .
Если
.
Если ,
то
,
то ,
но
,
но ,
т. е.
,
т. е. .
. . Доказательство. Если
. Доказательство. Если  ,
то
,
то и тогда.
Если
и тогда.
Если ,
то
,
то ,
и тогда.
,
и тогда.. Доказательство. Если
 , то
, то  ,
,  .
Отсюда
.
Отсюда ,
т. е..
Если
,
т. е..
Если ,
то
,
то ,
откуда
,
откуда .
Так как
.
Так как ,
то
,
то ,
или,
откуда,
т. е.
,
или,
откуда,
т. е. .
Поэтому.
Получаем, что .
.
Поэтому.
Получаем, что .
Теорема 1. Пусть 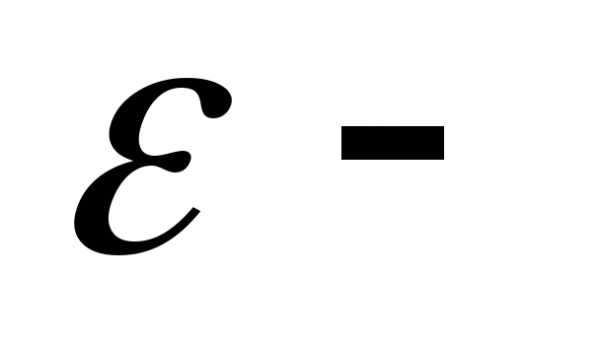 положительное число. Тогда неравенства
положительное число. Тогда неравенства иравносильны.(( , 0: х ) ( — х )).
иравносильны.(( , 0: х ) ( — х )).
Доказательство. Пусть 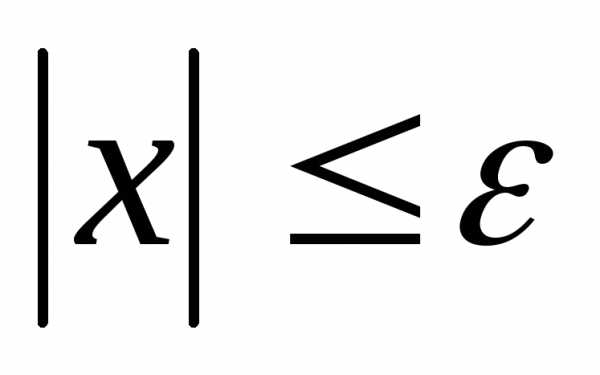 .
Если
.
Если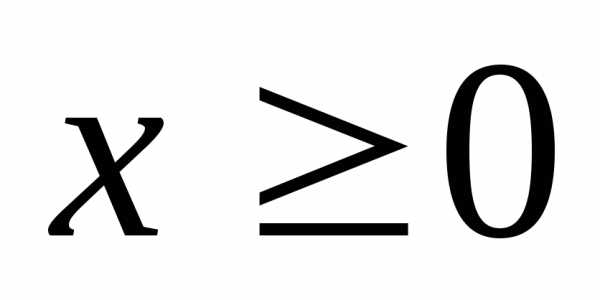 ,
то
,
то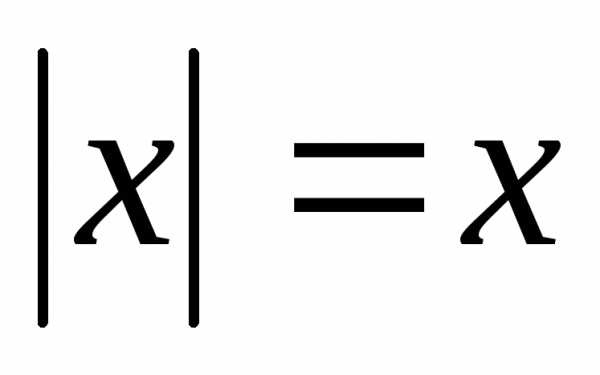 ,
поэтому
,
поэтому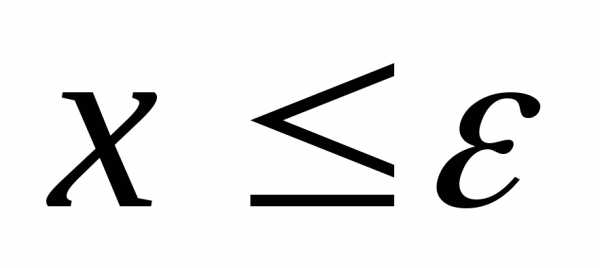 ,
таким образом,.
Если
,
таким образом,.
Если ,
то,
следовательно,
,
то,
следовательно,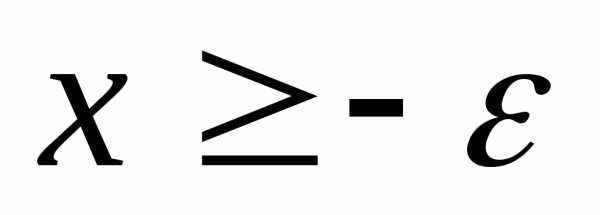 ,
откуда.
Объединяя неравенстваи,
получаем, что
,
откуда.
Объединяя неравенстваи,
получаем, что ,.
,.
Пусть
.
Это означает, что одновременно выполняются
неравенства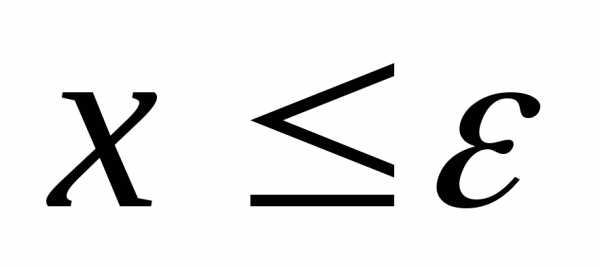 и
и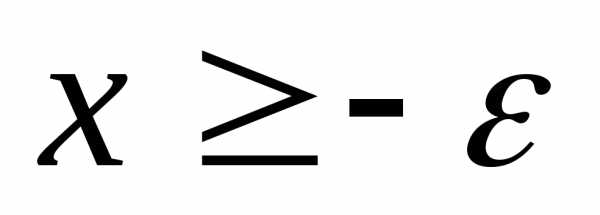 .
Из последнего неравенства следует, что
.
Из последнего неравенства следует, что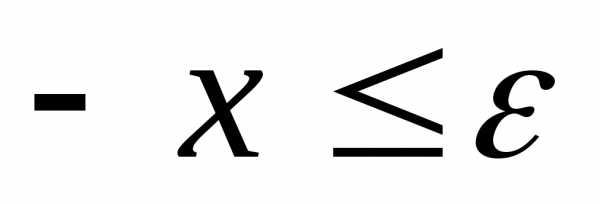 .
По определению,
.
По определению,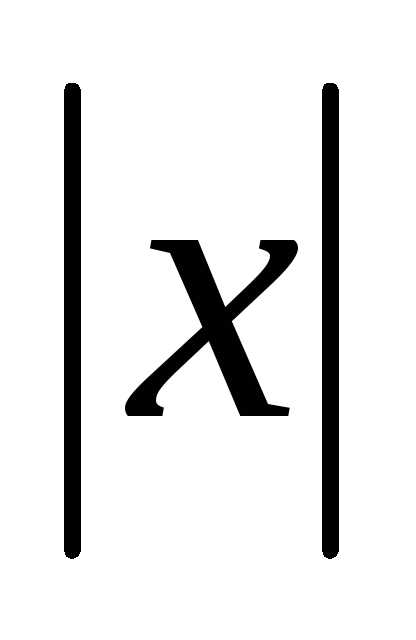 есть либо
есть либо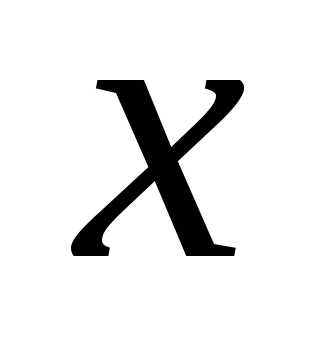 ,
либо
,
либо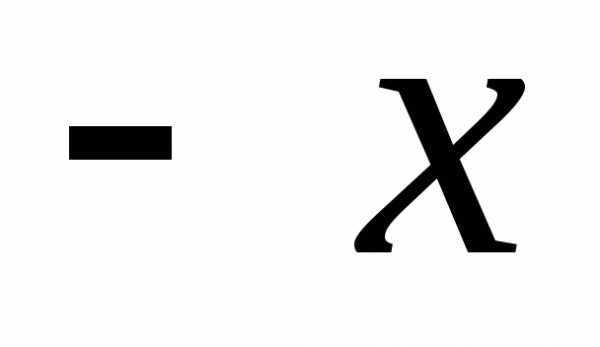 ,
поэтому
,
поэтому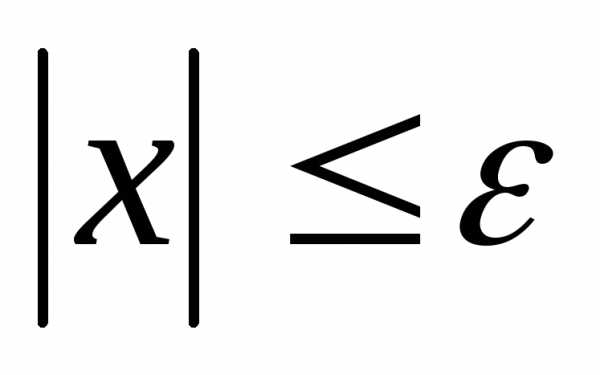 .
.
Теорема 2. Абсолютная величина суммы двух чисел не больше суммы абсолютных величин этих чисел, т. е. .
Доказательство. Пусть 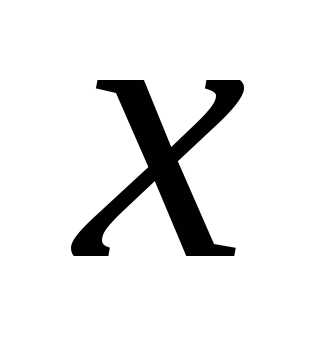 ,
, – произвольные числа. По свойству 3 для
них выполняются неравенства:,.
Поэтому, складывая эти неравенства,
получаем.
По предыдущей теореме это равносильно
неравенству.
– произвольные числа. По свойству 3 для
них выполняются неравенства:,.
Поэтому, складывая эти неравенства,
получаем.
По предыдущей теореме это равносильно
неравенству.
Из этой теоремы следует, что абсолютная величина разности двух чисел не больше суммы абсолютных величин этих чисел, т. е. .
Теорема 3. Абсолютная величина разности двух чисел не меньше разности абсолютных величин этих чисел, т. е. .
Доказательство. Для любых чисел 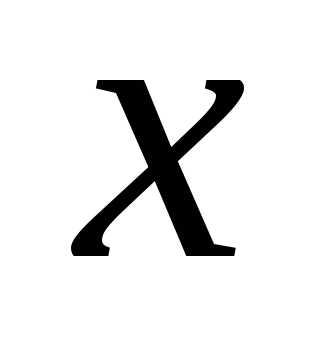 и
и :.
По предыдущей теореме.
Поэтому.
:.
По предыдущей теореме.
Поэтому.
Аналогично доказывается утверждение о том, что абсолютная величина суммы двух чисел не меньше разности абсолютных величин этих чисел, т. е. .
Замечание. Для любых чисел х и у имеют место легко
проверяемые соотношения 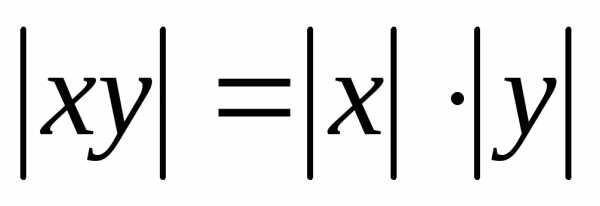 и
и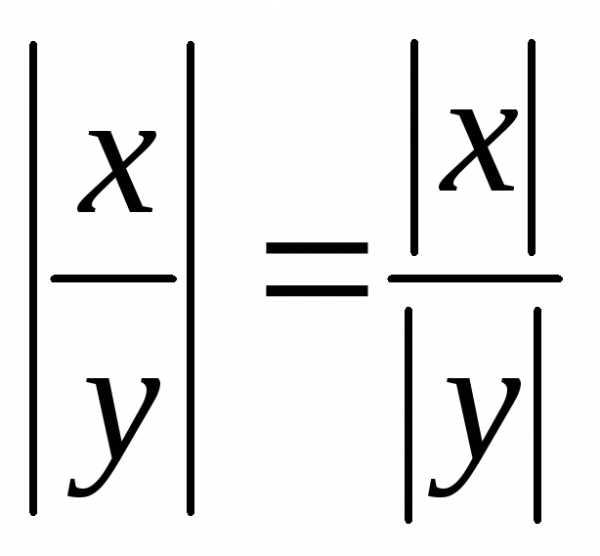 ,
если
,
если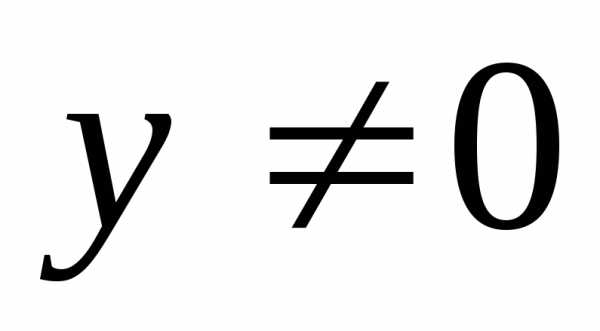 .
Эти соотношения предлагается доказать
самостоятельно.
.
Эти соотношения предлагается доказать
самостоятельно.
1.4. Геометрическое изображение вещественных чисел
Рассмотрим произвольную прямую. На ней можно указать два противоположных направления. Выберем одно из направлений и масштабную единицу для измерения длин отрезков.
Определение. Прямая с выбранным на ней направлением называется осью.
Рассмотрим на оси две произвольные точки А и В.
Определение. Отрезок с граничными точками А и В называется направленным, если указано, какая из этих точек считается началом, а какая – концом отрезка.
Направленный
отрезок с началом в точке А и концом в
точке В обозначим 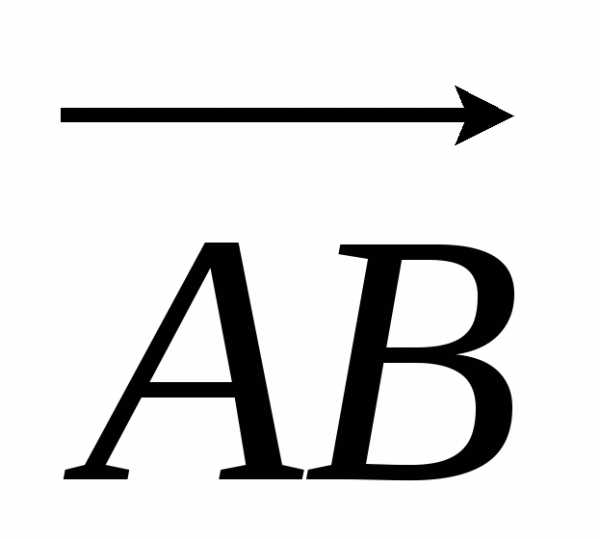 и будем считать, что он направлен от
начала отрезка к концу.Нулевыми
направленными отрезками будем называть те, у которых начало и
конец совпадают. Длина направленного
отрезка
и будем считать, что он направлен от
начала отрезка к концу.Нулевыми
направленными отрезками будем называть те, у которых начало и
конец совпадают. Длина направленного
отрезка 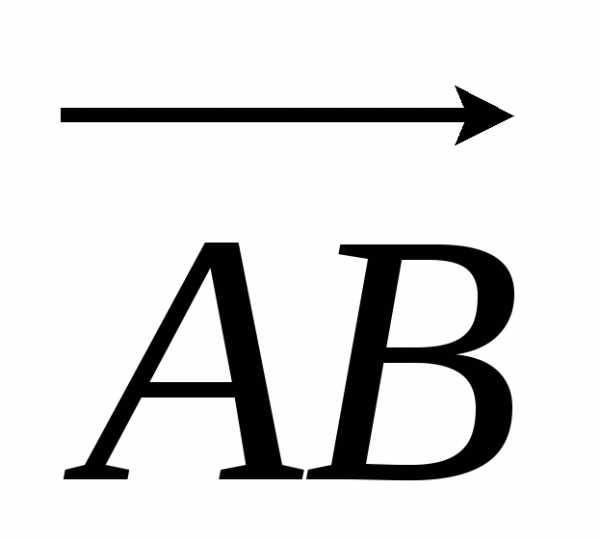 обозначается
обозначается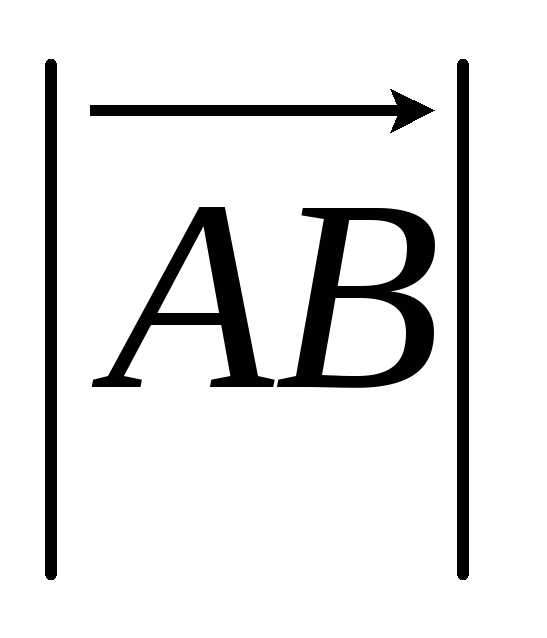 или.
или.
Для направленных отрезков, лежащих на оси (или на параллельных осях), вводится понятие величины направленного отрезка.
Определение.
Величиной АВ направленного
отрезка  называется число, равное
называется число, равное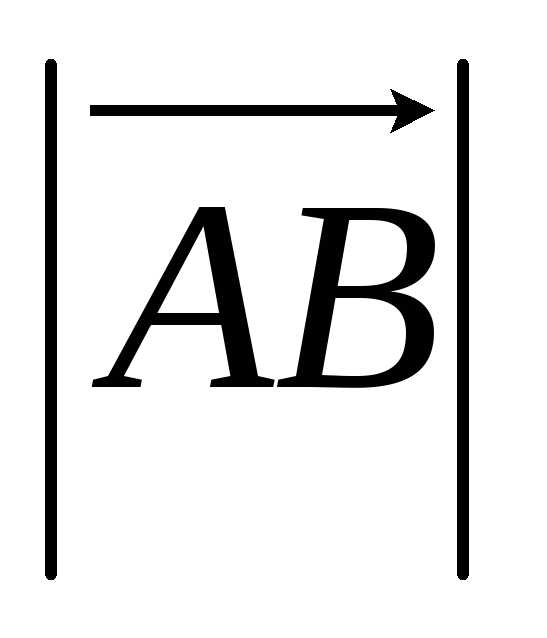 ,
если направления отрезка и оси совпадают,
и
,
если направления отрезка и оси совпадают,
и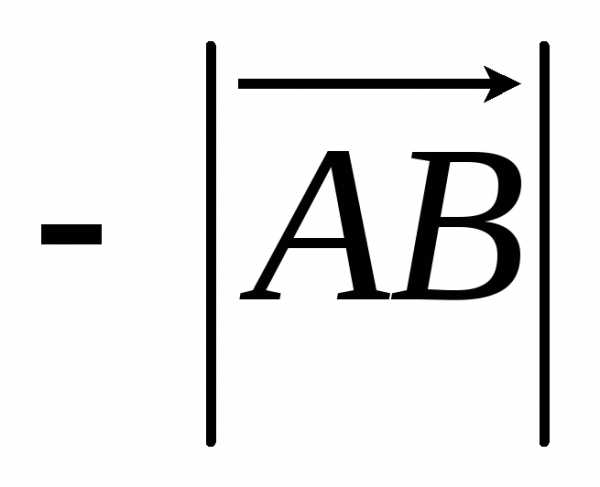 ,
если эти направления противоположны.
,
если эти направления противоположны.
Величины направленных
отрезков 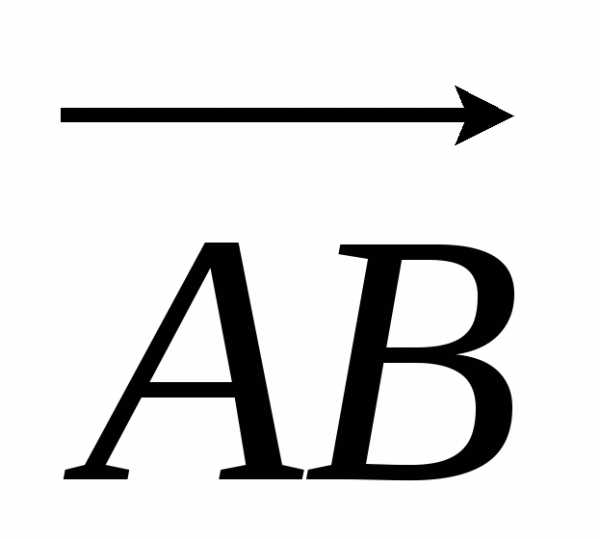 и
и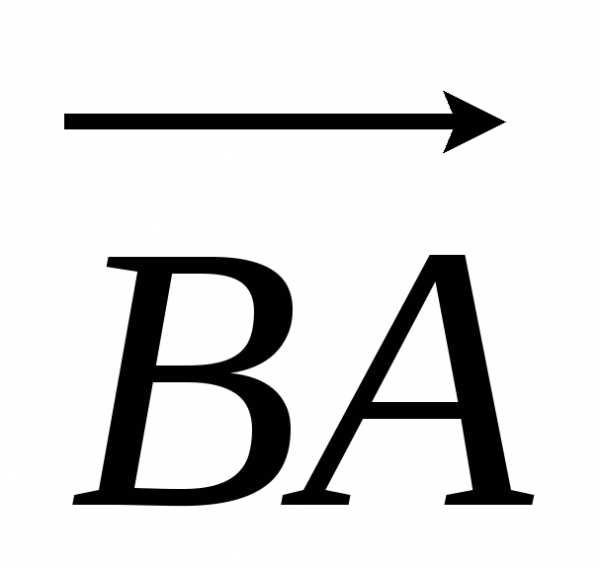 при любом направлении оси отличаются
знаками.
при любом направлении оси отличаются
знаками.
Если точки А и В
совпадают, то величина направленного
отрезка  считается равной нулю.
считается равной нулю.
Определение. Два ненулевых направленных отрезка называются равными, если при совмещении начал этих отрезков совпадают и их концы. Любые два нулевых направленных отрезка считаются равными.
Над направленными отрезками определены следующие операции операция сложения и умножения на число.
О
D
пределение. Суммой направленных отрезков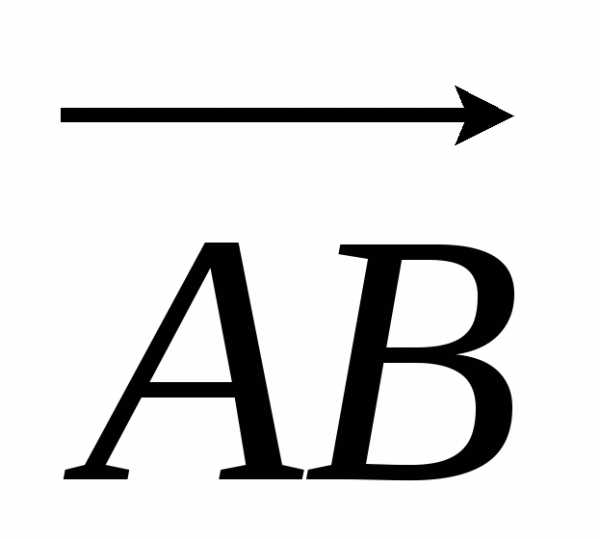 и
и называется направленный отрезок,
полученный при совмещении начала
называется направленный отрезок,
полученный при совмещении начала отрезка
отрезка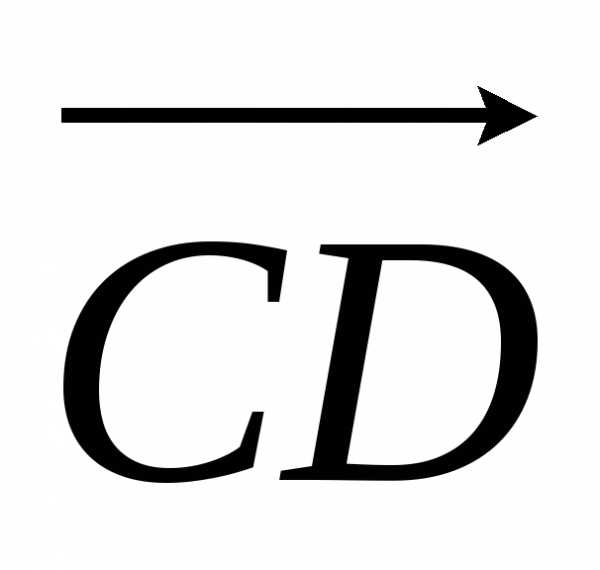 с концом
с концом отрезка
отрезка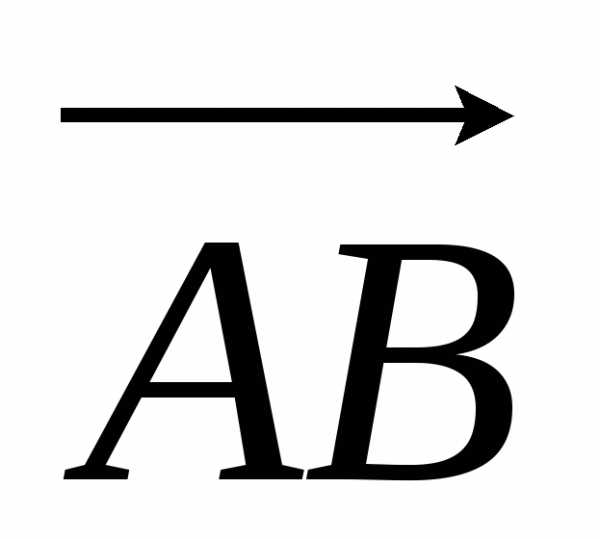 .
.В
С
А
Теорема. Величина суммы направленных отрезков равна сумме величин слагаемых отрезков.
Доказательство. Пусть хотя бы один из отрезков 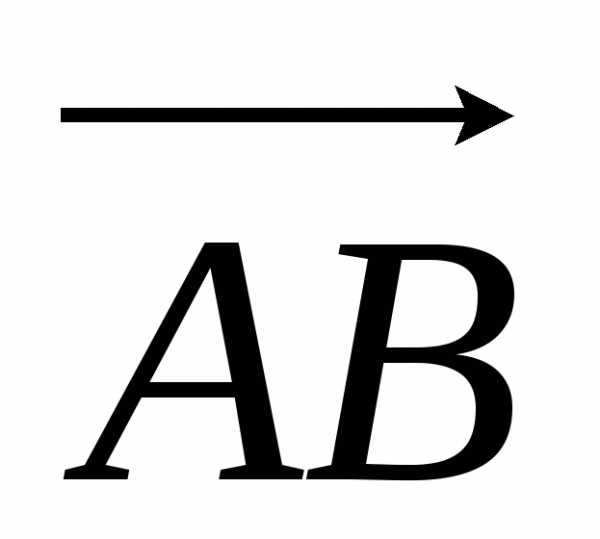 и
и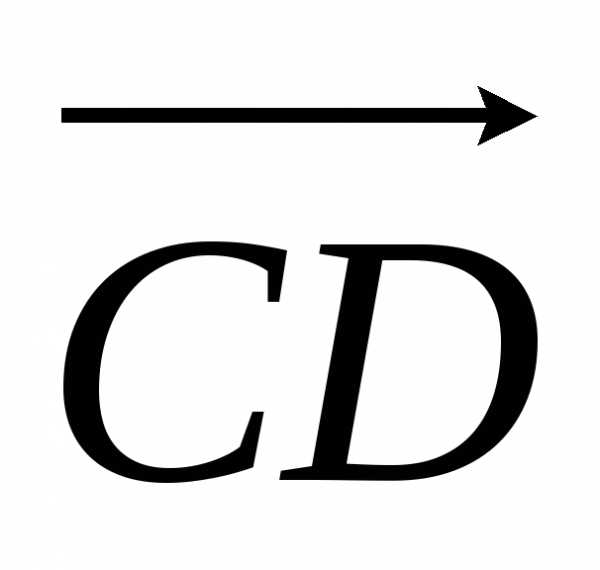 является нулевым, то в этом случае сумма
совпадает с другим отрезком и утверждение
теоремы справедливо. Если оба отрезка
ненулевые, то при совмещении начала
является нулевым, то в этом случае сумма
совпадает с другим отрезком и утверждение
теоремы справедливо. Если оба отрезка
ненулевые, то при совмещении начала отрезка
отрезка с концом
с концом отрезка
отрезка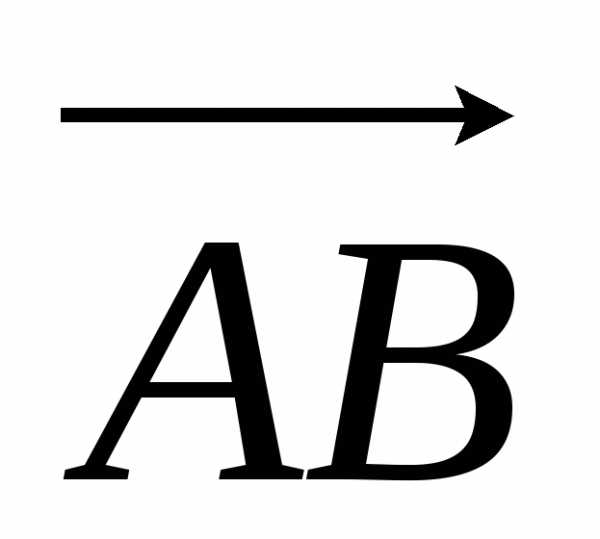 получим, что.
Рассмотрим случай, когда оба отрезка
получим, что.
Рассмотрим случай, когда оба отрезка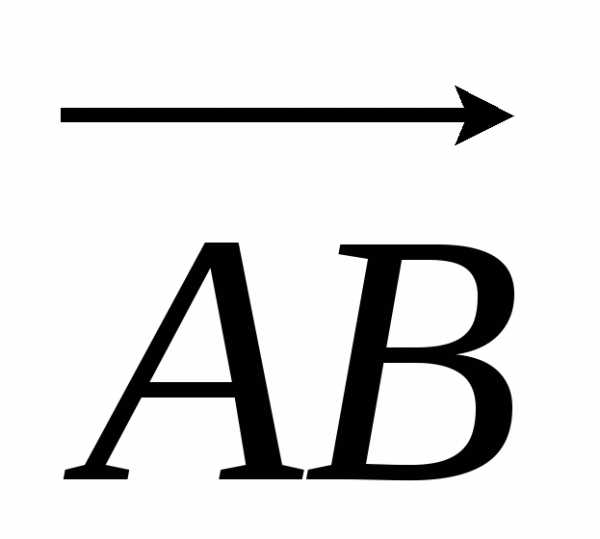 и
и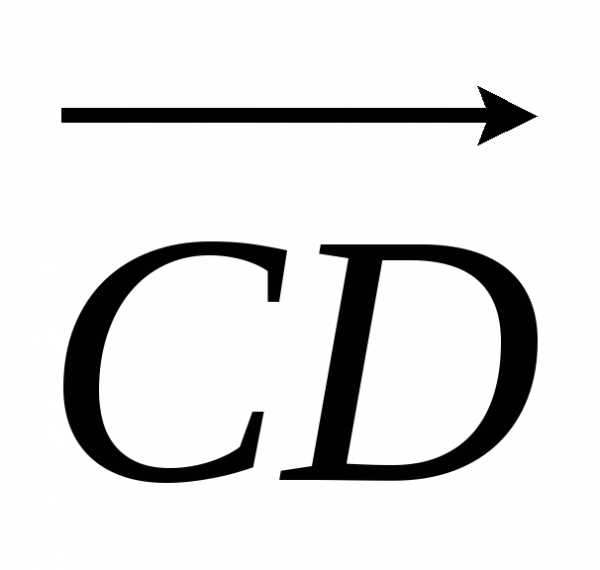 направлены в одну сторону. В этом случае
длина отрезка
направлены в одну сторону. В этом случае
длина отрезка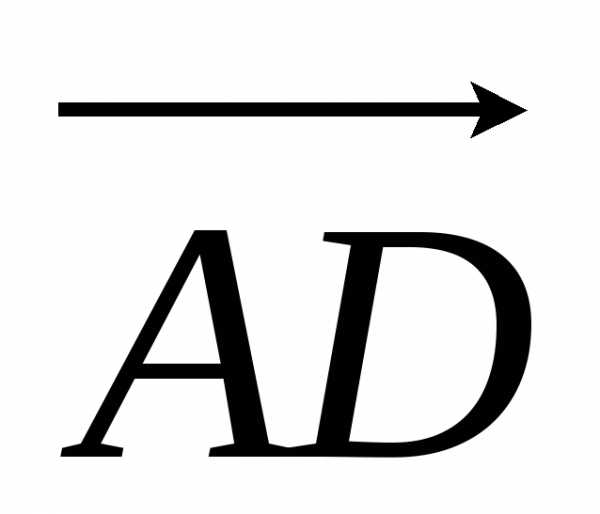 равна сумме длин отрезков
равна сумме длин отрезков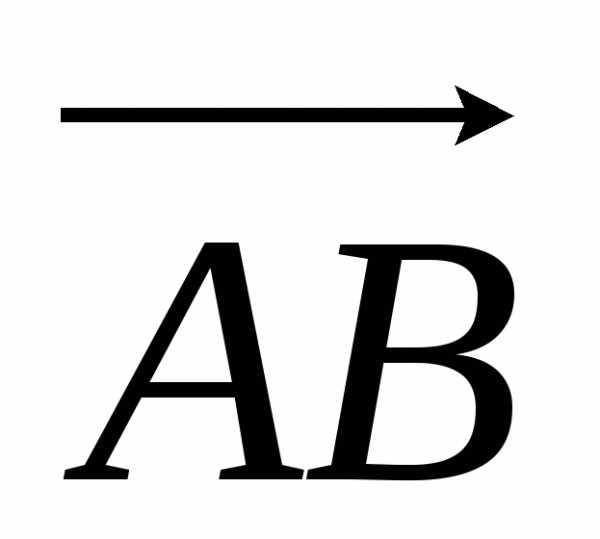 и
и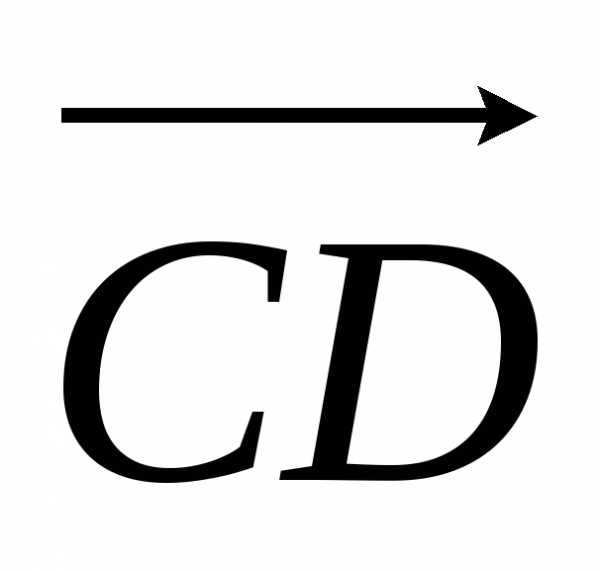 ,
причем направление
,
причем направление совпадает с направлением каждого из
отрезков
совпадает с направлением каждого из
отрезков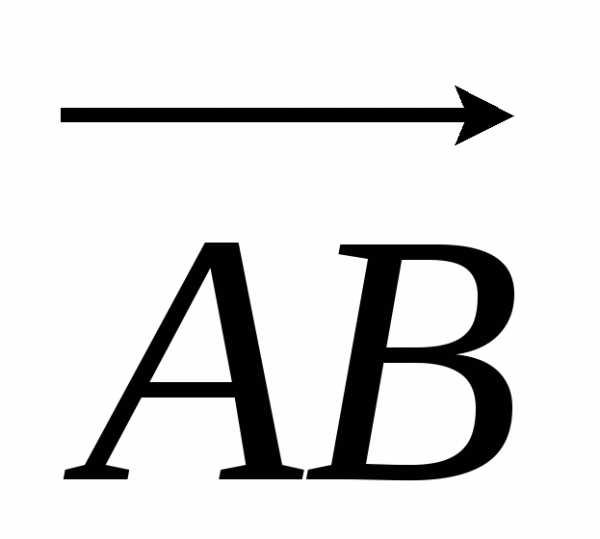 и
и .
Поэтому справедливо равенство.
Рассмотрим случай, когда отрезки
.
Поэтому справедливо равенство.
Рассмотрим случай, когда отрезки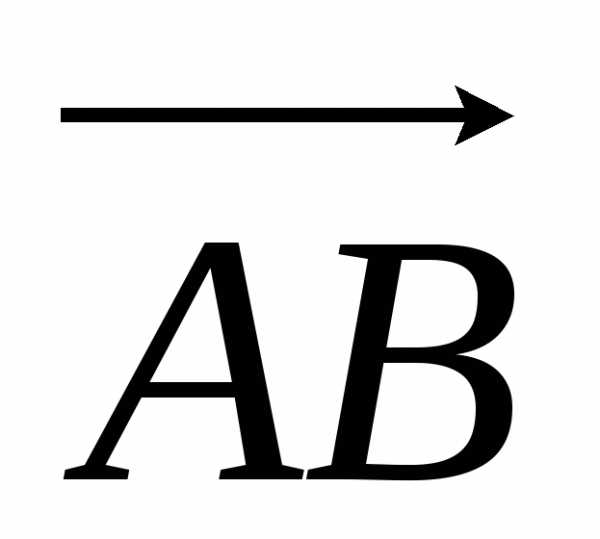 и
и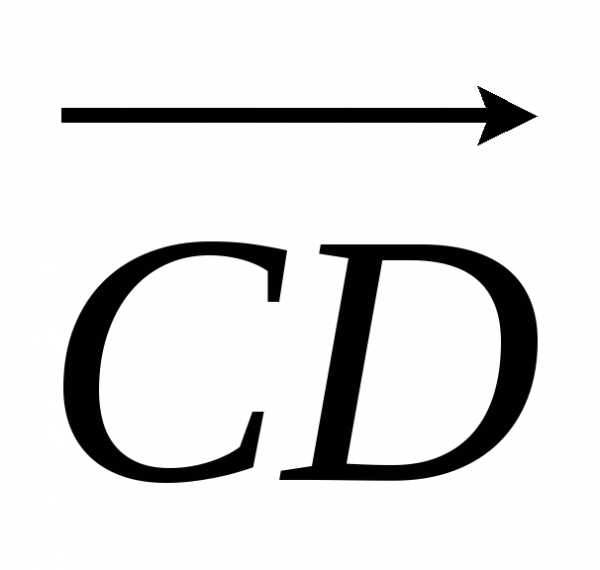 направлены в противоположные стороны.
В этом случае величины отрезков
направлены в противоположные стороны.
В этом случае величины отрезков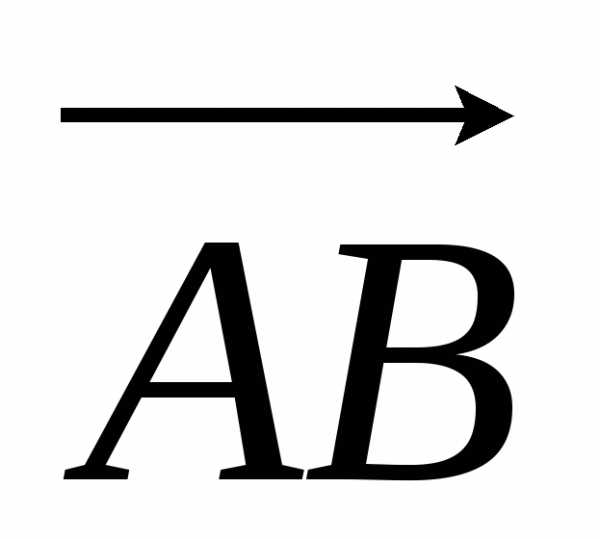 и
и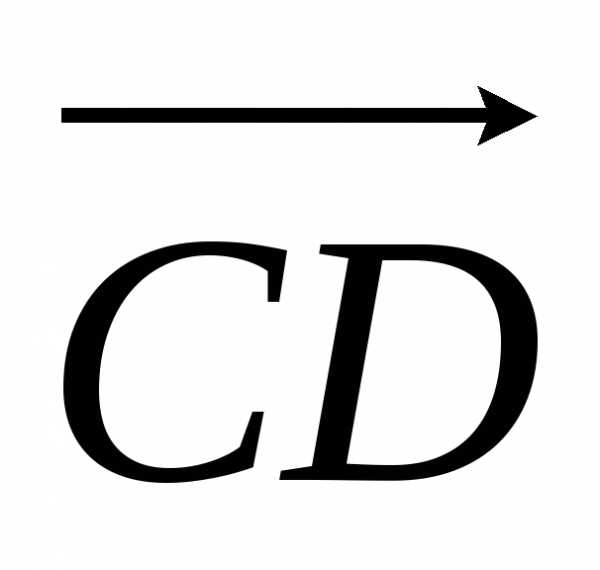 имеют разные знаки, поэтому.
Направление отрезка
имеют разные знаки, поэтому.
Направление отрезка совпадает с направлением наибольшего
по длине из отрезков
совпадает с направлением наибольшего
по длине из отрезков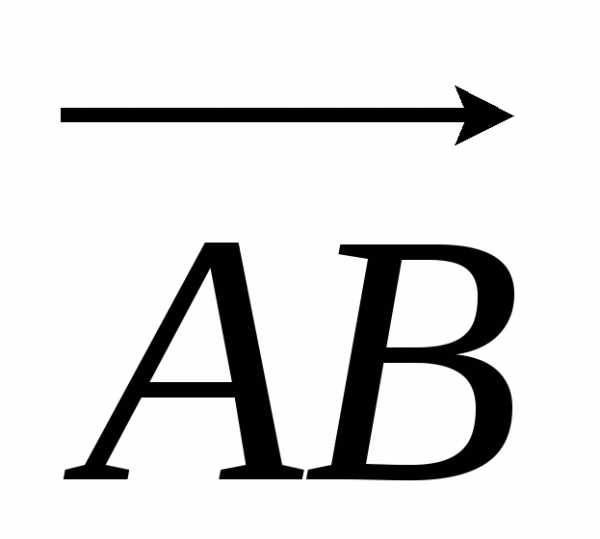 и
и ,
следовательно, знак величины отрезка
,
следовательно, знак величины отрезка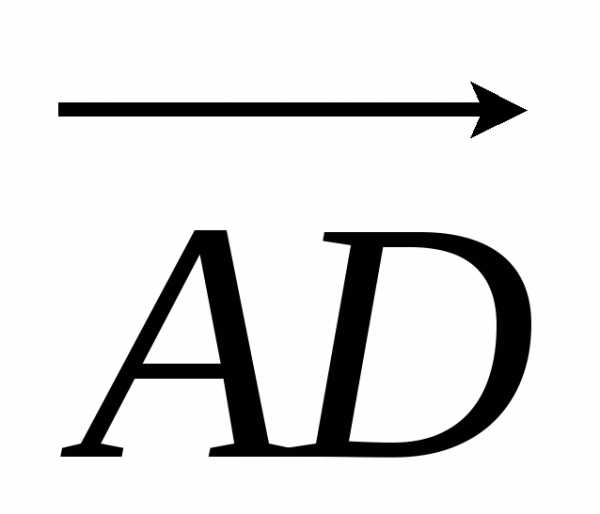 совпадает со знаком числа,
т. е. справедливо равенство.
Теорема доказана.
совпадает со знаком числа,
т. е. справедливо равенство.
Теорема доказана.
Основное тождество. Для любых
трех точек А, В, С, расположенных на оси,
величины направленных отрезков  ,
,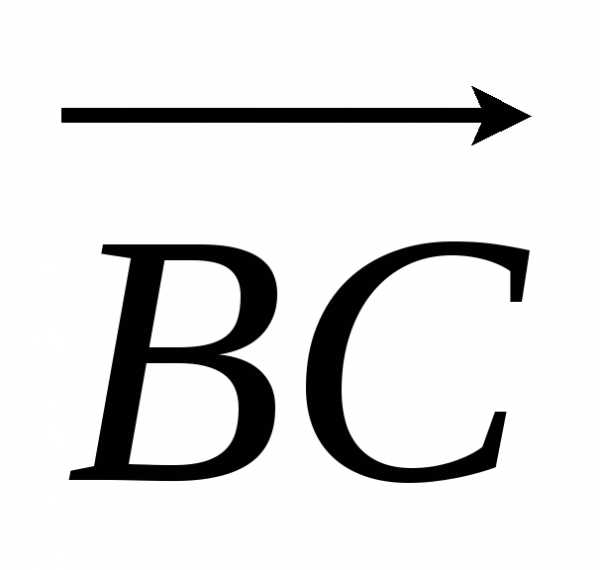 и
и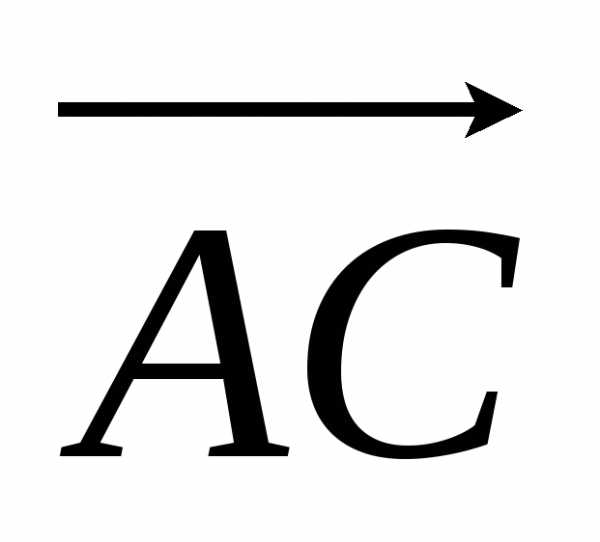 удовлетворяют соотношению.
удовлетворяют соотношению.
Это тождество следует из доказанной выше теоремы.
Определение.
Произведением направленного отрезка 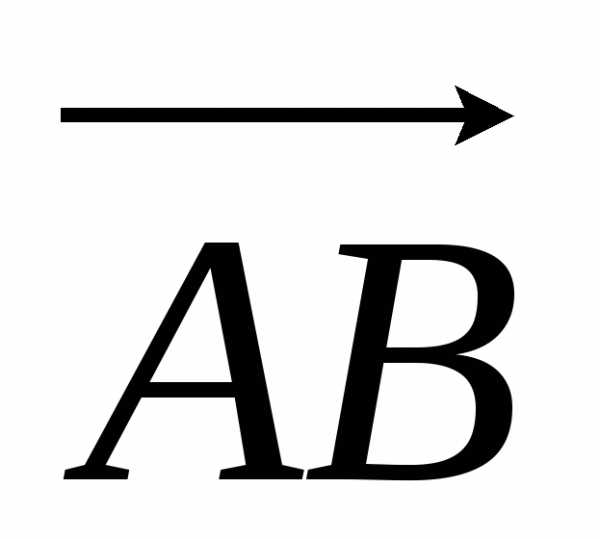 на число называется направленный отрезок,
обозначаемый
на число называется направленный отрезок,
обозначаемый 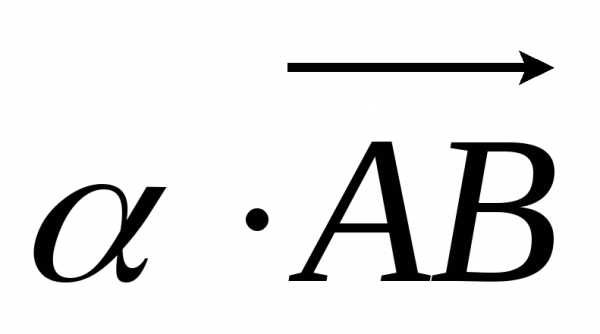 ,
длина которого равна произведению числа
,
длина которого равна произведению числа на длину отрезка
на длину отрезка 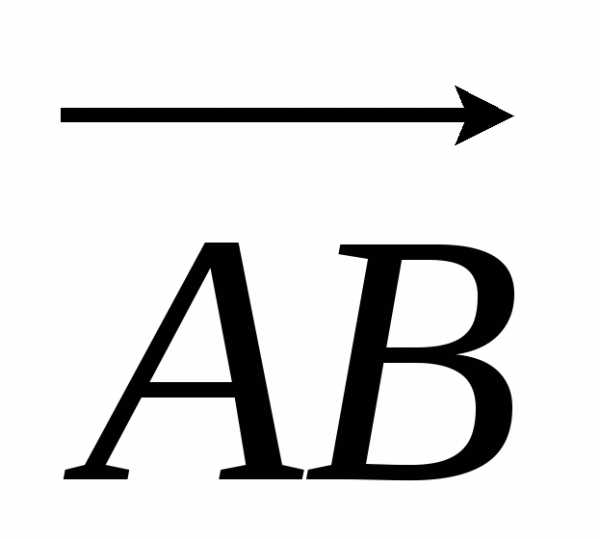 и направление которого совпадает с
направлением отрезка
и направление которого совпадает с
направлением отрезка 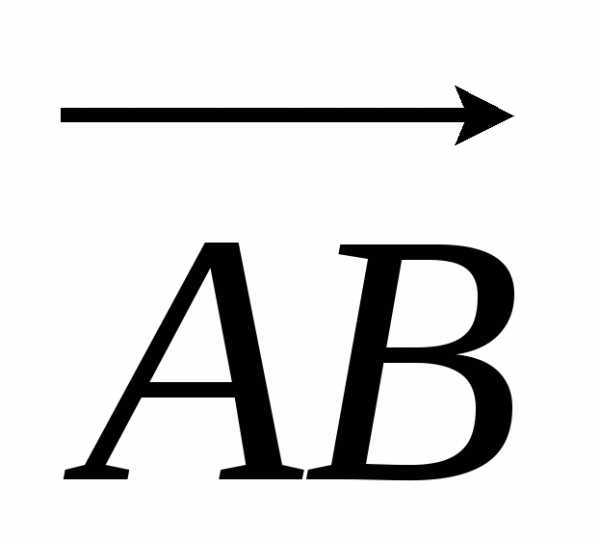 при
при  и противоположно направлению
и противоположно направлению 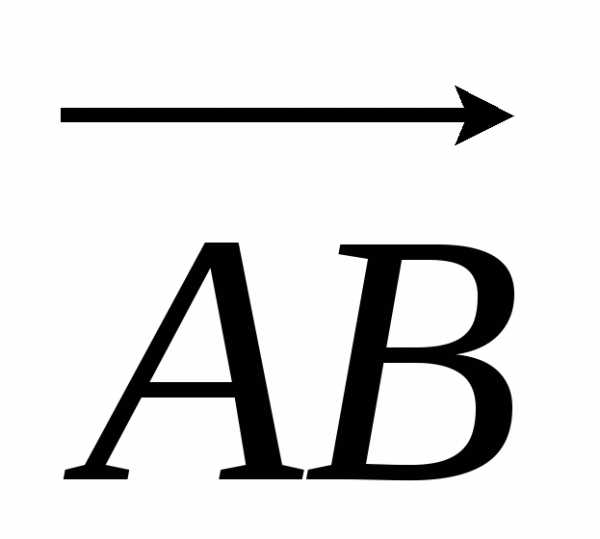 при
при  .
.
Рассмотрим произвольную прямую, на которой выбрано направление и некоторая точка О, называемая началом координат.
Определение. Прямая с выбранным направлением, масштабной единицей и началом координат называется координатной осью.
Пусть М – произвольная точка на выбранной прямой.
О
М
Точке М поставим в соответствие число х,
равное величине ОМ направленного отрезка 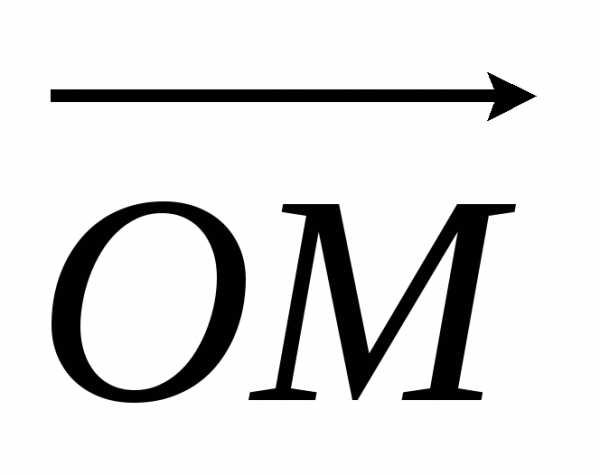 .
Числох называется координатой точки М.
.
Числох называется координатой точки М.
Таким образом, каждой точке координатной прямой соответствует определенное вещественное число – ее координата. Верно и обратное утверждение: любому вещественному числу х соответствует некоторая точка М на координатной прямой, координата которой равна х. Следовательно, вещественные числа можно изображать точками на координатной прямой. Поэтому около точки на координатной прямой часто указывают число – ее координату.
О
х
Пусть точка М1 имеет координату х1, а точка М2 – координату х2.
М1 (х1)
О
М2 (х2)
Выразим величину М1М2 направленного отрезка 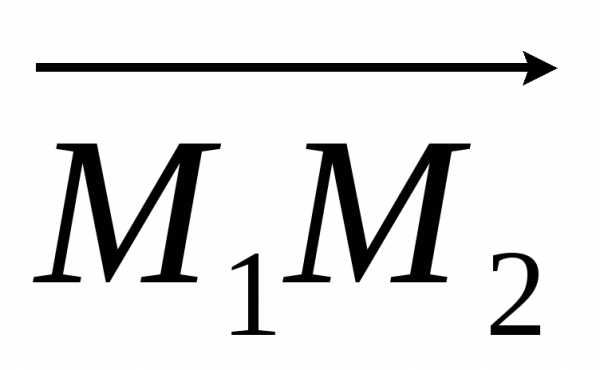 через координаты точекМ1и М2.
Согласно основному тождеству ОМ1 + М1М2 = ОМ2.
Тогда М1М2 = ОМ2 — ОМ1, но ОМ1 = х1, ОМ2 = х2,
поэтому М1М2 = х2 – х1.
через координаты точекМ1и М2.
Согласно основному тождеству ОМ1 + М1М2 = ОМ2.
Тогда М1М2 = ОМ2 — ОМ1, но ОМ1 = х1, ОМ2 = х2,
поэтому М1М2 = х2 – х1.
studfiles.net

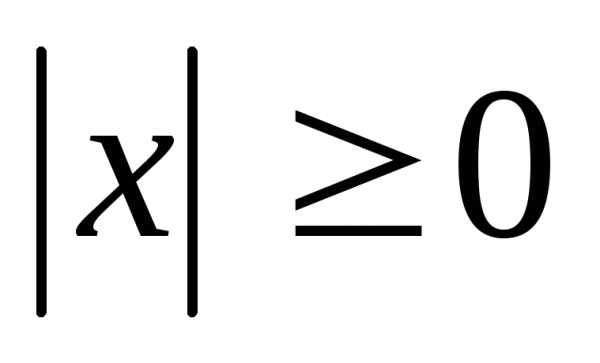 . Доказательство. Если
. Доказательство. Если 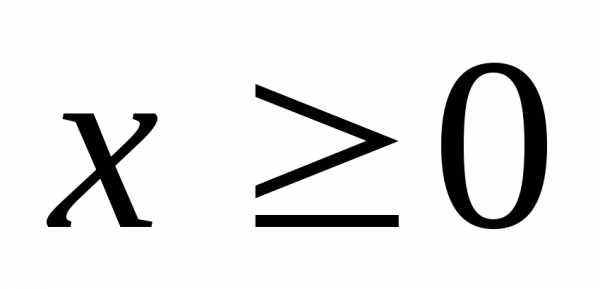 ,
то
,
то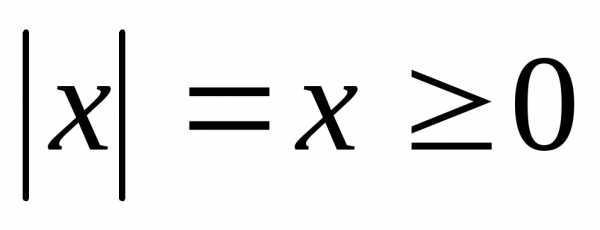 .
Если
.
Если ,
то
,
то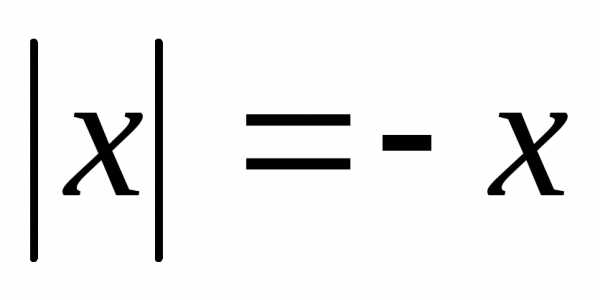 ,
но
,
но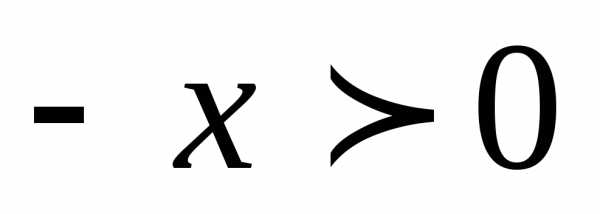 ,
т. е.
,
т. е. .
.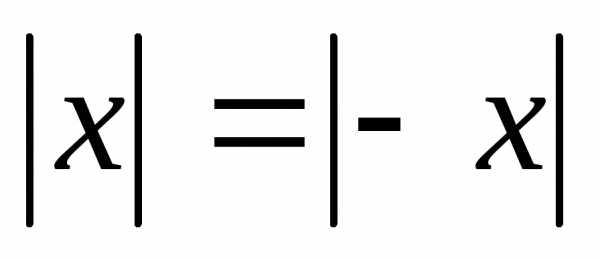 . Доказательство. Если
. Доказательство. Если 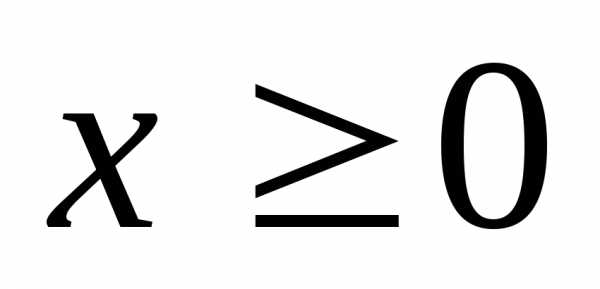 ,
то
,
то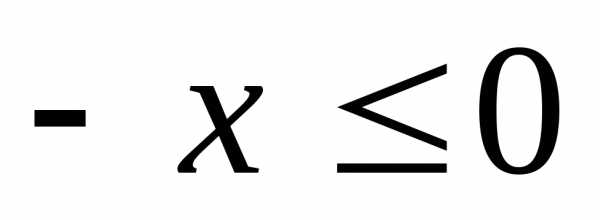 и тогда.
Если
и тогда.
Если ,
то
,
то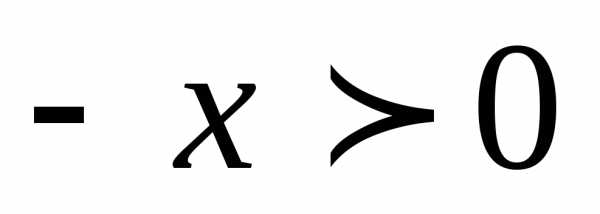 ,
и тогда.
,
и тогда. , то
, то 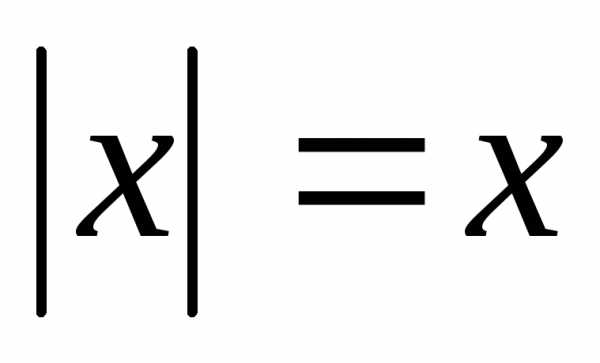 ,
, 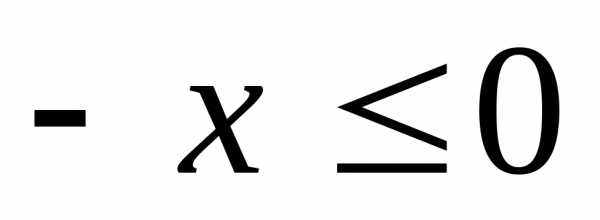 .
Отсюда
.
Отсюда ,
т. е..
Если
,
т. е..
Если ,
то
,
то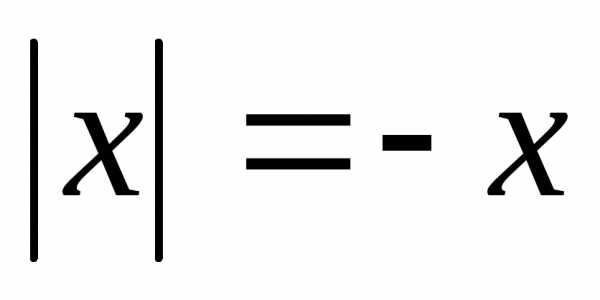 ,
откуда
,
откуда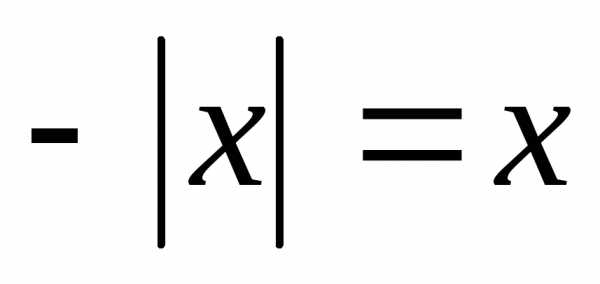 .
Так как
.
Так как ,
то
,
то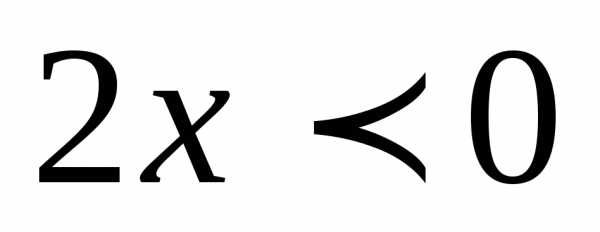 ,
или,
откуда,
т. е.
,
или,
откуда,
т. е.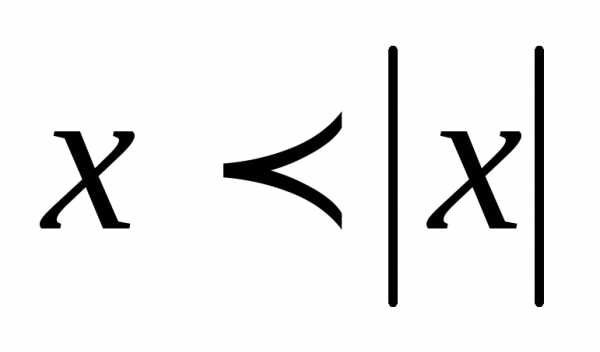 .
Поэтому.
Получаем, что .
.
Поэтому.
Получаем, что .