Алгоритм как решать – Алгоритмы. Разработка алгоритма решения задачи

Как построить блок-схему 🚩 блок схема онлайн 🚩 Компьютеры и ПО 🚩 Другое

3 августа 2011

Автор КакПросто!

В настоящее время программисты при написании программ обычно не чертят для них блок-схем. Но в школьном курсе информатики преподаватели нередко до сих пор требуют от учеников сопровождение программ такими схемами. Составлять их совсем несложно.

Статьи по теме:

Вам понадобится

• — трафарет для черчения блок-схем;
• — механический карандаш;
• — ластик;
• — бумага;
• — компьютер с доступом в интернет.

Инструкция

Начало и конец алгоритма обозначаются овалами. Внутри них помещают, соответственно, слова «Начало» и «Конец». От овала, символизирующего начало алгоритма, исходит одна стрелка вниз, к овалу, символизирующему конец алгоритма, приходит стрелка сверху. Шаги, соответствующие действиям, не связанным с вводом-выводом, обозначаются при помощи прямоугольников. Пример такого действия — вычисление по формуле и присвоение результата той или иной переменной. Стрелка от предыдущего шага приходит к прямоугольнику сверху, а снизу от него исходит стрелка к следующему шагу. Для обозначения шагов, соответствующих операциям ввода-вывода, используются параллелограммы. Такие операции бывают двух видов: присвоение поступивших откуда-либо данных переменной и вывод данных из переменной в файл, порт, на экран, принтер и т.п. Ветвления обозначаются ромбами. В верхний угол ромба приходит стрелка от предыдущего шага, а из его боковых углов исходят стрелки, помеченные как «Нет» и «Да». Они приходят, соответственно, к шагам, выполняемым при несоблюдении и соблюдении условия. Нижний угол ромба оставляется свободным. Само условие (например, равенство, строгое или нестрогое) записывается внутри ромба.

Прямоугольник, боковые стенки которого двойные, олицетворяет переход к подпрограмме. После того как в подпрограмме встретился оператор возврата, продолжается выполнение основной программы. Внутри прямоугольника указывается название подпрограммы. Блок-схемы всех подпрограмм помещаются под блок-схемой основной программы либо на отдельных страницах.

Чертить блок-схемы удобнее всего через специальные трафареты, пользуясь механическим карандашом. Его можно стирать ластиком, аналогично обычному карандашу, но не требуется точить.

Если вы желаете составлять блок-схемы в электронном виде, воспользуйтесь онлайн-приложением под названием Flowchart. При желании можно также освоить особые языки программирования, в которых сам процесс программирования заключается в составлении блок-схемы. Таких языков два: Дракон и HiAsm.

Первое и самое главное умение программиста — составить алгоритм. Знание языка это уже второе дело, их выбор — практически дело вкуса. А вот основы алгоритмизации едины всегда.

Инструкция

Изучите основные элементы и обозначения в алгоритме. Сначала вам может показаться это сложным и неуместным, однако, как только вам понадобится написать что-то действительно объёмное и комплексное, вы сами почувствуете, что канонично изображенный алгоритм легко читать. Прямоугольником обозначается формирование данных и новый процесс, ввод данных – параллелограммом, а ромбом – условие. Цикл начинается шестиугольником, использование подпрограммы – прямоугольником с дополнительными полосами сбоку. Начало и конец – круг. Вывод полученных значений – «оборванный лист», прямоугольник с нижней стороной в форме волны. Сокращайте! Главным требованием к любому алгоритму является его простота. Чем меньше элементов в вашей конструкции, тем надежнее она будет работать. Более того, приучите себя к тому, что после составления изначального варианта, наверняка можно будет исключить из него 2-3 лишних шага. Попытайтесь «взять себя на слабо», и воспринимайте процесс сокращения алгоритма как некий вызов, а не раздражитель. Помните – чем короче все выглядит в теории, тем проще будет написание программы.

Предпочитайте «отсев» «развилке». Гораздо более удобным с точки зрения программного кода, как правило, является проверка условий. Иными словами, стремитесь к более «прямой» структуре, а не разветвленной. Классическим примером послужит алгоритм задачи «определить четверть плоскости, в которой находится точка, по координатам». В данном случае лучше окажется алгоритм, составленный из условий: «x>0, y>0 –данет», «x<0, y>0 –данет», и т.д. Менее удобным окажется вариант: «если x>0, то…», на большинстве языков он потребует больше шагов для выполнения.

Внимательно изучите доступные библиотеки. Многие начинающие программисты грешат тем, что не знают основных команд даже встроенных библиотек, из-за чего им постоянно приходится изобретать велосипед. Вполне возможно (особенно при работе с текстом, для него существует огромный запас различных команд) что некоторое действие (к примеру сравнение длинны строк) может быть выполнено стандартной подпрограммой. Это сразу исключает 5-7 лишних шагов из вашего алгоритма.

Видео по теме

Обратите внимание

-Пишите алгоритм на бумаге. Из-за обилия геометрических фигур это просто удобнее.

-Спросите 2-3 человека как бы они решмили поставленную задачу. Вполне возможно вам покажут кардинально иной подход.

Полезный совет

-Алгоритм изображается сверху вниз.

Алгоритмирование — наука о создании алгоритмов и процессов, важнейшая компонента структурного программирования. Без алгоритмов не обойдется составление бизнес-плана, разработка приложения для мобильного или компьютерной игры. Умение создавать алгоритмы позволяет делать многие вещи многократно, с минимумом усилий, в автоматическом режиме.

Инструкция

Впервые слово «алгоритм» употребил один из создателей современной алгебры, мудрец и астроном Аль-Хорезми еще в 224 году н.э. в своих фундаментальных трудах. В его понимании алгоритм — инструкция, позволяющая решить задачу. Аль-Хорезми был уважаемым ученым среди своих коллег, и составление таких инструкций стало в математической среде нормой.

Важнейшую практическую и прикладную роль составление алгоритмов приобрело с появлением компьютеров. Огромные машины на электронных лампах были созданы с целью вычисления сложных выражений и решения задач. Компьютер мыслить творчески не умеет, понимая лишь указания (команды) в двоичном коде. Алгоритм в программировании — последовательность команд, ведущая к достижению результата.

Для того чтобы составить алгоритм, сначала нужно определить цель. Затем можно сформулировать своими словами (и записать на бумаге, пусть даже расплывчато), как этой цели достичь.

Основные черты алгоритма — краткость изложения, шаговая поэтапность, понятность исполнителю. Хороший пример алгоритма — кулинарный рецепт. Превратите ваше расплывчатое описание достижения цели в инструкцию, разбитую на конкретные действия, приближающие достижение цели. Команды должны быть ясными, возможными, не вызывающими вопросов, измеримыми. Например: «Возьмите 2 яйца. Варите их 10 минут в кастрюле. Очистите от скорлупы».

Для перевода алгоритма в программный код нужно максимально упростить его. Затем можно переписать его в «псевдокоде» — в этом языке все действия выполняются в стиле программирования, но человеческими, а не программными словами. По завершении псевдокод переводится в код на известном вам языке программирования, а сама программа компилируется (выполняется вычислительной машиной).

Видео по теме

Полезный совет

Научиться искусству алгоритмирования поможет изучение доказательств теорем математики. Изящные ходы интеллекта, минимализм решения и пошаговые действия – основа любых математических работ.

www.kakprosto.ru

Алгоритмы как их решать?

Последовательность точно определенных операций, описывающих необходимый порядок действий для решения поставленнойзадачи. Любая задача может быть решена с помощью алгоритма. Перед составлением инструкции в алгоритм вводятся переменные величины с учетом условия задачи. Наиболее простые типы алгоритма: линейные, циклические и алгоритмы с ветвлением. Каждый из них, путем конечного числа операций, осуществляет переход от вводных данных к искомому в задаче результату.

Инструкция

Внимательно ознакомьтесь с условием исходной задачи. Продумайте ее решение: имеется ли цикличность в задаче. Возможно, заданы операции, выполнение которых обусловлено удовлетворением разных условий. Выпишите все известные данные и искомые величины.



Как решать задачи с алгоритмом

Любой алгоритм требует формализованной записи. Если вам требуется составить блок-схему алгоритма, используйте специальные элементы для обозначения каждой операции создаваемой инструкции. Какправило, это блоки из прямоугольных и ромбическихфигур, соединенные в общеедерево.

Составьте общий алгоритмрешения задачи. На первом шаге введите в алгоритм переменные величины, обозначающие известные данные и результирующие значения. Присвойте переменным известные из условия задачизначения.Детализируйте алгоритм. Подробно распишите условиезадачи. Каждый шаг инструкции должен быть записан на отдельной строке. При необходимости задайте циклы или разветвления алгоритма.Все действия в шагах инструкции производите с заданнымипеременными. Если необходимо ввести вспомогательные переменные, включите их дополнительно в самом начале алгоритма.Часто из смысла исходной задачив процессе решения вытекают условия, при удовлетворении которых над данными проводится одно действие, а без удовлетворения – другое. В этом случае речь идет о разветвлении алгоритма. Оформите его двумя ветками дерева-инструкции.Если при разветвлении алгоритма после прохождения условия одну из веток необходимо вернутьназад по телу алгоритма, тообразуется циклический алгоритм. Четко проследите, чтобы цикл внутри инструкции не был бесконечен и имел конечное число итераций.Любая последовательность выполняемых действий должна привести к конечному результату, заданному в условии задачи. После получения искомой величины, завершите тело алгоритма и запишите полученный ответ.

istinaved.ru

Памятка -алгоритм по математике «Как решать задачи» (1класс)

Примерный план ответа-рассуждения ребенка при решении задачи:

Анализ задачи.

1. Известно, что… (расскажи условие задачи)

2. Надо узнать… (повтори вопрос)

3. Чтобы ответить на вопрос задачи, надо …

4. Сразу мы не можем ответить на вопрос задачи, так как не знаем…

5. Поэтому в первом действии мы узнаем …

6. Во втором действии мы ответим на вопрос задачи. Для этого…(какое действие выполняем)

«КАК РЕШАТЬ ЗАДАЧИ»

1. Прочитай задачу и представь себе то, о чем в ней говорится.

2. Выдели условие и вопрос.

3. Запиши условие кратко или выполни чертёж.

4.Подумай можно ли сразу

ответить на вопрос задачи.

Если нет, то почему.

Что надо узнать сначала, что

потом?

5. Составь план решения.

6. Выполни решение.

7. Проверь решение и запиши ответ задачи.

ПАМЯТКА

(алгоритм)  

«КАК РЕШАТЬ ЗАДАЧИ»

1  КЛАСС

5. Задачи на нахождение неизвестного вычитаемого и слагаемого.

*У Иры было 9 тетрадей. Когда несколько тетрадей Ира исписала, их осталось-6. Сколько тетрадей исписала Ира?

*На полке было 5 книг. Когда еще несколько книг поставили на полку, их стало 8. Сколько книг поставили на полку?

6. Задачи на нахождение уменьшаемого.

*Когда Коля раскрасил в книжке 4 картинки, их осталось 3. Сколько картинок в книжке?

7. Задачи на разностное сравнение.

*В саду 8 кустов малины и 5 кустов крыжовника. На сколько больше кустов малины, чем кустов крыжовника?

На сколько меньше кустов крыжовника, чем кустов малины?

8.Составные задачи на нахождение остатка.

*В классе учились 12 девочек и 10 мальчиков. Потом 4 человека ушли. Сколько человек осталось

ТИПЫ ЗАДАЧ

1. Задачи на нахождение суммы

*На ветке сидело 4 воробья и 3 снегиря. Сколько птиц сидело на ветке?

2. Задачи на увеличение и уменьшение числа на несколько единиц.

*В Северном Ледовитом океане 10 морей, а в Индийском на 5 меньше. Сколько морей в Индийском океане?

*Антон нашел 5 боровиков, а сыроежек  на 4 больше. Сколько сыроежек нашел Антон?

3. Задачи на нахождение неизвестного слагаемого.

*За два дня турист прошел 8 км. В первый день

он прошел 3 км. Сколько км он прошел во второй день?

4. Задачи на нахождение остатка.

*На дереве сидело 7 птиц. 3 улетели. Сколько птиц осталось?

12.Составные задачи на нахождение третьего слагаемого.

*У нашей кошки 11 котят: 3 белых 4 черных и несколько рыжих. Сколько рыжих котят у нашей кошки?

13.Составные задачи на нахождение суммы.

*На полке стояло 9 книг на немецком языке, а на английском на 14 книг больше, чем на немецком, а на французском языке на 12 книг меньше, чем на английском. Сколько всего книг стояло на полке?

14.Составные задачи на нахождение уменьшаемого.

*В банке были соленые огурцы. За завтраком съели 12 огурцов, а в обед 21. Сколько огурцов было в банке, если в ней осталось 15 огурцов?

15.Составные задачи на разностное сравнение.

*В тетради 6 чистых страниц, исписано на 4 страницы больше. На сколько меньше исписанных страниц, чем всего страниц в тетради?

*В коробке было 9 красных и зеленых ручек. Из них красных — 3 ручки. На сколько больше было зеленых ручек, чем красных?

9.Задачи с косвенными вопросами.

*Ров первого деревянного кремля имел глубину

5 м, что на 2 м больше, чем его ширина.

Какова ширина рва?

*Жук олень имеет длину 7 си, что на 4 см

меньше длины уссурийского усача. Какова

длина уссурийского усача?

10.Составные задачи на нахождение суммы.

*В магазин привезли 20 ящиков конфет, а

печенья на 6 ящиков больше. Сколько всего

ящиков привезли в магазин?

11.Составные задачи на нахождение слагаемого и вычитаемого.

*В классе 14 девочек и 15 мальчиков. В школу пришло 18 детей. Сколько детей заболело?

*Ежик собрал 28 яблок. 9 из них он отдал ежику

и еще несколько белочке. Сколько ежик отдал яблок белочке, если у него осталось 12 яблок?

infourok.ru

алгоритмы как их решать? — Математика

Последовательность точно определенных операций, описывающих необходимый порядок действий для решения поставленнойзадачи. Любая задача может быть решена с помощью алгоритма. Перед составлением инструкции в алгоритм вводятся переменные величины с учетом условия задачи. Наиболее простые типы алгоритма: линейные, циклические и алгоритмы с ветвлением. Каждый из них, путем конечного числа операций, осуществляет переход от вводных данных к искомому в задаче результату.

Инструкция

Внимательно ознакомьтесь с условием исходной задачи. Продумайте ее решение: имеется ли цикличность в задаче. Возможно, заданы операции, выполнение которых обусловлено удовлетворением разных условий. Выпишите все известные данные и искомые величины.



Как решать задачи с алгоритмом

Любой алгоритм требует формализованной записи. Если вам требуется составить блок-схему алгоритма, используйте специальные элементы для обозначения каждой операции создаваемой инструкции. Какправило, это блоки из прямоугольных и ромбическихфигур, соединенные в общеедерево.

Составьте общий алгоритмрешения задачи. На первом шаге введите в алгоритм переменные величины, обозначающие известные данные и результирующие значения. Присвойте переменным известные из условия задачизначения.Детализируйте алгоритм. Подробно распишите условиезадачи. Каждый шаг инструкции должен быть записан на отдельной строке. При необходимости задайте циклы или разветвления алгоритма.Все действия в шагах инструкции производите с заданнымипеременными. Если необходимо ввести вспомогательные переменные, включите их дополнительно в самом начале алгоритма.Часто из смысла исходной задачив процессе решения вытекают условия, при удовлетворении которых над данными проводится одно действие, а без удовлетворения – другое. В этом случае речь идет о разветвлении алгоритма. Оформите его двумя ветками дерева-инструкции.Если при разветвлении алгоритма после прохождения условия одну из веток необходимо вернутьназад по телу алгоритма, тообразуется циклический алгоритм. Четко проследите, чтобы цикл внутри инструкции не был бесконечен и имел конечное число итераций.Любая последовательность выполняемых действий должна привести к конечному результату, заданному в условии задачи. После получения искомой величины, завершите тело алгоритма и запишите полученный ответ.

otvetytut.com

примеры, элементы, построение. Блок-схемы алгоритмов :: SYL.ru

В этой статье будут рассмотрены примеры блок-схем, которые могут встретиться вам в учебниках по информатике и другой литературе. Блок-схема представляет собой алгоритм, по которому решается какая-либо задача, поставленная перед разработчиком. Сначала нужно ответить на вопрос, что такое алгоритм, как он представляется графически, а самое главное – как его решить, зная определенные параметры. Нужно сразу отметить, что алгоритмы бывают нескольких видов.

Что такое алгоритм?

Это слово ввел в обиход математик Мухаммед аль-Хорезми, который жил в период 763-850 года. Именно он является человеком, который создал правила выполнения арифметических действий (а их всего четыре). А вот ГОСТ от 1974 года, который гласит, что:

Алгоритм – это точное предписание, которое определяет вычислительный процесс. Причем имеется несколько переменных с заданными значениями, которые приводят расчеты к искомому результату.

Алгоритм позволяет четко указать исполнителю выполнять строгую последовательность действий, чтобы решить поставленную задачу и получить результат. Разработка алгоритма – это разбивание одной большой задачи на некую последовательность шагов. Причем разработчик алгоритма обязан знать все особенности и правила его составления.

Особенности алгоритма

Всего можно выделить восемь особенностей алгоритма (независимо от его вида):

1. Присутствует функция ввода изначальных данных.
2. Есть вывод некоего результата после завершения алгоритма. Нужно помнить, что алгоритм нужен для того, чтобы достичь определенной цели, а именно – получить результат, который имеет прямое отношение к исходным данным.
3. У алгоритма должна быть структура дискретного типа. Он должен представляться последовательными шагами. Причем каждый следующий шаг может начаться только после завершения предыдущего.
4. Алгоритм должен быть однозначным. Каждый шаг четко определяется и не допускает произвольной трактовки.
5. Алгоритм должен быть конечным – необходимо, чтобы он выполнялся за строго определенное количество шагов.
6. Алгоритм должен быть корректным – задавать исключительно верное решение поставленной задачи.
7. Общность (или массовость) – он должен работать с различными исходными данными.
8. Время, которое дается на решение алгоритма, должно быть минимальным. Это определяет эффективность решения поставленной задачи.

А теперь, зная, какие существуют блок-схемы алгоритмов, можно приступить к рассмотрению способов их записи. А их не очень много.

Словесная запись

Такая форма, как правило, применяется при описании порядка действий для человека: «Пойди туда, не знаю куда. Принеси то, не знаю что».

Конечно, это шуточная форма, но суть понятна. В качестве примера можно привести еще, например, привычную запись на стеклах автобусов:«При аварии выдернуть шнур, выдавить стекло».

Здесь четко ставится условие, при котором нужно выполнить два действия в строгой последовательности. Но это самые простые алгоритмы, существуют и более сложные. Иногда используются формулы, спецобозначения, но при обязательном условии – исполнитель должен все понимать.

Допускается изменять порядок действий, если необходимо вернуться, например, к предыдущей операции либо обойти какую-то команду при определенном условии. При этом команды желательно нумеровать и обязательно указывается команда, к которой происходит переход: «Закончив все манипуляции, повторяете пункты с 3 по 5».

Запись в графической форме

В этой записи участвуют элементы блок-схем. Все элементы стандартизированы, у каждой команды имеется определенная графическая запись. А конкретная команда должна записываться внутри каждого из блоков обычным языком или математическими формулами. Все блоки должны соединяться линиями – они показывают, какой именно порядок у выполняемых команд. Собственно, этот тип алгоритма более подходит для использования в программном коде, нежели словесный.

Запись на языках программирования

В том случае, если алгоритм необходим для того, чтобы задачу решала программа, установленная на ПК, то нужно его записывать специальным кодом. Для этого существует множество языков программирования. И алгоритм в этом случае называется программой.

Блок-схемы

Блок-схема – это представление алгоритма в графической форме. Все команды и действия представлены геометрическими фигурами (блоками). Внутри каждой фигуры вписывается вся информация о тех действиях, которые нужно выполнить. Связи изображены в виде обычных линий со стрелками (при необходимости).

Для оформления блок-схем алгоритмов имеется ГОСТ 19.701-90. Он описывает порядок и правила создания их в графической форме, а также основные методы решения. В этой статье приведены основные элементы блок-схем, которые используются при решении задач, например, по информатике. А теперь давайте рассмотрим правила построения.

Основные правила составления блок-схемы

Можно выделить такие особенности, которые должны быть у любой блок-схемы:

1. Обязательно должно присутствовать два блока – «Начало» и «Конец». Причем в единичном экземпляре.
2. От начального блока до конечного должны быть проведены линии связи.
3. Из всех блоков, кроме конечного, должны выходить линии потока.
4. Обязательно должна присутствовать нумерация всех блоков: сверху вниз, слева направо. Порядковый номер нужно проставлять в левом верхнем углу, делая разрыв начертания.
5. Все блоки должны быть связаны друг с другом линиями. Именно они должны определять последовательность, с которой выполняются действия. Если поток движется снизу вверх или справа налево (другими словами, в обратном порядке), то обязательно рисуются стрелки.
6. Линии делятся на выходящие и входящие. При этом нужно отметить, что одна линия является для одного блока выходящей, а для другого входящей.
7. От начального блока в схеме линия потока только выходит, так как он является самым первым.
8. А вот у конечного блока имеется только вход. Это наглядно показано на примерах блок-схем, которые имеются в статье.
9. Чтобы проще было читать блок-схемы, входящие линии изображаются сверху, а исходящие снизу.
10. Допускается наличие разрывов в линиях потока. Обязательно они помечаются специальными соединителями.
11. Для облегчения блок-схемы разрешается всю информацию прописывать в комментариях.

Графические элементы блок-схем для решения алгоритмов представлены в таблице:

Линейный тип алгоритмов

Это самый простой вид, который состоит из определенной последовательности действий, они не зависят от того, какие данные вписаны изначально. Есть несколько команд, которые выполняются однократно и только после того, как будет сделана предшествующая. Линейная блок-схема выглядит таким образом:

Причем связи могут идти как сверху вниз, так и слева направо. Используется такая блок-схема для записи алгоритмов вычислений по простым формулам, у которых не имеется ограничений на значения переменных, входящих в формулы для расчета. Линейный алгоритм – это составная часть сложных процессов вычисления.

Разветвляющиеся алгоритмы

Блок-схемы, построенные по таким алгоритмам, являются более сложными, нежели линейные. Но суть не меняется. Разветвляющийся алгоритм – это процесс, в котором дальнейшее действие зависит от того, как выполняется условие и какое получается решение. Каждое направление действия – это ветвь.

На схемах изображаются блоки, которые называются «Решение». У него имеется два выхода, а внутри прописывается логическое условие. Именно от того, как оно будет выполнено, зависит дальнейшее движение по схеме алгоритма. Можно разделить разветвляющиеся алгоритмы на три группы:

1. «Обход» – при этом одна из веток не имеет операторов. Другими словами, происходит обход нескольких действий другой ветки.
2. «Разветвление» – каждая ветка имеет определенный набор выполняемых действий.
3. «Множественный выбор» – это разветвление, в котором есть несколько веток и каждая содержит в себе определенный набор выполняемых действий. Причем есть одна особенность – выбор направления напрямую зависит от того, какие заданы значения выражений, входящих в алгоритм.

Это простые алгоритмы, которые решаются очень просто. Теперь давайте перейдем к более сложным.

Циклический алгоритм

Здесь все предельно понятно – циклическая блок-схема представляет алгоритм, в котором многократно повторяются однотипные вычисления. По определению, цикл – это определенная последовательность каких-либо действий, выполняемая многократно (более, чем один раз). И можно выделить несколько типов циклов:

1. У которых известно число повторений действий (их еще называют циклами со счетчиком).
2. У которых число повторений неизвестно – с постусловием и предусловием.

Независимо от того, какой тип цикла используется для решения алгоритма, у него обязательно должна присутствовать переменная, при помощи которой происходит выход. Именно она определяет количество повторений цикла. Рабочая часть (тело) цикла – это определенная последовательность действий, которая выполняется на каждом шаге. А теперь более детально рассмотрим все типы циклов, которые могут встретиться при составлении алгоритмов и решении задач по информатике.

Циклы со счетчиками

На рисунке изображена простая блок-схема, в которой имеется цикл со счетчиком. Такой тип алгоритмов показывает, что заранее известно количество повторений данного цикла. И это число фиксировано. При этом переменная, считающая число шагов (повторений), так и называется – счетчик. Иногда в учебниках можно встретить иные определения – параметр цикла, управляющая переменная.

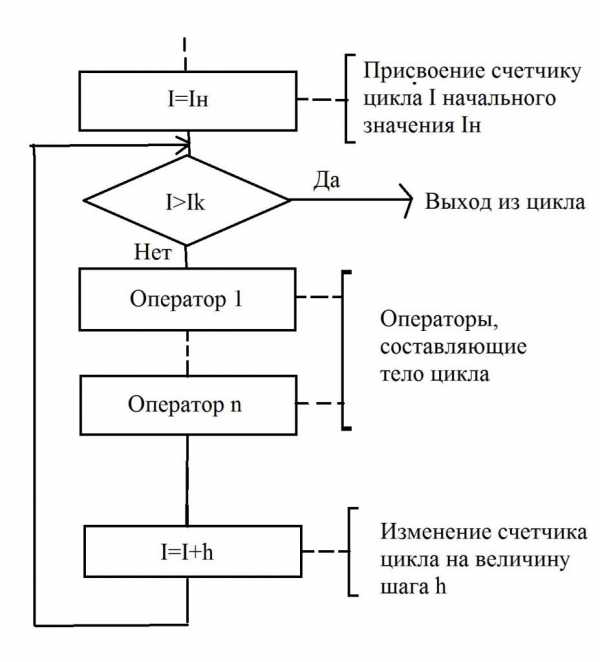
Блок-схема очень наглядно иллюстрирует, как работает цикл со счетчиком. Прежде чем приступить к выполнению первого шага, нужно присвоить начальное значение счетчику – это может быть любое число, оно зависит от конкретного алгоритма. В том случае, когда конечное значение меньше величины счетчика, начнет выполняться определенная группа команд, которые составляют тело цикла.

После того, как тело будет выполнено, счетчик меняется на величину шага счетчика, обозначенную буквой h. В том случае, если значение, которое получится, будет меньше конечного, цикл будет продолжаться. И закончится он лишь в тогда, когда конечное значение будет меньше, чем счетчик цикла. Только в этом случае произойдет выполнение того действия, которое следует за циклом.

Обычно в обозначениях блок-схем используется блок, который называется «Подготовка». В нем прописывается счетчик, а затем указываются такие данные: начальное и конечное значения, шаг изменения. На блок-схеме это параметры I н, Ik и h, соответственно. В том случае, когда h=1, величину шага не записывают. В остальных случаях делать это обязательно. Необходимо придерживаться простого правила – линия потока должна входить сверху. А линия потока, которая выходит снизу (или справа, в зависимости от конкретного алгоритма), должна показывать переход к последующему оператору.

Теперь вы полностью изучили описание блок-схемы, изображенной на рисунке. Можно перейти к дальнейшему изучению. Когда используется цикл со счетчиком, требуется соблюдать определенные условия:

1. В теле не разрешается изменять (принудительно) значение счетчика.
2. Запрещено передавать управление извне оператору тела. Другими словами, войти в цикл можно только из его начала.

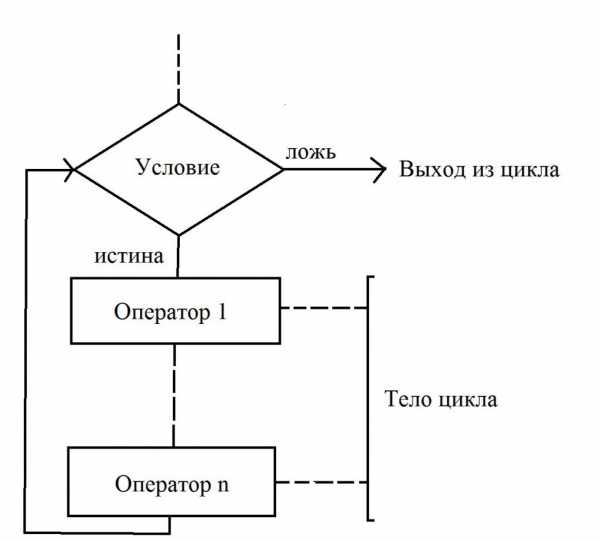
Циклы с предусловием

Этот тип циклов применяется в тех случаях, когда количество повторений заранее неизвестно. Цикл с предусловием – это тип алгоритма, в котором непосредственно перед началом выполнения тела осуществляется проверка условия, при котором допускается переход к следующему действию. Обратите внимание на то, как изображаются элементы блок-схемы.

В том случае, когда условие выполняется (утверждение истинно), происходит переход к началу тела цикла. Непосредственно в нем изменяется значение хотя бы одной переменной, влияющей на значение поставленного условия. Если не придерживаться этого правила, получим «зацикливание». В том случае, если после следующей проверки условия выполнения тела цикла оказывается, что оно ложное, то происходит выход.

В блок-схемах алгоритмов допускается осуществлять проверку не истинности, а ложности начального условия. При этом из цикла произойдет выход только в том случае, если значение условия окажется истинным. Оба варианта правильные, их использование зависит от того, какой конкретно удобнее использовать для решения той или иной задачи. Такой тип цикла имеет одну особенность – тело может не выполниться в случае, когда условие ложно или истинно (в зависимости от варианта, который применяется для решения алгоритма).

Ниже приведена блок-схема, которая описывает все эти действия:

Если внимательно присмотреться, то этот вид циклов чем-то похож на предыдущий. Самостоятельно построить блок-схему, описывающую этот цикл, мы сейчас и попробуем. Особенность заключается в том, что неизвестно заранее число повторений. А условие задается уже после того, как произошел выход из тела. Отсюда видно, что тело, независимо от решения, будет выполняться как минимум один раз. Для наглядности взгляните на блок-схему, описывающую выполнение условия и операторов:

Ничего сложного в построении алгоритмов с циклами нет, достаточно в них только один раз разобраться. А теперь перейдем к более сложным конструкциям.

Сложные циклы

Сложные – это такие конструкции, внутри которых есть один или больше простых циклов. Иногда их называют вложенными. При этом те конструкции, которые охватывают иные циклы, называют «внешними». А те, которые входят в конструкцию внешних – внутренними. При выполнении каждого шага внешнего цикла происходит полная прокрутка внутреннего, как представлено на рисунке:

Вот и все, вы рассмотрели основные особенности построения блок-схем для решения алгоритмов, знаете принципы и правила. Теперь можно рассмотреть конкретные примеры блок-схем из жизни. Например, в психологии такие конструкции используются для того, чтобы человек решил какой-то вопрос:

Или пример из биологии для решения поставленной задачи:

Решение задач с блок-схемами

А теперь рассмотрим примеры задач с блок-схемами, которые могут попасться в учебниках информатики. Например, задана блок-схема, по которой решается какой-то алгоритм:

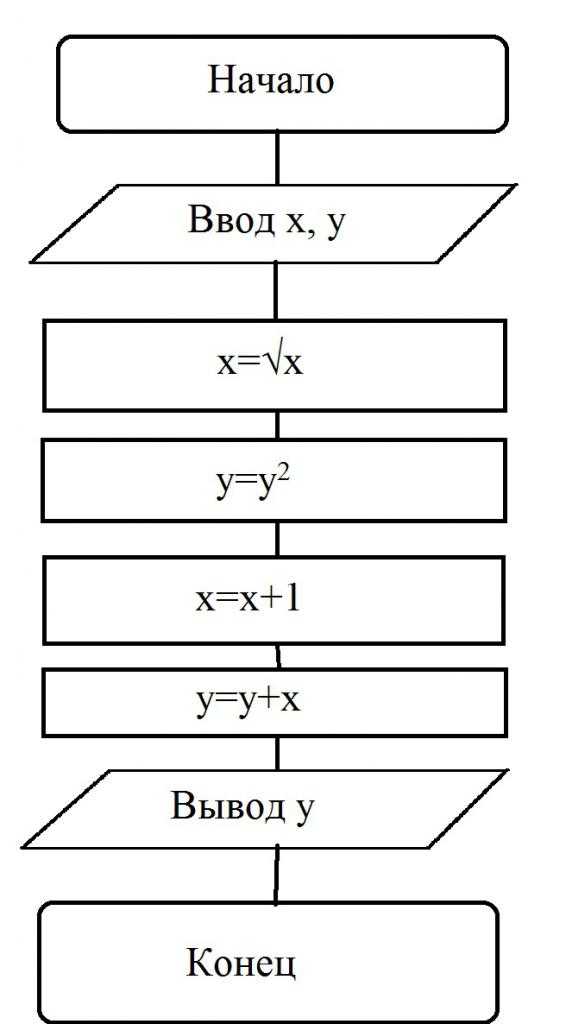
При этом пользователь самостоятельно вводит значения переменных. Допустим, х=16, а у=2. Процесс выполнения такой:

1. Производится ввод значений х и у.
2. Выполняется операция преобразования: х=√16=4.
3. Выполняется условие: у=у²=4.
4. Производится вычисление: х=(х+1)=(4+1)=5.
5. Дальше вычисляется следующая переменная: у=(у+х)=(5+4)=9.
6. Выводится решение: у=9.

На этом примере блок-схемы по информатике хорошо видно, как происходит решение алгоритма. Нужно обратить внимание на то, что значения х и у задаются на начальном этапе и они могут быть любыми.

www.syl.ru

Алгоритмы в математике

Разделы: Математика

---

Современные формы обучения, инновации в преподавании, введение новых технологий диктуют учителю необходимость постигать секреты мастерства, а значит, и совершенствовать методы обучения и воспитания учащихся.

Исследования психологов и педагогов, опыт коллег показывают: чтобы научить детей самостоятельно учиться и проявлять творчество необходимо применение деятельностного подхода в обучении. Для этого учащихся нужно замотивировать и обучить их приемам и способам учебной деятельности, которые помогут сформировать необходимые знания, умения и навыки.

Курс школьной математики имеет достаточно широкие возможности для применения различных приемов, методов и технологий. В последние годы в содержание школьного курса естественным образом закладывается алгоритмическая линия. Так как применение алгоритмов является приоритетным в моей работе, то нужно отметить что, между понятиями “прием” и “алгоритм” существует много общего, ни и есть принципиальные отличия, а именно:

– прием – это рациональный способ работы, который состоит из отдельных действий, он может быть выражен в виде правил или инструкций, его можно перестроить и на его основе создать новый прием. Приемы деятельности допускают самостоятельный выбор учениками конкретных действий по решению учебных задач;
– алгоритм – это общепонятное и однозначное предписание, которое определяет последовательность действий, позволяющее достичь искомый результат. Алгоритм предполагает жесткое выполнение шагов, а прием дает общее направление деятельности по решению учебных задач, не регламентируя каждый шаг. Поэтому я в своей работе выделяю два подхода: 1) обучение алгоритмам; 2) формирование приемов решения задач. Школьные задачи делятся на: алгоритмические, полуалгоритмические, полуэвристические и эвристические. Каждый тип задачи предполагает свои схемы решения, подходы, применение логики и изобретательности.

На начальном этапе обучения математике применение алгоритмов способствует формированию и прочному усвоению навыков владения математическими методами. Также осуществляется подготовка к формированию первоначальных представлений о математическом моделировании. Уже в начальных классах прослеживается применение простейших алгоритмов выполнения арифметических операций, дети овладевают навыками выполнения последовательных действий. Решают задачи с составлением схем и кратких записей. Это можно рассматривать как пропедевтику операционного стиля мышления.

Следующий уровень алгоритмической культуры учащихся – введение понятия алгоритма и формирование его основных свойств. Это происходит в среднем звене школы. Именно в этот период необходимо сочетания алгоритма и образца ответа, что дает возможность ученику, верно, ответить на поставленный вопрос, сопроводив его правильной речью. У учителя появляется возможность предлагать задачи с элементами творчества. А материал, предлагаемый в наших школьных учебниках, является хорошей базой для обучения составлению простейших алгоритмов и дальнейшей их записи в разных формах. Мы применяем табличную, графическую (блок-схема), словесную и формульную форму записи алгоритмов.

В качестве примера, иллюстрирующего процесс алгоритмизации как средство обучения, можно указать на решение задач методом уравнений. Примером графического алгоритма является блок-схема для отыскания количества решений системы двух линейных уравнений с двумя неизвестными (см. Рисунок 1).

Отыскания числа решений системы двух линейных уравнений (блок-схема)

Рис. 1
Графические алгоритмы

Табличную форму алгоритма можно продемонстрировать на примере таблицы, составляемой для исследования функций и дальнейшего построения графиков (см. рис. 2).

Исследование функции и построение графика

Функция задана уравнением у = f(x). Исследовать функцию и построить ее график.

1. Таблица исследования функции

2. Построение графика

Рис. 2
Табличный алгоритм

Пример формульного способа – последовательность нахождения компонентов при составлении уравнения касательной к графику той или иной функции (см. рис. 3).

Уравнение касательной к графику функции

Рис. 3
Формульный способ

Словесный алгоритм используется практически во всех правилах выполнения действий, например, правило сложения чисел с разными знаками (см. рис. 4).

Алгоритм сложения чисел с разными знаками

Рис. 4
Словесный алгоритм

В старших классах работа становится разнообразней и содержательней, появляется возможность включать упражнения разного типа и уровня сложности, предполагающее, что приемы деятельности могут быть разной степени сложности и обобщенности. Они состоят из большого числа действий, выполнение которых приводит к применению алгоритмов на отдельных этапах работы.

Такой подход к преподаванию математики в основной школе определяет условия для формирования у учащихся навыков, позволяющих в старших классах успешно изучать базовый курс “Информатики и ИКТ”. Применение алгоритмов в старших классах, по мнению некоторых учителей, отбивает творческий подход к решению задач, но с другой стороны, твердое знание основных задач курса и умение их решать, является твердым фундаментом для активизации самостоятельной и творческой работы учащихся.

Список литературы

1. Кухарев Н.В. На пути к профессиональному совершенству. – М.: Просвещение, 1990.
2. Епишева О.Б. Крутич В.И. Учить школьников учиться математике. – М.: Просвещение, 1990.
3. Сост. Глейзер Г.Д. Повышение эффективности обучения математике в школе. – М.: Просвещение, 1991.
4. Груденов Я.И. Совершенствование методики работы учителя математики. – М.: Просвещение, 1990.
5. Байдак В.А. и др. Формирование алгоритмической культуры у учащихся. – М.: Просвещение, 1989.

26.06.2011

xn--i1abbnckbmcl9fb.xn--p1ai

Виды алгоритмов в информатике: примеры

При изучении информатики немало внимания уделяется изучению алгоритмов и их видам. Не зная основных сведений о них, нельзя написать программу или проанализировать ее работу. Изучение алгоритмов начинается еще в школьном курсе информатики. Сегодня мы рассмотрим понятие алгоритма, свойства алгоритма, виды.

Понятие

Алгоритм – это определенная последовательность действий, которая приводит к достижению того или иного результата. Составляя алгоритм, детально прописывают каждое действие исполнителя, которое в дальнейшем приведет его к решению поставленной задачи.

Довольно часто алгоритмы используют в математике для решения тех или иных задач. Так, многим известен алгоритм решения квадратных уравнений с поиском дискриминанта.

Свойства

Прежде чем рассматривать виды алгоритмов в информатике, необходимо выяснить их основные свойства.

Среди основных свойств алгоритмов необходимо выделить следующие:

• Детерминированность, то есть определенность. Заключается в том, что любой алгоритм предполагает получение определенного результата при заданных исходных.
• Результативность. Означает, что при наличии ряда исходных данных после выполнения ряда шагов будет достигнут определенный, ожидаемый результат.
• Массовость. Написанный единожды алгоритм может использоваться для решения всех задач заданного типа.
• Дискретность. Она подразумевает, что любой алгоритм можно разбить на несколько этапов, каждый из которых имеет свое назначение.

Способы записи

Вне зависимости от того, какие виды алгоритмов в информатике вы рассматриваете, существует несколько способов их записи.

1. Словестный.
2. Формульно-словестный.
3. Графический.
4. Язык алгоритма.

Наиболее часто изображают алгоритм в виде блок-схемы, используя специальные обозначения, зафиксированные ГОСТами.

Основные виды

Выделяют три основных схемы:

1. Линейный алгоритм.
2. Ветвящийся алгоритм, или разветвленный.
3. Циклический.

Далее мы рассмотрим виды алгоритмов в информатике, примеры, которые помогут более детально понять, как они работают.

Линейный

Наиболее простым в информатике считается линейный алгоритм. Он предполагает последовательность выполнения действий. Приведем наиболее простой пример алгоритма такого вида. Назовем его «Сбор в школу».

1. Встаем, когда звенит будильник.

2. Умываемся.

3. Чистим зубы.

4. Делаем зарядку.

5. Одеваемся.

6. Кушаем.

7. Обуваемся и идем в школу.

8. Конец алгоритма.

Разветвляющийся алгоритм

Рассматривая виды алгоритмов в информатике, нельзя не вспомнить о разветвляющейся структуре. Данный вид предполагает наличие условия, при котором в случае его выполнения действия выполняются в одном порядке, а в случае невыполнения – в другом.

Например, возьмем следующую ситуацию – переход дороги пешеходом.

1. Подходим к светофору.

2. Смотрим на сигнал светофора.

3. Он должен быть зеленым (это условие).

4. Если условие выполняется, мы переходим дорогу.

4.1 Если нет – ждем, пока загорится зеленый.

4.2 Переходим дорогу.

5. Конец алгоритма.

Циклический алгоритм

Изучая виды алгоритмов в информатике, детально следует остановиться на циклическом алгоритме. Данный алгоритм предполагает участок вычислений или действий, который выполняется до выполнения определенного условия.

Возьмем простой пример. Если ряд чисел от 1 до 100. Нам необходимо найти все простые числа, то есть те, которые делятся на единицу и себя. Назовем алгоритм «Простые числа».

1. Берем число 1.

2. Проверяем, меньше ли оно 100.

3. Если да, проверяем простое ли это число.

4. Если условие выполняется, записываем его.

5. Берем число 2.

6. Проверяем, меньше ли оно 100.

7. Проверяем, простое ли оно.

…. Берем число 8.

Проверяем, меньше ли оно 100.

Проверяем, простое ли число.

Нет, пропускаем его.

Берем число 9.

Таким образом перебираем все числа, до 100.

Как видите, шаги 1 – 4 будут повторяться некоторое число раз.

Среди циклических выделяют алгоритмы с предусловием, когда условие проверяется в начале цикла, или с постусловием, когда проверка идет в конце цикла.

Другие варианты

Алгоритм может быть и смешанным. Так, он может быть циклическим и разветвленным одновременно. При этом используются разные условия на разных отрезках алгоритма. Такие сложные структуры приеняются при написании сложных программ и игр.

Обозначения в блок-схеме

Мы с вами рассмотрели, какие виды алгоритмов есть в информатике. Но мы не рассказали о том, какие обозначения используются при их графической записи.

1. Начало и конец алгоритма записываются в овальной рамке.
2. Каждая команда фиксируется в прямоугольнике.
3. Условие прописывается в ромбе.
4. Все части алгоритма соединяются при помощи стрелок.

Выводы

Мы с вами рассмотрели тему «Алгоритмы, виды, свойства». Информатика уделяет немало времени изучению алгоритмов. Их используют при написании различных программ как для решения математических задач, так и для создания игр и различного рода приложений.

fb.ru