2.1.12. Свойства биномиальных коэффициентов
Биномиальными коэффициентами являются величины
,
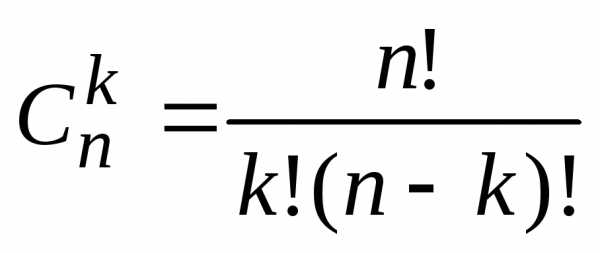которые выражают число сочетаний из nэлементов поk. Эти величины обладают следующими свойствами.
Свойство симметрии.
.
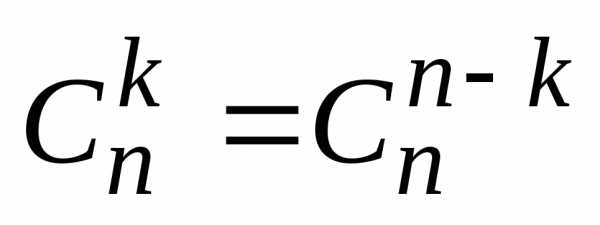В формуле бинома это означает, что коэффициенты, стоящие на одинаковых местах от левого и правого концов формулы, равны, например:
Действительно,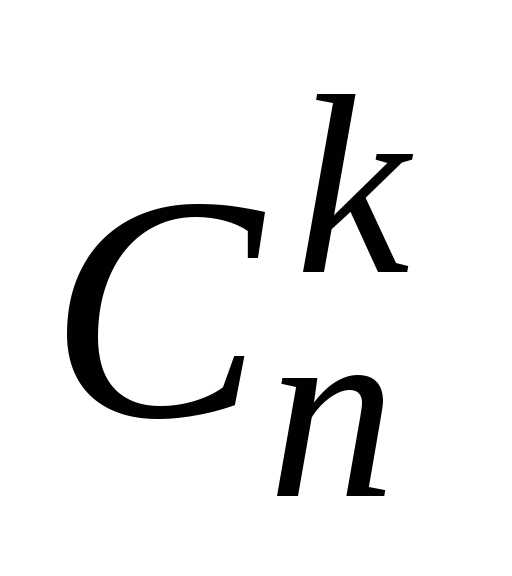 
—
это количество подмножеств, содержащихkэлементов, множества, содержащегоnэлементов. А
—
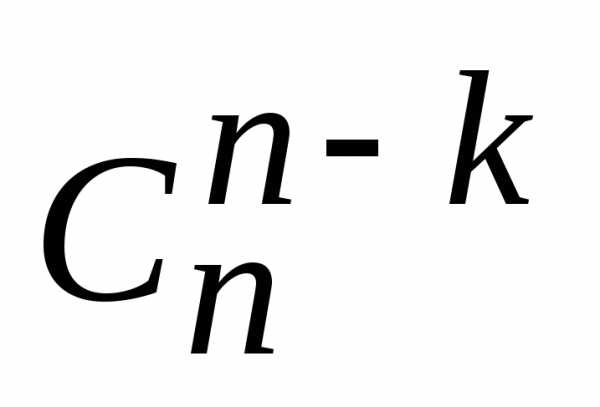количество дополнительных к ним
подмножеств. Сколько подмножеств,
столько и дополнений.
Свойство Паскаля.
Пусть .
Число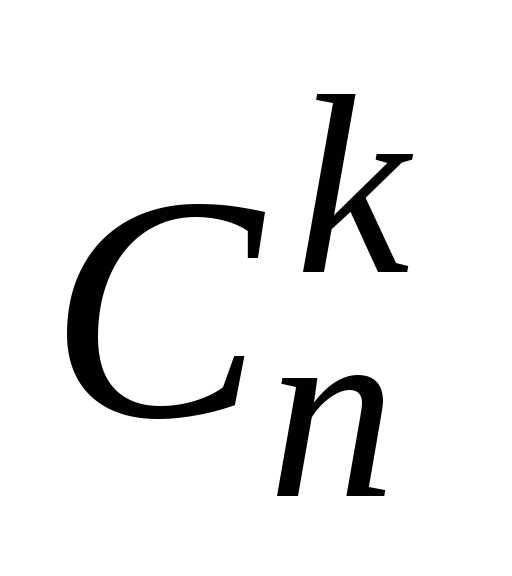
—
это количество подмножеств из k элементов множестваX.
Разделим все подмножества на два класса:
1) подмножества,
не содержащие элемен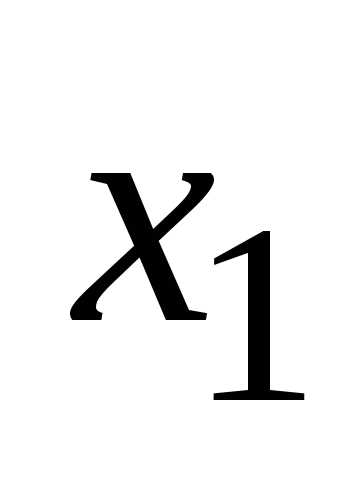т 
,
— их будет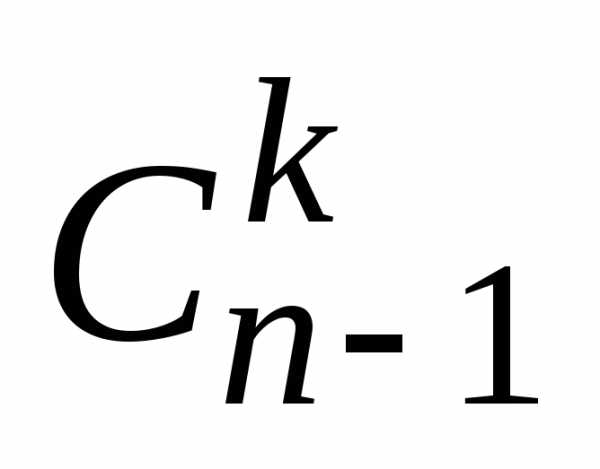
;
2) подмножества,
содержащие элемен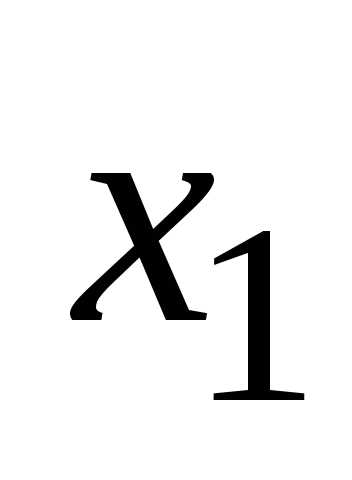т 
,
— их будет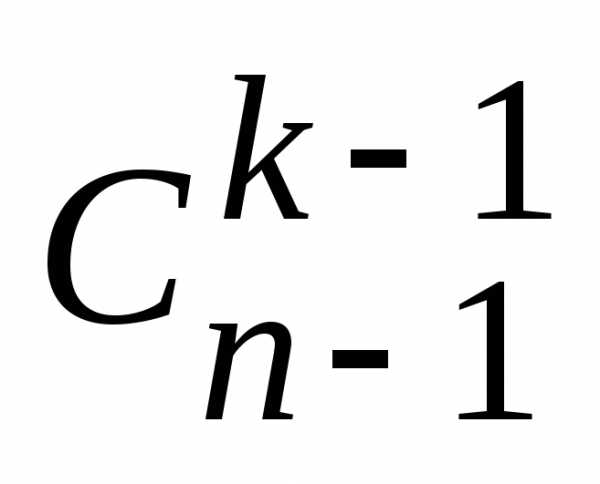
.
Т.к. эти классы не пересекаются, то по правилу суммы количество всех k-элементных подмножеств множестваXбудет равно
На этом свойстве
основано построение треугольника
Паскаля (рис. 2.2), в n-ой
строке которого стоят коэффициенты
разложения бинома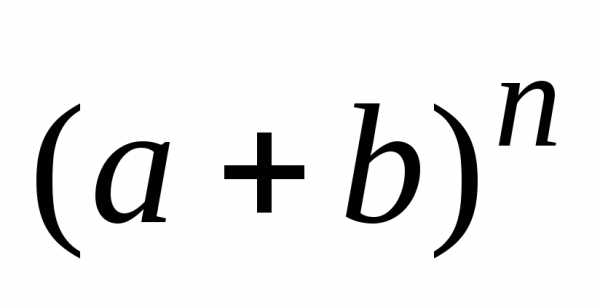
Свойство суммы.
Подставим в формулу бинома Ньютона
значения . Получим
Заметим, что с
точки зрения теории множеств сумма
выражает количество всех подмножествn-элементного
множества. По теореме о мощности булеана
(см. 1.4.4) это количество равно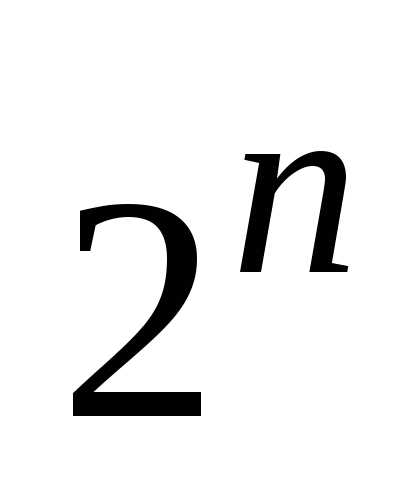
.
Свойство разности.
Положим в формуле
бинома Ньютона
.
Получим в левой части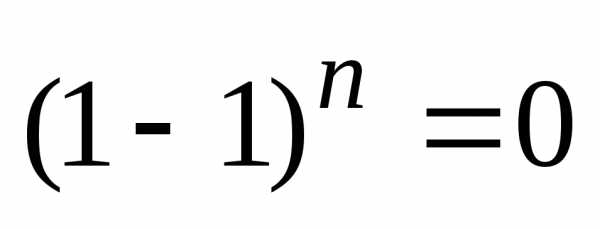
,
а в правой – биномиальные коэффициенты
с чередующимися знаками, что и доказывает
свойство.
Последнее свойство удобнее записать, перенеся все коэффициенты с отрицательными знаками в левую часть формулы:
тогда свойство легко запоминается в словесной формулировке: “ сумма биномиальных коэффициентов с нечетными номерами равна сумме биномиальных коэффициентов с четными номерами”.
Задача.
Найти член разложения бинома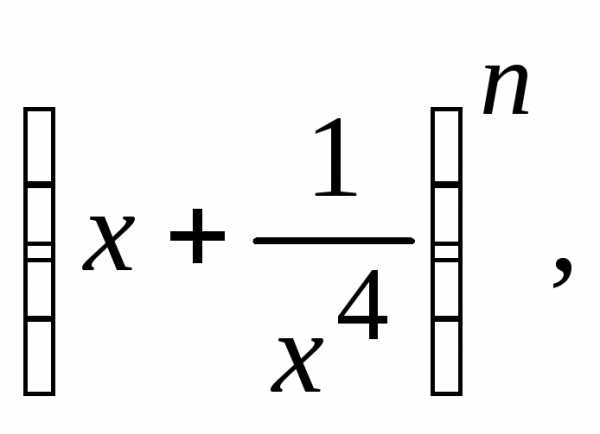
не содержащийx,
если сумма биномиальных коэффициентов
с нечетными номерами равна 512.
Решение. По
свойству разности сумма биномиальных
коэффициентов с четными номерами также
равна 512, значит, сумма всех коэффициентов
равна 512+512=1024. Но по свойству суммы это
число равно.
Поэтому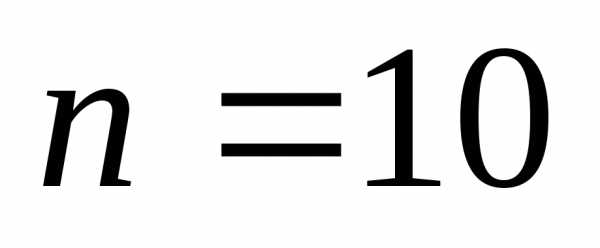
.
Запишем общий член разложения бинома
и преобразуем его:
при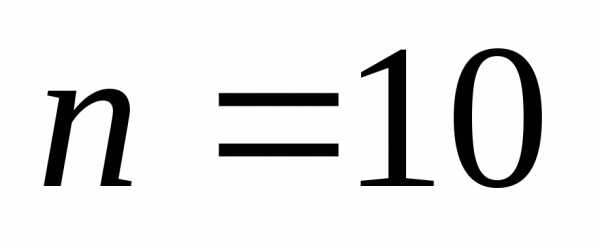 
получим:
Член разложения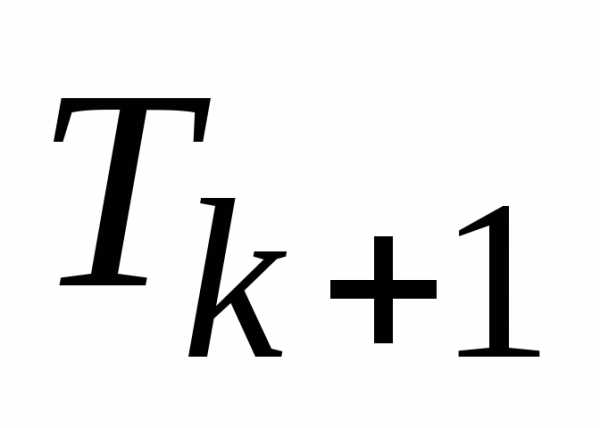 
не содержитx,
если
,
т.е.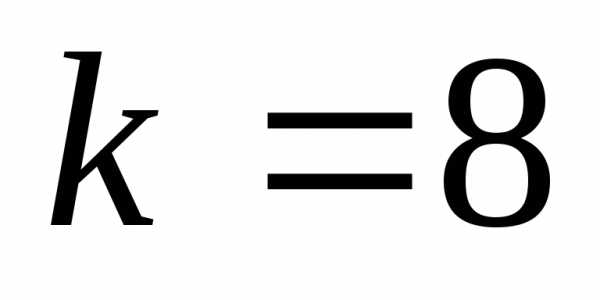
Свойство
максимума. Если степень биномаn– четное число, то среди биномиальных
коэффициентов есть один максимальный
при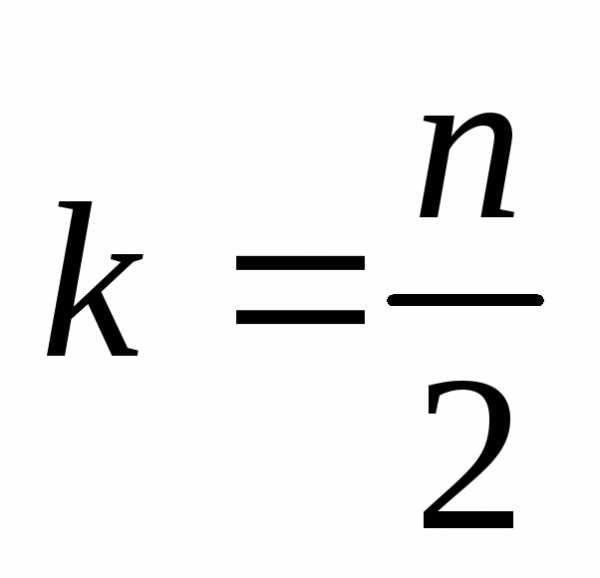
.
Если степень бинома нечетное число, то
максимальное значение достигается для
двух биномиальных коэффициентов пр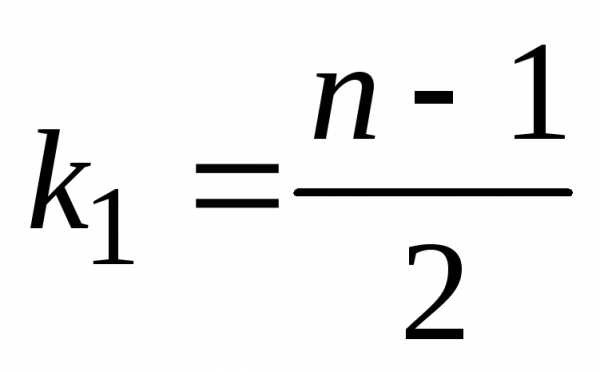и
и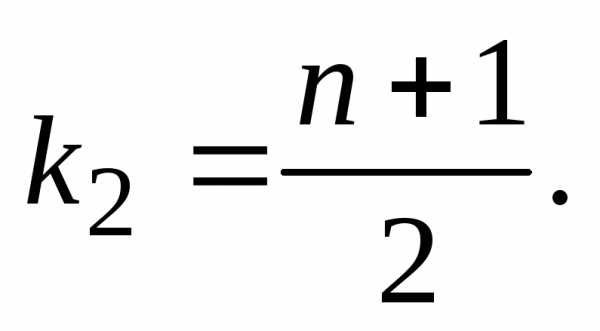
Так, при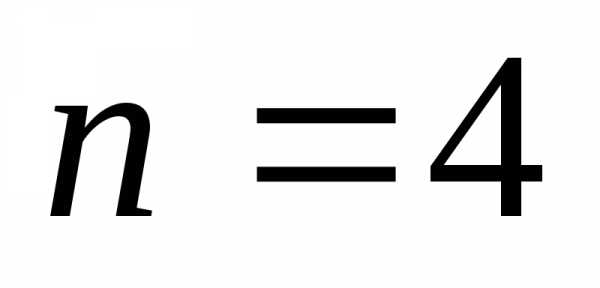 
максимальным
является коэффициент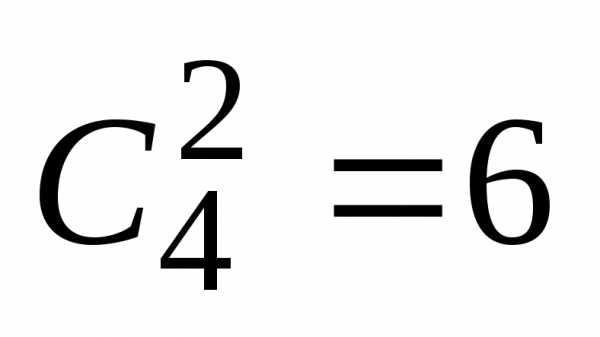
,
а при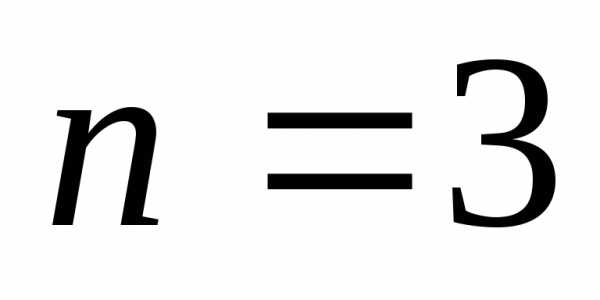
максимальное значение равно
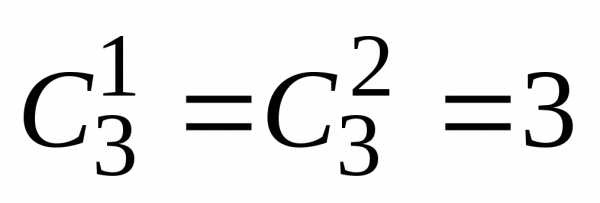(рис.
2.2).
2.1.13. Приближенные вычисления с помощью бинома Ньютона
Положим в формуле бинома Ньютона :
Эту формулу
удобно применять для приближенных
вычислений при малых значениях x(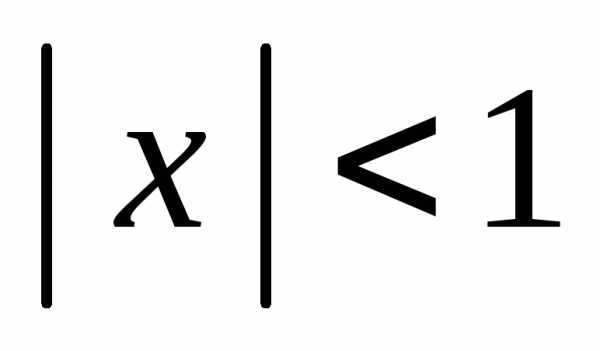
).
Пример 1.
Используя формулу бинома Ньютона,
вычислить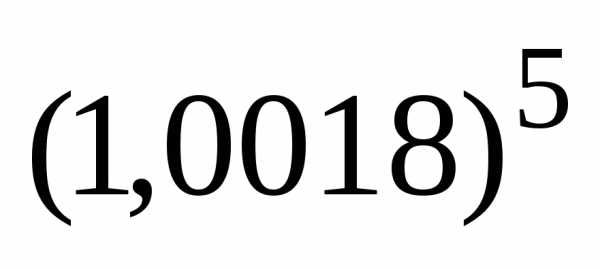
с
точностью до.
По приведенной выше формуле имеем:
Оценим третье слагаемое в этой сумме.
остальные слагаемые еще меньше. Поэтому все слагаемые, начиная с третьего, можно отбросить. Тогда
Пример 2.
Вычислить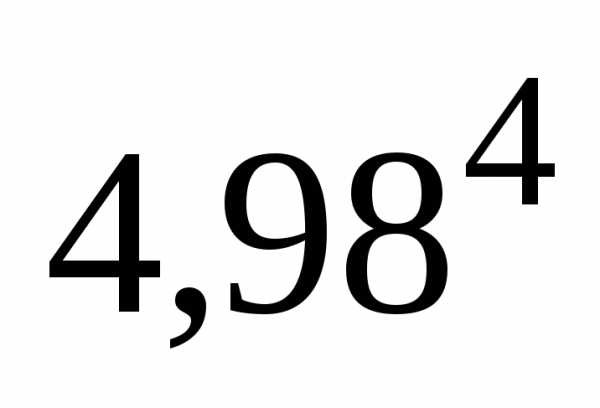
с
точностью до 0,01.
Оценим третье слагаемое:
.
Оценим четвертое слагаемое:
Значит все слагаемые, начиная с четвертого, можно отбросить. Получим
studfiles.net
Биномиальные коэффициенты :: Производящие функции
В данном очень важном приложении речь пойдёт о биномиальных коэффициентах, точнее, об их расширении на случай произвольных значений верхнего индекса. Иногда такая тема в литературе называется «расширенный треугольника Паскаля», поскольку расширение биномиальных коэффициентов влечёт за собой расширение треугольника Паскаля, который из этих коэффициентов состоит, а также рассматриваемая здесь функция (1+z)n (точнее, её разложение в ряд) называется биномиальным рядом.
Свойства биномиальных коэффициентов и доказательства основных тождеств в этом разделе не предусматривается, речь о них идёт только в контексте производящих функций. Предполагается, что читатель знаком с основными положениями комбинаторики или, по крайней мере, встречался с ними в реальной жизни. Ведь математика окружает нас со всех сторон. Числа, закономерности и разнообразные комбинации могут появиться где угодно: во время похода в магазин, расчета шансов на победу в казино, в теории управления и даже в футурологических прогнозах. В целом, все умеют считать. Но иногда комбинаторика оказывается более сложной, чем это необходимо в повседневной жизни. Скажем, при расчётах энтропии некоторой сложной физической системы, когда требуется вычислять количество допустимых конфигураций соответствующей физической модели. Так вот расширенные биномиальные коэффициенты как раз больше относятся к научным, а не повседневным расчетам.
Основные определения
Здесь я вынужден немного остановиться на определениях и обозначениях, чтобы не возникало недоразумений. Подготовленный читатель может пропустить этот пункт.
Биномиальный коэффициент обозначается символом , или (что часто встречается в русской литературе) .
Давайте сразу определимся с обозначениями. Правильное обозначение для биномиальных коэффициентов не , как учат в российских школах (и в университетах), а . К сожалению, я не знаю, по какой причине в России чаще используется обозначение , а в остальном Мире — . Поэтому учтите, что если вы пишите статью для российских журналов, вас поймут, как бы вы эти коэффициенты не обозначили, а для зарубежных журналов советую писать правильно.
Читается этот символ разными способами: «число сочетаний из n по k», или просто «из n по k», а также говорят «выбор k из n». Смысл указанных выражений заключён в комбинаторной интерпретации этого символа — это число способов выбрать k объектов из n различных объектов, причём порядок выбора не важен. Например, из множества {1,2,3,4,5} можно выбрать два элемента десятью способами:
Таким образом,
В общем случае известно, что
В процессе вычислений, чтобы не считать лишние факториалы, можно сразу часть множителей сократить:
От этой формулы и будем отталкиваться в будущем. Именно она и является правильным определением биномиальных коэффициентов. Число n называется верхним индексом, а k — нижним. В соответствии с комбинаторной интерпретацией, числа n и k должны быть целыми неотрицательными. Наша задача будет заключаться в том, чтобы расширить определение на произвольные значения n.
Биномиальные коэффициенты, упорядоченные специальным образом, образуют треугольник Паскаля.
В XVII веке французский математик, физик, философ Блез Паскаль впервые в своем «трактате об арифметическом треугольнике» наиболее полно рассказал о свойствах этого самого треугольника (хотя сам треугольник встречался в работах других математиков задолго до Паскаля).Строится этот замечательный треугольник очень просто:
По краям треугольника ставятся единицы, а любое число, стоящее не с краю, вычисляется как сумма двух чисел, расположенных сверху слева и сверху справа от него. Например, 10=4+6, или 3=1+2. Итак, речь зашла о треугольнике Паскаля в связи с тем, что он как раз образован биномиальными коэффициентами:
Для наших целей (и для удобства) лучше записывать треугольник, выравнивая его по левому краю:
Нули появляются за счёт нуля в числителе (когда k>n). Заметьте, что в нулевом столбце ставятся единицы, так как
В числителе стоит произведение нулевого числа элементов, которое по определению равно 1. Данная формула верна для любого (в том числе, комплексного) n.
Ну вот, мы уже приближаемся к тому, чтобы изучить биномиальные коэффициенты для любого n. Наше расширение, во-первых, должно быть таким, чтобы формула осталась прежней (для удобства), во-вторых, треугольник Паскаля, образованный биномиальными коэффициентами (с целым отрицательным значением индекса), не должен потерять своё основное свойство:
оно гласит, что число в клетке (n,k) равно сумме верхнего числа и верхнего левого (когда числа выровнены по левому краю).
В-третьих (что самое важное), должна остаться справедливой биномиальная теорема, утверждение которой напоминается в следующем пункте.
Биномиальная теорема
Содержание данной теоремы в классической формулировке известно еще из средних классов школы:
Это выражение также носит название бином Ньютона. Коэффициенты бинома Ньютона и называются биномиальными коэффициентами.
Теперь, пользуясь биномом Ньютона и треугольником Паскаля, можно посчитать, например (взяв третью строчку треугольника),
Данный сайт посвящён производящим функциям, поэтому нас данная теорема интересует лишь с этой позиции. Запишем производящую функцию в следующем виде:
Представленная производящая функция генерирует последовательность биномиальных коэффициентов с верхним индексом, равным n. Верхний индекс в сумме можно записать равным ∞, это ничего не меняет, когда n целое неотрицательное (почему?). Обратите внимание, что подстановка z=1 даёт замечательное тождество (ряд конечный, поэтому подстановка справедлива):
которое показывает, что сумма всех чисел в n-й строке треугольника Паскаля равняется двойке, возведённой в степень n.
Данное разложение функции (1+z)n в ряд согласуется с формулой Тейлора, в соответствие с которой коэффициент, стоящий при zk равен
Напомню, что для этой функции ряд Тейлора сходится при |z|<1 (когда n произвольно). Эта функция также носит название «Биномиальный ряд».
Расширение
Теперь нас интересует ответ на вопрос: можно ли допустить в биномиальной теореме, чтобы n было целым отрицательным? Можно, причём треугольник Паскаля расширяется «вверх» единственным образом, если мы хотим сохранить его основное свойство:
при этом . Рассмотрим отрицательные строчки подробнее:
Например, минус первая строка треугольника может быть только такой, и никакой иначе, поскольку , а остальные элементы вычисляются однозначно:
Для чего нужны расширенные биномиальные коэффициенты? Для того, чтобы раскладывать в ряд простые дроби. Например,
Поэтому, кстати (читайте о разложении 1/(1−z)),
Теперь выведем формулу для целых отрицательных биномиальных коэффициентов исходя не из их положения в треугольнике, а из их правильного определения:
Таким образом,
Данная формула также согласуется с разложением этой функции в ряд Тейлора для |z|<1.
Пойдём дальше. На практике могут пригодиться рациональные показатели степени, например, рассмотрим биномиальный ряд для n=1/2:
Эта формула даёт нам возможность раскладывать в ряд функцию
Аналогично (мы оставляем подробный вывод читателю),
а это, в свою очередь, позволяет записать ещё одну полезную производящую функцию:
www.genfunc.ru
Свойства биноминальных коэффициентов — Студопедия.Нет
Решение задач на перебор вариантов
Цель работы:
студент должен:
знать:
— определение соединений, их видов;
— определение вероятности;
— теоремы сложения, умножения вероятностей;
уметь:
— по условию задачи различать виды соединений;
— вычислять разные виды соединений;
— вычислять вероятность событий.
Сведения из теории:
Соединения, их виды
Группы, составленные из каких – либо элементов, называются соединениями.
Различаю три основных вида соединений: размещения, перестановки и сочетания.
Размещениями из n элементов по m в каждом называются такие соединения, которые отличаются друг от друга либо самими элементами, либо порядком их расположения.
Число размещений из n элементов по m обозначается и вычисляется по формуле:
.
Перестановками из n элементов называются такие соединения из всех n элементов, которые отличаются друг от друга порядком расположения элементов.
Перестановки представляют частный случай размещений из n элементов по n в каждом.
Число всех перестановок из n элементов равно произведению последовательных чисел от 1 до n включительно:
,
n!-читается «n-факториал», причем 0!=1 и 1!=1.
Используя приведенные выше определения имеем формулы:
,
при решении задач часто используется равенство:
.
Сочетаниями из n элементов по m в каждом называются такие соединения, которые отличаются друг от друга хотя бы одним элементом.
Число сочетаний из n элементов по m обозначается и вычисляется по формуле:
,
которую можно записать также в виде
или
.
Кроме того, при решении задач используются следующие формулы, выражающие основные свойства сочетаний:
,
Пример 94.
Найти число размещений из 10 элементов по 4.
Решение:
по формуле :
.
Пример 95.
Решить уравнение: .
Решение:
используя формулу для вычисления числа размещений имеем:
.
Разделим обе части на одинаковые выражения, получим:
,
и решим получившееся квадратное уравнение: .
Пример 96.
Решите систему: .
Решение:
решим второе уравнение:
.
Т. к. , то –11 не удовлетворяет условию задачи. Подставив х=12 в первое уравнение системы, получим
.
Используя основное свойство сочетаний, имеем:
,
тогда
.
Ответ: х=12, у=5.
Пример 97.
Сколькими способами из восьми кандидатов можно выбрать три лица на три должности?
Решение:
условию задачи соответствуют размещения 3 из 8, имеем:
.
Случайные события
Изучение каждого явления в порядке наблюдения или производства опыта связано с осуществлением некоторого комплекса условий (испытаний). Всякий результат или исход испытания называется событием.
Если событие при заданных условиях может произойти или не произойти, то оно называется случайным.
В том случае, когда событие должно непременно произойти, его называют достоверным, а в том случае, когда оно заведомо не может произойти, невозможным.
События называются несовместными, если каждый раз возможно появление только одного из них. События называются совместными, если в данных условиях появление одного из этих событий не исключает появление другого при том же испытании.
События называются противоположными, если в условиях испытания они, являясь единственными его исходами, несовместны.
Вероятность события рассматривается как мера объективной возможности появления случайного события.
Классическое определение вероятности.
Вероятностью событияА называется отношение числа благоприятных исходов m, к числу всех возможных исходов n:
.
Вероятность любого события не может быть меньше нуля и больше единицы, т. е. .
Невозможному событию соответствует вероятность Р(А)=0, а достоверному – вероятность Р(А)=1.
Пример 98.
В лотерее из 1000 билетов 200 выигрышных. Вынимают наугад один билет. Какова вероятность, что этот билет выигрышный?
Решение:
количество благоприятных событий, удовлетворяющих условию задачи m=200.
Число всех возможных вариантов n=1000.
По определению вероятности: Р(А)=200/1000=0,2.
Пример 99.
Из урны, в которой находятся 5 белых и 3 черных шара, вынимают один шар. Найти вероятность того, что этот шар черный?
Решение:
общее число шаров m=8, из них черных n=3, по определению: Р(А)=3/8=0,375.
Пример 100.
Из урны, в которой находятся 12 белых и 8 черных шара, вынимают наудачу два шара. Найти вероятность того, что оба шара окажутся черными?
Решение:
общее число возможных случаев n равно числу сочетаний из 20 (12+8) элементов по два:
;
число благоприятных исходов m равно числу сочетаний из 8 элементов по два:
.
По определению: Р(А)=28/190=0,147.
Пример 101.
В партии из 18 деталей находятся 4 бракованных. Наугад выбирают 5 деталей. Какова вероятность того, что из этих 5 деталей две окажутся бракованными?
Решение:
число всех равновозможных независимых исходов n равно числу сочетаний из 18 по 5:
.
Подсчитаем число благоприятных исходов m. Среди 5 взятых наугад деталей должно быть 3 качественных и 2 бракованных. Число способов выборки двух бракованных деталей из 4 имеющихся бракованных равно числу сочетаний из 4 по 2:
.
Число способов выборки трех качественных деталей из 14 имеющихся равно числу сочетаний из 14 по 3:
.
Любая группа качественных деталей может комбинироваться с любой группой бракованных, поэтому общее число комбинаций m равно:
,
по определению: Р(А)=2184/8568=0,255.
Задания для самостоятельного решения:
Решить следующие задачи, используя определение сочетаний, их видов:
| 1 вариант 1) Сколько двузначных чисел можно составить из цифр 1, 3, 5, 8, 9 так, чтобы в каждом числе не было одинаковых цифр? 2) Из 6 открыток надо выбрать 3. Сколькими способами это можно сделать? 3) Решите уравнение: . | 2 вариант 1) Сколькими способами могут разместиться 5 человек вокруг круглого стола? 2) Сколькими способами можно составить флаг, состоящий из трех горизонтальных полос различных цветов, если имеется материал семи различных цветов? 3) Решите уравнение: . |
| 3 вариант 1) Из 10 кандидатов нужно выбрать 3 человека на конференцию. Сколькими различными способами это можно сделать? 2) Сколько различных пятизначных чисел можно составить из цифр 0, 1, 3, 5, 7 так, чтобы в каждом числе не было одинаковых цифр? 3) Решите уравнение: . | 4 вариант 1) Бригадир должен отправить на работу бригаду из 3 человек. Сколько таких бригад можно составить из 8 человек? 2) На собрании должны выступить 5 человек (А, Б, В, Г, Д). Сколькими способами их можно разместить в списке выступающих, еслиА должен выступать первым? 3) Решите уравнение: . |
| 5 вариант 1) Сколькими способами можно расставить на полке 6 книг? 2) Сколькими способами можно выбрать гласную и согласную буквы из слова «журнал»? 3) Решите уравнение: . | 6 вариант 1) Сколькими способами можно составить список из 6 человек? 2) Сколькими способами собрание, состоящее из 18 человек, может из своего состава выбрать председателя собрания и секретаря? 3) Решите уравнение: . |
| 7 вариант 1) Среди перестановок из цифр 1, 2, 3, 4, 5 сколько таких, которые не начинаются цифрами 3 или 5? 2) Из города А в город В ведут 6 дорог, а из города В в город С –3 дороги. Сколькими способами можно попасть из города А в город С? 3) Решите систему: . | 8 вариант 1) В шахматном турнире принимали участие 15 шахматистов, причем каждый из них сыграл только одну партию с каждым из остальных. Сколько всего партий сыграно в этом турнире? 2) Имеется 8 пар перчаток различных размеров. Сколькими способами можно выбрать из них одну перчатку на левую руку и одну перчатку на правую руку так, чтобы эти перчатки были разных размеров? 3) Решите систему: . |
9 вариант 1) Группа учащихся изучает семь учебных дисциплин.сколькими способами можно составить расписание занятий на понедельник, если в этот учебный день должно быть четыре различных урока? 2) Сколько матчей будет сыграно в футбольном чемпионате с участием 16 команд, если каждые две команды встречаются между собой один раз? 3) Вычислить: . | |
Контрольные вопросы:
1. Дайте определение соединения, их виды?
2. Приведите формулы для вычисления разных видов соединений.
3. Дайте определение случайного события, их виды. Приведите примеры.
4. Дайте классическое определение вероятности.
Литература:[5, с. 234-238]
Практическая работа № 41
Свойства биноминальных коэффициентов
Цель работы:
студент должен:
знать:
— формулу бинома Ньютона;
— свойства биноминальных коэффициентов;
уметь:
— раскладывать бином по степеням х;
— возводить в различные степени трехчлены.
Сведения из теории:
Формула бинома Ньютона
Бином Ньютона – это формула разложения степени двучлена (бинома) (a+b)n в виде многочлена от a и b.
Запишем разложения бинома Ньютона для нескольких первых значений n:
Чтобы найти коэффициент при akbn—kв разложении бинома (a+b)n в общем случае, представим себе, что мы перемножаем n скобок и приводим подобные члены. Член akbn—kвстретится столько раз, сколько можно указать k скобок (из n возможных), из которых мы возьмем множитель а (а из остальных автоматически возьмем b). Это число равно числу выборок k скобок из n возможных, которое носит название числа сочетаний из n по k и обозначается .
В этих обозначениях формула имеет следующий вид:
.
Иными словами, число сочетаний из n по k равно коэффициенту при члене an—kbkв разложении n-ой степени двучлена (a+b) поэтому числа сочетаний называют иначе биномиальными коэффициентами.
Эту связь можно использовать для вывода свойств сочетаний алгебраическими методами. Такой подход к выводу свойств комбинаторных объектов носит название метода производящих функций.
Свойства биномиальных коэффициентов
Биномиальные коэффициенты обладают большим количеством свойств.
Свойство 1. .
Свойство2. – биномиальные коэффициенты, равноотстоящие от концов, равны между собой
Свойство3. – сумма биномиальных коэффициентов при фиксированномn равна .
Свойство4. – суммы биномиальных коэффициентов, стоящих на четных и на нечетных местах, равны между собой (и равны по половине от общей суммы).
Свойство5. – рекуррентное соотношение, связывающее биномиальные коэффициенты для соседних степеней.
Пример 102.
Разложить бином (1+х)6 по степеням x.
Решение:
применяем формулу бинома Ньютона:
.
Значения биномиальных коэффициентов находим последовательно по формуле :
Т.о.
Задача для самостоятельного решения №1.Разложить бином (1+х)5 по степеням x.
Пример 103.
Возвести трехчлен a+b+c в четвертую степень.
Решение:
применяем формулу бинома Ньютона:
Задача для самостоятельного решения №2.Возвести трехчлен a+b+c в третью степень.
Контрольные вопросы:
1. Запишите формулу бинома Ньютона.
2. Перечислите свойства биноминальных коэффициентов.
Литература: [16]
Практическая работа № 42
Треугольник Паскаля
Цель работы:
студент должен:
знать:
— принцип построения треугольника Паскаля;
уметь:
— возводить двучлен в любую натуральную степень.
Сведения из теории:
Треугольник Паскаля – бесконечная таблицабиномиальных коэффициентов, имеющая треугольную форму. В этом треугольнике на вершине и по бокам стоятединицы. Каждое число равно сумме двух расположенных над ним чисел. Строки треугольника симметричны относительно вертикальной оси. Назван треугольник в честьБлеза Паскаля.
Первая строка в этой таблице содержит биномиальные коэффициенты для n=1; вторая – дляn=2; третья – дляn=3 и т.д.
Пример 104.
Разложить выражение:(a+b)7.
Решение:
мы можем получить результат моментально, используя из таблицы разложение по седьмой строке (т.к. седьмая степень двучлена):
.
Задача для самостоятельного решения №1.Построить треугольник Паскаля до двадцатой строки.
Задача для самостоятельного решения №2.Разложить выражение:(a+b)n, гдеn–номер по журналу (если Ваш номер 1-7, то прибавьте к номеру число 5).
Контрольные вопросы:
1. Сформулируйте принцип построения треугольника Паскаля.
studopedia.net
3.5. Свойства биномиальных коэффициентов
Своим историческим названием числа Cnrобязаны формуле бинома Ньютона:
(a + b)n = Σrn = 0Cnrarbn—r . (3.13)
В этой формуле числа Cnr определяют число произведений arbn—r, которое равно числу всех сочетаний из n по r при суммировании этих произведений от r = 0 до n. Этот факт имеет вполне комбинаторное обоснование. Формула (3.13) относится к классу производящих функций, которые будут рассмотрены в 3.6. Здесь же нас интересуют свойства биномиальных коэффициентов.
Полагая в (3.13) a = b = 1, получим, что
Σrn = 0Cnr= 2n . (3.14)
Этой формулой выражается число всех r‑подмножеств n‑X множества .
Из формул (3.6) и (3.12) следует, что
Структура соединений
F: r‑ S → n‑X,
r = 3, n = 4.
Размещений:nr
111 112 113 114
121 122 123 124
131 132 133 134 Всех
141 142 143 144 инъективных (упорядоченных)
размещений:
211 212 213 214 Anr = n(n — 1)···(n — (r — 1))
221 222 223 224
231 232 233 234 123 132 213 231 312 321
241 242 243 244 124 142 214 241 412 421
134 143 314 341 413 431
311 312 313 314 234 243 324 342 423 432
321 322 323 324
331 332 333 334 перестановок: r!
341 342 343 344
Cочетаний, как классов
411 412 413 414 инъективных размещений:
421 422 423 424 Cnr = Anr / r! = n! / (r!(n -r)!)
431 432 433 434
441 442 443 444
Рисунок 3.4
Cnr = n(n — 1)…(n — (r — 1)) / r!.
Умножив и разделив обе части этого равенства на (n — r)!, получим
Cnr = n!/(r!(n — r)!). (3.15)
Из этой формулы при подстановках вместо rзначения (n—r) следует, чтоCnr=Cnn—r. Это свойство именуетсясимметрией биномиальных коэффициентов.
Далее, при r = 0 или r = n из (3.15) имеем
Cn0 = Cnn = 1. (3.16)
Докажем, что для Cnr имеет место соотношение:
Cnr = Cnr-1+ Cnr-1-1. (3.17)
Зафиксируем любой элемент xi в ‹x1, x2, …xn›. Тогда множество всех r‑элементных подмножеств n‑X множества распадается на два непересекающихся класса: тех, что не содержат xi и тех, что его содержат. Число элементов первого класса равно Cnr-1, так как r‑подмножество строится на (n-1)‑X множестве. Число элементов второго класса равно Cnr —— 11, поскольку эти элементы определяются всеми (r-1)‑подмножествами, построенными на (n-1)‑X множестве, с которыми комбинирует элемент xi. Доказательство окончено.
Свойства (3.16) и (3.17) позволяют расположить биномиальные коэффициенты в виде треугольника, по краям которого записаны единицы, а каждый элемент внутри вычисляется как сумма чисел, находящихся в верхнем ряду над ним. Строки имеют номера, идущие сверху вниз, начинаясь с нуля. Ими определяется значения n в (3.17). Значения r в этом же соотношении определяются номером элемента в строке. Эти значения также начинаются с нуля.
Построенная треугольная таблица чисел известна как треугольник Паскаля. Ниже приведены числа треугольника Паскаля для строк с номерами от нуля до пяти. Из таблицы видно, что она наглядно определяет значения биномиальных коэффициентов при малых значениях n и r.
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
…………………………..
studfiles.net
Биномиальный коэффициент — это… Что такое Биномиальный коэффициент?
В математике биномиальные коэффициенты — это коэффициенты в разложении бинома Ньютона по степеням x. Коэффициент при обозначается или и читается «биномиальный коэффициент из n по k» (или «це из n по k»):
В комбинаторике биномиальный коэффициент интерпретируется как количество сочетаний из n по k, то есть количество всех подмножеств (выборок) размера k в n-элементном множестве.
Биномиальные коэффициенты часто возникают в задачах комбинаторики и теории вероятностей. Обобщением биномиальных коэффициентов являются мультиномиальные коэффициенты.
Явные формулы
Значение биномиального коэффициента определено для всех целых чисел n и k. Явные формулы для вычисления биномиальных коэффициентов:
- для
- для или
- для
где обозначает факториал числа m.
Треугольник Паскаля
Тождество
позволяет расположить биномиальные коэффициенты для неотрицательных целых чисел n, k в виде треугольника Паскаля, в котором каждое число равно сумме двух вышестоящих:
Треугольная таблица, предложенная Паскалем в «Трактате об арифметическом треугольнике» (1654), отличается от выписанной здесь поворотом на 45°. Таблицы для изображения биномиальных коэффициентов были известны и ранее (Тарталье, О. Хайяму и др.).
Строки в треугольнике Паскаля в пределе стремятся к функции нормального распределения.
Если взять квадратную матрицу, отсчитав N элементов по катетам треугольника и повернув квадрат на любой из четырёх углов, то детерминант этих четырёх матриц по модулю равен 1 при любом N. Если поставить уголом из 1 в верхний левый угол, то детерминант матрицы будет равен 1.
В матрице числа на диагонали i + j = const повторяют числа строк треугольника Паскаля (i, j = 0…∞).
Матрицу , где i, j = 0..p можно разложить в произведение двух строго диагональных матриц. Первая нижнетреугольная, а вторая получается из первой путем транcпонирования. Матрицы удовлетворяет соотношению:
- где i, j = 0..p.
Обратная матрица к U имеет вид:
Таким образом, можно разложить обратную матрицу к в произведение двух строго диагональных матриц: первая матрица — верхнетреугольная, а вторая получается из первой путем транспонирования, что позволяет дать явное выражение для обратных элементов:
- , где i, j , m, n = 0..p.
Элементы обратной матрицы меняются при изменении её размера и, в отличие от матрицы , недостаточно приписать новую строку и столбец.
Свойства
Производящие функции
Для фиксированного значения n производящей функцией последовательности биномиальных коэффициентов является:
Для фиксированного значения k производящей функцией последовательности биномиальных коэффициентов является:
Двумерной производящей функцией биномиальных коэффициентов является:
Делимость
Из теоремы Люка следует, что:
Основные тождества
- (правило симметрии).
- (вынесение за скобки).
- (замена индексов).
Бином Ньютона и следствия
Свёртка Вандермонда и следствия
Другие тождества
- — m-ое гармоническое число.
- Мультисекция ряда даёт тождество, выражающее сумму биномиальных коэффициентов с произвольным шагом s и смещением t в виде замкнутой суммы из s слагаемых:
Асимптотика и оценки
где — энтропия.
- (неравенство Чернова).
Алгоритмы вычисления
Биномиальные коэффициенты могут быть вычислены с помощью формулы , если на каждом шаге хранить значения при . Этот алгоритм особенно эффективен, если нужно получить все значения при фиксированном . Алгоритм требует памяти ( при вычислении всей таблицы биномиальных коэффициентов) и времени (в предположении, что каждое число занимает единицу памяти и операции с числами выполняются за единицу времени).
При фиксированном значении k биномиальные коэффициенты могут быть вычислены по рекуррентной формуле с начальным значением . Для вычисления значения этот метод требует памяти и времени.
См. также
Ссылки
biograf.academic.ru
Биноминальные коэффициенты
Сnk(число сочетаний) — это число способов выбрать k различных (т.е. без повторений) предметов из n различных (0<=k<=n), без учета порядка выбора. Они могут быть вычислены по следующим формулам:
Треугольник Паскаля и Бином Ньютона:
В предыдущих примерах мы вычисляли числа Cnk непосредственно по формуле, делая много умножений и делений. Оказывается, есть метод вычислять сразу много разных Cnk, используя только сложение. Особенно важно это при программной реализации, поскольку компьютер складывает числа гораздо быстрее, чем умножает и тем более делит. Он основан на доказанном выше свойстве:
Cn+1k+1=Cnk+Cnk+1.
Давайте построим из чисел два бесконечных треугольника. В первом из них (см. рис. внизу слева) будем ставить единицы в самом верху и по краям каждом следующей строки, а каждое из остальных чисел будет равно сумме двух стоящих над ним слева и справа (этот треугольник называется треугольником Паскаля). Во втором (см. рис. внизу справа) будем последовательно выписывать значения Cnk, отводя по одной строке для каждого значения n и располагая в ней Cnk по возрастанию k. На самом деле эти треугольники одинаковы. Равенство первых нескольких строчек, можно заметить, а дальше надо уже доказывать.
Утверждение. Если строчки треугольника Паскаля и позиции в них нумеровать, начиная с нуля, то на k-м месте в n-й строке будет стоять значение Cnk (основное свойство треугольника Паскаля). Доказательство: Индукция по n (см. лекцию «Индукция», если вы еще не знакомы с этим методом). База: n=0 — действительно, C00=1 — как раз то, что стоит на верхушке треугольника Паскаля. Переход: от n к n+1. Пусть в n-й строчке все числа уже равны значениям Cnk из n по соответствующим k. Рассмотрим n+1-ю строчку. На ее краях (нулевое и n+1-е места) стоят две единицы — и значения Cn+10 и Cn+1n+1 как раз равны 1. Далее, при всех k от 1 до n число, стоящее на k-м месте в n+1-й строке, равно сумме чисел, стоящих в n-й строке на k-1-м и k-м местах соответственно (т.е. как раз двух стоящих над ним — по принципу построения треугольника Паскаля). По предположению индукции, они равны Cnk-1 и Cnk, а их сумма тогда будет Cnk-1+Cnk, что как раз равно Cn+1k, ч.т.д. Для справки мы приводим здесь первые 11 строчек (с нулевой по 10-ю) треугольника Паскаля — их можно посчитать и вручную. На компьютере, с помощью простой программы, можно вычислить значительно больше, и более быстрого алгоритма, чем треугольник Паскаля, пока не существует.
| |||||||||||||||||||||||||||||||||||||||||||||
1
1
1
2
1
1
3
3
1
1
4
6
4
1
1
5
10
10
5
1
1
6
15
20
15
6
1
Такие, казалось бы, чисто комбинаторные вещи, как числа Cnk и треугольник Паскаля, неожиданно встречаются и в алгебре. Выпишем известные формулы сокращенного умножения:
(a+b)0= (a+b)1= (a+b)2= (a+b)3= | 1 a+b a2+2ab+b2 a3+3a2b+3ab2+b3 |
Коэффициенты в этих формулах (и это лучше видно, когда выписаны еще нулевая и первая степень) — это числа из треугольника Паскаля, то есть Cnk. На самом деле, такая закономерность будет продолжаться и дальше, и называется она бином Ньютона. Точнее:
(a+b)n=an+Cn1an-1b+Cn2an-2b2+…+Cnn-1a1bn-1+bn.
Можно доказать эту формулу по индукции, как и основное свойство треугольника Паскаля. Приведем более простое объяснение:
(a+b)n=(a+b)(a+b)…(a+b) (n скобок). Раскрывая скобки, получаем в отдельных слагаемых произведения n букв, каждая из которых — a или b, т.е. an-kbk при каком-то k от 0 до n. Докажем, что для каждого такого k число таких слагаемых — ровно Cnk, откуда, приведя подобные, и получаем формулу бинома. Но это правда: an-kbk получается путем взятия a из k скобок и b из n-k оставшихся; разные такие слагаемые получаются путем разного выбора этих самых k скобок, а k скобок из n можно выбрать как раз Cnk способами, ч.т.д.
Именно из-за бинома Ньютона числа Cnk часто называют биномиальными коэффициентами.
Следствие 1
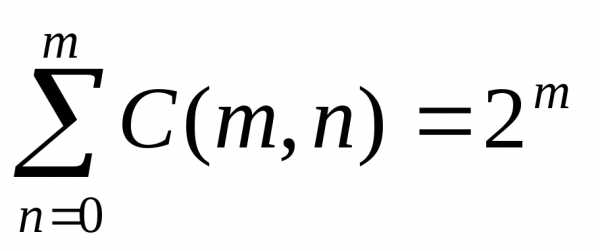
Доказательство. Заметим, что 2n=(1+1)n и раскроем по формуле бинома Ньютона (при a=b=1). Получим 1+Cn1+Cn2+…+Cnn-1+1 — с учетом того, что Cn0=Cnn=1, это как раз сумма из условия, ч.т.д.
Следствие 2
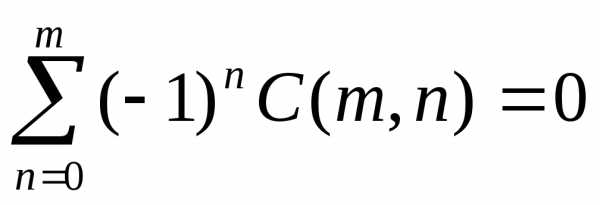(доказать
самостоятельно, при доказательстве
использовать формулу бинома Ньютона
при a=1, b=-1).
Свойства биномиальных коэффициентов
Биномиальные коэффициенты обладают целым рядом замечательных свойств.
Теорема
,.
,studfiles.net
3.5. Свойства биномиальных коэффициентов
Своим историческим названием числа Cnrобязаны формуле бинома Ньютона:
(a + b)n = Σrn = 0Cnrarbn—r . (3.13)
В этой формуле числа Cnr определяют число произведений arbn—r, которое равно числу всех сочетаний из n по r при суммировании этих произведений от r = 0 до n. Этот факт имеет вполне комбинаторное обоснование. Формула (3.13) относится к классу производящих функций, которые будут рассмотрены в 3.6. Здесь же нас интересуют свойства биномиальных коэффициентов.
Полагая в (3.13) a = b = 1, получим, что
Σrn = 0Cnr= 2n . (3.14)
Этой формулой выражается число всех r‑подмножеств n‑X множества .
Из формул (3.6) и (3.12) следует, что
Структура соединений
F: r‑ S → n‑X,
r = 3, n = 4.
Размещений:nr
111 112 113 114
121 122 123 124
131 132 133 134 Всех
141 142 143 144 инъективных (упорядоченных)
размещений:
211 212 213 214 Anr = n(n — 1)···(n — (r — 1))
221 222 223 224
231 232 233 234 123 132 213 231 312 321
241 242 243 244 124 142 214 241 412 421
134 143 314 341 413 431
311 312 313 314 234 243 324 342 423 432
321 322 323 324
331 332 333 334 перестановок: r!
341 342 343 344
Cочетаний, как классов
411 412 413 414 инъективных размещений:
421 422 423 424 Cnr = Anr / r! = n! / (r!(n -r)!)
431 432 433 434
441 442 443 444
Рисунок 3.4
Cnr = n(n — 1)…(n — (r — 1)) / r!.
Умножив и разделив обе части этого равенства на (n — r)!, получим
Cnr = n!/(r!(n — r)!). (3.15)
Из этой формулы при подстановках вместо rзначения (n—r) следует, чтоCnr=Cnn—r. Это свойство именуетсясимметрией биномиальных коэффициентов.
Далее, при r = 0 или r = n из (3.15) имеем
Cn0 = Cnn = 1. (3.16)
Докажем, что для Cnr имеет место соотношение:
Cnr = Cnr-1+ Cnr-1-1. (3.17)
Зафиксируем любой элемент xi в ‹x1, x2, …xn›. Тогда множество всех r‑элементных подмножеств n‑X множества распадается на два непересекающихся класса: тех, что не содержат xi и тех, что его содержат. Число элементов первого класса равно Cnr-1, так как r‑подмножество строится на (n-1)‑X множестве. Число элементов второго класса равно Cnr —— 11, поскольку эти элементы определяются всеми (r-1)‑подмножествами, построенными на (n-1)‑X множестве, с которыми комбинирует элемент xi. Доказательство окончено.
Свойства (3.16) и (3.17) позволяют расположить биномиальные коэффициенты в виде треугольника, по краям которого записаны единицы, а каждый элемент внутри вычисляется как сумма чисел, находящихся в верхнем ряду над ним. Строки имеют номера, идущие сверху вниз, начинаясь с нуля. Ими определяется значения n в (3.17). Значения r в этом же соотношении определяются номером элемента в строке. Эти значения также начинаются с нуля.
Построенная треугольная таблица чисел известна как треугольник Паскаля. Ниже приведены числа треугольника Паскаля для строк с номерами от нуля до пяти. Из таблицы видно, что она наглядно определяет значения биномиальных коэффициентов при малых значениях n и r.
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
…………………………..
studfiles.net
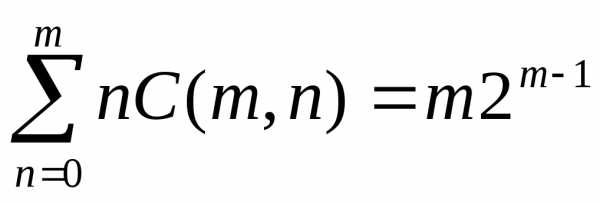