Формула и ряд Тейлора. Биноминальный ряд — Мегаобучалка
Рассмотрим многочлен -й степени
Его можно представить в виде суммы степеней , взятых с некоторыми коэффициентами. Продифференцируем его раз по переменной , а затем найдем значения многочлена и его производных в точке :
Таким образом, получаем, что
Полученное выражение называется формулой Маклорена для многочлена степени .
Рассуждая аналогично, можно разложить многочлен по степеням разности , где — любое число. В этом случае будем иметь:
Это выражение называется формулой Тейлора для многочлена в окрестности точки .
Пример
Задание. Разложить в ряд Тейлора функцию в точке .
Решение. Найдем производные:
Итак, , , . Значение функции в точке
Таким образом,
Ответ.
БИНОМИАЛЬНЫЙ РЯД — степенной ряд вида
где n — целое, а α — произвольное фиксированное число (вообще говоря, комплексное), z = x + iy — комплексное переменное, (αn) — биномиальные коэффициенты. Для целых α = m ≥ 0 Б. р. сводится к конечной сумме m + 1 слагаемых
называемой Ньютона биномом. Для остальных значений α Б. р. абсолютно сходится при |z| < 1 и расходится при |z| > 1. В граничных точках единичной окружности |z| = 1 Б. р. ведет себя следующим образом: 1) если Re α > 0, то он абсолютно сходится во всех точках окружности |z| = 1; 2) если Re α ≤ — 1, то он расходится во всех точках окружности |z| = 1; 3) если — 1 < Rе α ≤ 0, то Б. р. расходится в точке z = — 1 и условно сходится во всех остальных точках окружности |z| = 1. Во всех точках, в к-рых Б. р. сходится, он представляет главное значение функции (1 + z)α, равное 1 при z = 0. Б. р. является частным случаем гипергеометрического ряда.
Если z = x и α — действительные числа, причем α не есть целое неотрицательное число, то Б. р. ведет себя следующим образом: 1) если α > 0, то он абсолютно сходится при — 1 ≤ x ≤ 1 2) если α ≤ — 1, то Б. р. абсолютно сходится при — 1 < x < 1 и расходится при всех иных значениях х; 3) если — 1 < α ≤ 0, то Б. р. абсолютно сходится при — 1 < x < 1, условно сходится при х = 1 и расходится при х = — 1; при |х| > 1 Б. р. всегда расходится.
Теорема Эйлера. Правильные многогранники.
Выпуклый многогранник называется правильным, если его гранями являются равные правильные многоугольники, и в каждой вершине сходится одинаковое число граней.
Пусть дан топологически правильный многогранник, гранями которого являются n — угольники, и в каждой вершине сходится m ребер. Ясно, что n и m больше или равны трем. Обозначим, как и раньше, В — число вершин, Р — число ребер и Г — число граней этого многогранника. Тогда
nГ = 2P; Г = ; mB = 2P; В = .
По теореме Эйлера, В — Р + Г = 2 и, следовательно,
Откуда Р = .
Из полученного равенства, в частности, следует, что должно выполняться неравенство 2n + 2m – nm > 0, которое эквивалентно неравенству (n – 2)(m – 2) < 4.
Теорема Эйлера
Для любого выпуклого многогранника справедливо соотношение Г+В-Р=2, где Г – число граней, В – число вершин и Р – число ребер данного многогранника.
Доказательство теоремы, связанное с нахождением суммы плоских углов выпуклого многогранника:
Обозначим эту сумму, как . Напомним, что плоскими углами многогранника являются внутренние плоские углы его граней.
Например, найдем для таких многогранников:
а) тетраэдр имеет 4 грани – все треугольники. Таким образом, ;
б) куб имеет 6 граней – все квадраты. Таким образом, ;в) возьмем теперь произвольную пятиугольную призму. У нее две грани – пятиугольники и пять граней – параллелограммы. Сумма углов выпуклого пятиугольника равна . Сумма углов параллелограмма равна . Таким образом, .
Итак, для нахождения мы вычисляли сначала сумму углов, принадлежащих каждой грани. Воспользуемся этим приемом и в общем случае.
Введем следующие обозначения: , , …, — число сторон в 1, 2, 3-й и т.д. последней грани многогранника.
Тогда
Далее найдем общее число сторон всех граней многогранника. Оно равно . Так как каждое ребро многогранника принадлежит двум граням, имеем: .
Таким образом, получаем:
(1)
Сосчитаем теперь другим способом. Для этого будем менять форму многогранника таким образом, что бы у него не менялось число Г, В и Р. При этом может измениться каждый плоский угол в отдельности, но число останется прежним. Выберем такое преобразование многогранника: примем одну из его граней за основание, расположим его горизонтально и «растянем» для того, чтобы на него можно было спроектировать другие грани многогранника. Например, на рисунке 1а показано, к чему мы придем, в случае тетраэдра, а на рисунке 1б – в случае куба
Заметим, что спроектированный многогранник представляет слившиеся две наложенные друг на друга пластины с общим контуром, из которых верхняя разбита на (Г-1) многоугольник, а нижняя на грани не делится. Обозначим число сторон внешнего окаймляющего многоугольника через r. Теперь найдем спроектированного многоугольника. состоит из следующих трех сумм:
1) Сумма углов нижней грани, у которой r сторон, равна .
2) Сумма углов верхней пластины, вершинами которых являются вершины нижней грани, тоже равна .
3) Сумма «внутренних» углов верхней пластины равна , так как верхняя пластина имеет внутренних вершин и все углы группируются около них.
Итак, (2)
Таким образом, сравнивая выражения (1) и (2), получаем: Г+В-Р=2, что и требовалось доказать.
megaobuchalka.ru
4)Биномиальный ряд.
Разложим в ряд Маклорена функцию f(x)=(1+x)m, где m любое целое постоянное число. Непосредственная оценка остаточного члена и тут затруднена. Поступим следующим образом. Заметим, что функция f(x)=(1+x)m удовлетворяет дифференциальному уравнению (1+x)f'(x)=(m)f(x) (*), и условию f(0)=1. Найдем степенной ряд, сумма которого S(x) удовлетворяет уравнению (*) и условию S(0)=1: (5). Подставим в (*) получим . Приравняем коэффициенты при одинаковых степенях x:a1=m;a1+2a2=ma1; …;nan+(n+1)an+1=man. Отсюда найдем — это биномиальные коэффициенты. Подставляя их в формулу (5), получим:
(6).
Если m целое положительное число, то сумма (6) обрывается, т.к. начиная с члена содержащего xm+1 все коэффициенты равны нулю. При других m имеется бесконечный ряд. Определим его радиус сходимости: ,,.
Ряд (6) сходится при |x|<1. Получили, что в (-1;1) ряд (6) представляет функцию S(x), удовлетворяющую дифференциальному уравнению (*) и условиюS(0)=1. Но дифференциальному уравнению может удовлетворять только одна функция с таким условием, потому S(x)=(1+x)m в (-1;1). Итак:
(7).
Это и есть биноминальный ряд. При m целом положительным он обрывается и дает формулу бинома Ньютона.
5)Функция f(x)=arctg(x).
Рассмотрим ряд: сходится в (-1;1). Проинтегрируем на [0;x], |x|<1. Получим:
(8).
Можно доказать, что (4) верно на [-1,1].
9)Применение степенных рядов к приближенным вычислениям.
Если дана функции 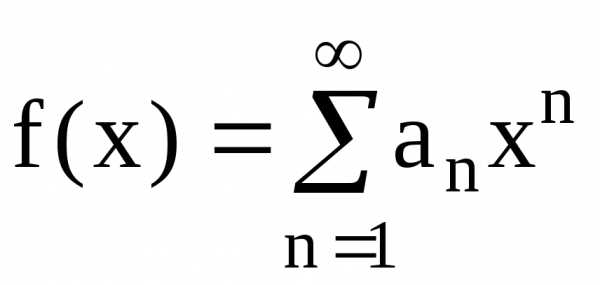 (1) и нужно вычислить ее приближенное
значение при некотором х, то достаточно
взять сумму нескольких ее первых членов
f(x)»Sn(x).
Сколько первых членов нужно взять, чтобы
обеспечить точность вычисления, на этот
вопрос дает ответ оценка остатка ряда
|rn(x)|.
(1) и нужно вычислить ее приближенное
значение при некотором х, то достаточно
взять сумму нескольких ее первых членов
f(x)»Sn(x).
Сколько первых членов нужно взять, чтобы
обеспечить точность вычисления, на этот
вопрос дает ответ оценка остатка ряда
|rn(x)|.
Если ряд типа Лейбница, то |rn(x)|£|an+1xn+1|. Отсюда находим n, начинаяс которого rn(x) не превосходит заданной точности. Если ряд другой, то применяют мажорируемый ряд (обычно геометрическую прогрессию) сумму остатка которой можно оценить легче.
Примеры:
1)Вычислить число е сточностью до 7 знаков.
Т.к. 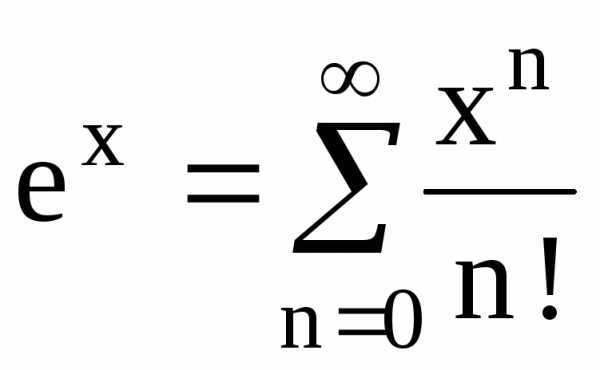 ,
то при x=1
имеем: Оценим |rn|.
,
то при x=1
имеем: Оценим |rn|.
.
Итак, 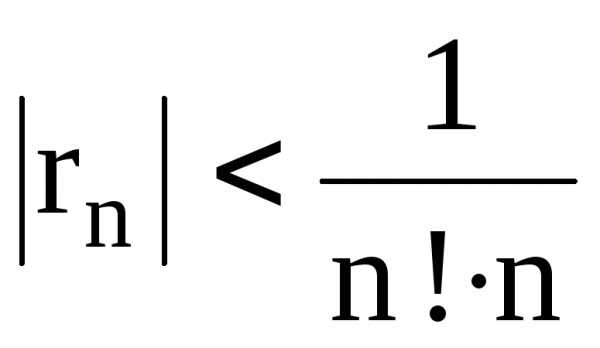 .
Должно быть
.
Должно быть 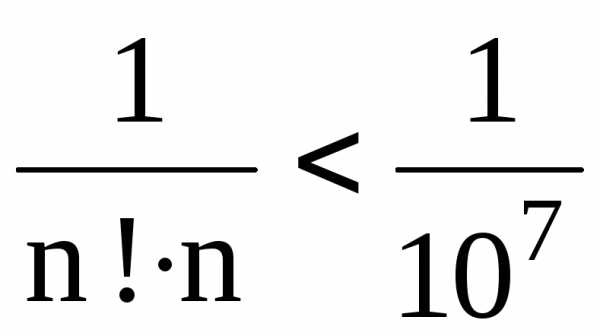 ;
видно, что при n=10 это уже есть. Поэтому
достаточно взять 11 первых членов:
;
видно, что при n=10 это уже есть. Поэтому
достаточно взять 11 первых членов:
.
2) Вычисление логарифмов чисел.
Если х принадлежит (-1;1), то (1). если заменитьх на -х, то (2) также справедливо в (-1;1).(1) и(2) применяются для вычисления ln чисел между 0 и 2. Как вычислить логарифмылюбых чисел? Сходящиеся ряды можно вычитать. Из (1) вычтем (2), получим:
(3)
верно в (-1;1).Всякое положительное
число t можно представить в виде 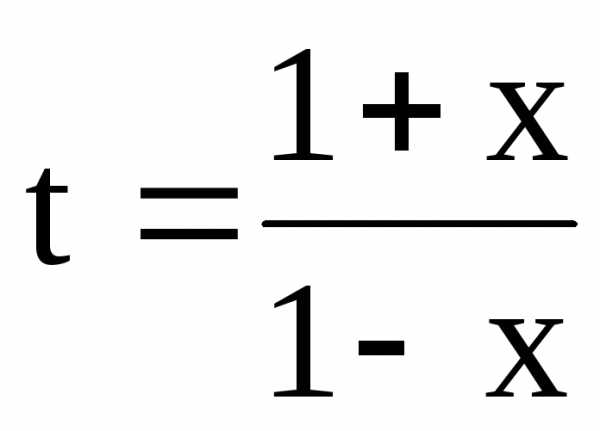 при хÎ(-1;1):
t-t×x=1+x,
при хÎ(-1;1):
t-t×x=1+x, 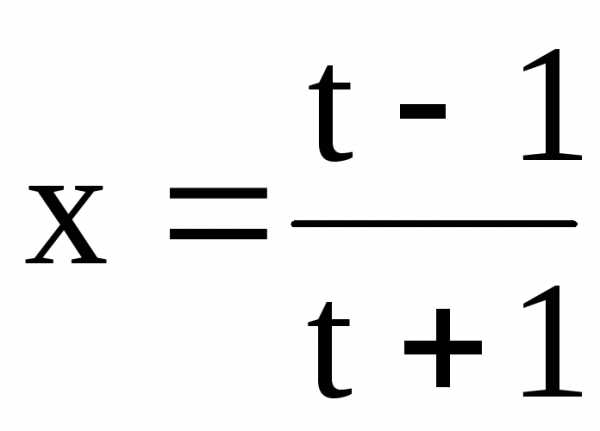 ,
потому можно вычислять:
,
потому можно вычислять:
.
3) Вычисление корней.
Надо с большой
точностью вычислить 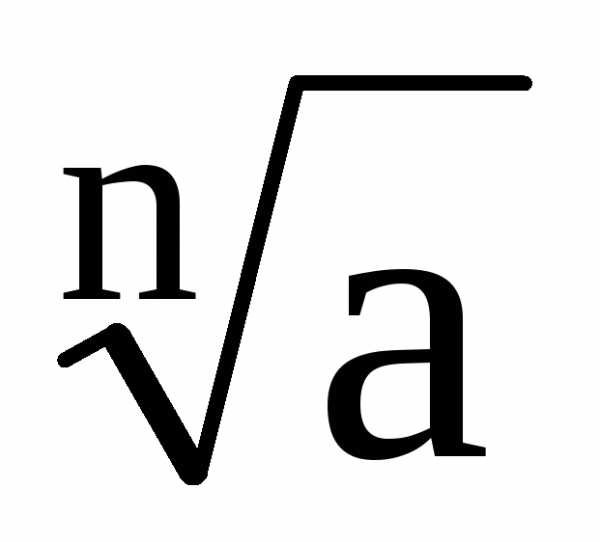
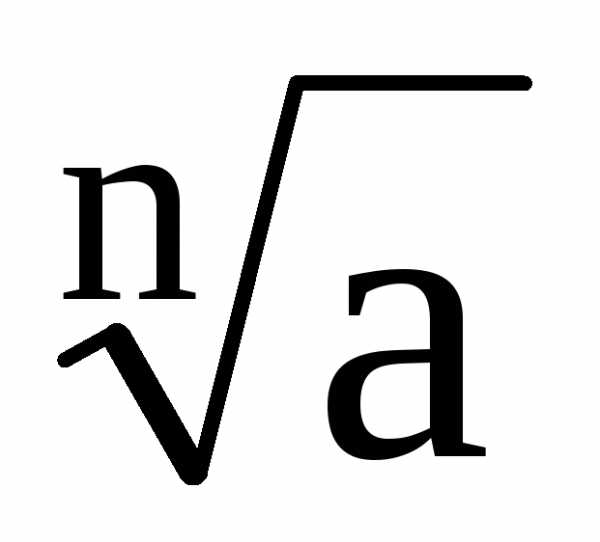 »b,
тогда a»bn,
»b,
тогда a»bn, 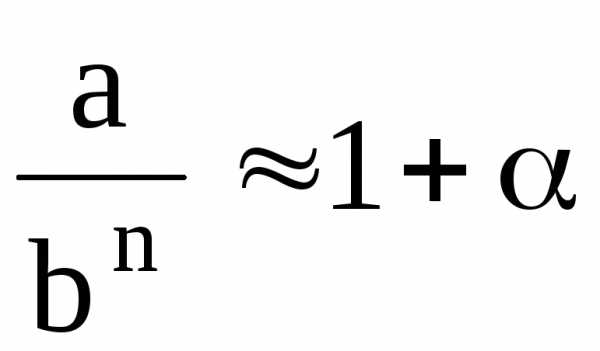 ,
где a-небольшая
величина: ½a½<1.
Тогда
,
где a-небольшая
величина: ½a½<1.
Тогда .
Разлагая 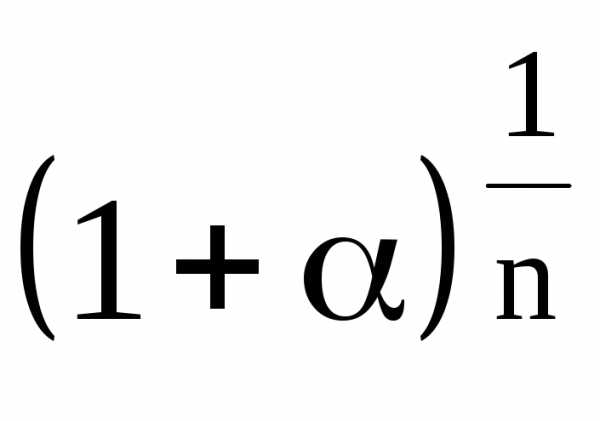 в биномиальный ряд, получим
в биномиальный ряд, получим 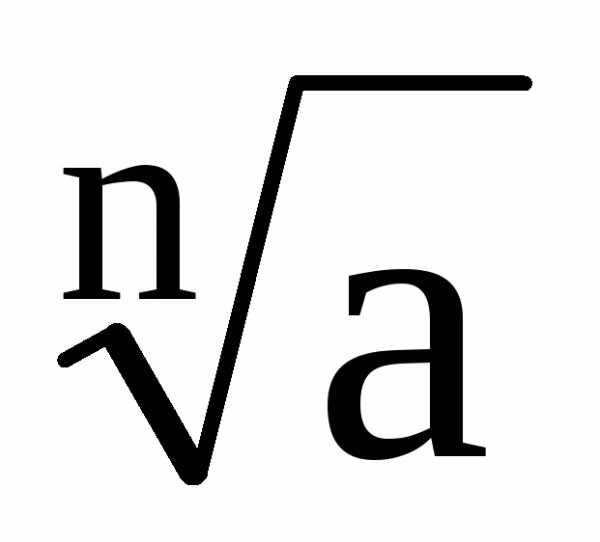 с любой точностью.
с любой точностью.
Пример: Поэтому
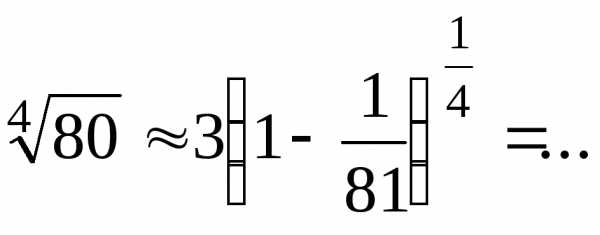
Вычисление интегралов.
Вычислить 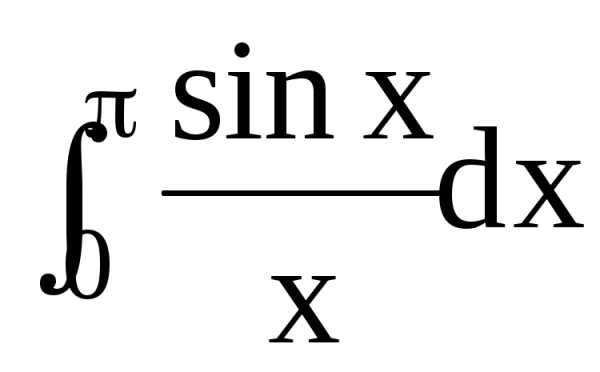 . Тогда
.
=
. Тогда
.
=
=
Выбирая нужное число членов полученного знакочередующегося ряда, мы и найдем значение данного интеграла с заданной точностью.
Степенные ряды применяются к вычислению пределов (раскрытию неопределенности), к приближенному решению дифференциальных уравнений и т.п.
studfiles.net
Бином Ньютона, биноминальное разложение с использованием треугольника Паскаля, подмножества
Биноминальное разложение с использованием треугольника Паскаля
Рассмотрим следующие выражения со степенями (a + b)n, где a + b есть любой бином, а n — целое число.
Каждое выражение — это полином. Во всех выражениях можно заметить особенности.
1. В каждом выражении на одно слагаемое больше, чем показатель степени n.
2. В каждом слагаемом сумма степеней равна n, т.е. степени, в которую возводится бином.
3. Степени начинаются со степени бинома n и уменьшаются к 0. Последний член не имеет множителя a. Первый член не имеет множителя b, т.е. степени b начинаются с 0 и увеличиваются до n.
4. Коэффициенты начинаются с 1 и увеличиваются на определенные значения до «половины пути», а потом уменьшаются на те же значения обратно к 1.
Давайте рассмотрим коэффициенты подробнее. Предположим, что мы хотим найти значение (a + b)6. Согласно особенности, которую мы только что заметили, здесь должно быть 7 членов
a6 + c1a5b + c2a4b2 + c3a3b3 + c4a2b4 + c5ab5 + b6.
Но как мы можем определить значение каждого коэффициента, ci? Мы можем сделать это двумя путями. Первый метод включает в себя написание коэффициентов треугольником, как показано ниже. Это известно как Треугольник Паскаля:
Есть много особенностей в треугольнике. Найдите столько, сколько сможете.
Возможно вы нашли путь, как записать следующую строку чисел, используя числа в строке выше. Единицы всегда расположены по сторонам. Каждое оставшееся число это сумма двух чисел, расположенных выше этого числа. Давайте попробуем отыскать значение выражения (a + b)6 путем добавления следующей строки, используя особенности, которые мы нашл
www.math10.com
БИНОМИАЛЬНЫЙ РЯД
степенной ряд вида
где — целое, а — произвольное фиксированное число (вообще говоря, комплексное), -. комплексное переменное, — биномиальные коэффициенты. Для целых Б. р. сводится к конечной сумме слагаемых называемой Ньютона биномом. Для остальных значений Б. р. абсолютно сходится при и расходится при .В граничных точках единичной окружности Б. р. ведет себя следующим образом: 1) если , то он абсолютно сходится во всех точках окружности ; 2) если , то он расходится во всех точках окружности ; 3) если то Б. р. расходится в точке и условно сходится во всех остальных точках окружности Во всех точках, в к-рых Б. р. сходится, он представляет главное значение функции , равное 1 при Б. р. является частным случаем гипергеометрического ряда.
Если — действительные числа, причем а не есть целое неотрицательное число, то Б. р. ведет себя следующим образом: 1) если , то он абсолютно сходится при ; 2) если , то Б. р. абсолютно сходится при и расходится при всех иных значениях х;3) если , то Б. р. абсолютно сходится при , условно сходится при и расходится при ; при Б. р. всегда расходится.
Б. р. появляется впервые, по-видимому, у И. Ньютона (I. Newton) в 1664-65. Исчерпывающее исследование Б. р. было проделано Н. Абелем [1]. Оно послужило началом теории степенных рядов в комплексной области.
Лит.:[1] Abel N.. «J. reine und angew. Math.», 1826, Bd 1, № 4; S. 311-39; [2] Knopp K., Theorie und Anwendung dcr unendlichen Rcihen, 5 Aufl., В., 1947; [3] Маркушевич А. И., Теория аналитических функций, 2 изр., т. 1, М. 1967. Е. Д. Соломенцев
slovar.wikireading.ru
Математическая энциклопедия — значение слова Биномиальный Ряд
степенной ряд вида где — целое, а — произвольное фиксированное число (вообще говоря, комплексное), -. комплексное переменное, — биномиальные коэффициенты. Для целых Б. р. сводится к конечной сумме слагаемых называемой Ньютона биномом. Для остальных значений Б. р. абсолютно сходится при и расходится при .В граничных точках единичной окружности Б. р. ведет себя следующим образом: 1) если , то он абсолютно сходится во всех точках окружности ; 2) если , то он расходится во всех точках окружности ; 3) если то Б. р. расходится в точке и условно сходится во всех остальных точках окружности Во всех точках, в к-рых Б. р. сходится, он представляет главное значение функции , равное 1 при Б. р. является частным случаем гипергеометрического ряда. Если — действительные числа, причем а не есть целое неотрицательное число, то Б. р. ведет себя следующим образом: 1) если , то он абсолютно сходится при ; 2) если , то Б. р. абсолютно сходится при и расходится при всех иных значениях х;3) если , то Б. р. абсолютно сходится при , условно сходится при и расходится при ; при Б. р. всегда расходится. Б. р. появляется впервые, по-видимому, у И. Ньютона (I. Newton) в 1664-65. Исчерпывающее исследование Б. р. было проделано Н. Абелем [1]. Оно послужило началом теории степенных рядов в комплексной области. Лит.:[1] Abel N.. «J. reine und angew. Math.», 1826, Bd 1, № 4; S. 311-39; [2] Knopp K., Theorie und Anwendung dcr unendlichen Rcihen, 5 Aufl., В., 1947; [3] Маркушевич А. И., Теория аналитических функций, 2 изр., т. 1, М. 1967. Е. Д. Соломенцев
Смотреть значение Биномиальный Ряд в других словарях
Ряд — линия
шеренга
Словарь синонимов
Ряд — м. вереница, строй, предметы по одной черте, по порядку, чередом. дерев. Улица в два ряда домов. ы на покосе, полосы в размах косы, валы. | Воен. каждый человек в шеренге, со……..
Толковый словарь Даля
В Ряд Нареч. — 1. Один около другого, в одну линию. 2. Наравне, рядом с кем-л., чем-л.
Толковый словарь Ефремовой
Динамический Ряд — Временная последовательность ретроспективных значений переменной объекта прогнозирования.
Политический словарь
Временной Ряд Продаж — Массив данных, содержащий информацию об объемах продаж в натуральных или денежных показателях за равные последовательные промежутки времени. Используется для анализа……..
Экономический словарь
Ряд — ряда (с числит. Два, три, четыре: ряда), в ряде и в ряду, мн. ряды, м. 1. (в ряду). Совокупность однородных предметов, расположенных в одну линию. Верхний ряд зубов. Стулья в……..
Толковый словарь Ушакова
Ряд — -а (с числительными: два, три, четыре ряда́), предл. в ря́де и в ряду́; мн. ряды́; м.
1. предл.: в ряду́. Совокупность однородных предметов, расположенных друг за другом, в……..
Толковый словарь Кузнецова
Ряд Временной — совокупность наблюдений, выполненных в хронологическом порядке и, как правило, через равные промежутки времени.
Экономический словарь
Ряд Динамики — хронологический ряд, ряд последовательно расположенных в хронологическом порядке значений показателя, который в своих изменениях отражает ход развития изучаемого явления во времени.
Экономический словарь
Адаптивный Ряд — совокупность последовательных стадий адаптации биологического вида к изменению какого-либо фактора окружающей среды.
Большой медицинский словарь
Ряд — — договор, соглашение в Древней Руси.
Юридический словарь
Ряд (др.рус.) — — договор, соглашение.
Юридический словарь
Боуэновский Ряд Реакций — , объяснение порядка кристаллизации минералов в остывающей магме, полученное на основании лабораторных экспериментов с расплавом пород, проведенных Норманом БОУЭНОМ………
Научно-технический энциклопедический словарь
Зубной Ряд — , тип, число и расположение ЗУБОВ (см. ЗУБНАЯ ФОРМУЛА). У взрослого человека зубной ряд состоит из 32 зубов. Резцы служат для разрезания пищи, клыки — для захвата и разрывания,……..
Научно-технический энциклопедический словарь
Динамический Ряд — ряд последовательных значений какого-либо статистического показателя, меняющихся во времени; широко используется при обработке материалов медико-биологических исследований.
Большой медицинский словарь
Радиоактивный Ряд — , последовательность изотопов, каждый из которых является продуктом РАДИОАКТИВНОГО РАСПАДА предыдущего, начиная с РАДИОИЗОТОПА и заканчивая одним из стабильных изотопов……..
Научно-технический энциклопедический словарь
Зубной Ряд — совокупность зубов, расположенных на одной челюсти, состоящая из 10 молочных или 14-16 постоянных зубов.
Большой медицинский словарь
Ряд — , математическое выражение (сумма), получаемое путем сложения чисел ПОСЛЕДОВАТЕЛЬНОСТИ. Таким образом, ряд 1+4+9+16+… образуется из последовательности 1, 4, 9, 16,…. Также как……..
Научно-технический энциклопедический словарь
Ряд Напряжений — (электрохимический ряд), перечень, в который включены металлы и один газ — водород, указывающий на относительную способность этих веществ к окислению (т.е. к потере электронов……..
Научно-технический энциклопедический словарь
Ряд Фурье — , ряд синусоидальных и косинусоидальных функций, посредством которого можно представить все ПЕРИОДИЧЕСКИЕ ФУНКЦИИ. Периодические функции, как правило, ограничены……..
Научно-технический энциклопедический словарь
Бесконечный Ряд — см. Ряд.
Большой энциклопедический словарь
Биномиальный Коэффициент — коэффициент в формуле разложения Ньютона бинома.
Большой энциклопедический словарь
Биномиальный Ряд — бесконечный степенной ряд, являющийся обобщениемформулы Ньютона бинома на случай дробных и отрицательных показателей.
Большой энциклопедический словарь
Вариационный Ряд — последовательность значений наблюденной величины,расположенных в порядке возрастания. Напр., вариационный ряд значений 1,- 3, 0, 5, 3, 4 имеет вид -3, 0, 1, 3, 4, 5.
Большой энциклопедический словарь
Гармонический Ряд — числовой рядЧлены гармонического ряда стремятся к нулю — однако гармонический рядрасходится.
Большой энциклопедический словарь
Гомологический Ряд — в химии (от греч. homologos — соответственный -подобный), последовательность органических соединений с одинаковымифункциональными группами и однотипным строением, каждый……..
Большой энциклопедический словарь
Пестрый Ряд — см. Гисса среды.
Большой медицинский словарь
Лиотропный Ряд — ряд ионов, расположенных в порядке усиления илиослабления их влияния на свойства растворителя. Известны лиотропные рядыионов по их способности адсорбироваться из……..
Большой энциклопедический словарь
Маклорена Ряд — (по имени К. Маклорена) — частный случай Тейлора ряда.
Большой энциклопедический словарь
Натуральный Ряд — бесконечная последовательность 1, 2, 3, 4, 5,…,состоящая из всех натуральных чисел, расположенных в порядке ихвозрастания. См. также Число.
Большой энциклопедический словарь
Посмотреть еще слова :
slovariki.org
Биномиальный ряд — Энциклопедия по машиностроению XXL
Разложим второе слагаемое в правой части равенства, определяющего х, в биномиальный ряд и ограничимся в этом разложении двумя первыми членами. Тогда приближенное выражение координаты х будет следующим [c.82]После разложения в биномиальный ряд и отбрасывания вследствие малости всех членов с множителями порядка АХ и выше получим [c.437]
Малые изменения давления, вызываемые малыми изменения-мп скорости, можно также вычислить по формуле, полученной путем разложения равенства (72) гл. I в биномиальный ряд и отбрасывания всех членов с множителями порядка и выше. [c.437]
Разложим теперь полученную зависимость в биномиальный ряд, ограничиваясь первыми тремя членами разложения [c.101]
Если заметим, что радиус-вектор 8 не может превзойти наибольший размер А тела S, то тотчас же увидим, что ш будет малой величиной первого порядка, так что если обозначим через (3) выражение третьего порядка по сравнению с отношением 8/р, то из разложения в биномиальный ряд будем иметь [c.90]
Бином Ньютона 74 — 76 Биномиальные ряды 152 Биномиальный закон распределения вероятности 323 [c.567]
Биномиальные ряды 152 Биномиальный закон распределения вероятности 323 Биномиальный коэффициент — Вычисление 74 [c.547]
Разложив правую часть выражения (1) в биномиальный ряд и ограничиваясь малыми первого порядка, получим [c.296]
Разложим это выражение в биномиальный ряд [c.76]
Разложим последнее выражение в биномиальный ряд [c.81]
Если уравнение (28) подставить в последний член уравнения (26), а подынтегральное выражение разложить в биномиальный ряд, то после почленного интегрирования получаем при Рг 1 [c.221]
Разложив (14-39) в биномиальный ряд, получим [c.358]
На рис. 2.1f, а показана нагруженная вертикальной нагрузкой Р = Pi sin (jto /Z) балка длиной I, концы которой могут свободно поворачиваться, но не могут перемещаться в горизонтальном направлении. Условия шарнирного закрепления и уравнение (2.4) могут, быть удовлетворены, если прогиб w задать в виде w — = Wi inx/V), где Wi — прогиб в середине пролета балки. Пусть AZ — разность между длинами изогнутой и не изогнутой осей стержня. Тогда, как видно из рис, 2,11,6 и представления для биномиального ряда (1 + а)» = 1 + па + п п — l)aV2 +. .. 1 + па, [c.88]
Решение Интегрального соотношения (25.43) относительно может быть получено приближенно, путем разложения подынтегральной функции в ряд. Вводя подстановку 0 = «, а затем разлагая подынтегральную функцию в биномиальный ряд относительно — Ь) и интегрируя его почленно, сводим уравнение [c.648]
Признак сходимости биномиального ряда 31 [c.739]
Но и в сравнении с г является очень малым, и если корень разложить в ряд по биному Ньютона (биномиальный ряд), а также пренебречь членами [c.228]
Раскладывая второй член уравнения в биномиальный ряд и пренебрегая членами высшего порядка, имеем [c.280]
Если разложить двучлен в биномиальный ряд и интегрировать почленно, то найдем [c.369]
Из математики известно, что биномиальный ряд [c.100]
Разлагая правую часть в биномиальный ряд при тех же ограничениях, накладываемых на скорость, что и в предыду- [c.102]
Производя разложение в биномиальный ряд и отбрасывая все члены, кроме первого и второго, получим [c.83]
Здесь г, е К, x(t) = xl(i), Х2 1)), и предположения относительно а 1, ), р х 1) — такие же, как перед формулировкой предложения 1. Доказательство аналогично доказательству предложения 1 разница только в том, что и t, х) = Н 1) х, где /г (/) = л (/) , и вместо биномиального ряда используется ряд для 1п[1 + 1]- [c.323]
Действительно, 1/Хр (О есть произведение биномов вида — с) , которые разлагаются в биномиальные ряды [c.399]
После разложения в биномиальный ряд с отбрасыванием всех членов со множителями АХ и более высокого порядка имеем [c.286]
Все биномиальные ряды сходятся для I д [[c.73]
Бинарные установки ртутно-водяные — Схема 2 — 95 Бинарные циклы паросиловых установок 2 — 95 Бинокли — Объективы 2 — 240 Бином Ньютона 1—74—76 Биномиальные ряды I — 152 Биномиальный закон распределения вероятности I — 323 Биномиальный коэффициент 1 — 74, 75, 80 [c.400]
Биномиальный ряд (1+х) . Воспользуемся равенствами d (l+x) /dx= =n(l+x) -i, 2 (l+x) /dx == (л—1) (l+x) — (l+x) /dx3=n (га—1) (n—2)X X(l+x) -5 и т.д. [c.510]
Оба биномиальных ряда, из которых образовано произведение и правой части (19), абсолютно сходятся при 1 а [c.109]
Функции P( , Pi,. . . являются полиномами Лежандра, уже определенными в гл. III, где рассматривались условия сходимости этого разложения. Легко видеть, что при 5 = 0, os 5= 4-1, выражение (3) принимает вид (1 — q) 1, а (4в) становится его разложением в биномиальный ряд вида [c.269]
Для практических расчетов применяют упрощенное уравнение 5 = /(а), полученное разложением корня в биномиальный ряд [c.72]
Эта формула получается разложением, в биномиальный ряд дроби 1/1 1 И [c.118]
Разлагая правую часть в биномиальный ряд, линеаризуя и сокращая, получаем [c.209]
Если колебания являются малыми, то-рг 1 и можно отбросить последующие члены биномиального ряда при этом [c.26]
Представив первый сомножитель в квадратных скобках в виде биномиального ряда, получим [c.168]
Выражение (1 + 1Д/Сц) — есть биномиальный ряд, тогда [c.134]
Малые изменения давления, вызываемые малыми изменениями скорости, можно также вычислить по формуле, полученной путём разложения равенства (78) главы I в биномиальный ряд с от-брасйвапием всех членов со множителями АХ и более высокого порядка. В самом деле, [c.287]
При небольших значениях величина Ар 1р(, мала, и, ограничиваясь двумя членами разло-жения в биномиальный ряд величины (1-1-ДуОц// он), получаем следующее выражение для адиабатической работы [c.511]
Интересно заметить, что приведенное в п. б разложение Со (Г//) не может быть преобразовано к членам (5 Я / 7 )р, г=о при использовании биномиального ряда для такая процедура приводит к разложению в виде знакопеременного ряда, однако все входящие в это разложение ряды, за исключением двух верхних, являются расходящимися. Это объясняется тем, что в общем случае С является педифференцируемой функцией в точке Т = О, как это видно из общего выражения для (д С/дТ )р (см. п. б ). Указанную трудность, однако, можно устранить, записывая члены разложения для С (Г//) при любом п в том же виде, в каком записан первый член в условиях задачи в п. в так, например, второй член будет иметь вид г [c.197]
mash-xxl.info
Биномиальный ряд — Большая Энциклопедия Нефти и Газа, статья, страница 1
Биномиальный ряд
Cтраница 1
Биномиальный ряд является основой многих дальнейших разложений функций в ряды. [1]
При помощи биномиального ряда можно быстро и довольно точно вычислять значения корней из чисел, а также значений различных функций. [2]
Определим радиус сходимости биномиального ряда, я этого составим ряд из модулей членов биномиаль — р ряда и воспользуемся признаком сходимости Далам-бера. [3]
Поставим себе задачей получить биномиальный ряд, исходя из логарифмического и показательного рядов. [4]
Внутри своего интервала сходимости биномиальный ряд ( как и всякий степенной ряд) сходится равномерно. [5]
Рассмотреть производные и использовать биномиальный ряд. [6]
Ряд ( 46) называется биномиальным рядом. [7]
Ряд ( 41) называется биномиальным рядом. [8]
Ряд ( 46) называется биномиальным рядом. [9]
Ряд ( 25) называется биномиальным рядом. [10]
Ряд ( 4) называется биномиальным рядом. [11]
При целом положительном показателе m этот биномиальный ряд будет содержать конечное число т — — 1 членов, ибо коэффициенты всех последующих членов будут равны нулю. В этом случае он обращается в элементарную формулу бинома Ньютона. [12]
Однако из одного лишь факта сходимости биномиального ряда (37.56) при jt l нельзя еще сделать заключение о том, что его сумма равна ( 1 х) а. [13]
Если г мало, то корень можно разложить в биномиальный ряд по возрастающим степеням г; каждый член эхого ряда представляет собой решение уравнения Лапласа. Коэффициенты при степенях г называются полиномами Лежандра Рп ( х) это и есть интересующие нас функции. [14]
Приводим без доказательства точные условия сходимости этого разложения в биномиальный ряд. При х 1 имеем в случае а0 абсолютную сходимость, в случае — 1 а 0 условную сходимость, а в случае а; — 1 расходим ость. Что при о 0 ряд сходится равномерно относительно х в замкнутом промежутке — 1 х; 0, легко получается из выводов Дополнений к гл. [15]
Страницы: 1 2 3
www.ngpedia.ru
