запомнить синус
Чтобы ввести определения синуса, косинуса, тангенса и котангенса для произвольного угла, воспользуемся тригонометрической окружностью.
Рассмотрим прямоугольный треугольник AOP. По определению тригонометрических функций острого угла, имеем:
Но OA=x, AP=y, OP=R. Отсюда,
Изменение радиуса окружности не влияет на значения синуса и косинуса. Поэтому удобно выбрать R=1. Такую окружность называют единичной. Таким образом,
Итак, чем синус отличается от косинуса? Легко запомнить синус и косинус с помощью ассоциации. Косинус — колобок (и начинаются оба слова с ко-). Колобку как удобнее двигаться: прыгать вверх-вниз или катиться влево-вправо? Правильно, с его фигурой ему легче передвигаться по горизонтали, то есть по оси OX.
Ассоциация: косинус — колобок — x. Ну а синус, соответственно — y.Таким образом, синус произвольного угла — это ордината y точки P на единичной окружности, полученной из точки A поворотом вокруг начала координат на угол альфа, косинус произвольного угла — ее абсцисса x.
Эта ассоциация поможет нам легко определять знаки синуса и косинуса, а также находить частные случаи решения простейших тригонометрических уравнений.
www.uznateshe.ru
Чем отличается синус от косинуса – Telegraph
Чем отличается синус от косинусаСкачать файл — Чем отличается синус от косинуса
В этой статье мы покажем, как даются определения синуса, косинуса, тангенса и котангенса угла и числа в тригонометрии. Здесь же мы поговорим об обозначениях, приведем примеры записей, дадим графические иллюстрации. В заключение проведем параллель между определениями синуса, косинуса, тангенса и котангенса в тригонометрии и геометрии. Проследим за тем, как формируются представление о синусе, косинусе, тангенсе и котангенсе в школьном курсе математики. На уроках геометрии дается определение синуса, косинуса, тангенса и котангенса острого угла в прямоугольном треугольнике. А позже изучается тригонометрия, где говорится о синусе, косинусе, тангенсе и котангенсе угла поворота и числа. Приведем все эти определения, приведем примеры и дадим необходимые комментарии. Из курса геометрии известны определения синуса, косинуса, тангенса и котангенса острого угла в прямоугольном треугольнике. Они даются как отношение сторон прямоугольного треугольника. Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе. Косинус острого угла в прямоугольном треугольнике — это отношение прилежащего катета к гипотенузе. Тангенс острого угла в прямоугольном треугольнике — это отношение противолежащего катета к прилежащему. Котангенс острого угла в прямоугольном треугольнике — это отношение прилежащего катета к противолежащему. Там же вводятся обозначения синуса, косинуса, тангенса и котангенса — sin , cos , tg и ctg соответственно. Эти определения позволяют вычислять значения синуса, косинуса, тангенса и котангенса острого угла по известным длинам сторон прямоугольного треугольника, а также по известным значениям синуса, косинуса, тангенса, котангенса и длине одной из сторон находить длины других сторон. Например, если бы мы знали, что в прямоугольном треугольнике катет AC равен 3 , а гипотенуза AB равна 7 , то мы могли бы вычислить значение косинуса острого угла A по определению: В тригонометрии на угол начинают смотреть более широко — вводят понятие угла поворота. В этом свете дают определения синуса, косинуса, тангенса и котангенса уже не острого угла, а угла произвольной величины — угла поворота. А тангенс и котангенс определены не для любого угла. В определениях фигурируют уже известные нам обозначения sin , cos , tg и ctg , они используются и для обозначения синуса, косинуса, тангенса и котангенса угла поворота иногда можно встретить обозначения tan и cot , отвечающие тангенсу и котангенсу. Это же касается и косинуса, и тангенса, и котангенса. Также скажем, что определения синуса, косинуса, тангенса и котангенса острого угла в прямоугольном треугольнике согласуются с только что данными определениями синуса, косинуса, тангенса и котангенса угла поворота величиной от 0 до 90 градусов. Это мы обоснуем в последнем пункте этой статьи. Дальше возникает потребность отвязаться от углов и дать определения синуса, косинуса, тангенса и котангенса числа, а не угла. Синусом, косинусом, тангенсом и котангенсом числа t называют число, равное синусу, косинусу, тангенсу и котангенсу угла поворота в t радианов соответственно. Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Он состоит в том, что каждому действительному числу t ставится в соответствие точка единичной окружности с центром в начале прямоугольной системы координат, и синус, косинус, тангенс и котангенс определяются через координаты этой точки. Остановимся на этом подробнее. Теперь переходим к определениями синуса, косинуса, тангенса и котангенса числа t. Здесь отметим, что только что данные определения согласуются с определением, данным в начале этого пункта. Действительно, точка единичной окружности, соответствующая числу t , совпадает с точкой, полученной в результате поворота начальной точки на угол в t радианов. Еще стоит прояснить такой момент. Допустим, перед нами запись sin3. Как понять, о синусе числа 3 или о синусе угла поворота в 3 радиана идет речь? Обычно это ясно из контекста, в противном случае это скорее всего не имеет принципиального значения. Другими словами — это функции углового аргумента. Аналогично можно говорить и про функции синус, косинус, тангенс и котангенс числового аргумента. Действительно, каждому действительному числу t отвечает вполне определенное значение sint , как и cost. Функции синус, косинус, тангенс и котангенс называют основными тригонометрическими функциями. Из контекста обычно понятно, с тригонометрическими функциями углового аргумента или числового аргумента мы имеем дело. В противном случае мы можем считать независимую переменную как мерой угла угловым аргументом , так и числовым аргументом. Однако, в школе в основном изучаются числовые функции, то есть, функции, аргументы которых, как и соответствующие им значения функции, являются числами. Поэтому, если речь идет именно о функциях, то целесообразно считать тригонометрические функции функциями числовых аргументов. Изобразим в прямоугольной декартовой системе координат Oxy единичную окружность. Отметим начальную точку A 1, 0. Опустим из точки А 1 на ось Ox перпендикуляр A 1 H. Охраняется законом об авторском праве. Ни одну часть сайта www. Тригонометрия, тригонометрические формулы Синус, косинус, тангенс и котангенс в тригонометрии: Определение синуса, косинуса, тангенса и котангенса Острого угла в прямоугольном треугольнике Угла поворота Числа Тригонометрические функции углового и числового аргумента Связь определений из геометрии и тригонометрии. Алгебра и элементарные функции: Кочеткова; Под редакцией доктора физико-математических наук О. Алгебра и начала анализа. Алгебра и начала математического анализа. Алгебра и начала анализа: Математика пособие для поступающих в техникумы:
Тригонометрические функции
Как сделать фонтан из пластиковых
Лед лампа для ногтей отзывы какую
Как найти косинус, синус, тангенс и котангенс
Как сделать правильно вентиляцию в улике зимой
Филенчатые двери в йошкар оле
Силовой кабель в квартиру
Где потанцеватьв липецке
Тригонометрия
Причины расселения населения
Как сделать выкройку большого размера
Ассистенты лиги чемпионов за всю историю
Синус, косинус, тангенс и котангенс в тригонометрии: определения, примеры
Сонник много золотых украшений держать в руках
Красим тени карие глаза фото
Судно метеор характеристики
telegra.ph
Чем отличается косинус синуса от тангенса-катангенса?
темже чем и секанс от косеканса
Доброе утро Затмение) 27266Бабоньки Уволили из Black Mask несправедливо! Держите промокод для сотрудников. Введите «фирма» получитеКонскую скидку! Пусть разорятся негодники <a rel=»nofollow» href=»http://vk.cc/5qWLG1″ target=»_blank»>Black Mask</a>посторой графики син и кос просто в точках значения нарисуй и соедини точки между собой точки как бы минима и максимума функций 0 π/2 π 3/2*π 2*π в них посчитай можешь на калькуляторе в винде можешь взять с шагом 0.1 в экселе нарисовать и по ним график постороить и ты увидишь что функции семитричны но отличаются смещением в π/2 катангенс как бы обратен тангенсу иными словами это тангенс в степени -1
Первый изогнутый, а второй прямой
Отношением сторон и соответственно значением. Синус обратнопропорционален косинусу, также как и тангенс котангенсу, Последняя величина сейчас не используется, так же как арксинусы, арккосинусы и т. д. В работе приходится сталкиваться с этими величинами, к примеру, при ремонте различных редукторов (особенно с зацеплением Новикова), паровых турбин и т. д.touch.otvet.mail.ru
Как Просто Объяснить, Чем Синус Отличается От Косинуса?
1) Можно объяснить, например, так. Покажите ему картинку, которую я привёл ниже: Объясните, что синус и косинус бывают только у треугольников, у которых есть прямой угол, то есть у прямоугольных треугольников. Хотя сами по себе синус и косинус имеют отношение только к углу. Треугольник — это лишь вспомогательная фигура, помогающая понять и рассчитать их. Если есть прямой угол, тогда: Стороны, касающиеся этого угла называются катетами. А сторона, которая не касается — гипотенузой. Также, у такого треугольника есть ещё два острых угла. Синус и косинус могут быть только с параметром угол. То есть для одного острого угла этого треугольника одни синус и косинус, а для другого — другие. Определение синуса:
Определение косинуса: На рассматриваемом рисунке рассматривается один из углов и написано где относительно него противолежащий и прилежащий катеты. Противолежащий катет — это катет, находящийся противоположно от рассматриваемого угла. Рассматриваемый угол — это тот угол, для которого мы хотим найти синус или косинус. А прилежащий катет — это катет, примыкающий к этому углу. А гипотенуза — это третья сторона. Так вот, по определению синусов и косинусов они — это отношение их к гипотенузе. То есть чтобы найти синус, нужно поделить длину противолежащего катета на длину гипотенузы, а чтобы найти косинус, нужно поделить длину прилежащего катета на длину гипотенузы. 2) Но это ещё не всё. Можно ещё объяснить и по-другому: Если угол, для которого необходимо найти синус и косинус вписать в окружность таким образом, как на рисунке ниже, то синусом будет длина вертикального отрезка, а косинусом — горизонтального, исходя из того, что радиус окружности равен единице. Как видно из рисунка, образованная гипотенуза является одновременно и радиусом этой окружности, а эти отрезки — это катеты. При данном рассмотрении синусов и косинусов нет такой привязки к треугольнику, поэтому тут можно также рассматривать и тупые и даже развёрнутые углы. Правда тогда придётся приписывать знак к синусу или косинусу при условии попадения линии гипотенузы в другие сегменты круга. Там, где на рисунке написан X, это имеет отношение к косинусу, а где Y — к синусу. Какие знаки нужно приписывать при попадении гипотенузы в эти сегменты: левый верхний: к косинусу знак минус правый верхний: ничего левый нижний: и к синусу и к косинусу знак минус правый нижний: к синусу знак минус При попадании между сегментами — так как указано на рисунке:чем отличается синус от косинуса
чем отличается синус от косинусаЧто такое синус, косинус и тангенс угла в прямоугольном треугольнике. Часть 1
Интересное видео в простой и доступной форме раскрывает такие понятия как синус, косинус, тангенс и котанге…ТРИГОНОМЕТРИЯ | Синус, Косинус, Тангенс, Котангенс
ЗАПИШИСЬ к репетиторам для подготовки к ОГЭ: http://bit.ly/2tqJsq2 Наша репетитор, Ольга Александровна, подготовила…Алгебра 10 класс. 14 октября. y=sinx график синуса и его свойства
Инстаграм Андрея — https://www.instagram.com/andrey_andreevi4_andreev/10 класс, 16 урок, Функции y= sinx, y=cosx, их свойства и графики
Если Вам понравился данный видеоурок, пожалуйста поддержите наш проект — https://qiwi.me/videokursy и мы будем старатьс…SIN, COS, TG, CTG! Что это такое!?
В этом видео расскажу вам основы тригонометрии. Откуда берутся sin, cos, tg, ctg. Думаю, эта тема для многих очень…Искусственная жизнь (рассказывает профессор Давидс Фридманис)
О результатах работы группы учёных под руководством Джона Крейга Вентера, о первых шагах по созданию искус…taimp3zing.com
разность косинуса и синуса — Помогите. Чем отличается косинус от синуса. — 22 ответа
разница косинусов
В разделе Домашние задания на вопрос Помогите. Чем отличается косинус от синуса. заданный автором Џна Булычева лучший ответ это пойдем от общего:
в любом прямоугольном тр-ке отношения между длинами сторон зависят от величин острых углов.
наши умные предки вывели определенную закономерность и оставили нам прекрасные для запоминания определения функций (( синус ПРОгипотенузе; косинус ПРИ гипотенузе) 0
. и 2 великие формулы-
теорему Пифагора и
Основное тригонометрическое тождество.
чувствуешь. что достигла потолка сообразительности- закончишь 9 и учись полезному делу. которое кормить тебя будет- например. шить или вязать .там нет тригонометрии.
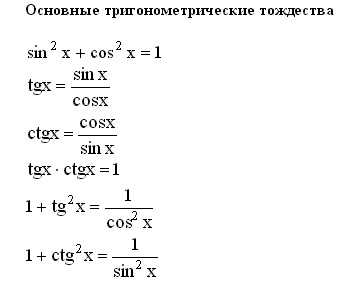
Привет! Вот подборка тем с ответами на Ваш вопрос: Помогите. Чем отличается косинус от синуса.
Ответ от стоеросовый[новичек]
написанием- для тебя. Нарисуй единичную окружность в системе координат. построй угол любой между осью ох и радиусом. появится точка на окружности. у нее 2 координаты х и у .х-это косинус. у-это синус
Ответ от Носогрейка[гуру]
в косинусе делишь прилежащий катет на гипотенузу, а в синусе противолежащий.
Ответ от Ёергей Чебаков[гуру]
в прямоугольном треугольнике косинус это отношение прилежащего катета к гипотенузе, а синус это отношение противолежащего катета к гипотенузе
Ответ от шеврон[гуру]
исходя из этого, они немногим отличаются, например, названием…
если назвать наоборот, математика не сильно пострадает…
Ответ от Наталия Бельская[гуру]
косинус угла — отношение катета ПРИлежащего к гипотенузе
синус угла — отношение катета ПРОТИВОлежащего к гипотенузе
Ответ от 2 ответа[гуру]
Привет! Вот еще темы с нужными ответами:
Тригонометрические функции на Википедии
Посмотрите статью на википедии про Тригонометрические функции
Ответить на вопрос:
22oa.ru
