П.3. Пространство элементарных событий
Каждый из равновозможных результатов испытаний называется элементарным исходом или (элементарным событием). Всякий мыслимый результат эксперимента называют элементарным событием и обычно обозначают буквами
Пространством элементарных событий называется множество всех взаимно исключающих исходов эксперимента такое, что результатом эксперимента всегда является один и только один исход.
Пространство элементарных событий обычно обозначается и считается заданным, если указаны все его элементы.
Из элементарных исходов можно составить более сложное событие. Результат испытания называется событием, независимо от его значимости. Результат испытания, который нельзя заранее прогнозировать, называется случайным событием.
Любое подмножество данного множества интерпретируется как событие (возможно, и ненаблюдаемое). Совокупность всех наблюдаемых событий составляет множество событий
Множество для данного испытания может быть дискретным, или иметь более сложную структуру. К дискретным относятся конечные или счетные множества элементарных исходов. Построение множества(если оно не задано при описании эксперимента) осуществляется на практике, исходя из требования, чтобы все интересующие нас результаты данного эксперимента могли быть однозначно описаны на основе построенного множества. Другими словами, если нас интересуют события и т.д., являющиеся наблюдаемыми событиями в данном эксперименте, то множество должно состоять из таких исходов, чтобы существовали подмножества данного множества, равносильные событиями т.д.
Каждое случайное событие определяется как подмножество в множестве элементарных событий. При этом те элементарные события из, при которых событиенаступает (т.е. принадлежит подмножеству) называютблагоприятствующими событию . Говорят, что событиепроизошло (наступило, осуществилось, реализовалось), если результатом эксперимента явился элементарный исход, принадлежащий().
Два события называются совместными (совместимыми) в данном опыте, если появление одного из них не исключает появления другого.
Два события называются несовместными (несовместимыми) в данном опыте, если они не могут произойти вместе при одном и том же испытании. Несколько событий называются несовместными, если они попарно несовместны.
Другими словами, события исовместны, если соответствующие множестваиимеют общие элементы, и несовместны в противном случае, если появление одного из них исключает появление другого, и соответствующие множестваине имеют общих элементов, т.е. пересечение этих множеств является пустым множеством.
Достоверным называют событие, которое обязательно произойдет, если будет осуществлена определенная совокупность условий .
Невозможным называют событие, которое заведомо не произойдет, если будет осуществлена определенная совокупность условий .
Событие, совпадающее с пустым множеством , называетсяневозможным событием, а событие, совпадающее со всем множеством , называетсядостоверным событием.
События называют равновозможными, если нет основания полагать, что одно событие является более возможным, чем другие.
Теория вероятностей есть наука, изучающая закономерности случайных событий. Одной из главных задач в теории вероятностей является задача определения количественной меры возможности появления события.
studfiles.net
Пространство элементарных событий
Будем считать фиксированным комплекс G условий и станем рассматривать некоторую F систему событий A, B, C, …, каждое из которых должно при каждом осуществлении комплекса G произойти или не произойти. Обозначим через U – достоверное событие, а через V – невозможное.
1) Если в результате
испытания, из того, что произойдет
событие A,
следует, что произойдет и событие B,
то говорят, что событие A влечет за собой событие B.
И обозначают:  .
.
2) Если , то говорят, что эти события равносильны и записываютА = В.
3) Событие, состоящее
в наступлении обоих событий А
и В, будем
называть их произведением и обозначать: АВ или  .
.
4) Событие, состоящее в наступлении хотя бы одного из событий А или В, называется их суммой и обозначается: .
6) Два события 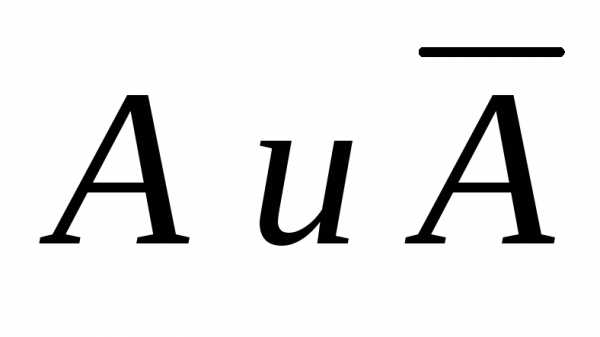 называются
противоположными, если одно из них
обязательно наступит, а другое нет, т.е.
выполняются одновременно равенства:.
называются
противоположными, если одно из них
обязательно наступит, а другое нет, т.е.
выполняются одновременно равенства:.
Пример: Комплекс условий G состоит в том, что на стол один раз бросается игральная кость. Обозначим:
соб. А – выпадение 6 очков,
соб. В – выпадение 3 очков,
соб. С – выпадение четного числа очков,
соб. D – выпадение числа очков, кратного 3.
Тогда события A, B, C, D связаны следующими соотношениями:
7) События А и В называются несовместными, если их совместное появление невозможно, т.е. АВ = V.
8) Если событие А представимо в виде суммы А = В1+В2+ … +Вк и события Bj попарно несовместны, то говорят, что событие А подразделяется на частные случаи. Например, при бросании игральной кости, событие С, состоящее в выпадении четного числа очков подразделяется на три частных случая Е2, Е4, Е6 (выпадение 2, 4, 6 очков).
9) Говорят, что события В1, В2, …, Bn образуют полную группу событий, если хотя бы одно из них непременно должно наступить при выполнении данного комплекса условий.
В дальнейшем нас будут интересовать полные группы попарно несовместных событий, т.е. единственно возможных:
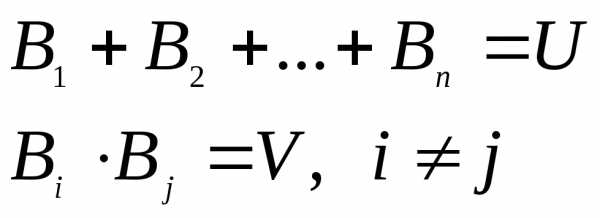
10) Для операций сложения и умножения событий справедливы законы:
Коммутативность: А+В = В+А; АВ =ВА,
Ассоциативность: А+(В+С) =(А+В)+С; А(ВС) = (АВ)С,
Тождества: А+А =А; АА = А,
Дистрибутивность: А(В+С) = АВ+АС;
* А+ВС = (А+В)(А+С).
Классическое определение вероятности случайного события
Классическое определение вероятности опирается на понятие равновозможность событий. «Равновозможность» в свою очередь базируется на симметрии явлений. Например, мы считаем, что выпадение любой из двух граней при бросании монеты равновозможно, если она сделана из однородного материала. Точно так же, мы предполагаем одинаковую возможность выпадения каждой грани при бросании игральной кости. Таким образом, каждый раз, когда мы хотим использовать классическое определение, необходимо проверить равновозможность рассматриваемых событий.
Зададим какую-либо полную группу Q попарно несовместных и равновозможных событий Е1, Е2, …,Еn. Образуем систему F, состоящую из:
а) невозможного события V;
б) достоверного события U = Е1+Е2+ … +Еn;
в) всех событий Еi, i = 1,2,…,n
г) всех событий А, которые могут быть подразделены на частные случаи, входящие в состав группы Q.
Тогда система F образует алгебраическое поле.
Пусть некоторое событие А поля F подразделяется на
Те элементарные исходы, в результате которых наступает событие А, называют благоприятствующими событию А.
Определение: Вероятностью P(A) события А называется отношение числа m-исходов, благоприятствующих событию А, к числу n всех возможных исходов испытания, образующих полную группу попарно несовместных и равновозможных событий. Записывают
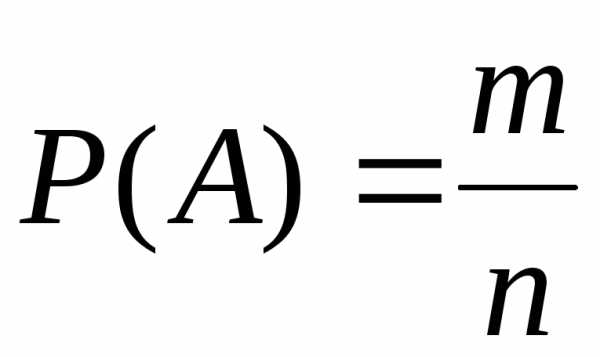
Так, например, вероятность выпадения i очков при бросании игральной кости равна
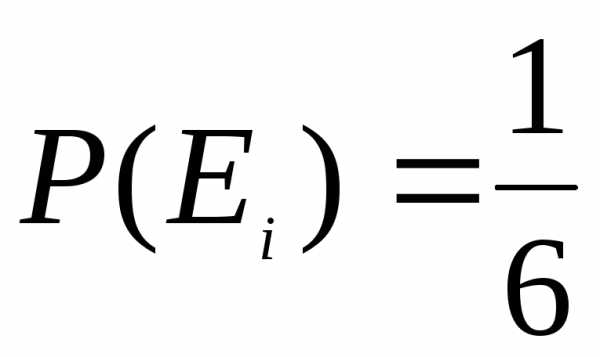
Событие С, состоящее в выпадении четного числа очков, подразделяется на три частных случая, входящих в полную группу равновозможных и попарно несовместных событий
С = Е2+Е4+Е6
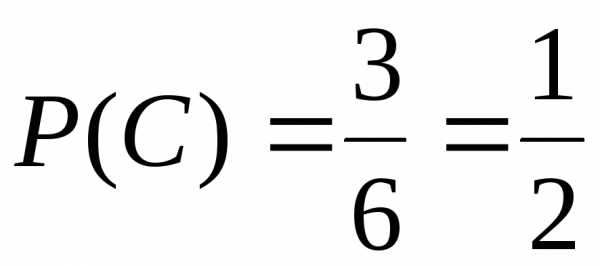
В соответствии с приведенным определением, каждому событию А, принадлежащему построенному полю F, ставится в соответствие определенная вероятность P(A). Таким образом, вероятность P(A) есть функция, определенная на поле F.
studfiles.net
Пространство элементарных событий. — КиберПедия
Лекция 1
Пространство элементарных событий.
Предметом теории вероятности являются математические модели случайных экспериментов.
Эксперимент (Э) называют случайным, если заранее нельзя предсказать его результат (исход).
1. Э – бросание одной монеты. Исходы – выпадение герба (Г) или решки (Р). Заранее нельзя предсказать исход.
2. Э – бросание одной игральной кости. Исходы – выпадение 1,2,3,4,5 или 6 очков.
Результаты (исходы) Э называются событиями. События бывают простыми (элементарными) и сложными (составными). Сложные события состоят из простых.
Множество всех возможных взаимоисключающих исходов эксперимента называется пространством элементарных исходов, обозначается Ω. Его элементами являются элементарные исходы, обозначающиеся ω.
Примеры.
3. Э – бросание одной монеты, .
4. Э–бросание одной игральной кости, (или , где — выпадение 1 очка и т.д.)
События обозначаются: А,B,C,…
Элементарные события, принадлежащие событию А, называют благоприятствующими (благоприятными) событию А.
Примеры.
5. Пусть событие А состоит в выпадении четного числа очков при бросании игральной кости. Тогда: , (или , ).
6. Монеты подбрасываются дважды. Пусть А – событие, состоящее в том, что хотя бы один раз появится решка, событие В – хотя один раз появится герб. Тогда: , , .
Само множество Ω также есть случайное событие, оно называется достоверным, потому что всегда происходит. Пустое множество Ø, не содержащее ни одного элемента, называется невозможным.
Алгебраические операции над событиями
Так как случайные события есть множества, то к ним применимы операции пересечения, объединения и дополнения множеств.
Событие, состоящее в наступлении хотя бы одного из событий А или В, называется суммой (объединением) событий А и В и обозначатся А+В (А В).
Событие, состоящее в наступлении обоих событий А и В, называется произведением (пересечением) этих событий и обозначается АВ ( ).
Разностью событий А–В (А\В) называется событие, состоящее из элементов множества А, не принадлежащих В. Оно состоит в том, что А произошло, а В не произошло.
Если А – событие, то противоположным к нему называют событие, обозначающееся и состоящее из тех элементов, которые не принадлежат А; , т.е. происходит в том и только том случае, когда А не происходит. Для противоположных событий одновременно выполняются два условия: а) — достоверное событие, б) — невозможное событие.
Два события называются совместными (несовместными), если в результате их осуществления возможно (или невозможно) их совместное осуществление, т.е. для несовместных событий выполняется: Ø.
События называют полной группой несовместных событий, если:
1. Ø для ,
2. Ø для ,
3. .
Замечание: Операции суммы и произведения аналогично определяются для любого числа событий.
Статистическая вероятность.
Статистической вероятностью (частотой) события А в проведенной серии экспериментов называется число
. (1)
Свойства:
1. ;
2. ;
3. (Ø) = 0;
4. если А и В несовместны, то (для любого числа событий).
5. обладает свойством устойчивости при , т.е. в различных сериях испытаний при больших п соответствующие частоты практически совпадают, группируясь около некоторого постоянного значения , называемого вероятностью.
Классическая вероятность.
Если пространство элементарных событий Ω, соответствующее случайному Э, удовлетворяет условиям:
1. множество Ω конечно: ;
2. все элементарные события равновозможны: ;
3. элементарные события попарно-несовместны и образуют полную группу событий.
Тогда вероятность любого события можно вычислить по формуле:
, (2)
где n – общее число исходов (событий) испытания; m – число событий, благоприятных событию А.
Свойства:
1. ;
2. ;
3. (Ø) = 0:
4. если А и В несовместны, то (для любого числа событий).
Примеры:
(Пр.5): ,
(Пр.6): .
Геометрическая вероятность.
Пусть проведен эксперимент, пространство элементарных исходов которого бесконечно. В этом случае нельзя воспользоваться классическим определением вероятности. В таких случаях вводят понятие геометрической вероятности – обобщение классической вероятности, т.е. вероятность попадания точки в область (отрезок, часть плоской области, часть пространственной области и т.д.)
Пусть — фигура в , .
Будем считать условия Э такими, что не зависит от местоположения в и пропорционально мере . Тогда:
, (3)
где — мера фигуры , — мера фигуры .
Правило суммы
Если некоторый объект А может быть выбран из совокупности объектов n способами, а другой объект В может быть выбран m способами, то выбрать либо объект А, либо объект В можно способами.
Правило произведения
Если объект А может быть выбран из совокупности объектов n способами и посла каждого такого выбора объект В может быть выбран m способами, то пара объектов (А,В) в указанном порядке может быть выбрана способами.
Примеры.
7. В первом ящике 8 шаров, во втором -10 шаров. Сколькими способами можно выбрать один шар из двух ящиков?
► Событие А – выбор шара из первого ящика, он может быть осуществлен 8-ю способами, событие В – выбор шара из второго ящика, он может быть осуществлен 10-ю способами, т.е. n=8, m=10. Событие А+В – выбор одного шара либо из первого ящика, либо из второго. По правилу суммы находим: =8+10=18.
8. Сколько можно составить пятизначных чисел так, чтобы любые две соседние цифры были различны?
► Первую цифру можно выбрать 9-ю способами, вторую – 9-ю способами и т.д., следовательно, всего цифр можно составить способами (правило произведения).
Выборки без повторений
Пусть дано конечное множество X, состоящее из n элементов.
Размещениемиз n элементов по m множества X называют любые наборы, которые отличаются либо составом элементов, либо их порядком:
. (4)
Частный случай размещения – перестановки: наборы, состоящие из n одних и тех же элементов, отличающиеся только порядком их расположения.
n!. (5)
Сочетанием из n элементов по m множества X называют любые неупорядоченные наборы, которые отличаются хотя бы одним элементом:
. (6)
Отсюда может быть выведена формула размещения, более удобная для счета:
. (7)
Примеры.
9. Сколько различных двузначных чисел можно составить из чисел 1,2,3,4?
► .
10. Сколько различных четырехзначных чисел можно составить из чисел 1,2,3,4?
► .
11. Сколькими способами можно выбрать две детали из ящика с десятью деталями?
►
Выборки с повторениями
Перестановки с повторениями – это различные конечные наборы из n элементов, в которых элементов принадлежат одному виду, элементов – другому виду и т.д. и .
= . (8)
Пример.
12. Сколько различных шестизначных чисел можно составить из трех единиц, одной двойки и двух троек?
►
Сочетания с повторениями
Сочетанием из n элементов множества X по m с повторениями называют любые неупорядоченные наборы, состоящие из m элементов, каждый из которых принадлежит к одному из n видов.
(9)
Например, из трех различных элементов можно составить следующие сочетания с повторениями: .
► .
Размещения с повторениями
Пусть X – множество из n элементов. Достаем один элемент, фиксируем, кладем элемент обратно. Выборку производим т раз. Число таких наборов из n элементов множества X по m равно
. (10)
Пример 13. Сколько существует трехзначных телефонных номеров?
► .
Условная вероятность.
Вероятность наступления события А при условии, что В произошло, называется условной вероятностью А при условии В:
, где . (11)
Независимость событий
Если события А и В таковы, что то существует условная вероятность . В случае когда
, (*)
мы говорим, что событие А не зависит от события В.
Если и то
, (14)
и из независимости А от В следует независимость В от А, т.е. понятие зависимости А и В симметрично и из формулы умножения вероятностей (12) следует, что для независимости событий А и В имеет место равенство
События А и В называются независимыми, если выполнено равенство:
(15)
Формула полной вероятности
Если события образуют полную группу событий и , то для любого события А имеет место формула
, (17)
где события называются гипотезами.
Доказательство:
Т.к. образуют полную группу событий, то событие A можно представить как:
,
где события попарно несовместны.
Используя свойство аддитивности вероятности и формулу умножения вероятностей, получим:
.
Формула Байеса
Если события образует полную группу событий, то для любого события А, для которого справедлива формула:
— (18)
Доказательство:
По определению условной вероятности и, используя формулу умножения вероятностей, имеем:
.
Формула Байеса используется в ситуации, когда эксперимент уже проведён, событие А наступило, и требуется переоценить шансы наступления гипотез , т.е. найти условные вероятности . Эти вероятности называются апостериорными (послеопытными), а гипотезы, которые рассматриваются до эксперимента – априорными (доопытными), при этом:
; .
Лекция 1
Пространство элементарных событий.
Предметом теории вероятности являются математические модели случайных экспериментов.
Эксперимент (Э) называют случайным, если заранее нельзя предсказать его результат (исход).
Примеры.
1. Э – бросание одной монеты. Исходы – выпадение герба (Г) или решки (Р). Заранее нельзя предсказать исход.
2. Э – бросание одной игральной кости. Исходы – выпадение 1,2,3,4,5 или 6 очков.
Результаты (исходы) Э называются событиями. События бывают простыми (элементарными) и сложными (составными). Сложные события состоят из простых.
Множество всех возможных взаимоисключающих исходов эксперимента называется пространством элементарных исходов, обозначается Ω. Его элементами являются элементарные исходы, обозначающиеся ω.
Примеры.
3. Э – бросание одной монеты, .
4. Э–бросание одной игральной кости, (или , где — выпадение 1 очка и т.д.)
События обозначаются: А,B,C,…
Элементарные события, принадлежащие событию А, называют благоприятствующими (благоприятными) событию А.
Примеры.
5. Пусть событие А состоит в выпадении четного числа очков при бросании игральной кости. Тогда: , (или , ).
6. Монеты подбрасываются дважды. Пусть А – событие, состоящее в том, что хотя бы один раз появится решка, событие В – хотя один раз появится герб. Тогда: , , .
Само множество Ω также есть случайное событие, оно называется достоверным, потому что всегда происходит. Пустое множество Ø, не содержащее ни одного элемента, называется невозможным.
cyberpedia.su
§ 2 Пространство элементарных событий,
АЛГЕБРА СОБЫТИЙ.
Будем различать элементарные (неразложимые) события и составные события (или просто события).
Пример
1:
подбрасывание игральной кости 1 раз.
Элемен -тарные события, обозначим их 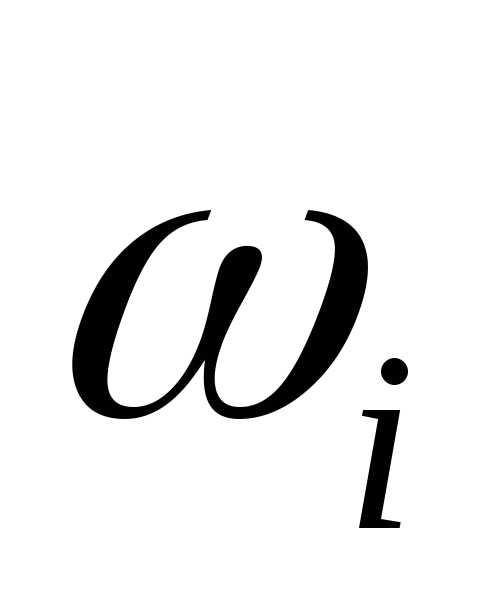 ,
число выпавших очков на верхней грани
(
,
число выпавших очков на верхней грани
(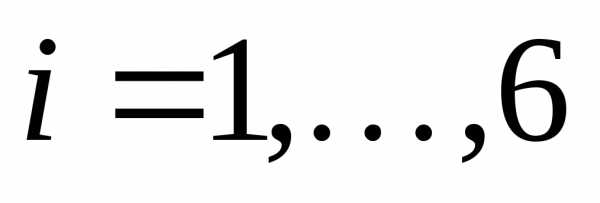 ),
Множество всех элементарных событий
в данном опыте.
Составные события, или просто события,
могут быть описаны как подмно- жества
множества всех элементарных событий.
Например,cо-
бытие А — «выпало чётное число очков»
можно выразить сле- дующим образом
),
Множество всех элементарных событий
в данном опыте.
Составные события, или просто события,
могут быть описаны как подмно- жества
множества всех элементарных событий.
Например,cо-
бытие А — «выпало чётное число очков»
можно выразить сле- дующим образом  .
.
Пример 2: Трёхкратное подбрасывание монеты.
Пусть 1 — выпал «герб», 0 – выпала «цифра». Тогда множество всех элементарных событий:
.
Событие А — «при первом подбрасывании выпал герб» можно представить следующим образом»:
.
Пример 3. Стрельба по плоскости.
Если
мы введём на плоскости прямоугольную
систему коор -динат 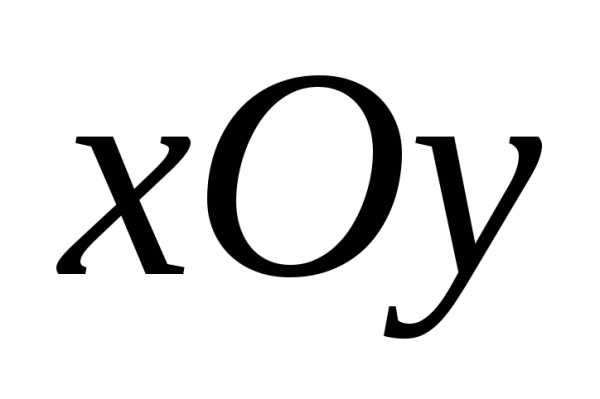 ,
то множнство элементарных событий
(попадание в некоторую точку плоскости)
записывается в виде:
,
то множнство элементарных событий
(попадание в некоторую точку плоскости)
записывается в виде:
.
Событие А — «попадание в круг единичного радиуса» можем записать в виде .
Итак, элементарные
события — это все мыслимые исходы опыта или
наблюдения. События могут быть описаны
как под- множества множества всех
элементарных событий. Совокуп -ность
всех элементарных событий данного
опыта будем назы- вать пространством
элементарных событий и обозначать 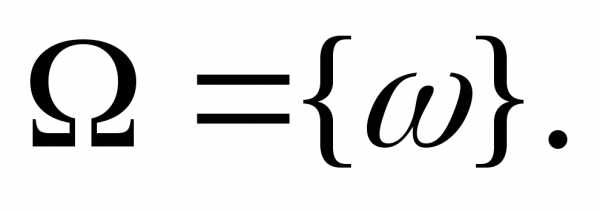 Оно может быть конечным, как в приерах
1 и 2, счётным ()
или бесконечным несчёт- ным, как в
примере 3. Любое подмножество иножества
Оно может быть конечным, как в приерах
1 и 2, счётным ()
или бесконечным несчёт- ным, как в
примере 3. Любое подмножество иножества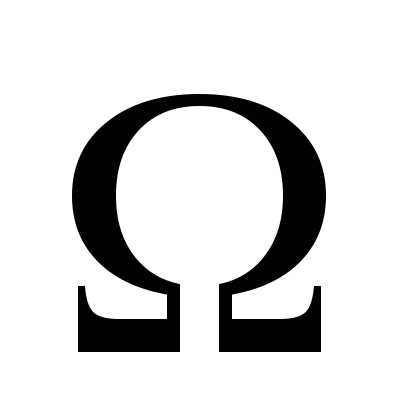 называетсясобытием.
называетсясобытием.
Суммой (или объединением) двух событий называется событие, состоящее из элементарных событий, вхо- дящих по крайней мере в одно из событий А или В.
Например:  = «попадание в цель при 1 — м выстреле»,
= «попадание в цель при 1 — м выстреле», — «попадание в цель при 2 – м выстреле»,
тогда
— «попадание в цель при 2 – м выстреле»,
тогда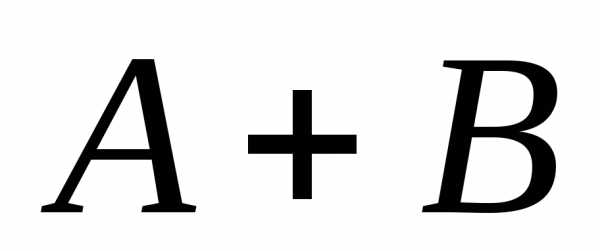 — «хотя бы одно попадание в цель».
— «хотя бы одно попадание в цель».
Следует помнить свойство: .
Произведением (или пересечением )
двух событий называется событие,
состоящее из элементарных со- бытий,
входящих и в событие и в событие
и в событие .
.
Например:  =
«попадание в цель при 1 — м выстреле»,
=
«попадание в цель при 1 — м выстреле», — «попадание в цель при 2 – м выстреле»,
тогда
— «попадание в цель при 2 – м выстреле»,
тогда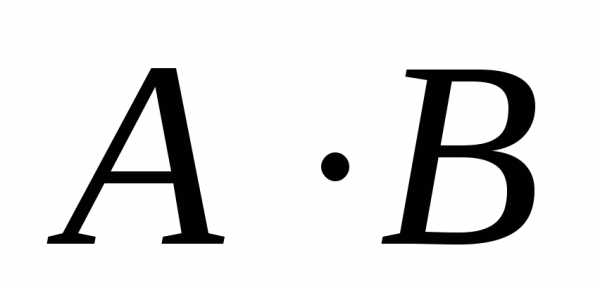 — попа- дание в цель при обоих выстрелах.
— попа- дание в цель при обоих выстрелах.
Свойство: .
Разностью 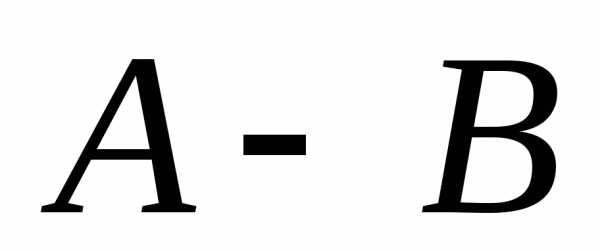 ( или
( или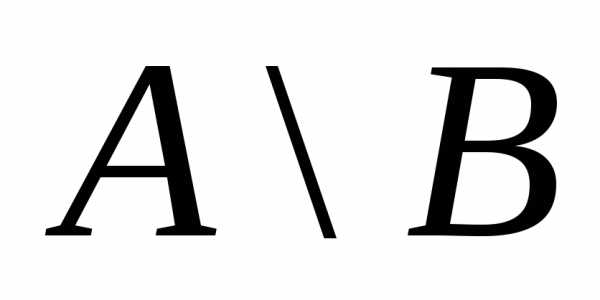 )
называется событие, состо- ящее из
элементарных событий, входящих в
множество
)
называется событие, состо- ящее из
элементарных событий, входящих в
множество ,
но не входящих в множество
,
но не входящих в множество .
( Другими словами, событие
.
( Другими словами, событие произошло, а событие
произошло, а событие не произошло.)
не произошло.)
Например,
при бросании игрального кубика:  — «выпала чётная цыфра», т.е.,
— «выпала чётная цыфра», т.е., — «выпала цыфра, крат- ная 3», т.е..
Тогда.
— «выпала цыфра, крат- ная 3», т.е..
Тогда.
Событие 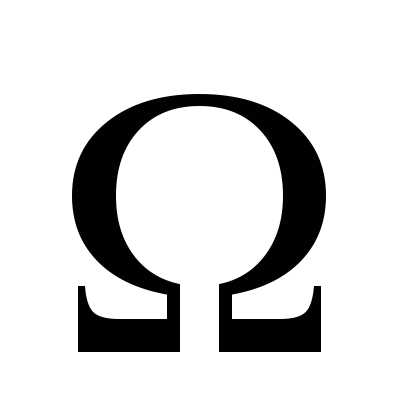 ,
состоящее из всех элементарных
исходов данного опыта, называетсядостоверным
событием (проис- ходит «всегда» в данном опыте).
,
состоящее из всех элементарных
исходов данного опыта, называетсядостоверным
событием (проис- ходит «всегда» в данном опыте).
Событие  ,
не содержащее ни одного из элементарных
исходов данного опыта, называетсяневозможным
событием.
,
не содержащее ни одного из элементарных
исходов данного опыта, называетсяневозможным
событием.
Например, при бросании игрального кубика «выпала цифра от 1 до 6» — достоверное событие, «выпала цифра 10» — не -возможное собтие.
Противоположное
событие  (событие
(событие не произошло) — это дополнение события
не произошло) — это дополнение события до достоверного, т.е.
до достоверного, т.е.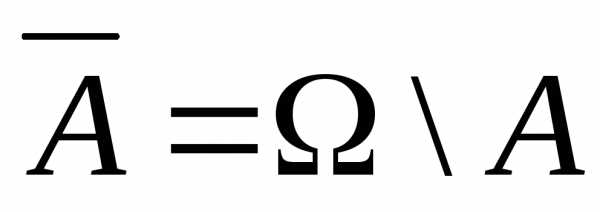 .
.
Например:  — «три дня подряд шёл дождь», тогда
— «три дня подряд шёл дождь», тогда — «хотя бы один день дождя не было»;
— «хотя бы один день дождя не было»; — «из пяти чисел хо -тя бы одно
чётное», тогда
— «из пяти чисел хо -тя бы одно
чётное», тогда — «все пять чисел нечётные».
— «все пять чисел нечётные».
Свойства:
События  и
и называютсянесовместными,
если невоз -можно их одновременное
появление в одном опыте, (т.е., если
).
называютсянесовместными,
если невоз -можно их одновременное
появление в одном опыте, (т.е., если
).
Например,
при бросании монеты:  — «выпал герб»,
— «выпал герб», — «выпала цифра» — несовместные
события.
— «выпала цифра» — несовместные
события.
 (
( влечёт
влечёт ,
т.е элементарные события, входя -щие
в событие
,
т.е элементарные события, входя -щие
в событие ,
входят и в событие
,
входят и в событие )
— из наступления события
)
— из наступления события следует наступление события
следует наступление события .
.
Например:  — «попадание при первом выстреле»,
— «попадание при первом выстреле», — «хотя бы одно попадание при трёх
выстрелах». Тогда
— «хотя бы одно попадание при трёх
выстрелах». Тогда .
.
Если  и
и ,
то говорят, что события
,
то говорят, что события и
и равносильны или эквивалентны.
равносильны или эквивалентны.
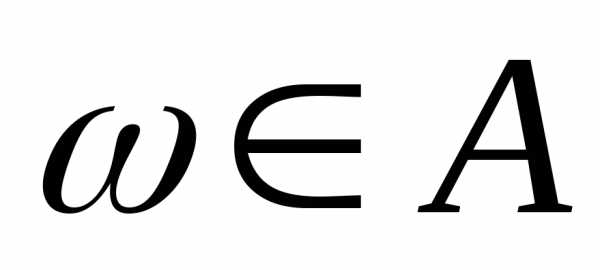 означает,
что элементарное событие
означает,
что элементарное событие  входит в событие
входит в событие .
.
Понятия произведения и суммы событий можно перенести на случай произвольной конечной или бесконечной последо -вательности событий:
Событие
состоит из элемен -тарных событий,
входящих хотя бы в одно из событий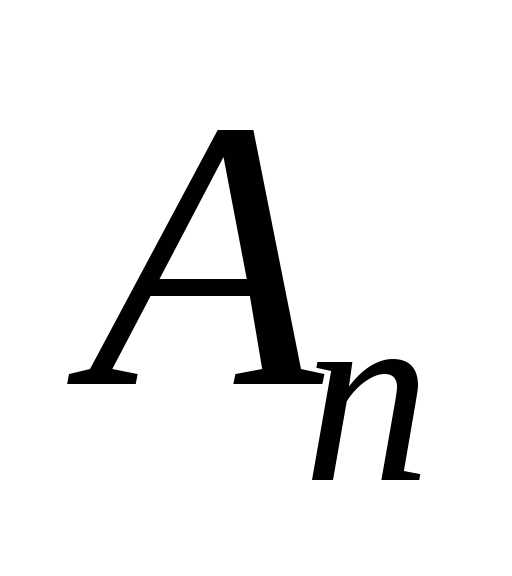 ,.
,.
Событие
состоит из элементарных событий,
входящих одновременно в каждое из
событий ,.
,.
Говорят, события образуютполную группу, если в результате опыта происходит хотя бы одно из них.
Пусть 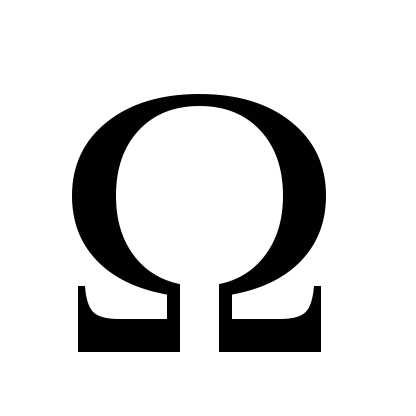 — произвольное пространство элементарных
собы- тий.
— произвольное пространство элементарных
собы- тий. — некоторый класс подмножеств
пространства
— некоторый класс подмножеств
пространства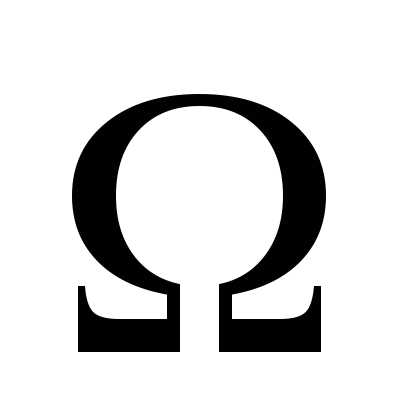 . Этот класс подмножеств называетсяалгеброй
событий,
если
. Этот класс подмножеств называетсяалгеброй
событий,
если  и для любых событий
и для любых событий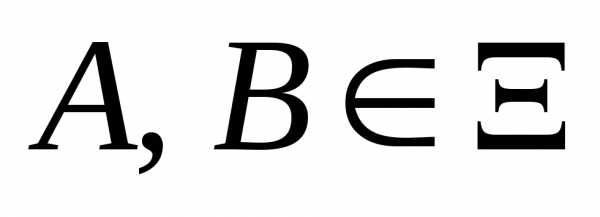 выполняется:,.
выполняется:,.
studfiles.net
Пространство элементарных исходов — КиберПедия
| Мощность множества измеряется не в лошадиных силах, а в кардинальных числах. Бывают множества с конечной, счетной, континуум мощностью и даже больше. Если элементы множества можно пересчитать,то есть поставить в взаимно однозначное соответствие каждому элементу множества натуральное число, оно называется «счетное множество». | Множество элементарных исходов опыта в теории вероятностей называется пространством элементарных исходов. Элементарные исходы являются элементами (точками) этого множества. В предыдущих примерах видно, что одному реальному опыту можно сопоставить несколько описаний пространства элементарных исходов. Таким образом, для описания экспериментов в качестве первичных математических понятий используются множества. В своей общей части теория вероятностей не использует никаких специфических свойств элементарных исходов и множеств, кроме числа элементов в них или их мощности. Поэтому любые два пространства элементарных исходов с одинаковым числом элементов или одинаковой мощностью с точки зрения теории вероятностей эквивалентны. Например, в опыте с бросанием монеты мы можем выбрать в качестве исходов слова «герб» и «решка» или числа «0» и «1». Обозначается пространство элементарных исходов обычно так: а сам элементарный исход так Можно записать отношение между пространством элементарных исходов и элементарными исходами так |
Советы по построению пространства элементарных исходов.
Имейте в виду задачу, которую вы хотите решить — то случайное событие, вероятность которого вам необходимо найти, должно описываться с помощью указания элементарных исходов, приводящих к этому событию.
На первых порах старайтесь вводить наиболее детальное описание опыта, – потом начнете понимать, в каких случаях можно, без ущерба для конечного результата, упростить модель.
Между разными подходящими моделями предпочтительнее выглядит модель, в которой элементарные исходы симметричны и равновероятны.
Очень удобно выбирать элементарные исходы в виде векторов (в смысле точек в пространстве), размерность которых равна количеству различных случайных факторов (источников) в случайном явлении, а координаты которых соответствуют различным вариантам значений этих факторов. Например, при бросании двух костей элементарный исход имеет размерность 2 и каждая координата 6 значений. При одновременном бросании монеты и кости вектор имеет размерность 2, первая координата 2 значения, вторая – 6 (или наоборот). Если бросаем 10 монет, то в качестве пространства элементарных исходов можно взять множество различных двоичных векторов размерности 10 из нулей и единиц.
Определения
Подмножества
Если пространство элементарных исходов определено, то появляется возможность описать любое событие, происшедшее в опыте, просто указав, какие элементарные исходы ему соответствуют.
· Пример.3.5 Элементарные исходы, 5 вариант: числа очков на костях с различением игральных костей [(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(2,1),(2,2),…] –36 исходов.
· Элементарный исход можно представить в виде
· ,
· где i – число очков на первой кости, j – второй кости.
· Тогда событие «на двух костях выпало в сумме 7 очков» можно представить в виде следующего подмножества элементарных исходов:
·
Заметим, что порядок перечисления элементарных исходов может быть произвольным. В дальнейшем подмножества пространства элементарных исходов будем обозначать большими латинскими буквами A, B, C…
A =
Пустое подмножество обозначим
Так как пустое подмножество не содержит никаких элементарных исходов, в теории вероятностей оно обозначает невозможное событие.
Множество всех элементарных событий W называется, естественно, достоверное событие.
Элементарный исход как случайное событие представляет собой одноточечное подмножество.
Операции над подмножествами
Стандартные операции над подмножествами применяются в теории вероятностей и имеют вероятностную интерпретацию.
Дополнение
Дополнение до подмножества A — это подмножество
т. е. дополнением к A является подмножество, включающее в себя все элементарные исходы, не содержащиеся в A. С точки зрения теории вероятностей подмножество A представляет событие, которое естественно назвать отрицание A или не-A. Т.е. A в опыте не произошло («не наступило»).
Объединение
Объединением двух подмножеств A и B является подмножество
Соответственно и интерпретация : произошло или A или B.
Пересечение
Пересечением двух подмножеств : A и B является подмножество
Соответственно и интерпретация : и A и B произошли одновременно.
Разность
Разностью двух подмножеств A и B является подмножество
Соответственно и интерпретация : A произошло, B — нет.
Симметричная разность
Симметричной разностью двух подмножеств A и B является подмножество
Соответственно и интерпретация : произошло только одно из этих двух событий.
cyberpedia.su
Пространство элементарных событий | Теория вероятностей
В основе теории вероятностей лежит понятие случайного эксперимента. Эксперимент считается случайным, если он может закончиться любым из совокупности известных результатов, но до осуществления эксперимента нельзя предсказать, каким именно. Примеры случайного эксперимента: бросание монеты, игральной кости, проведение лотереи, азартные игры, стрельба по цели, поступление звонков на телефонную станцию и т.п. Различные результаты эксперимента называют исходами.Определение 1. Множество всех взаимоисключающих исходов эксперимента называется пространством элементарных событий. Взаимоисключающие исходы — это те, которые не могут наступить одновременно. Пространство элементарных событий будем обозначать буквой Ω, а его исходы — буквой ω.
Определение 2. Произвольное подмножество пространства элементарных событий называется событием. Событие может состоять из одного или нескольких элементарных событий, а также из счетного или несчетного числа элементарных событий. Событие Ω, состоящее из всех исходов эксперимента, называется достоверным событием. Оно обязательно происходит, так как эксперимент всегда заканчивается каким-нибудь исходом. Пустое множество исходов эксперимента называется невозможным событием и обозначается символом ø.
Определение 3. Суммой двух событий А и В (обозначается A+B ) называется событие, состоящее из всех исходов, входящих либо в А, либо в В. Другими словами, под A+B понимают следующее событие: произошло или событие А, или событие В, либо они произошли одновременно, т.е. произошло хотя бы одно из событий А или В (рис. 1.1а).
Определение 4. Произведением двух событий А и В (обозначается АВ) называется событие, состоящее из тех исходов, которые входят как в А, так и в В. Иными словами, АВ означает событие, при котором события А и В наступают одновременно (рис. 1.1б).
Определение 5. Разностью двух событий А и В (обозначается A-B ) называется событие, состоящее из исходов, входящих в А, но не входящих в В. Смысл события A-B состоит в том, что событие А наступает, но при этом не наступает событие В (рис. 1.1в).
Определение 6. Противоположным (дополнительным) для события А (обозначается A) называется событие, состоящее из всех исходов, которые не входят в А. Наступление события A означает просто, что событие А не наступило. Если события изобразить на плоскости, то результат определенных операций над событиями выглядит следующим образом:
allworks.su
Пространство элементарных событий
Теория вероятностей изучает математические модели случайных явлений. Предположим, что производится некоторый эксперимент, исход (результат) которого непредсказуем. Множество тех исходов данного эксперимента, которые не могут происходить одновременно и появление одного и только одного из них обязательно произойдет, называют пространством элементарных событий, а сами исходы называют элементарными событиями. Пространство элементарных событий обозначают W, а элементарное событие — w. Пространство элементарных событий называют конечным, если множество элементарных событий конечно и — бесконечным в противном случае.
Рассмотрим некоторые примеры пространств элементарных событий.
Пример 1.4. Игральный кубик, имеющий шесть граней с изображением на каждой числа точек (1,2,3,4,5,6), подбрасывают один раз. Результатами этого эксперимента будем считать число очков, выпавшее на верхней грани кубика. Следовательно, пространство элементарных событий состоит из множества W = {w1, w2 , w3 , w4 , w5 ,w6}, где элементарное событие wi обозначает число очков i, выпавшее на верхней грани кубика.
Пример 1.5. Эксперимент состоит в наблюдении числа автомобилей, обслуживаемых автозаправочной станцией с 12 до 15 часов. В этом случае элементарные события можно выразить числами 0,1,2…. Очевидно, что число обслуживаемых автомобилей в течение рассматриваемого промежутка времени конечно, но точно предсказать их число невозможно. Поэтому будем считать, что пространство элементарных событий состоит из бесконечного множества
W = {0,1,2,…}.
Пример 1.6.Игральный кубик подбрасывают один раз. Рассмотрим следующие события: A = {выпало четное число},
B = {выпало нечетное число},
C = {выпало число £3}.
Каждое из этих событий отождествим с множеством всех исходов, при которых они наступают. Тогда события
A={ w2 ,w4 ,w6}, B ={w1,w3,w5}, C={w1,w2,w3}.
Отсюда видно, что все эти события являются подмножествами пространства элементарных событий.
Классификация событий
Для конечных пространств элементарных событий отождествим событие и множество всех исходов, при которых данное событие наступает. Эти исходы называют элементарными событиями, благоприятствующимиданному событию. Для конечных пространств элементарных событий событие – это множество всех исходов ему благоприятствующих. Такой подход к определению случайного события позволяет применять теорию множеств.
Определение. Невозможным событием называется событие, которое не может наступить в условиях данного эксперимента, т.е. это событие имеет пустое множество благоприятствующих исходов.
Например, пусть событие D = {на верхней грани кубика выпало число > 7}. Это событие является невозможным и ему соответствует пустое множество Æ благоприятствующих исходов. Будем невозможное событие обозначать символом Æ.
Определение. Достоверным называется событие W, которое всегда наступает в условиях данного эксперимента. Множество благоприятствующих исходов достоверного события совпадает с пространством элементарных событий W.
Пусть событие E = {на верхней грани кубика выпало число <= 7}. Это событие является достоверным и множество благоприятствующих ему исходов совпадает с пространством элементарных событий.
Определение.Если при каждом осуществлении события A происходит событие B,то говорят, что событие A влечет событие B. В этом случае множество благоприятствующих исходов события A содержится в множестве благоприятствующих исходов события B, т.е. .
Определение. События А и В называются эквивалентными, если событие А влечет событие В, а событие В влечет А.
Определение. Событие =W-A называется противоположнымсобытию A. Множество благоприятствующих исходов события является дополнением до пространства элементарных событий W множества благоприятствующих исходов события A ( или появление события —это непоявление события А ).
Определение. События A и B называются несовместными, если они не могут произойти вместе.
infopedia.su
