Чему равен факториал – Факториал числа — расчет онлайн

Содержание

Факториал — WiKi

Факториа́л — функция, определённая на множестве неотрицательных целых чисел. Название происходит от лат. factorialis — действующий, производящий, умножающий; обозначается n!, произносится эн факториа́л. Факториал натурального числа n определяется как произведение всех натуральных чисел от 1 до n включительно:

n!=1⋅2⋅…⋅n=∏k=1nk{\displaystyle n!=1\cdot 2\cdot \ldots \cdot n=\prod _{k=1}^{n}k}.

Например,

5!=1⋅2⋅3⋅4⋅5=120{\displaystyle 5!=1\cdot 2\cdot 3\cdot 4\cdot 5=120}.

Из определения факториала следует соотношение (n−1)!=n!n{\displaystyle (n-1)!={\frac {n!}{n}}}, откуда при n=1{\displaystyle n=1} формально находим

0!=1{\displaystyle 0!=1}.

Последнее равенство обычно принимают в качестве соглашения, хотя, как показано выше, оно следует из определения факториала для натуральных чисел при условии, что все значения функции связаны единым рекуррентным соотношением.

Факториалы всех чисел составляют последовательность A000142 в OEIS; значения в научной нотации округляются
n	n!
0	1
1	1
2	2
3	6
4	24
5	120
6	720
7	5040
8	40320
9	362880
10	3628800
11	39916800
12	479001600
13	6227020800
14	87178291200
15	1307674368000
16	20922789888000
17	355687428096000
18	6402373705728000
19	121645100408832000
20	2432902008176640000
25	≈1,551121004⋅10²⁵
50	≈3,041409320⋅10⁶⁴
70	≈1,197857167⋅10¹⁰⁰
100	≈9,332621544⋅10¹⁵⁷
450	≈1,733368733⋅10¹⁰⁰⁰
1000	≈4,023872601⋅10²⁵⁶⁷
3249	≈6,412337688⋅10¹⁰⁰⁰⁰
10000	≈2,846259681⋅10³⁵⁶⁵⁹
25206	≈1,205703438⋅10¹⁰⁰⁰⁰⁰
100000	≈2,824229408⋅10⁴⁵⁶⁵⁷³
205023	≈2,503898932⋅10^1000004
1000000	≈8,263931688⋅10^5565708
10¹⁰⁰	≈10^{9,956570552⋅10¹⁰¹}
10¹⁰⁰⁰	≈10^10¹⁰⁰³
10^10 000	≈10^{10^10 004}
10^100 000	≈10^{10^100 005}
10^10¹⁰⁰	≈10^{10^10¹⁰⁰}

Факториал активно используется в различных разделах математики: комбинаторике, математическом анализе, теории чисел, функциональном анализе и др.

Факториал является чрезвычайно быстро растущей функцией. Он растёт быстрее, чем любая показательная функция или любая степенная функция, а также быстрее, чем любая сумма произведений этих функций. Однако, степенно-показательная функция nn{\displaystyle n^{n}} растёт быстрее факториала, так же как и большинство двойных степенных, например een{\displaystyle e^{e^{n}}}.

Свойства

Рекуррентная формула

Факториал может быть задан следующей рекуррентной формулой:

n!={1n=0,n⋅(n−1)!n>0.{\displaystyle n!={\begin{cases}1&n=0,\\n\cdot (n-1)!&n>0.\end{cases}}}

Комбинаторная интерпретация

В комбинаторике факториал натурального числа n интерпретируется как количество перестановок (упорядочиваний) множества из n элементов. Например, для множества {A,B,C,D} из 4-х элементов существует 4! = 24 перестановки:

ABCD  BACD  CABD  DABC
ABDC  BADC  CADB  DACB
ACBD  BCAD  CBAD  DBAC
ACDB  BCDA  CBDA  DBCA
ADBC  BDAC  CDAB  DCAB
ADCB  BDCA  CDBA  DCBA

Комбинаторная интерпретация факториала подтверждает целесообразность соглашения 0!=1{\displaystyle 0!=1} — количество перестановок пустого множества равно единице. Кроме того, формула для числа размещений из n{\displaystyle n} элементов по m{\displaystyle m}

Anm=n!(n−m)!{\displaystyle A_{n}^{m}={\frac {n!}{(n-m)!}}}

при n=m{\displaystyle n=m} обращается в формулу для числа перестановок из n{\displaystyle n} элементов (порядка n{\displaystyle n} ), которое равно n!{\displaystyle n!} .

Связь с гамма-функцией

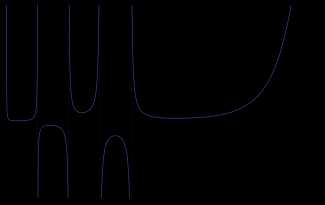Пи-функция, определённая для всех вещественных чисел, кроме отрицательных целых, и совпадающая при натуральных значениях аргумента с факториалом.

Факториал связан с гамма-функцией от целочисленного аргумента соотношением

n!=Γ(n+1){\displaystyle n!=\Gamma (n+1)} .

Это же выражение используют для обобщения понятия факториала на множество вещественных чисел. Используя аналитическое продолжение гамма-функции, область определения факториала также расширяют на всю комплексную плоскость, исключая особые точки при n=−1,−2,−3…{\displaystyle n=-1,-2,-3\ldots } .

Непосредственным обобщением факториала на множества вещественных и комплексных чисел служит пи-функция Π(z)=Γ(z+1){\displaystyle \Pi (z)=\Gamma (z+1)} , которая при Re(z)>−1{\displaystyle \mathrm {Re} (z)>-1} может быть определена как

Π(z)=∫0∞tze−tdt{\displaystyle \Pi (z)=\int _{0}^{\infty }t^{z}e^{-t}\,\mathrm {d} t} (интегральное определение).

Пи-функция натурального числа или нуля совпадает с его факториалом: Π(n)=n!{\displaystyle \Pi (n)=n!} . Как и факториал, пи-функция удовлетворяет рекуррентному соотношению Π(z)=zΠ(z−1){\displaystyle \Pi (z)=z\Pi (z-1)} .

Формула Стирлинга

Формула Стирлинга — асимптотическая формула для вычисления факториала:

n!=2πn(ne)n(1+112n+1288n2−13951840n3−5712488320n4+163879209018880n5+524681975246796800n6+O(n−7)),{\displaystyle n!={\sqrt {2\pi n}}\left({\frac {n}{e}}\right)^{n}\left(1+{\frac {1}{12n}}+{\frac {1}{288n^{2}}}-{\frac {139}{51840n^{3}}}-{\frac {571}{2488320n^{4}}}+{\frac {163879}{209018880n^{5}}}+{\frac {5246819}{75246796800n^{6}}}+O\left(n^{-7}\right)\right),}

см. O-большое^[1].

Во многих случаях для приближённого вычисления факториала достаточно рассматривать только главный член формулы Стирлинга:

n!≈2πn(ne)n.{\displaystyle n!\approx {\sqrt {2\pi n}}\left({\frac {n}{e}}\right)^{n}.}

При этом можно утверждать, что

2πn(ne)ne1/(12n+1)<n!<2πn(ne)ne1/(12n).{\displaystyle {\sqrt {2\pi n}}\left({\frac {n}{e}}\right)^{n}e^{1/(12n+1)}<n!<{\sqrt {2\pi n}}\left({\frac {n}{e}}\right)^{n}e^{1/(12n)}.}

Формула Стирлинга позволяет получить приближённые значения факториалов больших чисел без непосредственного перемножения последовательности натуральных чисел. Например, с помощью формулы Стирлинга легко подсчитать, что

100! ≈ 9,33×10¹⁵⁷;
1000! ≈ 4,02×10²⁵⁶⁷;
10 000! ≈ 2,85×10^35 659.

Разложение на простые числа

Каждое простое число p входит в разложение n! на простые множители в степени

⌊np⌋+⌊np2⌋+⌊np3⌋+….{\displaystyle \left\lfloor {\frac {n}{p}}\right\rfloor +\left\lfloor {\frac {n}{p^{2}}}\right\rfloor +\left\lfloor {\frac {n}{p^{3}}}\right\rfloor +\ldots .}

Таким образом,

n!=∏pp⌊np⌋+⌊np2⌋+…,{\displaystyle n!=\prod _{p}p^{\lfloor {\frac {n}{p}}\rfloor +\lfloor {\frac {n}{p^{2}}}\rfloor +\ldots },}

где произведение берётся по всем простым числам. Можно заметить, что для всякого простого p большего n соответствующий множитель в произведении равен 1; следовательно, произведение можно брать лишь по простым p, не превосходящим n.

Связь с производной от степенной функции

Для целого неотрицательного числа n:

(xn)(n)=n!{\displaystyle \left(x^{n}\right)^{(n)}=n!}

Например:

(x5)(5)=(5⋅x4)(4)=(5⋅4⋅x3)‴=(5⋅4⋅3⋅x2)″=(5⋅4⋅3⋅2⋅x)′=5⋅4⋅3⋅2⋅1=5!{\displaystyle \left(x^{5}\right)^{(5)}=\left(5\cdot x^{4}\right)^{(4)}=\left(5\cdot 4\cdot x^{3}\right)»’=\left(5\cdot 4\cdot 3\cdot x^{2}\right)»=\left(5\cdot 4\cdot 3\cdot 2\cdot x\right)’={5\cdot 4\cdot 3\cdot 2\cdot 1}=5!}

Другие свойства

Для натурального числа n:

n!2⩾nn⩾n!⩾n{\displaystyle n!^{2}\geqslant n^{n}\geqslant n!\geqslant n}

Для любого n>1:

n!{\displaystyle n!} не является квадратом целого числа.

История

Факториальные выражения появились ещё в ранних исследованиях по комбинаторике, хотя компактное обозначение n!{\displaystyle n!} предложил французский математик Кристиан Крамп только в 1808 году^[2]. Важным этапом стало открытие формулы Стирлинга, которую Джеймс Стирлинг опубликовал в своём трактате «Дифференциальный метод» (лат. Methodus differentialis, 1730 год). Немного ранее почти такую же формулу опубликовал друг Стирлинга Абрахам де Муавр, но в менее завершённом виде (вместо коэффициента 2π{\displaystyle {\sqrt {2\pi }}} была неопределённая константа)^[3].

Стирлинг подробно исследовал свойства факториала, вплоть до выяснения вопроса о том, нельзя ли распространить это понятие на произвольные вещественные числа. Он описал несколько возможных путей к реализации этой идеи и высказал мнение, что:

(12)!=π2{\displaystyle \left({1 \over 2}\right)!={\frac {\sqrt {\pi }}{2}}}

Стирлинг не знал, что годом ранее решение проблемы уже нашёл Леонард Эйлер. В письме к Кристиану Гольдбаху Эйлер описал требуемое обобщение^[4]:

x!=limm→∞mxm!(x+1)(x+2)…(x+m){\displaystyle x!=\lim _{m\to \infty }{\frac {m^{x}m!}{(x+1)(x+2)\dots (x+m)}}}

Развивая эту идею, Эйлер в следующем, 1730 году ввёл понятие гамма-функции в виде классического интеграла. Эти результаты он опубликовал в журнале Санкт-Петербургской Академии наук в 1729—1730 годах.

Обобщения

Двойной факториал

Двойной факториал числа n обозначается n‼ и определяется как произведение всех натуральных чисел в отрезке [1,n], имеющих ту же чётность, что и n.

n!!=2⋅4⋅6⋅…⋅n=∏i=1n22i=21n2⋅(n2)!{\displaystyle n!!=2\cdot 4\cdot 6\cdot \ldots \cdot n=\prod _{i=1}^{\frac {n}{2}}2i=2^{{\color {white}1}^{\!\!\!\!{\frac {n}{2}}}}\cdot \left({\frac {n}{2}}\right)!}

Для нечётного n:

n!!=1⋅3⋅5⋅…⋅n=∏i=0n−12(2i+1)=n!21n−12⋅(n−12)!{\displaystyle n!!={1\cdot 3\cdot 5\cdot \ldots \cdot n}=\prod _{i=0}^{\frac {n-1}{2}}(2i+1)={\frac {n!}{2^{{\color {white}1}^{\!\!\!\!{\frac {n-1}{2}}}}\cdot \left({\frac {n-1}{2}}\right)!}}}

Связь между двойными факториалами двух соседних целых неотрицательных чисел и обычным факториалом одного из них.

n!!=(n+1)!(n+1)!!{\displaystyle n!!={\frac {(n+1)!}{(n+1)!!}}}

Для нечётного n:

n!!=n!(n−1)!!{\displaystyle n!!={\frac {n!}{(n-1)!!}}}

Выведение формул

Осуществив замену n=2k{\displaystyle n=2k} для чётного n и n=2k+1{\displaystyle n=2k+1} для нечётного n соответственно, где k{\displaystyle k} — целое неотрицательное число, получим:

для чётного числа:

(2k)!!=2⋅4⋅6⋅…⋅2k=∏i=1k2i=2k⋅k!{\displaystyle (2k)!!=2\cdot 4\cdot 6\cdot \ldots \cdot 2k=\prod _{i=1}^{k}2i=2^{k}\cdot k!}

для нечётного числа:

(2k+1)!!=1⋅3⋅5⋅…⋅(2k+1)=∏i=0k(2i+1)=(2k+1)!2k⋅k!{\displaystyle (2k+1)!!=1\cdot 3\cdot 5\cdot \ldots \cdot (2k+1)=\prod _{i=0}^{k}(2i+1)={\frac {(2k+1)!}{2^{k}\cdot k!}}}

По договорённости: 0!!=1{\displaystyle 0!!=1} . Также это равенство выполняется естественным образом:

0!!=20⋅0!=1⋅1=1{\displaystyle 0!!=2^{0}\cdot 0!=1\cdot 1=1}

Двойной факториал, также как и обычный факториал, определён только для целых неотрицательных чисел.

Последовательность значений n!! начинается так^[5]:

1, 1, 2, 3, 8, 15, 48, 105, 384, 945, 3840, 10 395, 46 080, 135 135, 645 120, 2 027 025, 10 321 920, 34 459 425, 185 794 560, 654 729 075, 3 715 891 200, 13 749 310 575, 81 749 606 400, 316 234 143 225, 1 961 990 553 600, 7 905 853 580 625, 51 011 754 393 600, …

Кратный факториал

m-кратный факториал числа n обозначается n!!…!⏟m{\displaystyle \textstyle n\underbrace {!!\ldots !} _{m}} и определяется следующим образом. Пусть число n представимо в виде

www.ru-wiki.org

Чему равен факториал -1? т.е. (-1)!

Обобщением факториала является гамма-функция. Для всех целых чисел меньше 1 эта функция терпит разрыв (не существует) . А вот, например, чему она равна для -0,5 — ответить можно.

Ничему. Для отрицательных чисел факториал как функция не определен. А для целых неотрицательных не определено даже обобщение факториала — гамма-функция.

Факториал не определен для отрицательных чисел.

на сколько помню отрицательных фактариалов не бывает и вообще фактариалов с цифрой один тоже

touch.otvet.mail.ru

чему равен факториал (n-1)! ?

факториал равен произведению 1x2x3x….x(n-3)x(n-2)x(n-1) или, если известен n! то (n-1)!=n!/n

ну.. . можно например записать как n!/n

Можно воспользоваться формулой Стирлинга n! = sqrt(2*pi*n)*(n/e)^n где sqrt — квадратный корень только подставьте n-1

Я что, Пушкин что ли?

это что вопщё такое