Что следует из подобия треугольников – Подобие треугольников. Учебник по ЕГЭ и ОГЭ

Подобные треугольники | Математика

В двух треугольниках, имеющих равные углы, стороны, лежащие против одинаковых углов, называются сходственными (соответственными).

В треугольниках ABC и DEF (черт. 152), в которых

∠A = ∠D, ∠B = ∠E, ∠C = ∠F

стороны AB и DE, BC и EF, AC и DF, лежащие против равных углов C и F, A и D, B и E будут соответственными сторонами.

Определение подобных треугольников. Подобными называются такие два треугольника, у которых углы равны и сходственные стороны пропорциональны.

Если в двух треугольниках (черт. 152) ABC и DEF углы равны

∠A = ∠D, ∠B = ∠E, ∠C = ∠F

и соответственные стороны пропорциональны

AB/DE = AC/DF = BC/EF

то треугольники называются подобными.

Подобие обычно выражают знаком ∼.

Подобие двух треугольников изображают письменно:

ABC ∼ DEF.

Случаи подобия треугольников

Теорема 89. (Первый случай подобия.) Два треугольника подобны, если три угла одного равны трем углам другого треугольника.

Дано. В треугольниках ABC и DEF углы равны (черт. 153).

∠A = ∠D, ∠B = ∠E, ∠C = ∠F

Требуется доказать, что они подобны. Для этого нужно доказать, что их стороны пропорциональны, т. е. удовлетворяют отношениям:

AB/DE = AC/DF = BC/EF

Доказательство. Наложим треугольник DEF на ABC так, чтобы вершина E совпала с вершиной B, сторона ED со стороной AB. По равенству углов B и E сторона EF пойдет по стороне BC. Положим, точка D упадет в D’, а точка F в E’. Треугольник D’BE’ равен треугольнику DEF, следовательно,

∠D’ = ∠D, ∠D = ∠A

откуда

∠D’ = ∠A.

Если соответственные углы равны, то D’E || AC.

По теореме 86 имеют место равенства

AC/D’E’ = AB/BD’ = BC/BE’

Так как BD’ = ED, BE’ = EF, D’E’ = DF, то

AC/DF = AB/ED = BC/EF (ЧТД).

Теорема 90 (второй случай подобия). Два треугольника подобны, если они имеют по два равных угла.

Доказательство. Если в двух треугольниках ABC и DEF два угла равны (черт. 153).

A = D, B = E

то и третьи углы тоже равны, а в таком случае треугольники подобны (теорема 89).

Теорема 91 (третий случай подобия). Два треугольника подобны, если они имеют по равному углу, заключающемуся между пропорциональными сторонами.

Дано. В треугольниках ABC и DEF (черт. 153) углы B и E равны, и стороны, их содержащие, пропорциональны, т. е.

∠B = ∠E и AB/DE = BC/EF.

Требуется доказать, что треугольники подобны.

Доказательство. Совместим угол E с углом B, и отложим BD’ = ED, BE’ = EF, тогда ∆BD’E’ = ∆DEF, следовательно,

∠D’ = ∠D, ∠E’ = ∠F.

Так как имеет место пропорция

AB/BD’ = BC/BE’

то сторона D’E’ || AC (теорема 87).

Поэтому ∠D’ = ∠A, ∠C = ∠E’.

Следовательно,

∠A = ∠D, ∠C = ∠F, ∠B = ∠E

т. е. три угла одного равны трем углам другого треугольника.

В этом же случае треугольники ABC и DEF подобны (ЧТД).

Теорема 92 (четвертый случай подобия). Два треугольника подобны, если стороны одного пропорциональны сторонам другого.

Дано. В треугольниках ABC и abc (черт. 154) стороны пропорциональны:

AB/ab = BC/bc = AC/ac (1)

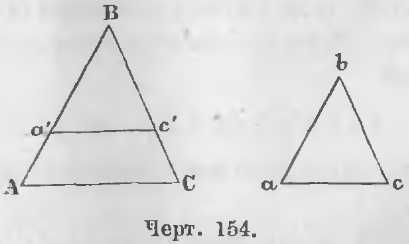
Требуется доказать, что у них углы равны, т. е.

A = a, B = b, C = c.

Доказательство. Отложим на стороне BA отрезок Ba’, равный ba, и проведем отрезок a’c’, параллельный AC, тогда будут иметь место отношения:

AB/Ba’ = BC/Bc’ = AC/a’c’

Так как Ba’ = ba, то рядом с этими имеют место отношения:

AB/ab = BC/Bc’ = AC/a’c’ (2)

Сопоставляя отношения (1) и (2), заключаем, что

Bc’ = bc, a’c’ = ac,

следовательно, два треугольника a’Bc’ и abc равны, откуда

∠B = ∠b, ∠Ba’c’ = ∠a, ∠Bc’a’ = ∠c

а так как

∠A = ∠a’, ∠C = ∠c’, то
B = b, A = a, C = c,

следовательно, углы двух треугольников ABC и abc равны (ЧТД).

Теорема 93 (пятый случай подобия). Два треугольника подобны, если стороны одного параллельны сторонам другого.

Доказательство. Здесь могут быть два случая:

1-й случай. Если углы двух треугольников с параллельными сторонами обращены в одну сторону. В таком случае в двух таких треугольниках ABC и abc (черт. 155) все углы одного соответственно равны углам другого, и, следовательно, треугольники подобны.

2-й случай. Когда углы с параллельными сторонами обращены в разные стороны. Так в треугольниках ABC и a’b’c’ стороны параллельны.

AB || a’b’, AC || a’c’, BC || b’c’.

Углы же между параллельными сторонами обращены в разные стороны.

В таком случае, продолжив стороны a’c’ и a’b’, откладываем на продолжении их части a’b» = a’b’ и a’c» = a’c’.

Треугольники a’b»c» и a’b’c’ равны. Треугольник a’b»c» подобен треугольнику ABC, ибо у него стороны параллельны и углы, направленные в одну сторону, равны, следовательно,

∆ABC ~ a’b»c», следовательно, ∆ABC ~ a’b’c’ и
AB/a’b’ = AC/a’c’ = BC/b’c’

Теорема 94 (шестой случай подобия). Два треугольника подобны, если стороны одного перпендикулярны к сторонам другого.

Даны два треугольника ABC и abc (черт. 156), стороны которых перпендикулярны:

ab ⊥ AB, ac ⊥ AC, bc ⊥ BC

Требуется доказать, что треугольники подобны.

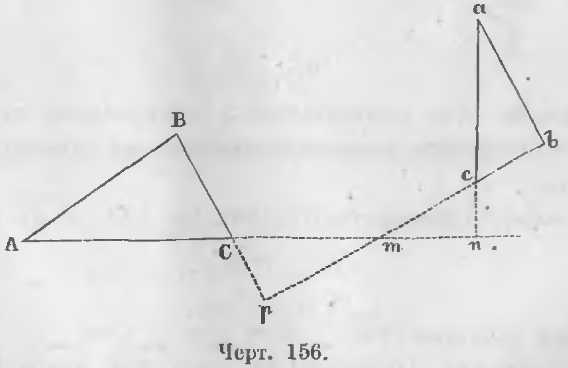
Доказательство. Продолжим стороны ac и bc до пересечения их со сторонами AC и BC в точках n и p. Тогда в двух треугольниках mcn и mCp все углы равны, ибо

n = p как прямые

Углы при точке m равны как вертикальные,

а следовательно, и третьи углы равны ∠pCm = ∠mcn.

Так как

∠pCm = ∠ACB, ∠mcn = ∠acb

следовательно,

∠ACB = ∠acb

Подобным же образом можно доказать, что A = a, B = b, следовательно, треугольники ABC и abc подобны и имеет место пропорция

AB/ab = AC/ac = BC/bc

Подобие прямоугольных треугольников

Теорема 95. Два прямоугольных треугольника подобны, если они имеют по равному острому углу.

Дано. У прямоугольных треугольников ABC и abc (черт. 157) острые углы C и c равны.

Требуется доказать, что треугольники ABC и abc подобны.

Доказательство. Углы B и b равны как прямые, углы C и c равны по условию, следовательно, они подобны (теорема 90).

Теорема 96. Два прямоугольных треугольника подобны, если катет и гипотенуза одного пропорциональна катету и гипотенузе другого.

Дано. В прямоугольных треугольниках ABC и abc (черт. 157)

AC/ac = AB/ab (a)

Требуется доказать, что ∠A = ∠a, ∠C = ∠c.

Доказательство. Отложим на отрезке BA отрезок Bm, равный ba и из точки m проведем отрезок mn, параллельный ac, тогда имеет место пропорция:

AC/mn = AB/Bm (b)

Так как Bm = ab по построению, то, сравнивая две пропорции (a) и (b), заключаем, что ac = mn, следовательно, два прямоугольных треугольника Bmn и abc, имея по равному катету и равной гипотенузе, равны.

Действительно, у них Bm = ab, mn = ac. У равных треугольников и углы равны:

∠m = ∠a = ∠A и ∠n = ∠c = ∠C

следовательно, два треугольника ABC и abc подобны.

Теорема 97. В подобных треугольниках высоты пропорциональны сторонам.

Даны два подобных треугольника ABC и FED (черт. 158), следовательно,

∠A = ∠F, ∠B = ∠E, ∠C = ∠D и
AB/FE = BC/ED = AC/DF

и проведены высоты BH и Eh.

Требуется доказать, что AB/FE = BH/Eh.

Доказательство. Прямоугольные треугольники ABH и FEh подобны, ибо ∠A = ∠F по условию, ∠AHB = ∠FhE как прямые, следовательно,

AB/FE = BH/Eh (ЧТД).

Теорема 98. Прямая, разделяющая угол треугольника пополам, делит его противоположную сторону на части пропорциональные двум другим сторонам.

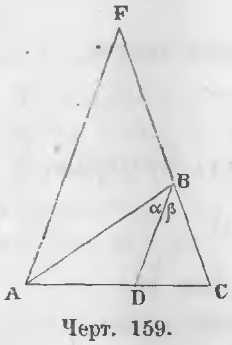
Дано. Отрезок BD делит угол B треугольника ABC пополам (черт. 159).

∠ABD = ∠DBC или ∠α = ∠β

Требуется доказать, что AB/BC = AD/DC.

Доказательство. Проведем из точки A отрезок AF параллельный BD до пересечения его с прямой BC в точке F. В треугольнике FBA

∠AFB = ∠β как соответственные углы,
∠FAB = ∠α как внутренние накрест-лежащие углы от пересечения параллельных AF и BD третьей прямой AB.

Так как ∠α = ∠β по условию, то

∠AFB = ∠FAB, т. е. треугольник FAB равнобедренный, поэтому FB = AB.

Из того, что AF || BD вытекает пропорция:

FB/BC = AD/DC

Заменяя FB равным отрезком AB, получим пропорцию:

AB/BC = AD/DC (ЧТД).

Теорема 99 (обратная 98). Прямая, проведенная из вершины треугольника и делящая противоположную сторону на части, пропорциональные двум другим сторонам, делит угол при вершине пополам.

Дано. В треугольнике ABC (черт. 159) прямая BD рассекает противоположную сторону так, что имеет место пропорция:

AB/BC = AD/DC (a)

Требуется доказать, что ∠α = ∠β.

Доказательство. Проведем отрезок AF параллельно BD, тогда из треугольника AFC вытекает пропорция:

FB/BC = AD/DC (b)

Сравнивая две пропорции (a) и (b), заключаем, что FB = AB, следовательно,

∠AFB = ∠FAB.

Так как ∠α = ∠FAB, ∠β = ∠AFB, то и

∠α = ∠β (ЧТД).

Отношения в прямоугольном треугольнике

Теорема 100. Перпендикуляр, опущенный из вершины прямого угла на гипотенузу, среднепропорционален между частями гипотенузы.

Дано. В треугольнике ABC угол ABC прямой (черт. 160) и BD ⊥ AC.

Требуется доказать, что AD/BD = BD/DC.

Доказательство. Треугольники ABD и BDC подобны, ибо углы при точке D равны как прямые; кроме того из равенств ∠A + ∠α = d, ∠α +∠β = d вытекает

A + α = α + β, или A = β, следовательно и C = α.

Из подобия треугольников ABD и BDC вытекает пропорция

AD/BD = BD/DC (ЧТД).

Примечание. Если составляют одно отношение из сторон одного треугольника, то другое отношение составляется из соответственных сторон другого треугольника. При этом рассуждают следующим образом: против стороны AD лежит угол α, которому в подобном треугольнике BCD равен угол C, а против него лежит сходственная сторона BD треугольника BCD и т. д.

Теорема 101. Каждый катет среднепропорционален между целой гипотенузой и отрезком, прилежащим катету.

Доказательство. a) Треугольники ABC и ABD (черт. 160) подобны, ибо ∠ABC = ∠ADB как прямые, ∠A общий, следовательно,

∠C = ∠α

Из подобия треугольников вытекает пропорция:

AD/AB = AB/AC (a)

b) Треугольники ABC и BCD подобны, ибо ∠ABC = ∠BDC как прямые, ∠C общий, следовательно,

∠A = ∠β, откуда
DC/BC = BC/AC (b)

Теорема 102. Квадрат гипотенузы равен сумме квадратов катетов.

Из предыдущих пропорций (a) и (b) вытекают равенства:

AB² = AD · AC
BC² = DC · AC

Складывая их, получим:

AB² + BC² = AD · AC + DC · AC или
AB² + BC² = AC (AD + DC) = AC · AC = AC², т. е.
AC² = AB² + BC²

откуда

a) Гипотенуза равна корню квадратному из суммы квадратов катетов.

b) Катет равен корню квадратному из квадрата гипотенузы без квадрата другого катета.

Теорема 103. Диагональ квадрата несоизмерима с его стороной, или гипотенуза равнобедренного прямоугольного треугольника несоизмерима с катетом.

Дано. В квадрате ABCD проведена диагональ AC (черт. 161).

Требуется доказать, что отношение AC/AD есть величина несоизмеримая.

Доказательство. Станем сравнивать больший отрезок AC с меньшим BC по обыкновенным приемам нахождения общей меры, т. е. наложим меньший отрезок на больший, первый остаток на меньший и т. д.

a) Наложим отрезок BC на отрезок AC. Отложив отрезок AE, равный AB или BC, мы видим, что отрезок BC уложился один раз, ибо

AB + BC > AC.

Так как AB = BC, то 2BC > AC и BC > ½AC, следовательно, первый остаток EC < BC.

b) Наложим первый остаток EC на отрезок BC. Для этого из точки E восставим перпендикуляр EF и соединим точку F с A.

c) Треугольник FEC равнобедренный, ибо ∠EFC = ∠BAC как углы с перпендикулярными сторонами

∠BAC = ∠ECF, следовательно,
∠EFC = ∠ECF

На этом основании стороны EF и EC равны:

EF = EC (1)

Треугольники ABF и AEF равны, ибо они прямоугольны и у них

AF сторона общая
AB = AE по построению, следовательно,
BF = EF (2)

Таким образом из равенств (1) и (2) выходит, что

EC = EF = BF

Не трудно видеть, что первый остаток укладывается в отрезке BC не более двух раз. Отложив EC два раза на отрезке BC, найдем точку G и второй остаток GC. Таким образом, остаток после наложения сторон квадрата на диагональ укладывается в стороне квадрата не более двух раз.

d) Наложим второй остаток GC на первый EC.

В прямоугольном и равнобедренном треугольнике FEC соотношение между отрезками GC, FC и EC то же самое как и соотношение между данными отрезками EC, AC и BC в треугольнике ABC, ибо треугольник FEC прямоугольный и равнобедренный, следовательно, при дальнейшем наложении мы будем снова получать остаток. Продолжая так поступать, мы всегда будем получать остатки, поэтому общей меры мы никогда не получим, следовательно, отрезки AC и BC несоизмеримы.

Обозначив длину диагонали черед l, длину стороны квадрата через a, последовательные величины остатков через d₁, d₂ и т. д., т. е. положив

AC = l, BC = a, CE = d₁, GC = d₂ и т. д.

имеем равенства:

l = a + d₁, a = 2d₁ + d₂, d₁ = 2d₂ + d₃ и т. д.

откуда

l/a = 1 + d₁/a
a/d₁ = 2 + d₂/d₁ или d₁/a = ½ + d₂/d₁
d₁/d₂ = 2 + d₃/d₂ или d₂/d₁ = ½ + d₃/d₂

следовательно,

l/a = 1 + ½ + ½ + …

Отношение между длинами l и a выражается бесконечной непрерывной дробью. Несоизмеримость впрочем прямо вытекает из выражения диагонали квадрата по катетам.

Действительно,

AC² = AB² + BC².

Так как AB = BC, то AC² = 2AB², откуда AC = AB√2 и AC/AB = √2 величина несоизмеримая.

Соотношение между сторонами остроугольного и тупоугольного треугольника

Теорема 104. Квадрат стороны, лежащей против острого угла, равен сумме квадратов прочих двух сторон треугольника без удвоенного произведения основания на отрезок, заключающийся между вершиной острого угла и высотой.

Здесь могут быть два случая: 1) когда перпендикуляр, выражающий высоту, пойдет внутри и 2) когда он пойдет вне треугольника.

Первый случай. Перпендикуляр BD (черт. 162), опущенный из вершины B на основание AC треугольника ABC, пойдет внутри треугольника.

Требуется доказать, что AB² = BC² + AC² — 2AC · DC.

Доказательство. Для прямоугольного треугольника ABD имеем равенство:

AB² = BD² + AD² (a)
AD = AC — DC, AD² = (AC — DC)² = AC² + DC² — 2AC · DC

Из прямоугольного треугольника BDC имеем:

BD² = BC² — DC²

Вставляя величины BD² и AD² в равенство (a), получим:

AB² = BC² — DC² + AC² + DC² — 2AC · DC, откуда
AB² = BC² + AC² — 2AC · DC (ЧТД).

2-й случай. Перпендикуляр BD (черт. 163) лежит вне треугольника ABC.

Доказательство. Из прямоугольного треугольника ABD имеем:

AB² = BD² + DA²

Из прямоугольного треугольника BCD имеем:

BD² = BC² — CD²

следовательно,

AB² = BC² — CD² + DA².

Так как

DA = CD — AC
DA² = (CD — AC)² = CD² + AC² — 2CD · AC, то
AB² = BC² — CD² + CD² + AC² — 2CD · AC, откуда
AB² = BC² + AC² — 2CD · AC (ЧТД).

Теорема 105. Квадрат стороны, лежащей против тупого угла, равен сумме квадратов прочих двух сторон треугольника с удвоенным произведением основания на отрезок его от вершины тупого угла до высоты.

Дано. В тупоугольном треугольнике ABC отрезок CD (черт. 164) есть отрезок, лежащий между вершиной тупого угла и высотой.

Требуется доказать, что

AB² = AC² + BC² + 2AC · CD

Доказательство. Из тупоугольного треугольника ABC имеем:

AB² = BD² + AD² (a)
AD = AC + CD, AD² = AC² + CD² + 2AC · CD

Из прямоугольного треугольника BCD вытекает, что

BD² = BC² — CD²

Заменяя AD² и BD² в равенстве (a), получим:

AB² = BC² — CD² + AC² + CD² + 2AC · CD

откуда

AB² = BC² + AC² + 2AC · CD (ЧТД).

Теорема 106. Сумма квадратов диагоналей равна сумме квадратов всех четырех сторон параллелограмма.

Дан параллелограмм ABCD (черт. 165) и проведены его диагонали AC и BD.

Требуется доказать, что

AC² + BD² = AB² + BC² + CD² + AD²

Доказательство. Опустив перпендикуляры BE и CF, имеем из косоугольного треугольника ABD равенство:

BD² = AB² + AD² — 2AD · AE (1)

Из тупоугольного треугольника ACD равенство:

AC² = CD² + AD² + 2AD · DF (2)

Отрезки AE и DF равны, ибо прямоугольные треугольники ABE и DCF равны, так как они имеют по равному катету и равной гипотенузе.

Сложив равенства (1) и (2), имеем:

BD² + AC² = AB² + AD² + CD² + AD²

Так как AD = BC, то

BD² + AC² = AB² + BC² + CD² + AD² (ЧТД).

Теорема 107. Сумма квадратов двух сторон треугольника равна сумме удвоенного квадрата отрезка, соединяющей вершину с серединой основания, с удвоенным квадратом половины основания.

Дано. Соединим вершину B с серединой основания D треугольника ABC так, что AD = DC (черт. 166).

Требуется доказать, что

AB² + BC² = 2AD² + 2BD²

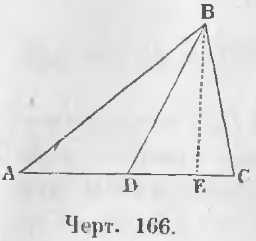
Доказательство. Проведем высоту BE.

Из прямоугольных треугольников ABE и BCE вытекают равенства:

AB² = BE² + AE²
BC² = BE² + CE²

Сложив их, находим:

AB² + BC² = 2BE² + AE² + CE² (a)

Так как AE = AD + DE = CD + DE, CE = CD — DE, то

AE² = (CD + DE)² = CD² + DE² + 2CD · DE
CE² = (CD — DE)² = CD² + DE² — 2CD · DE

откуда

AE² + CE² = 2CD² + 2DE² (b)

Заменяя в равенстве (a) сумму AE² + CE² из равенства (b), имеем:

AB² + BC² = 2BE² + 2CD² + 2DE².

Из прямоугольного треугольника BDE видно, что

BE² = BD² — DE²

следовательно

AB² + BC² = 2BD² — 2DE² + 2CD² + 2DE²

откуда

AB² + BC² = 2BD² + 2CD² (ЧТД).

 

maths-public.ru

Использование подобия треугольников — FizikaKlass.ru

Треугольник, образованный векторами и подобен треугольнику, образованному векторами и потому что оба треугольника равнобедренные, а углы при их вершинах равны.Модули векторов и равны а модули векторов и равны поэтому из подобия указанных треугольников получаем Поскольку для малого промежутка времени можно принять где и — модули ускорения и скорости, получаем Отсюда следует, что модуль центростремительного ускорения

fizikaklass.ru

Первый признак подобия треугольников

Вспомним, что подобными называются треугольники, у которых углы соответственно равны, а сходственные стороны пропорциональны.

На одном из предыдущих уроков мы отмечали, что подобие треугольников можно установить, проверив только некоторые из равенств. И сейчас мы познакомимся с первым признаком подобия треугольником.

Теорема (1-й признак подобия треугольников). Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.

Доказательство.

, .

, , ,

, следовательно, .

Так как , то .

Так как , то .

, .

Так как , то .

, .

Следовательно, .

Выше мы доказали, что соответственные углы этих треугольников равны, а значит, они треугольники подобны.

Что и требовалось доказать.

Из доказанной теоремы следует, что прямая, параллельная одной из сторон треугольника, отсекает от него треугольник, подобный данному.

Давайте возьмём некоторый треугольник ABC и проведём прямую MN, параллельную стороне AC.

 как соотв. при  и секущей ,  

 как соотв. при  и секущей , 

следовательно,  по 1-му признаку.

Также из доказанного признака следует, что прямоугольные треугольники подобны по острому углу.

Действительно. Если у прямоугольных треугольников ABC и A₁B₁C₁ угол А равен углу А₁, то  по 1-му признаку.

А теперь давайте посмотрим на следующие треугольники и найдём среди них подобные.

Итак, треугольники а и в подобны по первому признаку, так как два угла одного треугольника соответственно равны двум углам другого треугольника.

Треугольники д и е являются подобными, так как они прямоугольные и у них острые углы равны.

И у нас остались треугольники б и г. Так как сумма углов треугольника равна ста восьмидесяти градусам, то несложно найти градусную меру третьего угла треугольника б. Она равна 40º. А тогда эти треугольники подобны по двум углам, то есть по первому признаку.

Задача. На стороне  параллелограмма отмечена точка . Прямые  и  пересекаются в точке . Найдите  и , если  см,  см,  см,  см.

Решение.

Рассмотрим  и .

 как вертикальные,  как внутр. накрест лежащие  при  и секущей . 

Значит,  по 1-му признаку.

, то есть .

, ,  (см).

 см.

, ,  (см).

Ответ:  см;  см.

Задача. На рисунке  см,  см,  см, а . Найдите .

Решение.

 

Рассмотрим  и .

 по условию задачи,  – общий.  

Значит,  по 1-му признаку.

, ,   (см).

Ответ:  см.

Итак, на уроке мы доказали первый признак подобия треугольников: если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.

Убедились, что прямая, параллельная одной из сторон треугольника, отсекает от него треугольник, подобный данному. А также, что прямоугольные треугольники подобны по острому углу.

Кроме этого решили задачи на закрепление нового материала.

videouroki.net

Признаки подобия треугольников. Теория | Учеба-Легко.РФ

Подобие треугольников играет важную роль в геометрии. Она широко применяется при черчении и построении моделей. Два треугольника называются подобными, если их соответственные углы равны, а соответствующие стороны пропорциональны.

Обратите внимание!

При обозначении подобных треугольников следите за тем, чтобы в названиях подобных треугольников вершины соответствующих равных углов стояли на одинаковых местах.

Для того чтобы два треугольника были сходными, достаточно, чтобы их стороны или углы удовлетворяли определенные условия, изложенные в признаках сходства.

Признаки подобия треугольников:

1. Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.

2. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы между этими сторонами равны, то такие треугольники подобны.

3. Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники равны.

4. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и крупнейший из противоположных им углов одного треугольника равен соответствующему углу другого треугольника, то такие треугольники подобны.

Признаки подобия прямоугольных треугольников:

За острым углом. Если прямоугольные треугольники имеют по равному острому углу, то такие треугольники подобны. У прямоугольного треугольника один угол прямой, поэтому для подобия двух прямоугольных треугольников достаточно, чтобы у них было по ровному острому углу.

За двумя пропорциональными катетами. Если катеты одного прямоугольного треугольника пропорциональны катетам второго прямоугольного треугольника, то такие треугольники подобны.

По пропорциональным катетом и гипотенузой. Если катет и гипотенуза одного прямоугольного треугольника пропорциональны катету и гипотенузе второго прямоугольного треугольника, то такие треугольники подобны.

Обратите внимание! Высота прямоугольного треугольника, проведенная к гипотенузы, делит его на два треугольника, подобны друг другу и подобные данном треугольнике.

uclg.ru