Что такое функция в алгебре определение – . . . .

Определение, понятие, свойства и значение функций в алгебре

Одним из основных понятий в математике, если не самым основным, является понятие функции. Для понимания этого термина, его значения, смысла и необходимости, обратимся к следующему примеру:

Вообразим себе обыкновенный автомобиль. Предположим, что он постоянно двигается со скоростью 80 км/ч и не меняет её на протяжении всего пути. А теперь попробуем выяснить: сколько километров проедет автомобиль, если в пути он будет находиться 5 часов? Итак, нам известна скорость и время. Попробуем составить зависимость:

Вконтакте

Одноклассники

Facebook

Мой мир

Twitter

Сколько времени находится в пути автомобиль?	Сколько километров автомобиль проехал?
1 ч	80 км
2 ч	160 км
3 ч	240 км
4 часа	320 км
5 часов	400 км

Нам были известны всего две величины: скорость автомобиля и время, которое он находился в пути. Взглянув на таблицу, можно понять, что между временем, которое находился автомобиль в пути, и пройденным им расстоянием есть чёткая зависимость — каждый час автомобиль проезжает на 80 километров больше. Что ж, давайте немного приблизимся к алгебре и введём две переменные: y и x.

Y — это наше расстояние, а x — время пути. Составим уравнение: y = 80 * x. Теперь вместо x подставим время:

• Y = 80 * 1. Получается 80 — значение расстояния, которое автомобиль пройдёт за 1 час.
• Теперь вместо x подставим 2. Получается: y = 80 * 2 = 160. Это значение расстояния, которое пройдёт автомобиль при условии, что он будет ехать 2 часа.

Теперь введём следующую запись: y(x). Эта запись означает зависимость первой переменной от второй, а наше окончательное уравнение для движения автомобиля будет выглядеть следующим образом: y(x)=80x. Y в алгебре принято называть функцией, а x — аргументом.

Это интересно: какой вектор называется разностью двух векторов?

Смысл

Пользуясь приведённым примером, мы чётко и ясно можем понять, что определение функции — это зависимость одной переменной от другой.

Очень важно понимать, что y = 80 * x — не единственная зависимость. Стоит нам лишь изменить скорость автомобиля, то все ý при тех же значениях аргумента будут совсем другие. Кроме того, существует огромное множество зависимостей, которые могут иметь другой вид.

Способы задания

Всего в математике существует три способа задания функции:

• «Формульный способ». С помощью формулы мы всегда можем определить ý. Допустим, что у нас есть зависимость y = 5x + 1. Чтобы найти все y, нам просто нужно подставить вместо x любое число, например: если x = 0, y = 1, если x = 5, y = 26. В этой функции мы можем принимать любые значения аргумента, но если нам встретится следующая зависимость: y = √x, то мы сможем взять за x все числа, кроме отрицательных, так как число под корнем не может быть с минусом.
• Табличный способ задания также очень сильно распространён. Мы уже встречались с таблицей, когда приводили пример про автомобиль. Для того чтобы составить таблицу, необходимо всего лишь найти несколько значений y при нескольких значениях аргумента.
• Графический способ задания. Когда только начинают знакомятся с функциями, обязательно вводят такое понятие, как график. Давайте рассмотрим, что же он из себя представляет.

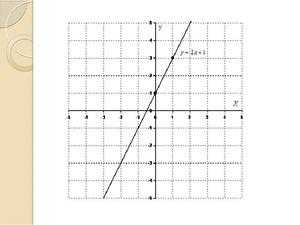
Перед вами координатная плоскость — основа для графика. Она состоит из вертикальной оси Y — оси значений, и из горизонтальной оси X — аргумента. У координатной плоскости обязательно есть начало отсчёта, которая обозначается нулём, и единичный отрезок (в данном примере единичный отрезок равен одной клетке).

На координатной плоскости мы можем взять любой единичный отрезок. Например, если нам удобно, значение одной клетки будет ни 1, а 100. Следовательно, две клетки — 200 и так далее. Здесь мы можем построить любой график и, соответственно, увидеть любую зависимость.

На координатной плоскости мы видим график 2x — 1. Графиком является прямая. Как же определить зависимость? Давайте приметим любое значение аргумента, например, 0. Когда x = 0, значение равно 1, что чётко видно на графике. Когда аргумент = -1, значение также равно -1.

Свойства

В алгебре есть невообразимое количество свойств функции, но основными и действительно важными являются лишь некоторые.

• «Область определения». Это понятие очень простое: оно подразумевает собой абсолютно все числа, которые может принимать переменная x. Например, в функции y = x — 2, переменная x может принимать все значения, то есть от минус бесконечности до плюс бесконечности. Другое дело, например, такая функция: y = √x. Так как под корнем не может стоять отрицательное число, допустимыми значениями аргумента могут быть все числа от нуля до плюс бесконечности.
• Если область определения все значения аргумента, то следующее свойство функции, называемое «область значений» — это все значения, которые может принимать переменная y. Поскольку значения функции зависимы от аргумента, то тут ничего выдумывать не надо, а просто вычислять.
• «Ограниченность» определить очень просто: если в рассматриваемой функции существует максимальное или минимальное значение y, то мы говорим, что функция будет называться ограниченной либо сверху, либо снизу.
• «Непрерывность» —тоже очень простое свойство. Например, зависимость ý = 2x — 1, которую мы уже рассматривали, непрерывна, так как её график нигде не прерывается. Если же в какой-либо функции график будет прерываться, можно говорить, что она прерывается на определённом промежутке.
• «Выпуклость» также присуща не всем графикам. У линейной зависимости её быть не может, поскольку это прямая и она не может быть выпуклой. А, например, парабола может быть выпуклой либо вверх, либо вниз.
• Нули функции — это пересечение с осями. То есть, если нам необходимо описать данное свойство, нужно будет найти, в каком месте график пересекается с осью абсцисс и в каком месте с осью ординат.

Подводя итог, мы можем сказать, что функция — это важнейшее понятие в математике, ведь, по сути, ею можно описать любые процессы.

obrazovanie.guru

Определение функции

Определение
Функцией y = f(x) называется закон (правило, отображение), согласно которому, каждому элементу x множества X ставится в соответствие один и только один элемент y множества Y.

Множество X называется областью определения функции.
Множество элементов y ∈ Y, которые имеют прообразы во множестве X, называется множеством значений функции (или областью значений).

Область определения функции иногда называют множеством определения или множеством задания функции.

Элемент x ∈ X называют аргументом функции или независимой переменной.
Элемент y ∈ Y называют значением функции или зависимой переменной.

Само отображение  f  называется характеристикой функции.

Характеристика  f  обладает тем свойством, что если два элемента и из множества определения имеют равные значения: , то .

Символ, обозначающий характеристику, может совпадать с символом элемента значения функции. То есть можно записать так: . При этом стоит помнить, что y – это элемент из множества значений функции, а – это правило, по которому для элемента x ставится в соответствие элемент y.

Сам процесс вычисления функции состоит из трех шагов. На первом шаге мы выбираем элемент x из множества X. Далее, с помощью правила , элементу x ставится в соответствие элемент множества Y. На третьем шаге этот элемент присваивается переменной y.

Частным значением функции называют значение функции при выбранном (частном) значении ее аргумента.

Графиком функции  f  называется множество пар .

Сложные функции

Определение
Пусть заданы функции и . Причем область определения функции f содержит множество значений функции g. Тогда каждому элементу t из области определения функции g соответствует элемент x, а этому x соответствует y. Такое соответствие называют сложной функцией:  .

Сложную функцию также называют композицией или суперпозицией функций и иногда обозначают так:  .

В математическом анализе принято считать, что если характеристика функции обозначена одной буквой или символом, то она задает одно и то же соответствие. Однако, в других дисциплинах, встречается и другой способ обозначений, согласно которому отображения с одной характеристикой, но разными аргументами, считаются различными. То есть отображения и считаются различными. Приведем пример из физики. Допустим мы рассматриваем зависимость импульса от координаты . И пусть мы имеем зависимость координаты от времени . Тогда зависимость импульса от времени является сложной функцией . Но ее, для краткости, обозначают так: . При таком подходе и – это различные функции. При одинаковых значениях аргументов они могут давать различные значения. В математике такое обозначение не принято. Если требуется сокращение, то следует ввести новую характеристику. Например . Тогда явно видно, что и – это разные функции.

Действительные функции

Область определения функции и множество ее значений могут быть любыми множествами.
Например, числовые последовательности – это функции, областью определения которых является множество натуральных чисел, а множеством значений – вещественные или комплексные числа.
Векторное произведение тоже функция, поскольку для двух векторов и имеется только одно значение вектора . Здесь областью определения является множество всех возможных пар векторов . Множеством значений является множество всех векторов.
Логическое выражение является функцией. Ее область определения – это множество действительных чисел (или любое множество, в котором определена операция сравнения с элементом “0”). Множество значений состоит из двух элементов – “истина” и “ложь”.

В математическом анализе большую роль играют числовые функции.

Числовая функция – это функция, значениями которой являются действительные или комплексные числа.

Действительная или вещественная функция – это функция, значениями которой являются действительные числа.

Максимум и минимум

Действительные числа имеют операцию сравнения. Поэтому множество значений действительной функции может быть ограниченным и иметь наибольшее и наименьшее значения.

Действительная функция называется ограниченной сверху (снизу), если существует такое число M, что для всех выполняется неравенство:
.

Числовая функция называется ограниченной, если существует такое число M, что для всех :
.

Максимумом M (минимумом m) функции f, на некотором множестве X называют значение функции при некотором значении ее аргумента , при котором для всех ,
.

Верхней гранью или точной верхней границей действительной, ограниченной сверху функции называют наименьшее из чисел, ограничивающее область ее значений сверху. То есть это такое число s, для которого для всех и для любого , найдется такой аргумент , значение функции от которого превосходит s′: .
Верхняя грань функции может обозначаться так:
.

Верхней гранью неограниченной сверху функции является бесконечно удаленная точка .

Нижней гранью или точной нижней границей действительной, ограниченной снизу функции называют наибольшее из чисел, ограничивающее область ее значений снизу. То есть это такое число i, для которого для всех и для любого , найдется такой аргумент , значение функции от которого меньше чем i′: .
Нижняя грань функции может обозначаться так:
.

Нижней гранью неограниченной снизу функции является бесконечно удаленная точка .

Таким образом, любая действительная функция, на не пустом множестве X, имеет верхнюю и нижнюю грани. Но не всякая функция имеет максимум и минимум.

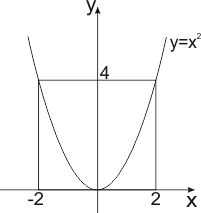
В качестве примера рассмотрим функцию , заданную на открытом интервале .
Она ограничена, на этом интервале, сверху значением 1 и снизу – значением 0:
для всех .
Эта функция имеет верхнюю и нижнюю грани:
.
Но она не имеет максимума и минимума.

Если мы рассмотрим туже функцию на отрезке , то она на этом множестве ограничена сверху и снизу, имеет верхнюю и нижнюю грани и имеет максимум и минимум:
для всех ;
;
.

Монотонные функции

Определения возрастающей и убывающей функций
Пусть функция определена на некотором множестве действительных чисел X. Функция называется строго возрастающей (строго убывающей), если для всех таких что выполняется неравенство:
.
Функция называется неубывающей (невозрастающей), если для всех таких что выполняется неравенство:
.

Определение монотонной функции
Функция называется монотонной, если она неубывающая или невозрастающая.

Многозначные функции

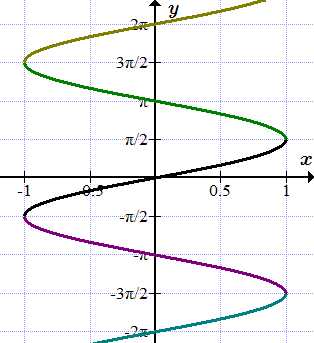
Пример многозначной функции. Различными цветами обозначены ее ветви. Каждая ветвь является функцией.

Как следует из определения функции, каждому элементу x из области определения, ставится в соответствие только один элемент из множества значений. Но существуют такие отображения, в которых элемент x имеет несколько или бесконечное число образов.

В качестве примера рассмотрим функцию арксинус: . Она является обратной к функции синус и определяется из уравнения:
(1)   .
При заданном значении независимой переменной x, принадлежащему интервалу , этому уравнению удовлетворяет бесконечно много значений y (см. рисунок).

Наложим на решения уравнения (1) ограничение. Пусть
(2)   .
При таком условии, заданному значению , соответствует только одно решение уравнения (1). То есть соответствие, определяемое уравнением (1) при условии (2) является функцией.

Вместо условия (2) можно наложить любое другое условие вида:
(2.n)   ,
где n – целое. В результате, для каждого значения n, мы получим свою функцию, отличную от других. Множество подобных функций является многозначной функцией. А функция, определяемая из (1) при условии (2.n) является ветвью многозначной функцией.

Многозначная функция – это совокупность функций, определенных на некотором множестве.

Ветвь многозначной функции – это одна из функций, входящих в многозначную функцию.

Однозначная функция – это функция.

Использованная литература:
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.

Автор: Олег Одинцов.     Опубликовано: 10-04-2018   Изменено: 08-10-2018

1cov-edu.ru

Что такое функция и ее свойства

Если задано множество чисел X и указан способ f, по которому для каждого значения хЄX ставится в соответствие только одно число у. Тогда считается заданной функция y = f(х), у которой область определения X (обычно обозначают D(f) = X). Множество Y всех значений у, для которых есть как минимум одно значение хЄX, такое, что y = f(х), такое множество называют множеством значений функции f (чаще всего обозначают E(f)= Y).

Или зависимость одной переменной у от другой х, при которой каждому значению переменной х из определенного множества D соответствует единственное значение переменной у, называется функцией.

Функциональную зависимость переменной у от х часто подчеркивают записью у(х), которую читают игрек от икс.

Область определения функции у(х), т. е. множество значений ее аргумента х, обозначают символом D(y), который читают дэ от игрек.

Область значений функции у(х), т. е. множество значений, которые принимает функция у, обозначают символом Е(у), который читают е от игрек.

Основными способами задания функции являются:

а) аналитический (с помощью формулы y = f(х)). К этому способу можно отнести и случаи, когда функция задается системой уравнений. Если функция задана формулой, то область ее определения составляют все те значения аргумента, при которых выражение, записанное в правой части формулы, имеет значения.

б) табличный (с помощью таблицы соответствующих значений х и у). Таким способом часто задается температурный режим или курсы валют, но этот способ не такой наглядный, как следующий;

в) графический (с помощью графика). Это один из самых наглядных способов задания функции, поскольку по графику сразу «читаются» изменения. Если функция у(х) задана графиком, то область ее определения D(y) есть проекция графика на ось абсцисс, а область значений Е(у) — проекция графика на ось ординат (смотри рисунок).

г) словестный. Этот способ часто применяется в задачах, а точнее в описании их условия. Обычно этот способ заменяют одним из приведенных выше.

Функции y = f(х), xЄX, и y = g(х), xЄX, называются тождественно равными на подмножестве МСX, если для каждого x₀ЄМ справедливо равенство f(х₀) = g

(х₀).

График функции y = f(х) можно представить, как множество таких точек (х; f(х)) на координатной плоскости, где х — произвольная переменная, из D(f). Если f(х₀) = 0, где х₀ то точка с координатами (x₀; 0) — это точка, в которой график функции y = f(х) пересекается с осью Оx. Если 0ЄD(f), то точка (0; f(0)) — это точка, в которой график функции у = f(x) пересекается с осью Оу.

Число х₀ из D(f) функции y = f(х)  это нуль функции, тогда, когда f(х₀) = 0.

Промежуток МСD(f) это промежуток знакопостоянства функции y = f(х

), если либо для произвольного xЄМ верно f(х) > 0, либо для произвольного хЄМ верно f(х) < 0.

Есть приборы, которые вырисовывают графики зависимостей между величинами. Это барографы — приборы для фиксации зависимости атмосферного давления от времени, термографы — приборы для фиксации зависимости температуры от времени, кардиографы — приборы для графической регистрации деятельности сердца. У термографа есть барабан, он равномерно вращается. Бумаги, намотанной на барабан, касается самописец, который в зависимости от температуры поднимается и опускается и вырисовывает на бумаге определенную линию.

От представления функции формулой можно перейти к ее представлению таблицей и графиком.

При изучении математики очень важно понимать, что такое функция, ее области определения и значения. С помощью исследования функций на экстремум можно решить многие задачи по алгебре. Даже задачи по геометрии иногда сводятся к рассмотрению уравнений геометрических фигур на плоскости.

belmathematics.by

Что такое функция

 

Понятие функции – одно из основных в математике.

На уроках математики вы часто слышите это слово. Вы строите графики функций, занимаетесь исследованием функции, находите наибольшее или наименьшее значение функции. Но для понимания всех этих действий давайте определим, что такое функция.

Определение функции можно дать несколькими способами. Все они будут дополнять друг друга.

1. Функция – это зависимость одной переменной величины от другой. Другими словами, взаимосвязь между величинами.

Любой физический закон, любая формула отражает такую взаимосвязь величин. Например, формула – это зависимость давления жидкости от глубины .

Чем больше глубина, тем больше давление жидкости. Можно сказать, что давление жидкости является функцией от глубины, на которой его измеряют.

Знакомое вам обозначение как раз и выражает идею такой зависимости одной величины от другой. Величина у зависит от величины по определенному закону, или правилу, обозначаемому .

Другими словами: меняем (независимую переменную, или аргумент) – и по определенному правилу меняется .

Совсем необязательно обозначать переменные и . Например, – зависимость длины от температуры , то есть закон теплового расширения. Сама запись означает, что величина зависит от .

2. Можно дать и другое определение.

Функция – это определенное действие над переменной.

Это означает, что мы берем величину , делаем с ней определенное действие (например, возводим в квадрат или вычисляем ее логарифм) – и получаем величину .

В технической литературе встречается определение функции как устройства, на вход которого подается – а на выходе получается .

Итак, функция – это действие над переменной. В этом значении слово «функция» применяется и в областях, далеких от математики. Например, можно говорить о функциях мобильного телефона, о функциях головного мозга или функциях депутата. Во всех этих случаях речь идет именно о совершаемых действиях.

3. Дадим еще одно определение функции – то, что чаще всего встречается в учебниках.

Функция – это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один и только один элемент второго множества.

Например, функция каждому действительному числу ставит в соответствие число в два раза большее, чем .

Это соответствие можно изобразить так:

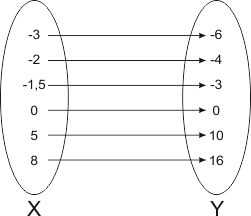
Повторим еще раз: каждому элементу множества по определенному правилу мы ставим в соответствие элемент множества . Множество называется

областью определения функции. Множество – областью значений.

Но зачем здесь такое длинное уточнение: «каждому элементу первого множества соответствует один и только один элемент второго»? Оказывается, что соответствия между множествами тоже бывают разные.

Рассмотрим в качестве примера соответствие между двумя множествами – гражданами России, у которых есть паспорта, и номерами их паспортов. Ясно, что это соответствие взаимно-однозначное – у каждого гражданина только один российский паспорт. И наоборот – по номеру паспорта можно найти человека.

В математике тоже есть такие взаимно-однозначные функции. Например, линейная функция . Каждому значению соответствует одно и только одно значение . И наоборот – зная , можно однозначно найти .

	-3	-2	-1	0	1	2
	-7	-4	-1	2	5	8

Могут быть и другие типы соответствий между множествами. Возьмем для примера компанию друзей и месяцы, в которые они родились:

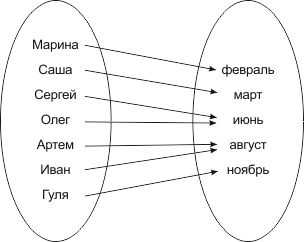
Каждый человек родился в какой-то определенный месяц. Но данное соответствие не является взаимно-однозначным. Например, в июне родились Сергей и Олег.

Пример такого соответствия в математике – функция . Один и тот же элемент второго множества соответствует двум разным элементам первого множества – и .

А каким должно быть соответствие между двумя множествами, чтобы оно не являлось функцией? Очень просто! Возьмем ту же компанию друзей и их хобби:

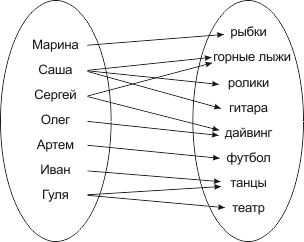
Мы видим, что в первом множестве есть элементы, которым соответствует два или три элемента из второго множества.

Очень сложно было бы описать такое соответствие математически, не правда ли?

Вот другой пример. На рисунках изображены кривые. Как вы думаете, какая из них является графиком функции, а какая – нет?

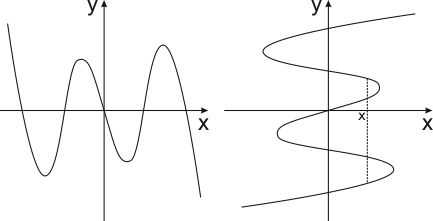
Ответ очевиден. Первая кривая – это график некоторой функции, а вторая – нет. Ведь на ней есть точки, где каждому значению соответствует не одно, а целых три значения .

Перечислим способы задания функции.

1. С помощью формулы. Это удобный и привычный для нас способ. Например:

, , , – примеры функций, заданных формулами.

2. Графический способ. Он является самым наглядным. На графике сразу видно все – возрастание и убывание функции, наибольшие и наименьшие значения, точки максимума и минимума. В следующей статье будет рассказано об исследовании функции с помощью графика.

К тому же не всегда легковывести точную формулу функции. Например, курс доллара (то есть зависимость стоимости доллара от времени) можно показать только на графике.

3. С помощью таблицы. С этого способа вы когда-то начинали изучение темы «Функция» — строили таблицу и только после этого – график. А при экспериментальном исследовании какой-либо новой закономерности, когда еще неизвестны ни формула, ни график, этот способ будет единственно возможным.

4. С помощью описания. Бывает, что на разных участках функция задается разными формулами. Известная вам функция задается описанием:

Звоните нам: (495) 984 09 27 Образовательная компания «МастерВУЗ».
Или нажмите на кнопку «Запишитесь в группу», чтобы заполнить контактную форму. Мы обязательно вам перезвоним.

Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России)                        +7 (495) 984-09-27 (бесплатный звонок по Москве)

Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.

ege-study.ru

Функция

Функция

График функции

Функция

Примеры функций

Простой пример функции

y = x + 5

Где здесь функция?

Игрек – это функция, икс – это аргумент функции, математический закон в данном примере состоит в том, что к иксу надо прибавить пять.

Как найти значение функции? Надо вместо аргумента, т.е. икса, подставить его значение и вычислить чему равен игрек.

Игрек и есть значение функции.

Итак, пусть икс = 5. Найдем значение функции, т.е. значение игрека: 5 + 5 = 10.

Значит значение функции при икс = 5 будет 10.

Пример функции.

Площадь квадрата равна квадрату стороны:

S = a²

Где здесь функция? S – это функция, «a» – это аргумент функции, математический закон в данном примере состоит в том, что «a» нужно возвести в квадрат.

Как найти значение функции?

Надо вместо аргумента, т.е. “а” подставить его значение и вычислить чему равена площадь S. S и есть значение функции.

Итак, пусть a = 5. Найдем значение функции, т.е. значение S. Имеем 5 * 5 = 25. Значит значение функции при a = 5 будет 25.

Составим небольшую таблицу соответствия значений “а” значениям площадей S:

Площадь S	0	1	4	9	16
Сторона a	0	1	2	3	4

Используя математический закон, в данном случае это возведение в квадрат, мы каждому значению длины стороны а поставили в соответствие значение площади S.

В нашем выражении

S = a²

S – это зависимая переменная или функция, ведь её значение зависит от значения длины стороны а;
длина стороны а – это независимая переменная или аргумент функции.

www.sbp-program.ru

Презентация к уроку по алгебре (9 класс) по теме: Что такое функция.

Графиком функции называют множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции.
Координатная плоскость
ось абсцисс
8
-8
Рис. 6
Рис. 7
1. Функция задана формулой
f(x)=-3x²+10
. Найдите: а)
f(-1)
;

б)
f(0)
; в)
f(
0,
3)
.
Приложение2

2. Известно, что
f(x)=-5x+6
. Найдите значение
x
, при котором:
а)
f(x)
=17; б)
f(x)
=-3; в)
f(x)
=0.
Приложение3.

3. На рис.16 построен график функции
y=g(x)
, где
D
есть [-6;5].
С помощью графика найдите:
а)
g(-4)
;
g(-1)
;
g(1)
;
g(5)
;
g(2)
.
б)
x
при котором
g(x)=4
;
g(x)=-4
;
g(x)=0
.

в)наибольшее и наименьшее зна-
чения функции.
г)область значений функции.
Приложение4.

ДОМАШНЕЕ ЗАДАНИЕ
: Выучить все опреде-
ления данной темы урока. Выполнить
№№3,8,20. Построить графики

любых

известных 3 функции МО
PowerPoint
.

Применим полученные знания.
Рис.16
y
x
0
1
5
1
-6
История вопроса
Понятие функции заложили в 17 веке французские учёные Франсуа Виет и Рене Декарт; они разработали единую буквенную символику. Введено было единое обозначение: неизвестных последними буквами латинского алфавита –
x
,
y
,
z
, известных – начальными буквами того же алфавита –
a
,
b
,
c
.
Все значения, которые принимает зависимая переменная,
образуют область значений функции.

На рис5. график функции
y=f(x)
, область определения
которой является промежу-
ток [-3;7].

Область значений функции
служит промежуток [-2;4].

С помощью графика можно
найти, например,

что
f(-3)=-2
.

Область значений функции
Y=f(x)
Рис. 5
Обратной пропорциональностью является зависимость силы
тока
I
на участке цепи от сопротивления проводника
R
при постоянном напряжении
U(
I
=
U/R
)
рис.
12
, зависимость времени
t
,
которое затрачивает равномерно движущееся тело

на путь
s
,
от скорости
v
(
t=s/v
) рис.
13

I
,А
R
,Ом
0
1
2
3
4
1
0,5
2
Рис.14
0
t
,час
s
,км
30
60
40
120
1
2
4
3
v=
120
/s
Рис.15
Что такое функция?
Что такое область определения функции?
Что такое область значений функции?
График функции и способы её задания!
Презентацию выполнила Пухальская Н.А.
Учитель математики МБОУ СОШ №14 имени А.Ф.Лебедева г. Томска

1. Сторона квадрата.
2.Числа 0, 1, 4, 9, 16, 25.
3.
x
.
4. 0, 2, 4, 6, 8, 10, 12. На 3 слайде все эти значения
,
будут
находиться в области
D
.

Переменную
x
называют независимой переменной или

аргументом.

Переменную
y
называют зависимой переменной, говорят
также, что переменная
y
является функцией от перемен-
ной
x
. Читают:

y
равно
f
от
x
, т.е.
Y=f(x)
.

Область определений функции
Например прямой пропорциональностью является зависимость

массы тела
m
от его объёма
V
при постоянной плотности
ρ
(
m=
ρ
V)

рис.10, зависимости длины окружности от её радиуса

R (C=2
π
R)
рис.11.
Функциями описываются многие реальные процессы
и закономерности
Рис. 11
R
Рис. 10
Вопрос. К какому номеру задания относится способ задания
функции: аналитический, табличный,описательный,графи-
ческий.
1. Определённой стороне квадрата соответствует единствен-
ная для её длины площадь.
Примеры функций
2
.
x
y
0
0
1
1
4
2
1
9
3
16
4
25
5

Y= 2x +0
,
3
3.
4.
T˚C
0
t
,
час
2
4
6
8
10
12
+5
+10
+15
-5
-10
-15
Рис. 2
Рис. 3
Рис. 4
График функции
Y=ax+b
пусть
a=-2
;
b
=3,

тогда
Y=-2x
+3

Y
X
2
4
6
-2
-4
-6
0
2
4
6
8
-2
-4
-6
-8
X
0
4
Y
3
-5
Рис. 9
Каждому значению
x
соответствует единственное значение
y
. Математическая запись
y=f(x)
.
Функцией называют такую зависимость переменной
y
от
x
, при которой каждому значению переменной
y
соответствует единственное значение переменной
x
.
D
E
x
4
x
2
x
1
y
1
y
2
y
3
y
4
x
2
Рис. 1
График функции
Y=X
²

Y
X
-2
-4
2
4
6
8
-6
-8
0
2
4
6
8
-2
-4
-6
-8

Y
X
9
-3
9
3
4
-2
4
2
1
-1
1
1
0
0
Рис. 8
Приложение1
.

nsportal.ru

АЛГЕБРА ФУНКЦИИ — это… Что такое АЛГЕБРА ФУНКЦИИ?

— полупростая коммутативная банахова алгебра А , реализованная в виде алгебры непрерывных функций на пространстве максимальных идеалов. Если и f — нек-рая функция, определенная на спектре элемента а(т. е. на множестве значений функции есть нек-рая функция на Условие конечно, не обязано выполняться. Если, однако, f — целая функция, то для любого Использование интегральной формулы Коши позволяет существенно усилить этот результат: если функция f регулярна в нек-рой окрестности спектра элемента а, то и отображение является гомоморфизмом А. ф., аналитических в нек-рой окрестности спектра элемента в алгебру Это утверждение остается справедливым и для неполупростых коммутативных банаховых алгебр. Кроме того, класс функций, аналитических в окрестности спектра данного элемента, может оказаться не расширяемым: напр., если спектр к-рых принадлежит отрезку аналитична в нек-рой окрестности этого отрезка.

В отдельных случаях элемент можно определить и для многозначных аналитпч. функций f, но это определение встречает естественные затруднения. Напр., пусть А — алгебра непрерывных функций в круге аналитических в круге н удовлетворяющих условию Единичный круг естественно отождествляется с пространством максимальных идеалов А. Непрерывная на пространстве максимальных идеалов функция не принадлежит алгебре А, но является решением квадратного уравнения

где

Если А — полупростая алгебра с пространством максимальных идеалов

(простой корень), то . Аналогично, если и то .

А. ф. наз. алгеброй с равномерной сходимостью, если норма в этой алгебре определяет сходимость, эквивалентную равномерной сходимости функций на пространстве максимальных идеалов. Если для всех — алгебра с равномерной сходимостью. Общим примером алгебры с равномерной сходимостью является замкнутая подалгебра в алгебре ограниченных непрерывных функций на некотором топологич. пространстве, наделенной естественной sup-нормой.

Если А — алгебра с равномерной сходимостью, и ее пространство максимальных идеалов метризуемо, то среди всех кольцевых границ (не только замкнутых) существует минимальная граница Г ₀, замыканием к-рой служит граница Шилова. Множество Г ₀ состоит из «точек пика»: наз. точкой пика, если существует такая функция что для всех В рассматриваемом случае для любой точки из пространства максимальных идеалов существует представляющая мера, сосредоточенная на

А. ф. наз. аналитической, если всякая функция из этой алгебры, равная нулю на непустом открытом подмножестве пространства максимальных идеалов, равна нулю тождественно. Аналогично определяются алгебры, аналитические относительно границы. Всякая аналитич. алгебра является аналитической относительно границы Шилова; обратное, вообще говоря, неверно.

А. ф. Аназ. регулярной, если для любого замкнутого множества Fв пространстве Xмаксимальных идеалов алгебры Аи любой не содержащейся в Fточки х ₀ найдется такая функция что для всех Всякая регулярная алгебра нормальна, т. е. для любой пары непересекающихся замкнутых множеств существует элемент такой, что для всех для всех Более того, в регулярной алгебре для любого конечного открытого покрытия пространства Xимеется разбиение единицы, принадлежащее А, т. е. система функций для к-рых

и

Функция gназ. локально принадлежащей А. ф. А, если для любой точки существует такая окрестность, в к-рой эта функция совпадает с нек-рой функцией из алгебры. Всякая функция, локально принадлежащая регулярной алгебре, сама является элементом этой алгебры.

Элемент А. ф. наз. вещественным, если вещественно при всех Если А — алгебра с вещественными образующими и

для всех то Арегулярна.

Идеал в банаховой алгебре наз. примарным, если он содержится только в одном максимальном идеале. Если А — регулярная А. ф., то в каждом максимальном идеале х ₀ имеется наименьший замкнутый примерный идеал к-рый содержится в любом замкнутом примерном идеале, содержащемся в х ₀ ; идеал есть замыкание идеала, образованного функциями , равными нулю в нек-рой (зависящей от f) окрестности точки

В алгебре абсолютно сходящихся интегралов Фурье с присоединенной единицей всякий максимальный идеал совпадает с соответствующим примарным идеалом.

Пусть А — замкнутая подалгебра алгебры где X- нек-рый компакт (не обязательно совпадающий с пространством максимальных идеалов алгебры А). Пусть Аразделяет точки компакта X,

т. е. для любых двух различных точек существует такая функция f из алгебры А, для к-рой АлгебраЛ наз. симметричной, если вместе с функцией f алгебре принадлежит и функция Согласно теореме Стоуна-Вейерштрасса, если Асимметрична, то Алгебра A наз. антисимметричной, если из условий следует, что — постоянная функция. Антисимметричными являются, в частности, алгебры аналитич. функций. Подмножество наз. множеством антисимметрии (относительно алгебры А), если любая функция вещественная на S, постоянна на этом множестве. Согласно этому определению алгебра Аантисимметрична, если все Xявляются множеством антисимметрии. В общем случае пространство Xможно представить в виде объединения непересекающихся замкнутых максимальных множеств антисимметрии. Каждое максимальное множество антисимметрии является пересечением множеств пика (множество Рназ. множеством пика, если существует такая функция что . Отсюда следует, что сужение А |_Y алгебры Ана максимальное множество антисимметрии есть замкнутая (антисимметричная) подалгебра алгебры Если Xесть пространство максимальных идеалов алгебры А, то максимальные множества антисимметрии связны. Если непрерывная функция такова, что на каждом максимальном множестве антисимметрии она совпадает с нек-рой функцией из алгебры А, то и сама эта функция принадлежит А. Это обобщение теоремы Стоуна- Вейерштрасса позволяет в принципе свести изучение произвольных алгебр с равномерной сходимостью к изучению антисимметричных алгебр А. Вместе с тем изучение произвольных алгебр Ане может быть сведено к аналитическим алгебрам: существует пример алгебры тина (замкнутой подалгебры алгебры ), не совпадающей с , антисимметричной и регулярной.

Пусть — вещественное пространство функций вида где если Re A -алгебра, или если Re A замкнуто в Пространство Xможно рассматривать как часть пространства максимальных идеалов алгебры А; поэтому на X можно рассматривать не только обычную топологию пространства максимальных идеалов, но и метрику, индуцированную вложением Xв пространство, сопряженное А. Расстояние в смысле этой метрики обозначим Для любых точек имеет место неравенство отношение является отношением эквивалентности, и классы эквивалентности наз. долями Глисона. Если X — круг и A- замкнутая подалгебра в С (X), состоящая из аналитических при функций, то метрика неевклидова, а долями Глисона служат одноточечные множества на границе и внутренность круга. Доли Глисона не всегда обладают аналитич. структурой: любое s-компактное вполне регулярное пространство гомеоморфно доле Глисона пространства максимальных идеалов нек-рой алгебры, такой, что сужение алгебры на эту долю содержит всякую ограниченную непрерывную функцию. Принадлежность двух точек к одной и той же доле Глисона может быть охарактеризована в терминах представляющих мер на границе Шилова: такие две точки обладают взаимно абсолютно непрерывными представляющими мерами с ограниченными производными. Алгебра, для к-рой плотно в наз. алгеброй Дирихле; если Р- доля Глисона в пространстве максимальных идеалов алгебры Дирихле, состоящая более, чем из одной точки, то существует такое непрерывное взаимно однозначное отображение круга на Р, что для любой функции функция аналитична при Таким образом, Робладает структурой, относительно к-рой функции аналитичны; отображение вообще говоря, не является гомеоморфизмом, если Рснабжено обычной топологией пространства максимальных идеалов, но является гомеоморфизмом, если снабдить Рметрикой

Лит. см. при статье Банахова алгебра. Е. А. Горин.

Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.

dic.academic.ru