Изготовьте математический маятник: Изготовьте математический маятник длиной рассчитанной в контрольном вопросе 1….

Содержание

Математический маятник — урок. Физика, 9 класс.

Математическим маятником называют материальную точку (тело небольших размеров), подвешенную на тонкой невесомой нерастяжимой нити или на невесомом стержне.

В положении равновесия сила тяжести и сила упругости нити уравновешивают друг друга, и материальная точка находится в покое.

При отклонении материальной точки от положения равновесия на малый угол α на тело будет действовать возвращающая сила $F$, которая является тангенциальной составляющей силы тяжести:

F=mgsinα.

Далее материальная точка проходит по инерции положение равновесия и, двигаясь далее, сбавляет скорость. В крайнем положении материальная точка останавливается и затем начинает двигаться в обратном направлении.

Период малых собственных колебаний математического маятника длины $l$, неподвижно подвешенного в однородном поле тяжести с ускорением свободного падения $g$, равен

T=2πlg.

Обрати внимание!

Период колебаний математического маятника не зависит от амплитуды колебаний и массы груза.

Наиболее известным практическим использованием маятника является применение его в часах для измерения времени. Впервые это сделал голландский физик X. Гюйгенс.

Поскольку период колебаний маятника зависит от ускорения свободного падения $g$, то часы, которые идут верно в Москве, будут идти вперёд в Ленинграде. Чтобы эти часы шли верно в Ленинграде, приведённую длину их маятника нужно увеличить.

В геологии маятник применяют для опытного определения числового значения ускорения свободного падения $g$ в разных точках земной поверхности. Для этого по достаточно большому числу колебаний маятника в том месте, где измеряют $g$, находят период его колебаний, а затем вычисляют ускорение свободного падения, выразив его из формулы периода маятника.

Заметное отклонение величины $g$ от нормы для какой-либо местности называют гравитационной аномалией.

Определение аномалий помогает находить залежи полезных ископаемых.

Опыт показывает, что качающийся маятник сохраняет плоскость, в которой происходят его колебания. Это означает, что если привести в движение маятник, установленный на диске центробежной машины, а диск заставить вращаться, то плоскость качания маятника относительно комнаты изменяться не будет. Это позволяет с помощью опыта обнаружить вращение Земли вокруг своей оси.

В $1850$ г. Ж. Фуко подвесил маятник под куполом высокого здания так, что острие маятника при качании оставляло след на песке, насыпанном на полу. Оказалось, что при каждом качании острие оставляет на песке новый след. Таким образом, опыт Фуко показал, что Земля вращается вокруг своей оси. В условиях вращения Земли при достаточно большой нити подвеса плоскость, в которой маятник совершает колебания, медленно поворачивается относительно земной поверхности в сторону, противоположную направлению вращения Земли.

Любое тело, насаженное на горизонтальную ось вращения, способно совершать в поле тяготения свободные колебания и, следовательно, также является маятником. Такой маятник принято называть физическим.

Обрати внимание!

Физический маятник отличается от математического только распределением масс.

В положении устойчивого равновесия центр масс $C$ физического маятника находится ниже оси вращения $O$ на вертикали, проходящей через ось. При отклонении маятника на угол $φ$ возникает момент силы тяжести, стремящийся возвратить маятник в положение равновесия:

M=−mgsinϕd.

Здесь $d$ — расстояние между осью вращения и центром масс $C$. Знак «минус» в этой формуле означает, что момент сил стремится повернуть маятник в направлении, противоположном его отклонению из положения равновесия.

Источники:

Физика. 9 кл.: учебник / Перышкин А. В., Гутник Е. М. — М.: Дрофа, 2014. — 319 с.
www.ru.wikipedia.org

www.ru.solverbook.com

www.lib.sernam.ru

www.bourabai.ru

Математический маятник: задачи среднего уровня

Рассмотрим задачи среднего уровня, связанные с колебаниями тела на нити – то есть с математическим маятником. Навык решения задач – основной навык, который гарантирует высокие баллы на ЕГЭ.

Математический маятник

Задача 1. Один математический маятник имеет период Т_1 =3 с. ‚ другой – с. Каков период колебаний математического маятника, длина которого равна сумме длин данных маятников

Запишем периоды колебаний обоих маятников:

$T_1=2 \pi \sqrt{\frac{l_1}{g}}$

$T_2=2 \pi \sqrt{\frac{l_2}{g}}$

Возведем в квадрат оба уравнения:

$T_1^2=4\pi^2 \frac{l_1}{g}$

$T_2^2=4 \pi^2 \frac{l_2}{g}$

Выразим длины нитей обоих маятников:

$l_1=\frac{ gT_1^2}{4\pi^2 }$

$l_2=\frac{ gT_2^2}{4\pi^2 }$

Сложим длины нитей:

$l_1+ l_2=\frac{ g(T_1^2+T_2^2)}{4\pi^2 }$

Определим период маятника с такой длиной нити:

$T=2 \pi \sqrt{\frac{l_1+l_2}{g}}=2 \pi \sqrt{\frac{ T_1^2+T_2^2}{4\pi^2 }}=\sqrt{ T_1^2+T_2^2}$

Ответ: $T=\sqrt{ T_1^2+T_2^2}$
Задача 2. Математический маятник подвешен вблизи вертикальной стены и колеблется в плоскости, параллельной стене. В стену вбит гвоздь так, что середина нити маятника наталкивается на него каждый раз, когда маятник проходит положение равновесия справа налево (рис.). Найти длину нити, если период колебаний такого маятника (с помехой в виде гвоздя) с.

К задаче 2

Период колебаний такого маятника состоит из двух частей: одна часть, соответствующая длине нити , и вторая, соответствующая длине нити $\frac{l}{2}$ .

Тогда

$T_1=2 \pi \sqrt{\frac{l}{g}}$

$T_2=2 \pi \sqrt{\frac{l}{2g}}$

Период равен

$T=\frac{T_1}{2}+\frac{T_2}{2}=\pi \sqrt{\frac{l}{g}}+\pi \sqrt{\frac{l}{2g}}=\pi \sqrt{\frac{l}{g}}\left(1+\frac{1}{\sqrt{2}}\right)$

Чтобы найти длину нити, возведем в квадрат период:

$T^2=\pi^2\frac{l}{g}\left(1+\frac{1}{\sqrt{2}}\right)^2$

«Вытащим» :

$l=\frac{gT^2}{\pi^2\left(1+\frac{1}{\sqrt{2}}\right)^2}$

Немного «причешем»:

$l=\frac{gT^2}{\pi^2\left(1+\frac{2}{\sqrt{2}}+\frac{1}{2}\right)}$

Домножим на 2 числитель и знаменатель:

$l=\frac{2gT^2}{\pi^2\left(2+\frac{4}{\sqrt{2}}+1\right)}$

$l=\frac{2gT^2}{\pi^2\left(3+2\sqrt{2}\right)}$

Ответ: $l=\frac{2gT^2}{\pi^2\left(3+2\sqrt{2}\right)}$
Задача 3. Шарик подвешен на длинной нити. Первый раз его поднимают по вертикали до точки подвеса, второй раз отклоняют на небольшой угол. В каком из этих случаев шарик быстрее возвратится к начальному положению?

Если шарик висел на нити длиной и его подняли на высоту , то, когда он будет отпущен, он упадет за время t_1 согласно формулам кинематики:

$t_1=\sqrt{\frac{2l}{g}}$

Если шарик отклонить, то для возвращения ему потребуется полпериода:

$t_2=\frac{T}{2}=\pi\sqrt{\frac{l}{g}}$

Понятно, что число $\pi$ больше, чем $\sqrt{2}$ .

Задача 4. Два математических маятника начинают колебаться одновременно. Когда первый маятник совершил полных колебаний, второй совершил только N_2=10 полных колебаний. Какова длина l_1 первого маятника, если длина второго l_2= 4 м?

Так как второй маятник успевает выполнить вдвое меньше колебаний, то, следовательно, период этих колебаний вдвое больше, чем у первого маятника:

. Вычислим отношение периодов:

$\frac{T_2}{T_1}=\sqrt{\frac{l_2}{l_1}}$

По условию, отношение периодов равно 2:

$\sqrt{\frac{l_2}{l_1}}=2$

$\frac{l_2}{l_1}=4$

Если l_2=4 , то l_1=1

Ответ: l_1=1 м.
Задача 5. Маятниковые часы за t = 1 сут отстают на 1 час. Что нужно сделать с маятником, чтобы они шли верно?

Если часы отстают на 1 час, то, следовательно, то количество качаний, которые эти часы должны выполнять за 24 часа, они выполняют за 23 часа. Пусть это количество качаний . Найдем положенный период и фактический:

$T=\frac{24}{N}$

$T_{fakt}=\frac{23}{N}$

Отношение периодов маятников

$\frac{T_{fakt}}{T}=\sqrt{\frac{l_{fakt}}{l}}=\frac{23}{24}$

Тогда, возводя в квадрат, получим:

$\frac{l_{fakt}}{l}=\frac{23^2}{24^2}$

$l_{fakt}=\frac{529}{576}l=0,918l$

То есть фактическая длина меньше, чем надо, следовательно, нить маятника нужно удлинить на 0,082l .

Математические маятники: задачки посложнее

В задачах этой статьи мы столкнемся с необходимостью вспомнить формулу ускорения свободного падения, наши маятники будут подниматься в лифтах и скатываться по наклонным плоскостям.

Математический маятник

Задача 1. Одно из самых высоких мест на Земле, где постоянно проживают люди, находится на высоте h= 5200 м над уровнем моря. На сколько будут уходить за сутки маятниковые часы, выверенные на этой высоте, если их перенести на уровень моря? Радиус Земли известен.
Можно установить, на сколько будут уходить часы, если сопоставить два периода: период маятника фактический (на фактической высоте в h= 5200 м над уровнем моря) и период, каким бы он был, спусти мы этот маятник с гор на уровень моря.

Период фактический:

$T=2\pi \sqrt{\frac {l}{g_h}}$

$T^2=4\pi ^2\frac {l}{g_h}$

Откуда

$g_h=\frac{4\pi ^2 l }{T_h^2}$

Тогда на уровне моря у маятника был бы период , и

$g=\frac{4\pi ^2 l }{T^2}$

То есть

$\frac{g_h}{g}=\frac{T^2}{T_h^2}$

А так как ускорение свободного падения зависит от высоты над уровнем моря, то можно записать, что

$\frac{g_h}{g}=\left(\frac{T}{T_h}\right)^2=\left(\frac{R_Z}{R_Z+h}\right)^2$

Тогда

$\frac{T}{T_h}=\frac{R_Z}{R_Z+h}$

Или

$T=T_h\cdot \frac{R_Z}{R_Z+h}$

Когда маятник был на вершине, он совершал колебаний в сутки, и получалось, что nT_h=24 часа.

Теперь, на уровне моря, колебаний уже не есть 24 часа, поэтому маятник уйдет на определенное время, равное nT_h-nT :

$\Delta t=86400-86400\cdot \frac{T}{T_h}=86400-86400\cdot\frac{R_Z}{R_Z+h}=\frac{86400h}{R_Z+h}=\frac{86400\cdot5200}{6400000+5200}=70$

Ответ: 70 с
Задача 2. Какую длину должен иметь маятник Фуко, если представить себе, что он установлен на планете, плотность которой равна плотности Земли, а радиус в 2 раза меньше? Маятник совершает три колебания в минуту.

Период маятника равен T=20 с. По периоду можно установить длину такого маятника, если известно ускорение свободного падения. Но на планете с радиусом меньшим, чем земной, ускорение будет равно

$g_1=G\cdot \frac{M_1}{R_1^2}= G\cdot \frac{\frac{4\pi R^3\rho}{3}}{8\frac{R^2}{4}}=G\cdot \frac{M}{2R^2}=\frac{g}{2}$

Тогда длина маятника равна

$T=2\pi \sqrt{\frac {l}{g_1}}$

$T^2=4\pi ^2\frac {l}{\frac{g}{2}}$

$l=\frac{T^2g}{8\pi^2}=\frac{4000}{8 \cdot3,14^2}=50,7$

Ответ: T=50,7 м.

Задача 3. Вблизи рудного месторождения период колебаний маятника изменился на $\eta= 0,1$ % . Плотность руды в месторождении $\rho = 8$ г/см. Оценить радиус месторождения R_1 , если средняя плотность Земли $\rho_z = 5,6$ г/см.

Очевидно, что в районе месторождения средняя плотность породы больше, следовательно, больше и ускорение свободного падения, ведь оно прямо зависит от плотности:

$g=G\frac{M}{R^2}= G\frac{\rho_z V}{R^2}$

Поскольку зависимость периода математического маятника от ускорения свободного падения обратная: $T=2\pi \sqrt{\frac{l}{g}}$ , то очевидно, что период с увеличением плотности уменьшается. Тогда можно записать период маятника вдали от месторождения:

$T=2\pi \sqrt{\frac{l}{g}}$

Период маятника вблизи месторождения:

$T_1=2\pi \sqrt{\frac{l}{g_1}}$

Отношение периодов:

$\frac{T}{T_1}=\sqrt{\frac{g_1}{g}}$

$\left(\frac{T}{T_1}\right)^2=\frac{g_1}{g}$

С другой стороны, так как период уменьшился вблизи месторождения, то

$\frac{T_1}{T}=1- \eta$

То есть

$\frac{T}{T_1}=\frac{1}{1- \eta}$

$\left(\frac{T}{T_1}\right)^2=\left(\frac{1}{1- \eta}\right)^2$

$\frac{g_1}{g}=\left(\frac{1}{1- \eta}\right)^2$

Теперь нужно записать ускорение свободного падения и его изменение в районе месторождения:

$g=G\frac{M}{R^2}= G\frac{\rho V}{R^2}= G\frac{\rho 4 \pi R^3\rho_z}{3R^2}= G\frac{4 \pi R\rho_z}{3}$

А в районе месторождения

$g_1= G\frac{4 \pi R_1\rho}{3}$

Теперь вычтем из последнего равенство предыдущее:

$g_1-g= G\frac{4 \pi R_1(\rho-\rho_z)}{3}$

И разделим на :

$\frac{g_1-g}{g}= \frac{G\frac{4 \pi R_1(\rho-\rho_z)}{3}}{ G\frac{4 \pi R\rho_z}{3}}$

$\frac{g_1}{g}-1=\frac{R_1}{R}\frac{\rho-\rho_z }{\rho_z }$

$\frac{g_1}{g}=\frac{R_1}{R}\frac{\rho-\rho_z }{\rho_z }+1$

Подставим отношение ускорений:

$\left(\frac{1}{1- \eta}\right)^2=\frac{R_1}{R}\frac{\rho-\rho_z }{\rho_z }+1$

Выразим радиус месторождения:

$R_1=\frac{1-(1-\eta)^2}{(1-\eta)^2}\cdot \frac{R\rho_z }{\rho- \rho_z }$

$R_1=\frac{2\eta -\eta^2}{(1-\eta)^2}\cdot \frac{R\rho_z }{\rho- \rho_z }$

В числителе можно пренебречь величиной $\eta^2$ , в знаменателе $1-2\eta+\eta^2$ можно $\eta^2-2\eta$ можно приближенно заменить на $-\eta$ , получим:

$R_1=\frac{2\eta}{1-\eta}\cdot \frac{R\rho_z }{\rho- \rho_z }$

Подставим числа и рассчитаем радиус месторождения. При этом радиус земли подставим в км, при этом результат тоже получится в км, а плотности можно подставить в любых единицах – эти единицы сократятся при делении:

$R_1=\frac{2\cdot 0,001}{1-0,001}\cdot \frac{6400\cdot 5,6 }{8- 5,6 }=29,9$

Ответ: радиус месторождения около 30 км.

Задача 4. Один конец нити прикреплен к потолку лифта, а на другом укреплен груз пренебрежимо малого размера. Лифт начинает опускаться с ускорением а=0,81 м/с. Каков период малых колебаний груза, если длина нити l= 1 м?

Так как лифт спускается с ускорением, то в формулу для вычисления периода нужно подставить не ускорение свободного падения, а то результирующее ускорение, которое действует на груз, а именно a_1=g-a :

$T=2 \pi \sqrt{\frac{l}{a_1}}=2 \pi \sqrt{\frac{l}{g-a}}=2 \pi \sqrt{\frac{1}{9,81-0,81}}=\frac{2 \pi}{3}=2,09$

Ответ: T=2,09 с

Математический маятник, формулы и примеры

Определения и формулы математического маятника

Рис.1. Математический маятник

Математический маятник – это модель системы, совершающей гармонические колебания. Свободные колебания математического маятника при малых углах отклонения описываются уравнением гармонических колебаний.

В положении равновесия сила тяжести и сила упругости нити уравновешивают друг друга, и материальная точка находится в покое. При отклонении материальной точки от положения равновесия на малый угол на тело будет действовать возвращающая сила , которая является тангенциальной составляющей силы тяжести:

Эта сила сообщает материальной точке тангенциальное ускорение, направленное по касательной к траектории, и материальная точка начинает двигаться к положению равновесия с возрастающей скоростью. По мере приближения к положению равновесия возвращающая сила, а следовательно, и тангенциальное ускорение точки, уменьшаются. В момент прохождения положения равновесия угол отклонения , тангенциальное ускорение также равно нулю, а скорость материальной точки максимальна. Далее материальная точка проходит по инерции положение равновесия и, двигаясь в направлении, противоположном силе , сбавляет скорость. В крайнем положении материальная точка останавливается, и затем начинает двигаться в обратном направлении.

Период колебаний математического маятника

Период колебаний математического маятника не зависит от массы груза и амплитуды колебаний.

Примеры решения задач

Понравился сайт? Расскажи друзьям!

Маятники: задачи посложнее

В статье предложены задачи немного сложнее, чем вводные задачи на определение периодов математического и пружинного маятников. Также придется вспомнить, как раскладывать вектора на проекции и кинематические формулы.

Задача 1. В ракете помещены математический и пружинный маятники с одинаковым периодом колебаний Т= 1 с. Ракета начинает движение вертикально вверх с ускорением a=10g . На выcоте H= 50 км двигатель выключается и ракета продолжает подниматься по инерции. Сколько колебаний сделает каждый маятник за время работы двигателя ракеты и за все время подъема? Сопротивлением воздуха и уменьшением силы земного тяготения с высотой пренебречь.

Сначала разберемся с ракетой. Сколько времени ей потребовалось на подъем до 50 км? Как высоко она вообще забралась? Сколько времени длился подъем? Давайте выясним.

Ракета движется равноускоренно в течение времени , с нулевой начальной скоростью, и преодолевает 50 км:

$H=\frac{at^2}{2}$

$t^2=\frac{2H}{a}$

$t=\sqrt{\frac{2H}{a}}$

За это время скорость ракеты все время растет и к моменту выключения двигателя она равна

$\upsilon=at$

Теперь полет равнозамедленный, ускорение тянет ракету к земле, поэтому скорость ее будет постепенно уменьшаться, пока не станет равной нулю в наивысшей точке полета через время t_1 :

$\upsilon-gt_1=0$

$t_1=\frac{\upsilon }{g}=\frac{at}{g}=10t$

То есть общее время полета – 11t . Теперь давайте с маятниками разбираться. Сначала пружинный, так как ему все равно, с каким ускорением двигалась ракета – его период от этого не зависит:

$T_{pr}=2\pi \sqrt{\frac{m}{k}}$

Поэтому за время работы двигателя он сделает $N_{1pr}$ колебаний, а когда двигатель отключится – $N_{2pr}$ колебаний:

$N_{1pr}=\frac{t}{T}=\sqrt{\frac{2H}{aT^2}}$

$N_{2pr}=\frac{10t}{T}=\sqrt{\frac{200H}{aT^2}}$

Всего за время подъема

$N_{1pr}+ N_{2pr}=\frac{t}{T}+\frac{10t}{T}=\frac{11t}{T}=\sqrt{\frac{242H}{aT^2}}=\sqrt{\frac{242H}{10gT^2}}$

Подставим числа:

$N_{1pr}=\sqrt{\frac{2\cdot50000}{10 \cdot 9,8}}=10\sqrt{10}=31,9$

$N_{1pr}+ N_{2pr}=\sqrt{\frac{242\cdot50000}{98,1}}=11\sqrt{1020}=351,4$

Теперь посмотрим, как колебался математический маятник.

Его период зависит от ускорения, которое воздействует на маятник:

$T_{mat}=2\pi \sqrt{\frac{l}{a}}$

На участке подъема, где двигатель работал, на маятник действовало ускорение 10g+g , следовательно, его период колебаний уменьшился в $\sqrt{11}$ раз, тогда

$N_{1mat}=\frac{t}{T_1}=\sqrt{\frac{2H}{aT_1^2}}=\sqrt{\frac{22H}{aT^2}}$

Потом, когда двигатель отключился, на маятник ускорение не действовало, так как ракета просто падает, неважно, что у нее есть определенная скорость, пусть даже и большая. Тогда период маятника станет равным бесконечности, следовательно,

$N_{2mat}=0$

$N_{1mat}=\sqrt{\frac{22\cdot50000}{98,1}}=106$

Получается, что

$N_{1mat}+ N_{2mat}=106$

Ответ: $N_{1pr}=32$ , $N_{1pr}+ N_{2pr}=351$ , $N_{1mat}=106$ , $N_{1mat}+ N_{2mat}=106$ .
Задача 2. Математический маятник длиной l= 1 м подвешен в вагоне, движущемся горизонтально с ускорением a = 6 м/с. Найти период колебаний этого маятника. Какой угол составляет линия отвеса маятника с вертикалью в движущемся вагоне при отсутствии колебаний?

На маятник будет воздействовать ускорение, являющееся суммой $\vec{a}$ и $\vec{g}$ :

$a_1=\sqrt{a^2+g^2}$

Период колебаний такого маятника равен

$T=2 \pi \sqrt{\frac{l}{a_1}}=2 \pi \sqrt{\frac{l}{\sqrt{a^2+g^2}}}$

$T=2 \cdot (3,14) \sqrt{\frac{1}{\sqrt{6^2+10^2}}}=1,84$

Линия отвеса тоже поменяет положение, отклонившись от вертикали на угол:

$\alpha=\operatorname{arctg}\frac{a}{g}=\operatorname{arctg}0,6=31^{\circ}$

Ответ: T=1,84 с, $\alpha=31^{\circ}$ .
Задача 3. Математический маятник укреплен на тележке. Его период колебаний Т = 1 с. Тележка скатывается (без трения) с наклонной плоскости, образующей угол $\alpha =30^{\circ}$ с горизонтом. Найти период колебаний маятника во время скатывания тележки.

Так как тележка скатывается вниз с ускорением, то на маятник будет воздействовать уже не полное ускорение , а только его проекция – $g \cos{\alpha}$ .

Когда тележка была неподвижна, период маятника был равен

$T=2 \pi \sqrt{\frac{l}{g}}$

Но, когда тележка покатилась вниз, период стал равен

$T_1=2 \pi \sqrt{\frac{l}{ g \cos{\alpha}}}$

Поэтому, разделив одно выражение на другое, получим:

$\frac{T_1}{T}=\sqrt{\frac{1}{\cos{\alpha}}}$

$T_1= \frac{T}{\sqrt {\cos{\alpha}}}$

Ответ: $T_1= \frac{T}{\sqrt {\cos{\alpha}}}$

Исследование гармонических колебаний. Изготовление лабораторной работы

Гунько Н.Е. 1

1МАОУ СОШ № 15 г. Челябинска

Васильева И.В. 1

1МАОУ «СОШ № 15 г. Челябинска»

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

Введение

Интерес к теме гармонических колебаний появился у меня после того, как я наблюдал за часами, находясь в гостях у бабушки. У нее на стене висят большие механические часы с маятником. Мне стало интересно почему так равномерно двигается маятник, каждый час издавая бой. В интернете я нашел историю возникновения таких часов. Оказалось, что первым подумал об использовании маятника в часах великий ученый Галилео.

В 1583 году в Пизанском соборе любознательный юноша по имени Галилео Галилей (тогда ему было 12 лет) не столько слушал проповедь, сколько любовался движением люстр. Наблюдения за светильниками показались ему интересными и, когда он вернулся домой, изготовил опытную установку для исследования колебаний маятников. Она состояла из свинцовых шариков, укрепленных на тонких нитях. Время он засекал с помощью своего пульса.

Так при помощи своих экспериментов он открыл законы колебания маятника, которые сегодня изучают в каждой школе. Но Галилей в то время был слишком молод, чтобы думать о внедрении в жизнь своего изобретения. И только в конце жизни его осенило — приставить к маятнику счетчик колебаний, — в результате чего могут получиться часы. Но ученый смог сделать только чертеж часов.

Первые часы, с маятником были изготовлены в 1656 году, Христианам Гюйгенсом. Часы дали прекрасный результат и с тех времён в большие часы стали устанавливать маятник. Изобретению часов с маятником мы обязаны голландцу, Христиану Гюйгенсу, математику, астроному и физику.

На основании полученных данных нами была сформулирована следующая цель исследования: изучение понятия математического маятника и создание лабораторной работы для школьников.

Для достижения цели были поставлены следующие задачи:

Изучить понятие математического маятника и гармонических колебаний;

Изучить основные характеристики математического маятника;

Создать образец математического маятника

Изготовить и описать лабораторную работу с математическим маятником.

Предметом моего исследования является математический маятник, а объектом – гармонические колебания.

Глава 1. Теоретическая часть

Математический маятник

Математический маятник — это материальная точка, подвешенная на длинной невесомой нерастяжимой нити (Рис 1.)

Маятник будет считаться математическим, если длинна его нити, во много раз больше, чем размер подвешенного на нее тела. Также учитывается то, что по сравнению с массой тела, нить имеет ничтожно малую массу.

Рис. 1. Математический маятник

Математический маятник так же называют нитяным, так как тело подвешивается на нить.

Математический маятник использовали многие выдающиеся ученые прошлого, начиная с античности, в частности Архимед, Аристотель, Платон, Плутарх. Так Архимед и вовсе использовал математический маятник во всех своих вычислениях, а некоторые люди даже верили, что маятник может влиять на судьбы людей и пытались делать с его помощью предсказания будущего. [1]

Галилео первый убедился, что математический маятник может служить для измерения времени. если бы он поддерживался в своем движении колесным механизмом и, в свою очередь, регулирующее влиял бы на эти колесики. Первые часы, с маятником были изготовлены в 1656 году, Христианам Гюйгенсом. Часы дали прекрасный результат и с тех времён в большие часы стали устанавливать маятник. Изобретению часов с маятником мы обязаны голландцу, Христиану Гюйгенсу, математику, астроному и физику (1629 г.-1695 г.). [2]

Математический маятник описывает гармонические колебания — колебания, при которых физическая величина изменяется с течением времени по гармоническому (синусоидальному или косинусоидальному) закону.

Основные характеристики математического маятника

К основным характеристикам математического маятника относятся:

1.Амплитуда колебания — это наибольшее смещение колеблющегося тела от положения равновесия (Рис. 2).

Рис. 2. Амплитуда колебаний

2.Частота колебаний — это количество колебаний в единицу времени.

3.Период – это время одного полного колебания.

Кроме этого, период математического маятника можно рассчитать. Он рассчитывается по следующей формуле: , где

L – длина нити математического маятника

g – ускорение свободного падения

π – число Пи.

В процессе своих исследований древний ученый Галилей подвешивал различные предметы к потолку, а время считал, замеряя свой пульс. Галилей убедился, что легкие предметы качаются так же часто, как и тяжелые, если они висят на нитках одинаковой длины. А зависят качания только от длины нити: чем нитка длиннее, тем реже качается маятник, а чем короче, тем качания чаще. Частота качаний зависит только от длины маятника, а не от его веса

. В результате своих опытов Галилей убедился, что время одного качания заметным образом не меняется — оно остается одинаковым.

Применение математических маятников в повседневной жизни

Проанализировав разные источники литературы, мной был сделан вывод, что математический маятник нашел свое применение в геологоразведке и при отсчёте времени (часах). Таким образом, мной была составлена следующая схема применения математического маятника в повседневной жизни, которая представлена на рис. 3.

Математический маятник
Геологоразведка	Часы
С его помощью ищут полезные ископаемые. Получается так, что ускорение свободного падения изменяется с географической широтой, зависит это от плотности земной кары. В разных местах нашей планеты плотность неравномерная и там, где залегают породы с большей плотностью, ускорение будет чуть-чуть больше. Например, руда и каменный уголь имеют большую плотность по сравнению с другими полезными ископаемыми, поэтому именно их можно отыскать в глубинах земли. Для этого подсчитывается количество колебаний маятника на разных участках земли, там, где их больше и есть залежи полезных ископаемых.	Маятник работает путём преобразования кинетической энергии в потенциальную и обратно. Когда маятник находится в крайнем положении он имеет максимальную накопленную энергию (потенциальную энергию). В самой нижней точке, максимально близкой к земле потенциальная энергия переходит в кинетическую и имеет её максимальное значение в этой точке. Таким образом, маятник постоянно переводит потенциальную и кинетическую энергии друг в друга, что является примером простого гармонического колебания.
Раньше с маятником в руках искали воду, а сейчас ведут поиск затонувших кораблей и мест скопления рыбы. Знаменитый экстрасенс Ури Геллер свой первый миллион долларов заработал, летая на самолёте на малой высоте над непроходимыми джунглями Бразилии, с маятником в руках. Он искал нефть, и нашёл.	Если бы трение соприкасающихся элементов и сопротивление среды(воздуха) отсутствовало, то есть были созданы идеальные условия, то маятник бы совершал колебания вечно. Но в реальных условиях маятник учитывая вышеперечисленные факторы замедляется. Но что является очень важным для хронометража, даже при уменьшении амплитуды колебания время колебания маятника не изменяется.

Рис. 3. Применение математического маятника в повседневной жизни

Глава 2. Практическая часть

2.1. Описание установки

Для демонстрации работы математического маятника мной была сделана установка. Установка представлена на рисунке (Приложение А).

Для её создания мне понадобились следующие материалы: доска, колесики, железный кронштейн, рейки, конус, нить и песок.

Сборка установки:

Подвижная поверхность на колесиках размером 15,5х90 см (Приложение Б).

Данная поверхность была вырезана из необходимого размера из доски. Для обеспечения её подвижности к нижней части прикручены четыре колеса.

Вертикальная стойка размером 45,5х22х45,5 см (Приложение В).

Данная стойка является отдельным элементом установки. Для её создания были использованы деревянные рейки, которые скреплены между собой и представляют П-образную фигуру.

Подвесной механизм, который состоит из кронштейна, нити и груза

Данный механизм крепится посередине вертикальной стойки.

Кронштейн 9,5 см

Нить длиной 32,5 см

Груз- конус с отверстием внизу (Приложение Г)

2.2. Выполнение работы

Цель работы: вычислить основные характеристики математического маятника.

Оборудование: собственная установка с математическим маятником; телефон или секундомер; линейка.

Ход работы:

1.Насыпать в конус песок;

2.Установить конус в начальное положение;

3.Отклонить конус на небольшое расстояние и отпустить, чтоб он совершал колебания.

4. Во время колебаний необходимо двигать равномерно подвижную поверхность.

5. Включить секундомер и считайте количество полных 5 колебаний;

6. На доске песок нарисует плавную синусоиду, которую мы будем исследовать.

Определите по песочному рисунку амплитуду;

Зафиксируйте время полных трех колебаний;

Вычислите период, разделив время на количество колебаний;

Вычислите частоту, разделив единицу на период.

7. Повторите исследования с другой амплитудой (Приложение Д).

8. Запишите полученные данные в таблицу 1.

Таблица 1

Исследование гармонических колебаний

№	Амплитуда	Время, с	Количество колебаний	Период, с	Частота, Гц
1	6,5	3,46	3	1,15	0,87
2	7	6,05	5	1,21	0,82
3	6,75	9,53	8	1,19	0,84

Вывод: измерили основные характеристики математического маятника.

Заключение

На основании полученных данных нами была достигнута следующая цель исследования: изучили понятия математического маятника и создали лабораторную работу для школьников.

Для достижения цели были выполнены следующие задачи:

Изучили понятие математического маятника и гармонических колебаний;

Изучили основные характеристики математического маятника;

Создали образец математического маятника

Изготовили и описали лабораторную работу с математическим маятником.

Целью исследовательской работы было, доказать, что возможно сделать и испытать маятник, близкий по своим характеристикам к математическому маятнику, в домашних условиях.

И еще одно обстоятельство, на которое хотелось бы обратить внимание, это то, что несмотря на свою простоту, математический маятник связан с рядом интересных фактов их применения: геологоразведка; часовые механизмы.

В заключении можно сказать, что изготовление собственными руками устройства несет минимальные денежные затраты и приносит огромную моральную удовлетворенность как в самом процессе изготовления, так и в процессе воспроизведения.

Список литературы

1.https://foxford.ru/wiki/fizika/matematicheskiy-mayatnik

2.https://history.wikireading.ru/415480

3.https://mywatch.ru/articles/art_305.html

4.https://fb.ru/article/148323/matematicheskiy-mayatnik-period-uskorenie-i-formulyi

Приложение А

Рис. 1. Установка

Приложение Б

Рис. 2. Подвижная поверхность

Приложение В

Рис. 3. Вертикальная стойка

Приложение Г

Рис. 4. Груз математического маятника

Приложение Д

Рис.5. Изображение песочной синусоиды

Просмотров работы: 23

Исследовательская работа «Колебания и маятники» 9 класс

АРХАНГЕЛЬСКИЙ ОБЛАСТНОЙ КОНКУРС ЮНОШЕСКИХ ИССЛЕДОВАТЕЛЬСКИХ РАБОТ ИМЕНИ М.В. ЛОМОНОСОВА

Секция Прикладная физика

Колебания и маятники

Исследовательская работа

Выполнена учеником 9 класса муниципального казённого образовательного учреждения средняя общеобразовательная школа № 3 города Мирного Архангельской области

Черновым Георгием Романовичем

Научный руководитель — учитель муниципального казённого образовательного учреждения средняя общеобразовательная школа № 3 города Мирного Архангельской области

Михей Мирослава Олеговна

г. Мирный, 2014Оглавление.

1. Введение ………………………………………………………………….3 стр.

2. Колебания…………………………………………………………………4 стр.

3. Маятники………………………………………………………………….4 стр.

Математический маятник……………………………………………5 стр.
Пружинный маятник………………………………………………..5 стр.
Маятник Фуко……………………………………………………….6 стр.
Крутильный маятник………………………………………………….6 стр.
Маятник Ньютона……………………………………………………7 стр.

4. Эксперименты по применению и изготовлению маятников………….7 стр.

Эксперимент № 1
Эксперимент № 2
Эксперимент № 3
Эксперимент № 4
Эксперимент № 5
Эксперимент № 6.

5. Заключение………………………………………………………………11 стр.

6. Библиографический список…………………………………………….12 стр.

7. Приложение………………………………………………………………13 стр.

Введение.

Учась в школе меня очень заинтересовала тема колебания и маятники. Они окружают нас повсюду: колебания веток деревьев на ветру, качелей, автомобиля на рессорах, иглы швейной машины и так далее. Маятники используются в часах, детских кроватках, в автомобилях (механизм рулевого управления). Так же используется в строительстве, геодезии, гравиметрии, для измерении дульной энергии крупнокалиберного стрелкового оружия , в биолокациях и т.д. Но мы рассматриваем не все виды маятников, а только пружинный и математический, и мне захотелось изучить различные виды маятников.

В связи с этим возникла проблема исследования: рассмотреть колебательные движения различные виды маятников, выявить их применение в жизни и технике, сконструировать их с помощью подручных материалов. Отсюда вытекает тема исследования: «Колебания и маятники».

Объект исследования: различные маятники.
Предмет исследования: конструирование моделей маятников.
Цель исследования: изучить теоретические основы колебательного движения различных маятников, провести серию опытов по конструированию их, рассмотреть применение в жизни.
Задачи исследования:

Изучить учебную литературу о колебаниях и маятниках.
Изучить методику проведения экспериментов.
Провести эксперименты и сделать выводы.

Основные методы работы – поисковый, метод обобщенного анализа (сравнение имеющихся знаний с полученными данными), лабораторно – практический метод.

Этапы исследования:

Изучение и анализ литературы по этой теме.
Создание модели проведения экспериментов.
Проведение экспериментов.
Систематизация работы
Подбор наглядного материала. Написание работы.

Благодаря этой работе, я научусь применять полученные знания на практике, с помощью физических законов описывать различные явления; узнаю, из каких материалов можно сделать различные модели маятников, и попытаюсь экспериментально это доказать.

Я старался использовать не только электронные ресурсы Интернета, но и библиотечные ресурсы МКОУ СОШ № 3.

Колебания.

Колебательные движения широко распространены в окружающей нас жизни.
Первыми учеными, изучавшими колебания, были Галилео Галилей (1564-1642) и Христиан Гюйгенс (1629-1692).

Галилей сконструировал первые маятниковые часы. (приложение, рис №1 ) [3] В 1656 году в возрасте 27 лет Гюйгенсом были сконструированы первые маятниковые часы со спусковым механизмом. (приложение, рис № 2)

Следует особо отметить работы с маятниками гениальных русских учёных Михаила Васильевича Ломоносова и Дмитрия Ивановича Менделеева. (приложение, рис № 3)

Маятники.

Свободно колеблющиеся тела всегда взаимодействуют с другими телами и вместе образуют систему тел, которая получила название колебательной системы. Мы будем рассматривать колебательные системы называемые маятниками.

Под словом «маятник» понимают твердое тело, совершающее под действием приложенных сил колебания около неподвижной токи или вокруг оси.[5]

Существует несколько типов маятников, я рассмотрю наиболее распространённые и интересные.

Математический маятник

Математическим маятником – это материальная точка, висящая на невесомой нерастяжимой нити. [7]

Реальный маятник можно считать математическим, если длина нити много больше размеров подвешенного на ней тела, масса нити ничтожно мала по сравнению с массой тела. (приложение, рис № 4)

Период колебаний математического маятника определяется по формуле . Мы видим, что период прямо пропорционален длине маятника и обратно пропорционален ускорению свободного падения.

Математический маятник нашёл широко применение в жизни.

Ускорение свободного падения меняется с географической широтой, так как плотность земной коры различна, поэтому прибор с маятником применили для разведки полезных ископаемых. Подсчитав число качаний, можно обнаружить в земных недрах руды или уголь.

Сейчас очень популярна такая методика, как биолокация. Биолокация позволяют человеку посредством индикатора — рамки или маятника определять наличие каких либо предметов или объектов в пространстве, а также получать ответы с уровня информационного поля. [3]

В наше время круг задач, решаемых биолокацией, еще более расширился. Эта техника применяется экстрасенсами для диагностики заболеваний, поиска пропавших людей, предметов и т.д. Активно используется биолокация в археологии, геологии, гидрогеологии, строительстве и т.д.

Следующий маятник, которым мы изучаем в школе, это пружинный.

Пружинный маятник

Это груз, прикрепленный к пружине, массой которой можно пренебречь. [2] (приложение, рис № 5) Пружинный маятник характеризуется массой тела и жесткостью пружины, поэтому период для такого маятника находиться по формуле .

Пружинные маятники широко используются в качестве акселерометра в системах управления баллистических ракет, контактных взрывателях артиллеристских и авиационных боеприпасов и т.п.

Следующий вид маятника – это разновидность математического маятника.

Маятник Фуко.

Маятник Фуко служит для демонстрации вращения Земли вокруг своей оси. Все мы с вами знаем, что Земля вращается вокруг своей оси и совершает полный оборот за 24 часа. Вращение Земли можно доказать многими физическими опытами. Самым знаменитым из них был опыт, проведенный Жаном Бернаром Леоном Фуко в 1851 году в парижском Пантеоне в присутствии императора Наполеона. Под куполом здания физик подвесил металлический шар массой 28 кг на стальной проволоке длиной 67 м. Под ним было сделано ограждение с радиусом 6 м, внутри которого насыпали песок, чьей поверхности касалось острие маятника. После того как маятник привели в движение, все заметили, что плоскость качания поворачивается относительно пола по часовой стрелке. Это следовало из того, что при каждом следующем качании острие маятника делало отметку на 3 мм дальше предыдущего. Это отклонение и объясняет то, что Земля совершает вращение вокруг своей оси.Таким образом, маятник Фуко имеет важное научное применение.

Следующий вид, это крутильный маятник.

Крутильный маятник.

Это маятник Максвелла, он позволяет выявить ряд интересных закономерностей движения твердого тела. Небольшой маховичок падает, разматывая навитые на его ось нити, и приобретает постепенно столь значительную энергию вращения, что, развернув нити до конца, продолжать вращаться, вновь наматывая их и, следовательно, поднимаясь вверх. (приложение, рис № 7) [1]

Обычно крутильный маятник применяется в механических наручных часах. Колесико-балансир под действием пружины вращается то в одну, то в другую сторону. Его равномерные движения обеспечивают точность хода часов.

Несколько лет назад большую популярность на Западе, особенно в Америке, приобрела знаменитая игрушка, называемая «йо-йо». Это – катушка, которая спускается на разматывающейся ленте и сама затем поднимается. Игрушка – не новость: ею развлекались ещё солдаты наполеоновских армий, и даже герои Гомера.

Маятник Ньютона.

Колыбель Ньютона (маятник Ньютона) — механическая система, придуманная Исааком Ньютоном для демонстрации преобразования энергии различных видов друг в друга: кинетической в потенциальную и наоборот. В отсутствие противодействующих сил трения система могла бы действовать вечно, но в реальности это недостижимо. (приложение, рис № 6) [3]

Эту популярную игрушку-сувенир, придуманную английским актёром Саймоном Пребблом в 1967 году, а сегодня часто встречаемую на письменных столах в кабинетах и офисах, можно поместить и в музей физики. Я считаю этот маятник самым интересным и в тоже время самым сложным в изготовлении.

Эксперименты по применению и изготовлению маятников.

Эксперимент № 1.

Определение ускорения свободного падения с помощью математического маятника.

Цель работы: определить ускорение свободного падения на основе зависимости периода колебаний маятника на подвесе от длины подвеса.

Оборудование: секундомер, измерительная лента, шарик с отверстием, нить, штатив с муфтой.

Проведение эксперимента

1. Устанавливаю на краю стола штатив. У его верхнего конца укрепляю шарик на нити. Шарик должен висеть на расстоянии 1—2 см от пола.

2. Измеряю лентой длину l маятника.

3. Возбуждаю колебания маятника, отклонив шарик в сторону на 5—8 см и отпустив его.

4. Измеряю в нескольких экспериментах время t 50 колебании маятника и вычисляю t_cp:

где n— число опытов по измерению времени. [4]

5. Результаты заношу в таблицу

Номер опыта

t, с

t_ср, с

l, м

g, м/с²

120,2

1,425

120,4

120,1

120,2

9,72

120,3

120,1

120,2

6. Вычислить ускорение свободного падения по формуле

7. Вывод: ускорения свободного падения получилось равным 9,72 м/с². (приложение, рис № 8)

Эксперимент № 2.

Измерение жесткости пружины.

Цель: изготовить пружинный маятник и измерить жесткость пружины.

Оборудование: пружина неизвестной жесткости, штатив с перекладиной и муфтой, груз массой 102 г, крючок, секундомер.

Проведение эксперимента

1. Собираю установку: укрепляю пружину на штативе, к пружине подвешиваю груз массой 102 г.

2. Возбуждаю колебания маятника, оттянув его немного вниз.

3. Измеряю в нескольких экспериментах время t 10 колебании маятника и вычисляю t_cp:

где n— число опытов по измерению времени.

4. Результаты заношу в таблицу

Номер опыта

t, с

t_ср, с

m, кг

k, Н/м

5,1

0,102

4,5

4,3

4,32

4,5

3,8

3,7

5. Вычисляем жесткость пружины по формуле:

Вывод: жесткость пружины равна 22 Н/м.

Эксперимент № 3.

Изготовление модели маятника Фуко.

Оборудование: легкий маятник с острием, пробку, булавку, три вилки, тарелка с солью.

Проведение эксперимента:

Возьмём лёгкий маятник с острым концом. Свободный конец нитки привяжем к булавке, воткнутой в пробку. Установим эту пробку на трех вилках, воткнутых в нее наискось. Поставим свой треножник на тарелку и отрегулируем длину нитки так, чтобы нижний конец острия доходил почти до дна тарелки.
У краев тарелки насыпаем две грядочки из мелкой соли. Они заменят песок в опыте Фуко.
Качнем теперь маятник. Острие прочертит следы в грядках соли. При каждом качании маятника конец острия будет проходить по прежним следам.
Наша скромная тарелка изображает земной шар. Подражая вращению Земли, начнём тихо, без толчков поворачивать тарелку. Замечаем, что острие маятника будет чертить уже другую траекторию.
Из опыта следует, что плоскость колебания маятника не поменялась – это наша тарелка-Земля обернулась вокруг своей оси.

Вывод: с помощью нашей модели маятника мы продемонстрировали опыт Фуко и доказали суточное вращение Земли. (приложение, рис № 9)

Эксперимент № 4.

Изготовление игрушки «йо-йо» как один из видов крутильного маятника.

Цель: с помощью подручных материалов изготовить игрушку и продемонстрировать работу крутильного маятника.

Оборудование: две одинаковые пластмассовые крышки (можно от йогурта или кофе), капроновую нить, трубочку и пластилин.

Проведение эксперимента:

Проделаем отверстия в крышках по центру, вставим трубочку (внутрь трубочки необходимо поместить пластилин или вату для твёрдости).
Для утяжеления в крышки помещаем пластилин. Привязываем нить и игрушка готова.
Наблюдаем, как при раскручивании нити до конца, катушка не останавливается, а за счет энергии поднимается вверх.

Вывод: с помощью видоизмененного крутильного маятника мы продемонстрировали его действие. (приложение, рис № 10)

Эксперимент 5.

Изготовление маятника Ньютона.

Цель: с помощью подручных материалов изготовить маятник Ньютона и пронаблюдать его действие.

Оборудование: шесть шариков от подшипника, капроновые нити, клей, коробка из прочного картона для основания.

Проведение эксперимента:

Приклеим нити к шарикам с двух сторон.
Из коробки сделаем каркас основания для маятника.
Приклеиваем маятники так, чтобы их центры располагались вдоль одной прямой и касались друг друга.
Отводим крайний шарик на пару сантиметров в сторону и отпускаем. Наблюдаем, что импульс передаётся от одного шарика к другому и последний шарик откланяется на точно такое же расстояние, что и первый.
Сложность этого эксперимента в том, то очень трудно подвесить маятники так, чтобы практический не происходило потери энергии.

Вывод: мы изготовили модель маятника Ньютона. (приложение, рис № 11)

Заключение.

В ходе работы я рассмотрел различные маятники и познакомился с ними, узнал много фактов, касающихся истории маятников.

Мы доказали, что маятники находят широко применение в жизни, в различных приборах.

Я научился планировать эксперимент, отбирать приборы для его выполнения, выполнять эксперимент и делать выводы. Определили ускорение свободного падения и жесткость пружины.

Самое главное, что я понял, что с помощи физики можно и нужно познавать мир, так как познание физики – это движение вперед.

Библиографический список

Занимательная физика. Знаете ли вы физику? / Я. И. Перельман. – М.: АСТ, 2007. – 462 c.
Интернет ресурсы: class-fizika.narod.ru
Интернет ресурсы: ru.wikipedia.org
Универсальные поурочные разработки по физике: 11 класс.- М.: ВАКО, 2009. – 464 с. – ( в помощь школьному учителю).
Физика. 9 кл.: учебник для общеобразовательных учреждений/ А.В. Перышкин, Е.М. Гутник. – 14-е изд., стереопит. – М.: Дрофа, 2009. – 300, [4] с.
Физика в школе. Научно-методический журнал, 2012, № 1, 1-72 с.
Физика в школе. Научно-методический журнал, 2009, № 3, 1-64 с.

7. Приложение.

Рисунок № 1 Маятниковые часы Галилея

Рисунок № 2 Маятниковые часы, сконструированные Гюйгенсом.

Рисунок № 3. Маятник-диск и маятник-подкова, сконструированные Д.И. Менделеевым.

Рисунок № 4. Математический маятник.

Рисунок № 5 Пружинный маятник.

Рисунок № 6 Маятник Ньютона

Рисунок № 7. Крутильный маятник

Рисунок № 8. Измерение ускорения свободного падения.

Рисунок № 9 Модели маятника Фуко

Рисунок № 10 «Игрушка Йо-Йо».

Рисунок № 11 «Маятник Ньютона».

Маятник

Простой маятник — это маятник, который можно рассматривать как точечную массу, подвешенную на струне или стержне с незначительной массой. Это резонансная система с единственной резонансной частотой. Для малых амплитуд период такого маятника может быть приблизительно равен:

(Введите данные для двух переменных, а затем щелкните активный текст для третьей переменной, чтобы вычислить ее.)

Обратите внимание, что угловая амплитуда не появляется в выражении для периода. Это выражение для периода достаточно точное для углов в несколько градусов, но обработка маятник большой амплитуды намного больше сложный.

Если масса стержня немалая, то его следует рассматривать как физический маятник.

Шон Кэрролл рассказывает историю открытия Галилеем того факта, что для малых амплитуд период и частота не зависят от амплитуды.»В 1581 году молодой Галилео Галилей, как сообщается, сделал прорывное открытие, когда ему было скучно во время церковной службы в Пизе. Люстра над головой мягко раскачивалась взад и вперед, но, казалось, она двигалась быстрее, когда она раскачивалась широко (после порыва ветра. ветра, например) и медленнее, когда он не двигался так далеко. Заинтригованный, Галилей решил измерить, сколько времени требуется для каждого колебания, используя единственное приблизительно периодическое событие, к которому у него был свободный доступ: биение его собственный пульс.Он обнаружил кое-что интересное: количество ударов сердца между колебаниями люстры было примерно одинаковым, независимо от того, были ли качели широкими или узкими. Размер колебаний — насколько далеко маятник качнулся вперед и назад — не повлиял на частоту этих колебаний ».

Индекс

Концепции периодического движения

Кэрролл
Eternity to Here, p16

Маятник

Простой — или математический — маятник состоит из твердого тела, подвешенного на фиксированной горизонтальной оси, вокруг которой тело может колебаться в вертикальной плоскости под действием силы тяжести.

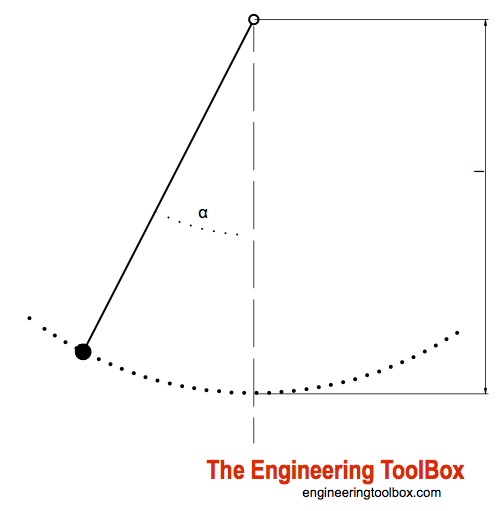
Период колебаний простого маятника можно рассчитать как

T = 2 π (л / год _г) ^1/2 (1)

где

T = период колебаний для одного цикла (с)

l = длина маятника (м, фут)

a _g = ускорение свободного падения (9.81 м / с ², 32,17 фут / с ²)

Пример — Рассчитайте длину маятника с периодом колебаний 1 с, 10 с и 100 с

Длина маятника с данный период колебаний может быть рассчитан путем преобразования (1) в:

l = (T / (2 π)) ² a _g

Длина для 1 сек — обычно для старых модные маятниковые часы:

l = ((1 с) / (2 π)) ² (9.81 м / с ²)

= 0,249 (м)

Маятниковые часы были мировым стандартом для точного измерения времени в течение 270 лет, пока в 1927 году не были изобретены кварцевые часы.

Длина для 10 секунд :

l = ((10 с) / (2 π)) ² (9,81 м / с ²)

= 24,9 (м)

Длина для 100 с :

l = ((100 с) / (2 π)) ² (9,81 м / с ²)

= 2487 (м)

Четыре типа маятников

Это обычное дело Чтобы различать четыре типа маятников:

Составной или физический маятник — твердое тело, подвешенное к неподвижной горизонтальной оси.Тело может колебаться в вертикальной плоскости под действием силы тяжести.
Простой или математический маятник — Подобен составному или физическому маятнику, но масса сосредоточена в одной точке и колеблется взад и вперед в вертикальной плоскости. Массовая точка соединена с горизонтальной осью невесомой хордой.
Конический маятник — Подобен простому маятнику, за исключением того, что груз, подвешенный на хорде, движется с одинаковой скоростью по окружности в горизонтальной плоскости.
Торсионный маятник — Диск, закрепленный на тонком стержне. Штанга крепится к неподвижной раме. Если диск скручен, он будет колебаться вперед и назад вокруг оси стержня.

.
Математических моделей
Математика может использоваться для «моделирования» или представления того, как работает реальный мир.
Пример: сколько места внутри этой картонной коробки?
Нам известны три измерения:
л (длина),
w (ширина) и
h (высота),
, а формула объема кубоида:
Объем = д × ш × в
Итак, у нас есть (очень простая) математическая модель пространства в этом ящике.
Точно?
Модель не такая как настоящая.
В нашем примере мы не задумывались о толщине картона и многих других вещах из «реального мира».
Но, надеюсь, это достаточно хорошо, чтобы быть полезным .
Если мы взимаем плату за объем отправленной коробки, мы можем сделать несколько измерений и узнать, сколько нужно заплатить.
Это также может быть полезно при принятии решения, какую коробку купить, когда нам нужно упаковать вещи.
Так что модель пригодилась!
Но, возможно, нам нужно больше точности, возможно, нам придется отправлять сотни коробок каждый день, а толщина картона имеет значение. Итак, давайте посмотрим, сможем ли мы улучшить модель :
Толщина картона «t», все размеры вне коробки … сколько места внутри?
Необходимо уменьшить внутренние размеры на толщину каждой стороны:
Внутренняя длина l-2t
Внутренняя ширина w-2t ,
Внутренняя высота h-2t
и теперь формула:
Внутренний объем = (l-2t) × (w-2t) × (h-2t)
Теперь у нас есть модель лучше .Все еще не идеально (мы учитывали потраченное впустую пространство, потому что мы не могли аккуратно упаковать вещи и т. Д.), Но лучше.
Итак, модель не реальна, но должна быть достаточно хорошей, чтобы быть полезной.
Играет с моделью
Теперь у нас есть модель, мы можем использовать ее по-разному:
Пример: Ваша компания использует коробки размером 200x300x400 мм, а картон имеет толщину 5 мм.
Кто-то предлагает использовать картон 4мм … насколько это лучше?
Сравним два тома:
Текущий объем = (200-2 × 5) × (300-2 × 5) × (400-2 × 5) = 21,489,000 мм ³
Новый объем = (200-2 × 4) × (300-2 × 4) × (400-2 × 4) = 21 977 088 мм ³
Это изменение:
(21,977,088-21,489,000) / 21,489,000 ≈ 2% больше объема
Так что модель полезная .Это дает нам понять, что внутри коробки будет на 2% больше места (при тех же внешних размерах).
Но есть еще вещи «реального мира», о которых стоит подумать, например, «будет ли он достаточно сильным?»
Мыслить ясно
Чтобы создать математическую модель, нам также нужно ясно думать о фактах!
Пример: на нашей улице собак вдвое больше, чем кошек. Как нам записать это в виде уравнения?
Пусть D = количество собак
Пусть C = количество кошек
Сейчас… вот что: 2D = C
или должно быть: D = 2C
Подумайте внимательно!
Правильный ответ: D = 2C
( 2D = C — распространенная ошибка, так как в вопросе написано «дважды … собаки … кошки»)
Вот еще один:
Пример: вы являетесь руководителем 8-часовой смены. Недавно они сократили время перерыва на 10 минут, но общий объем производства не улучшился.
На первый взгляд моделировать нечего, потому что в производстве не было изменений.
Но подождите … они работают на 10 минут больше, но производят столько же, так что производительность в час , должно быть, упала!
Допустим, они работали 7 часов (420 минут):
Изменение производства в час = 410/420 = 0,976 …
Что означает снижение более чем на 2%
Но что еще хуже: на первые несколько часов смены более короткое время перерыва не влияет, поэтому позднее в смену оно может быть сокращено на 4 или 5%.
Вы можете порекомендовать:
с учетом производительности за каждый час смены
пробует разное время перерывов, чтобы увидеть, как они влияют на производство
Пример побольше: самый экономичный размер
Хорошо, давайте попробуем построить и использовать математическую модель для решения реального вопроса.
Ваша компания будет делать коробки своими руками!
Было решено, что ящик должен содержать 0.02m ³ (0,02 кубометра, что равно 20 литрам) гаек и болтов.
Коробка должна иметь квадратное основание и двойную толщину сверху и снизу.
Картон стоит 0,30 $ за квадратный метр.
Выбирайте наиболее экономичный размер.
Шаг первый: Нарисуйте эскиз!
Это помогает обрисовать то, что мы пытаемся решить!
Основание квадратное, поэтому мы будем использовать просто «w» для обеих длин.
Коробка имеет 4 стороны, а также двойные верх и низ.
Форму коробки можно вырезать вот так (но, вероятно, сложнее):
Шаг второй: составляйте формулы.
Без учета толщины для этой модели:
Объем = ш × ш × в = ш ² ч
И нам говорят, что объем должен быть 0,02 м. ³:
w ² h = 0,02
Площади:
Площадь 4-х сторон = 4 × w × h = 4wh
Площадь двойных вершин и оснований = 4 × w × w = 4w ²
Всего картона необходимо:
Площадь картона = 4 Вт + 4 Вт ²
Шаг третий: составьте единую формулу для стоимости
Нам нужна единая формула стоимости:
Стоимость = 0 $.30 × Площадь Картона
= 0,30 доллара США × (4wh + 4w ²)
И это стоимость, когда мы знаем ширину и высоту .
Может быть сложно работать с … функцией с двумя переменными.
Но мы можем сделать это проще! Поскольку ширина и высота уже связаны объемом:
Объем = w ² h = 0,02
… который можно переставить на …
h = 0,02 / w ²
… и это можно положить в формулу стоимости …
Стоимость = 0,30 доллара США × (4w × 0,02 / w ² + 4w ²)
А теперь стоимость напрямую связана с шириной только .
С небольшим упрощением получаем:
Стоимость = 0,30 USD × (0,08 / w + 4w ²)
Шаг четвертый: Постройте график и найдите минимальную стоимость
Что строить? Что ж, формула имеет смысл только для ширины больше нуля, и я также обнаружил, что для ширины больше 0.5 стоимость становится все больше и больше.
Вот график этой формулы стоимости для шириной от 0,0 м до 0,55 м :

График y = 0,3 (0,08 / x + 4x ²)
x — ширина, а y — стоимость
На глаз я вижу, что стоимость достигает минимума примерно (0,22, 0,17) . Другими словами:
при ширине около 0,22 м (значение x),
минимальная стоимость около 0 $.17 в коробке (значение y).
На самом деле, если посмотреть на график, ширина может быть где-то между 0,20 и 0,24, не сильно влияя на минимальную стоимость.
Шаг пятый: рекомендации
Используя эту математическую модель, вы можете рекомендовать:
Ширина = 0,22 м
Высота = 0,02 / ширина ² = 0,02 / 0,22 ² = 0,413 м
Стоимость = 0,30 USD × (0,08 / w + 4w ²) = 0 USD.30 × (0,08 / 0,22 + 4 × 0,22 ²) = 0,167 USD
Или около 16,7 цента за коробку
Но любая ширина от 0,20 м до 0,24 м подойдет.
Вы также можете предложить улучшения для этой модели:
Включите стоимость клея / скоб и сборки
Учитывать потери при вырезании коробки из картона.
Подходит ли эта коробка для упаковки, обращения и хранения?
Любые другие идеи, которые могут у вас возникнуть!
Предсказание будущего
Математические модели также могут использоваться для прогнозирования будущего поведения.
Пример. Компания по производству мороженого отслеживает, сколько мороженого продается в разные дни.
Сравнивая это с погодой в каждый день, они могут построить математическую модель продаж по сравнению с погодой .
Затем они могут предсказать будущие продажи на основе прогноза погоды и решить, сколько мороженого им нужно приготовить … заранее!
Компьютерное моделирование
Математические модели могут быть очень сложными, поэтому математические правила часто записываются в компьютерные программы, чтобы создать компьютерную модель.
Поиграйте с простой компьютерной моделью отражения внутри эллипса
или с анимацией двойного маятника.
Более сложные примеры включают:
Прогноз погоды
Экономические модели (прогнозирование процентных ставок, безработицы и т. Д.)
Модели поведения больших конструкций при нагрузке (мосты, небоскребы и т. Д.)
Многие другие …
Если вы станете экспертом в любой из этих областей, у вас будет работа на всю жизнь!
.
Маятник Рисование стало проще — Kids STEAM Lab
Узнайте о силах движения и гравитации с помощью новой техники рисования, заменив кисть на качающийся маятник. Вовлеките своего ребенка в учебную деятельность STEAM, сочетая искусство и науку.
STEAM — это сочетание науки, технологий, инженерии, искусства и математики. Хотя вы, возможно, знаете о популярности обучения STEM, мы считаем, что для создания STEAM следует добавить букву «A» для искусства.Именно благодаря творческому и критическому мышлению ваш ребенок сможет успешно решать проблемы и мыслить.
Наука позади маятниковой живописи
Маятник — это неподвижный объект, подвешенный за точку, поэтому он может свободно качаться вперед и назад под действием силы тяжести. При обсуждении концепции с детьми отличным примером для использования являются качели. Когда качели движутся вперед и назад, они демонстрируют физику маятника. Качели движутся вперед и назад из-за силы тяжести на качелях.

Материалы
Стакан из пенопласта или бумаги, ножницы, веревка, скотч, 2 стула, метла, большая бумага (мы использовали рулон коричневой крафт-бумаги), пластиковая скатерть или другая ткань
Учебник
Шаг 1: Подготовьте рабочее место, накрыв пол тканью. Подготовьте маятник, проделав отверстие в дне бумажного стаканчика и по одному отверстию с каждой стороны стакана под ободком. Проденьте веревку через два отверстия на боковой стороне чашки, образуя ручку для чашки.

Шаг 2: Поместите метлу горизонтально между двумя стульями и сдвиньте завязанную веревкой чашку к середине метлы.

Шаг 3: Перед тем, как добавить краску в чашку, проверьте маятник водой. Это простой способ убедиться, что ваше рабочее место покрыто краской. Это также дает вашему художнику время поэкспериментировать с раскачиванием чашки.

Когда ваш ребенок будет готов, приклейте кусок ленты, закрывающий нижнее отверстие чашки, и наполните чашку смесью смываемой краски и воды.Это может зависеть от толщины краски, но мы использовали соотношение 2: 1, 2 части краски на 1 часть воды. Раскатайте и поместите бумагу под маятник.

Удалите ленту и поверните чашку. Обратите внимание, какие узоры маятник создает на бумаге.

Шаг 4: Дайте картине полностью высохнуть.

Поэкспериментируйте с разным временем качания чашки, разной длиной струны или опусканием и подъемом чашки.

Боишься беспорядка? Попробуйте снаружи!
Этот проект может немного запутаться (но с помощью ветоши его было очень легко очистить).
Если идея рисования внутри вас пугает… попробуйте вынести маятниковую картину снаружи. Мы использовали моющуюся краску для тротуаров, чтобы проверить маятник снаружи.
Рецепт моющейся краски для тротуаров своими руками
1/3 с. кукурузного крахмала
1/3 с. воды
столовая ложка моющейся краски
Смешайте ингредиенты в миске.Обязательно сначала протестируйте краску на небольшом участке, чтобы убедиться, что она смывается. Мы обнаружили, что краски некоторых марок смываются легче, чем другие.

Вопросы, которые стоит задать ребенку:
Какой узор рисует маятник краской?
Что произойдет, если повернуть маятник мягко или сильнее?
Как эта картина выглядит или напоминает вам?
Чтобы получить больше удовольствия от практических занятий в STEAM, ознакомьтесь с нашей книгой-бестселлером!

.
No related posts.