Функция y=cos t, её основные свойства и график. Видеоурок. Алгебра 10 Класс
Тема: Тригонометрические функции
Урок: Функция y=cost, её основные свойства и график
Функцией называется закон, по которому каждому значению независимого аргумента ставится в соответствие единственное значение функции.
Вспомним определение функции Пусть t – любое действительное число. Ему соответствует единственная точка M на числовой окружности. У точки M есть единственная абсцисса. Она и называется косинусом числа t. Каждому значению аргумента t соответствует только одно значение функции (рис. 1).
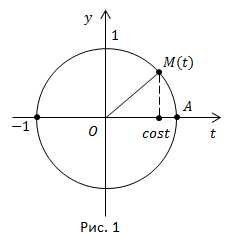
Центральный угол численно равен величине дуги в радианах, т.е. числу Поэтому аргументом может быть и действительное число, и угол в радианах.
Если мы умеем для каждого значения определить то можем построить график функции
Можно получить график функции и другим способом. По формулам приведения поэтому график косинуса – это синусоида, сдвинутая по оси

Свойства функции
1) Область определения:
2) Область значений:
3) Функция четная:
4) Наименьший положительный период:
5) Координаты точек пересечения с осью абсцисс:
6) Координаты точки пересечения с осью ординат:
7) Промежутки, на которых функция принимает положительные значения:
8) Промежутки, на которых функция принимает отрицательные значения:
9) Промежутки возрастания:
10) Промежутки убывания:
11) Точки минимума:
12) Минимум функции: .
13) Точки максимума:
14) Максимум функции:
Мы рассмотрели основные свойства и график функции Далее они будут использоваться при решении задач.
Список литературы
1. Алгебра и начала анализа, 10 класс (в двух частях). Учебник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2009.
2. Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.
3. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 10 класса (учебное пособие для учащихся школ и классов с углубленным изучением математики).-М.: Просвещение, 1996.
4. Галицкий М.Л., Мошкович М.М., Шварцбурд С.И. Углубленное изучение алгебры и математического анализа.-М.: Просвещение, 1997.
5. Сборник задач по математике для поступающих во ВТУЗы (под ред. М.И.Сканави).-М.:Высшая школа, 1992.
6. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебраический тренажер.-К.: А.С.К., 1997.
7. Саакян С.М., Гольдман А.М., Денисов Д.В. Задачи по алгебре и началам анализа (пособие для учащихся 10-11 классов общеобразов. учреждений).-М.: Просвещение, 2003.
8. Карп А.П. Сборник задач по алгебре и началам анализа : учеб. пособие для 10-11 кл. с углубл. изуч. математики.-М.: Просвещение, 2006.
Домашнее задание
Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.
№№ 16.6, 16.7, 16.9.
Дополнительные веб-ресурсы
1. Математика (Источник).
2. Интернет-портал Problems.ru (Источник).
3. Образовательный портал для подготовки к экзаменам (Источник).
interneturok.ru
Функция y=cos t, её свойства и график. Видеоурок. Алгебра 9 Класс
На этом уроке вы узнаете, что такое функция y=cost. Мы проведем аналогии между функциями косинуса и синуса, изучим основные свойства и терминологию
Вспомним определение косинуса:
– любое действительное число, ему соответствует единственная точка на числовой окружности. Как эта точка получается: начало отсчета – точка , дуга откладывается против часовой стрелки, если – положительное число и по часовой стрелке, если отрицательное. Длина дуги равняется модулю числа . Задали произвольное и получили единственную точку , у которой есть единственная пара координат . Первую координату назвали косинусом (), а вторую – синусом () (рис. 1).
В соответствии с данным правилом, мы дали определение двум функциям: и .
Рис. 1. Иллюстрация для определения косинуса
Построим график функции из определения по точкам.
Если мы захотим узнать значение косинуса в иных точках, то используем формулу .
Например:
Получается, зная значения косинуса при и данную формулу, вполне можно узнать значения косинуса для любых значений . Для этого используется симметрия функции косинуса (благодаря ее четности) и периодичность, учитывая, что период у косинуса равен .
Построим график косинуса по точкам (рис. 2):
На отрезке отметим точки, кратные , , как показано на рисунке, это значения аргумента.
Рис. 2. График функции косинуса по точкам
Для начала необходимо нарисовать график лишь на отрезке . Так как функция четная, график симметричен относительно оси ординат – получим и график на отрезке . В результате имеем график на отрезке . Так как этот промежуток длиной в период (, то этого достаточно, чтобы впоследствии нарисовать весь график.
Изучим функцию и построим график косинуса, используя график синуса и связь между синусом и косинусом:
Эта формула позволяет, зная график синуса, сдвинуть его на в нужную сторону и получить график косинуса.
Докажем данную формулу.
Произвольному числу соответствует единственная точка , тогда числу будет соответствовать тоже единственная точка . Мы знаем, как получились точки и , причем или длина дуги (рис. 3).
Рис. 3. Иллюстрация к доказательству формулы связи синуса и косинуса
Итак, имеется две точки и . Косинус – это отрезок . Синус – это отрезок . Докажем, что эти отрезки равны.
Исходя из графика, можно сделать вывод, что эти отрезки равны по знаку. Оба отрезка входят в соответствующие треугольники в качестве сторон, значит, нам можно доказать равенство треугольников, чтобы доказать равенство сторон.
Докажем, что дуга равна дуге .
Дуга получается, если отнять от дуги дугу : .
Дуга получается, если отнять от дуги дугу : .
Из этих двух равенств следует, что дуги и равны. А значит, центральный угол равен центральному углу . Получается, что накрест лежащие углы также равны, а значит, . В результате получаем, что по углу и гипотенузе, так как они прямоугольные, и гипотенузы являются радиусами в одной и той же окружности. Из равенства треугольников получаем равенство отрезков , значит, .
Построим теперь график (здесь заменена буква на более привычную ), или, что то же самое, график . Этот график можно построить, если синусоиду сдвинуть влево на . Итак, строится график , сдвигаем каждую точку на влево, получаем кривую (рис. 4).
interneturok.ru
Свойства функции косинуса
Понятие косинуса
Перед изучением функции косинуса и её свойств, вспомним понятие самого косинуса. Определение косинуса можно ввести двумя способами: с помощью прямоугольного треугольника и с помощью тригонометрической окружности.
Определение 1
Косинусом острого угла называется отношение длины прилежащего катета к гипотенузе прямоугольного треугольника (рис 1):
\[cos\alpha =\frac{b}{c}\]Рисунок 1. Прямоугольный треугольник.
Определение 2
Косинусом острого угла называется абсцисса единичной окружности, которая получается из точки $(1,\ 0)$ путем поворота на угол $\alpha $ радиан (рис. 2).

Рисунок 2. Значение косинуса с помощью единичной окружности.
Введем таблицу некоторых значений косинуса (таблица 1).
Рисунок 3. Значения косинуса.
Свойства функции $f(x)=cosx$
Рассмотрим теперь свойства функции $f\left(x\right)=cosx$.
- Область определения — все числа.
- Так как по определению 2 значение косинуса определяется с помощью единичной окружности, то область значения данной функции отрезок $[-1,\ 1]$.
- $f\left(-x\right)={cos \left(-x\right)\ }=cosx=f(x)$, следовательно, функция $f\left(x\right)=cosx$ четна.
- $f\left(x+2\pi \right)={cos \left(x+2\pi \right)\ }=cosx=f(x)$, следовательно, функция $f\left(x\right)=cosx$ периодическая с минимальным периодом $2\pi $.
Пересечение с осями координат: При $x=0$, $f\left(0\right)=cos0=1$. При $y=0$, $x=\frac{\pi }{2}+\pi n,n\in Z$.
Функция выше оси $Ox$ при $x\in \left(-\frac{\pi }{2}+2\pi n,\frac{\pi }{2}+2\pi n\right),n\in Z$.
- Функция ниже оси $Ox$ при $x\in \left(\frac{\pi }{2}+2\pi n,\frac{3\pi }{2}+2\pi n\right),n\in Z$.
- $f’ (x)=(cosx)’=-sinx$.\[-sinx=0\] \[sinx=0\] \[x=\pi n,\ n\in Z\]
Функция $f\left(x\right)=cosx$ возрастает, при $x\in (-\pi +2\pi n,2\pi n)$. Функция $f\left(x\right)=cosx$ убывает при $x\in (2\pi n,\pi +2\pi n)$ Точки максимума $(2\pi n,1)$. Точки минимума $(\pi +2\pi n,-1)$.
9.Функция непрерывна на всей области определения.
График функции $y=cosx$
Графиком функции $y=cosx$ является косинусоида (рис. 3).
Рисунок 4. Косинусоида.
Задачи на построение косинусоид
Пример 1
Построить график функции $y=2cosx$.
График данной функции получается из функции $y=cosx$ растяжением вдоль оси $Oy$ в 2 раза:
Рисунок 5.
Пример 2
Построить график функции $y=cos\left(x-\frac{\pi }{2}\right)$.
График данной функции получается из функции $y=cosx$ путем смещения вдоль оси $Ox$ на $\frac{\pi }{2}$ единиц вправо.
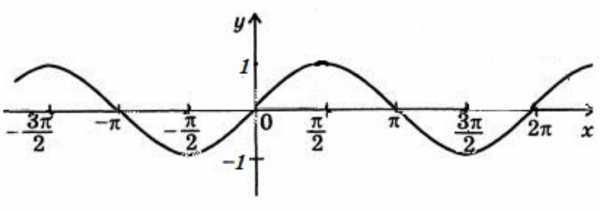
Рисунок 6.
spravochnick.ru
