Формула косинуса угла между векторами, которые заданы координатами
Теперь у нас есть полная информация, чтобы ранее выведенную формулу косинуса угла между векторами выразить через координаты векторов :
Косинус угла между векторами плоскости и , заданными в ортонормированном базисе , выражается формулой:
.
Косинус угла между векторами пространства , заданными в ортонормированном базисе , выражается формулой:
Пример 16
Даны три вершины треугольника . Найти (угол при вершине ).
Решение:По условию чертёж выполнять не требуется, но всё-таки: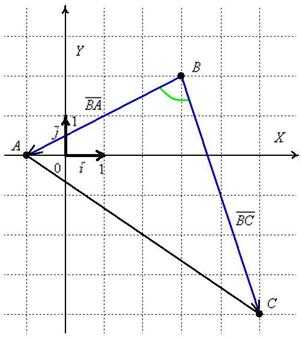
Требуемый угол помечен зелёной дугой. Сразу вспоминаем школьное обозначение угла: – особое внимание на среднюю букву – это и есть нужная нам вершина угла. Для краткости можно было также записать просто .
Из чертежа совершенно очевидно, что угол треугольника совпадает с углом между векторами и , иными словами: .
Проведённый анализ желательно научиться выполнять мысленно.
Найдём векторы:
Вычислим скалярное произведение:
И длины векторов:
Косинус угла:
Именно такой порядок выполнения задания рекомендую чайникам. Более подготовленные читатели могут записывать вычисления «одной строкой»:
Вот и пример «плохого» значения косинуса. Полученное значение не является окончательным, поэтому нет особого смысла избавляться от иррациональности в знаменателе.
Найдём сам угол:
Если посмотреть на чертёж, то результат вполне правдоподобен. Для проверки угол также можно измерить и транспортиром. Не повредите покрытие монитора =)
Ответ:
В ответе не забываем, что спрашивалось про угол треугольника
(а не про угол между векторами), не забываем указать точный ответ: и приближенное значение угла: , найденное с помощью калькулятора.Те, кто получил удовольствие от процесса, могут вычислить углы , и убедиться в справедливости канонического равенства
Пример 17
В пространстве задан треугольник координатами своих вершин . Найти угол между сторонами и
Это пример для самостоятельного решения. Полное решение и ответ в конце урока
Небольшой заключительный раздел будет посвящен проекциям, в которых тоже «замешано» скалярное произведение:
Проекция вектора на вектор. Проекция вектора на координатные оси.
Направляющие косинусы вектора
Рассмотрим векторы и :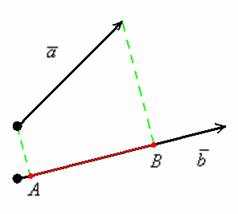
Спроецируем вектор на вектор , для этого из начала и конца вектора опустим
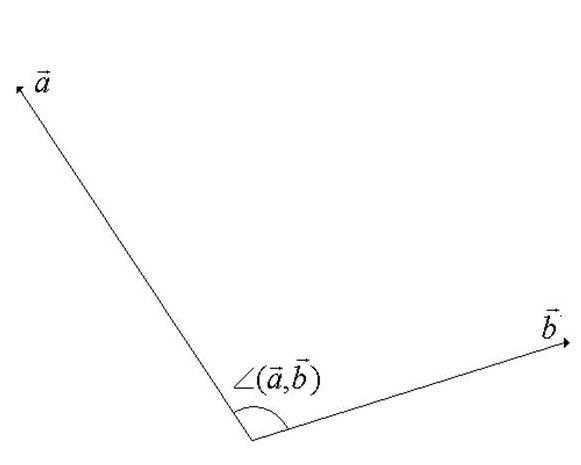
Данное ЧИСЛО обозначается следующим образом: , «большим вектором» обозначают вектор КОТОРЫЙ проецируют, «маленьким подстрочным вектором» обозначают вектор НАкоторый проецируют.
Сама запись читается так: «проекция вектора «а» на вектор «бэ»».
Что произойдёт, если вектор «бэ» будет «слишком коротким»? Проводим прямую линию, содержащую вектор «бэ». И вектор «а» будет проецироваться уже на направление вектора «бэ», попросту – на прямую, содержащую вектор «бэ». То же самое произойдёт, если вектор «а» отложить в тридесятом царстве – он всё равно легко спроецируется на прямую, содержащую вектор «бэ».
Если угол
между векторами острый (как на рисунке), тоЕсли векторы ортогональны, то (проекцией является точка, размеры которой считаются нулевыми).
Если угол между векторами тупой(на рисунке мысленно переставьте стрелочку вектора ), то (та же длина, но взятая со знаком минус).
Отложим данные векторы от одной точки:
infopedia.su
Как найти косинус угла между векторами
Давайте разберем как найти косинус угла между векторами на примерах, но изначально рассмотрим формулы, с помощью которых, собственно, и вычисляется этот косинус.
Чтобы вычислить косинус угла между векторами необходимо использовать скалярное произведение данных векторов и длины векторов.
Рассмотрим два случая:
1-й случай. Векторы заданы на плоскости.
В таком случае координаты векторов будут заданы двумя координатами х и у и косинус можно будет найти по следующей формуле:
2-й случай. Векторы заданы в пространстве.
Тогда координаты векторов задаются тремя координатами x, y и z и косинус рассчитывается по такой же формуле, но с использованием всех трех координат.
Теперь рассмотрим использование этих формул на практических примерах.
Пример 1.
Найдем косинус угла между двумя заданными на плоскости векторами и .
Решение.
По условию имеем, что векторы заданы на плоскости, поэтому используем первую формулу и подставим в нее известные координаты векторов:
Ответ. .
Аналогично решается пример для векторов, которые заданы в пространстве с использованием второй формулы.
ru.solverbook.com
Как найти косинус угла между векторами
Автор КакПросто!
Вектором в геометрии называют направленный отрезок или упорядоченную пару точек евклидова пространства. Длиной вектора — скаляр, равный арифметическому квадратному корню из суммы квадратов координат (компонент) вектора.

Статьи по теме:
Вам понадобится
- Базовые знания по геометрии и алгебре.
Инструкция
Косинус угла между векторами находят из их скалярного произведения. Сумма произведения соответствующих координат вектора равна произведению их длин на косинус угла между ними. Пусть даны два вектора: a(x1, y1) и b(x2, y2). Тогда скалярное произведение можно записать в виде равенства: x1*x2 + y1*y2 = |a|*|b|*cos(U), где U — угол между векторами.Например, координаты вектора a(0, 3), а вектора b(3, 4).
Выражая из полученного равенства cos(U) получается, что cos(U) = (x1*x2 + y1*y2)/(|a|*|b|). В примере формула после подстановки известных координат примет вид: cos(U) = (0*3 + 3*4)/(|a|*|b|) или cos(U) = 12/(|a|*|b|).
Длина векторов находится по формулам: |a| = (x1^2 + y1^2)^1/2, |b| = (x2^2 + y2^2)^1/2. Подставив в качестве координат векторов a(0, 3), b(3, 4) получается, соответственно, |a|=3, |b|=5.
Подставляя полученные значения в формулу cos(U) = (x1*x2 + y1*y2)/(|a|*|b|), найдите ответ. Пользуясь найденными длинами векторов, получите, что косинус угла между векторами a(0, 3), b(3, 4) равен: cos(U) = 12/15.
Обратите внимание
Если все посчитано правильно, косинус угла должен быть меньше единицы. Также длины векторов не могут принимать отрицательные значения.
Полезный совет
Если длина одного из векторов равна нулю, значит это нулевой вектор, и тогда угол между ним и другим вектором равен 90 градусов.
www.kakprosto.ru
Угол между двумя векторами
Пусть в n-мерном пространстве задан ортонормированный базис
Как известно скалярное произведение ненулевых векторов x и y называется произведение
| (1) |
где |·|-модуль вектора, φ -угол между векторами.
Если x=0 или y=0, то скалярное произведение равно нулю.
Вариант 1. Начальные точки всех векторов совпадают с началом координат.
Так как рассматривается пространство с ортонормированным базисом, то скалярное произведение можно вычислить также из выражения
| (2) |
где
координаты векторов x и y соответственно.
Из выражений (1) и (2) следует, что косинус угла между двумя векторами равен
И, следовательно, угол между двумя векторами будет равен
Вариант 2. Начальные точки векторов произвольные.
Пусть заданы векторы x=AB и y=CD, где ,,,.
Переместим параллельно векторы x и y так, чтобы начальные точки векторов совпали с началом координат. Получим векторы x’ и y’ с координатами (т.е. с конечными точками):
где
При таком перемещении угол между векторами x и y равен углу между векторами x’ и y’. Следовательно косинус угла между двумя векторами равен:
| (3) |
Угол между двумя векторами будет равен:
| (4) |
Примеры вычисления угла между двумя векторами
Вариант 1. Начальные точки всех векторов совпадают с началом координат.
Пример . Найти угол между векторами x=(7,2) и y=(4,5).
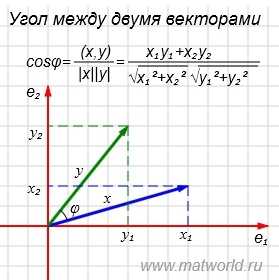
Рис. 1
На рисунке Рис. 1 в двухмерном пространстве представлены векторы x=(7,2) и y=(4,5).
Для вычисления угла между векторами x и y, вычислим нормы векторов x и y:
Косинус угла между векторами x и y, будет равен:
| (5) |
Из выражения (5) вычисляем угол φ:
Вариант 2. Начальные точки векторов произвольные.
Пример . Найти угол между векторами x=AB и y=CD, где A(-1,1), B(3, 7), C(3,2), D(12,5).
На рисунке Рис. 2 в двухмерном пространстве представлены векторы x=AB и y=CD.
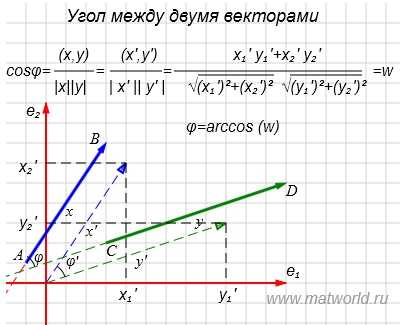
Рис. 2
Переместим параллельно векторы x и y так, чтобы начальные точки векторов совпали с началом координат. Получим векторы x’ и y’ с координатами (т.е. с конечными точками): x’=(3-(-1),7-1)=(4,6), y’=(12-3,5-2)=(9,3).
Угол φ между векторами x и y равен углу φ’ между векторами x’ и y’. Поэтому вычисляя угол φ’ , получим угол между векторами x и y.
Вычислим норму векторов x’ и y’:
Косинус угла между векторами x’ и y’:
Угол между двумя векторами будет равен:
matworld.ru
угол между векторами | C++ для приматов
Условие:
Найти угол в градусах, минутах и секундах между векторами [latex]\overrightarrow{a}=(a_x,a_y,a_z)[/latex] и [latex]\overrightarrow{b}=(b_x,b_y,b_z)[/latex].
Входные данные:
Координаты векторов [latex] \overrightarrow{a}[/latex] и [latex]\overrightarrow{b}[/latex].
Выходные данные:
Угол в градусах, минутах и секундах.
Тесты
| № | Входные данные | Выходные данные |
| 1 | 1 1 4 20 31 12 | 53° 1′ 23″ |
| 2 | 1 61 12 1 11 1 | 7° 17′ 33″ |
| 3 | 1 0 0 0 0 1 | 90° 0′ 0″ |
| 4 | -1 0 1 -2 2 1 | 44° 59′ 59″ |
Код
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
#define _USE_MATH_DEFINES #include #include using namespace std;
int main() { double ax, ay, az, bx, by, bz, mdla, mdlb, mdlab, ccos, ugl; int gr = 0,mn=0, sc=0; cin >> ax >> ay >> az >> bx >> by >> bz; mdla = sqrt(ax*ax + ay*ay + az*az); //формула длины вектора mdlb = sqrt(bx*bx + by*by + bz*bz); mdlab = mdla*mdlb; ccos = (ax*bx + ay*by + az*bz) / mdlab; // формула косинус угла между векторами ugl = acos(ccos)*180/M_PI;// получим угол по формуле перевода радиан в градусы gr = ugl; // найдем градусы ugl -= gr; mn = ugl * 60; // оставшаяся часть угла в минутах ugl -= (double)mn / 60; sc = ugl * 3600; // оставшаяся часть угла в секундах cout << gr << «° » << mn << «‘ » << sc << «»»; return 0; } |
Решение:
Для решения данной задачи необходимо найти косинус между векторами, а после перевести радианы в градусы.
Косинус между векторами найдем по формуле [latex] \cos \alpha = \frac{\vec{a}\vec{b}}{\left|\vec{a} \right|\left|\vec{b} \right|}[/latex] .
Скалярное произведение найдем по формуле [latex] \left|\vec{a} \right| \left|\vec{b} \right|={a}_{x}{b}_{x}+{a}_{y}{b}_{y}+{a}_{z}{b}_{z} [/latex] .
Модуль вектора найдем по формуле [latex] \left|\vec{a} \right| = \sqrt{ {{a}_{x}}^{2}+{{a}_{y}}^{2}+{{a}_{z}}^{2} } [/latex] ; [latex] \left|\vec{b} \right| = \sqrt{ {{b}_{x}}^{2}+{{b}_{y}}^{2}+{{b}_{z}}^{2} } [/latex] .
Затем переведем радианы в градусы по формуле [latex] \frac{180}{ \arccos (-1.0) \arccos (\cos \alpha )} [/latex] .
[latex] \arccos (-1.0) [/latex] это число [latex] \pi [/latex] .
Ссылки:
Решение задачи на ideone.com: http://ideone.com/Gx3IVU
Косинус угла между векторами: http://ru.onlinemschool.com/math/library/vector/angl/
Скалярное произведение векторов: http://ru.onlinemschool.com/math/library/vector/multiply/
Модуль вектора: http://ru.onlinemschool.com/math/library/vector/length/
Перевод радиан в градусы: http://www.cleverstudents.ru/trigonometry/radian_and_degree_conversion.html
Условие задачи: http://cpp.mazurok.com/mtasks/
cpp.mazurok.com
Как найти угол между векторами 🚩 Нахождение угла между векторами 🚩 Математика
Автор КакПросто!
Вектор — это отрезок с заданным направлением. Угол между векторами имеет физическое значение, например при нахождении длины проекции вектора на ось.

Статьи по теме:
Инструкция
Угол между двумя ненулевыми векторами определяется с помощью вычисления скалярного произведения. По определению скалярное произведение равно произведению длин векторов на косинус угла между ними. С другой стороны, скалярное произведение для двух векторов a с координатами (x1; y1) и b с координатами (x2; y2) вычисляется по формуле: ab = x1x2 + y1y2. Из этих двух способов нахождения скалярного произведения легко найти угол между векторами.Найдите длины или модули векторов. Для наших векторов a и b: |a| = (x1² + y1²)^1/2, |b| = (x2² + y2²)^1/2.
Найдите скалярное произведение векторов, перемножив их координаты попарно: ab = x1x2 + y1y2. Из определения скалярного произведения ab = |a|*|b|*cos α, где α — угол между векторами. Тогда получим, что x1x2 + y1y2 = |a|*|b|*cos α. Тогда cos α = (x1x2 + y1y2)/(|a|*|b|) = (x1x2 + y1y2)/((x1² + y1²)(x2² + y2²))^1/2.
Найдите угол α с помощью таблиц Брадиса.
В случае трехмерного пространства добавляется третья координата. Для векторов a (x1; y1; z1) и b (x2; y2; z2) формула для косинуса угла представлена на рисунке.
Видео по теме
Обратите внимание
Скалярное произведение — это скалярная характеристика длин векторов и угла между ними.
Для решения многих задач, как прикладных, так и теоретических, в физике и линейной алгебре необходимо вычислять угол между векторами. Эта простая на первый взгляд задача способна доставить множество трудностей, если вы четко не усвоите сущность скалярного произведения и какая величина появляется в результате этого произведения.
Инструкция
Угол между векторами в векторном линейном пространстве – минимальный угол при повороте, на который достигается сонаправленность векторов. Осуществляется поворот одного из векторов вокруг его начальной точки. Из определения становится очевидно, что значение угла не может превышать 180 градусов (cм. рисунок к шагу).При этом совершенно справедливо предполагается, что в линейном пространстве при осуществлении параллельного переноса векторов угол между ними не меняется. Поэтому для аналитического расчета угла пространственная ориентация векторов не имеет значения.
При нахождении угла используйте определение скалярного произведения для векторов. Данная операция обозначается следующим образом (см. рисунок к шагу).Результат скалярного произведения – число, иначе скаляр. Запомните (это важно знать), чтобы не допустить в дальнейших расчетах ошибок. Формула скалярного произведения, расположенных на плоскости либо в пространстве векторов, имеет вид (см. рисунок к шагу).
Это выражение справедливо только для ненулевых векторов. Отсюда выразите угол между векторами (см. рисунок к шагу).
Если система координат, в которой располагаются векторы, является декартовой, то выражение для определения угла можно переписать в следующем виде (см. рисунок к шагу).
Если вектора располагаются в пространстве, то расчет производите аналогичным способом. Единственным отличием будет появление третьего слагаемого в делимом — это слагаемое отвечает за аппликату, т.е. третью компоненту вектора. Соответственно, при вычислении модуля векторов компоненту z также необходимо учесть, тогда для векторов, расположенных в пространстве, последнее выражение преобразуется следующим образом (см. рисунок 6 к шагу).
www.kakprosto.ru
Как определить угол между векторами
Автор КакПросто!
Операции с векторами нередко вызывают сложности у школьников. Несмотря на наличие ограниченного ряда формул, с которыми нужно оперировать, некоторые задачи вызывают сложности и проблемы с решением. В частности, не все учащиеся старших классов способны вычислить угол между векторами.

Статьи по теме:
Инструкция
Обратите внимание на то, что вычисление угла между двумя любыми векторами сводится к нахождению такого между векторами, имеющими общую точку. Это часто вызывает непонимание, однако объясняется достаточно просто. Чтобы два лежащих в одной плоскости вектора начинались в одной точке, вам необходимо совершить операцию параллельного переноса. Но эта процедура никак не влияет на искомую величину. Запомните общее определение угла между двумя векторами: это поможет вам сложить представление о том, что требуется в задаче. Ведь угол – это не цифры, а определенная реальность, обозначающая ту кратчайшую величину, на которую необходимо повернуть один вектор (относительно своей начальной точки) до сонаправленности со вторым. Важно учитывать, что искомая величина угла должна быть в пределах от нуля до 3,14 радиан.Не забывайте, что если вы имеете дело с коллинеарными или параллельными векторами, величина угла составляет ноль градусов в случае их сонаправленности и 180 – для разнонаправленных векторов. Это следует из определения, так как вам необходимо повернуть второй вектор, чтобы поменять его направление.
Воспользуйтесь простой формулой, позволяющей быстро вычислить величину косинуса угла между векторами. Для этого вам необходимо знать соответствующие координаты. Косинус угла представляет собой дробь, в числителе которой стоит скалярное произведение векторов, а в знаменателе – произведение их модулей. Для нахождения первой величины для векторов с координатами а1, а2, а3 и с1, с2, с3, найдите сумму произведений а1с1, а2с2, а3с3. Модуль каждого вектора есть корень второй степени из суммы квадратов его координат.
Обратитесь к помощи электронных калькуляторов, которые по заданным параметрам векторов вычислят требуемый угол.
www.kakprosto.ru
