|
www.reshim.su
Задача на Диаграмму Эйлера-Венна — Ответ Прост!
Задание 3. С помощью диаграмм Эйлера-Венна определите, в каких отношениях находятся нижеследующие понятия.
Книга и учебник, живая природа и неживая природа, ребенок и инвалид, наука и математика, библиотека и столовая, динозавр и мамонт, азбука и согласная буква.
Теория:
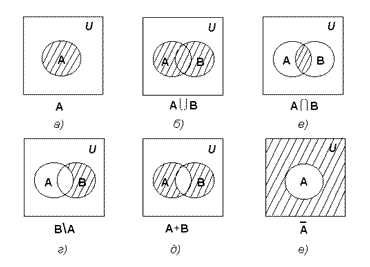
ДИАГРАММА ВЕННА
, схематическое представление отношений между математическими МНОЖЕСТВАМИ или логическими утверждениями, названное по имени английского логика Джона Венна (1834-1923). Множества изображаются в виде геометрических фигур, обычно — кругов, которые перекрываются, если различные множества имеют общие элементы.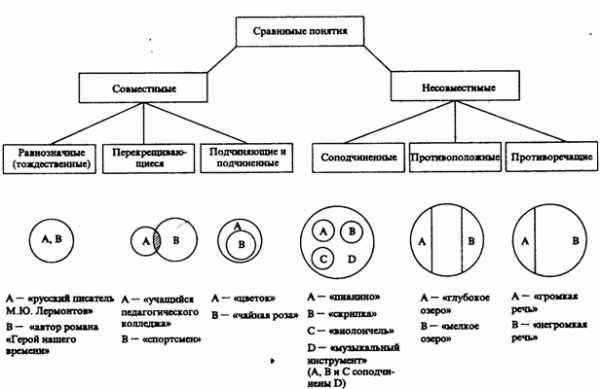
Ответ:
Любой учебник является книгой. Понятие «учебник» находится в отношении подчинения относительно понятия «книга».
Понятия «живая природа» и «неживая природа» находятся в отношении соподчинения.
Понятия «ребенок» и «инвалид» находятся в отношении пересечения, так как инвалидом может быть ребенок.
Математика – это наука. Поэтому понятие «математика» будет подчиняться (полностью входить) понятию «наука».
Понятия «библиотека» и «столовая» находятся в отношении соподчинения.
Понятия «динозавр» и «мамонт» находятся в отношении соподчинения. При чем, если их рассматривать относительно понятия «вымершие животные», то можно сказать, что понятия «динозавр» и «мамонт» соподчинены понятию «вымершие животные».
Понятие «согласная буква» и «азбука» находятся в отношении подчинения, так как азбука – это набор букв, в том числе и гласных и согласных.
1,138 просмотров всего, 2 просмотров сегодня
otvet-prost.ru
1.3. Диаграммы Эйлера — Венна
Диаграммы Эйлера-Венна позволяют представить множества, как множества точек на плоскости, оганиченные замкнутыми кривыми круглой или овальной формы. Прямоугольная рамка ограничивает универсум. Обычно, если не требуется иное, рисуют так называемый общий случай: когда каждое из множеств имеет свои собственные точки и точки, общие с другими множествами.U
II
III
I
A
B
AB – зоны I, II, III.
AB – зона III.
A\B — зона I.
A — все, кроме круга А.
AB — зоны I, III.
Диаграмма для общего случая c тремя множествами будет иметь вид:
U
A B
C
Построение диаграммы Эйлера-Венна для общего случая с четырьмя и более множествами можно предложить для самостоятельных развлечений.
1.4. Алгебра множеств
Операции над множествами дают в результате новые множества.
Для операций справедлив ряд законов. Приведем наиболее часто используемые.
Для упрощения записи, уменьшения числа скобок, определяющих последовательность операций, можно использовать соглашение о «силе» операций (в порядке убывания): дополнение, пересечение, объединение.
Остальные операции можно выразить через эти три.
Законы:
1. Коммутативный:
A B = B A A B = B A2. Ассоциативный:
A (B C) = (A B) C = A B C A (B C) = (A B) C = A B С
3. Дистрибутивный:
A (B С)= (A B) (A C) A (B С) = (A B) (A C)
4. Поглощения:
A (A B) = A A (A B) = A
5. Идемпотентности:
A A = A A A = A
6. Исключенноготретьего:Противоречия:
A A = U A A =
7. A = A A =
8. A U = U A U = A
Де Моргана:
____ ___
A B = A B A B = A B
10.= U U =
11. Двойного отрицания: A = A
12. A \ B =A B
13. A B =A B A B
Пример доказательства варианта дистрибутивного закона:
A (B С) = (A B) (A C)
I. Докажем, что левая часть включена в правую:
A (B C) (A B) (A C)
Пусть х А(ВС), тогда у х есть две возможности
1. х A . Тогда хAB и хACх(AB)(AC).
2. х BC. Тогда хB и хCхAB и хAC,
то есть х (AB)(AC).
studfiles.net