Расчет значения функции Эйлера
Функция Эйлера — такая функция от целого положительного числа, значение которой равно количеству натуральных чисел, меньших заданного числа и взаимно простых с ним.
При этом полагают, что число 1 взаимно просто со всеми натуральными числами.
Если заданное число N является простым то логично предложить что функция Эйлера будет равна N-1, так как все числа меньше N, являются взаимно простыми к заданному.
Например, значение функции Эйлера числа 33 равно 20. Как такое получилось?
Разложим 33 на множители получим 3*11. Запомним их и будем сравнивать с рядом чисел от 1 до 32.
Напомним, что взаимно простыми числами являются таки числа, которые не имеют общих делителей.
Считаем взаимно простые числа: 1,2 ,3(не учитывем),4,5,6(делится на 3),7,8,9,10,11(делится на 11),
Посчитаем сколько получилось зачеркнутых чисел?
Их 12, ряд чисел содержит 32 элемента ( от 1 до 33) тогда количество незачеркнтуых (взаимно простых) чисел будет 32-12 =20
Есть еще простой способ рассчитывать значения функции
Разложим произвольное число например 4832 на простые множители.
Получим
Функция Эйлера равна
То есть, если у вас число N представлено в виде простых сомножителей вида
то функция Эйлера будет равна
Вот еще пример
Рассчитаем значение фунции числа 100
тогда значение функции Эйлера равно
Применимость числа Эйлера в теории чисел и криптографии достаточно велико, но мы будем её использовать для расчета линейных диофантовых уравнений с двумя неизвестными.
Удачных расчетов!
abakbot.ru
Функция Эйлера
Функция Эйлера φ(а) определяется для всех натуральных чисел а и представляет собой количество натуральных чисел взаимно простых с а, и не превосходящих а. При этом считается, что φ(1)=1. Вычисляется эта функция по формуле
где – простые делители в каноническом разложении числаа .
Число чисел, составляющих приведенную систему вычетов равно φ(m).
Общее свойство полной и приведенной системы вычетов
Если числа представляют собой полную (
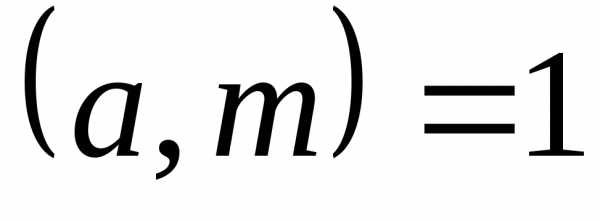 ,
так же представляют собой полную или
приведенную систему вычетов по модулюm.
,
так же представляют собой полную или
приведенную систему вычетов по модулюm.Пример.
Показать, что числа 25,-20,16,46,-21,18,37,-17 составляют полную систему вычетов по модулю 8.
Решение.
Образуем полную систему наименьших неотрицательных чисел
, ,,,,,,.
Итак, данные числа 0,1,2,3,4,5,6,7 образуют полную систему вычетов по модулю 8.
Теоремы Эйлера и Ферма
1. Теорема Эйлера.
При m>1 и (a,m)=1 имеем
. (1)
Доказательство.
Пусть x пробегает приведенную систему вычетов  ,
где
,
где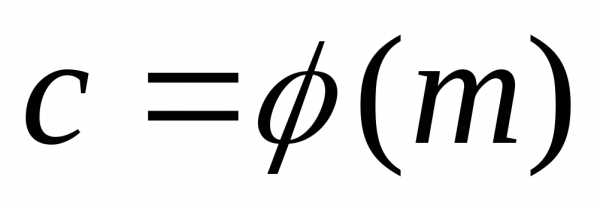 составленную из наименьших неотрицательных
вычетов. Наименьшие неотрицательные
вычетычисел ax будут побегать ту же систему, но
расположенную (в общем случае) в ином
порядке. Перемножив почленно сравнения
.
Откуда получим .
Откуда, деля обе части на произведение
,
получим
или
.
составленную из наименьших неотрицательных
вычетов. Наименьшие неотрицательные
вычетычисел ax будут побегать ту же систему, но
расположенную (в общем случае) в ином
порядке. Перемножив почленно сравнения
.
Откуда получим .
Откуда, деля обе части на произведение
,
получим
или
.
2. Теорема Ферма.
При простом p и a, не делящемся на p, имеем
. (2)
Эта теорема является частным случаем теоремы Эйлера, при m=p. Из (2) можно легко получить очень важное сравнение
,
справедливое при всех целых а, так как оно верно и при a кратном p.
Пример.
Проверить теорему Эйлера при a=5 и .
Решение.
,
.
Действительно, .
Пример.
Найти остаток от
деления 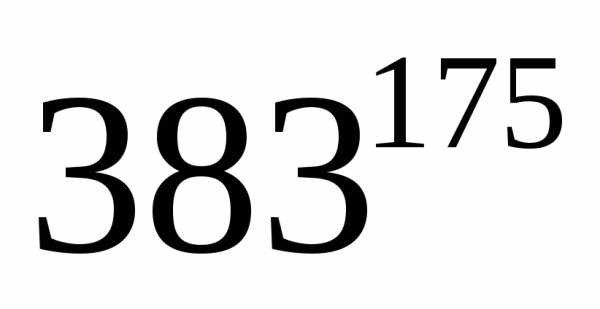 на 45.
на 45.
Решение.
Так как , то. Так каки (23,45)=1, то по теореме Эйлера
Значит
, но
, но
.
Итак, .
Ответ: искомый остаток равен 32.
Сравнения первой степени (решение задач)
Пример 1.
Решить способом Эйлера сравнение . Правильность ответа проверить подстановкой.
Решение.
(3,5)=1, значит, данное
сравнение имеет единственное решение
(в смысле класса чисел x
по modm).
По формуле Эйлера имеем
,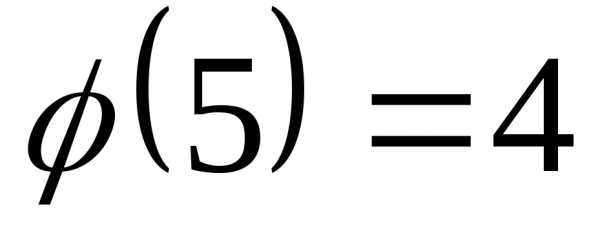 ,
тогда получимилиили.
,
тогда получимилиили.
Проверка ,верно.
Ответ: .
Пример 2.
Решить способом Эйлера сравнение .
Решение.
(5,10)=5, но 7 не делится на 5, значит, данное сравнение не имеет решений.
Пример 3.
Решить способом Эйлера сравнение .
Решение.
Так как (25,17)=1, то данное сравнение имеет решение. Данное сравнение равносильно сравнению . По формуле Эйлера имеем., тогда
Рассмотрим
.
Итак, , тогда.
Проверка ,верно.
Ответ: .
Пример 4.
Решить одним из способов сравнение
, (1)
Решение.
(12,15)=3. Значит, данное сравнение имеет 3 решения (в смысле классов). Рассмотрим сравнение
, (2)
которое получено из данного после сокращения на 3.
По формуле Эйлера имеем,.
Итак, .
Проверка .
Мы нашли решение сравнения (2). Решение сравнения (1) находится по формуле ,k=0,1,2.
; ; .
Проверка:
1) , .
2) ,
3) ,
Ответ: , , .
Пример 5.
Приписать справа к числу 523 такие три цифры, чтобы полученное шестизначное число делилось на 7,8,9.
Решение.
Пусть приписываемое
число x,
тогда,
откудаили.
Значениеx
будет трехзначным числом при t=0
и t=1.
Получаем 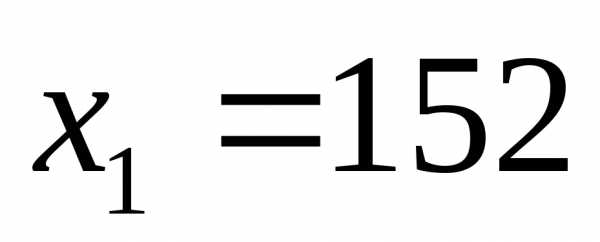
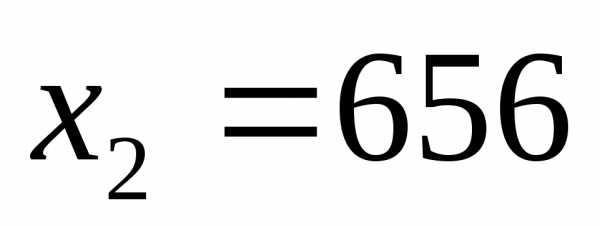 .
.Проверки.
523152 делится на 7,8,9;
523656 делится на 7,8,9.
studfiles.net
Функция Эйлера — Национальная библиотека им. Н. Э. Баумана
Материал из Национальной библиотеки им. Н. Э. Баумана
Последнее изменение этой страницы: 13:25, 9 мая 2016.
Определение
| Определение « Функция Эйлера» |
|---|
Функцией Эйлера φ(m){\displaystyle \varphi(m)} называется функция, равная количеству натуральных чисел не превосходящих m{\displaystyle m} и взаимно простых с ним. |
Таблица значений
| n{\displaystyle n} | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| φ(n){\displaystyle \varphi(n)} | 0 | 1 | 2 | 2 | 4 | 2 | 6 | 4 |
Свойства
- Пусть p{\displaystyle p}-простое. Тогда φ(pk)=pk−pk−1{\displaystyle \varphi(p^k)=p^k-p^{k-1}} для любого натурального k{\displaystyle k}.
- Для любых взаимно простых натуральных a{\displaystyle a} и b{\displaystyle b} справедливо равенство φ(ab)=φ(a)φ(b){\displaystyle \varphi(ab)=\varphi(a)\varphi(b)}
- Если m=p1k1p2k2…pnkn{\displaystyle m=p_1^{k_1}p_2^{k_2} \dots p_n^{k_n}}, то
φ(m)=m(1−1p1)(1−1p2)…(1−1pn){\displaystyle \varphi(m)=m(1-\frac{1}{p_1})(1-\frac{1}{p_2})\dots(1-\frac{1}{p_n})}
Пример
Найдем φ(120){\displaystyle \varphi(120)}.
Так как 120=23⋅3⋅5{\displaystyle 120=2^3 \cdot 3 \cdot 5}, то φ(120)=4⋅2⋅4=32{\displaystyle \varphi(120)=4 \cdot 2 \cdot 4 = 32}.
Теорема Эйлера
Теорема Эйлера
Литература
ru.bmstu.wiki
Функция Эйлера — WiKi
Первая тысяча значений φ(n){\displaystyle \varphi (n)}Фу́нкция Э́йлера φ(n){\displaystyle \varphi (n)} — мультипликативная арифметическая функция, равная количеству натуральных чисел, меньших n{\displaystyle n} и взаимно простых с ним. При этом полагают по определению, что число 1 взаимно просто со всеми натуральными числами, и φ(1)=1{\displaystyle \varphi (1)=1}[1].
Например, для числа 24 существует 8 меньших его и взаимно простых с ним чисел (1, 5, 7, 11, 13, 17, 19, 23), поэтому φ(24)=8{\displaystyle \varphi (24)=8}.
Названа в честь Эйлера, который впервые использовал её в 1760 году в своих работах по теории чисел для доказательства малой теоремы Ферма, а затем и для доказательства более общего утверждения — теоремы Эйлера. Позднее функцию использовал Гаусс в своем труде «Арифметические исследования», вышедшем в свет в 1801 году. Гаусс ввёл ставшее стандартным обозначение φ(n){\displaystyle \varphi (n)}[2].
Функция Эйлера находит применение в вопросах, касающихся теории делимости и вычетов (см. сравнение по модулю), теории чисел, криптографии. Функция Эйлера играет ключевую роль в алгоритме RSA[3].
| φ(n){\displaystyle \varphi (n)} | +0 | +1 | +2 | +3 | +4 | +5 | +6 | +7 | +8 | +9 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0+ | 1 | 1 | 2 | 2 | 4 | 2 | 6 | 4 | 6 | |
| 10+ | 4 | 10 | 4 | 12 | 6 | 8 | 8 | 16 | 6 | 18 |
| 20+ | 8 | 12 | 10 | 22 | 8 | 20 | 12 | 18 | 12 | 28 |
| 30+ | 8 | 30 | 16 | 20 | 16 | 24 | 12 | 36 | 18 | 24 |
| 40+ | 16 | 40 | 12 | 42 | 20 | 24 | 22 | 46 | 16 | 42 |
| 50+ | 20 | 32 | 24 | 52 | 18 | 40 | 24 | 36 | 28 | 58 |
| 60+ | 16 | 60 | 30 | 36 | 32 | 48 | 20 | 66 | 32 | 44 |
| 70+ | 24 | 70 | 24 | 72 | 36 | 40 | 36 | 60 | 24 | 78 |
| 80+ | 32 | 54 | 40 | 82 | 24 | 64 | 42 | 56 | 40 | 88 |
| 90+ | 24 | 72 | 44 | 60 | 46 | 72 | 32 | 96 | 42 | 60 |
Общие сведения
Функция Эйлера φ(n){\displaystyle \varphi (n)} показывает, сколько натуральных чисел из отрезка [1,n−1]{\displaystyle [1,\;n-1]} имеют c n{\displaystyle n} только один общий делитель — единицу. Функция Эйлера определена на множестве натуральных чисел, и значения её лежат в множестве натуральных чисел.
Как следует из определения, чтобы вычислить φ(n){\displaystyle \varphi (n)} , нужно перебрать все числа от 1{\displaystyle 1} до n−1{\displaystyle n-1} , и для каждого проверить, имеет ли оно общие делители с n{\displaystyle n} , а затем подсчитать, сколько чисел оказались взаимно простыми с n{\displaystyle n} . Эта процедура для больших чисел n{\displaystyle n} весьма трудоёмка, поэтому для вычисления φ(n){\displaystyle \varphi (n)} используют другие методы, которые основываются на специфических свойствах функции Эйлера.
В таблице справа представлены первые 99 значений функции Эйлера. Анализируя эти данные, можно заметить, что значение φ(n){\displaystyle \varphi (n)} не превосходит n−1{\displaystyle n-1} , и в точности ему равно, если n{\displaystyle n} — простое. Таким образом, если в координатах (n,y){\displaystyle (n,\;y)} провести прямую y=n−1{\displaystyle y=n-1} , то значения y=φ(n){\displaystyle y=\varphi (n)} будут лежать либо на этой прямой, либо ниже её. Также, глядя на график, приведенный в начале статьи, и на значения в таблице, можно предположить, что существует прямая, проходящая через ноль, которая ограничивает значения φ(n){\displaystyle \varphi (n)} снизу. Однако, оказывается, такой прямой не существует. То есть, какую бы пологую прямую мы ни провели, всегда найдется натуральное число n{\displaystyle n} , такое, что φ(n){\displaystyle \varphi (n)} лежит ниже этой прямой. Ещё одной интересной особенностью графика является наличие некоторых прямых, вдоль которых концентрируются значения функции Эйлера. Так, например, помимо прямой y=n−1{\displaystyle y=n-1} , на которой лежат значения φ(n)=n−1{\displaystyle \varphi (n)=n-1} , где n{\displaystyle n} — простое, выделяется прямая, примерно соответствующая y=n/2{\displaystyle y=n/2} , на которую попадают значения φ(2n)=φ(n)=n−1{\displaystyle \varphi (2n)=\varphi (n)=n-1} , где n{\displaystyle n} — простое.
Более подробно поведение функции Эйлера рассматривается в разделе #Асимптотические соотношения.
Мультипликативность функции Эйлера
Одним из основных свойств функции Эйлера является её мультипликативность. Это свойство было установлено ещё Эйлером и формулируется оно следующим образом: для любых взаимно простых чисел m{\displaystyle m} и n{\displaystyle n} [4]
- φ(mn)=φ(m)φ(n).{\displaystyle \varphi (mn)=\varphi (m)\varphi (n).}
Доказательство мультипликативности
Для доказательства мультипликативности функции Эйлера потребуется следующая вспомогательная теорема[5].
- Теорема 1. Пусть (m,m′)=1{\displaystyle (m,\;m’)=1} и a{\displaystyle a} пробегает приведённую систему вычетов по модулю m{\displaystyle m} , в то время как a′{\displaystyle a’} пробегает приведённую систему вычетов по модулю m′{\displaystyle m’} . Тогда a′m+am′{\displaystyle a’m+am’} пробегает приведённую систему вычетов по модулю mm′{\displaystyle mm’} .
- Доказательство. Если
- a1′m+a1m′≡a2′m+a2m′(modmm′),{\displaystyle a_{1}’m+a_{1}m’\equiv a_{2}’m+a_{2}m'{\pmod {mm’}},}
- тогда
- a1m′≡a2m′(modm),{\displaystyle a_{1}m’\equiv a_{2}m'{\pmod {m}},}
- поэтому
- a1≡a2(modm);{\displaystyle a_{1}\equiv a_{2}{\pmod {m}};}
- аналогично
- a1′≡a2′(modm′).{\displaystyle a_{1}’\equiv a_{2}'{\pmod {m’}}.}
- Поэтому существует mm′{\displaystyle mm’} несравнимых по модулю чисел, которые образуют приведённую систему вычетов по модулю mm′{\displaystyle mm’} .
Теперь можно доказать основное утверждение[6].
- Теорема 2. Функция Эйлера мультипликативна.
- Доказательство. Если (m,m′)=1{\displaystyle (m,\;m’)=1} , то по Теореме 1 a′m+am′{\displaystyle a’m+am’} пробегает приведённую систему вычетов по модулю mm′{\displaystyle mm’} , когда a{\displaystyle a} и a′{\displaystyle a’} пробегают приведённые системы вычетов по модулям m{\displaystyle m} и m′{\displaystyle m’} соответственно. Также:
- (a′m+am′,mm′)=1{\displaystyle (a’m+am’,\;mm’)=1}
- ⇔(a′m+am′,m)=1,(a′m+am′,m′)=1{\displaystyle \Leftrightarrow (a’m+am’,\;m)=1,\;(a’m+am’,\;m’)=1}
- ⇔(am′,m)=1,(a′m,m′)=1{\displaystyle \Leftrightarrow (am’,\;m)=1,\;(a’m,\;m’)=1}
- ⇔(a,m)=1,(a′,m′)=1.{\displaystyle \Leftrightarrow (a,\;m)=1,\;(a’,\;m’)=1.}
- Поэтому φ(mm′){\displaystyle \varphi (mm’)} чисел, которые меньше числа mm′{\displaystyle mm’} и взаимно просты с ним, являются наименьшими положительными вычетами среди φ(m)φ(m′){\displaystyle \varphi (m)\varphi (m’)} значений a′m+am′{\displaystyle a’m+am’} , для которых a{\displaystyle a} взаимно просто с m{\displaystyle m} и a′{\displaystyle a’} взаимно просто с m′{\displaystyle m’} . Отсюда следует, что
- φ(mm′)=φ(m)φ(m′).{\displaystyle \varphi (mm’)=\varphi (m)\varphi (m’).}
Функция Эйлера от простого числа
Для простого p{\displaystyle p} значение функции Эйлера задаётся явной формулой[7]:
- φ(p)=p−1,{\displaystyle \varphi (p)=p-1,}
которая следует из определения. Действительно, если p{\displaystyle p} — простое, то все числа, меньшие p{\displaystyle p} , взаимно просты с ним, а их ровно p−1{\displaystyle p-1} штук.
Для вычисления функции Эйлера от степени простого числа используют следующую формулу[7]:
- φ(pn)=pn−pn−1.{\displaystyle \varphi (p^{n})=p^{n}-p^{n-1}.}
Это равенство обосновывается следующим образом. Подсчитаем количество чисел от 1{\displaystyle 1} до pn{\displaystyle p^{n}} , которые не взаимно просты с pn{\displaystyle p^{n}} . Все они, очевидно, кратны p{\displaystyle p} , то есть, имеют вид: p,2p,3p,…,pn−1p.{\displaystyle p,\;2p,\;3p,\;\ldots ,\;p^{n-1}p.} Всего таких чисел pn−1{\displaystyle p^{n-1}} . Поэтому количество чисел, взаимно простых с pn{\displaystyle p^{n}} , равно pn−pn−1{\displaystyle p^{n}-p^{n-1}} .
Функция Эйлера от натурального числа
Вычисление φ(n){\displaystyle \varphi (n)} для произвольного натурального n{\displaystyle n} основывается на мультипликативности функции Эйлера, выражении для φ(pn){\displaystyle \varphi (p^{n})} , а также на основной теореме арифметики. Для произвольного натурального числа значение φ(n){\displaystyle \varphi (n)} представляется в виде[7]:
- φ(n)=n∏p∣n(1−1p),n>1,{\displaystyle \varphi (n)=n\prod _{p\mid n}\left(1-{\frac {1}{p}}\right),\;\;n>1,}
где p{\displaystyle p} — простое число и пробегает все значения, участвующие в разложении n{\displaystyle n} на простые сомножители.
Доказательство
Обобщённая мультипликативность
Функция Эйлера является мультипликативной арифметической функцией, то есть
- φ(mn)=φ(m)φ(n)∀m,n∈N:(m,n)=1.{\displaystyle \varphi (mn)=\varphi (m)\varphi (n)\;\;\;\forall m,\,n\in \mathbb {N} \colon (m,\,n)=1.}
Здесь существенно, что наибольший общий делитель m{\displaystyle m} и n{\displaystyle n} равен единице. Оказывается, существует обобщение этой формулы на случай, когда m{\displaystyle m} и n{\displaystyle n} имеют общие делители, отличные от единицы. А именно, для любых натуральных m{\displaystyle m} и n{\displaystyle n} [8]:
- φ(m⋅n)=φ(m)⋅φ(n)⋅dφ(d),{\displaystyle \varphi (m\cdot n)=\varphi (m)\cdot \varphi (n)\cdot {\frac {d}{\varphi (d)}},}
где d{\displaystyle d} — наибольший общий делитель m{\displaystyle m} и n.{\displaystyle n.} Это свойство является естественным обобщением мультипликативности.
Доказательство обобщённой мультипликативности
Пусть (m,n)=d,{\displaystyle (m,\,n)=d,} тогда m=m′d,n=n′d,{\displaystyle m=m’d,\;n=n’d,} причем в общем случае (m′,d)≠1{\displaystyle (m’,\,d)\neq 1} и (n′,d)≠1.{\displaystyle (n’,\,d)\neq 1.} Поэтому можно записать:
- d=d1δ1⋅…⋅dkδk⋅dk+1δk+1⋅…⋅dKδK,{\displaystyle d=d_{1}^{\delta _{1}}\cdot \ldots \cdot d_{k}^{\delta _{k}}\cdot d_{k+1}^{\delta _{k+1}}\cdot \ldots \cdot d_{K}^{\delta _{K}},}
- m′=d1α1⋅…⋅dkαk⋅p1β1⋅…⋅prβr,{\displaystyle m’=d_{1}^{\alpha _{1}}\cdot \ldots \cdot d_{k}^{\alpha _{k}}\cdot p_{1}^{\beta _{1}}\cdot \ldots \cdot p_{r}^{\beta _{r}},}
- n′=dk+1γk+1⋅…⋅dKγK⋅q1ε1⋅…⋅qsεs.{\displaystyle n’=d_{k+1}^{\gamma _{k+1}}\cdot \ldots \cdot d_{K}^{\gamma _{K}}\cdot q_{1}^{\varepsilon _{1}}\cdot \ldots \cdot q_{s}^{\varepsilon _{s}}.}
Здесь первые k{\displaystyle k} делителей d{\displaystyle d} являются также делителями m′,{\displaystyle m’,} а последние K−k{\displaystyle K-k} делителей d{\displaystyle d} являются делителями n′.{\displaystyle n’.} Распишем:
- φ(mn)=φ(d2⋅m′n′)=φ((d1δ1⋅…⋅dkδk⋅dk+1δk+1⋅…⋅dKδK)2⋅d1α1⋅…⋅dkαk⋅p1β1⋅…⋅prβr⋅dk+1γk+1⋅…⋅dKγK⋅q1ε1⋅…⋅qsεs).{\displaystyle \varphi (mn)=\varphi (d^{2}\cdot m’n’)=\varphi ((d_{1}^{\delta _{1}}\cdot \ldots \cdot d_{k}^{\delta _{k}}\cdot d_{k+1}^{\delta _{k+1}}\cdot \ldots \cdot d_{K}^{\delta _{K}})^{2}\cdot d_{1}^{\alpha _{1}}\cdot \ldots \cdot d_{k}^{\alpha _{k}}\cdot p_{1}^{\beta _{1}}\cdot \ldots \cdot p_{r}^{\beta _{r}}\cdot d_{k+1}^{\gamma _{k+1}}\cdot \ldots \cdot d_{K}^{\gamma _{K}}\cdot q_{1}^{\varepsilon _{1}}\cdot \ldots \cdot q_{s}^{\varepsilon _{s}}).}
В силу мультипликативности функции Эйлера, а также с учётом формулы
- φ(pn)=pn(1−1p),{\displaystyle \varphi (p^{n})=p^{n}(1-{\frac {1}{p}}),}
где p{\displaystyle p} — простое, получаем:
- φ(mn)=d1α1+δ1(1−1d1)⋅…⋅dkαk+δk(1−1dk)⋅p1β1(1−1p1)⋅…⋅prβr(1−1pr)⋅dk+1δk+1(1−1dk+1)⋅…⋅dKδK(1−1dK)××dk+1γk+1+δk+1(1−1dk+1)⋅…⋅dKγK+δK(1−1dK)⋅q1ε1(1−1q1)⋅…⋅qsεs(1−1qs)⋅d1δ1(1−1d1)⋅…⋅dk+1δk+1(1−1dk+1)××1(1−1d1)⋅…⋅(1−1dK).{\displaystyle {\begin{aligned}\varphi (mn)&=d_{1}^{\alpha _{1}+\delta _{1}}\left(1-{\frac {1}{d_{1}}}\right)\cdot \ldots \cdot d_{k}^{\alpha _{k}+\delta _{k}}\left(1-{\frac {1}{d_{k}}}\right)\cdot p_{1}^{\beta _{1}}\left(1-{\frac {1}{p_{1}}}\right)\cdot \ldots \cdot p_{r}^{\beta _{r}}\left(1-{\frac {1}{p_{r}}}\right)\cdot d_{k+1}^{\delta _{k+1}}\left(1-{\frac {1}{d_{k+1}}}\right)\cdot \ldots \cdot d_{K}^{\delta _{K}}\left(1-{\frac {1}{d_{K}}}\right)\times \\&\;\times \;d_{k+1}^{\gamma _{k+1}+\delta _{k+1}}\left(1-{\frac {1}{d_{k+1}}}\right)\cdot \ldots \cdot d_{K}^{\gamma _{K}+\delta _{K}}\left(1-{\frac {1}{d_{K}}}\right)\cdot q_{1}^{\varepsilon _{1}}\left(1-{\frac {1}{q_{1}}}\right)\cdot \ldots \cdot q_{s}^{\varepsilon _{s}}\left(1-{\frac {1}{q_{s}}}\right)\cdot d_{1}^{\delta _{1}}\left(1-{\frac {1}{d_{1}}}\right)\cdot \ldots \cdot d_{k+1}^{\delta _{k+1}}\left(1-{\frac {1}{d_{k+1}}}\right)\times \\&\;\times \;{\frac {1}{\left(1-{\frac {1}{d_{1}}}\right)\cdot \ldots \cdot \left(1-{\frac {1}{d_{K}}}\right)}}.\end{aligned}}}
В первой строке записано φ(m),{\displaystyle \varphi (m),} во второй — φ(n),{\displaystyle \varphi (n),} а третью можно представить, как d/φ(d).{\displaystyle d/\varphi (d).} Поэтому:
- φ(m⋅n)=φ(m)⋅φ(n)⋅dφ(d).{\displaystyle \varphi (m\cdot n)=\varphi (m)\cdot \varphi (n)\cdot {\frac {d}{\varphi (d)}}.}
Некоторые частные случаи:
- φ(nm)=nm−1φ(n).{\displaystyle \;\varphi \left(n^{m}\right)=n^{m-1}\varphi (n).}
- φ(2m)={2φ(m),m=2k,k∈N,φ(m),m=2k−1,k∈N.{\displaystyle \varphi (2m)={\begin{cases}2\varphi (m),&m=2k,\;k\in \mathbb {N} ,\\\varphi (m),&m=2k-1,\;k\in \mathbb {N} .\end{cases}}}
- φ(M)⋅φ(d)=φ(m)⋅φ(n),{\displaystyle \varphi (M)\cdot \varphi (d)=\varphi (m)\cdot \varphi (n),} где M{\displaystyle M} — наименьшее общее кратное m{\displaystyle m} и n{\displaystyle n} , а d{\displaystyle d} — их наибольший общий делитель.
Теорема Эйлера
Наиболее часто на практике используется свойство, установленное Эйлером:
- aφ(m)≡1(modm),{\displaystyle a^{\varphi (m)}\equiv 1{\pmod {m}},}
если a{\displaystyle a} и m{\displaystyle m} взаимно просты.
Это свойство, которое называют теоремой Эйлера, вытекает из Теоремы Лагранжа и того факта, что φ(m){\displaystyle \varphi (m)} равна порядку группы обратимых элементов кольца вычетов по модулю m{\displaystyle m} .
В качестве следствия теоремы Эйлера можно получить малую теорему Ферма. Для этого нужно взять не произвольное m,{\displaystyle m,} а простое. Тогда:
- am−1≡1(modm).{\displaystyle a^{m-1}\equiv 1{\pmod {m}}.}
Последняя формула находит применение в различных тестах простоты.
Другие свойства
Исходя из представимости φ(n){\displaystyle \varphi (n)} произведением Эйлера, несложно получить следующее полезное утверждение:
- a∣b⇒φ(a)∣φ(b).{\displaystyle a\mid b\Rightarrow \varphi (a)\mid \varphi (b).}
Следующее равенство[9][10] является следствием теоремы Зигмонди (англ.):
- φ(an+bn)≡0(modn),a>b⩾1.{\displaystyle \varphi (a^{n}+b^{n})\equiv 0{\pmod {n}},\;a>b\geqslant 1.}
Всякое натуральное число представимо в виде суммы значений функции Эйлера от его натуральных делителей[11]:
- ∑d∣nφ(d)=n.{\displaystyle \sum _{d\mid n}\varphi (d)=n.}
Сумма всех чисел, меньших данного, и взаимно простых с ним, выражается через функцию Эйлера:
- ∑1⩽k⩽n(k,n)=1k=12nφ(n),n>1.{\displaystyle \sum _{1\leqslant k\leqslant n \atop (k,\;n)=1}k={\frac {1}{2}}n\varphi (n),\;n>1.}
ru-wiki.org
Функция Эйлера Википедия
Первая тысяча значений φ(n){\displaystyle \varphi (n)}Фу́нкция Э́йлера φ(n){\displaystyle \varphi (n)} — мультипликативная арифметическая функция, равная количеству натуральных чисел, меньших n{\displaystyle n} и взаимно простых с ним. При этом полагают по определению, что число 1 взаимно просто со всеми натуральными числами, и φ(1)=1{\displaystyle \varphi (1)=1}[1].
Например, для числа 24 существует 8 меньших его и взаимно простых с ним чисел (1, 5, 7, 11, 13, 17, 19, 23), поэтому φ(24)=8{\displaystyle \varphi (24)=8}.
Названа в честь Эйлера, который впервые использовал её в 1760 году в своих работах по теории чисел для доказательства малой теоремы Ферма, а затем и для доказательства более общего утверждения — теоремы Эйлера. Позднее функцию использовал Гаусс в своем труде «Арифметические исследования», вышедшем в свет в 1801 году. Гаусс ввёл ставшее стандартным обозначение φ(n){\displaystyle \varphi (n)}[2].
Функция Эйлера находит применение в вопросах, касающихся теории делимости и вычетов (см. сравнение по модулю), теории чисел, криптографии. Функция Эйлера играет ключевую роль в алгоритме RSA[3].
ru-wiki.ru
