Длина дуги кривой через интеграл
В декартовой системе координат
Пусть в декартовой системе координат задана плоская кривая уравнением , . Если функция и ее производная непрерывны на отрезке , то длина дуги кривой вычисляется по формуле:
ПРИМЕР 1
| Задание | Вычислить длину кривой |
| Решение | Найдем производную :
Тогда
Итак, искомая длина
|
| Ответ |
Если кривая задана параметрически
Если уравнение кривой задано параметрически , где и – непрерывные функции с непрерывными производными, то длина заданной кривой находится по формуле:
ПРИМЕР 2
| Задание | Найти длину дуги кривой
|
| Решение | Найдем
Тогда
Итак, искомая длина дуги
|
| Ответ |
В полярной системе координат
Пусть кривая задана уравнением в полярных координатах , . Предположим, что функция и ее производная непрерывны на отрезке . Тогда длина дуги кривой вычисляется по формуле:
ПРИМЕР 3
| Задание | Найти длину дуги кардиоиды |
| Решение | Найдем выражение:
Отсюда
Тогда искомая длина
|
| Ответ |
Виды интегралов
Применение интегралов в физике и математике
Геометрический и физический смысл интеграла
Решение интегралов методом подстановки
ru.solverbook.com
Вычисление длины дуги плоской кривой
20)
Пусть известна функция и требуется найти длину дуги, заданной функцией , где .
Для определения длины дуги необходимо вычислитьопределенный интеграл:
Рассмотрим случай параметрического задания кривой:
где . В этом случае для определения длина дуги вычисляется определенный интеграл:
Рассмотрим случай, когда кривая задается в полярных координатах где. Тогда для определения длины дугивычисляется следующийопределенный интеграл:
21)
Как вычислить объем тела вращения с помощью определенного интеграла?
Помимо нахождения площади плоской фигуры с помощью определенного интегралаважнейшим приложением темы является вычисление объема тела вращения. Материал простой, но читатель должен быть подготовленным: необходимо уметь решатьнеопределенные интегралы средней сложности и применять формулу Ньютона-Лейбница в определенном интеграле. Как и для задачи нахождения площади, нужны уверенные навыки построения чертежей – это чуть ли не самое важное (поскольку интегралы сами по себе чаще будут лёгкими). Освоить грамотную и быструю технику построения графиков можно с помощью методических материалов Графики и свойства Элементарных функций и Геометрические преобразования графиков. Но, собственно, о важности чертежей я уже неоднократно говорил на уроке Определенный интеграл. Как вычислить площадь фигуры .
Вообще в интегральном исчислении очень много интересных приложений, с помощью определенного интеграла можно вычислить площадь фигуры, объем тела вращения,длину дуги, площадь поверхности вращения и многое другое. Поэтому будет весело, пожалуйста, настройтесь на оптимистичный лад!
Представьте некоторую плоскую фигуру на координатной плоскости. Представили? … Интересно, кто что представил… =))) Её площадь мы уже находили. Но, кроме того, данную фигуру можно ещё и вращать, причем вращать двумя способами:
– вокруг оси абсцисс ; – вокруг оси ординат .
В
данной статье будут разобраны оба
случая. Особенно интересен второй способ
вращения, он вызывает наибольшие
затруднения, но на самом деле решение
практически такое же, как и в более
распространенном вращении вокруг оси
абсцисс. В качестве бонуса я вернусь
к задаче
нахождения площади фигуры,
и расскажу вам, как находить площадь
вторым способом – по оси
Начнем с наиболее популярной разновидности вращения.
Вычисление объема тела, образованного вращением плоской фигуры вокруг оси
Пример 1
Вычислить объем тела, полученного вращением фигуры, ограниченной линиями ,вокруг оси.
Решение: Как и в задаче на нахождение площади, решение начинается с чертежа плоской фигуры. То есть, на плоскости необходимо построить фигуру, ограниченную линиями,, при этом не забываем, что уравнениезадаёт ось. Как рациональнее и быстрее выполнить чертёж, можно узнать на страницахГрафики и свойства Элементарных функций и Определенный интеграл. Как вычислить площадь фигуры. Это китайское напоминание, и на данном моменте я больше не останавливаюсь.
Чертёж здесь довольно прост:
studfiles.net
Калькулятор длины дуги кривой линии в декартовых координатах
Одним из приложений определенного интеграла является вычисление длины дуги плоской кривой. На рисунке изображен график функции y(x) = x2
Для того, чтобы узнать длину дуги кривой линии изображенной на рисунке, необходимо вычислить определенный интеграл:
В более общем случае, если у нас задана функция y = f(x) в декартовых координатах и стоит задача найти длину дуги этой кривой между точками a и b, нам необходимо вычислить интеграл:
В приведенной выше формуле, выражение означает, что сначала нужно вычислить производную функции f(x), а затем полученное выражение возвести в квадрат.
Наш онлайн калькулятор, построенный на основе системы Wolfram Alpha, позволяет вычислить длину кривой, заданной в декартовых координатах для любой, даже очень сложной функции.
www.mathforyou.net
Длина дуги кривой линии в декартовой системе координат
Длина дуги кривой линии в декартовой системе координат на Math34.biz для закрепления студентами пройденного материала. Вычислить длину дуги кривой от явно заданной функции с помощью приложения интеграла сводится к базовому вычислению определенного интеграла на отрезке, который задан условием задачи. Зачастую приходится знать, как длина кривой рассчитывается на практике без использования подручных средств. Как никому математикам эта поставленная задача известна еще с древних времен, когда кривую спрямляли, разбивая на множество прямых отрезков, и вычисляли их сумму. Тогда еще не знали великие умы, что значение длины дуги вычисляется точно только через интеграл, при этом зная ее формулу. Именно функция от аргумента, описывающая линию, подставляется в формулу и вычислить длину кривой после таких манипуляций очень и очень просто. Можно использовать наш калькулятор Math34.biz для этого, специально предназначенный для студентов и школьников, чтобы им не тратить много времени. На нашем ресурсе множество решебников, среди которых длина кривой решается онлайн в считанные секунды и с высокой точностью результат выводится на странице сайта. В современной математике каждому учащемуся необходимо вычислить длину дуги кривой в рамках некоторой конкретной задачи, а может быть и попутно при выполнении более сложной работы. Даже выделили спец занятия, в котором изучаются приложения определенного интеграла с помощью множества выведенных учеными формул, среди которых есть такая задача, как найти длину дуги кривой от явно или неявно заданной функции. Math34.biz — это и есть калькулятор для вычисления длины дуги кривой в заданной системе координат, которые изучают в школьной и вузовской программах. Помимо пройденного пути по условию текстовой задачи, еще вычисляется длина дуги кривой через интеграл, именно той, которая соответствует траектории движения пешехода. Не касаясь абстрактных объектов или заурядных сложных систем исчисления, например, таких как риманово пространство, затрагивающих аффинные преобразования, будем считать, что длина дуги кривой находится в декартовой системе координат. Поэтому смело обращайтесь к сайту Math34.biz, где представлен раздел по нахождению длины дуги онлайн. Вообще-то говоря, значение длины кривой в разных системах координат будет тоже разным и это неоспоримый факт, но очень любопытный. Допустим мы имеем криволинейную систему координат в трехмерном пространстве, и длина кривой зависит от начальной и конечной точки исследуемого отрезка. Так вот, если по точкам отобразить кривую в этой системе, то визуально она будет представлять прямую относительно прямоугольных координат и длина дуги определится через обычный интеграл. Но к этому неочевидному факту порой очень сложно прийти опытным путем, да и представить визуально криволинейное пространство человек не в силе по своей природе. Мы все сводим к сравнению к привыкшей прямоугольной декартовой системе. Однако вычислить длину кривой можно в любой системе координат, если она спрямляема, что является основой при решении такой задачи. Существуют кривые не спрямляемые, длина кривой онлайн которой не найдёт ни один калькулятор. Вообще такую кривую не задать в нормальном представлении. Есть правило, по которому она строится и все. А вот вычислить длину дуги кривой не получится никому, потому что ее просто не существует. Помимо расчета массы тела или моментов инерции тел и пластин, с помощью приложения определенного интеграла можно с легкостью найти длину дуги кривой линии в различных системах координат, даже в полярной, к слову это даже легче сделать, нежели в декартовой. Переход из первой системы координат во вторую выполняется несложным преобразованием через тригонометрические функции, определяя зависимость между углом и радиусом-функции от начала координат. Далее можно воспользоваться бесплатным калькулятором длины дуги кривой и получить результат сразу здесь в окне браузера. Используйте Math34.biz в своих целях для достижения результата сразу. Не тратьте свое драгоценное время на то, чтобы, зная материал, по несколько раз проделывать сложные действия и искать длину дуги кривой самому, в то время как то же самое и мгновенно сможет выполнить сайт Math34.biz и поможет в решении поставленной задачи. При этом длина дуги онлайн будет найдена от любой функции из любого задачника по высшей математике. По ходу математического решения длину кривой возможно найти через определенный интеграл от заданной функции по нижнему и верхнему пределам интегрирования. Одновременно с нахождением общего решения задачи, длина дуги через конкретный интеграл определяется моментально при подстановке требуемых величин в итоговую сумму подынтегральной функции, что приводит нас к исследованию радикальной функции на концах отрезка. Единовременно к математической задаче присоединяется параллельная, а именно правильно вычислить длину кривой линии по переменной t, как зависимость функции от временной шкалы по ходу движения материальной точки. Однако траектория движения тела как совокупности материальных точек, либо конкретной точки в отдельности, не может представить полного характера движения, не имея закон, по которому описывается ее линия движения. Но можно, используя конечно математический анализ, с легкостью исследовать ее движение, в том числе ускорения на определенных участках, а также определить, чему равна длина кривой с вычислением этой величины онлайн на сайте Math34.biz. Как находится длина дуги кривой через интеграл известно давным-давно ученым во всем мире, но донести это до студентов вовремя не так-то просто, как кажется на первый вид. Это замечательный и полезный для студентов и учеников школ ресурс позволяет вычислить длину дуги кривой, как говорится, здесь и сейчас прямо на ваших глазах, и при этом ответ будет абсолютно без погрешностей с точностью до тысячных знаков. Поскольку приложения определенного интеграла не в полной мере изучаются в ВУЗах, потому что на это отводится немного учебного времени, студентам необходимо самим приложить усилия в познании данного важного раздела математики, потому что это пригодится в дальнейшем в жизни. Аналогичные сайты, в отличие от Math34.biz, тоже помогут вам найти длину дуги кривой от заданной функции, но мы рекомендуем все-таки вычислительные результаты сравнить с полученным ответом нашего ресурса, за который мы отвечаем совей репутацией. Какой бы современный и мощнейший калькулятор длины дуги кривой вы ни использовали для исследования задачи по математике, ни один такой калькулятор или компьютер не сможет помочь научиться решать такие задачи самому. От вас требуется внимательность, усидчивость, а главное терпение при изучении любого математического раздела, поскольку это наука точная и требует постепенного освоения, в силу своей специфики. Возвращаясь к нашей тематике, подытожим мысли о том, как все-таки без особых затруднений выяснить, что длина дуги кривой может быть найдена по заранее заданной формуле и вычислена правильно. Мы настоятельно советуем каждому кто примется за познание науки математики, уметь и знать, как вычисляется длина дуги онлайн на сайте Math34.biz. Как обычно в таких задачах необходима такая длина дуги кривой, вычисленная через интеграл, поскольку от этого зависит ход дальнейшего решения задачи. Назначение условия по выявлению критических точек не связано напрямую с поставленной задаче, но длина кривой находится по тем же принципам математических законов. Правильно заметили ученики, что длина дуги как определенный интеграл дает максимум ответов на все поставленные вопросы при исследовании участка движения материальной точки. При изучении движения материальной пластины, достаточно знать траекторию движения хотя бы двух ее точек, потому что линии всех остальных ее точек можно определить исходя из геометрических связей, тем более затем вычислить длину кривой движения любой точки на пластине. Используя калькулятор на Math34.biz, длина кривой онлайн определяется практически сразу и с высочайшей точностью в ответе, поскольку мы используем современные технологии в подходе решения подобных математических проблем. И если вам вдруг предстоит вычислить длину дуги кривой от явной или неявной функции, то не расстраивайтесь сразу, пока не посетите наш ресурс, поскольку помимо приложения определенного интеграла для площадей или вычисления объемов тел, вам с легкостью представится возможность найти длину дуги кривой прямо здесь и сию минуту. Рациональное использование ресурсов, а время — это самый важный и главный ресурс, которым обладает человек, позволяет экономить время с калькулятором длины дуги кривой, потому что этот уникальный по своей сути инструмент в руках умельца, даст наибольший результат, нежели от простого заучивания сложных математических формул без отработанных практических навыков. Вовсе не секрет тот факт, что усидчивость и терпение — залог успешности любой личности, поскольку только в трудных ситуациях студент учится быть самостоятельным и прививает себе качество лидера. Ваши друзья и коллеги не смогут быстрее вас выявить, что длина дуги кривой будет больше у первой функции, но не у второй функции, хотя отрезки берутся одинаковые от первой точки до последней. Бывает так, что длина дуги онлайн имеет значение отличное от того, которое получилось при ручном подсчете при помощи подручных калькуляторов и таблиц, но не стоит раньше времени делать необоснованные выводы, потому что естественная погрешность допустима при вычислениях вручную. В заключение все же студентам необходимо рекомендовать сайт Math34.biz и однозначно сказать, что длина дуги кривой через интеграл вычисляется гораздо более быстрее, продуктивнее и намного точнее, чем использовать численные методы по приблизительным вычислениям. Повсеместно принято на уровне учащихся такое мнение, что длина кривой не может быть вычислена через математические формулы, если не знать их. Однако нет, это ошибочное суждение, потому что существуют современные сервисы в интернете, специально заточенные под студентов, где есть калькуляторы по математике и длина дуги как интеграл рассчитывается в считанные секунды прямо на глазах пользователей сайтом. Такие калькуляторы могут вычислить длину кривой от любой заданной функции, используя математические законы для этого, определяя и выбирая оптимальные расчеты, как бы это сделал грамотный преподаватель. Ведь запрограммировать сколь угодно сложный вычислительный процесс выгоднее и менее затратнее, чем постоянно лезть в заумные книги, искать подходящую формулу, определять вид функции и так далее и тому подобное. Используйте все преимущества сайта Math34.biz для своих поставленных целей, будьте гибче в подходе к изучению точных наук, таких как математика, физика или химия, выжимайте по максимуму их аналогичных ресурсов, уделяя больше времени к изучению теоретических моментов, чем практических, поскольку практика хоть и является основой закрепления пройденного материала, но все же теория заставляет шевелить мозгами более интенсивно и тем самым развивая ваш кругозор. Если длина кривой онлайн находится сразу и дает достаточно точный ответ, то принимая во внимание условия подзадачи, сразу переходите к следующим вычислениям, и завершайте до логического заключения выводы. Math34.biz позволит вам и всем остальным ученикам вычислить длину дуги кривой по траектории движения материальной точки и завязать формулировку задачи на базовом определении местоположения объекта как материального тела. Из приложения определенного интеграла с легкостью и наибольшей точностью, чем численными методами, которые дают приближенные результаты, можно и нужно решать такие задачки, как объем тела вращения фигуры вокруг оси в декартовой системе координат, или, например, определение массы пластины материальной, с заданной плотностью, и много чего полезного в изучении точных наук. А мы с вами в свое время сможем найти длину дуги кривой для функции, которая задана явно или параметрически, базируясь на принципах правильного подхода к решению такого рода задач математического анализа. Как известно, найти или однозначно определить решение нельзя, не опираясь на фундаментальные законы матери природы. Зачастую в аспекте изучения науки студенты ошибаются довольно редко, если под рукой имеется качественный калькулятор длины дуги кривой и он доступен 24 часа в сутки, с помощью которого выполняются сложнейшие математические расчеты. Прямо укажем такую очевидную вещь как правильный и своевременный подход к изучению теории и практики в совокупности по мере возрастания и прибавления знаний ученика. Длина дуги кривой имеет огромный прикладной смысл, поскольку инженерам дает возможность так сконструировать строительный объект, чтобы не было аварийных ситуаций при его эксплуатации в ближайшем и далеком будущем. Взять, например, проект моста через крупную реку. Просто километры тросов свисают гирляндами над проезжей или прохожей частями этого моста, огромный массы металла нагружают конструкцию, делая ее с одной стороны гигантским искусственным бесподобием, с дугой — уникальным достижением человеческой мысли и его возможностями в этом мире. Как никогда при расчетах длина дуги онлайн вычисляется с незамедлительным результатом, поскольку миллионы математических функций должны отработать в разумные периоды времени, описывая конструкцию как единый живой механизм со своими естественными деформациями вдоль и поперек. И если вам скажут, что длина дуги кривой через интеграл — это бесполезное занятие, то вы знаете как дать ответ этим глупостям. Все, чем мы пользуемся повседневно и чем гордится наша страна — плод развития человека в этой среде. Как только истинная длина кривой достигнет своего верхнего предельного значения, используя метод спрямляемой линии, то есть вписыванием все новых отрезков половинного деления, так сразу в ответе математической задачи получим приближенное значение интегрального метода. То есть, другими словами говоря, длина дуги через интеграл нам дает абсолютно точное значение той величины, которой соответствует в пространстве прямоугольных координат применяемый метод решения. Студенты на этом этапе постановки задачи немного теряются и допускают простейшие ошибки. Если все-таки не удалось в полной мере вычислить длину кривой с использованием явной формулы для ее вычисления, то разбейте задачу на несколько подпунктов, так вам станет визуально легче ее воспринимать и в дальнейшем избавиться от математических неточностей. Рекомендуем индивидуально использовать ресурс Math34.biz, чтобы знать, как длина кривой онлайн вычисляется за несколько секунд после того, как ввести данные по условию задачи и нажать на кнопку «Решение». Предположим вы знаете как вычислить длину дуги кривой и имеете достаточный практический опыт в этом, но не забывайте, что, экономя свое время на простых вещах, вы оставляете за собой право распоряжаться личным свободным временем для дальнейшего изучения математики онлайн. Известные всем приложения определенного интеграла дают массу возможностей ученым применять их повсеместно в строительстве, монтаже конструкций и просто в целях безопасности окружающей среды. Поможет вам и всем остальным студентам найти длину дуги кривой сайт Math34.biz, который специально разработан упростить и облегчить труд учащихся. но тем самым наставляя их на путь правильного понимания сущности теоретических знаний. Вы сможете без проблем в Google или в Yandex по соответствующему запросу найти калькулятор длины дуги кривой и воспользоваться им в полной мере, но будьте бдительны, когда наталкиваетесь на недобросовестных исполнителей, которым лишь бы взять с вас оплату за услуги, тем самым, не думая, как вам сдать успешно экзамен или сессию. Потому что преподаватели уже умеют распознавать заказал ли студент работу, или выполнил ее самостоятельно. Попробуйте решать математику все-таки сами, не поленитесь изучить нужный для этого материал и подсказками решебников, а в помощь вам мы предлагаем мощный математический инструмент под названием Math34.biz и задачи, в которых требуется длина дуги кривой для дальнейших действий, решаются в два счета! Вам только нужно грамотно ввести все скобки выражения, проставить знаки сложения, вычитания, делении и умножения, возможно с радикалами, короче правильно применить синтаксис, и длина дуги вычистится онлайн прямо тут же и на мониторе вы увидите свой ответ. Как бы вы ни дробили шаг интегрирования, разумеется в допустимых пределах, лучше, чем длина дуги кривой через интеграл она вычислена быть не сможет, поскольку это наиточнейший способ добиться высокой точности ответа. Заслуга в этом принадлежит ученым из позапрошлого века и даже еще раньше. А теперь в заключение хотим поговорить о длине кривой f=f(x) или любой другой явно заданной функции, которые часто встречаются в задачниках в школах и вузах. Если вы заметили все задачи разделены на подтипы, это сделано для наилучшего восприятия учащимися пройденного материала. Как только преподаватель объяснит какую-то теорию, то сразу приводит пример для закрепления пройденного материала. Так длина кривой может быть найдена с помощью численных методов или же с помощью интеграла, что более предпочтительней. Потому что длина дуги как интеграл от функции вычислить можно по-разному, но это в точности дает нужный результат и его можно далее применять в расчетах любого типа задач. Поскольку вычислить длину кривой требуется практически на каждом занятии, в то время как учитель доносит материал по мере усложнения, то мы советуем выбрать наш сайт с названием Math34.biz и облегчить себе труд. поскольку так делают современные молодые люди. Они не зацикливаются на каком-то сложном примере, а как только встречают на своем пути преграды, то берут и в лоб решают задачи с помощью калькулятора. Зная, как длина кривой онлайн вычисляется с помощью сервиса Math34.biz, то нет сомнений, что ответ из любого другого раздела этого ресурса будет как никогда тоже точным и правильным. А в ряде калькуляторов доступны пошаговые решения, что вообще дает насказанное преимущество перед теми, кто ими не пользуется, ну или не знает, как использовать калькуляторы и правильно вычислить длину дуги кривой. Не забываем проверять себя после каждого действия, будь то обыкновенное извлечение корня, или умножение столбиком, или деление многочлена на многочлен, в ряде случаев приложения определенного интеграла дают колоссальный результат по определению веса тела или пластины, нахождения моментов инерции, что в механике представляют очень существенные показатели при проектировании, тем более помогают найти длину дуги кривой, что тоже будет важно для инженеров. Как мы ранее указали вам, пользуйтесь калькулятор длины дуги кривой на сайте Math34.biz и будет ваше ожидание удовлетворено в полной мере, так как математические задачи тут решаются как дважды два! Об этом вы можете в интернете узнать о положительных отзывах о нас, так как мы не взимаем плату за решение математики онлайн, и гарантируем точность вычислений любой сложности, благодаря мощной вычислительной системе. На сегодняшний день известно множество способов определить, что длина дуги кривой не представляет сложности при проектировании сооружений, потому что уже в инженерных калькуляторах запрограммировано вычисление этого важного этапа. Но все-таки существуют, и их множество, специально заточенных под нахождение длины дуги онлайн калькуляторов, в которых кривая может быть задана различными способами. Отсюда универсальность таких изобретений. Однако каким бы хорошим численным методом ни была найдена длина дуги кривой, но через интеграл эта длина все равно будет иметь точное значение, так сказать эталонное по сравнению с аналогичными по сути численными результатами.
math24.biz
22. Вычисление длины дуги плоской кривой
1 случай. Пусть в прямоугольных координатах на плоскости дана кривая . Вычислим длину дуги кривой, заключенной между точкамии(рис. 12).
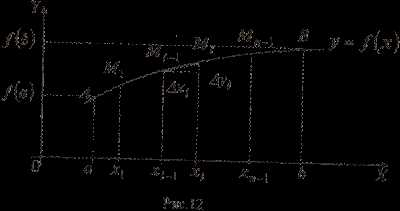
Возьмем на дуге точкис абсциссамии проведем хорды, длины которых обозначим соответственно. Тогда получим ломанную, вписанную в дугу. Длина ломанной равна
.
Определение. Длиной дугиназывается тот предел, к которому стремится длина вписанной ломанной, когда длина ее наибольшего звена стремится к нулю:
.
Длина всей дуги , заключенной между точкамии, вычисляется по формуле
.
Пример 16. Найти длину окружности .
Решение. Вычислим сначала длину четверти окружности, расположенной в 1 четверти.
Из уравнения окрежности ,.
Тогда .
Длина всей окрежности
Ответ: (лин.ед).
23. Вычисление объема тела, образованного вращением плоской фигуры вокруг оси
Пример 1
Вычислить объем тела, полученного вращением фигуры, ограниченной линиями ,вокруг оси.
Решение: Как и в задаче на нахождение площади, решение начинается с чертежа плоской фигуры. То есть, на плоскости необходимо построить фигуру, ограниченную линиями,, при этом не забываем, что уравнениезадаёт ось. Как рациональнее и быстрее выполнить чертёж, можно узнать на страницахГрафики и свойства Элементарных функцийи Определенный интеграл. Как вычислить площадь фигуры. Это китайское напоминание, и на данном моменте я больше не останавливаюсь.
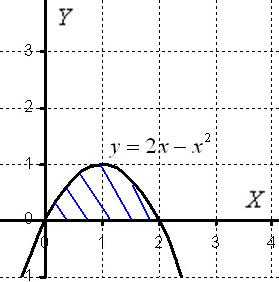
Чертёж здесь довольно прост:
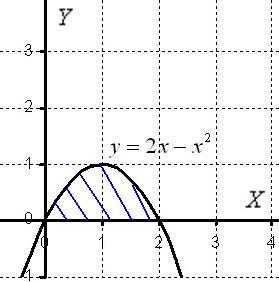
Искомая плоская фигура заштрихована синим цветом, именно она и вращается вокруг оси В результате вращения получается такая немного яйцевидная летающая тарелка, которая симметрична относительно оси. На самом деле у тела есть математическое название, но по справочнику что-то лень уточнять, поэтому едем дальше.
Как вычислить объем тела вращения?
Объем тела вращения можно вычислить по формуле:
В формуле перед интегралом обязательно присутствует число . Так повелось – всё, что в жизни крутится, связано с этой константой.
Как расставить пределы интегрирования «а» и «бэ», думаю, легко догадаться из выполненного чертежа.
Функция … что это за функция? Давайте посмотрим на чертеж. Плоская фигура ограничена графиком параболысверху. Это и есть та функция, которая подразумевается в формуле.
В практических заданиях плоская фигура иногда может располагаться и ниже оси . Это ничего не меняет – подынтегральная функция в формуле возводится в квадрат:, таким образоминтеграл всегда неотрицателен, что весьма логично.
Вычислим объем тела вращения, используя данную формулу:
Как я уже отмечал, интеграл почти всегда получается простой, главное, быть внимательным.
Ответ:
В ответе нужно обязательно указать размерность – кубические единицы . То есть, в нашем теле вращения примерно 3,35 «кубиков». Почему именно кубическиеединицы? Потому что наиболее универсальная формулировка. Могут быть кубические сантиметры, могут быть кубические метры, могут быть кубические километры и т.д., это уж, сколько зеленых человечков ваше воображение поместит в летающую тарелку.
24. Определение двойного интеграла
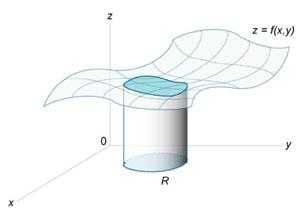
Понятие интеграла может быть расширено на функции двух и большего числа переменных. Рассмотрим, например, функцию двух переменных z = f (x,y). Двойной интеграл от функции f (x,y) обозначается как
где R — область интегрирования в плоскости Oxy. Если определенный интеграл от функции одной переменнойвыражает площадь под кривойf (x) в интервале от x = a до x = b, то двойной интеграл выражает объем под поверхностью z = f (x,y) выше плоскости Oxy в области интегрирования R (рисунок 1).
|
| |
Рис.1 |
25. Геометрический смысл двойного интеграла. Если f(x,y) ?0 в области D, то двойной интеграл (1) равен объему “цилиндрического” тела, изображенного на рис.1:
V = (2)
Пояснение. Цилиндрическое тело ограничено снизу областью D, сверху — частью поверхности z=f(x,y), с боков — вертикальными отрезками прямых, соединяющих границы этой поверхности и области D.
26. Основные свойства двойного интеграла:
1. Постоянный множитель выносится за знак интегр.
2. Интеграл от суммы равен сумме интегралов
3. Если область D разбить на 2 части, то
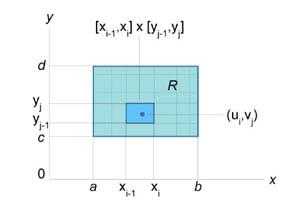
27. Вычисление двойного интеграла в декартовых координатах
Пусть требуется вычислить двойной интегр. Где ф-ция f(x;y) непрерывна в области D
Пусть область D представляет собой криволин. Трапецию ограниченную кривыми и прямыми D: ;x=a; x=b
Такая область правильная в направлении оси OY, то есть любая прямая параллельная OY пересекает границу области на более чем в 2-х точках
Если область правильная, тогда вычисление 2-го интегр. сводится к вычислению двукратного (повторного) интеграла.
28. Замена переменной в двойном интеграле. Вычисление двойного интеграла в полярных координатах
Заменим независимые переменные х и у через функцию ;, если эти функции имеют в некоторой областинепрерывные частные производные и отличный от нуля определитель
А f(x;y) интегрируема в области D, тогда имеет место замена переменных
I(u;v) – определитель Якоби (якобиан)
Пусть в полярных координатах
x=rcosφ
y=rsinφ
I(φ;r)=-r
Пусть область ограничена лучами,и кривыми
29. Физические приложения двойного интеграла
Физический смысл двойного интеграла заключен в нахождении массы плоской пластины
30. Определение криволинейного интеграла 1 рода
Если существует предел интегральной суммы, который не зависит ни от способа разбиения кривой на части, ни от выбора в них точек, то он называется криволинейный интеграл от ф-ции f(x;y) по длине кривой AB
31. Основные свойства криволинейного интеграла 1 рода
1. Постоянный множитель выносится за знак интегр.
2. Интеграл от суммы равен сумме интегралов
3. Если кривую АВ разбить на части такие, что их объединение = АВ и они имеют только 1 общую точку разделяющую их, тогда
4. Криволинейный интеграл 1-го порядка не зависит от направления пути направления кривой
32. Вычисление криволинейного интеграла 1 рода
а. Параметрическое представление кривой
б. Явно заданная функция
33. Приложения криволинейного интеграла 1 рода
1. Длина кривой
2. Площадь цилиндрической поверхности
Если направляющей цилиндрической поверхности служит кривая АВ, а образующая параллельна оси OZ, то площадь такой поверхности z=f(x;y) вычисляется по формуле
3. Масса плоской кривой (провод)
4. Статические моменты
5. Координаты центра тяжести
6. Момент инерции
34. Определение криволинейного интеграла 2 рода
Предположим, что кривая C задана векторной функцией , где переменная s − длина дуги кривой. Тогда производная векторной функции
представляет собой единичный вектор, направленный вдоль касательной к данной кривой. В приведенной выше формуле α, β и γ − углы между касательной и положительными направлениями осей Ox, Oy и Oz, соответственно.
Введем векторную функцию F(P;Q;R), определенную на кривой C, так, чтобы для скалярной функции
существовал криволинейный интеграл . Такой интеграл называетсякриволинейным интегралом второго рода от векторной функции вдоль кривойC и обозначается как
35. Основные свойства криволинейного интеграла 2 рода
1. Если в КИ2 изменить направление интегрирования, то он поменяет знак на противоположный
2. Если кривая АВ разбита точкой С на части, то
3. Если кривая лежит в плоскости перпендикулярной ОХ, то
Аналогично для OY
4. Криволинейный интеграл по замкнутой кривой не зависит от выбора начальной точки, а зависит только от направления обхода прямой
36. Вычисление криволинейного интеграла 2 рода
а. Параметрическое представление кривой
б. Явно заданная функция
37. Приложения криволинейного интеграла 2 рода
C помощью криволинейных интегралов вычисляются:
— Масса кривой
— Центр масс и моменты инерции кривой
— Работа при перемещении тела в силовом поле
— Магнитное поле вокруг проводника с током (Закон Ампера)
— Электромагнитная индукция в замкнутом контуре при изменении магнитного потока (Закон Фарадея)
38. Формула Остроградского-Грина
Пусть на плоскости OXY задана область D, ограниченная кривой пересекающейся с прямыми параллельными координатным осям не более чем в 2-х точках то есть, область D правильная.
Если ф-ции P(x;y) и Q(x;y) непрерывны вместе со своими частными производными в области D, то имеет место формула:
39. Основные понятия о дифференциальных уравнениях (определение, решение, порядок, обыкновенные ДУ, ДУ в общих производных, вид, общее решение, частные решения, начальные условия, задача Коши)
40. ДУ с разделяющимися переменными
Среди обыкновенных дифференциальных уравнений первого порядка существуют такие, в которых возможно переменные x и y разнести по разные стороны знака равенства. В уравнениях вида переменные уже разделены, а в ОДУпеременные разделяются посредством преобразований. Кроме того, некоторые дифференциальные уравнения сводятся к уравнениям с разделяющимися переменными после введения новых переменных.
41. Однородные ДУ 1-го порядка
ДУ вида – однородныеn-го порядка, если при умножении каждого элемента функции на множитель t вся функция умножится на
42. Линейные ДУ 1-го порядка. Метод вариации произвольной постоянной
Линейные ДУ 1-го порядка имеют такой вид
Характерная особенность – функция и ее производные входят в уравнение в 1 степени и между собой не перемножаются
Метод Лагранжа (Метод вариаций произвольной постоянной)
Метод вариации произвольной постоянной состоит в том, что постоянную С в полученном решении заменяем С=с(x), тогда решение исходного уравнения будем искать в виде
После находим производную и подставляем в исходное уравнение
43. Линейные ДУ 1-го порядка. Метод Бернулли
Линейные ДУ 1-го порядка имеют такой вид
Характерная особенность – функция и ее производные входят в уравнение в 1 степени и между собой не перемножаются
Метод Бернулли
Решение данного уравнения ищется в виде производной 2-х функция то, есть с помощью подстановки
y=U*V, где U=u(x) и V=v(x)
Подставим выражение для y и в исходное уравнение
Сгруппируем 1 и 3 слогаемые, или 2 и 3 и вынесем общий множитель за скобки
(*)
Функцию v подберём таким образом, чтобы выражение в скобках было равно нулю
–уравнение с разд. переменными, получаем:
Подставляем полученное в уравнение (*), учитывая, что выражение в скобках равно нулю
Ответ:
44. ДУ высших порядков, допускающие понижения порядка. ДУ вида
Рассмотрим дифференциальное уравнение вида , где– производная «энного» порядка, а правая частьзависиттолько от «икс». В простейшем случае может быть константой.
Данное дифференциальное уравнение решается последовательным интегрированием правой части. Причём интегрировать придется ровно раз.
На практике наиболее популярной разновидность является уравнение второго порядка: . Дважды интегрируем правую часть и получаем общее решение. Уравнение третьего порядканеобходимо проинтегрировать трижды, и т.д.
45. ДУ высших порядков, допускающие понижения порядка. ДУ вида
Порядок такого уравнения можно понизить на единиц заменой. Тогда уравнение примет вид
Из последнего уравнения, если это возможно, определяем , а затем находимиз уравненияk-кратным интегрированием.
46. ДУ высших порядков, допускающие понижения порядка. ДУ вида
Отличительная особенность данного диффура состоит в том, что в нём в явном виде отсутствует независимая переменная «икс». То есть, в исходном дифференциальном уравнении нет «икса».
Подстановка позволяет понизить порядок уравнения на единицу. При этомрассматривается как новая неизвестная функция от. Все производныевыражаются через производные от новой неизвестной функциипо
Подставив эти выражения вместо в уравнение, получим дифференциальное уравнение (n–1)-го порядка
47. Линейные однородные ДУ второго порядка. Определитель Вронского. Структура общего решения
Рассмотрим линейное дифференциальное уравнение вида
где p, q − постоянные коэффициенты. Для каждого такого дифференциального уравнения можно записать так называемое характеристическое уравнение:
Общее решение однородного дифференциального уравнения зависит от корней характеристического уравнения, которое в данном случае будет являться квадратным уравнением. Возможны следующие случаи:
Дискриминант характеристического квадратного уравнения положителен: D > 0. Тогда корни характеристического уравнения k1 и k2 действительны и различны. В этом случае общее решение описывается функцией
где C1 и C2 − произвольные действительные числа.
Дискриминант характеристического квадратного уравнения равен нулю: D = 0. Тогда корни действительны и равны. В этом случае говорят, что существует один корень k1 второго порядка. Общее решение однородного дифференциального уравнения имеет вид:
Дискриминант характеристического квадратного уравнения отрицателен: D < 0. Такое уравнение имеет комплексно-сопряженные корни k1 = α + βi, k1 = α − βi. Общее решение записывается в виде
48. Интегрирование ЛОДУ второго порядка с постоянными коэффициентами
Эйлер предложил искать частные решения в виде:
k – некоторое число
–характеристическое уравнение
Случ.1 D>0 =>
Общее решение записываем в виде
Случ.2 D=0 =>
Случ.3 D<0 =>
49. Интегрирование ЛНДУ второго порядка с постоянными коэффициентами. Случай
Общее решение ЛНДУ выглядит так:
Для ЛНДУ с правой частью специального вида частное решение можно найти пользуясь методом неопределённых коэффициентов. Суть метода: по виду правой части уравнения запишем ожидаемую форму частного решения с неопределённым коэффициентом, затем дважды её продифференцируем и полученные выражения подставим в исходное уравнение после чего найдём неопределённые коэффициенты
Частное для такого уравнения будет находиться в виде
r – число равное кратности α, как корня характеристического уравнения
а. Если
б. Если
в. Если
50. Интегрирование ЛНДУ второго порядка с постоянными коэффициентами. Случай
Общее решение ЛНДУ выглядит так:
Для ЛНДУ с правой частью специального вида частное решение можно найти пользуясь методом неопределённых коэффициентов. Суть метода: по виду правой части уравнения запишем ожидаемую форму частного решения с неопределённым коэффициентом, затем дважды её продифференцируем и полученные выражения подставим в исходное уравнение после чего найдём неопределённые коэффициенты
l = max (n;m)
r – число равное кратности как корень характеристического уравнения
studfiles.net
Вычисление длин дуг с помощью определённого интеграла. Теория, примеры и рисунки.: wrtorr
При вычислении любой длины следует помнить, что это величина конечная, то есть просто число. Если имеется в виду длина дуги кривой, то такая задача решается с помощью определенного интеграла (в плоском случае) или криволинейного интеграла первого рода (по длине дуги). Дуга АВ будет обозначаться UАВ.Первый случай (плоский). Пусть UАВ задана плоской кривой y = f(x). Аргумент функции изменятся в пределах от а до b и она непрерывно дифференцируема этом отрезке. Найдем длину L дуги UАВ (см. рис. 1а). Для решения этой задачи разбейте рассматриваемый отрезок на элементарные отрезки ∆xi, i=1,2,…,n. В результате UАВ разобьется на элементарные дуги ∆Ui, участков графика функции y=f(x) на каждом из элементарных отрезков. Найдете длину ∆Li элементарной дуги приближенно, заменив ее соответствующей хордой. При этом можно приращения заменить дифференциалами и использовать теорему Пифагора. После вынесения из квадратного корня дифференциала dx получите результат, приведенный на рисунке 1b.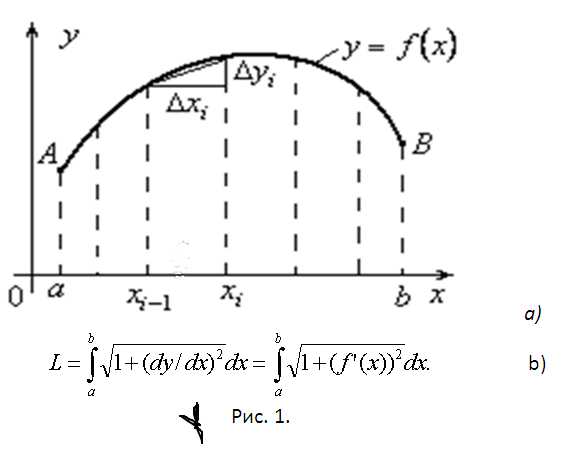
Как вычислить длину кривой
Второй случай (дуга UАВ задана параметрически). x=x(t), y=y(t), tє[α,β]. Функции x(t) и y(t) имеют непрерывные производные на отрезке этом отрезке. Найдите их дифференциалы. dx=f’(t)dt, dy=f’(t)dt. Подставьте эти дифференциалы в формулу для вычисления длины дуги в первом случае. Вынесите dt из квадратного корня под интегралом, положите х(α)=а, x(β)=b и придете к формуле для вычисления длины дуги в данном случае (см. рис. 2а).
Третий случай. Дуга UАВ графика функции задана в полярных координатах ρ=ρ(φ) Полярный угол φ при прохождении дуги изменяется от α до β. Функция ρ(φ)) имеет непрерывную производную на отрезке ее рассмотрения. В такой ситуации проще всего использовать данные, полученные на предыдущем шаге. Выберите φ в качестве параметра и подставьте в уравнения связи полярных и декартовых координат x=ρcosφ y=ρsinφ. Продифференцируйте эти формулы и подставьте квадраты производных в выражение на рис. 2а. После небольших тождественных преобразований, основанных в основном, на применении тригонометрического тождества (cosφ)^2+(sinφ)^2=1, получите формулу для вычисления длины дуги в полярных координатах (см. рис.2b).
Четвертый случай (пространственная кривая, заданная параметрически). x=x(t), y=y(t), z=z(t) tє[α,β]. Строго говоря, здесь следует применить криволинейный интеграл первого рода (по длине дуги). Криволинейные интегралы вычисляют переводом их в обычные определенные. В результате ответ останется практическим таким же как и случае два, с тем лишь отличием, что под корнем появится добавочное слагаемое – квадрат производной z’(t) (см рис. 2с).
Примеры:
Пример 1. Пусть в прямоугольных координатах дана плоская кривая АВ, уравнение которой у=ƒ(х), где а≤х≤ b.
Под длиной дуги АВ понимается предел, к которому стремится длина ломаной линии, вписанной в эту дугу, когда число звеньев ломаной неограниченно возрастает, а длина наибольшего звена ее стремится к нулю. Покажем, что если функция у=ƒ(х) и ее производная у’ = ƒ'(х) непрерывны на отрезке [а; b], то кривая АВ имеет длину, равную

Применим схему I (метод сумм).
1. Точками х0 = а, х1…, хn = b (х0 < x1 < …< хn) разобьем отрезок [а; b] на n частей (см. рис. 183). Пустьэтим точкам соответствуют точки М0 = А, M1,…,Mn =В на кривой АВ. Проведем хорды М0M1, M1M2,…, Мn-1Мn, длины которых обозначим соответственно через ΔL1, AL2,…, ΔLn. Получим ломаную M0M1M2 … Mn-ιMn, длина которой равна Ln=ΔL1 + ΔL2+…+ ΔLn =
2. Длину хорды (или звена ломаной) ΔL1 можно найти по теореме Пифагора из треугольника с катетами Δxi и Δуi:
По теореме Лагранжа о конечном приращении функции Δуi=ƒ'(сi)•Δхi, где ci є (xi-1;xi). Поэтому
а длина всей ломаной M0M1… Мn равна
3.Длина l кривой АВ, по определению, равна
.
Заметим, что при ΔLi→0 также и Δxi→0 ΔLi =и, следовательно, |Δxi|<ΔLi).
Функция непрерывна на отрезке [а; b], так как, по условию, непрерывна функция ƒ'(х). Следовательно, существует предел интегральной суммы (41.4), когда max Δxi→ 0:
Таким образом,или в сокращенной записи l =
Если уравнение кривой АВ задано в параметрической форме
где x(t) и y(t) — непрерывныефункции с непрерывными производными и х(а) = а, х(β) = b, то длина l кривой АВ находится по формуле
Формула (41.5) может быть получена из формулы (41.3) подстановкой x = x(t),dx = x'(t)dt,
Пример 2. Определить длину окружности x2 + y2 = r2. Решение. Вычислим сначала длину четвертой части окружности, лежащей в первом квадранте. Тогда уравнение дуги AB будет, откуда,следовательно,
Длина всей окружности L = 2πr.
Пример 3. Найти длину дуги кривой y2 = x3 от x = 0 до x = 1 (y > 0). Решение. Дифференцируя уравнение кривой, найдем y’ = (3/2)x1/2, откуда
Пример 4. Пусть кривая лежит в плоскости x0y и описывается уравнением y = f(x).
Для нахождения длины дуги этой кривой, заключенной между точками с абсциссами a и b, разобьем дугу на столь малые элементы, чтобы каждый из них можно было аппроксимируовать прямолинейным участком (см. рисунок 1).Рис. 1. Аппроксимация элемента дуги кривой прямолинейным участком.
Длину dL бесконечно малого участка можно выразить через dx и dy с помощью теоремы Пифагора:
| (1) |
Длина дуги равна сумме длин составляющих ее элементов:
| . |
Пример 5.
.

Пример 6.
wrtorr.livejournal.com
2.Длина дуги кривой.
Вычисление
длины дуги кривой в декартовых координатах.Введем понятие длины дуги. Пусть на
плоскости введена кривая, являющаяся
графиком непрерывной функции на отрезке
на отрезке .
Разобьем отрезок
.
Разобьем отрезок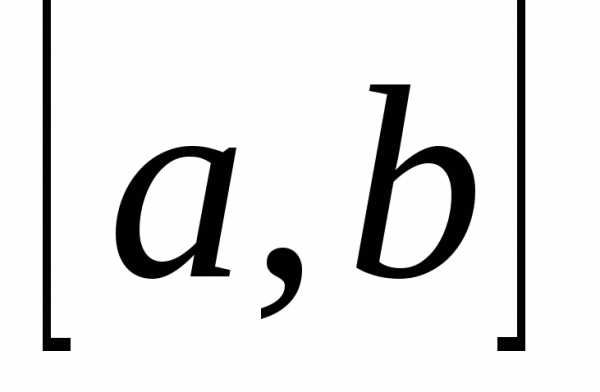 точками наnчастей.
Из каждой точки
точками наnчастей.
Из каждой точки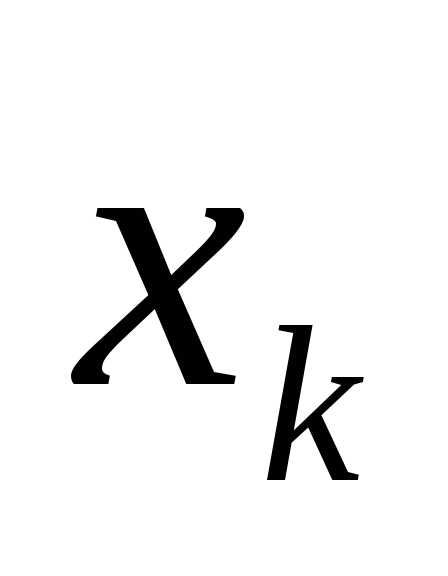 восстановим перпендикуляр к осиOx;
тогда дугаABразобьется
наnчастей точками(рис.4). Заменим каждый участок дуги
восстановим перпендикуляр к осиOx;
тогда дугаABразобьется
наnчастей точками(рис.4). Заменим каждый участок дуги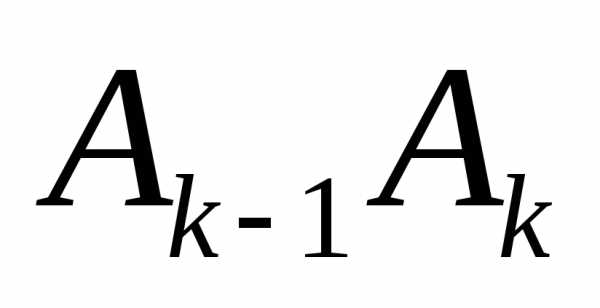 участком прямой
участком прямой .
.
Определение.Длиной дуги называется пределL,
к которому стремится длина ломаной,
вписанной в дугуAB, при
стремлении к нулю наибольшей из ее
сторон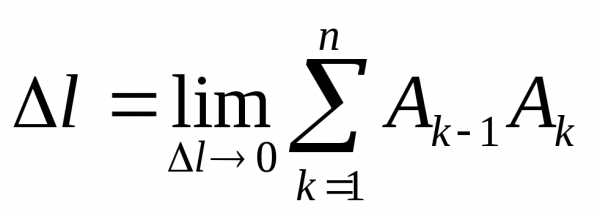 ,
а значит, и при,
т.е.
,
а значит, и при,
т.е.
 (8)
(8)
Рис. 4 Рис.5
Пусть
функция 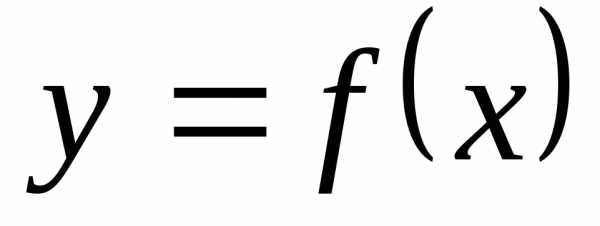 и ее производная
и ее производная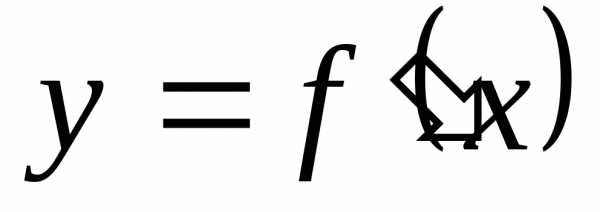 непрерывны на отрезке
непрерывны на отрезке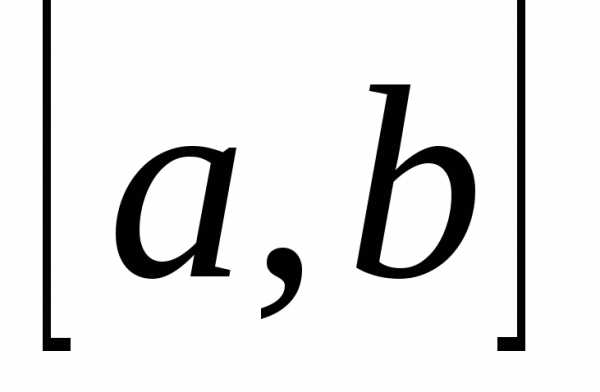 .
Согласно теореме Пифагора имеем.
Обозначим.
Так каки,
то на основании теоремы Лагранжа получим
.
Согласно теореме Пифагора имеем.
Обозначим.
Так каки,
то на основании теоремы Лагранжа получим
.
Тогда
.
В следствие непрерывности производной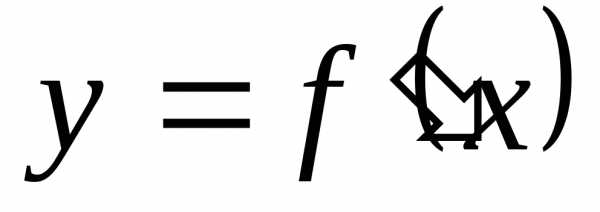 существует предел (8) интегральной суммы.
Таким образом,
существует предел (8) интегральной суммы.
Таким образом,
(9)
По
определению предел (9) равен определенному
интегралу от функции 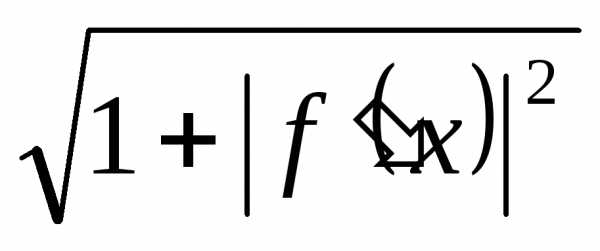 на отрезке
на отрезке :
:
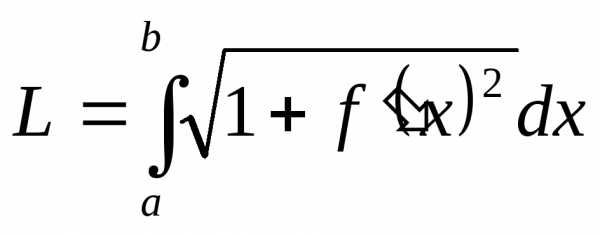 .
(10)
.
(10)
Это и есть формула для вычисления длины дуги.
Пример
4. Найти длину дуги кривой  ,
отсеченной прямой
,
отсеченной прямой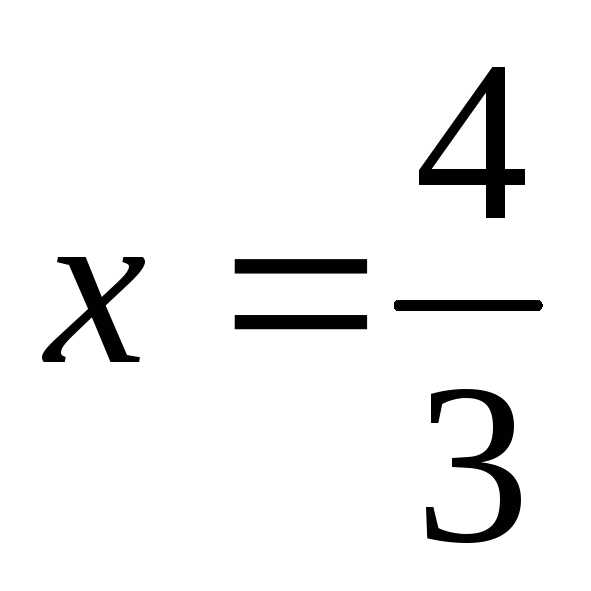 (рис.5).
(рис.5).
Решение.
Найдем производную функции y=f(x),
заданной неявно соотношением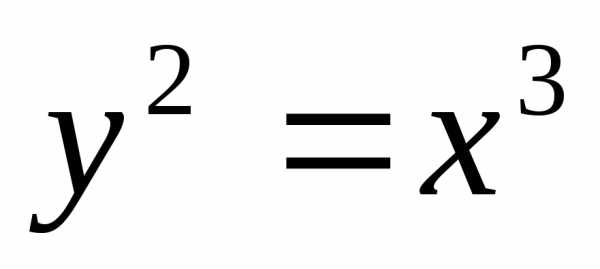 ;
имеем,
откуда
;
имеем,
откуда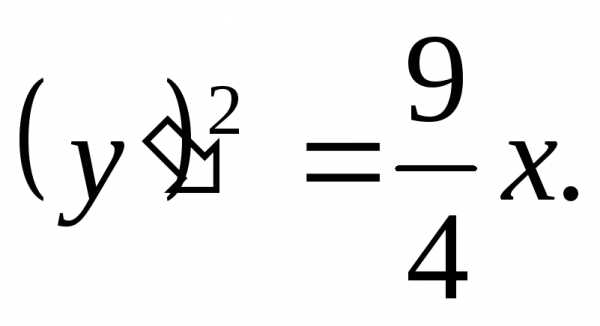 В силу симметрии достаточно вычислить
длину половины кривой
В силу симметрии достаточно вычислить
длину половины кривой .
По формуле (10) получим
.
По формуле (10) получим
,
при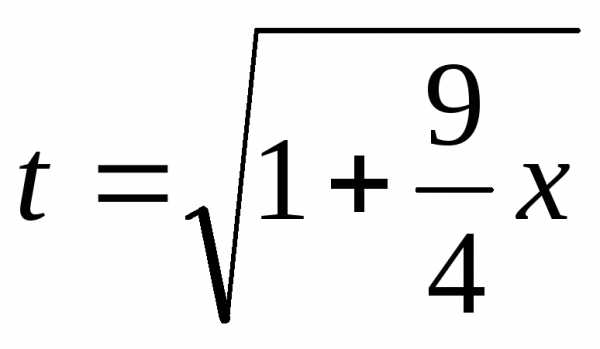 .
.
Вычисление
дуги плоской кривой, заданной в
параметрической форме. Рассмотрим
параметрически заданную кривуюгде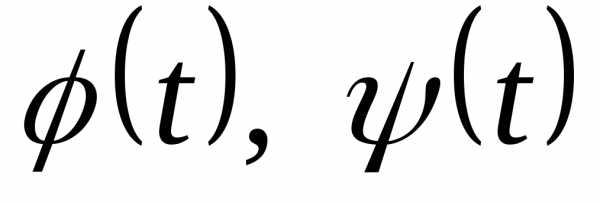 — непрерывные и имеющие непрерывные
производные функции, причем
— непрерывные и имеющие непрерывные
производные функции, причем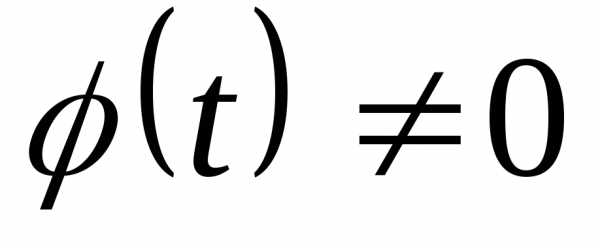 .
Пусть.
В интеграле (10) произведем подстановку;
так как
.
Пусть.
В интеграле (10) произведем подстановку;
так как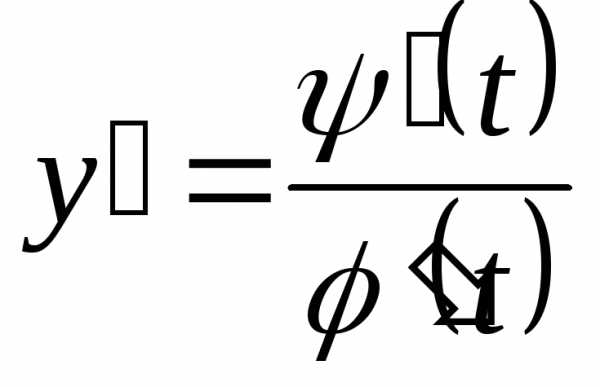 ,
то получим
,
то получим
. (11)
Пример 5. Найти длину окружности радиуса R.
Решение. Уравнения окружности в параметрической форме имеют вид Найдем четвертую часть длины окружности. По формуле (11) имеем
Что согласуется с общеизвестным результатом.
Вычисление
длины дуги плоской кривой в полярных
координатах.Воспользуемся формулами
перехода от полярных координат к
декартовым:(учли,
что радиусrесть функция
полярного угла). Эти уравнения можно
рассматривать, как параметрические
уравнения кривой при изменении параметра в пределах.
Тогда по формуле (11) находим
в пределах.
Тогда по формуле (11) находим
. (12)
3. Вычисление объемов и площадей поверхностей вращения.
Пусть криволинейная трапеция, ограниченная графиком непрерывной функции y=f(x), осьюOxи прямымиx=a,x=b, вращается вокруг осиOx.
(рис.6)
Найдем
объем Vполученного тела
вращения. Ясно, что произвольное
поперечное сечение этого тела представляет
собой круг. Площадь круга, образованного
при сечении тела вращения плоскостьюx=x, есть.
Тогда используя формулу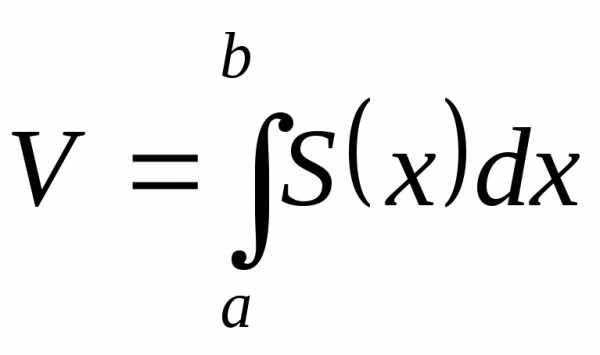 ,
получим
,
получим
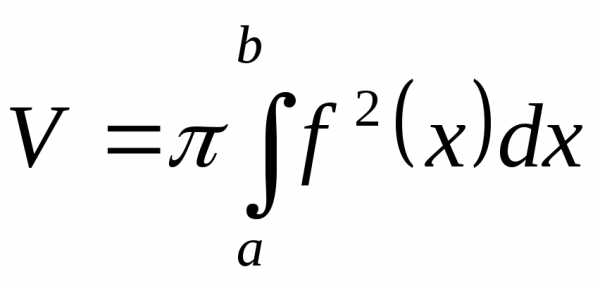 (13)
(13)
Если
криволинейная трапеция, ограниченная
непрерывной функцией 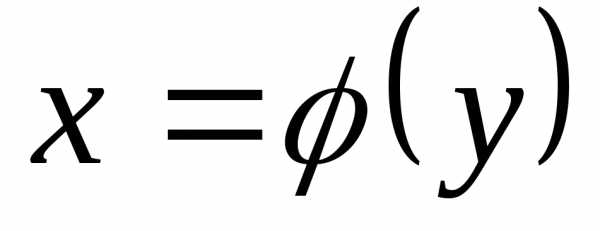 ,
осьюOyи прямымиy=aиy=b, вращается
вокруг осиOy, то объем
полученного тела вычисляется по формуле
,
осьюOyи прямымиy=aиy=b, вращается
вокруг осиOy, то объем
полученного тела вычисляется по формуле
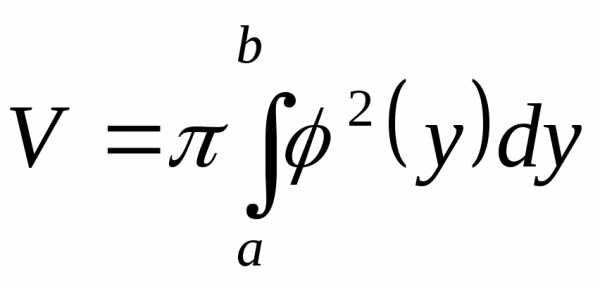 (14)
(14)
Пример 6. Найти объем конуса с радиусом основания Rи высотойh.
Решение. Конус можно считать телом, полученным вращением прямоугольного треугольника с катетами hиRотносительно осиOx. Найдем уравнение гипотенузы этого треугольника. Имеемy=kx, где. По формуле (13) получим
Вычисление площади поверхности тела вращения.
Определение.Площадью поверхности
тела, полученного при вращении дугиABвокруг осиOxназывается
предел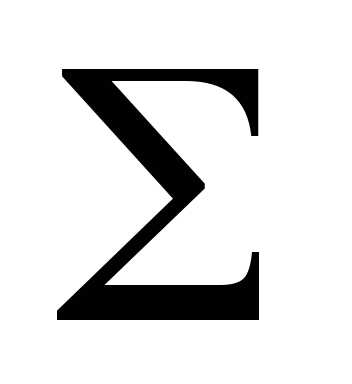 ,
к которому стремится площадь поверхности,
образованной вращением вокруг осиOxломаной,
вписанной в дугуAB, при
стремлении к нулю наибольшей из ее
сторон
,
к которому стремится площадь поверхности,
образованной вращением вокруг осиOxломаной,
вписанной в дугуAB, при
стремлении к нулю наибольшей из ее
сторон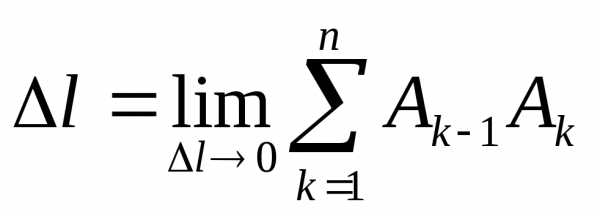 ,
а значит, и при,
т.е.
,
а значит, и при,
т.е.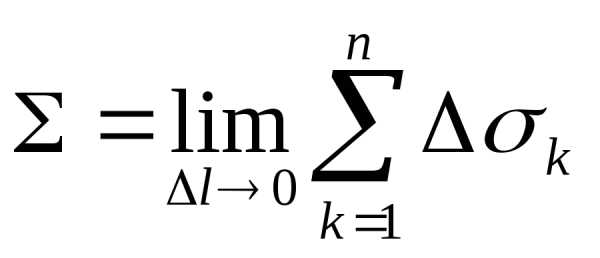 .
.
Формула для вычисления площади поверхности вращения вокруг оси Ox
(15)
Если кривая вращается вокруг оси Oy, то формула имеет вид
(16)
studfiles.net