Частные случаи решения тригонометрических уравнений
Частные случаи решения тригонометрических уравнений
Рассмотрим некоторые возможные стандартные варианты решений тригонометрических уравнений.
Частными случаями решения уравнения являются следующие уравнения:
То есть в роли возможных значений переменной а выступают табличные значения 0; —1 и 1.
Графически решение уравнения можно обосновать с помощью рисунка: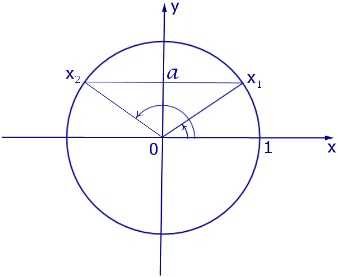
Для частных случаев решения можно найти несколькими способами, в частности их принято вносить в справочную информацию по тригонометрии. Наведем решения этих уравнений:
:
:
:
Частными случаями решения уравнения являются:
:
:
:
Графически решение уравнения можно обосновать с помощью рисунка: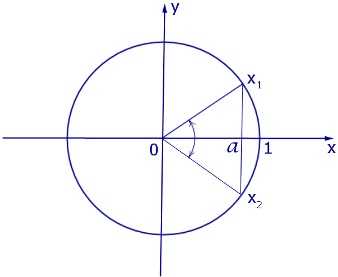
Частные случаи решения уравнения :
:
:
Графически решение уравнения можно обосновать с помощью рисунка:
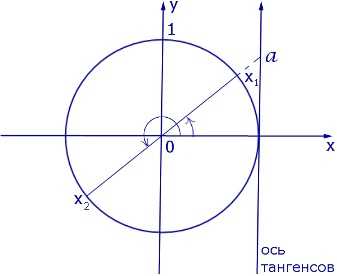
Частные случаи решения уравнения :
:
:
:
Графически решение уравнения можно обосновать с помощью рисунка:
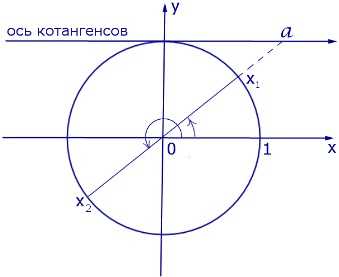
К частным случаям решения тригонометрических уравнений можно отнести также и другие табличные значения, которым равны тригонометрические функции по таблице значений. Например, к частным случаям решения уравнения можно также отнести уравнения вида:
ru.solverbook.com
Решение простейших тригонометрических уравнений
Решение простейших тригонометрических уравнений.
Решение тригонометрических уравнений любого уровня сложности в конечном итоге сводится к решению простейших тригонометрических уравнений. И в этом наилучшим помощником снова оказывается тригонометрический круг.
Вспомним определения косинуса и синуса.
Косинусом угла называется абсцисса (то есть координата по оси ) точки на единичной окружности, соответствующей повороту на данный угол .
Синусом угла называется ордината (то есть координата по оси ) точки на единичной окружности, соответствующей повороту на данный угол .
Положительным направлением движения по тригонометрическому кругу считается движение против часовой стрелки. Повороту на 0 градусов ( или 0 радиан) соответствует точка с координатами (1;0)
Используем эти определения для решения простейших тригонометрических уравнений.
1. Решим уравнение
Этому уравнению удовлетворяют все такие значения угла поворота , которые соответствуют точкам окружности, ордината которых равна .
Отметим на оси ординат точку с ординатой :
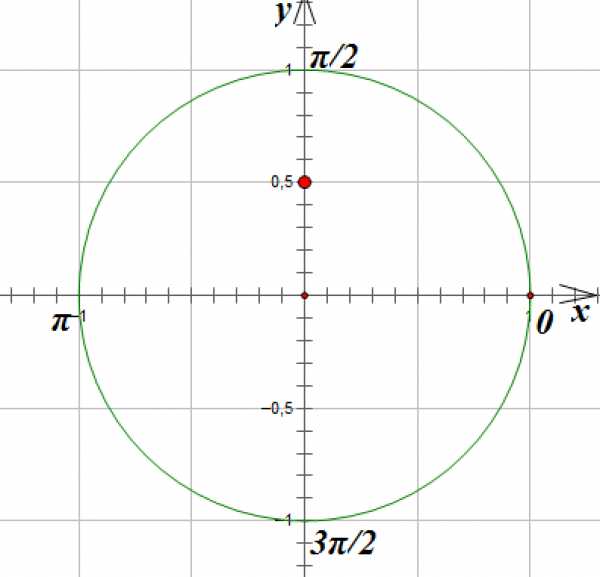
Проведем горизонтальную линию параллельно оси абсцисс до пересечения с окружностью. Мы получим две точки, лежащие на окружности и имеющие ординату. Эти точки соответствуют углам поворота на и радиан:
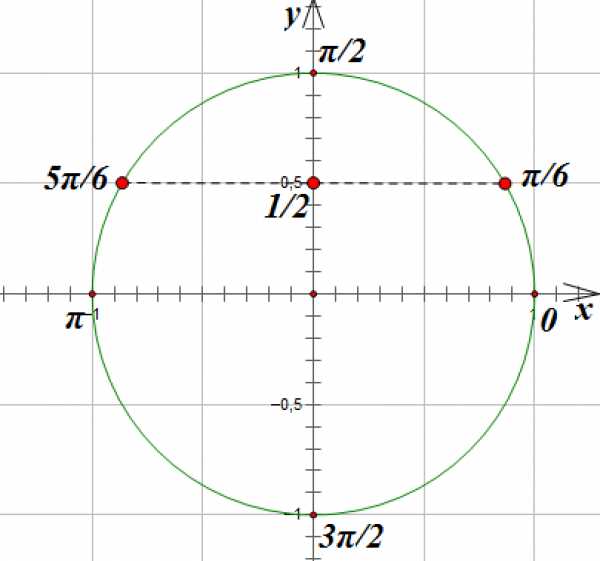
Если мы, выйдя из точки, соответствующей углу поворота на радиан, обойдем полный круг, то мы придем в точку, соответствующую углу поворота на радиан и имеющую ту же ординату. То есть этот угол поворота также удовлетворяет нашему уравнению. Мы можем делать сколько угодно «холостых» оборотов, возвращаясь в ту же точку, и все эти значения углов будут удовлетворять нашему уравнению. Число «холостых» оборотов обозначим буквой (или ). Так как мы можем совершать эти обороты как в положительном, так и в отрицательном направлении, (или ) могут принимать любые целые значения.
То есть первая серия решений исходного уравнения имеет вид:
, , — множество целых чисел (1)
Аналогично, вторая серия решений имеет вид:
, где , . (2)
Как вы догадались, в основе этой серии решений лежит точка окружности, соответствующая углу поворота на .
Эти две серии решений можно объединить в одну запись:
Если мы в этой записи возьмем ( то есть четное ), то мы получим первую серию решений.
Если мы в этой записи возьмем ( то есть нечетное ), то мы получим вторую серию решений.
2. Теперь давайте решим уравнение
Так как — это абсцисса точки единичной окружности, полученной поворотом на угол , отметим на оси точку с абсциссой :
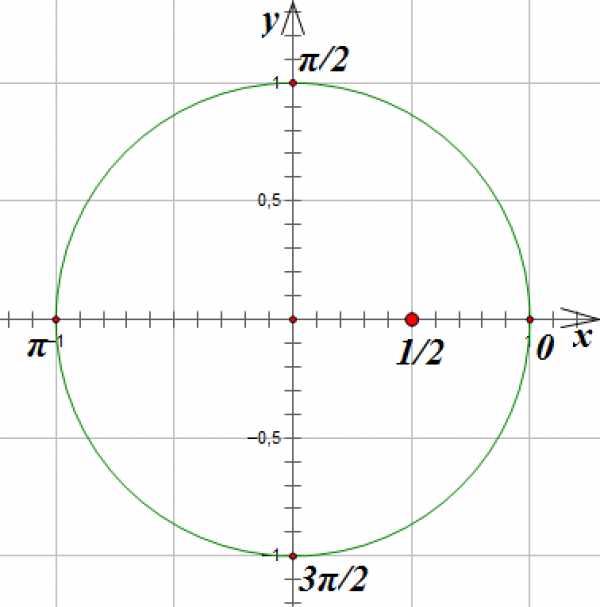
Проведем вертикальную линию параллельно оси до пересечения с окружностью. Мы получим две точки, лежащие на окружности и имеющие абсциссу . Эти точки соответствуют углам поворота на и радиан. Вспомним, что при движении по часовой стрелки мы получаем отрицательный угол поворота:
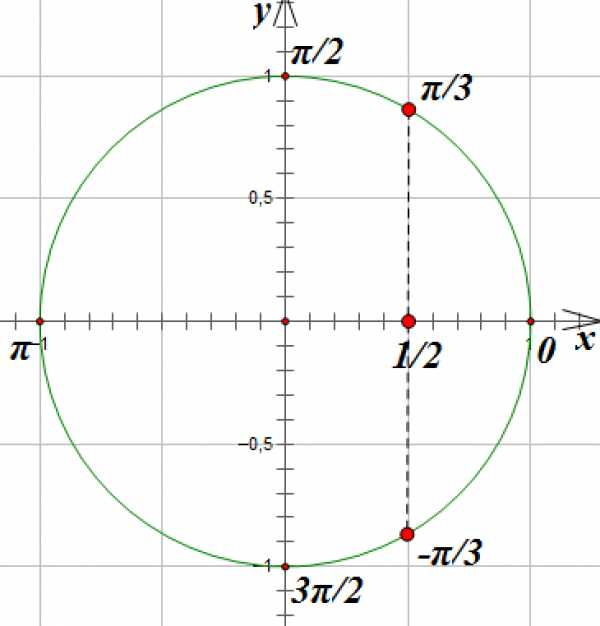
Запишем две серии решений:
,
,
(Мы попадаем в нужную точку, пройдя из основной полный круг, то есть .
Объедим эти две серии в одну запись:
3. Решим уравнение
Линия тангенсов проходит через точку с координатами (1,0) единичной окружности параллельно оси OY
Отметим на ней точку, с ординатой равной 1 (мы ищем, тангенс каких углов равен 1):
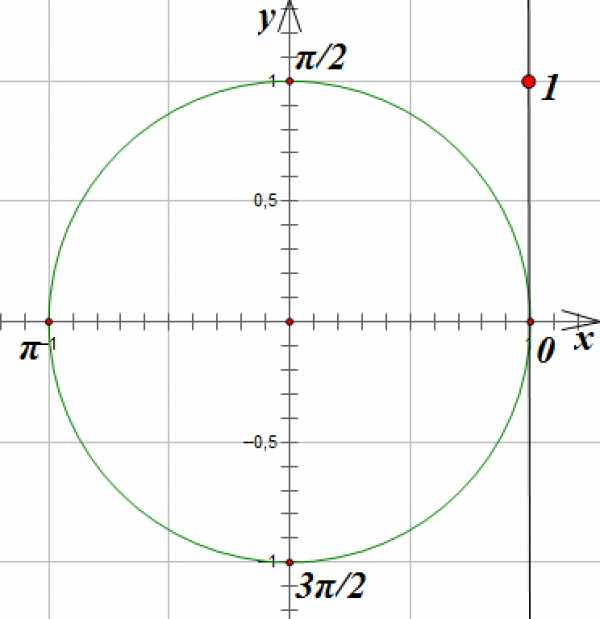
Соединим эту точку с началом координат прямой линией и отметим точки пересечения прямой с единичной окружностью. Точки пересечения прямой и окружности соответствуют углам поворота на и :

Так как точки, соответствующие углам поворота, которые удовлетворяют нашему уравнению, лежат на расстоянии радиан друг от друга, то мы можем записать решение таким образом:
,
4. Решим уравнение
Линия котангенсов проходит через точку с координатами единичной окружности параллельно оси .
Отметим на линии котангенсов точку с абсциссой -1:
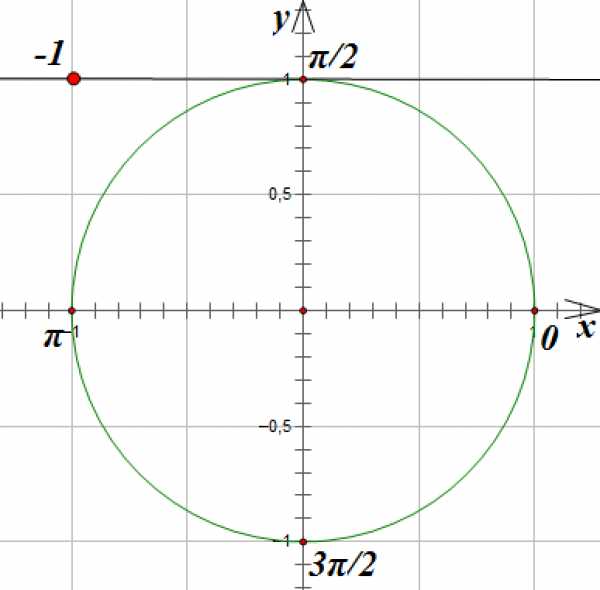
Соединим эту точку с началом координат прямой и продолжим ее до пересечения с окружностью. Эта прямая пересечет окружность в точках, соответствующих углам поворота на и радиан:
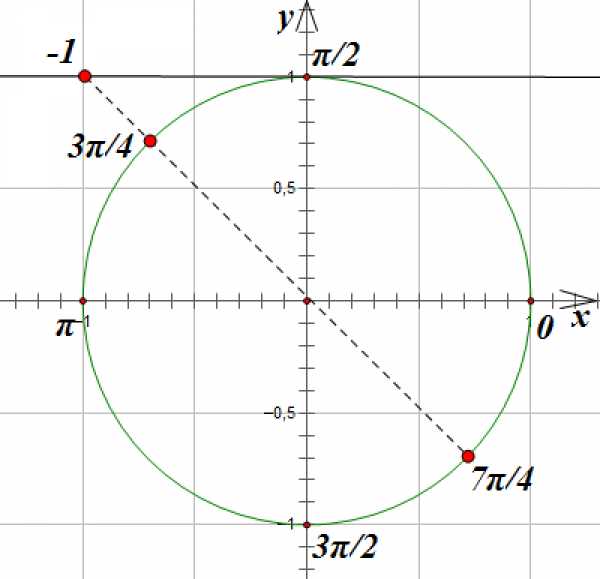
Поскольку эти точки отстоят друг от друга на расстояние, равное , то общее решение этого уравнения мы можем записать так:
В приведенных примерах, иллюстрирующих решение простейших тригонометрических уравнений были использованы табличные значения тригонометрических функций.
Однако, если в правой части уравнения стоит не табличное значение, то мы в общее решение уравнения подставляем значение обратной тригонометрической функции:

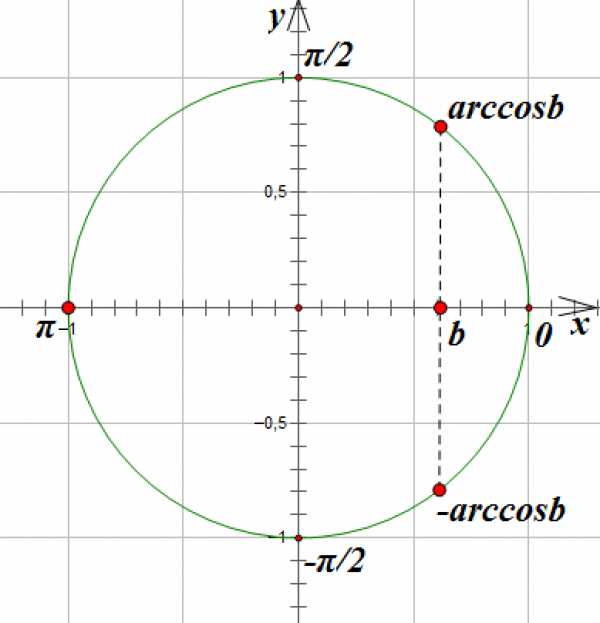
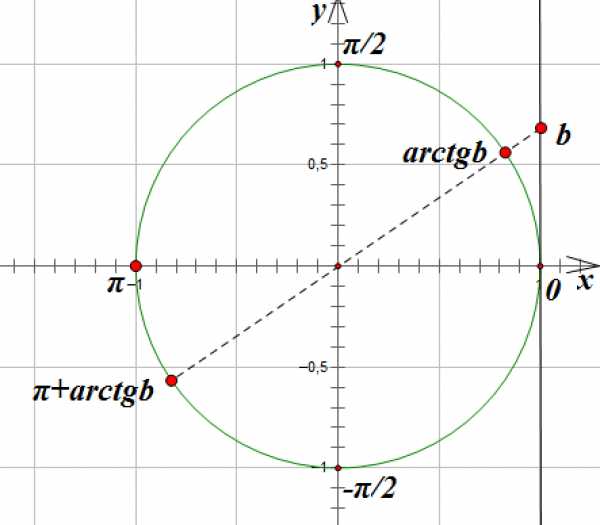
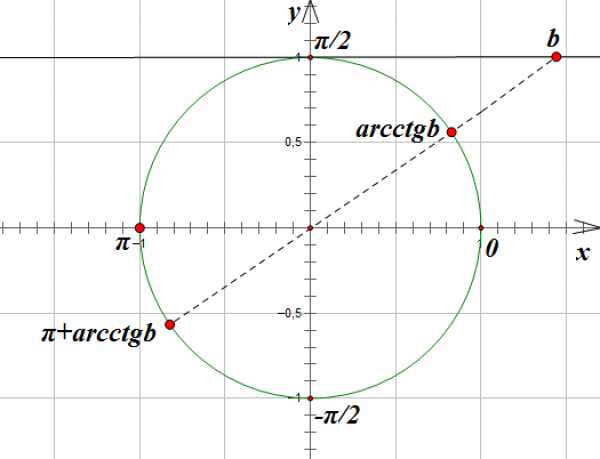
ОСОБЫЕ РЕШЕНИЯ:
1
Отметим на окружности точки, ордината которых равна 0:
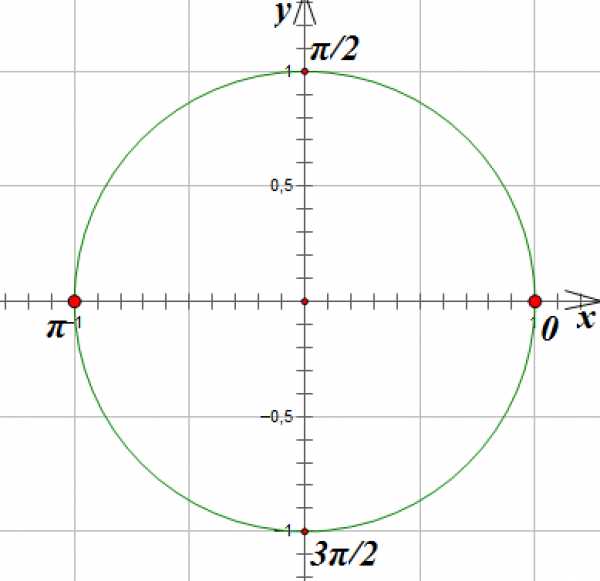
2.
Отметим на окружности единственную точку, ордината которой равна 1:
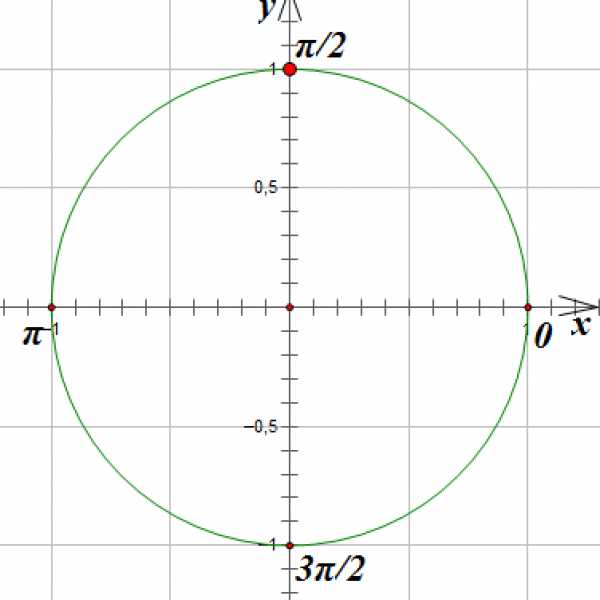
3.
Отметим на окружности единственную точку, ордината которой равна -1:
Так как принято указывать значения, наиболее близкие у нулю, решение запишем так:
4.
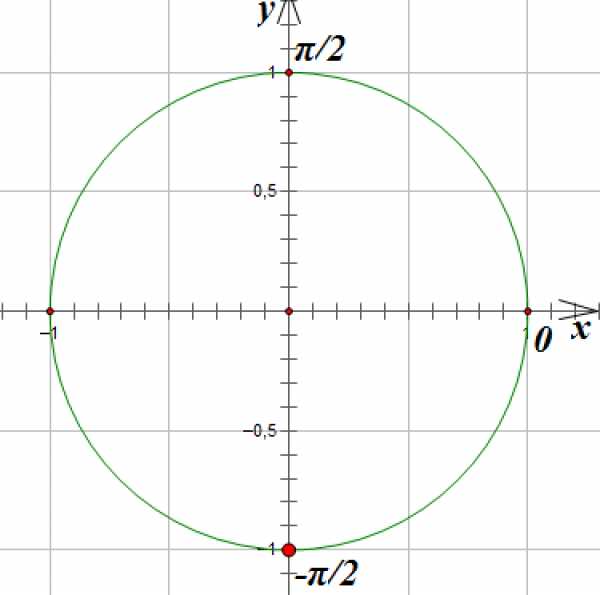
Отметим на окружности точки, абсцисса которых равна 0:
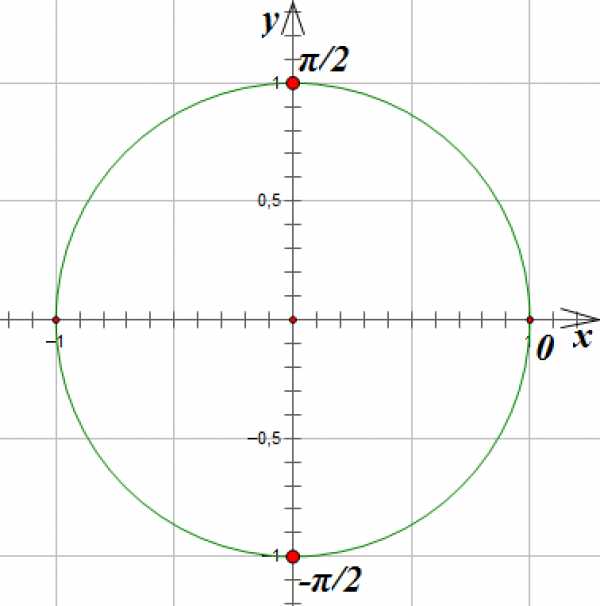
5.
Отметим на окружности единственную точку, абсцисса которой равна 1:
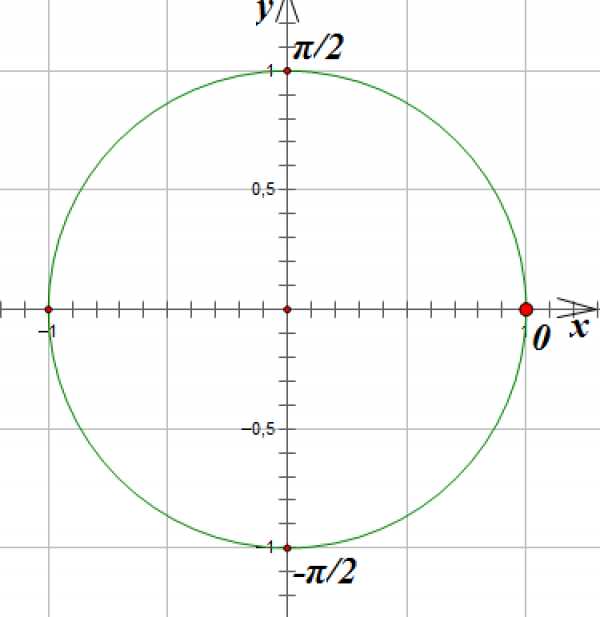
6.
Отметим на окружности единственную точку, абсцисса которой равна -1:
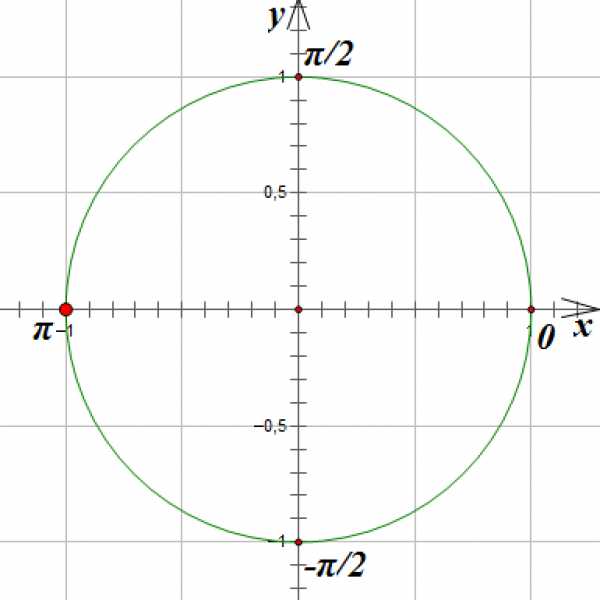
И чуть более сложные примеры:
1.
Синус равен единице, если аргумент равен
Аргумент у нашего синуса равен , поэтому получим:
. Разделим обе части равенства на 3:
Ответ:
2.
Косинус равен нулю, если аргумент косинуса равен
Аргумент у нашего косинуса равен , поэтому получим:
Выразим , для этого сначала перенесем вправо с противоположным знаком:
Упростим правую часть:
Разделим обе части на -2:
Заметим, что перед слагаемым знак не меняется, поскольку k может принимать любые целые значения.
Ответ:
И в заключение посмотрите видеоурок «Отбор корней в тригонометрическом уравнении с помощью тригонометрической окружности»
На этом разговор о решении простейших тригонометрических уравнений мы закончим. Следующий раз мы с вами поговорим о том, как решать простейшие тригонометрические неравенства.
И.В. Фельдман, репетитор по математике.
Купить видеокурс «ВСЯ ТРИГОНОМЕТРИЯ. Часть В и Задание 13»
ege-ok.ru
sin x = 1 решение
Доброй ночи!
Уравнения вида, которое вы нам предоставили — очень часто вызывает различные затруднение. Но это, на самом деле, не так страшно и не так сложно. Прежде, чем разобраться с Вашей уравнением sin x = 1, нужно подумать, в каком виде можно представить данное уравнение, чтоб понять как его решать.
Вот так будет выглядеть Ваше условие на математическом языке:
Да, я понимаю, что это Вам особо не помогло. Но для этого есть определённое правило решения подобных уравнений, которое примет такой общий вид:
Как только мы разобрались с общим решением, то теперь можем преступить к решению именно Вашего уравнения:
Значение мы найдём при помощи таблицы. И исходя из этого получаем, что
Так как с основным разобрались, то теперь можем и решить до конца Ваше уравнение:
Ответ:
Чему равен Sin 1 (синус единицы) ?
Синус одного градуса или синус одного радиана?
девяносто градусов.
синус единицы в радианной мере равен углу в 90 градусов.
Если это синус градуса то 90, а если радиана то????
sin 1” = π/(180•60•60) eto sinus 1 sekunda
Синус дуги, которая равна радиусу, есть 1/1! — 1/3! + 1/5! — 1/7! + 1/9! — etc. = 1 — 1/6 + 1/120 — 1/5040 + 1/362880 — etc. Сложим эти пять чисел: (362880 — 60480 + 3024 — 72 + 1) / 362880 = (302400 + 3025 — 72) / 362880 = 305353 / 362880 ~ 0.8414710097. Отсюда нужно ещё вычесть малое положительное число 1/11! — 1/13! + 1/15! — 1/17! + etc. < 1/11! = 1/39.916.800 ~ 2.5*10^(-8). Достаточно запомнить sin(1) = 0.841471.
sin(-1) = -0.0175 <a rel=»nofollow» href=»http://tehtab.ru/Guide/GuideMathematics/GuideMathematicsFiguresTables/sinusTable0to360by1/» target=»_blank»>http://tehtab.ru/Guide/GuideMathematics/GuideMathematicsFiguresTables/sinusTable0to360by1/</a>
touch.otvet.mail.ru
