Длина векторов по координатам – .

Вычисление длины (модуля) вектора в MS EXCEL. Примеры и методы

Найдем длину вектора по его координатам (в прямоугольной системе координат), по координатам точек начала и конца вектора и по теореме косинусов (задано 2 вектора и угол между ними).

Вектор – это направленный отрезок прямой. Длина этого отрезка определяет числовое значение вектора и называется длиной вектора или модулем вектора.

1. Вычисление длины вектора по его координатам

Если даны координаты вектора в плоской (двухмерной) прямоугольной системе координат, т.е. известны a_x и a_y, то длину вектора можно найти по формуле

В случае вектора в пространстве добавляется третья координата

В MS EXCEL выражение =КОРЕНЬ(СУММКВ(B8:B9)) позволяет вычислить модуль вектора (предполагается, что координаторы вектора введены в ячейки B8:B9, см. файл примера).

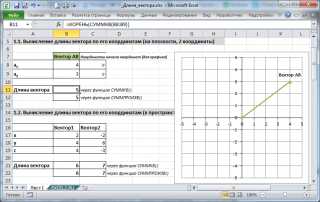
Функция СУММКВ() возвращает сумму квадратов аргументов, т.е. в данном случае эквивалентна формуле =B8*B8+B9*B9.

В файле примера также вычислена длина вектора в пространстве.

Альтернативной формулой является выражение =КОРЕНЬ(СУММПРОИЗВ(B8:B9;B8:B9)).

2. Нахождение длины вектора через координаты точек

Если вектор задан через координаты точек его начала и конца, то формула будет другой =КОРЕНЬ(СУММКВРАЗН(C28:C29;B28:B29))

В формуле предполагается, что координаты точек начала и конца введены в диапазоны C28:C29 и B28:B29 соответственно.

Функция СУММКВРАЗН() возвращает сумму квадратов разностей соответствующих значений в двух массивах.

По сути, в формуле сначала вычисляются координаты вектора (разности соответствующих координат точек), затем вычисляется сумма их квадратов.

3. Нахождение длины вектора по теореме косинусов

Если требуется найти длину вектора по теореме косинусов, то обычно заданы 2 вектора (их модули и угол между ними).

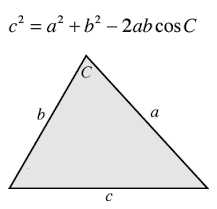
Найдем длину вектора с используя формулу =КОРЕНЬ(СУММКВ(B43:C43)-2*B43*C43*COS(B45))

В ячейках B43:B43 содержатся длины векторов а и b, а в ячейке В45 — угол между ними в радианах (в долях числа ПИ()).

Если угол задан в градусах, то формула будет немного отличаться =КОРЕНЬ(B43*B43+C43*C43-2*B43*C43*COS(B46*ПИ()/180))

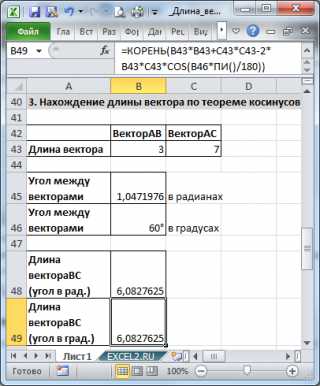
Примечание: для наглядности в ячейке со значением угла в градусах можно применить пользовательский формат, см. например, статью Отображение широты и долготы в MS EXCEL

4. Нахождение длины вектора через координаты точек треугольника

Пусть заданы 3 точки треугольника, образованного векторами.

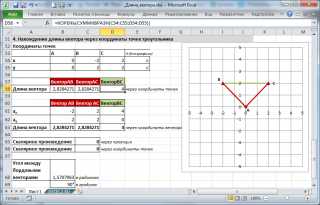
Найдем длину вектора ВС через координаты соответствующих точек (аналогично 2-й задаче, рассмотренной выше) по формуле =КОРЕНЬ(СУММКВРАЗН(C54:C55;D54:D55)).

Зная координаты точек можно найти все длины сторон (длины векторов) и углы треугольника (по теореме косинусов).

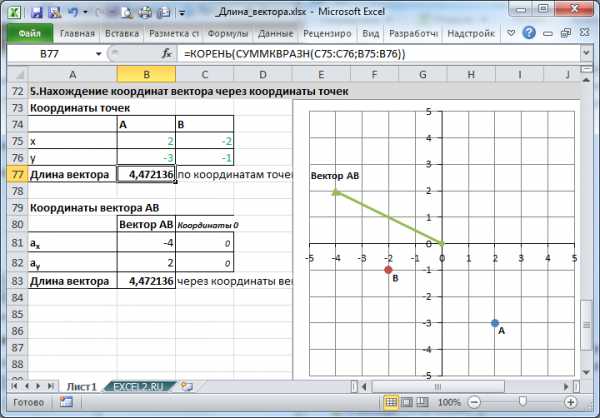
5. Нахождение координат вектора через координаты точек

Сделаем в MS EXCEL удобную форму для вычисления координат вектора и его длины через координаты точек. Также отобразим как сами точки, так и сам вектор.

excel2.ru

[Зачет 70] Определение ортонормированного базиса и прямоугольной декартовой системы координат (ПДСК). Вывод формул для вычисления длины вектора, заданного своими координатами в ортонормированном базисе, расстояния между двумя точками.

Определение. Базис называется ортонормированным, если его векторы попарно ортогональны и равны единице.

Определение. Декартова система координат, базис которой ортонормирован называется декартовой прямоугольной системой координат.

Вывод формул для вычисления длины вектора, заданного своими координатами в ортонормированном базисе, расстояния между двумя точками. 

Нахождение длины вектора по координатам.

Длину вектора  будем обозначать . Аналогичное обозначение имеет модуль числа, и длину вектора часто называют модулем вектора.

Начнем с нахождения длины вектора на плоскости по координатам.

Отложим от начала координат (от точки О) вектор . Обозначим проекции точки А на координатные оси как  и  соответственно и рассмотрим прямоугольник  с диагональю ОА. Таким образом, формула для нахождения длины вектора  по его координатам на плоскости имеет вид .

Рассмотрим пример.

Найдите длину вектора , заданного в декартовой системе координат. Сразу применяем формулу для нахождения длины вектора по координатам :
. Теперь получим формулу для нахождения длины вектора  по его координатам в прямоугольной системе координат Oxyz в пространстве. В этом случае  (так как ОА – диагональ прямоугольного параллелепипеда), откуда . Определение координат вектора позволяет нам записать равенства , а длина  ОА равна искомой длине вектора, следовательно, . Таким образом, длина вектора  в пространстве равна корню квадратному из суммы квадратов его координат, то есть, находится по формуле .

Длина вектора через координаты точек его начала и конца.

А как найти длину вектора, если даны координаты точек его начала и конца?

В предыдущем пункте мы получили формулы для нахождения длины вектора по его координатам на плоскости и в трехмерном пространстве. Тогда мы можем ими воспользоваться, если найдем координаты вектора по координатам точек его начала и конца.

Рассмотрим решения примеров.

Нахождение длины вектора по теореме косинусов.

Большинство задач на нахождение длины вектора решаются в координатах. Однако, когда координаты вектора не известны приходится искать другие пути решения.

Пусть известны длины двух векторов ,  и угол между ними (или косинус угла), а требуется найти длину вектора  или . В этом случае можно по теореме косинусов в треугольнике 

АВС вычислить длину стороны ВС, которая равна искомой длине вектора.

Разберем решение примера для пояснения сказанного.

Итак, для нахождения длины вектора по координатам используем формулы
 или ,
по координатам точек начала и конца вектора —
 или ,
в некоторых случаях к результату приводит теорема косинусов.

Расстояние между двумя точкамиA1(x1;y1) и A2(x2;y2) в прямоугольной системе координат выражается формулой: Порядок точек не играет роли. Расстояние считается положительным. поэтому корень берется с одним знаком (плюс).

Расстояние между двумя точками

fizmatinf.blogspot.com

Как найти длину вектора

Понятие длины вектора

Для того, чтобы разобраться с понятием длины вектора, прежде всего надо разобрать само понятие вектора. Для того, чтобы ввести определение геометрического вектора вспомним, что такое отрезок. Введем следующее определение.

Определение 1

Отрезком будем называть часть прямой, которая имеет две границы в виде точек.

Отрезок может иметь 2 направления. Для обозначения направления будем называть одну из границ отрезка его началом, а другую границу — его концом. Направление указывается от его начала к концу отрезка.

Определение 2

Вектором или направленным отрезком будем называть такой отрезок, для которого известно, какая из границ отрезка считается началом, а какая его концом.

Обозначение: Двумя буквами: $\overline{AB}$ – (где $A$ его начало, а $B$ – его конец).

Одной маленькой буквой: $\overline{a}$ (рис. 1).

Введем теперь, непосредственно, понятие длин вектора.

Определение 3

Длиной вектора $\overline{a}$ будем называть длину отрезка $a$.

Обозначение: $|\overline{a}|$

Понятие длины вектора связано, к примеру, с таким понятием, как равенство двух векторов.

Определение 4

Два вектора будем называть равными, если они удовлетворяют двух условиям: 1. Они сонаправлены; 1. Их длины равны (рис. 2).

Для того, чтобы определять векторы вводят систему координат и определяют координаты для вектора во введенной системе. Как мы знаем, любой вектор можно разложить в виде $\overline{c}=m\overline{i}+n\overline{j}$, где $m$ и $n$ – действительные числа, а $\overline{i}$ и $\overline{j}$ — единичные векторы на оси $Ox$ и $Oy$, соответственно.

Определение 5

Коэффициенты разложения вектора $\overline{c}=m\overline{i}+n\overline{j}$ будем называть координатами этого вектора во введенной системе координат. Математически:

$\overline{c}={m,n}$

Как найти длину вектора?

Для того, чтобы вывести формулу для вычисления длины произвольного вектора по данным его координатам рассмотрим следующую задачу:

Пример 1

Дано: вектор $\overline{α}$, имеющий координаты ${x,y}$. Найти: длину этого вектора.

Решение.

Введем на плоскости декартову систему координат $xOy$. От начал введенной системы координат отложим $\overline{OA}=\overline{a}$. Построим проекции $OA_1$ и $OA_2$ построенного вектора на оси $Ox$ и $Oy$, соответственно (рис. 3).

Построенный нами вектор $\overline{OA}$ будет радиус вектором для точки $A$, следовательно, она будет иметь координаты ${x,y}$, значит

$[OA_1 ]=x$, $[ OA_2]=y$

Теперь мы легко можем найти искомую длину с помощью теоремы Пифагора, получим

$|\overline{α}|^2=[OA_1]^2+[OA_2]^2$

$|\overline{α}|^2=x^2+y^2$

$|\overline{α}|=\sqrt{x^2+y^2}$

Ответ: $\sqrt{x^2+y^2}$.

Вывод: Чтобы найти длину вектора, у которого задан его координаты, необходимо найти корень из квадрата суммы этих координат.

Пример задач

Пример 2

Найдите расстояние между точками $X$ и $Y$, которые имеют следующие координаты: $(-1,5)$ и $(7,3)$, соответственно.

Решение.

Любые две точки можно легко связать с понятием вектора. Рассмотрим, к примеру, вектор $\overline{XY}$. Как мы уже знаем, координаты такого вектора можно найти, вычтя из координат конечной точки ($Y$) соответствующие координаты начальной точки ($X$). Получим, что

$\overline{XY}=(7+1,3-5)=(8,-2)$

Теперь, найдя длину этого вектора по формуле, выведенной выше, мы и получим искомую длину. Получим:

$d=\sqrt{8^2+(-2)^2}=\sqrt{64+4}=\sqrt{68}=2\sqrt{17}$

Ответ: $2\sqrt{17}$.

Замечание 1

Из этой задачи можно вывести формулу для вычисления такого расстояния. Пусть две точки имеют координаты ${(x’,y’)}$ и ${(x»,y»)}$. Тогда длину между такими точками можно найти по следующей формуле:

$d=\sqrt{(x’-x»)^2+(y’-y»)^2}$

Пример 3

Пусть нам дан треугольник своими координатами вершин $(5,-9)$, $(12,-2)$ и $(4,0)$. Найдем его периметр.

Решение.

Найдем для начала длины всех его сторон по формуле из замечания к задаче 2.

Первая сторона равняется:

$\sqrt{(5-12)^2+(-9+2)^2}=\sqrt{(-7)^2+(-7)^2}=\sqrt{98}=7\sqrt{2}$

Вторая сторона равняется:

$\sqrt{(5-4)^2+(-9-0)^2}=\sqrt{1^2+(-9)^2}=\sqrt{82}$

Третья сторона равняется:

$\sqrt{(12-4)^2+(-2-0)^2}=\sqrt{8^2+(-2)^2 }=\sqrt{68}=2\sqrt{17}$

Складывая, получим

Ответ: $7\sqrt{2}+\sqrt{82}+2\sqrt{17}$

spravochnick.ru

Нахождение длины вектора по координатам. — КиберПедия

Нахождение длины вектора по координатам.

Длину вектора будем обозначать . Из-за такого обозначения длину вектора часто называют модулем вектора.

Начнем с нахождения длины вектора на плоскости по координатам.

Введем на плоскости прямоугольную декартову систему координат Oxy. Пусть в ней задан вектор и он имеет координаты . Получим формулу, позволяющую находить длину вектора через координаты и .

Отложим от начала координат (от точки О) вектор . Обозначим проекции точки А на координатные оси как и соответственно и рассмотрим прямоугольник с диагональю ОА.

В силу теоремы Пифагора справедливо равенство , откуда . Из определения координат вектора в прямоугольной системе координатмы можем утверждать, что и , а по построению длина ОА равна длине вектора , следовательно, .

Таким образом, формула для нахождения длины вектора по его координатам на плоскости имеет вид .

Если вектор представлен в виде разложения по координатным векторам , то его длина вычисляется по этой же формуле , так как в этом случае коэффициенты и являются координатами вектора в заданной системе координат.

Рассмотрим пример.

Пример.

Найдите длину вектора , заданного в декартовой системе координат.

Решение.

Сразу применяем формулу для нахождения длины вектора по координатам :

Ответ:

.

Теперь получим формулу для нахождения длины вектора по его координатам в прямоугольной системе координат Oxyz в пространстве.

Отложим от начала координат вектор и обозначим проекции точки А на координатные оси как и . Тогда мы можем построить на сторонах и прямоугольный параллелепипед, в котором ОА будет диагональю.

В этом случае (так как ОА – диагональ прямоугольного параллелепипеда), откуда . Определение координат вектора позволяет нам записать равенства , а длина ОА равна искомой длине вектора, следовательно, .

Таким образом, длина вектора в пространстве равна корню квадратному из суммы квадратов его координат, то есть, находится по формуле .

Пример.

Вычислите длину вектора , где — орты прямоугольной системы координат.

Решение.

Нам дано разложение вектора по координатным векторам вида , следовательно, . Тогда по формуле нахождения длины вектора по координатам имеем .

Ответ:

.

Прямая на плоскости

Общее уравнение

 

Ax + By + C ( > 0).

Вектор = (А; В) — нормальный вектор прямой.

В векторном виде: + С = 0, где — радиус-вектор произвольной точки на прямой (рис. 4.11).

Частные случаи:

1) By + C = 0 — прямая параллельна оси Ox;

2) Ax + C = 0 — прямая параллельна оси Oy;

3) Ax + By = 0 — прямая проходит через начало координат;

4) y = 0 — ось Ox;

5) x = 0 — ось Oy.

Уравнение прямой в отрезках

 

где a, b — величины отрезков, отсекаемых прямой на осях координат.

Нормальное уравнение прямой (рис. 4.11)

 

где — угол, образуемый нормально к прямой и осью Ox; p — расстояние от начала координат до прямой.

Приведение общего уравнения прямой к нормальному виду:

Здесь — нормируемый множитель прямой; знак выбирается противоположным знаку C, если и произвольно, если C = 0.

 

Нахождение длины вектора по координатам.

Длину вектора будем обозначать . Из-за такого обозначения длину вектора часто называют модулем вектора.

Начнем с нахождения длины вектора на плоскости по координатам.

Введем на плоскости прямоугольную декартову систему координат Oxy. Пусть в ней задан вектор и он имеет координаты . Получим формулу, позволяющую находить длину вектора через координаты и .

Отложим от начала координат (от точки О) вектор . Обозначим проекции точки А на координатные оси как и соответственно и рассмотрим прямоугольник с диагональю ОА.

В силу теоремы Пифагора справедливо равенство , откуда . Из определения координат вектора в прямоугольной системе координатмы можем утверждать, что и , а по построению длина ОА равна длине вектора , следовательно, .

Таким образом, формула для нахождения длины вектора по его координатам на плоскости имеет вид .

Если вектор представлен в виде разложения по координатным векторам , то его длина вычисляется по этой же формуле , так как в этом случае коэффициенты и являются координатами вектора в заданной системе координат.

Рассмотрим пример.

Пример.

Найдите длину вектора , заданного в декартовой системе координат.

Решение.

Сразу применяем формулу для нахождения длины вектора по координатам :

Ответ:

.

Теперь получим формулу для нахождения длины вектора по его координатам в прямоугольной системе координат Oxyz в пространстве.

Отложим от начала координат вектор и обозначим проекции точки А на координатные оси как и . Тогда мы можем построить на сторонах и прямоугольный параллелепипед, в котором ОА будет диагональю.

В этом случае (так как ОА – диагональ прямоугольного параллелепипеда), откуда . Определение координат вектора позволяет нам записать равенства , а длина ОА равна искомой длине вектора, следовательно, .

Таким образом, длина вектора в пространстве равна корню квадратному из суммы квадратов его координат, то есть, находится по формуле .

Пример.

Вычислите длину вектора , где — орты прямоугольной системы координат.

Решение.

Нам дано разложение вектора по координатным векторам вида , следовательно, . Тогда по формуле нахождения длины вектора по координатам имеем .

Ответ:

.

cyberpedia.su

Длина вектора, онлайн калькулятор

Наш онлайн калькулятор позволяет найти длину вектора всего за пару кликов. Для нахождения длины вектора заданного координатами или по точкам — выберите размерность и способ задания вектора, введите все координаты и нажмите кнопку «Вычислить», калькулятор выдаст пошаговое решение и ответ! Каждый шаг будет подробно расписан, это поможет вам понять решение и закрепить пройденный материал.

Введите данные для вычисления длины вектора  

Размерность вектора:

2 3

Форма представления вектора:

координатами точками

Формула :

Решили сегодня: раз, всего раз

Понравился сайт? Расскажи друзьям!

ru.solverbook.com

Определение координат вектора заданного координатами его начальной и конечной точки.

Основное соотношение.Чтобы найти координаты вектора AB, зная координаты его начальной точек А и конечной точки В, необходимо из координат конечной точки вычесть соответствующие координаты начальной точки.

Формулы определения координат вектора заданного координатами его начальной и конечной точки

Формула определения координат вектора для плоских задач

В случае плоской задачи вектор AB заданный координатами точек A(A_x ; A_y) и B(B_x ; B_y) можно найти воспользовавшись следующей формулой

AB = {B_x — A_x ; B_y — A_y}

Формула определения координат вектора для пространственных задач

В случае пространственной задачи вектор AB заданный координатами точек A(A_x ; A_y ; A_z) и B(B_x ; B_y ; B_z) можно найти воспользовавшись следующей формулой

AB = {B_x — A_x ; B_y — A_y ; B_z — A_z}

Формула определения координат вектора для n -мерного пространства

В случае n-мерного пространства вектор AB заданный координатами точек A(A₁ ; A₂ ; … ; A_n) и B(B₁ ; B₂ ; … ; B_n) можно найти воспользовавшись следующей формулой

AB = {B₁ — A₁ ; B₂ — A₂ ; … ; B_n — A_n}

Примеры задач связанных с определением координат вектора по двум точкам

Примеры для плоских задач

Пример 1. Найти координаты вектора AB, если A(1; 4), B(3; 1).

Решение: AB = {3 — 1; 1 — 4} = {2; -3}.

Пример 2. Найти координаты точки B вектора AB = {5; 1}, если координаты точки A(3; -4).

Решение:

AB_x = B_x — A_x   =>   B_x = AB_x + A_x   =>   B_x = 5 + 3 = 8
AB_y = B_y — A_y   =>   B_y = AB_y + A_y   =>   B_y = 1 + (-4) = -3

Ответ: B(8; -3).

Пример 3. Найти координаты точки A вектора AB = {5; 1}, если координаты точки B(3; -4).

Решение:

AB_x = B_x — A_x   =>   A_x = B_x — AB_x   =>   A_x = 3 — 5 = -2
AB_y = B_y — A_y   =>   A_y = B_y — AB_y   =>   A_y = -4 — 1 = -5

Ответ: A(-2; -5).

Примеры для пространственных задач

Пример 4. Найти координаты вектора AB, если A(1; 4; 5), B(3; 1; 1).

Решение: AB = {3 — 1; 1 — 4; 1 — 5} = {2; -3; -4}.

Пример 5. Найти координаты точки B вектора AB = {5; 1; 2}, если координаты точки A(3; -4; 3).

Решение:

AB_x = B_x — A_x   =>   B_x = AB_x + A_x   =>   B_x = 5 + 3 = 8
AB_y = B_y — A_y   =>   B_y = AB_y + A_y   =>   B_y = 1 + (-4) = -3
AB_z = B_z — A_z   =>   B_z = AB_z + A_z   =>   B_z = 2 + 3 = 5

Ответ: B(8; -3; 5).

Пример 6. Найти координаты точки A вектора AB = {5; 1; 4}, если координаты точки B(3; -4; 1).

Решение:

AB_x = B_x — A_x   =>   A_x = B_x — AB_x   =>   A_x = 3 — 5 = -2
AB_y = B_y — A_y   =>   A_y = B_y — AB_y   =>   A_y = -4 — 1 = -5
AB_z = B_z — A_z   =>   A_z = B_z — AB_z   =>   A_z = 1 — 4 = -3

Ответ: A(-2; -5; -3).

Примеры для n -мерного пространства

Пример 7. Найти координаты вектора AB, если A(1; 4; 5; 5; -3), B(3; 0; 1; -2; 5).

Решение: AB = {3 — 1; 0 — 4; 1 — 5; -2 — 5; 5 — (-3)} = {2; -4; -4; -7; 8}.

Пример 8. Найти координаты точки B вектора AB = {5; 1; 2; 1}, если координаты точки A(3; -4; 3; 2).

Решение:

AB₁ = B₁ — A₁   =>   B₁ = AB₁ + A₁   =>   B₁ = 5 + 3 = 8
AB₂ = B₂ — A₂   =>   B₂ = AB₂ + A₂   =>   B₂ = 1 + (-4) = -3
AB₃ = B₃ — A₃   =>   B₃ = AB₃ + A₃   =>   B₃ = 2 + 3 = 5
AB₄ = B₄ — A₄   =>   B₄ = AB₄ + A₄   =>   B₄ = 1 + 2 = 3

Ответ: B(8; -3; 5; 3).

Пример 9. Найти координаты точки A вектора AB = {5; 1; 4; 5}, если координаты точки B(3; -4; 1; 8).

Решение:

AB₁ = B₁ — A₁   =>   A₁ = B₁ — AB₁   =>   A₁ = 3 — 5 = -2
AB₂ = B₂ — A₂   =>   A₂ = B₂ — AB₂   =>   A₂ = -4 — 1 = -5
AB₃ = B₃ — A₃   =>   A₃ = B₃ — AB₃   =>   A₃ = 1 — 4 = -3
AB₄ = B₄ — A₄   =>   A₄ = B₄ — AB₄   =>   A₄ = 8 — 5 = 3

Ответ: A(-2; -5; -3; 3).

ru.onlinemschool.com

Формулы векторов

1. Координаты вектора

Если вектор задан координатами своих начала и конца: , то его координаты равны разности соответствующих координат конца и начала:

   

2. Длина или модуль вектора

Если вектор , то его длина равна корню квадратному из суммы квадратов координат:

   

3. Сумма векторов

Если векторы и заданы своими координатами, то суммой этих векторов есть вектор, координаты которого равны сумме соответствующих координат векторов-слагаемых:

   

4. Умножение вектора на число

Чтобы найти произведение вектора на некоторое число , нужно каждую координату заданного вектора умножить на это число:

   

5. Скалярное произведение векторов

Если векторы и заданы своими координатами, то их скалярное произведение равно сумме произведений соответствующих координат:

   

6. Векторное произведение векторов

Если векторы и заданы своими координатами в некотором ортонормированном базисе , то их векторное произведение находится по формуле:

   

7. Смешанное произведение векторов

Если заданы три вектора и , то их смешанное произведение равно определителю, по строкам которого записаны координаты этих векторов:

   

Замечание. Обычно такой определитель вычисляется методом треугольников.

8. Угол между векторами

Косинус угла между двумя векторами и , заданными своими координатами, равен частному скалярного произведения этих векторов и произведению их модулей:

   

9. Проекция вектора на вектор

Проекция вектора на направление вектора равна отношение скалярного произведения этих векторов к модулю вектора :

   

Понравился сайт? Расскажи друзьям!

ru.solverbook.com