Инструмент для работы с графами онлайн
Задайте матрицу смежности. Используйте запятую «,» в качестве разделителя
Мартрица имеет неправильный формат. Используйте запятую «,» в качестве разделителя. Матрица должна иметь одинаковое количество столбцов и строк.
Задайте матрицу инцидентности. Используйте запятую «,» в качестве разделителя
Мартрица имеет неправильный формат. Используйте запятую «,» в качестве разделителя.
Ваш алгоритм отправлен на модерацию и в случае успеха он будет добавлен на сайт.
Ошибка создания графа. Матрица смежности имеет неправильный формат. Нажимте кнопку «исправить матрицу» чтобы исправить матрицу или кнопку «справка» чтобы открыть справку о формате матрицы
Ошибка создания графа. Матрица инцидентности имеет неправильный формат. Нажимте кнопку «исправить матрицу» чтобы исправить матрицу или кнопку «справка» чтобы открыть справку о формате матрицы
Задайте матрицу инцидентности. Используйте запятую «,» в качестве разделителя
Мартрица имеет неправильный формат. Используйте запятую «,» в качестве разделителя.
Выделите и перемещайте объекты или перемещайте рабочую область
Перемещайте курсор для перемещения объекта
Выделите и перемещайте объекты или перемещайте рабочую область
Перемещайте курсор для перемещения объекта
Кликните на рабочую область, чтобы добавить вершину. Нумерация вершин
Выделите первую вершину для создания дуги
Выделите вторую вершину, которую хотите соединить
Выделите вершину, из которой хотите найти кратчайших путь
Выделите конечную вершину кратчайшего пути
Расстояние между вершинами %d
Пути не существует
Кликните по объекту, который хотите удалить
Добавить ребро
Ориентированную
Неориентированную
Матрица смежности
Сохранить граф
Отмена
Мин. расстояние =
Матрица инцидентности
Сохранение графа
закрыть
Число компонентов связности графа равно
Число слабо связных компонентов равно
Что вы думаете о сайте?
Имя (email для ответа)
Написать
Отправить
Напишите нам
исправить матрицу
справка
Матрица имеет неправильный формат
Сохранение изображения графа
Полный отчёт
Краткий отчёт
Граф не содержит Эйлеров цикл
Граф содержит Эйлеров цикл
Обработка…
Добавить вершину
Переименовать вершину
Переименовать
ru
Изменить вес
ненагруженный
Групповое переименование
Опрос
Рекомендовать алгоритмы
Граф не содержит Эйлерову цепь
Граф содержит Эйлерову цепь
Граф минимальных расстояний.
Нажмите для сохранения
Показать матрицу расстояний
Матрица расстояний
Выделите исток максимального потока
Выделите сток максимального потока
Максимальный поток из %2 в %3 равен %1
Поток из %1 в %2 не существует
Исток
Сток
Граф не содержит Гамильтонов цикл
Граф содержит Гамильтонов цикл
Граф не содержит Гамильтонову цепь
Граф содержит Гамильтонову цепь
Выбирете начальную вершину обхода
Порядок обхода:
Изгиб дуги
Отменить
graphonline.ru
Новости сервиса Граф Онлайн
Ниже представлены последнии обновления нашего сервиса
Изгиб дуг
Добавили возможность изгибать дуги. Выделите дугу и нажимайте на кнопку + или -.
Админ 15.02.2019
Завершение сбора стредств
Благодаря неравнодушным пользователям нашего сервиса мы завершили сбор средств для разработки новых алгоритмов для сайта. Мы уже добавили алгоритм поиска диаметра и радиуса графа, далее будет поиск максимального потока и раскраска графа.
Админ 07.04.2018
Алгоритм Флойда — Уоршелла
Добавили алгоритм Флойда — Уоршелла. Теперь вы можете получить матрицу расстояний графа.
Админ 10.12.2017
Опрос
Мы завершили опрос о функциях, которые вы хотели бы видеть на graphonline.ru. Результаты распределились следующим образом:
- Больше алгоритмов — 53%
- Улучшение визуализации — 24%
- Личный кабинет — 13%
- Улучшение поддержки больших графов — 8%
Админ 13.09.2017
Завершение сбора стредств
Мы рады сообщить, что сбор на хостинг завершён. Благодаря 20 неравнодушным пользователям нам удалось собрать 1500р, для продления хостинга на год. Теперь мы можем не боясть блокировки до 2019 года.
Админ 02.07.2017
Обновления
По постоянно работаем над улучшением сайта, за последние несколько месяцев было сделано следующее: обновлены ролики у на нашем канале на Youtube https://www.youtube.com/channel/UCrUEnaF7yz6sclCZi1-7XMA, добавлены примеры графов, добавлен алгоритм поиска минимального остовного дерева, улучшена мобильная версия сайта и другие мелкие правки.
Админ 10.03.2017
Произвольный текст для вершин
Добавили возможноть задавать произвольный текст для вершин.
Админ 04.07.2016
Размещение графа на плоскости
Добавлен алгоритм для красивого размещения графа на плоскости. Мы будем улучшать этот алгоритм.
Админ 12.06.2016
Масштабирование
Добавлена функциональность для управления масштабом рабочей области.
Админ 11.06.2016
Анимация
Мы добавили анимацию для алгоритмов поиска кратчайшего пути и Эйлерового цикла. Также улучшили отчёт.
Админ 23.01.2016
Эйлеров цикл
Добавили алгоритм поиска Эйлеровго цикла. Также немного улучшили интерфейс главной страницы.
Админ 09.01.2016
graphonline.ru
Создания собственого алгоритма на JavaScript для графов онлайн
Задайте матрицу смежности. Используйте запятую «,» в качестве разделителя
Мартрица имеет неправильный формат. Используйте запятую «,» в качестве разделителя. Матрица должна иметь одинаковое количество столбцов и строк.
Задайте матрицу инцидентности. Используйте запятую «,» в качестве разделителя
Мартрица имеет неправильный формат. Используйте запятую «,» в качестве разделителя.
Ваш алгоритм отправлен на модерацию и в случае успеха он будет добавлен на сайт.
Ошибка создания графа. Матрица смежности имеет неправильный формат. Нажимте кнопку «исправить матрицу» чтобы исправить матрицу или кнопку «справка» чтобы открыть справку о формате матрицы
Ошибка создания графа. Матрица инцидентности имеет неправильный формат. Нажимте кнопку «исправить матрицу» чтобы исправить матрицу или кнопку «справка» чтобы открыть справку о формате матрицы
Задайте матрицу инцидентности. Используйте запятую «,» в качестве разделителя
Мартрица имеет неправильный формат. Используйте запятую «,» в качестве разделителя.
Выделите и перемещайте объекты или перемещайте рабочую область
Перемещайте курсор для перемещения объекта
Выделите и перемещайте объекты или перемещайте рабочую область
Перемещайте курсор для перемещения объекта
Кликните на рабочую область, чтобы добавить вершину. Нумерация вершин
Выделите первую вершину для создания дуги
Выделите вторую вершину, которую хотите соединить
Выделите вершину, из которой хотите найти кратчайших путь
Выделите конечную вершину кратчайшего пути
Расстояние между вершинами %d
Пути не существует
Кликните по объекту, который хотите удалить
Добавить ребро
Ориентированную
Неориентированную
Матрица смежности
Сохранить граф
Отмена
Мин. расстояние =
Матрица инцидентности
Сохранение графа
закрыть
Число компонентов связности графа равно
Число слабо связных компонентов равно
Что вы думаете о сайте?
Имя (email для ответа)
Написать
Отправить
Напишите нам
исправить матрицу
справка
Матрица имеет неправильный формат
Сохранение изображения графа
Полный отчёт
Краткий отчёт
Граф не содержит Эйлеров цикл
Граф содержит Эйлеров цикл
Обработка…
Добавить вершину
Переименовать вершину
Переименовать
ru
Изменить вес
ненагруженный
Групповое переименование
Опрос
Рекомендовать алгоритмы
Граф не содержит Эйлерову цепь
Граф содержит Эйлерову цепь
Граф минимальных расстояний.
Нажмите для сохранения
Показать матрицу расстояний
Матрица расстояний
Выделите исток максимального потока
Выделите сток максимального потока
Максимальный поток из %2 в %3 равен %1
Поток из %1 в %2 не существует
Исток
Сток
Граф не содержит Гамильтонов цикл
Граф содержит Гамильтонов цикл
Граф не содержит Гамильтонову цепь
Граф содержит Гамильтонову цепь
Выбирете начальную вершину обхода
Порядок обхода:
Изгиб дуги
Отменить
graphonline.ru
Построить граф и найти его характеристики
Студенты-математики и программисты изучают теорию графов в курсе дискретной математики. С практических позиций граф востребованное понятие. Говоря простым языком — это совокупность вершин и ребер, которые эти вершины соединяют. Примеры графов: карта с населенными пунктами и дорогами, структура сайта со страницами и переходами по этим страницам (карта сайта). Чаще всего студентам предлагают построить граф по заданному множеству вершин и ребер (дуг) если задана матрица смежности или матрица инцидентности. Или, наоборот, по заданнам вершинам и ребрам составить матрицу смежности и матрицу инцидентности. Еще предлагается часто посчитать хроматическое число графа — минимальное число цветов, в которые можно раскрасить вершины графа так, чтобы концы любого ребра имели разные цвета.Пользуясь нашим сервисом, вы можете построить граф по заданным соотношениям между вершинами (смотрите пример ввода внизу). Если вы введете пример и нажмете кнопку «Решить», то получите изображение графа и несколько вариантов компоновки вершин и ребер. Кроме того, будут выданы основные характеристики графа: число вершин — vertex count, число ребер — edge count, радиус графа — radius, диаметр графа — diameter, матрица смежности — adjacency matrix, матрица инцидентности — incidence matrix и целый ряд других характеристик. Напомним, что радиус графа — наименьший из эксцентриситетов его вершин; эксцентриситет вершины — максимальное расстояние от этой вершины до других вершин графа, диаметр графа — максимальный эксцентриситет его вершин. Можно получить и дополнительные характеристики, например, цикломатическое число графа. Очень удобно использовать этот сервис для построения больших графов. Вам останется только скопировать картинку и вставить в ваш отчет или семестровое задание. Ниже пример ввода:
1->2, 2->3, 3->1, 3->4, 4->1, 2->1, 2->2, 4->3
studlab.com
Graphviz – рисуем графы – Ещегодник
Достаточно часто встречается задача, когда надо нарисовать нечто, представляющее из себя граф. Это может быть иерархическая сструктура работ проекта, иерархическая структура рисков, организационная структура, топология сети и т.п. Если же количество вершин и ребер достаточно велико, то нарисовать это красиво становится нетривиальной задачей. К счастью, существует программа Graphviz, которая использует язык описания графов dot и имеет графический интерфейс под Windows.
Сама программа бесплатна и может быть скачена по ссылке. После установки в Windows в меню “Пуск” появится приложение gvedit, которое является графическим интерфесом к установленному пакету программ. В Mac OS X такого не произойдет и обходное решение описано ниже (если, конечно, вы не готовы работать в терминале).
Рассмотрим направленный граф, описывающий все возможные коммуникации между четырьмя участниками проекта. Листинг, описывающий граф привожу ниже:
digraph test{
1->2;
1->3;
1->4;
2->1;
2->3;
2->4;
3->1;
3->2;
3->4;
4->1;
4->2;
4->3;
}В приложении это будет выглядеть следующим образом:
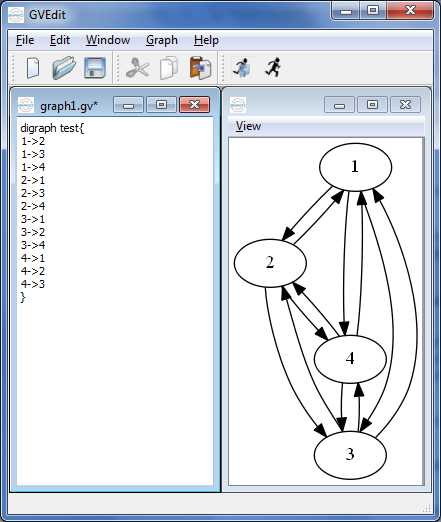
В данном случае, был использован параметр по умолчанию и для построения графа использована утилита dot.
Для примера, тот же граф, построенный с помощью:
Подробнее это описано в документации на сайте. Если кратко, то dot, а далее в статье используется только он, рисует граф в заданном в порядке ветвления; twopi – использует радиальное построение, когда вершины располагаются на концентрических окружностях, circo – связанные вершины располагаются по кругу.
В данном случае, у нас был изображен орграф. Если граф не ориентирован, иными словами “стрелочки” на рисунке нам не важны, то граф описывается следующим образом (обратите внимание на первой слово “graph” вместо “digraph”, как задаются связи (“–” вместо “->”), а также на команду node [shape = box] – задающую прямоугольники в качестве вершин). Несомненно, формат стрелок можно определить и в самом графе на языке dot, но алгоритмы построения для ориентированных и неориентированных графов имеют небольшое отличие.
graph test{
node [shape = box];
"Проект А"--"Фаза 1";
"Проект А"--"Фаза 2";
"Проект А"--"Фаза 3";
"Фаза 1"--"Задача 1";
"Фаза 1"--"Задача 2";
"Фаза 2"--"Задача 3";
"Фаза 2"--"Задача 4";
}Результат выглядит так:
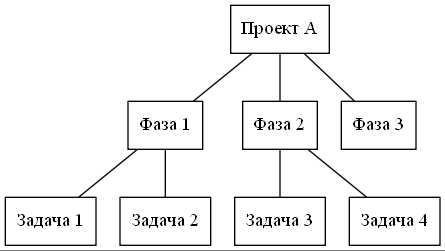
Пример из заметки по динамическому программированию: меняем ориентацию графа (строится справа налево), добавляем подписи и стили линий и задаем размер листа.
digraph ex01 {
rankdir=LR;
size="8,5"
node [shape = box];
"1" -> "2" [ label = "3",style=bold,color=red ];
"1" -> "3" [ label = "7",style=dotted];
"1" -> "4" [ label = "2",style=dotted ];
"2" -> "5" [ label = "9",style=dotted ];
"2" -> "6" [ label = "11",style=bold,color=red ];
"3" -> "5" [ label = "5",style=dotted ];
"3" -> "6" [ label = "10",style=dotted ];
"3" -> "7" [ label = "7",style=dotted ];
"4" -> "6" [ label = "15",style=dotted ];
"4" -> "7" [ label = "13",style=dotted ];
"5" -> "8" [ label = "7",style=dotted ];
"5" -> "9" [ label = "5",style=dotted ];
"6" -> "8" [ label = "3",style=bold,color=red ];
"6" -> "9" [ label = "4",style=dotted ];
"7" -> "8" [ label = "7",style=dotted ];
"7" -> "9" [ label = "1",style=dotted ];
"8" -> "10" [ label = "1",style=bold,color=red ];
"9" -> "10" [ label = "4",style=dotted ];
}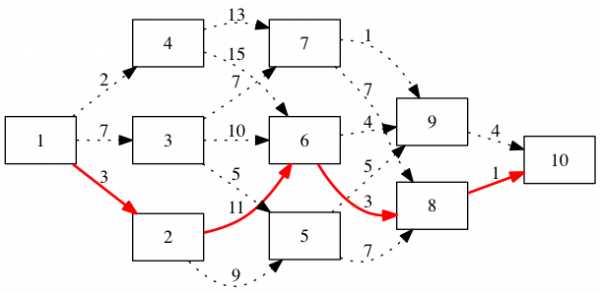
Более сложные пример приведен в заметке по методу анализа иерархии.
При выборе формата записи результирующего графа, определенный интерес представляет формат svg в поле Output File Type. Формат svg — векторный формат, файлы в этом формате можно редактировать, например, с помощью Inkscape. Также обратите внимание на векторный формат emf, позволяющий внедрять и масштабировать рисунки в Word без потери качества. Для этого сайта был использован растровый формат png.
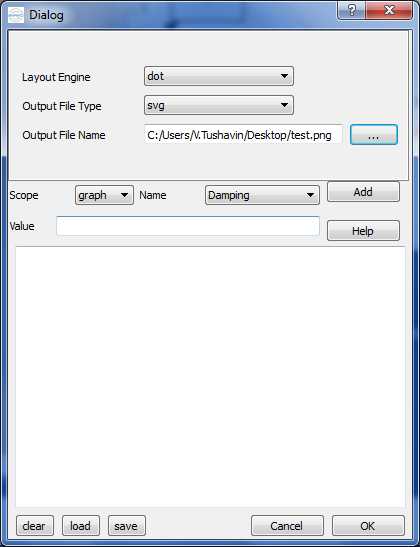
И последний пример, использование структуры в качестве вершины графа.
digraph structs {
node [shape=record,];
struct1 [label="<f0> Инициация|<f1> Планирование|<f2> Исполнение|<f3> Завершение",
fillcolor=yellow];
struct2 [label="<f0> Мониторинг|<f1> Контроль"];
struct1:f0-> struct2:f0;
struct1:f1-> struct2:f0;
struct1:f2-> struct2:f0;
struct1:f3-> struct2:f0;
struct2:f1 -> struct1:f0 [color="red"];
struct2:f1 ->struct1:f1 [color="red"];
struct2:f1 ->struct1:f2 [color="red"];
struct2:f1 ->struct1:f3 [color="red"];
}
Самый простой вариант создать диаграмму – это запустить в консоли соответсвующую команду (на рисунке показано окно Терминала под Mac OS X), например, dot. Если файл называется test.gv, а на выходе мы хотим получить png, то команда будет такая, как это показано ниже (а также выше на рисунке). Решение универсально и работает в любой операционной системе.
dot -Tpng -O test.gvСледует отметить, что в Mac OS X при установке graphviz такой удобной графической оболочки как в Windows, вы не получите. Если вариант собрать его из исходников из портов (если вы хоть что-то поняли из написанных слов, значит инструкции не нужны), можно использовать консоль, как это показано выше, но также имеется возможноть использовать средства языка R и RStudio. Возможно, что кому-то это будет проще.
Для корректной работы вам понадобится пакет DiagrammeR. Установите его из меню или командой
install.packages("DiagrammeR")После установки создайте файл, скопируйте туда код, сохраните его с расширением .gv, поставьте галочку “Preview on Save”. Обратите внимание, если вы работаете в Windows, то файл необходимо сохранять в кодировке cp1251, иначе вместо русского языка вы получите кракозябры.
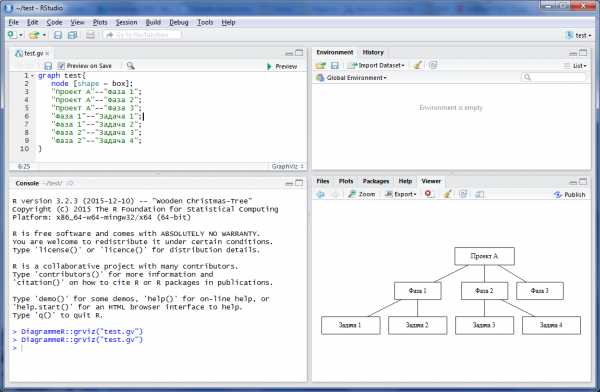
Дальше, используя кнопку Export, можно сохранить получившуюся диаграмму в формате png или jpeg.
Следует отметить, что DiagrammeR позволяет работать и с диаграммами в формате mermaid. В таком случае, файлы надо сохра
tushavin.ru
Онлайн редактор для схем, графиков и диаграмм
Визуальный редактор Gliffy предоставляет шаблоны для различных целей, в том числе для веб-дизайна, для разработки программного обеспечения, блок-схем, сетевых диаграмм, схем для архитекторских проектов и мн. др.
Ключевые особенности онлайн редактора Gliffy
Онлайн редактор Gliffy отличается разнообразием форм, стилей, цветов и форматов, доступных для широкого круга проектов. Использование флэш-технологии позволяет оперативно размещать диаграммы на экране методом drag-n-drop. Отдельные части можно легко удалять, достаточно их выделить и нажать на клавиатуре клавишу «Delete».
Редактор Gliffy предлагает возможность вести совместную работу над проектом, просто активируйте плагин и отправьте приглашение единомышленникам. Можно делиться своими диаграммами с пользователями, которые используют компьютер, планшет или смартфон с доступом к приложению Confluence.
По сравнению с аналогичными приложениями
Gliffy предоставляет пользователям список понятных шаблонов, цветные изображения с различными аспектами, профессионально созданные диаграммы проектов, а также стандартный чистый лист, с которого можно начать.
Цены
Бесплатная учетная запись пользователя имеет большую функциональность предоставляемых инструментов, но не сохраняет проекты. Тем не менее, можно просто сделать скриншот экрана и таким образом сохранить своё творчество)
Также недоступно совместное использование и печать. Вы можете экспортировать схемы в JPG, PNG, SVG или XML файлы и сохранять их локально.
Стандартный аккаунт позволяет сохранять до 200 диаграмм одновременно. За него взимается плата 4.95 долларов в месяц с одного пользователя.
Учетная запись для профессиональных пользователей обходится в 9.95 долларов в месяц и предлагает не ограниченное пространство для хранения схем.
Программа Gliffy отличается большой функциональностью для различных проектов, понятным пользовательским интерфейсом и многочисленными вариантами дизайна.
Видео
cameralabs.org
Центр графа
Вспомним, что центром является любая вершина х с наименьшим значением МВВ(х) (макимальное расстояние вершина-вершина), т. е. центр — это любая вершина х, такая, что расстояние от нее до наиболее отдаленной вершины минимально.
МВВ(х) =min{МВВ(i)}
Центр отыскивается как один из элементов матрицы DN, значение i, j-го элемента которой — di,j есть кратчайшее расстояние от вершины i к вершине j. Элементы матрицы могут быть вычислены с помощью алгоритма Флойда или алгоритма Данцига. Максимальное расстояние МВВ(i) от вершины i до любой вершины графа является элементом i-й строки матрицы DN, имеющим максимальное значение. Центром является произвольная вершина х с наименьшим среди всех вершин графа звачеявем МВВ(х), т. е. центр — это произвольная вершина х, которой соответствует строка матрицы DN, содержащая элемент с наименьшим максимальным значением.
Алгоритм поиска центра
- находим D – матрицу, элементами которой являются ai,j – длины кратчайших дуг.
- Ищем DN – матрицу длин кратчайших расстояний по Флойду или Данцегу.
- Определяем МВВ(i) для каждой вершины графа.
- Из всех МВВ(i) выбираем минимальное соответствующая вершина и будет центром.
Пример
Необходимо найти центр графа представленого на рисунке:
Составим матрицу длин кратчайших дуг между каждой парой вершин — D, в случае, если дуги между вершиной i и j не существует, элементу ai,j матрицы присваивается значение ∞. Матрица D:
| D0= | 30 | ∞ | ∞ | 45 | ∞ | ∞ | 23 | |
| 30 | ∞ | 17 | ∞ | ∞ | 122 | ∞ | ||
| ∞ | 34 | 12 | ∞ | 52 | ∞ | ∞ | ||
| ∞ | 11 | 23 | ∞ | ∞ | ∞ | 67 | ||
| 45 | ∞ | ∞ | ∞ | 40 | ∞ | ∞ | ||
| ∞ | ∞ | 52 | ∞ | 43 | ∞ | ∞ | ||
| ∞ | 12 | ∞ | ∞ | ∞ | ∞ | ∞ | ||
| ∞ | ∞ | ∞ | 67 | ∞ | ∞ | ∞ |
C помощью алгоритма Флойда или Данцега получаем матрицу длин кратчайших путей между каждой парой вершин графа:
| D8= | 30 | 70 | 47 | 45 | 85 | 152 | 23 | |
| 30 | 40 | 17 | 75 | 92 | 122 | 53 | ||
| 53 | 23 | 12 | 95 | 52 | 145 | 76 | ||
| 41 | 11 | 23 | 86 | 75 | 133 | 64 | ||
| 45 | 75 | 92 | 92 | 40 | 197 | 68 | ||
| 88 | 75 | 52 | 64 | 43 | 197 | 111 | ||
| 42 | 12 | 52 | 29 | 87 | 104 | 65 | ||
| 108 | 78 | 90 | 67 | 153 | 142 | 200 |
Теперь, основываясь на полученой нами матрице длин кратчайших путей, найдем МВВ(i) для каждой вершины графа
МВВ(i)=max{di,j}.
МВВ(1)=max{d(1, j)}=152
МВВ(2)=max{d(2, j)}=122
МВВ(3)=max{d(3, j)}=145
МВВ(4)=max{d(4, j)}=133
МВВ(5)=max{d(5, j)}=197
МВВ(6)=max{d(6, j)}=197
МВВ(7)=max{d(7, j)}=104
МВВ(8)=max{d(8, j)}=200
Центром графа является такая вершина x, для которой МВВ(x)=min{МВВ(i)}.. Минимальное значение имеет МВВ(7)=104, а это значит, что вершина 7 является центром графа.
www.uchimatchast.ru
