Экспонента онлайн калькулятор exp – Калькулятор онлайн значения экспоненциальной функции

Уравнение экспоненты онлайн калькулятор

Применение уравнений широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Уравнения человек использовал еще в древности и с тех пор их применение только возрастает. Экспонента представляет собой показательную функцию \[y(x) =e^x,\] производная которой равна самой функции. Экспоненту обозначают: \[e^x, exp(x), Exp(x) \]

\[e^x=exp(x)=Exp(x) \]

Экспонента обладает свойствами показательной функции с основанием степени е > 1. Основанием степени экспоненты является число «е». Это иррациональное число. Оно примерно равно:

\[e\approx 2,718281828459045\cdots \]

Выражение числа «е» через предел последовательности. Число «е» можно выразить через предел последовательности. Это, так называемый, второй замечательный предел:

\[e=\lim_{n\to\infty} \left(1+\frac~xn\right)^n\]

Выражение числа е в виде ряда

\[e = 2+1/2!+1/3!+1/3!+ \cdots +1/n!+ \cdots \]

График экспоненты

На графике представлена экспонента, \[e\] в степени \[x:\]

\[y(x) = e^x\]

На графике видно, что экспонента монотонно возрастает.

Так же читайте нашу статью «Решить уравнения с факториалом онлайн решателем»

Что касается основных формул, то они такие же, как и для показательной функции с основанием степени \[е.\]

\[e^p \cdot e^q=e^{p+q}\]

\[ (e^p)^p=e{pq}=(e^p)^p\]

\[e^p=e^{pq}=1/e^p\]

\[e^p/e^q = e^{p-q} \]

Выражение показательной функции через экспоненту:

\[q^x=e^{xln a}\]

Где можно решить уравнение с экспонентой онлайн?

Решить уравнение вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.

www.pocketteacher.ru

Функция экспонента в Excel

Одной из самых известных показательных функций в математике является экспонента. Она представляет собой число Эйлера, возведенное в указанную степень. В Экселе существует отдельный оператор, позволяющий её вычислить. Давайте разберемся, как его можно использовать на практике.

Вычисление экспоненты в Эксель

Экспонента является числом Эйлера, возведенным в заданную степень. Само число Эйлера приблизительно равно 2,718281828. Иногда его именуют также числом Непера. Функция экспоненты выглядит следующим образом:

f(x) = e^n,

где e – это число Эйлера, а n – степень возведения.

Для вычисления данного показателя в Экселе применяется отдельный оператор – EXP. Кроме того, эту функцию можно отобразить в виде графика. О работе с этими инструментами мы и поговорим далее.

Способ 1: вычисление экспоненты при помощи ручного ввода функции

Для того чтобы рассчитать в Экселе величину экспоненты для значения e в указанной степени, нужно воспользоваться специальным оператором EXP. Его синтаксис является следующим:

=EXP(число)

То есть, эта формула содержит только один аргумент. Он как раз и представляет собой степень, в которую нужно возвести число Эйлера. Этот аргумент может быть как в виде числового значения, так и принимать вид ссылки на ячейку, содержащую в себе указатель степени.

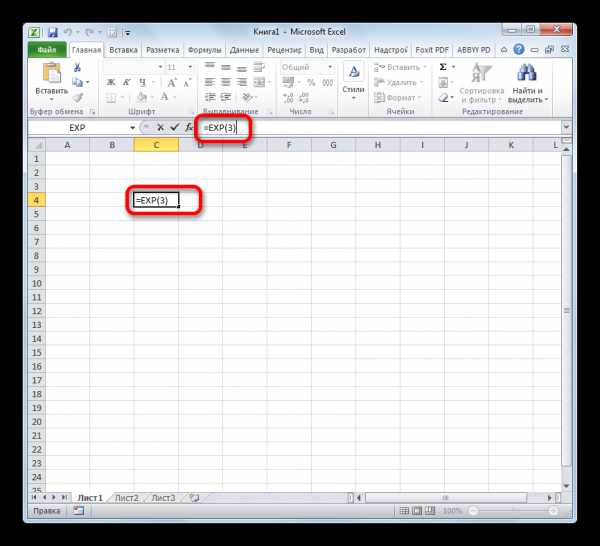
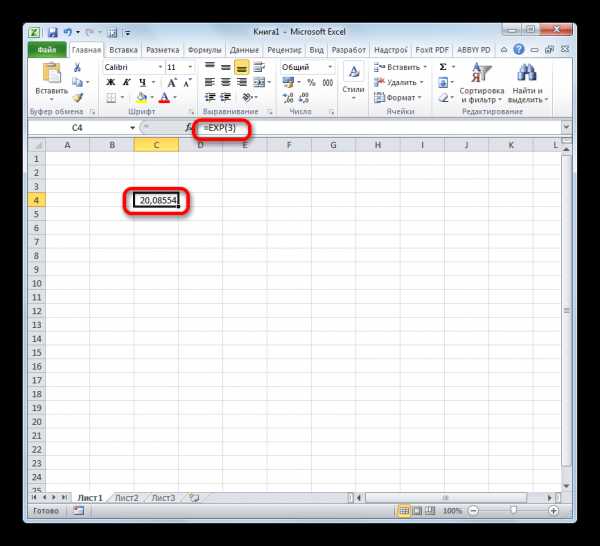
1. Таким образом для того, чтобы рассчитать экспоненту для третьей степени, нам достаточно ввести в строку формул или в любую незаполненную ячейку на листе следующее выражение:

   =EXP(3)



2. Для выполнения расчета щелкаем по кнопке Enter. Итог выводится в заранее указанную ячейку.

Урок: Другие математические функции в Эксель

Способ 2: использование Мастера функций

Хотя синтаксис расчета экспоненты предельно прост, некоторые пользователи предпочитают применять Мастер функций. Рассмотрим, как это делается на примере.

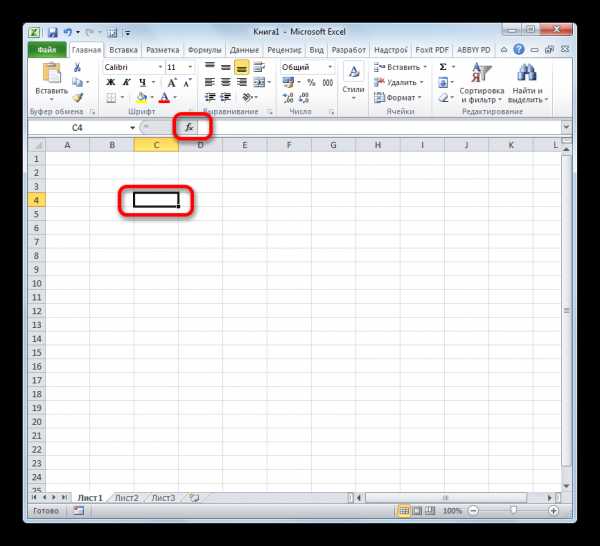
1. Устанавливаем курсор на ту ячейку, где должен будет выводиться итоговый результат расчета. Щелкаем по значку в виде пиктограммы «Вставить функцию» слева от строки формул.



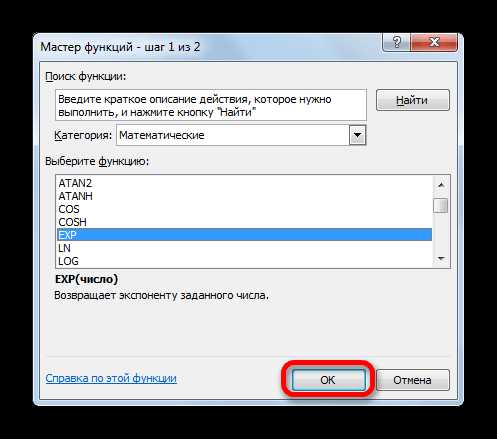
2. Открывается окошко Мастера функций. В категории «Математические» или «Полный алфавитный перечень» производим поиск наименования «EXP». Выделяем это название и жмем на кнопку
   «OK».



3. Открывается окно аргументов. Оно имеет только одно поле – «Число». Вбиваем в него цифру, которая будет означать величину степени числа Эйлера. Жмем на кнопку «OK».



4. После вышеперечисленных действий результат расчета будет показан в той ячейке, которая была выделена в первом пункте данного способа.

Если в качестве аргумента используется ссылка на ячейку, которая содержит показатель степени, то нужно поставить курсор в поле «Число» и просто выделить ту ячейку на листе. Её координаты тут же отобразятся в поле. После этого для расчета результата щелкаем по кнопке «OK».

Урок: Мастер функций в Microsoft Excel

Способ 3: построение графика

Кроме того, в Экселе существует возможность построить график, взяв за основу результаты, полученные вследствие вычисления экспоненты. Для построения графика на листе должны уже иметься рассчитанные значения экспоненты различных степеней. Произвести их вычисление можно одним из способов, которые описаны выше.

1. Выделяем диапазон, в котором представлены экспоненты. Переходим во вкладку «Вставка». На ленте в группе настроек «Диаграммы» нажимаем на кнопку «График». Открывается список графиков. Выбирайте тот тип, который считаете более подходящим для выполнения конкретных задач.



2. После того, как тип графика выбран, программа построит и отобразит его на том же листе, согласно указанным экспонентам. Далее его можно будет редактировать, как и любую другую диаграмму Экселя.

Урок: Как сделать график в Excel

Как видим, рассчитать экспоненту в Экселе при помощи функции EXP элементарно просто. Эту процедуру легко произвести как в ручном режиме, так и посредством Мастера функций. Кроме того, программа предоставляет инструменты для построения графика на основе этих расчетов.

Мы рады, что смогли помочь Вам в решении проблемы.
Опишите, что у вас не получилось. Наши специалисты постараются ответить максимально быстро.

Помогла ли вам эта статья?

ДА НЕТ

lumpics.ru

Экспонента комплексного числа

Аргумент экспоненты

Рассчитана экспонента комплексного числа/выражения

Описание

Ряд имеющий вид   расходится  и стремиться  к бесконечности,

с другой стороны ряд вида

стремится к определенному числу имеющее значение и названного в честь математика Эйлера, числом Эйлера.

Применение этого числа в жизни настолько велико, что практически любая мало-мальская сложная задача, имеет в своем решении это значение.

В электротехнике колебательных контуров — оно присутствует,  в телекоммуникации тоже, в физике, в статистике, в экономике и  так далее. 

Экспонента комплексного выражения

Синтаксис

Для тех кто пользуется XMPP клиентами, отдельной команды нет. Можно воспользоваться  командой calc_i или step_i

Примеры

Экспонента комплексной единицы

---

Экспонента комплексного выражения

---

Экспонента комплексного синуса

abakbot.ru

Онлайн калькулятор: Экспоненциальное сглаживание

Я тут было собрался написать еще одну статью о технических индикаторах и рассказать про экспоненциальное скользящее среднее (exponential moving average, EMA), однако получилось так, что, изучая теорию этого индикатора, я наткнулся на довольно интересные вещи, относящиеся все-таки больше к статистике, нежели к рынку акций или forex.

Поскольку на этом сайте статистика уже затрагивалась, я решил написать отдельную статью на эту тему, а именно, статью, посвященную методу экспоненциального сглаживания (exponential smoothing) в анализе рядов динамики (time series)

Тема рядов динамики уже затрагивалась в статье Сезонные колебания. Индексы сезонности. Метод постоянной средней, и там было сказано, в частности, что расчет средних индексов сезонности методов постоянной средней

может применяться для рядов динамики, где отсутствуют какие-либо тенденции повышения/понижения, либо же они незначительны. Иными словами, наблюдаемая величина колеблется около какого-то постоянного значения.

Что это значит? Это значит, что постоянное среднее, оно постоянное, и поэтому не может захватить тенденцию.
Проиллюстрируем это графиком

Постоянная средняя

addimport_exportmode_editdelete

Ряд динамики

Размер страницы: 5102050100chevron_leftchevron_right

Сохранить share extension

Вообще говоря, все методы усреднения направлены на то, чтобы исключить «шум» от случайного разброса данных, что позволяет более явно выявить тенденцию, либо же сезонные или циклические изменения, то есть внутреннюю структуру данных, кажущихся случайными, и использовать это для построения модели с последующим анализом и прогнозированием будущих значений — но, как видим, метод простого усреднения не работает при наличии явно выраженной тенденции, и спрогнозировать с его помощью ничего нельзя.

Нужно уметь получать не одно, постоянное, среднее, а, опять-таки, ряд средних, который бы пытался отражать тенденцию изменения данных. Ну и самым популярным (и простым) методом для получения таких рядов стал метод экспоненциального сглаживания.

На словах его можно описать так — При прогнозировании, более новым значениям наблюдаемой величины присваивается больший вес по сравнению с более старыми значениями. При этом более старым значениями присваиваются экспоненциально убывающие веса.

Теперь опишем это определение формулами.
Традиционно обозначим наблюдаемую величину как , а сглаженное среднее как .
Тогда,
не определено

и, обобщенно

где, принимает значение из диапазона [0;1)

Откуда берется экспонента — раскроем предыдущие средние

и, обобщенно

, для t > 2

Таким образом, веса перед — это бесконечно убывающая геометрическая прогрессия с множителем
И чем дальше S, тем меньше на нее влияют начальные значения.

Предположим, что , посмотрим, как меняется его вклад для различных S.

Точность вычисления

Знаков после запятой: 4

Изменение веса значения при экспоненциальном сглаживании

Сохранить share extension

Для S2 берется как есть, а вот в S3 при коэффициенте альфа равном 0.5, вклад y1 будет всего только 250, в S4 — 125, и так далее.

При этом большое значение имеет выбор коэффициента . Если поиграться с параметром «a» в калькуляторе (см. выше), то становится ясно, что чем выше его значение, тем быстрее отсчет фактически перестает влиять на сглаженное среднее, и наоборот — чем ниже, тем дольше сохраняется его влияние.

Соответственно, при малых , метод получения S2 оказывает большое влияние на результат. Присвоение это только один из методов. В качестве альтернативы начальным значением может выступать простое среднее по первым нескольким значениям y, например.

Но как же выбрать ? Какой показатель больше всего подходит для моделирования данного ряда динамики? Никаких математических формул по точному расчету нет. Этот показатель чаще всего выбирается методом подбора, или методом «проб и ошибок» (англ. trial and errors). Я еще пару раз видел название «метод научного тыка» 🙂

Метод заключается в том, что берется несколько значений и потом среди них выбирается одно лучшее. Что же является критерием «лучшести» в нашем случае?

Таким критерием является минимизация среднеквадратической ошибки (mean of squared errors). Ошибка — это отклонение фактического значения от прогнозного. Для каждого значения S ее возводят в квадрат, чтобы избавиться от влияния знака, и затем вычисляют среднее по всем значениям. Тот показатель , для которого среднее значение минимально и является лучшим из нескольких.

Теперь пару слов про прогнозирование.

Следующее значение ряда прогнозируется прямо по формуле

В случае если надо получить прогноз на большее число отсчетов, используется техника под названием bootstrapping (даже не знаю, какой адекватный русский термин здесь подойдет). Последнее известное значение «y» принимается за константу, и используется в рекурсивной формуле

Теперь применим полученные знания при расчете сглаженного среднего для графика, приведенного в начале статьи. Чтобы было интереснее, рассчитаем сглаженное среднее сразу для трех значений , и заодно посчитаем среднеквадратическую ошибку.

На графике для справки показано следующее прогнозируемое значение, т. е. сглаженные средние продлены на один отсчет дальше фактических данных.

planetcalc.ru