Сопротивление онлайн калькулятор – Калькулятор цветовой маркировки резисторов

Онлайн калькулятор цветовой маркировки сопротивления резисторов

 

Основная задача любого резистора – линейное преобразование силы тока (ампер) в напряжение (вольт), ограничение силы тока, ослабление источника питания и поглощение электроэнергии. Резисторы используют во всех сложных схемах и для работы сложных полупроводников. С учетом малого размера элемента нанесение читаемых буквенных или цифровых обозначений невозможно, поэтому применяется цветная маркировка. В статье мы разберем, что означают цветные точки и линии, их цвет, и объясним, как правильно подобрать резистор.

Вводные данные

Для начала обратимся к Википедии, которая дает четкое понимание, что из себя представляет любой резистор. В дословном переводе с английского термин означает сопротивление. И действительно, назначение резисторов с постоянным или переменным значение – линейное преобразование силы тока в напряжение, напряжения в силу и т.д.

Маркировочный цвет, порядок и шифрование цифровых кодов в резисторах определены ГОСТ 175-72 в соответствии с требованиями Публикации 62 Международной электротехнической комиссии. Согласно этим нормативам для идентификации применяются кольца, цвет и количество которых четко регламентированы

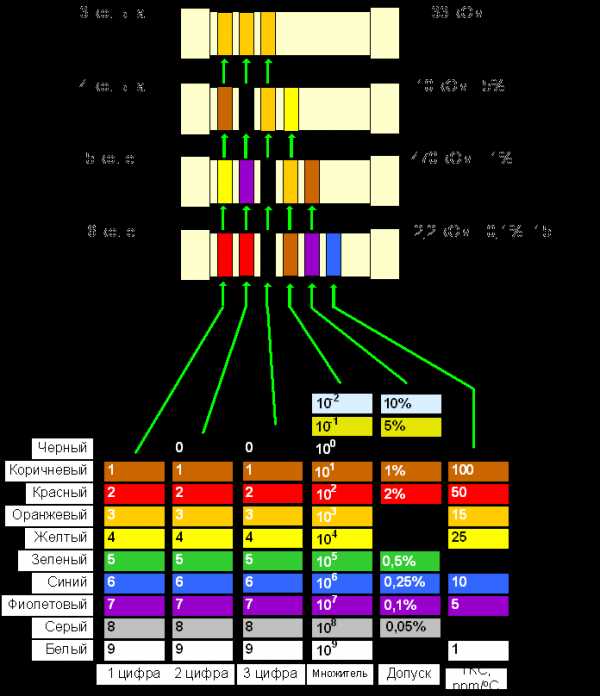
Полосы всегда смещены относительно одного вывода, читаются при этом как в арабской письменности — слева направо. Если размер пассивного элемента не позволяет визуально заметно обозначить начало, ширину первой полосы делают толще других приблизительно в 1,5-2 раза.

На резисторах с минимальной величиной допуска (до 10%) наносятся 5 колец, из которых:

• 1, 2, 3 – коэффициент сопротивления, ед.изм. Ом;
• 4 – множитель;
• 5 – максимально допустимое отклонение.

С допустимым отклонением от 10% уже четыре полосы, где:

• 1, 2, 3 – коэффициент сопротивления, ед.изм. Ом;
• 4 – множитель.

Резисторы с допуском 20% имеют только 3 полосы, где также отклонение не указано, но на коэффициент сопротивления отведено только первых 2 кольца.

Мощность резистора можно определить по его габаритам.

Нечасто, но можно встретить и 6-полосное маркирование, где:

• 1, 2, 3 – величина сопротивления, ед.изм. Ом;
• 4 – множитель;
• 5 – нормативный допуск;
• 6 — температурный коэффициент изменения

Последняя (шестая) полоса нужна для понимания того, насколько будет изменяться сопротивление, если корпус пассивного элемента начнет нагреваться.

ВИДЕО: Как работает резистор

Для чего нужны опознавательные признаки?

Самые маленькие резисторы мощностью 0,125 wt длиной всего 3-4 мм, а диаметр – 1 мм. Даже прочитать любую информацию на такой миниатюрке сложно, не говоря уже о том, чтобы нанести ее. Можно, конечно, написать силу тока, например, 4К7, что соответствует 4700 Ом, но этой информации крайне недостаточно.

Цветовая маркировка резисторов гораздо более практична ввиду следующего:

• наносится очень просто;
• легко читаема;
• содержит всю требуемую информацию о номинальных параметрах;
• остается сохранной и видимой в течение всего срока работы.

Также с помощью подсчета количества полос можно определить точность параметров:

• 3 – погрешность 20%;
• 4 – 5-10%;
• 5-6 – 0-0,9%

Для того, чтобы точно узнать, какой именно нужен резистор и с какими полосками, можно самостоятельно установить по таблице или воспользоваться онлайн-калькулятором (в конце статьи).

Универсальная таблица:

С помощью этих табличных значений можно быстро определить номинал пассивного элемента, при этом значение имеет очередность полоски или точки, что позволяет получить числовые данные.

Цвета означают разные данные – цифра отметки, множитель и допустимое отклонение.

Пример:

С помощью универсальной таблицы прочтем, что скрыто на данном элементе. Итак, имеем 4 полосы:

• коричневая,
• черная,
• красная,
• серебристая.

Напоминаем, читать полосы надо слева направо, а единица измерения Ом.

Никогда не маркируется первыми черный, золотой и белый цвета.

Расшифровка:

1. Первое место занимает коричневая полоса, которая обозначает одновременно цифровой символ (1) и множитель (10).
2. Черная (0) – при таком сочетании электрическое сопротивление обозначает 1 кОм – 1К0.
3. Красная – множитель, равен 100.
4. Серебристая – обозначение максимально допустимое отклонение, которое здесь составляет 10%. Эти же данные можно получить путем простого подсчета количества полосок.

Как «прочитать» проволочные резисторы

К этой разновидности пассивных элементов применяется все тот же ГОСТ 175-72 и Публикация 62 МЭК, соответственно, цвета, количество полос и порядок аналогичны «бочонкам», но есть определенные нюансы:

• самая широкая полоса – белая, не читается и обозначает только тип элемента;
• более 4-х десятичных показателей не наносятся;
• последняя в ряду полоса определяет отличительные свойства, зачастую это огнеупорность.

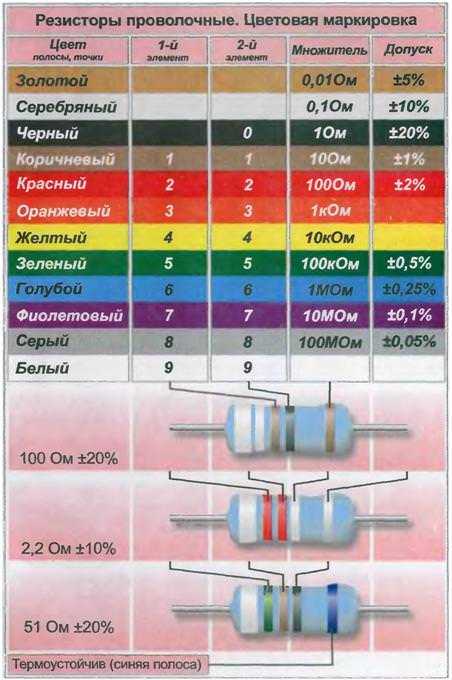
С учетом указанных особенностей лучше сопоставлять данные со сводной таблицей именно проволочных образцов.

Зарубежная продукция

{add_n26}

И хотя наши стандарты полностью соответствуют международным, а Публикация 62 и вовсе является императивным стандартом, некоторые компании используют свои правила нанесения полос и выбора цвета, с которыми нужно считаться:

Philips

Имеет свой стандарт символов и цветов, согласно которым наравне с номинальными показателями, резистор передает информацию о технологии производства и характеристике компонентов.

CGW и Panasonic

Используют дополнительные цвета для обозначения дополнительных свойств пассивных элементов цепи.

В целом, все маркировки совпадают с ранее приведенными значениями и таблицами, только эти компании еще больше упростили задачу идентификации номинала. При этом резисторы взаимозаменяемы и никаких требований относительно оригинала ни Philips, ни CGW и Panasonic не выдвигают.

Для того, чтобы точно понимать, какие рабочие характеристики требуются и какие резисторы следует покупать для определенной цели, воспользуйтесь простым сервисом

Путем введения исходных данных можно получить информацию по каждому маркировочному цвету, которому соответствует определенный цифровой код.

ВИДЕО: Расчет сопротивления резистора

www.diodgid.ru

Параллельное соединение резисторов. Калькулятор для расчета

Параллельное соединение резисторов

 — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую резисторы соединяют последовательно или параллельно для того, чтобы создать более сложные электронные схемы.

Схема параллельного соединения резисторов показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:

Формула параллельного соединения резисторов

Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:

Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:

Параллельное соединение резисторов — расчет

Пример  №1

При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.

Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:

Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:

Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.

Пример расчета №2

Найти общее сопротивление  R из трех параллельно соединенных резисторов:

Общее сопротивление R рассчитывается по формуле:

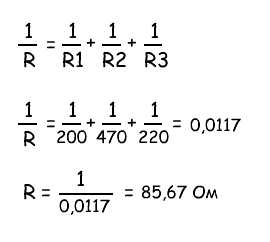
Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.

Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.

Как рассчитать сложные схемы соединения резисторов

Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:

Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).

Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:

В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:

Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.

Ток, протекающий в цепи параллельно соединенных резисторах

Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.

Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).

Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов ( I1 и I2 ) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .

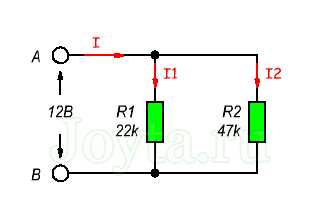
Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».

Таким образом, протекающий общий ток в цепи  можно определить как:

I = I1 + I2

Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:

Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА

Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА

Таким образом, общий ток будет равен:

I = 0,545 мА + 0,255 мА = 0,8 мА

Это также можно проверить, используя закон Ома:

I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)

где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)

И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать здесь.

Параллельное соединение резисторов — онлайн калькулятор

Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:

Подведем итог

Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.

Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора входящего в параллельное соединение.

www.joyta.ru

SMD резисторы. Маркировка SMD резисторов, размеры, онлайн калькулятор

В общем, термин SMD (от англ. Surface Mounted Device) можно отнести к любому малогабаритному электронному компоненту, предназначенному для монтажа на поверхность платы по технологии SMT (технология поверхностного монтажа).

SMT технология (от англ. Surface Mount Technology) была разработана с целью удешевления производства, повышению эффективности изготовления печатных плат с использованием более мелких электронных компонентов: резисторов, конденсаторов, транзисторов и т. д. Сегодня рассмотрим один из таких видов резисторов  – SMD резистор.

SMD резисторы

SMD резисторы – это миниатюрные резисторы, предназначенные для поверхностного монтажа. SMD резисторы значительно меньше, чем их традиционный аналог. Они часто бывают квадратной, прямоугольной или овальной формы, с очень низким профилем.

Вместо проволочных выводов обычных резисторов, которые вставляются в отверстия печатной платы, у SMD резисторов имеются небольшие контакты, которые припаяны к поверхности корпуса резистора. Это избавляет от необходимости делать отверстия в печатной плате, и тем самым позволяет более эффективно использовать всю ее поверхность.

Типоразмеры SMD резисторов

В основном термин типоразмер включает в себя размер, форму и конфигурацию выводов (тип корпуса) какого-либо электронного компонента. Например, конфигурация обычной микросхемы, которая имеет плоский корпус с двусторонним расположением выводов (перпендикулярно плоскости основания), называется DIP.

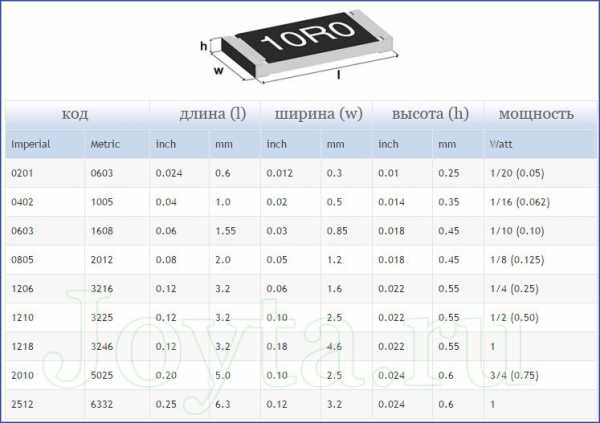
Типоразмер SMD резисторов стандартизированы, и большинство производителей используют стандарт JEDEC. Размер SMD резисторов обозначается числовым кодом, например, 0603. Код содержит в себе информацию о длине и ширине резистора. Таким образом, в нашем примере код 0603 (в дюймах) длина корпуса составляет 0,060 дюйма, шириной 0,030 дюйма.

Такой же типоразмер резистора в метрической системе будет иметь код 1608 (в миллиметрах), соответственно длина равна 1,6 мм, ширина 0,8мм. Чтобы перевести размеры в миллиметры, достаточно размер в дюймах перемножить на 2,54.

Размеры SMD резисторов и их мощность

Размер резистора SMD зависит главным образом от необходимой мощности рассеивания. В следующей таблице перечислены размеры и технические характеристики наиболее часто используемых SMD резисторов.

Маркировка SMD резисторов

Из-за малого размера SMD резисторов, на них практически невозможно нанести традиционную цветовую маркировку резисторов.

В связи с этим был разработан особый способ маркировки. Наиболее часто встречающаяся маркировка содержит три или четыре цифры, либо  две цифры и букву, имеющая название EIA-96.

Маркировка с 3 и 4 цифрами

В этой системе первые две или три цифры обозначают численное значение сопротивления резистора, а последняя цифра показатель множителя. Эта последняя цифра указывает степень, в которую необходимо возвести 10, чтобы получить окончательный множитель.

Еще несколько примеров определения сопротивлений в рамках данной системы:

• 450 = 45 х 10⁰ равно 45 Ом
• 273 = 27 х 10³ равно 27000 Ом (27 кОм)
• 7992 = 799 х 10² равно 79900 Ом (79,9 кОм)
• 1733 = 173 х 10³ равно 173000 Ом (173 кОм)

 

Буква “R” используется для указания положения десятичной точки для значений сопротивления ниже 10 Ом. Таким образом, 0R5 = 0,5 Ом и 0R01 = 0,01 Ом.

Маркировка EIA-96

SMD резисторы повышенной точности (прецизионные)  в сочетании с малыми размерами, создали необходимость в новой, более компактной маркировке. В связи с этим был создан стандарт EIA-96. Данный стандарт предназначен для резисторов с допуском по сопротивлению в 1%.

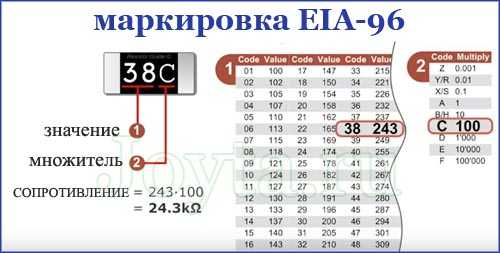
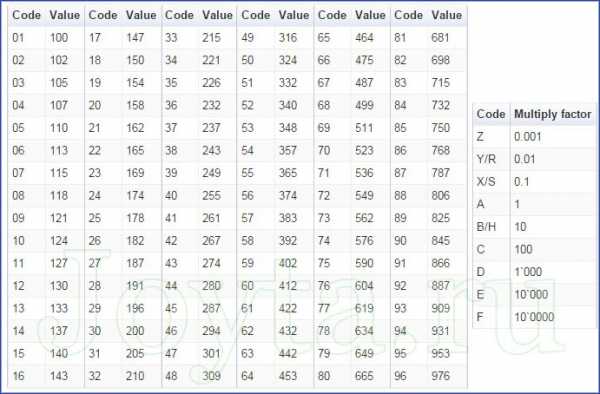
Эта система маркировки состоит из трех элементов: две цифры указывают код номинала резистора, а следующая за ними буква определяет множитель. Две цифры представляют собой код, который дает трехзначное число сопротивления (см. табл.)

Например, код 04 означает 107 Ом, а 60 соответствует 412 Ом. Множитель дает конечное значение резистора, например:

• 01А = 100 Ом ±1%
• 38С = 24300 Ом ±1%
• 92Z = 0.887 Ом ±1%

Онлайн калькулятор SMD резисторов

Этот калькулятор поможет вам найти величину сопротивления SMD резисторов. Просто введите код, написанный на резисторе и его сопротивление отразится внизу.

Калькулятор может быть использован для определения сопротивления SMD резисторов, которые маркированы 3 или 4 цифрами, а так же по стандарту EIA-96 (2 цифры + буква).

Хотя мы сделали все возможное, чтобы проверить функцию данного калькулятора, мы не можем гарантировать, что он вычисляет правильные значения для всех резисторов, поскольку иногда производители могут использовать свои пользовательские коды.

Поэтому чтобы быть абсолютно уверенным в значении сопротивления, лучше всего дополнительно измерить сопротивление с помощью мультиметра.

www.joyta.ru

Расчёт реактивного сопротивления

Реактивное сопротивление – электрическое сопротивление переменному току, обусловленное передачей энергии магнитным полем в индуктивностях или электрическим полем в конденсаторах.

Элементы, обладающие реактивным сопротивлением, называют реактивными.

Реактивное сопротивление катушки индуктивности.

При протекании переменного тока I в катушке, магнитное поле создаёт в её витках ЭДС, которая препятствует изменению тока.
При увеличении тока, ЭДС отрицательна и препятствует нарастанию тока, при уменьшении — положительна и препятствует его убыванию, оказывая таким образом сопротивление изменению тока на протяжении всего периода.

В результате созданного противодействия, на выводах катушки индуктивности в противофазе формируется напряжение U, подавляющее ЭДС, равное ей по амплитуде и противоположное по знаку.

При прохождении тока через нуль, амплитуда ЭДС достигает максимального значения, что образует расхождение во времени тока и напряжения в 1/4 периода.

Если приложить к выводам катушки индуктивности напряжение U, ток не может начаться мгновенно по причине противодействия ЭДС, равного -U, поэтому ток в индуктивности всегда будет отставать от напряжения на угол 90°. Сдвиг при отстающем токе называют положительным.

Запишем выражение мгновенного значения напряжения u исходя из ЭДС (ε), которая пропорциональна индуктивности L и скорости изменения тока: u = -ε = L(di/dt).
Отсюда выразим синусоидальный ток .

Интегралом функции sin(t) будет -соs(t), либо равная ей функция sin(t-π/2).
Дифференциал dt функции sin(ωt) выйдет из под знака интеграла множителем 1/ω.
В результате получим выражение мгновенного значения тока со сдвигом от функции напряжения на угол π/2 (90°).
Для среднеквадратичных значений U и I в таком случае можно записать .

В итоге имеем зависимость синусоидального тока от напряжения согласно Закону Ома, где в знаменателе вместо R выражение ωL, которое и является реактивным сопротивлением:

Реактивное сопротивлениие индуктивностей называют индуктивным.

Реактивное сопротивление конденсатора.

Электрический ток в конденсаторе представляет собой часть или совокупность процессов его заряда и разряда – накопления и отдачи энергии электрическим полем между его обкладками.

В цепи переменного тока, конденсатор будет заряжаться до определённого максимального значения, пока ток не сменит направление на противоположное. Следовательно, в моменты амплитудного значения напряжения на конденсаторе, ток в нём будет равен нулю. Таким образом, напряжение на конденсаторе и ток всегда будут иметь расхождение во времени в четверть периода.

В результате ток в цепи будет ограничен падением напряжения на конденсаторе, что создаёт реактивное сопротивление переменному току, обратно-пропорциональное скорости изменения тока (частоте) и ёмкости конденсатора.

Если приложить к конденсатору напряжение U, мгновенно начнётся ток от максимального значения, далее уменьшаясь до нуля. В это время напряжение на его выводах будет расти от нуля до максимума. Следовательно, напряжение на обкладках конденсатора по фазе отстаёт от тока на угол 90 °. Такой сдвиг фаз называют отрицательным.

Ток в конденсаторе является производной функцией его заряда i = dQ/dt = C(du/dt).
Производной от sin(t) будет cos(t) либо равная ей функция sin(t+π/2).
Тогда для синусоидального напряжения u = U_ampsin(ωt) запишем выражение мгновенного значения тока следующим образом:

i = U_ampωCsin(ωt+π/2).

Отсюда выразим соотношение среднеквадратичных значений .

Закон Ома подсказывает, что 1/ωC есть не что иное, как реактивное сопротивление для синусоидального тока:

Реактивное сопротивление конденсатора в технической литературе часто называют ёмкостным. Может применяться, например, в организации ёмкостных делителей в цепях переменного тока.

---

Онлайн-калькулятор расчёта реактивного сопротивления

Необходимо вписать значения и кликнуть мышкой в таблице.
При переключении множителей автоматически происходит пересчёт результата.

Реактивное сопротивление ёмкости XC = 1 /(2πƒC)

Реактивное сопротивление индуктивности XL = 2πƒL

Расчитать ёмкость или индуктивность для реактивного сопротивления:

Расчёт ёмкости: C = 1 /(2πƒXC)

Расчёт индуктивности: L = XL /(2πƒ)

---

Похожие страницы с расчётами:

Расcчитать импеданс.
Расcчитать частоту резонанса колебательного контура LC.
Расcчитать реактивную мощность и компенсацию.

tel-spb.ru

Номиналы резисторов. Таблица, онлайн калькулятор

В 1952 году IEC (IEC — международная электротехническая комиссия) утвердила стандартные значения для резисторов, называемый номинальный ряд резисторов.

История создание номинального ряда резисторов началась в первые годы прошлого века, в то время когда большинство резисторов были углеродно-графитовыми с относительно большими производственными допусками (отклонениями).

Идея создания номинального ряда довольно простая — установить стандартные значения для резисторов на основе допусков, с которыми они могут быть изготовлены.

Номиналы резисторов

Рассмотрим это на простом примере. Допустим, есть группа резисторов имеющих 10% отклонение от номинала (как в большую, так и в меньшую сторону).

Предположим, что первое предпочтительное значение должно быть равно 100 Ом. Следовательно, не имеет смысла изготавливать резистор, например на 105 Ом, так как резистор с сопротивлением 105 Ом падает в 10% диапазон допуска резистор на 100 Ом (90…110 Ом).

Поэтому следующее рациональное значение сопротивления должно быть в районе 120 Ом, поскольку резисторы на 100 Ом с допуском 10% имеют значение где-то между 90 Ом и 110 Ом, резистор 120 Ом имеет значение в диапазоне между 108 и 132 Ом, перекрывая тем самым диапазон между 100 и 120 Ом.

Следуя этой логике, стандартные номиналы резисторов с отклонением 10% в диапазоне между 100 и 1000 Ом будут следующие: 100, 120, 150, 180, 220, 270, 330 и так далее (с соответствующим округлением). Это серия резисторов, имеющая маркировку E12, приведена в таблице ниже.

Номиналы резисторов — таблица

Буква «Е» обозначает, что резистор из номинального ряда EIA. Идущее после буквы «Е» число указывает на количество логарифмических шагов в диапазоне от 100 до 1000.

Ниже, в таблице номиналов резисторов, приведены значения сопротивления в диапазоне 100…1000. Сопротивление в любом другом диапазоне (Ом, кОм, мОм) могут быть получены простым делением или умножением данных из таблицы на 10.

Отличия между сериями:

• Е6 — допуск 20%,
• E12 — допуск 10%
• E24 — допуск 5% (и 2%)
• Е48 — допуск 2%
• E96 — допуск 1%
• E192 — допуск 0,5, 0,25, 0,1% и выше

Номиналы резисторов — онлайн калькулятор

Для удобства приводим калькулятор для быстрого подбора сопротивления из стандартного номинального ряда резисторов.

Примечание: в окошко «Введите необходимое сопротивление» вписывайте значение без префиксов (кОм, МОм). Например, для поиска ближайшего значения для сопротивления 38 Ом – вводим 38. То же самое справедливо и для 38 кОм – вводим 38 (не забывая, что результат относится к кОм)

www.joyta.ru

Делитель напряжения на резисторах. Формула расчета, онлайн калькулятор

Делитель напряжения — это простая схема, которая позволяет получить из высокого напряжения пониженное напряжение.

Используя только два резистора и входное напряжение, мы можем создать выходное напряжение, составляющее определенную часть от входного. Делитель напряжения является одной из наиболее фундаментальных схем в электронике. В вопросе изучения работы делителя напряжения следует отметить два основных момента – это сама схема и формула расчета.

Схема делителя напряжения на резисторах

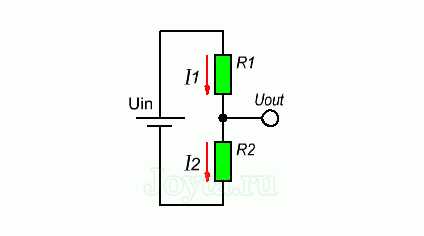
Схема делителя напряжения включает в себя входной источник напряжения и два резистора. Ниже вы можете увидеть несколько схематических вариантов изображения делителя, но все они несут один и тот же функционал.

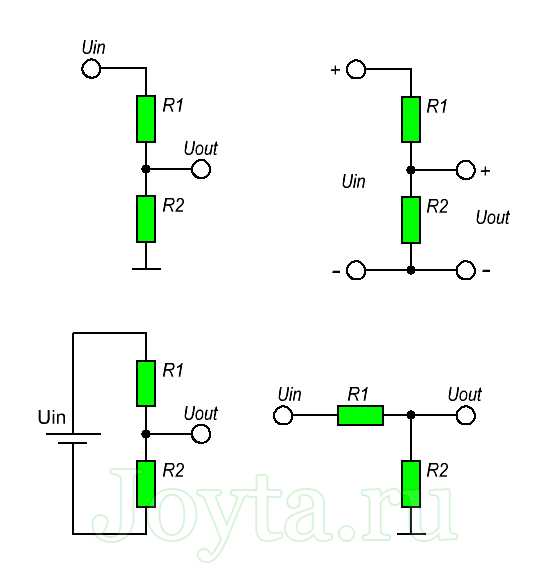Обозначим резистор, который находится ближе к плюсу входного напряжения (Uin) как R1, а резистор находящийся ближе к минусу как R2. Падение напряжения (Uout) на резисторе R2 — это пониженное напряжение, полученное в результате применения резисторного делителя напряжения.

Расчет делителя напряжения на резисторах

Расчет делителя напряжения предполагает, что нам известно, по крайней мере, три величины из приведенной выше схемы: входное напряжение и сопротивление обоих резисторов. Зная эти величины, мы можем рассчитать выходное напряжение.

Формула делителя напряжения

Это не сложное упражнение, но очень важное для понимания того, как работает делитель напряжения. Расчет делителя основан на законе Ома.

Для того чтобы узнать какое напряжение будет на выходе делителя, выведем формулу исходя из закона Ома. Предположим, что мы знаем значения Uin, R1 и R2. Теперь на основании этих данных выведем формулу для Uout. Давайте начнем с обозначения токов I1 и I2, которые протекают через резисторы R1 и R2 соответственно:

Наша цель состоит в том, чтобы вычислить Uout, а это достаточно просто используя закон Ома:

Хорошо. Мы знаем значение R2, но пока неизвестно сила тока I2. Но мы знаем кое-что о ней. Мы можем предположить, что I1 равно I2. При этом наша схема будет выглядеть следующим образом:

Что мы знаем о Uin? Ну, Uin это напряжение на обоих резисторах R1 и R2. Эти резисторы соединены последовательно, при этом их сопротивления суммируются:

И, на какое-то время, мы можем упростить схему:

Закон Ома в его наиболее простом вид: Uin = I *R. Помня, что R состоит из R1+R2, формула может быть записана в следующем виде:

А так как I1 равно I2, то:

Это уравнение показывает, что выходное напряжение прямо пропорционально входному напряжению и отношению сопротивлений R1 и R2.

Делитель напряжения — калькулятор онлайн



 Применение делителя напряжения на резисторах

В радиоэлектронике есть много способов применения делителя напряжения. Вот только некоторые примеры где вы можете обнаружить их.

Потенциометры

Потенциометр представляет собой переменный резистор, который может быть использован для создания регулируемого делителя напряжения.

Изнутри потенциометр представляет собой резистор и скользящий контакт, который делит резистор на две части и передвигается между этими двумя частями. С внешней стороны, как правило, у потенциометра имеется три вывода: два контакта подсоединены к выводам резистора, в то время как третий (центральный) подключен к скользящему контакту.

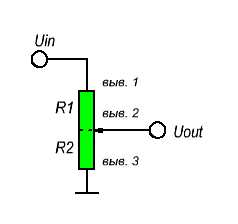
Если контакты резистора подключения к источнику напряжения (один к минусу, другой к плюсу), то центральный вывод потенциометра будет имитировать делитель напряжения.

Переведите движок потенциометра в верхнее положение и напряжение на выходе будет равно входному напряжению. Теперь переведите движок в крайнее нижнее положение и на выходе будет нулевое напряжение. Если же установить ручку потенциометра в среднее положение, то мы получим половину входного напряжения.

Резистивные датчики

Большинство датчиков применяемых в различных устройствах представляют собой резистивные устройства. Фоторезистор представляет собой переменный резистор, который изменяет свое сопротивление, пропорциональное количеству света, падающего на него. Так же есть и другие датчики, такие как датчики давления, ускорения и термисторы и др.

Так же резистивный делитель напряжения помогает измерить напряжение при помощи микроконтроллера (при наличии АЦП).

Пример работы делителя напряжения на фоторезисторе.

Допустим, сопротивление фоторезистора изменяется от 1 кОм (при освещении) и до 10 кОм (при полной темноте). Если мы дополним схему постоянным сопротивлением примерно 5,6 кОм, то мы можем получить широкий диапазон изменения выходного напряжения при изменении освещенности фоторезистора.

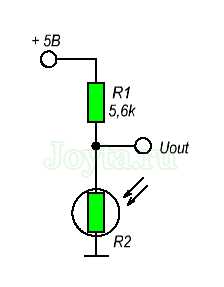
Как мы видим, размах выходного напряжения при уровне освещения от яркого до темного получается в районе 2,45 вольт, что является отличным диапазоном для работы большинства АЦП.

www.joyta.ru

Онлайн расчёт сопротивлений проводов. Площадь сечения проводов от мощности.

На первый взгляд может показаться, что эта статья из рублики «Электрику на заметку».
С одной стороны, а почему бы и нет, с другой — так ведь и нам, пытливым электронщикам, иногда нужно рассчитать сопротивление обмотки катушки индуктивности, или самодельного нихромового резистора, да и чего уж там греха таить — акустического кабеля для высококачественной звуковоспроизводящей аппаратуры.

Формула тут совсем простая R = p*l/S, где l и S соответственно длина и площадь сечения проводника, а p — удельное сопротивление материала, поэтому расчёты эти можно провести самостоятельно, вооружившись калькулятором и Ля-минорной мыслью, что все собранные данные надо привести к системе СИ.

Ну а для нормальных пацанов, решивших сберечь своё время и не нервничать по пустякам, нарисуем незамысловатую таблицу.

ТАБЛИЦА ДЛЯ РАСЧЁТА СОПРОТИВЛЕНИЯ ПРОВОДНИКА

Страница получилась сиротливой, поэтому помещу-ка я сюда таблицу для желающих связать своё время с прокладкой электропроводки, подключить мощный источник энергопотребления, либо просто посмотреть в глаза электрику Василию и, «похлёбывая из котелка» задать справедливый вопрос: «А почему, собственно? Может разорить меня решил? Зачем мне тут четыре квадрата из бескислородной меди для двух лампочек и холодильника? Из-за чего, собственно?»

И расчёты эти мы с вами сделаем не от вольного и, даже не в соответствии с народной мудростью, гласящей, что «необходимая площадь сечения провода равна максимальному току, делённому на 10», а в строгом соответствии нормативными документами Минэнерго России по правилам устройства электроустановок.
Правила эти игнорируют провода, сечением, меньшим 1,5 мм². Проигнорирую их и я, а за компанию и алюминиевые, в силу их вопиющей архаичности.
Итак.

РАСЧЁТ ПЛОЩАДИ СЕЧЕНИЯ ПРОВОДОВ В ЗАВИСИМОСТИ ОТ МОЩНОСТИ НАГРУЗКИ

Потери в проводниках возникают из-за ненулевого значения их сопротивления, зависящего от длины провода.
Значения мощности этих потерь, выделяемых в виде тепла в окружающее пространство, приведены в таблице.
В итоге к потребителю энергии на другом конце провода напряжение доходит в несколько урезанном виде — меньшим, чем оно было у источника. Из таблицы видно, что к примеру, при напряжении в сети 220 В и 100 метровой длине провода, сечением 1,5мм², напряжение на нагрузке, потребляющей 4 кВт, окажется не 220, а 199 В.
Хорошо, это или плохо?
Для каких-то приборов — безразлично, какие-то работать будут, но при пониженной мощности, а какие-то взбрыкнут и пошлют Вас к едрене фене вместе с вашими длинными проводами и умными таблицами.
Поэтому Минэнерго — минэнергой, а собственная голова не повредит ни при каких обстоятельствах. Если ситуация складывается подобным примеру образом — прямая дорога к выбору проводов, большего сечения.

 

vpayaem.ru