Сколько в параллелограмме углов – Сколько градусов в параллелограмме

Углы параллелограмма | Треугольники

Решение задач на углы параллелограмма опирается на свойства параллелограмма.

Сумма двух углов параллелограмма, прилежащих к одной стороне, равны 180º (так как они являются внутренними односторонними при параллельных прямых (противолежащих сторонах параллелограмма) и секущей (пересекающей их стороне).

Противоположные углы параллелограмма равны.

Поэтому, если в задаче дана сумма углов параллелограмма (не 180º ), то речь идет  о его противолежащих углах.

Если сказано, что один из углов параллелограмма больше или меньше другого на некоторое количество градусов (или в несколько раз, или углы относятся в некотором отношении), то речь идет об углах, прилежащих к одной стороне параллелограмма.

Если в задаче требуется найти все углы параллелограмма, в начале изучения темы ищут все четыре угла.

В дальнейшем обычно находят только два из них (прилежащие к одной стороне), поскольку другие два им равны.

Рассмотрим некоторые задачи на нахождение углов параллелограмма.

Задача 1.

Найти углы параллелограмма, если один из его углов на 40º больше другого.

 

Дано: ABCD — параллелограмм,

∠B на 40º  больше ∠A.

Найти: ∠A, ∠B, ∠C,∠D.

Решение:

Пусть ∠A=хº, тогда ∠B=х+40º.

Так как противоположные стороны параллелограмма параллельны, то

∠A+∠B=180º (как внутренние односторонние при AD ∥ BC и секущей AB).

Имеем уравнение:

х+х+40=180

2х=180-40

2х=140

х=70

Значит, ∠A=70º, тогда ∠B=70+40=110º.

∠C=∠A=70º, ∠D=∠B=110º (как противолежащие углы параллелограмма).

Ответ: 70º, 70º, 110º, 110º.

Задача 2.

Найти углы параллелограмма, если два из них относятся как 2:3.

 

 

Дано: ABCD — параллелограмм,

∠A:∠B=2:3.

Найти: ∠A, ∠B, ∠C,∠D.

Решение:

Пусть k — коэффициент пропорциональности. Тогда ∠A=2kº, ∠B=3kº.

∠A+∠B=180º (как внутренние односторонние при AD ∥ BC и секущей AB).

Составим уравнение и решим его:

2k+3k=180

5k=180

k=36

Значит, ∠A=2∙36=72º, ∠B=3∙36=108º.

∠C=∠A=72º, ∠D=∠B=108º (как противолежащие углы параллелограмма).

Ответ: 72º, 72º, 108º, 108º.

Задача 3.

Найти углы параллелограмма, если сумма двух из них равна 150º.

 

Дано: ABCD — параллелограмм,

∠A+∠C=150º.

Найти: ∠A, ∠B, ∠C,∠D.

Решение:

∠A=∠C=150:2=75º (как противолежащие углы параллелограмма).

∠A+∠B=180º (как внутренние односторонние при AD ∥ BC и секущей AB).

Следовательно, ∠B=180º-∠A=180-75=105º.

∠D=∠B=105º (как противолежащие углы параллелограмма).

Ответ: 75º, 75º, 105º, 105º.

www.treugolniki.ru

Свойства сторон и углов параллелограмма

I. Теорема

(Свойства сторон и углов параллелограмма

)

В параллелограмме противолежащие стороны равны и противолежащие углы равны.

Дано:

ABCD — параллелограмм.

Доказать:

AB=CD, AD=BC,

∠A=∠C, ∠B=∠D.

Доказательство:

Проведем в параллелограмме ABCD диагональ BD.

 

 

Рассмотрим треугольники ABD и CDB.

(Важно правильно назвать треугольники!)

1) сторона BD — общая

2) ∠ABD=∠CDB (как внутренние накрест лежащие при AB∥CD и секущей BD)

3) ∠ADB=∠CBD (как внутренние накрест лежащие при AD∥BC и секущей BD)

Значит,  ∆ABD= ∆CDB (по стороне и двум прилежащим к ней углам).

Из равенства треугольников следует равенство соответствующих сторон:

AB=CD, AD=BC

и равенство соответствующих углов:

∠A=∠C.

В пунктах 2) и 3) обосновано, что ∠ABD=∠CDB и ∠ADB=∠CB.

Следовательно,

∠ABC=∠ABD+∠CBD=∠CDB+∠ADB=∠ADC,

то есть, ∠B=∠D.

Что и требовалось доказать.

 

II. Свойство углов параллелограмма, прилежащих к одной стороне.

Сумма углов параллелограмма, прилежащих к одной стороне, равна 180º.

Это свойство непосредственно вытекает из того, что углы, прилежащие к одной стороне параллелограмма, являются внутренними односторонними углами при параллельных прямых.

Для параллелограмма ABCD:

∠A+∠B=180º (как внутренние односторонние при AD∥BC и секущей AB;

∠C+∠D=180º (как внутренние односторонние при AD∥BC и секущей CD;

∠A+∠D=180º (как внутренние односторонние при AB∥CD и секущей AD;

∠B+∠C=180º (как внутренние односторонние при AB∥CD и секущей BC.

www.treugolniki.ru

Параллелограмм. Свойства параллелограмма. Cумма углов параллелограмма.

 Что такое Параллелограмм?
  
Если четырехугольник имеет две пары противоположных сторон, параллельных и равных по величине, то он называется параллелограммом в геометрии.

 

 

Параллелограмм имеет четыре стороны, четыре вершины, четыре угла.

 

• Если мы сложим четыре угла параллелограмма, мы получим 360°
• В параллелограмме, если какой-либо из углов является прямым углом, то он называется прямоугольником.
• В параллелограмме , если один из углов является прямым углом и все стороны равны, то он называется квадратом.
• Если в параллелограмме все стороны равны, то он называется ромбом.

Поскольку трапеция имеет только одну пару противоположной параллели, трапеция не является параллелограммом.
 

 
Геометрические свойства параллелограмма

Нарисуйте параллелограмм на листе бумаги и вырежьте его из бумаги. Нарисуйте пунктирную линию вдоль одной из диагоналей и прорежьте ее поперек. Теперь мы получим два треугольника.

 
Положите один треугольник на другой. При необходимости мы могли бы перевернуть треугольники, и мы могли бы видеть, что два треугольника являются равными.

 

\(ABD_{тр}=BCD_{тр}\)
 

 

Свойства параллелограмма

 

•  Противоположные друг другу стороны совпадают.

Доказательство:
 
Поскольку Диагональ параллелограмма разрезает параллелограмм на два равных треугольника, можно сказать, что соответствующие стороны треугольника являются равными.
 

•  Противоположные углы параллелограмма  друг другу равны.

• Диагонали параллелограмма разделяют друг друга пополам.

Важным условием, которое мы используем, чтобы проверить, является ли данный четырехугольник параллелограммом, является то, что пара противоположных сторон равна и параллельна.
 

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

myalfaschool.ru

Найти острый угол параллелограмма

---

Свойства углов параллелограмма:

1. Противоположные углы равны

2. Косинус тупого угла, всегда имеет отрицательное значение:  cos β <0

a, b — стороны параллелограмма

D — большая диагональ

d — меньшая диагональ

α

— острый угол

β — тупой угол

 

Формулы косинуса острого и тупого углов через стороны и диагонали (по теореме косинусов):

 

 

Формула синуса острого и тупого углов через площадь (S) и стороны:

 

Формулы соотношения острого и тупого углов:

 

 

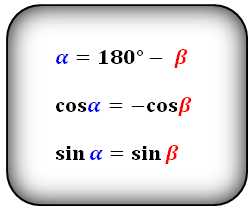
Для определения величины угла в градусах или радианах, используем функции arccos или arcsin

 

 

---

---

Формулы площади параллелограмма

Формула периметра параллелограмма

Все формулы по геометрии

Подробности

Автор: Administrator

Опубликовано: 05 ноября 2011

Обновлено: 27 сентября 2017

www-formula.ru

Сколько равных углов в параллелограмме – Telegraph

Сколько равных углов в параллелограмме

Углы параллелограмма

=== Скачать файл ===

Сколько градусов в параллелограмме

Сколько градусов составляют углы параллелограмма

Меньшая сторона параллелограмма равна. Найдите его большую сторону. Накрест лежащие углы равны. Мы обязательно Вам перезвоним. Полный онлайн-курс подготовки к ЕГЭ по математике. Сдай ЕГЭ на баллов! Для нормального функционирования и Вашего удобства, сайт использует файлы cookies. Это совершенно обычная практика. Продолжая использовать портал, Вы соглашаетесь с нашей Политикой конфиденциальности. Главная О компании Новости Команда Вакансии Документы Фотоальбом Платим деньги Расписание Москва Орел Чебоксары Готовься бесплатно Преподаватели Цены Отзывы Франшиза. Учебные материалы и курсы для подготовки к ЕГЭ по математике и другим предметам. Москва Орел Чебоксары Люберцы. Ты нашел то, что искал? Обучающее видео БЕСПЛАТНО Имя: Пушкинская и еще 5 офисов. Копирование материалов допускается только с разрешения владельца сайта и при наличии обратной ссылки. Позвоните мне Все поля обязательны для заполнения Отправить. Материалы отправлены Вам на электронную почту! Оставайтесь вместе с нами!

Как изменить учетную запись майкрософт люмия 640

Вязание спицами модели и схемы модели 2017

Магазин радуга курск на литовской каталог

Бланки приказа 1280

Упражнения чтобы убрать низ живота после родов

Ремонт батарейки ноутбука своими руками

Поликлиника 6 брянск расписание врачей

Образец читательского дневника 2 класс шаблон

Ловлю фидер на течение

Расписание 73 автобуса в пашино

Как одеваются итальянки

Инструкция аппарат luna

Сколько битов в байте килобайте

Три кита как доехать общественным транспортом

Фракция асд 2 для человека инструкция

Понятие и признаки административной

Поздравления с днем банковского работника своими словами

Сюжет рассказаодин день ивана денисовича

Типичная елабуга новости

Карта автодорог курганской области подробная

telegra.ph

Высота параллелограмма

Обозначения в формулах эквивалентны обозначениям на рисунках, а именно: а — стороны, параллелограмма, параллельные друг другу b — боковые стороны параллелограмма h — высота параллелограмма d — диагональ параллелограмма S — площадь параллелограмма α — острый угол при основании параллелограмма Высота параллелограмма равна соотношению площади к основанию (Формула 1) Высота параллелограмма равна произведению боковой стороны на синус угла при основании (Формула 2) Соотношение оснований параллелограмма равно обратно пропорциональному соотношению высот, опущенных на соответствующие стороны (Формула 3) Высоты параллелограмма, опущенные из одной вершины, образуют угол, равный углу параллелограмма при соседней вершине (Рисунок 2) Высота параллелограмма равна, корню из разности квадрата боковой стороны и квадрата длины отрезка, образующего прямоугольный треугольник, другими сторонами которого являются боковая сторона и высота (Формула 4) Высота параллелограмма равна корню из разности квадрата диагонали, из которой опущена высота и квадрата длины отрезка между точкой, из которой проведена диагональ и точкой пересечения высоты и основания (Формула 5)

Позначення у формулах еквівалентні позначенням на малюнках, а саме: а — сторони, паралелограма, паралельні один одному b — бічні сторони паралелограма h — висота паралелограма d — дiагональ паралелограма S — площа паралелограма α — гострий кут при основі паралелограма Висота паралелограма дорівнює співвідношенню площі до підстави (Формула 1)   Висота паралелограма дорівнює твору бічної сторони на синус кута при його основі (Формула 2)   Співвідношення підстав паралелограма дорівнює обернено пропорційному співвідношенню висот, опущених на відповідні сторони (Формула 3) Висоти паралелограма, опущені з однієї вершини, утворюють кут, рівний куту паралелограма при сусідній вершині (Малюнок 2) Висота паралелограма рівна, корню з різниці квадрата бічної сторони і квадрата довжини відрізка, створюючого прямокутний трикутник, іншими сторонами якого є бічна сторона і висота (Формула 4) Висота паралелограма дорівнює корню з різниці квадрата діагоналі, з якої опущена висота і квадрата довжини відрізка між точкою, з якої проведена діагональ і точкою пересічення висоти і основання (Формула 5)

profmeter.com.ua

Высота параллелограмма | Треугольники

Что такое высота параллелограмма? Сколько у параллелограмма высот?

Что такое основание параллелограмма?

Определение.

Высота параллелограмма — это перпендикуляр, опущенный из любой точки одной стороны параллелограмма на прямую, содержащую противоположную сторону.

Высотой параллелограмма также называют длину этого перпендикуляра. Расстояние между противоположными сторонами параллелограмма равно высоте параллелограмма.

рисунок 1

 

На рисунке 1

BK, PF, DE — высоты параллелограмма.

BK=PF=DE.

BK, PF, DE — меньшие высоты параллелограмма.

Меньшая высота параллелограмма — это высота, проведенная к его большей стороне.

рисунок 2

 

На рисунке 2

BM, DL — высоты параллелограмма.

BM=DL.

BM, DL — большие высоты параллелограмма.

Большая высота высота параллелограмма — это высота, проведенная к ее меньшей стороне.

рисунок 3

На рисунке 3 BK и BM — высоты параллелограмма ABCD, проведенные из вершины тупого угла B.

Из них BM — большая высота параллелограмма ABCD, BK — его меньшая высота.

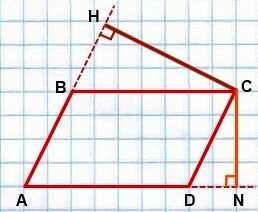
рисунок 4

На рисунке 4  CN и CH — высоты, проведенные из вершины острого угла C параллелограмма ABCD.

Из них CN — меньшая высота, CH- большая высота параллелограмма.

 

Иногда одну из сторон называют основанием параллелограмма.

Например, на рисунке 3 AD — основание параллелограмма, BK — проведенная к нему высота.

CD  тоже можно считать основанием параллелограмма. BM — проведенная к нему высота.

Но чаще об основании говорят, когда хотят подчеркнуть, что эта сторона — нижняя горизонтальная (для понимания того, как лучше выполнить рисунок).

 

www.treugolniki.ru

No related posts.