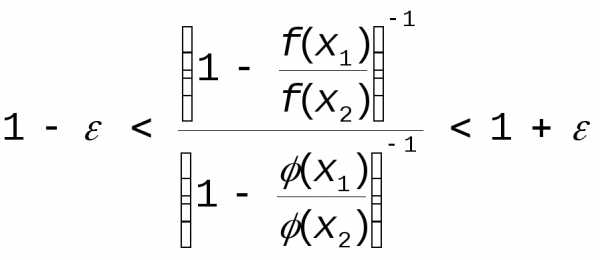формула Лейбница — ПриМат
$\Box$ Рассмотрим производную заданной функции по определению
$${ J }^{ \prime }\left( y \right) =\lim _{ \Delta y\rightarrow 0 }{ \frac { J\left( y+\Delta y \right) -J\left( y \right) }{ \Delta y } }.$$
Тогда для доказательства теоремы нам необходимо убедиться в равенстве
$$\lim _{ \Delta y\rightarrow 0 }{ \frac { J\left( y+\Delta y \right) -J\left( y \right) }{ \Delta y } } =\intop _{ a }^{ b }{ \frac { \partial }{ \partial y } f\left( x,y \right) dx } \Rightarrow$$ $$\Rightarrow \lim _{ \Delta y\rightarrow 0 }{ \left( \frac { J\left( y+\Delta y \right) -J\left( y \right) }{ \Delta y } -\intop_{ a }^{ b }{ \frac { \partial }{ \partial y } f\left( x,y \right) dx } \right) } =0\quad \left( 1 \right).$$
Для дальнейшей работы проанализируем отношение
$${ \frac { J\left( y+\Delta y \right) -J\left( y \right) }{ \Delta y } }=\intop _{ a }^{ b }{ \frac { f\left( x,y+\Delta y \right) -f\left( x,y \right) }{ \Delta y } dx }.$$
Так как функция $f$ и ее производная – дифференцируемые на заданном прямоугольнике функции, то мы имеем право воспользоваться теоремой Лагранжа о среднем значении*
$${ \frac { J\left( y+\Delta y \right) -J\left( y \right) }{ \Delta y } }=\intop _{ a }^{ b }{ \frac { f\left( x,y+\Delta y \right) -f\left( x,y \right) }{ \Delta y } dx }=$$ $$ =\intop_{ a }^{ b }{ \frac { \partial }{ \partial y } f\left( x,y+{ \theta }_{ x }\Delta y \right) dx },\quad { \theta }_{ x }\in \left( 0,1 \right).$$
Вернемся к отношению находящемуся под знаком предела формулы $(1)$:
$$\frac { J\left( y+\Delta y \right) -J\left( y \right) }{ \Delta y } -\intop _{ a }^{ b }{ \frac { \partial }{ \partial y } f\left( x,y \right) dx } =$$ $$ =\intop_{ a }^{ b }{ \frac { \partial }{ \partial y } f\left( x,y+{ \theta }_{ x }\Delta y \right) dx }-\intop_{ a }^{ b }{ \frac { \partial }{ \partial y } f\left( x,y \right) dx }=$$ $$ =\intop_{ a }^{ b }{ \left( \frac { \partial }{ \partial y } f\left( x,y+{ \theta }_{ x }\Delta y \right) -\frac { \partial }{ \partial y } f\left( x,y \right) \right) dx }.$$
Аналогично доказательству предыдущего свойства, так как $\frac { \partial }{ \partial y } f\left( x,y \right)$ непрерывна на заданном прямоугольнике, то по теореме Кантора она равномерно непрерывна на нем же. Тогда запишем условие равномерной непрерывности, что поможет оценить нам выражение под знаком предела формулы $(1)$:
$$\forall \varepsilon > 0 \quad \exists { \delta }_{ \varepsilon }>0:\forall x\in \left[ a,b \right] ; \forall y,y+\Delta y\in \left[ c,d \right]:\left| y+\Delta y-y \right|=$$ $$=\left| \Delta y \right| <{ \delta }_{ \varepsilon }\Rightarrow \left| \frac { \partial }{ \partial y } f\left( x,y+\Delta y \right) -\frac { \partial }{ \partial y } f\left( x,y \right) \right| <\frac { \varepsilon }{ b-a }.$$
Принимая во внимание тот факт, что ${ \theta }_{ x } \in \left( 0,1 \right)$, автоматически при тех же условиях будет выполняться неравенство
Тогда можем записать
$$\left| \frac { J\left( y+\Delta y \right) -J\left( y \right) }{ \Delta y } -\intop _{ a }^{ b }{ \frac { \partial }{ \partial y } f\left( x,y \right) dx } \right| =$$ $$=\left| \intop _{ a }^{ b }{ \left( \frac { \partial }{ \partial y } f\left( x,y+{ \theta }_{ x } \Delta y \right) -\frac { \partial }{ \partial y } f\left( x,y \right) \right) dx } \right| \le$$ $$\le \intop _{ a }^{ b }{ \left| \frac { \partial }{ \partial y } f\left( x,y+{ \theta }_{ x } \Delta y \right) -\frac { \partial }{ \partial y } f\left( x,y \right) \right| dx } \le \left( b-a \right) \frac { \varepsilon }{ b-a } =\varepsilon.$$
Отсюда следуя определению предела функции по Коши
$$\lim _{ \Delta y\rightarrow 0 }{ \left( \frac { J\left( y+\Delta y \right) -J\left( y \right) }{ \Delta y } -\intop _{ a }^{ b }{ \frac { \partial }{ \partial y } f\left( x,y \right) dx } \right) } =0\Rightarrow$$ $$\Rightarrow\lim _{ \Delta y\rightarrow 0 }{ \frac { J\left( y+\Delta y \right) -J\left( y \right) }{ \Delta y } } =\intop _{ a }^{ b }{ \frac { \partial }{ \partial y } f\left( x,y \right) dx } ={ J }^{ \prime }\left( y \right). \blacksquare$$
[свернуть]
ib.mazurok.com
Формула Лейбница
формула лейбница, формула лейбница для матрицФормулой Лейбница в интегральном исчислении называется правило дифференцирования под знаком интеграла, зависящего от параметра, пределы которого зависят от переменной дифференцирования. Формула названа в честь немецкого математика Готфрида Лейбница.
Формулировка
Пусть функция f ( x , y ) {\displaystyle f(x,\;y)} непрерывна вместе со своей первой производной ∂ f ( x , y ) ∂ y {\displaystyle {\partial f(x,\;y) \over \partial y}} на прямоугольнике [ α , β ] × [ c , d ] {\displaystyle \times } (отрезок [ α , β ] {\displaystyle } включает в себя множества значений a ( y ) , b ( y ) {\displaystyle a(y),\;b(y)\ } ), a функции a ( y ) , b ( y ) {\displaystyle a(y),\;b(y)} дифференцируемы на [ c , d ] {\displaystyle } ). Тогда интеграл I ( y ) = ∫ a ( y ) b ( y ) f ( x , y ) d x {\displaystyle I(y)=\int \limits _{a(y)}^{b(y)}f(x,\;y)\,dx} дифференцируем по y {\displaystyle y} на [ c , d ] {\displaystyle } и справедливо равенство
I ′ ( y ) = ∫ a ( y ) b ( y ) ∂ ∂ y f ( x , y ) d x + f ( b ( y ) , y ) b ′ ( y ) − f ( a ( y ) , y ) a ′ ( y ) . {\displaystyle I'(y)=\int \limits _{a(y)}^{b(y)}{\partial \over \partial y}f(x,\;y)\,dx+f(b(y),\;y){b'(y)}-f(a(y),\;y){a'(y)}.}Литература
- Ильин В. А., Садовничий В. А., Сендов Бл. Х. Математический анализ. Ч.1. — 2-е изд., перераб. — М.: Изд-во МГУ, 1985. — 662 с.
кривизна плоской кривой формула лейбница, формула лейбница, формула лейбница для матриц, формула лейбница пример
Формула Лейбница Информацию О

Формула Лейбница Комментарии
Формула Лейбница
Формула Лейбница
Формула Лейбница Вы просматриваете субъект
Формула Лейбница что, Формула Лейбница кто, Формула Лейбница описание
There are excerpts from wikipedia on this article and video
www.turkaramamotoru.com
Формула Лейбница для детерминантов • ru.knowledgr.com
В алгебре формула Лейбница выражает детерминант квадратной матрицы
:
с точки зрения перестановок матричных элементов. Названный в честь Готтфрида Лейбница, формула —
:
для матрицы n×n, где sgn — функция знака перестановок в группе S перестановки, которая возвращается +1 и −1 для четных и нечетных перестановок, соответственно.
Другое общее примечание, используемое для формулы, с точки зрения символа Леви-Чивиты и использует примечание суммирования Эйнштейна, где это становится
:
который может быть более знаком физикам.
Непосредственно оценка формулы Лейбница из определения требует операций в целом — то есть, много операций, асимптотически пропорциональных n факториалу — потому что n! число перестановок заказа-n. Это непрактично трудно для большого n. Вместо этого детерминант может быть оценен в O (n) операции, формируя разложение ЛЮТЕЦИЯ (как правило, через Гауссовское устранение или подобные методы), когда и детерминанты треугольных матриц L и U — просто продукты своих диагональных записей. (В практическом применении числовой линейной алгебры, однако, редко требуется явное вычисление детерминанта.) Посмотрите, например, Trefethen и Bau (1997).
Формальное заявление и доказательство
Теорема.
Там существует точно одна функция
:
который является дополнительными мультилинейными w.r.t. колонками и таким образом что.
Доказательство.
Уникальность: Позвольте быть такой функцией и позволить быть матрицей. Назовите-th колонку, т.е., так, чтобы
Кроме того, позвольте, обозначают-th вектор колонки матрицы идентичности.
Теперь каждый пишет каждый из с точки зрения, т.е.
:.
Как мультилинейно, у каждого есть
:
\begin {выравнивают }\
F (A) & = F\left (\sum_ {k_1 = 1} ^n a_ {k_1} ^1 E^ {k_1}, \dots, \sum_ {k_n = 1} ^n a_ {k_n} ^n E^ {k_n }\\право) \\
& = \sum_ {k_1, \dots, k_n = 1} ^n \left (\prod_ {я = 1} ^n a_ {k_i} ^i\right) F\left (E^ {k_1}, \dots, E^ {k_n }\\право).
\end {выравнивают }\
От чередования из этого следует, что любой термин с повторными индексами — ноль. Сумма может поэтому быть ограничена кортежами с неповторяющимися индексами, т.е. перестановками:
:
Поскольку F чередуется, колонки могут быть обменяны, пока это не становится идентичностью. Функция знака определена, чтобы посчитать число обменов необходимым и составлять получающееся изменение знака. Каждый наконец добирается:
:
\begin {выравнивают }\
F (A) & = \sum_ {\\сигма \in S_n} \sgn (\sigma) \left (\prod_ {я = 1} ^n a_ {\\сигма (i)} ^i\right) F (I) \\
& = \sum_ {\\сигма \in S_n} \sgn (\sigma) \prod_ {я = 1} ^n a_ {\\сигма (i)} ^i
\end {выравнивают }\
как требуется, чтобы быть равным.
Поэтому никакая функция помимо функции, определенной Формулой Лейбница, не является мультилинейной переменной функцией с.
Существование: Мы теперь показываем, что у F, где F — функция, определенная формулой Лейбница, есть эти три свойства.
Мультилинейный:
:
\begin {выравнивают }\
F (A^1, \dots, cA^j, \dots) & = \sum_ {\\сигма \in S_n} \sgn (\sigma) ca_ {\\сигма (j)} ^j\prod_ {я = 1, я \neq j} ^n a_ {\\сигма (i)} ^i \\
& = c \sum_ {\\сигма \in S_n} \sgn (\sigma) a_ {\\сигма (j)} ^j\prod_ {я = 1, я \neq j} ^n a_ {\\сигма (i)} ^i \\
&=c F (A^1, \dots, A^j, \dots) \\
\\
F (A^1, \dots, b+A^j, \dots) & = \sum_ {\\сигма \in S_n} \sgn (\sigma) \left (b_ {\\сигма (j)} + a_ {\\сигма (j)} ^j\right) \prod_ {я = 1, я \neq j} ^n a_ {\\сигма (i)} ^i \\
& = \sum_ {\\сигма \in S_n} \sgn (\sigma)
\left (\left (b_ {\\сигма (j) }\\prod_ {я = 1, я \neq j} ^n a_ {\\сигма (i)} ^i\right) + \left (a_ {\\сигма (j)} ^j\prod_ {я = 1, я \neq j} ^n a_ {\\сигма (i)} ^i\right) \right) \\
& = \left (\sum_ {\\сигма \in S_n} \sgn (\sigma) b_ {\\сигма (j) }\\prod_ {я = 1, я \neq j} ^n a_ {\\сигма (i)} ^i\right)
+ \left (\sum_ {\\сигма \in S_n} \sgn (\sigma) \prod_ {я = 1} ^n a_ {\\сигма (i)} ^i\right) \\
&= F (A^1, \dots, b, \dots) + F (A^1, \dots, A^j, \dots) \\
\\
\end {выравнивают }\
Чередование:
:
\begin {выравнивают }\
F (\dots, A^ {j_1}, \dots, A^ {j_2}, \dots)
& = \sum_ {\\сигма \in S_n} \sgn (\sigma) \left (\prod_ {я = 1, я \neq j_1, i\neq j_2} ^n a_ {\\сигма (i)} ^i\right) a_ {\\сигма (j_1)} ^ {j_1} a_ {\\сигма (j_2)} ^ {j_2 }\\\
\end {выравнивают }\
Поскольку любой позволил быть кортежем, равным с и переключенные индексы.
:
\begin {выравнивают }\
F (A) & = \sum_ {\\sigma\in S_ {n}, \sigma (j_ {1})
Таким образом, если тогда.
Наконец:
:
\begin {выравнивают }\\\
F (I) & = \sum_ {\\сигма \in S_n} \sgn (\sigma) \prod_ {я = 1} ^n I_ {\\сигма (i)} ^i \\
& = \sum_ {\\сигма = (1,2, \dots, n)} \prod_ {я = 1} ^n I_ {я} ^i \\
& = 1
\end {выравнивают }\
Таким образом единственные функции, которые являются мультилинейным чередованием с, ограничены функцией, определенной формулой Лейбница, и у этого фактически также есть эти три свойства. Следовательно детерминант может быть определен как единственная функция
:
с этими тремя свойствами.
См. также
- Лапласовское расширение
- Правление Крамера
- Ллойд Н. Трефетэн и Дэвид Бо, числовая линейная алгебра (СИАМ, 1997) ISBN 978-0898713619
ru.knowledgr.com
Формула Лейбница
y=uv
y=uv+vu
y=uv+2uv+vu
y=uv+3uv+3uv+vu
…..
Отсюда вытекает общее формальное правило:
Чтобы найти производную (дифференциал) от (uv)(n) надо по формуле бинома Ньютона разложить n-ю степень суммы (u+v)n и затем заменить показатели степеней u и v указателями порядка производных, причем нулевые степени (u0 и v0), входящие в крайние члены разложения заменить самими функциями u и v (то есть, «производными нулевого порядка»).
Для дифференциала n-го порядка справедлива формула
dn(uv)=(uv)(n)dxn
dy=vdu+udv
d2y=vd2u+2dudv+ud2v
d3y=vd3u+3d2udv+3dud2v
Применение производных к исследованию свойств функций.
Возрастание и убывание функций.
Экстремум.
Определение1. Функция y=f(x) называется возрастающей в промежутке (a,b), если для любых x1, x2(a,b) большему из них соответствует и большее значение функции.
x1(a,b), x2(a,b), x2>x1 f(x2)>f(x1)
Определение 2. Функция y=f(x) называется убывающей на (a,b), если для любых x1 , x2(a,b) большему x соответствует меньшее значение f(x).
x1(a,b), x2(a,b), x2>x1 f(x2)<f(x1)
Из этих определений следует, что для возрастающих функции sign(y)=sign(x), в силу чего их отношение положительно:
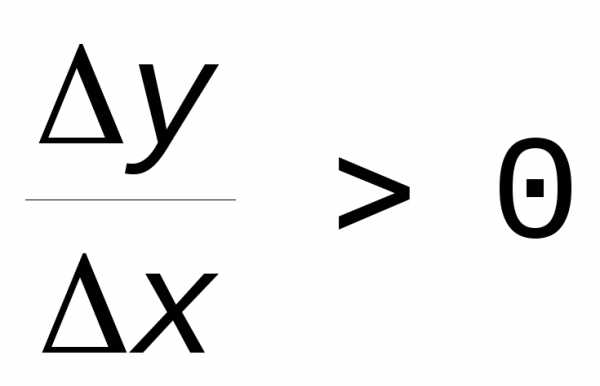
Для убывающей функции sign(y)=-sign(x)
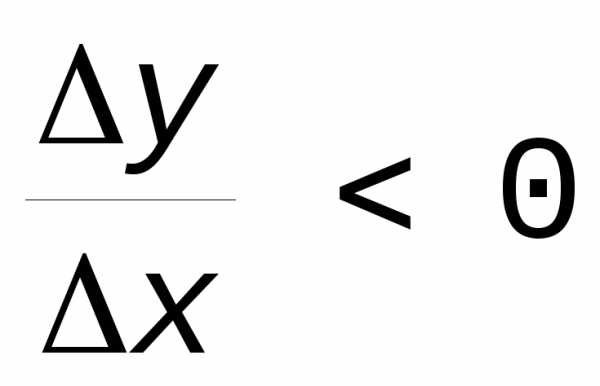
Если функция на переходит от возрастания к убыванию, или наоборот, ее называют колеблющейся на (a,b).
Значения x, при которых f(x) достигает своих наибольших или наименьших значений по сравнению с соседними, называют точками максимума и минимума.
Определение 3. x=x0 — точка максимума f(x), а f(x0) — максимум функции, если существует некоторая окрестность x0 (т.е. x0—, x0+) такая, что значение функции в любой точке x1(x0—, x0+) будет меньше , чем ее значение в x0, то есть меньше, чем максимум f(x0)
f(x0+x)<f
(x0) при любом |x|<Аналогично определяются точки максимума и минимума функции
f(x0+x)>f(x0) при любом |x|<
Дать графические примеры.
Точки минимума и максимума объединяются под общим названием – точки экстремума (экстремальные точки), а минимум и максимум функции – экстремумы функции.
Экстремумы функции, определенные выше, часто называют строгими экстремумами, в отличие нестрогих
f(x0+x)f(x0) и f(x0+x)f(x0)
Из определения вытекает, что вне -окрестности
Например за пределами (x0—, x0+), f(x+x)>f(x0) – где x0 — точка максимума, и аналогично f(x+x)<f(x0), если x0 — точка минимума f(x).
Таким образом понятия максимальной и минимальной функции носят локальный (местный) характер. Далее мы установим признаки возрастания и убывания функций и признаки экстремума функций, основанные на понятии производной.
Теоремы Ферма, Ролля, Лагранжа и Коши.
Теорема Ферма
. Если f(x) непрерывна на (a,b) и в x0(a,b) достигает максимума (минимума) и дифференцируема в x0, то ее производная в этой точке равна 0:f(x0)=0
Доказательство. Допустим, что f(x0) – максимум (минимум) функции. При достаточно малых x, точка x0+x независимо от знака x.
Пусть x>0 , переходя к пределу при x+0 получим: , как предел неположительной величины.
b) x<0
Так как для дифференцируемой в x0 функции производная слева равна производной справа
Аналогично проводится доказательство и для x0 — точки минимума, и для случая строгих неравенств.
Геометрический смысл очевиден: касательная к графику f(x) в точке экстремума, в которой f(x) дифференцируема, параллельна оси OX.
рисунок
Теорема Ролля. Если f(x) непрерывна на [a,b] и дифференцируема в (a,b), а на концах [a,b] принимает равные значения: f(a)=f(b)=c, то в промежутке (a,b) найдется точка x0 (по крайней мере одна), в которой f(x0)=0.
Доказательство. Рассмотрим случай f(x)c, x[a,b], удовлетворяющий условиям теоремы: f(x)=(c)=0 для любых x0.
Если же f(x)c будучи непрерывной на [a,b], она достигает своих наибольших и наименьших значений – M и m (см. свойства непрерывной функции). При этом возможны 3 случая:
a) f(a)=f(b)=m, f(x) достигнет наибольшего M в x0(a,b), то есть внутренней точке [a,b]. В точке x0 функция дифференцируема и тогда по теореме Ферма f(x0)=0.
b) f(a)=f(b)=M, f(x) достигнет минимума в некоторой x0(a,b), и снова, по теореме Ферма f(x0)=0.
c) Пусть теперь f(x) такова, что f (x0)=M и f (x0)=m, x0,x0(a,b), f(x0)=0 и f( x0)=0 по теореме Ферма.
Геометрический смысл теоремы Ролля: при выполнении условий теоремы Ролля на графике f(x) найдется хотя бы одна точка x0, касательная в которой будет параллельна оси ОХ.
Нарушение хотя бы одного из условий ведет к нарушению вывода из теоремы.
Рисунок Рисунок Рисунок
В частном случае, когда f(a)=f(b)=0 теорема Ролля имеет очень полезное для приложений толкование: Между двумя нулями дифференцируемой функции всегда заключен по крайней мере один нуль ее производной, то есть эта точка может оказаться max или min.
Теорема Коши. Если f(x) и (x) непрерывны на [a,b] и дифференцируемы в (a,b), при чем (x)0 на (a,b), то отношение конечных приращений этих функций на отрезке [a,b] равно отношению их производных в некоторой точке, которая может быть не единственной:
(b)(a) т.к. (x) 0 на (a,b) т.Ролля.
Доказательство. Введем вспомогательную F(x)=f(x)-(x), где =const. Выберем теперь такое, чтобы F(x) удовлетворяла условиям теоремы Ролля. Достаточно потребовать, чтобы F(a)=F(b). Другими словами:
F(a)-(a)=f(b)-(b)
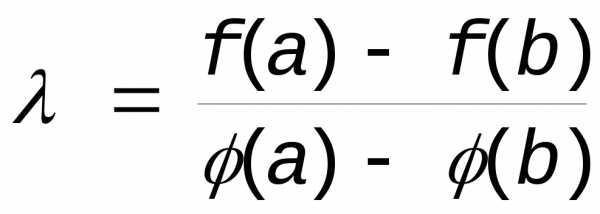 — конечное
значение, т.к. (b)(a)
— конечное
значение, т.к. (b)(a)
Тогда
хотя бы в одной точке c(a,b) F(c)=0 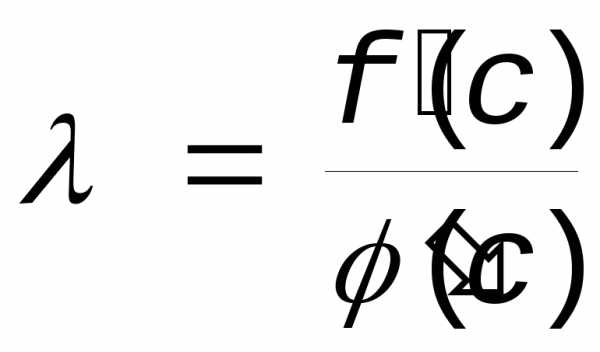
Теорема доказана.
Теорема Лагранжа (частный случай теоремы Коши). Пусть f(x) непрерывна на [a,b] и дифференцируема в (a,b). Тогда конечное приращение f(x) на [a,b] равно произведению длины отрезка [a,b] на значение производной в некоторой внутренней точке (a,b):
f(a)-f(b)=f(c)(b—a)
Полагая в теореме Коши (x)=x получим: (b)-(a)=b—a, (x)1 (c)=1
Поэтому
(*) т.е.
f(b)-f(a)=f(c)(b-a)
Геометрический смысл теоремы Лагранжа определяется формулой (*) . В ней левая часть есть угловой коэффициент хорды MN, соединяющей концы графической функции
РИСУНОК
Правая часть формулы – угловой коэффициент в точке P с абсциссой x=c(a,b)
f(c)=tg tg =tg , то есть хорда и касательная параллельны.
Таким образом, на произвольной дуге графика дифференцируемой функции всегда найдется хотя бы одна точка, в которой касательная будет параллельна хорде, стягивающей концы дуги.
Тот же геометрический смысл можно придать и теореме Коши, если рассматривать y=f(t) и x=(t) как параметрические уравнения кривой в плоскости XOY, а x считать параметром этой кривой.
Раскрытие неопределенностей.
Правило Бернулли-Лопиталя.
Раскрытием
неопределенности в математическом
анализе называют нахождение предела 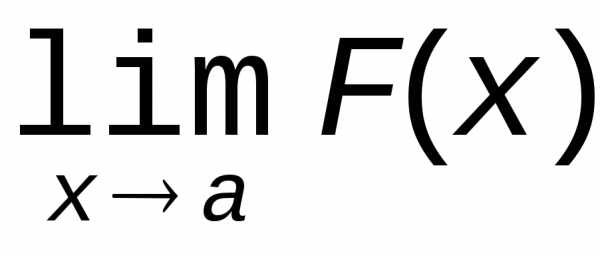 ,
когдаf(x) непрерывна вблизи a,
но не определена в самой этой точке, а
непосредственная подстановка в функцию x=a приводит к выражению неопределенного
вида
,
когдаf(x) непрерывна вблизи a,
но не определена в самой этой точке, а
непосредственная подстановка в функцию x=a приводит к выражению неопределенного
вида
 ,
,  ,
0, —,
1,0,0.
,
0, —,
1,0,0.
Опираясь на теорему Коши, выведем правило Бернулли-Лопиталя для раскрытия неопределенностей, используя производные.
Основными видами неопределенностей являются две:
 и
и  ,
,
раскрытие которых сводится к нахождению предела отношения двух бесконечно малых или бесконечно больших величин. Остальные виды сводятся к двум последним.
Рассмотрим неопределенность
 (приxa),
требуется найти
(приxa),
требуется найти  , когда
и .
Примем f(a)=(a)=0. Тогда f(x) и (x) будут непрерывными в x=a.
Предположим также, что f(x) и (x) дифференцируемы
вблизи x=a причем
(a)0.
В этом случае:
, когда
и .
Примем f(a)=(a)=0. Тогда f(x) и (x) будут непрерывными в x=a.
Предположим также, что f(x) и (x) дифференцируемы
вблизи x=a причем
(a)0.
В этом случае:
, (L — конечно или нет)
Доказательство. Применим к f(x) и (x) теорему Коши на отрезке [x0,a), где x0 окрестности a, в которой f и непрерывны и дифференцируемы (может за исключением a). Тогда
В силу того, что f(a)=(a)=0
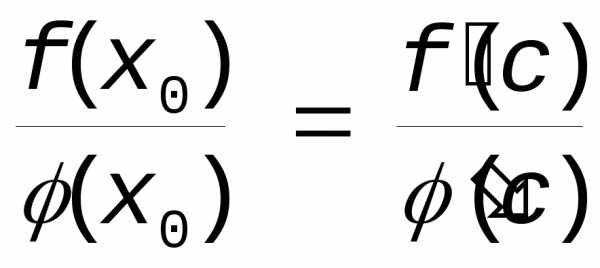 ,
где c(x0,a)
,
где c(x0,a)
Если теперь x0a, и ca, поэтому
Теперь, если положить x0=x, c=x
то есть в данном случае правило Бернулли-Лопиталя выполняется.
Примеры: 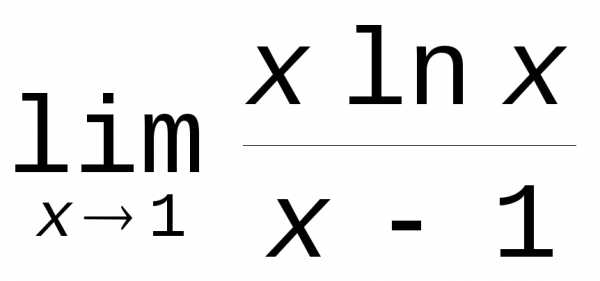
Неопределенность
 (x).
Докажем справедливость правила
Бернулли-Лопиталя и в этом случае.
(x).
Докажем справедливость правила
Бернулли-Лопиталя и в этом случае.
Итак
требуется найти 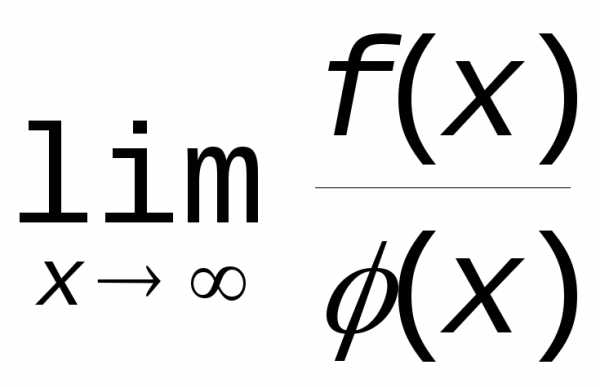 ,
еслии .
,
еслии .
Предположим,
что для достаточно больших x (|x|>M) обе функции дифференцируемы, (x)0 и что существует (конечный
или бесконечный) 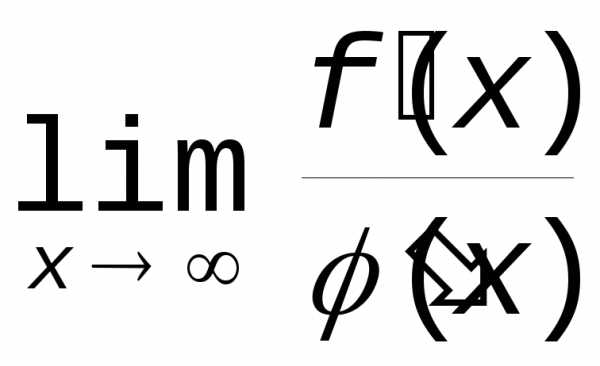 .
.
Докажем, что
Доказательство.
Перейдем к новому аргументу 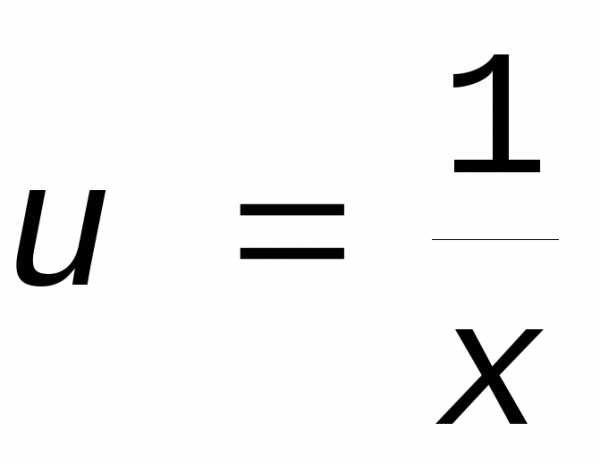 .
Тогда, x u0.
Нетрудно видеть, что к отношению
.
Тогда, x u0.
Нетрудно видеть, что к отношению 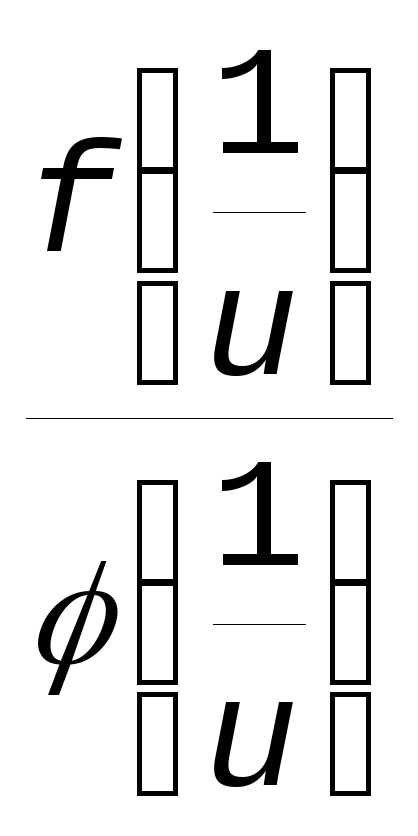 правило Бернулли-Лопиталя применимо:
в окрестности u=0 f и дифференцируемы, а
правило Бернулли-Лопиталя применимо:
в окрестности u=0 f и дифференцируемы, а 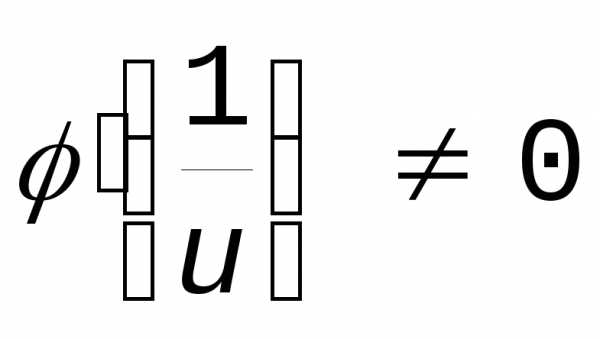 и существует
и существует
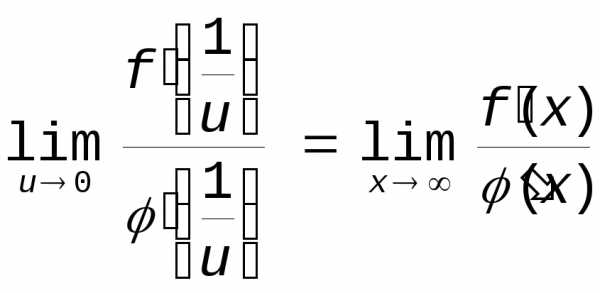
Тогда, принимая правило Бернулли-Лопиталя, получим
Возвращаясь к x, получим:
Правило остается в силе при x+ или x—.
Пример. 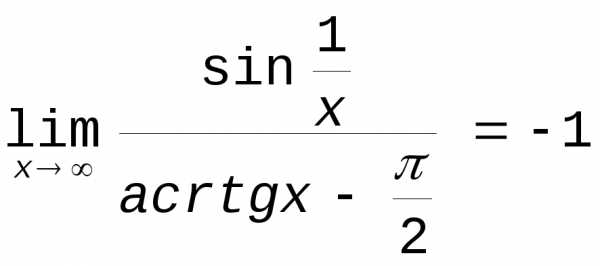 .
.
3.
Неопределенность  (xa).
Пусть теперь нужно найти
(xa).
Пусть теперь нужно найти 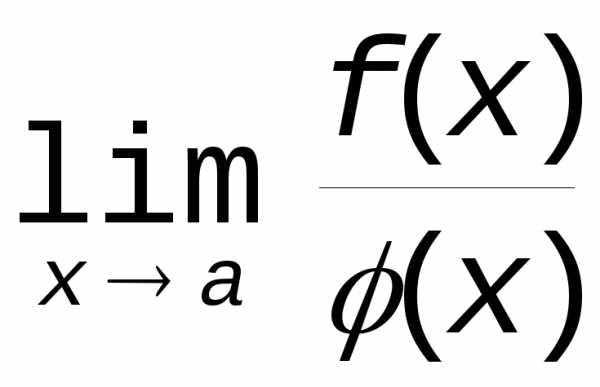 ,
если .
,
если .
Как и в случае 1., пусть f и дифференцируемы вблизи a, и (x)0.
Тогда,
если существует (конечный или бесконечный) 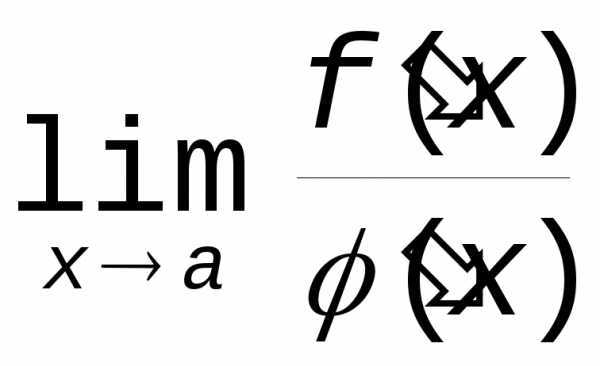 ,
то
,
то
Доказательство. Пусть x1 и x2 окрестности x=a, и пусть x1<x2<a, если точки берутся слева от a, или x1>x2>a — если справа. Тогда на отрезке [x1,x2] или [x2,x1]) к отношению f(x) и (x) применима теорема Коши:
c[x1,x2]
Далее пусть
Зададим теперь >0 и найдем ()>0 такое, что при |x—a|<()
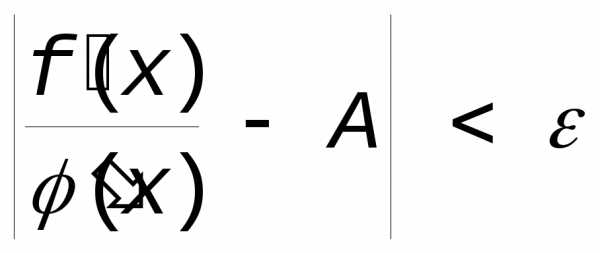 (*)
(*)
Выберем теперь x так, чтобы |x1—a|<() и зафиксируем его. Тогда, согласно условию выбора x2 |x2—a|<() и |c—a|<(), так как c[x1,x2]. Поэтому, в силу (*) будем иметь:
 или
или
Заменяя в этом неравенстве отношение производных отношением конечных приращений функций, получим
(1)
Если теперь x2a, не изменяя x1, то, так как ,
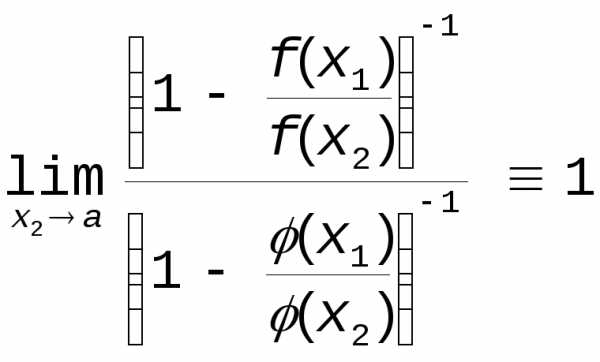
другими словами при заданном , найдется 1(), что при |x2—a|<1()
 или
или
Перемножая теперь почленно неравенства (1) и (2) (что возможно , так как все члены неравенства (2) положительны), получим
и
Другими
словами разность между 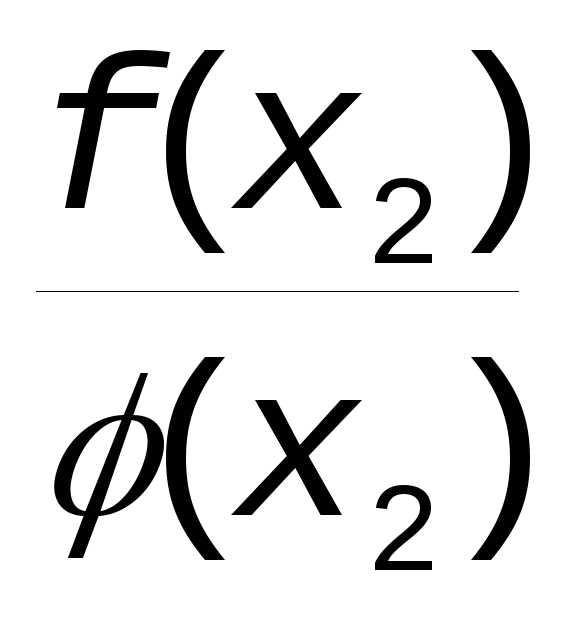 и постоянной A будет бесконечно малой величиной.
и постоянной A будет бесконечно малой величиной.
Следовательно 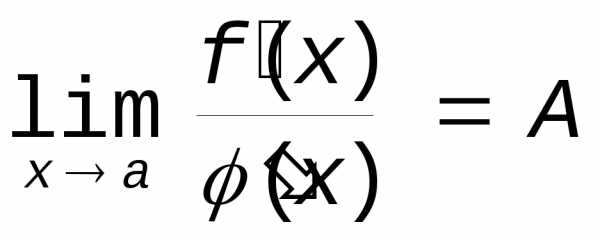 и
следовательно
и
следовательно
(3)
Пусть
теперь 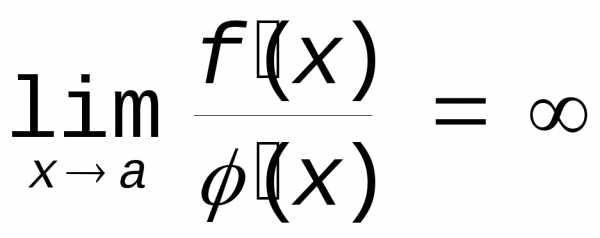 . Тогда f(x)0 в некоторой малой окрестности a (иначе
. Тогда f(x)0 в некоторой малой окрестности a (иначе 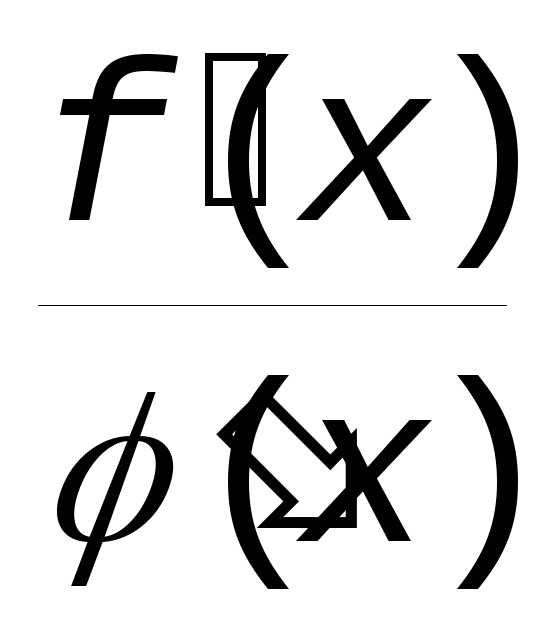 не было бы бесконечно большой величиной).
С другой стороны
не было бы бесконечно большой величиной).
С другой стороны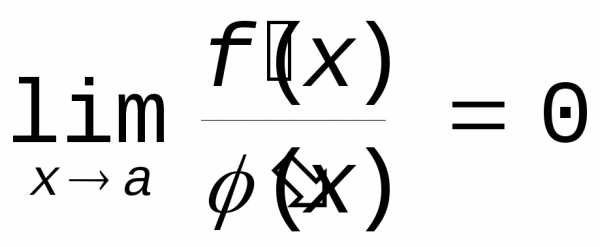 ,
а поэтому к обратному отношению применимо
предыдущее правило:
,
а поэтому к обратному отношению применимо
предыдущее правило:
Из последней формулы вытекает справедливость и формулы (3).
Пример. 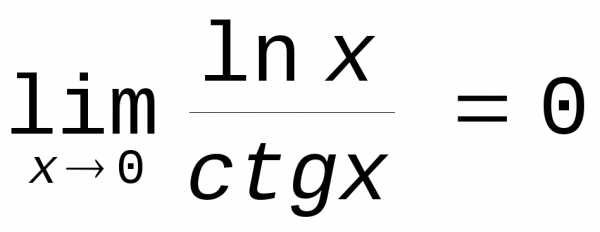
4. Неопределенность  (x). Правило
применимо, если f(x) и (x) дифференцируемы при любом x, |x|<M,
причем (x)0 и при условии,
что существует (конечный или бесконечный)
(x). Правило
применимо, если f(x) и (x) дифференцируемы при любом x, |x|<M,
причем (x)0 и при условии,
что существует (конечный или бесконечный) 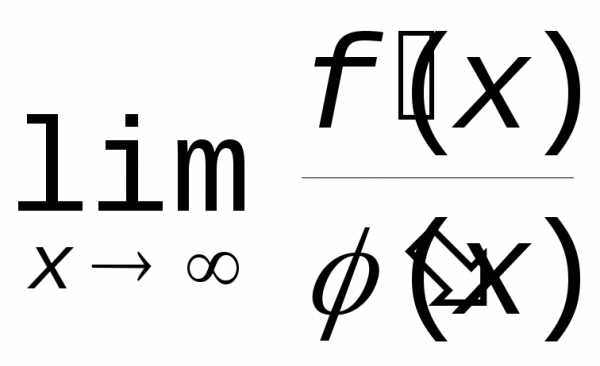 .
.
Для
доказательства достаточно перейти к
новому 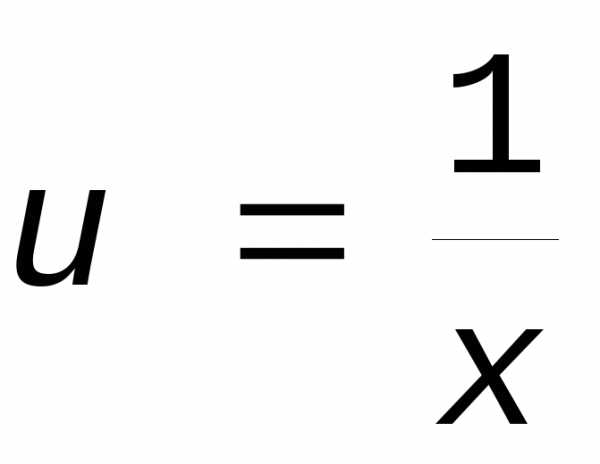 *
и использовать правило для случая 3.
*
и использовать правило для случая 3.
Пример. .
Правило
Бернулли-Лопиталя иногда приходится
применять несколько раз, если появляется
неопределенность в отношении 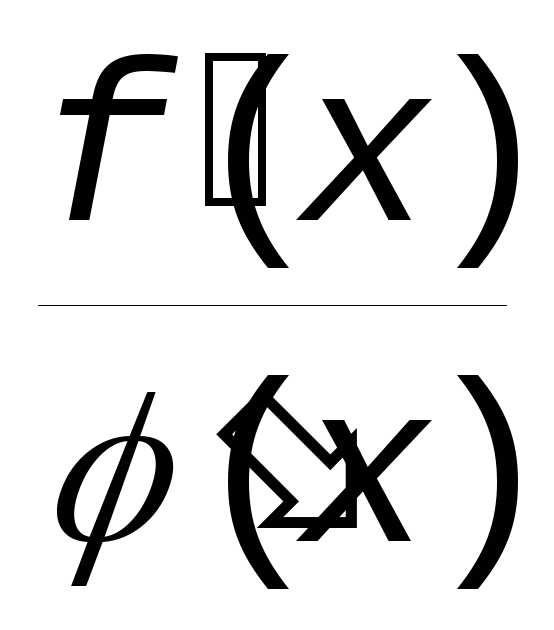 .
Для этого необходимо соблюдение условий
применимости теоремы Коши к производной
.
Для этого необходимо соблюдение условий
применимости теоремы Коши к производной
.
Примеры 1) 3 раза правило Бернулли-Лопиталя
2) . n раз правило Бернулли-Лопиталя
Примение правила Лопиталя к раскрытию неоределенности
0, —,
1,0,0 покажем на
примерах. Идея — эти
неопределенности сводятся в виду  или
или ,
а в последних 3-х случаях с применением
логарифмирования.
,
а в последних 3-х случаях с применением
логарифмирования.
Пример 1.
Представим
в виде: 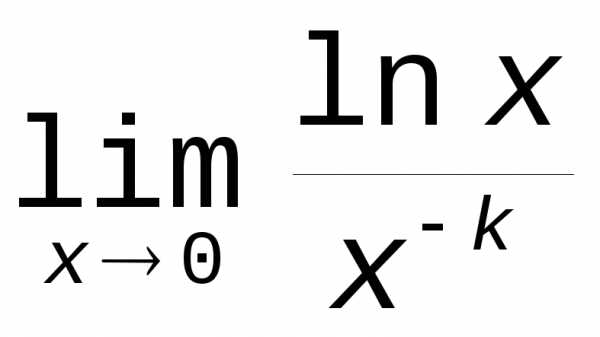 (xk – бесконечно
малая величина,
(xk – бесконечно
малая величина, 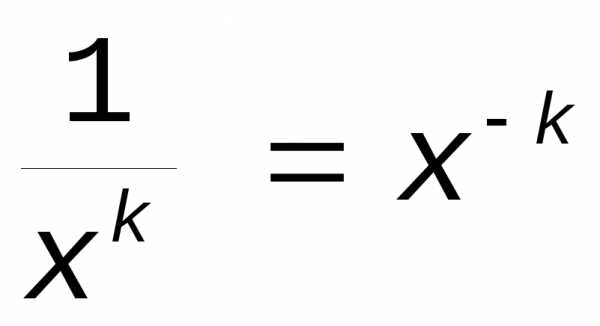 — бесконечно
большая величина)
— бесконечно
большая величина)  . x0
. x0
Пример
2.  —,
но
—,
но
, применяя правило Лопиталя, получим:
Пример 3.
Пример 4.
Правило
Лопиталя не применимо, если не существует 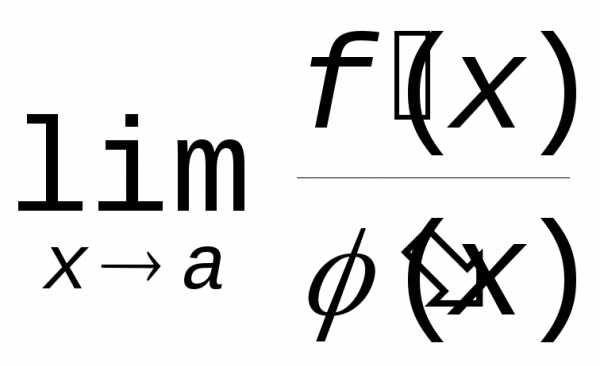 .
Однако это еще не означает, что не
существует
.
Однако это еще не означает, что не
существует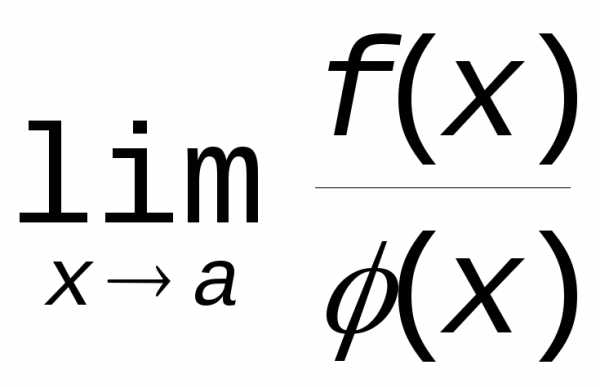 .
Просто в этом случае правило Лопиталя
нельзя использовать.
.
Просто в этом случае правило Лопиталя
нельзя использовать.
Пример. , тогда как .
Признаки возрастания и убывания функций.
Определения возрастания и убывания функций было дано ранее.
Теорема 1) Если f(x), дифференцируемая на отрезке [a,b], возрастает на этом отрезке, то f(x) неотрицательна на [a,b], то есть
f(x)0, x[a,b], если f(x),
2) Если f(x)непрерывна на[a,b]и дифференцируема в(a,b), причемf(x)>0, x(a,b), f(x)возрастает на[a,b].
studfiles.net

 (приxa),
требуется найти
(приxa),
требуется найти 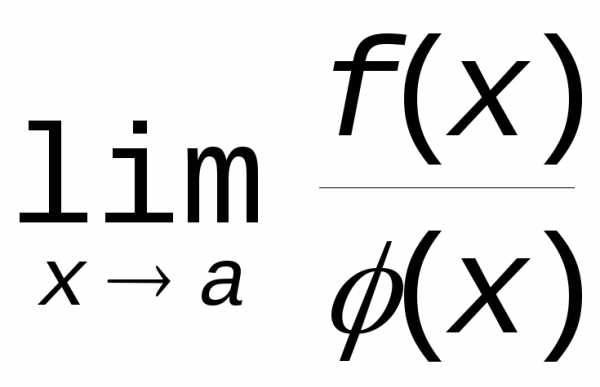 , когда
и .
Примем f(a)=(a)=0. Тогда f(x) и (x) будут непрерывными в x=a.
Предположим также, что f(x) и (x) дифференцируемы
вблизи x=a причем
(a)0.
В этом случае:
, когда
и .
Примем f(a)=(a)=0. Тогда f(x) и (x) будут непрерывными в x=a.
Предположим также, что f(x) и (x) дифференцируемы
вблизи x=a причем
(a)0.
В этом случае: (x).
Докажем справедливость правила
Бернулли-Лопиталя и в этом случае.
(x).
Докажем справедливость правила
Бернулли-Лопиталя и в этом случае.