Факториалы формулы – Факториал — урок. Алгебра, 9 класс.

alexxlab / / Школьная жизнь

Содержание

ФАКТР (функция ФАКТР) — Служба поддержки Office

Примечание:  Мы стараемся как можно оперативнее обеспечивать вас актуальными справочными материалами на вашем языке. Эта страница переведена автоматически, поэтому ее текст может содержать неточности и грамматические ошибки. Для нас важно, чтобы эта статья была вам полезна. Просим вас уделить пару секунд и сообщить, помогла ли она вам, с помощью кнопок внизу страницы. Для удобства также приводим ссылку на оригинал (на английском языке) .

Допустим, у вас есть шесть поговорим, причем каждый объект с другой звуковой сигнал, и вы хотите найти число уникальных последовательностей, в которых каждый колокольчика прозвучит один раз. В данном примере выполняется расчет факториал числа 6. Как правило Факториал используется для подсчета количества способами, в котором могут располагаться группы различных элементов (также называемые перестановок). Чтобы вычислить факториал числа, используйте функцию ФАКТОВ.

В этой статье описаны синтаксис формулы и использование функции ФАКТР в Microsoft Excel.

Описание

Возвращает факториал числа. Факториал числа — это значение, равное 1*2*3*…* число.

Синтаксис

ФАКТР(число)

Аргументы функции ФАКТР описаны ниже.

  • Число    — обязательный аргумент. Неотрицательное число, для которого вычисляется факториал. Если число не является целым, оно усекается.

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Формула

Описание

Результат

=ФАКТР(5)

Факториал числа 5 или 1*2*3*4*5

120

=ФАКТР(1,9)

Факториал целой части числа 1,9

1

=ФАКТР(0)

Факториал числа 0

1

=ФАКТР(-1)

Факториал отрицательного числа возвращает значение ошибки

#ЧИСЛО!

=ФАКТР(1)

Факториал числа 1

1

support.office.com

Факториал в Excel, Факториал в Эксель, формула ФАКТР, функция ФАКТР()

Как возвести в степень в Excel? И найти корень числа Как округлить число в Excel?

Понял, что на нашем сайте очень мало описаний математических функций. Хотя в Excel их превеликое множество. Есть описание НДС, всяких там печатных документов и форм. А вот описания основы основ табличного редактора — математических функций, почти нет. «Надо бы заняться этим пробелом» — подумал я. Вот занимаюсь. Первым очереди факториал. Почему? Просто на днях, делал одну задачу с этой функцией. Подробнее читаем далее про факториал в Excel.

Факториал в Excel. Введение

Думаю углубляться в мат. часть сильно не стоит. Считаю нужно рассказать для чего используется эта функция и как ее считать в Excel.

Начнем с определения, как говорит нам Википедия — Факториал числа n (от лат. factorialis — умножающий, действующий) — это произведение всех натуральных чисел от 1 до n включительно.

Для чего это может понадобится? В первую очередь — это обозначение умножения нескольких чисел 3! = 1*2*3. Факториал очень часто используется в комбинаторике. Что такое комбинаторика? Как следует из названия — это наука изучающая математические комбинации.

Пример: Сколько сочетаний цветов получится из 10 разных цветов? Сходу знаете? Я например, нет. Для вычисления кол-ва комбинаций применяется факториал.

Рассчитаем для 3 цветов: количество комбинаций цветов (желтый, красный, зеленый) = 3! =1*2*3 = 6. Какие это комбинации:

  1. ЖКЗ
  2. ЖЗК
  3. КЖЗ
  4. КЗЖ
  5. ЗЖК
  6. ЗКЖ

Действительно 6 🙂

В более сложных задачах в жизни, часто нужно узнать, к примеру, какое количество, вариантов выполнения маршрута из 7 точек. Как видите, штука полезная!

Факториал в Excel. Как посчитать.

Для факториала есть специальная функция =ФАКТР() Реквизиты предельно просты — один аргумент, то число до которого нужно рассчитать факториал

Пример такой формулы

=ФАКТР(A1)

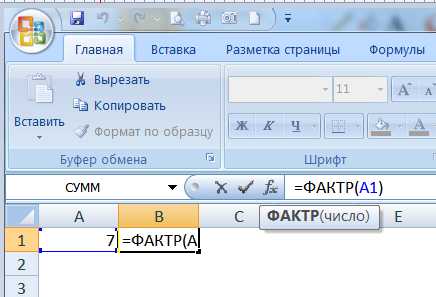
Рассчитав факториал 7, мы узнаем, что количество вариантов маршрута из 7 точек равно 5040. По-моему это впечатляет!

Удачной комбинаторики!

 

Поделитесь нашей статьей в ваших соцсетях:

Похожие статьи

Как возвести в степень в Excel? И найти корень числа Как округлить число в Excel?

excelworks.ru

Факториал — Википедия

Факториа́л числа

n (лат. factorialis — действующий, производящий, умножающий; обозначается n!, произносится эн факториа́л) — произведение всех натуральных чисел от 1 до n включительно:

Например:

.

По договорённости: . Также это равенство выполняется естественным образом:

Факториал определён только для целых неотрицательных чисел.

Последовательность факториалов неотрицательных целых чисел начинается так[1]:

1, 1, 2, 6, 24, 120, 720, 5040, 40 320, 362 880, 3 628 800, 39 916 800, 479 001 600, 6 227 020 800, 87 178 291 200, 1 307 674 368 000, 20 922 789 888 000, 355 687 428 096 000, 6 402 373 705 728 000, 121 645 100 408 832 000, 2 432 902 008 176 640 000, …

Факториалы часто используются в комбинаторике, теории чисел и функциональном анализе.

Факториал является чрезвычайно быстро растущей функцией. Он растёт быстрее, чем многочлен любой степени, и быстрее, чем экспоненциальная функция (но медленнее, чем двойная экспоненциальная функция ).

Рекуррентная формула[править]

Комбинаторная интерпретация[править]

В комбинаторике факториал натурального числа n интерпретируется как количество перестановок (упорядочиваний) множества из n элементов. Например, для множества {A,B,C,D} из 4-х элементов существует 4! = 24 перестановки:

ABCD  BACD  CABD  DABC
ABDC  BADC  CADB  DACB
ACBD  BCAD  CBAD  DBAC
ACDB  BCDA  CBDA  DBCA
ADBC  BDAC  CDAB  DCAB
ADCB  BDCA  CDBA  DCBA

Комбинаторная интерпретация факториала служит обоснованием тождества 0! = 1, так как пустое множество упорядочено единственным способом.

Связь с гамма-функцией[править]

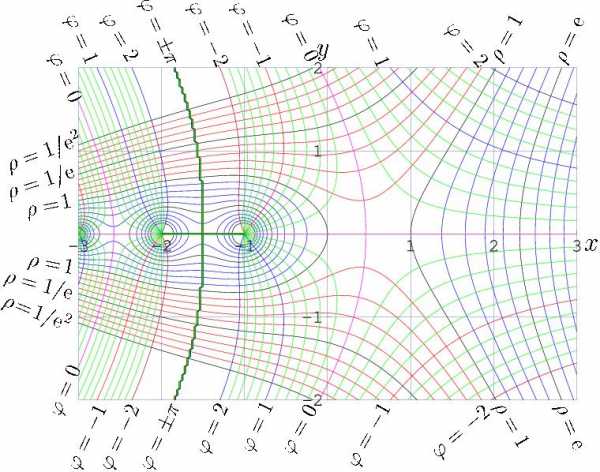Амплитуда и фаза факториала комплексного аргумента.

Факториал связан с гамма-функцией от целочисленного аргумента соотношением:

Таким образом, гамма-функцию рассматривают как обобщение факториала для положительных вещественных чисел.

Путём аналитического продолжения её также расширяют и на всю комплексную плоскость, исключая особые точки при .

Пи-функция, определённая для всех вещественных чисел, кроме отрицательных целых, и совпадающая при натуральных значениях аргумента с факториалом.

Более непосредственным обобщением факториала на множество вещественных (и комплексных) чисел является пи-функция, определяемая как

.

Поскольку то пи-функция натурального числа совпадает с его факториалом: Как факториал, пи-функция удовлетворяет рекурсивному соотношению

Формула Стирлинга[править]

Формула Стирлинга — асимптотическая формула для вычисления факториала:

см. O-большое[2].

Во многих случаях для приближённого значения факториала достаточно рассматривать только главный член формулы Стирлинга:

При этом можно утверждать, что

Формула Стирлинга позволяет получить приближённые значения факториалов больших чисел без непосредственного перемножения последовательности натуральных чисел. Так, с помощью формулы Стирлинга легко подсчитать, что

  • 100! ≈ 9,33×10157;
  • 1000! ≈ 4,02×102567;
  • 10 000! ≈ 2,85×1035 659.

Разложение на простые числа[править]

Каждое простое число p входит в разложение n! на простые множители в степени

Таким образом,

где произведение берётся по всем простым числам. Нетрудно видеть, что для всякого простого p большего n соответствующий множитель в произведении равен 1, а потому произведение можно брать лишь по простым p, не превосходящим n.

Связь с производной от степенной функции[править]

Для целого неотрицательного числа n:

Например:

Другие свойства[править]

  • Для натурального числа
    n    :

Двойной факториал[править]

Двойной факториал числа n обозначается n‼ и определяется как произведение всех натуральных чисел в отрезке [1,n], имеющих ту же чётность, что и n.

  • Для нечётного n:

Связь между двойными факториалами двух соседних целых неотрицательных чисел и обычным факториалом одного из них.

  • Для нечётного n:

Выведение формул

Осуществив замену для чётного n и для нечётного n соответственно, где  — целое неотрицательное число, получим:

  • для чётного числа:
  • для нечётного числа:

По договорённости: . Также это равенство выполняется естественным образом:

</div></div>

Двойной факториал, также как и обычный факториал, определён только для целых неотрицательных чисел.

Последовательность значений n!! начинается так[3]:

1, 1, 2, 3, 8, 15, 48, 105, 384, 945, 3840, 10 395, 46 080, 135 135, 645 120, 2 027 025, 10 321 920, 34 459 425, 185 794 560, 654 729 075, 3 715 891 200, 13 749 310 575, 81 749 606 400, 316 234 143 225, 1 961 990 553 600, 7 905 853 580 625, 51 011 754 393 600, …

Кратный факториал[править]

m-кратный факториал числа n обозначается и определяется следующим образом. Пусть число n представимо в виде где Тогда[4]

Обычный и двойной факториалы являются частными случаями m-кратного факториала для m = 1 и m = 2 соответственно.

Кратный факториал связан с гамма-функцией следующим соотношением[5]:

Неполный факториал[править]

Убывающий факториал[править]

Убывающим факториалом называется выражение

.

Например:

n = 7; k = 4,
(n − k) + 1 = 4,
3k = 7 • 6 • 5 • 4 = 840.

Убывающий факториал даёт число размещений из n по k.

Возрастающий факториал[править]

Возрастающим факториалом называется выражение

Праймориал или примориал[править]

Праймориал или примориал (англ. primorial) числа n обозначается pn# и определяется как произведение n первых простых чисел. Например,

.

Иногда праймориалом называют число , определяемое как произведение всех простых чисел, не превышающих заданное n.

Последовательность праймориалов (включая ) начинается так[6]:

1, 2, 6, 30, 210, 2310, 30 030, 510 510, 9 699 690, 223 092 870, 6 469 693 230, 200 560 490 130, 7 420 738 134 810, 304 250 263 527 210, 13 082 761 331 670 030, 614 889 782 588 491 410, 32 589 158 477 190 044 730, 1 922 760 350 154 212 639 070, …

Суперфакториалы[править]

Нейл Слоан и Саймон Плоуф (англ.) в 1995 году определили суперфакториал как произведение первых n факториалов. Согласно этому определению, суперфакториал четырёх равен

(поскольку устоявшегося обозначения нет, используется функциональное).

В общем

Последовательность суперфакториалов чисел начинается так[7]:

1, 1, 2, 12, 288, 34 560, 24 883 200, …

Идея была обобщена в 2000 году Генри Боттомли (англ.), что привело к гиперфакториалам (англ. Superduperfactorial), которые являются произведением первых n суперфакториалов. Последовательность гиперфакториалов чисел начинается так[8]:

1, 1, 2, 24, 6912, 238 878 720, 5 944 066 965 504 000, 745 453 331 864 786 829 312 000 000, 3 769 447 945 987 085 350 501 386 572 267 520 000 000 000, 6 916 686 207 999 802 072 984 424 331 678 589 933 649 915 805 696 000 000 000 000 000 …

Продолжая рекуррентно, можно определить факториал кратного уровня, или m-уровневый факториал числа n, как произведение (m − 1)-уровневых факториалов чисел от 1 до n, то есть

где для и

Субфакториал[править]

Субфакториал !n определяется как количество беспорядков порядка n, то есть перестановок n-элементного множества без неподвижных точек.

www.wiki-wiki.ru

Вычислить факториал

Начнем с определения: факториалом числа n называется произведение всех натуральных чисел от 1 до числа n включительно. Формула для вычисления факториала записывается так: $$n!=1\cdot 2\cdot 3\cdot …\cdot n$$ Надо еще знать соглашение: 0!=1. Почему факториал нуля равен единице можно спорить до бесконечности. Часто приводится и Гамма функция для объяснений и выражение типа: n!=(n-1)!n, в которое подставляют n=1 и радостно доказывают потом, что: из выражения 1!=(1-1)!1 следует 1=0!. Но на самом деле, это последнее выражение только доказывает, что правильно таки математики договорились считать, что 0!=1 для того, чтобы не нарушались правила вычисления факториала и в формулах не появлялось противоречие. А больше нигде это равенство 0!=1 и не используется. Поэтому и можно было договориться, чтобы не морочить себе голову в будущем. Но не об этом сейчас речь. Нас будет интересовать способ, как быстро (в домашних условиях) и правильно вычислить факториал большого числа. Проблема в том, что для вычисления факториалов больших чисел часто не хватает или памяти или числа знаков, поддерживаемых или калькулятором или компьютером. Ведь результат получается огромным, если число большое. Посмотрите на картинку (кликабельно) — на ней результат вычисления значения 500!. Но, теперь проблема решена — вы можете вычислять факториал от огромных чисел. Зачем только вам это может понадобиться не очень понятно. Ну, например, чтобы удивить вашего учителя или получить оригинальную заставку для вашего телефона. Правда иногда, программистам предлагают такую задачку решить, чтобы они помучились. Теперь все просто — вводите в строку ваше число, набираете восклицательный знак и жмете кнопку «Решить». Пример ввода приведен ниже.
500!
Важно. Чтобы получить все цифры огромного числа надо будет нажать надвпись More digits (больше цифр), если в конце выведенного числа есть троеточие. Нажимайте More digits до тех пор, пока троеточие в конце не исчезнет (для больших чисел несколько раз).

studlab.com

Факториал — Википедия

Факториа́л числа n (лат. factorialis — действующий, производящий, умножающий; обозначается n!, произносится эн факториа́л) — произведение всех натуральных чисел от 1 до n включительно:

Например:

.

По договорённости: . Также это равенство выполняется естественным образом:

Факториал определён только для целых неотрицательных чисел.

Последовательность факториалов неотрицательных целых чисел начинается так[1]:

1, 1, 2, 6, 24, 120, 720, 5040, 40 320, 362 880, 3 628 800, 39 916 800, 479 001 600, 6 227 020 800, 87 178 291 200, 1 307 674 368 000, 20 922 789 888 000, 355 687 428 096 000, 6 402 373 705 728 000, 121 645 100 408 832 000, 2 432 902 008 176 640 000, …

Факториалы часто используются в комбинаторике, теории чисел и функциональном анализе.

Факториал является чрезвычайно быстро растущей функцией. Он растёт быстрее, чем многочлен любой степени, и быстрее, чем экспоненциальная функция (но медленнее, чем двойная экспоненциальная функция ).

Рекуррентная формула[править]

Комбинаторная интерпретация[править]

В комбинаторике факториал натурального числа n интерпретируется как количество перестановок (упорядочиваний) множества из n элементов. Например, для множества {A,B,C,D} из 4-х элементов существует 4! = 24 перестановки:

ABCD  BACD  CABD  DABC
ABDC  BADC  CADB  DACB
ACBD  BCAD  CBAD  DBAC
ACDB  BCDA  CBDA  DBCA
ADBC  BDAC  CDAB  DCAB
ADCB  BDCA  CDBA  DCBA

Комбинаторная интерпретация факториала служит обоснованием тождества 0! = 1, так как пустое множество упорядочено единственным способом.

Связь с гамма-функцией[править]

Амплитуда и фаза факториала комплексного аргумента.

Факториал связан с гамма-функцией от целочисленного аргумента соотношением:

Таким образом, гамма-функцию рассматривают как обобщение факториала для положительных вещественных чисел.

Путём аналитического продолжения её также расширяют и на всю комплексную плоскость, исключая особые точки при .

Пи-функция, определённая для всех вещественных чисел, кроме отрицательных целых, и совпадающая при натуральных значениях аргумента с факториалом.

Более непосредственным обобщением факториала на множество вещественных (и комплексных) чисел является пи-функция, определяемая как

.

Поскольку то пи-функция натурального числа совпадает с его факториалом: Как факториал, пи-функция удовлетворяет рекурсивному соотношению

Формула Стирлинга[править]

Формула Стирлинга — асимптотическая формула для вычисления факториала:

см. O-большое[2].

Во многих случаях для приближённого значения факториала достаточно рассматривать только главный член формулы Стирлинга:

При этом можно утверждать, что

Формула Стирлинга позволяет получить приближённые значения факториалов больших чисел без непосредственного перемножения последовательности натуральных чисел. Так, с помощью формулы Стирлинга легко подсчитать, что

  • 100! ≈ 9,33×10157;
  • 1000! ≈ 4,02×102567;
  • 10 000! ≈ 2,85×1035 659.

Разложение на простые числа[править]

Каждое простое число p входит в разложение n! на простые множители в степени

Таким образом,

где произведение берётся по всем простым числам. Нетрудно видеть, что для всякого простого p большего n соответствующий множитель в произведении равен 1, а потому произведение можно брать лишь по простым p, не превосходящим n.

Связь с производной от степенной функции[править]

Для целого неотрицательного числа n:

Например:

Другие свойства[править]

  • Для натурального числа n:

Двойной факториал[править]

Двойной факториал числа n обозначается n‼ и определяется как произведение всех натуральных чисел в отрезке [1,n], имеющих ту же чётность, что и n.

  • Для нечётного n:

Связь между двойными факториалами двух соседних целых неотрицательных чисел и обычным факториалом одного из них.

  • Для нечётного n:

Выведение формул

  • Формула для чётного n:
Выведение формулы:
\begin{align} n!! & = {\color{Gray}\underbrace{\color{Black}2 \cdot 4 \cdot 6 \cdot \ldots \cdot n}_{\color{Black}\tfrac{n}{2}}} = {\color{Gray}\underbrace{\color{OliveGreen}2 \cdot 2 \cdot 2 \cdot \ldots \cdot 2}_{\color{Black}\tfrac{n}{2}}} \; \cdot \; \frac{\; 2 \cdot 4 \cdot 6 \cdot \ldots \cdot n \;}{\color{Gray}\underbrace{\color{OliveGreen}2 \cdot 2 \cdot 2 \cdot \ldots \cdot

www.wiki-wiki.ru

Реферат Факториал

скачать

Реферат на тему:

План:

    Введение
  • 1 Свойства
    • 1.1 Рекуррентная формула
    • 1.2 Комбинаторная интерпретация
    • 1.3 Связь с гамма-функцией
    • 1.4 Формула Стирлинга
    • 1.5 Разложение на простые числа
    • 1.6 Другие свойства
  • 2 Обобщения
    • 2.1 Двойной факториал
    • 2.2 Убывающий факториал
    • 2.3 Возрастающий факториал
    • 2.4 Праймориал или примориал
    • 2.5 Суперфакториалы
    • 2.6 Субфакториал

Введение

Факториа́л числа n (обозначается n!, произносится эн факториа́л) — произведение всех натуральных чисел до n включительно:

.

По определению полагают 0! = 1. Факториал определён только для целых неотрицательных чисел.

Последовательность факториалов неотрицательных целых чисел начинается так:

1, 1, 2, 6, 24, 120, 720, 5040, 40320, 362880, 3628800, 39916800, 479001600, 6227020800, … (последовательность A000142 в OEIS)

Факториалы часто используются в комбинаторике, теории чисел и функциональном анализе.


1. Свойства

1.1. Рекуррентная формула

1.2. Комбинаторная интерпретация

В комбинаторике факториал натурального числа n интерпретируется как количество перестановок множества из n элементов. Например, для множества {A,B,C,D} из 4-х элементов существует 4!=24 перестановки:

ABCD  BACD  CABD  DABC
ABDC  BADC  CADB  DACB
ACBD  BCAD  CBAD  DBAC
ACDB  BCDA  CBDA  DBCA
ADBC  BDAC  CDAB  DCAB
ADCB  BDCA  CDBA  DCBA

1.3. Связь с гамма-функцией

Факториал связан с гамма-функцией от целочисленного аргумента соотношением:

n! = Γ(n + 1)

Таким образом, гамма-функцию рассматривают как обобщение факториала для положительных вещественных чисел.

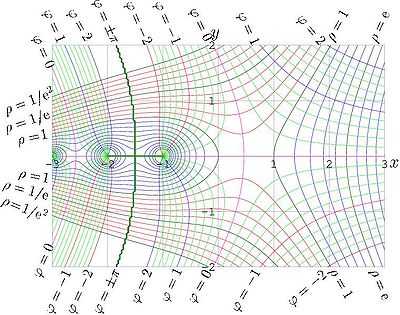
Амплитуда и фаза факториала комплексного аргумента.

Путём аналитического продолжения её также расширяют и на всю комплексную плоскость, исключая особые точки при .


1.4. Формула Стирлинга

Формула Стирлинга — асимптотическая формула для вычисления факториала:

см. O-большое. Коэффициенты этого разложения дают последовательность A001163 в OEIS (числители) и последовательность A001164 в OEIS (знаменатели).

Во многих случаях для приближённого значения факториала достаточно рассматривать только главный член формулы Стирлинга:

При этом можно утверждать, что


1.5. Разложение на простые числа

Каждое простое число p входит в разложение n! на простые в степени

Таким образом,

,

где произведение берётся по всем простым числам.

1.6. Другие свойства

  • Для натурального числа n

2. Обобщения

2.1. Двойной факториал

Двойной факториал числа n обозначается n!! и определяется как произведение всех натуральных чисел в отрезке [1,n], имеющих ту же чётность что и n. Таким образом,

По определению полагают 0!! = 1.

Последовательность значений n!! начинается так:

1, 1, 2, 3, 8, 15, 48, 105, 384, 945, … (последовательность A006882 в OEIS)

2.2. Убывающий факториал

Убывающим факториалом (или неполным факториалом) называется выражение

Убывающий факториал даёт число размещений из n по k.

2.3. Возрастающий факториал

Возрастающим факториалом называется выражение

2.4. Праймориал или примориал

Праймориал или примориал (англ. primorial) числа n обозначается n#  и определяется как произведение простых чисел, не превышающих n. Например,

Последовательность праймориалов (включая ) начинается так:

1, 2, 6, 30, 210, 2310, 30030, 510510, 9699690, … (последовательность A002110 в OEIS)

2.5. Суперфакториалы

Нейл Слоан и Саймон Плоуф (англ.) в 1995 году определили суперфакториал как произведение первых n факториалов. Согласно этому определению суперфакториал четырёх равен (поскольку устоявшегося обозначения нет, используется функциональное)

В общем

Последовательность суперфакториалов чисел n⩾0 начинается так:

1, 1, 2, 12, 288, 34560, 24883200, … (последовательность A000178 в OEIS)

Идея была обобщена в 2000 году Генри Боттомли (англ.), что привело к гиперфакториалам (англ. Super-duper-factorial), которые являются произведением первых n суперфакториалов. Последовательность гиперфакториалов чисел n⩾0 начинается так:

1, 1, 2, 24, 6912, 238878720, 5944066965504000, … (последовательность A055462 в OEIS)

Продолжая рекуррентно, можно определить факториал кратного уровня, где m-уровневый факториал числа n как произведение первых n (m-1)-уровневых факториалов, то есть

где для n > 0 и .


2.6. Субфакториал

Субфакториал определяется как количество беспорядков порядка , то есть перестановок -элементного множества без неподвижных точек.

wreferat.baza-referat.ru

Таблица факториалов

1! = 1

2! = 2

3! = 6

4! = 24

5! = 120

6! = 720

7! = 5040

8! = 40320

9! = 362880

10! = 3628800

11! = 39916800

12! = 479001600

13! = 6227020800

14! = 87178291200

15! = 1307674368000

16! = 20922789888000

17! = 355687428096000

18! = 6402373705728000

19! = 121645100408832000

20! = 2432902008176640000

21! = 51090942171709440000

22! = 1124000727777607680000

23! = 25852016738884976640000

24! = 620448401733239439360000

25! = 15511210043330985984000000

26! = 403291461126605635584000000

27! = 10888869450418352160768000000

28! = 304888344611713860501504000000

29! = 8841761993739701954543616000000

30! = 265252859812191058636308480000000

31! = 8222838654177922817725562880000000

32! = 263130836933693530167218012160000000

33! = 8683317618811886495518194401280000000

34! = 295232799039604140847618609643520000000

35! = 10333147966386144929666651337523200000000

36! = 371993326789901217467999448150835200000000

37! = 13763753091226345046315979581580902400000000

38! = 523022617466601111760007224100074291200000000

39! = 20397882081197443358640281739902897356800000000

40! = 815915283247897734345611269596115894272000000000

41! = 33452526613163807108170062053440751665152000000000

42! = 1405006117752879898543142606244511569936384000000000

43! = 60415263063373835637355132068513997507264512000000000

44! = 2658271574788448768043625811014615890319638528000000000

45! = 119622220865480194561963161495657715064383733760000000000

46! = 5502622159812088949850305428800254892961651752960000000000

47! = 258623241511168180642964355153611979969197632389120000000000

48! = 12413915592536072670862289047373375038521486354677760000000000

49! = 608281864034267560872252163321295376887552831379210240000000000

50! = 30414093201713378043612608166064768844377641568960512000000000000

ru.onlinemschool.com

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *