Формула a2 b2 – Формулы сокращённого умножения

Формулы сокращенного умножения.

Формулы сокращенного умножения.

Формулы сокращенного умножения. Разность квадратов, сумма кубов и разность кубов и разность четвертых степеней. Квадрат суммы и квадрат разности и куб суммы и куб разности.

Разность квадратов	a2-b2 = (a-b)(a+b)
Квадрат суммы	(a+b)2 = a2+2ab+b2
Квадрат разности	(a-b)2 = a2-2ab+b2
Куб суммы	(a+b)3 = a3+3a2b+3ab2+b3
Куб разности	(a-b)3 = a3-3a2b+3ab2-b3
Сумма кубов	a3+b3 = (a+b)(a2-ab+b2)
Разность кубов	a3-b3 = (a-b)(a2+ab+b2)
Разность четвертых степеней	a4-b4 = (a2-b2)(a2+b2)=(a-b)(a+b)(a2+b 2)

Справочно, только для тех кто хочет больше представлять тему: Бином Ньютона. Целая положительная степень n суммы. (a + b)ⁿ=

dpva.ru

мне нужны формулы «сокращенного умножения»? все полностью

и чего? ? в гугл не пробовал забить? так даже быстрее было бы

(a+b)2=a2+2ab+b2 (a-b)2=a2-2ab+b2 (a+b)(a-b)=a2-b2 (a+b)3=a3+3a2b+3ab2+b3 (a-b)3=a3-3a2b+3ab2-b3 (a+b)(a2-ab+b2)=a3+b3 (a-b)(a2+ab+b2)=a3-b3

Формулы для квадратов a2 − b2 = (a + b)(a − b) (a + b − c)2 = a2 + b2 + c2 + 2ab − 2ac − 2bc Формулы для кубов Формулы для четвёртой степени Формулы для n-ой степени an − bn = (a − b)(an − 1 + an − 2b + an − 3b2 + .+a2bn − 3 + abn − 2 + bn − 1) a2n − b2n = (a + b)(a2n − 1 − a2n − 2b + a2n − 3b2 − …− a2b2n − 3 + ab2n − 2 − b2n − 1), где n ϵ N a2n + 1 + b2n + 1 = (a + b)(a2n − a2n − 1b + a2n − 2b2 − …+a2b2n − 2 − ab2n − 1 + b2n), где n ϵ N Некоторые свойства формул (a − b)2n = (b − a)2n, где (a − b)2n + 1 = − (b − a)2n + 1, где Интересные формулы a4 − b4 = (a − b)(a + b)(a2 + b2) (выводится из a2 − b2)

touch.otvet.mail.ru

Ответы@Mail.Ru: а^2+b^2=(a-b)(a+b)????

a^2 + b^2= a^2 + 2*a*b + b^2

Выражение справа — разность квадратов. a^2 — b^2 = (a-b)(a+b)

это тождество исходим из правой части равенства (a-b)(a+b)=a^2-ab+ab-b^2(сокращаем -ab и +ab(получится 0)) остается a^2-b^2 а не a^2 + b^2

сумма квадратов на произведение НЕ раскладывается. [1] ( a + b )² = a² + 2ab + b² , [2] ( a – b )² = a² – 2ab + b² , [3] ( a + b ) ( a – b ) = a² – b², [4] ( a + b )³ = a³ + 3a² b + 3ab² + b³ , [5] ( a – b )³ = a ³ – 3a² b + 3ab² – b³ , [6] ( a + b )( a² – ab + b² ) = a³ + b³ , [7] ( a – b )( a ² + ab + b² ) = a³ – b³

a^2+b^2=a^2+ab-ab-b^2 a^2+b^2=a^2-b^2 2*b^2=0

a^2+b^2=a^2+ab-ab-b^2 a^2+b^2=a^2-b^2 2*b^2=0

я токое незнаю

а^2+b^2=(a+b)^2-2ab и только так) ) (a-b)(a+b)=a^2-b^2

да формулы сокращённого умножения

нет, это не правильно, ТОЛЬКО: a^2 — b^2 = (a-b)(a+b) обрати внимание на минус между квадратами a и b

touch.otvet.mail.ru

A 2 b 2 c 2, сложение квадратов

Выражения, преобразование выражений

Формулы сокращенного умножения (ФСУ): таблица, формулировки, примеры применения.

Для умножения и возведения в степень чисел и выражений (в частности многочленов) в некоторых случаях могут быть использованы так называемые формулы сокращенного умножения. Из названия понятно, что эти формулы позволяют проводить умножение сокращенно, то есть, быстрее при более компактной записи решения.

В этой статье мы перечислим все основные наиболее часто используемые формулы сокращенного умножения. Для удобства запоминания занесем их в таблицу. Дальше дадим формулировки – они позволят читать формулы сокращенного умножения. После этого остановимся на принципах доказательства этих формул. Наконец, дадим обзор задач, для решения которых применяются формулы сокращенного умножения, и рассмотрим несколько примеров с подробными решениями.

Список формул сокращенного умножения (ФСУ) в виде таблицы

Формулы сокращенного умножения (фсу) изучаются на уроках алгебры в 7 классе после разговора про действия с многочленами и одночленами, при этом рассматриваются 7 основных формул. Перечислим их по порядку в виде списка:

• (a+b)²=a²+2·a·b+b² – так называемая формула квадрата суммы;
• (a−b)²=a²−2·a·b+b² – эта формула имеет название квадрат разности;
• (a+b)³=a³+3·a²·b+3·a·b²+b³ – эта формула представляет собой куб суммы;
• (a−b)³=a³−3·a²·b+3·a·b²−b³ – формула куба разности;
• (a−b)·(a+b)=a²−b²;
• (a+b)·(a^2−a·b+b^2)=a^3+b^3;
• (a−b)·(a²+a·b+b²)=a³−b³.

Под буквами a и b понимаются числа, переменные, или, вообще, любые числовые и буквенные выражения.

Формулы сокращенного выражения очень часто применяются на практике, так что их все желательно выучить наизусть. До этого момента нам будет служить верой и правдой таблица формул сокращенного умножения, которую мы рекомендуем распечатать и все время держать перед глазами:

Первые четыре формулы из составленной таблицы формул сокращенного умножения позволяют возводить в квадрат и куб сумму или разность двух выражений. Пятая предназначена для краткого умножения разности и суммы двух выражений. А шестая и седьмая формулы используются для умножения суммы двух выражений a и b на их неполный квадрат разности (так называют выражение вида a²−a·b+b²) и разности двух выражений a и b на неполный квадрат их суммы (a²+a·b+b²) соответственно.

Стоит отдельно заметить, что каждое равенство в таблице представляет собой тождество. Этим объясняется, почему формулы сокращенного умножения еще называют тождествами сокращенного умножения.

При решении примеров, особенно в которых имеет место разложение многочлена на множители, ФСУ часто используют в виде с переставленными местами левыми и правыми частями:

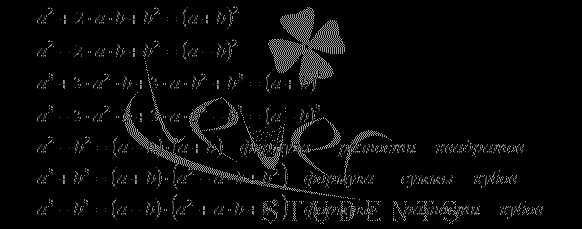
Три последних тождества в таблице имеют свои названия.

Формула a²−b²=(a−b)·(a+b) называется формулой разности квадратов, a³+b³=(a+b)·(a²−a·b+b²) — формулой суммы кубов, а a³−b³=(a−b)·(a²+a·b+b²) — формулой разности кубов. Обратите внимание, что соответствующим формулам с переставленными частями из предыдущей таблицы фсу мы никак не назвали.

К началу страницы

Дополнительные формулы

В таблицу формул сокращенного умножения не помешает добавить еще несколько тождеств.

Во-первых, полезной будет формула бинома Ньютона вида , где — биномиальные коэффициенты, стоящие в строке под номером n в треугольнике Паскаля. С ее помощью можно сокращенно возводить сумму двух выражений в любую натуральную степень. Кстати, ФСУ квадрата и куба суммы и разности являются частными случаями формулы бинома Ньютона при n=2 и n=3.

Во-вторых, полезной бывает формула возведения в квадрат суммы трех, четырех и большего количества слагаемых вида
(a₁+a₂+…+a_n)²=a₁²+a₂²+…+a_n−1²+a_n²+
+2·a₁·a₂+2·a₁·a₃+2·a₁·a₄+…+
+2·a₁·a_n−1+2·a₁·a_n+
+2·a₂·a₃+2·a₂·a₄+…+2·a₂·a_n−1+2·a₂·a_n+
+…+
+2·a_n−1·a_n.

Она читается так: квадрат суммы n слагаемых равен сумме квадратов всех этих слагаемых и удвоенных произведений всех возможных пар этих слагаемых. Для примера возведем в квадрат с использованием этой формулы сумму трех слагаемых a, b и c, имеем (a+b+c)²=a²+b²+c²+2·a·b+2·a·c+2·b·c. В частном случае при n=2 эта формула становится уже известной нам формулой квадрата суммы двух слагаемых.

И еще не помешает держать перед глазами формулу разности n-ых степеней двух слагаемых вида aⁿ−bⁿ=
=(a−b)·(aⁿ⁻¹+aⁿ⁻²·b+aⁿ⁻³·b²+…+a·bⁿ⁻²+bⁿ⁻¹), которую обычно представляют раздельно для четных и нечетных показателей. Для четных показателей 2·m она имеет вид a^2·m−b^2·m=
=(a²−b²)·(a^2·m−2+a^2·m−4·b²+a^2·m−6·b⁴+…+b^2·m−2), а для нечетных показателей 2·m+1 – вид a^2·m+1−b^2·m+1=
=(a−b)·(a^2·m+a^2·m−1·b+a^2·m−2·b²+…+b^2·m).

Частными случаями этой формулы являются формулы разность квадратов (при n=2), разность кубов (при n=3) и сумма кубов (при n=3 и если b заменить на −b).

К началу страницы

Как читаются формулы сокращенного умножения?

Чтобы рассказать решение примера, в котором были использованы формулы сокращенного умножения, нужно знать, как эти формулы читаются. Дадим соответствующие формулировки.

Сначала разберемся с принципом чтения формул сокращенного умножения. Это удобнее всего сделать, рассмотрев любую и них, например, первую формулу квадрата суммы вида (a+b)²=a²+2·a·b+b².

В левой ее части находится выражение (a+b)², которое представляет собой квадрат суммы двух выражений a и b, оно так и читается (отсюда понятно и название формулы). Дальше стоит знак равно, он и произносится как равно. В правой части формулы расположена сумма трех слагаемых a², 2·a·b и b². a² и b² – это квадраты первого и второго выражений соответственно, а 2·a·b читается как удвоенное произведение выражений a и b, слово «удвоенное» отвечает числовому коэффициенту2. Осталось соединить все эти рассуждения в одно предложение, которое будет ответом на вопрос, как читается формула квадрата суммы.

Итак, квадрат суммы двух выражений a и b равен сумме квадрата первого выражения, удвоенного произведения первого и второго выражений и квадрата второго выражения.

Аналогично читаются и остальные фсу.

Так квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение этих выражений плюс квадрат второго выражения. Эта формулировка второй фсу вида (a−b)²=a²−2·a·b+b

2.

Дальше читаем формулу (a+b)³=a³+3·a²·b+3·a·b²+b³. Куб суммы двух выражений a и b равен сумме куба первого выражения, утроенного произведения квадрата первого выражения на второе, утроенного произведения первого выражения на квадрат второго и куба второго выражения.

Аналогично читается и формула куба разности (a−b)³=a³−3·a²·b+3·a·b²−b³. Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого на квадрат второго выражения минус куб второго выражения.

Переходим к чтению пятой по списку формулы сокращенного выражения (a−b)·(a+b)=a²−b². Произведение разности двух выражений и их суммы равно разности квадратов первого и второго выражений.

А для удобства чтения шестой и, последней, седьмой ФСУ используют термины «неполный квадрат суммы» и «неполный квадрат разности» выражений a и b, которыми называют выражения a

2+a·b+b² и a²−a·b+b² соответственно. (В свою очередь выражения a²+2·a·b+b² и a²−2·a·b+b² называют полным квадратом суммы и разности соответственно.)

Итак, произведение суммы двух выражений на их неполный квадрат разности равно сумме кубов этих выражений.

Теорема косинусов. Доказательство теоремы косинусов.

Так читается формула (a+b)·(a²−a·b+b²)=a³+b³. И произведение разности двух выражений на неполный квадрат их суммы равен разности кубов этих выражений, этому утверждению отвечает формула сокращенного умножения вида (a−b)·(a²+a·b+b²)=a³−b³.

К началу страницы

Доказательство

Сейчас самое время остановиться на доказательстве формул сокращенного умножения.

Доказать их достаточно легко – для этого нужно лишь выполнить возведение в степень или умножение выражений, находящихся в левых частях формул, основываясь на свойствах умножения.

Для примера докажем формулу квадрата разности (a−b)²=a²−2·a·b+b². Возведем разность a−b во вторую степень. Для этого степень заменяем умножением, и выполняем это действие: (a−b)²=(a−b)·(a−b)=
=a·(a−b)−b·(a−b)=a·a+a·(−b)−b·a−b·(−b)=
=a²−a·b−b·a+b·b=a²−a·b−a·b+b²=
=a²−2·a·b+b².

Абсолютно аналогично доказывается любая другая из 7 основных формул сокращенного умножения.

Доказательство дополнительных ФСУ можно провести с использованием метода наименьших квадратов.

К началу страницы

Сферы применения формул сокращенного умножения (фсу) и примеры

Основное предназначение формул сокращенного умножения (фсу) объясняется их названием, то есть, оно состоит в кратком умножении выражений. Однако сфера применения ФСУ намного шире, и не ограничивается кратким умножением. Перечислим основные направления.

Несомненно, центральное приложение формулы сокращенного умножения нашли в выполнении тождественных преобразований выражений. Наиболее часто эти формулы используются в процессе упрощения выражений.

Упростите выражение 9·y−(1+3·y)².

В данном выражении возведение в квадрат можно выполнить сокращенно, имеем 9·y−(1+3·y)²=9·y−(1²+2·1·3·y+(3·y)²). Остается лишь раскрыть скобки и привести подобные члены: 9·y−(1²+2·1·3·y+(3·y)²)=9·y−1−6·y−9·y²=3·y−1−9·y².

9·y−(1+3·y)²=3·y−1−9·y².

И если в 7 классе речь идет о преобразовании целых выражений с помощью формул сокращенного умножения, то в старших классах можно будет видеть применение ФСУ к преобразованию выражений всех других видов – дробных, иррациональных, логарифмических, тригонометрических и других. К примеру, тождества сокращенного умножения с переставленными частями позволяют представлять выражения в виде степеней или произведений, в частности, выполнять разложение многочленов на множители. Это очень полезно, к примеру, при сокращении алгебраических дробей.

Формулы сокращенного умножения иногда позволяют рационально вычислять значения выражений. В качестве примера покажем, как можно возвести число 79 в квадрат с помощью формулы квадрата разности: 79²=(80−1)²=80²−2·80·1+1²=6 400−160+1=6 241. Такой подход позволяет выполнять подобные вычисления даже устно.

В заключение скажем еще про одно важное преобразование – выделение квадрата двучлена, в основе которого лежит формула сокращенного умножения квадрат суммы. Например, выражение 4·x²+4·x−3 может быть преобразовано к виду (2·x)²+2·2·x·1+1²−4, и первые три слагаемых заменяются с использованием формулы квадратом суммы. Так что выражение принимает вид (2·x+1)²−4. Подобные преобразования широко используются, например, при интегрировании.

Профиль автора статьи в Google+

К началу страницы

• Алгебра: учеб. для 7 кл. общеобразоват. учреждений / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. — 17-е изд. — М. : Просвещение, 2008. — 240 с. : ил. — ISBN 978-5-09-019315-3.
• Мордкович А. Г. Алгебра. 7 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович. — 13-е изд., испр. — М.: Мнемозина, 2009. — 160 с.: ил. ISBN 978-5-346-01198-9.
• Гусев В. А., Мордкович А. Г. Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с., ил.

laservirta.ru

Кто-нибудь знает эту формулу сокращенного умножения?? а2+в2

На это выражение нет формулы.

есть формула а2-б2,а вот ее раскрытие (а-б) (а+б)

будет (a + bi)(a — bi), где i — мнимая единица (корень (-1)

Есть <img src=»//otvet.imgsmail.ru/download/95728496_f43725387c22f7325c994d053c060757_800.jpg» data-lsrc=»//otvet.imgsmail.ru/download/95728496_f43725387c22f7325c994d053c060757_120x120.jpg»>

a²+b²=(a+b)²-2ab Это 100 процентов

touch.otvet.mail.ru

Ответы@Mail.Ru: Формулы сокращенного умножения: (a +_ b)2

Формулы сокращенного умножения Ключевые слова: квадрат суммы, квадрат разности, куб суммы, куб разности, разность квадратов, сумма кубов, разность кубов Квадрат суммы двух величин равен квадрату первой плюс удвоенное произведение первой на вторую плюс квадрат второй. (a+b)2=a2+2ab+b2 Квадрат разности двух величин равен квадрату первой минус удвоенное произведение первой на вторую плюс квадрат второй. (a-b)2=a2-2ab+b2 Произведение суммы двух величин на их разность равно разности их квадратов. (a+b)(a-b)=a2-b2 Куб суммы двух величин равен кубу первой плюс утроенное произведение квадрата первой на вторую плюс утроенное произведение первой на квадрат второй плюс куб второй. (a+b)3=a3+3a2b+3ab2+b3 Куб разности двух величин равен кубу первой минус утроенное произведение квадрата первой на вторую плюс утроенное произведение первой на квадрат второй минус куб второй. (a-b)3=a3-3a2b+3ab2-b3 Произведение суммы двух величин на неполный квадрат разности равно сумме их кубов. ( a+b)(a2-ab+b2)=a3+b3 Произведение разности двух величин на неполный квадрат суммы равно разности их кубов. (a-b)(a2+ab+b2)=a3- b3 Очень часто приведение многочлена к стандартному виду можно осуществить путём применения формул сокращённого умножения . Все они доказываются непосредственным раскрытием скобок и приведением подобных слагаемых. Формулы сокращённого умножения нужно знать наизусть: Пример. Докажите формулу a 3 + b 3 = ( a + b )( a 2 – ab + b 2 ). Решение. Имеем ( a + b )( a 2 – ab + b 2 ) = a 3 – a 2 b + ab 2 + ba 2 – ab 2 – b 3. Приводя подобные слагаемые, мы видим, что ( a + b )( a 2 – ab + b 2 ) = a 3 + b 3, что и доказывает нужную формулу. Пример. Упростите выражение (2 x 3 – 5 z )(2 x 3 + 5 z ). Решение. Воспользуемся формулой разности квадратов, получим: (2 x 3 – 5 z )(2 x 3 + 5 z ) = (2 x 3 ) 2 – (5 z ) 2 = 4 x 6 – 25 z 2. Ответ. 4 x 6 – 25 z 2.

Петька с Василь Иванычем угнали самолет. Летят. Вдруг В. И. орет: — Петька, приборы ? — 20 !!! — Че «20» ?!! — А че «приборы «?

А для чего, если человеку лень не только посмотреть в учебнике, но и найти в интернете (что проще простого), переписывать здесь учебник или знания из головы? Если он не хочет ничего, то и переписывать здесь бесполезно для него.

touch.otvet.mail.ru

Формулы сокращенного умножения

При выполнении различных алгебраических преобразований встречаются часто некоторые частные случаи умножения. Получающиеся при этом произведения полезно запомнить наизусть, чтобы в дальнейшем, когда эти случаи встретятся, можно было сразу написать результат, не производя каждый раз почленного умножения. Равенства, выражающие эти частные случаи умножения, называются формулами сокращенного умножения.

1. Квадрат суммы. Возведем в квадрат сумму двух чисел a и b.

(a + b)² = (a+b)(a+b) = a² + ab + ab + b²

Приведя подобные члены получим:

(a + b)² = a² + 2ab + b².

Эту формулу следует запомнить как в приведенной записи, так и в словесном выражении.

Квадрат суммы двух чисел равен квадрату первого числа, плюс удвоенное произведение первого числа на второе, плюс квадрат второго числа.

Примеры:
1)

(3a + 2b)² = (3a)² + 2 * 3a * 2b + (2b)² = 9a² + 12ab + 4b².

Следует приобрести навык писать сразу окончательный результат, не проводя промежуточной записи, которая показана в этом примере.

2) Эта формула применяется при устном возведении в квадрат чисел, немного больших «круглого» числа, например:

41² = (40 + 1)² = 40² + 2 * 40 * 1 + 12 = 1681;
32² = (30 + 2)² = 30² + 2 * 2 * 30 + 2² = 900 + 120 + 4 = 1024.

3) Особенно легко запомнить прием возведения в квадрат чисел, оканчивающихся пятеркой. Положим, число имеет a десятков и 5 единиц. Тогда его можно записать так:

10a + 5.

Возведем это число в квадрат по формуле:

(10a + 5)² = 100a² + 2 * 5 * 10a + 5² = 100a² + 100a + 25 = 100a(a + 1) + 25.

Полученное выражение показывает, что для возведения в квадрат числа, оканчивающегося пятеркой, надо число его десятков умножить на число, единицей большее, и к произведению приписать 25. Например:

65² = 6 * 7 * 100 + 25 = 4225;
85² = 8 * 9 (сотен) + 25 = 7225;
3,5² = 3 * 4 + 0,25 = 12,25.

Последний пример можно записать так:
Значит, чтобы возвести в квадрат смешанное число, дробная которого равна , достаточно целую часть умножить на число, единицей большее, и к произведению прибавить .2. Квадрат разности.

(a – b)² = (a – b)(a – b) = a² – ab – ab + b².
(a – b)² = a² – 2ab + b².

Квадрат разности двух чисел равен квадрату первого числа, минус удвоенное произведение первого числа на второе, плюс квадрат второго числа.

Эта формула отличается от ранее выделенной формулы только знаком среднего члена. Поэтому часто пишут сразу обе формулы так:
Примеры:

1)

(4a²b – ab)² = 16a⁴b² – 8a²b * ab + a²b² = 16a⁴b² – 8a³b² + a²b².

И здесь следует стараться написать сразу результат, производя промежуточные вычисления в уме.

2) Эта формула применяется при устном возведении в квадрат чисел, немного меньших «круглого» числа, например:

39² = (40 – 1)² = 40² – 2 * 40 + 1 = 1521;
48² = (50 – 2)² = 2500 – 2 * 2 * 50 + 4 = 2304;
79² = (80 – 1)² = 6400 – 160 + 1 = 6241.

3. Произведение суммы двух чисел на их разность.

(a + b)(a – b) = a² + ab – ab – b².
(a + b)(a – b) = a² – b².

Произведение суммы двух чисел на их разность равно разности квадратов этих чисел.

Примеры.

1) (5a + 2b)(5a – 2b) = 25a² – 4b².

2) (2a² + 3b³)(2a² – 3b³) = 4a⁴ – 9b⁶.

3) Эта формула применяется при устном умножении двух чисел, из которых одно на несколько единиц больше «круглого» числа, на сколько другое меньше его, например: 47 и 53, 68 и 72.

47 * 53 = (50 – 3)(50 + 3) = 50² – 3² = 2491;
68 * 72 = 70² – 4 = 4896;
33 * 27 = 900 – 9 = 891.

4) Но иногда бывает полезно поступить наоборот: для вычисления разности квадратов двух чисел заменить эту разность произведением суммы оснований на их разность, например:

102² — 101² = (102 – 101)(102 + 101) = 203;
54² — 46² = (54 – 46)(54 + 46) = 800;

4. Куб суммы.

(a + b)³ = (a + b)²(a + b) = (a² + 2ab + b²)(a + b) = a³ + 2a²b + ab² + a²b + 2ab² + b³;
(a + b)³ = a³ + 3a²b + 3ab² + b³.

Куб суммы двух чисел равен кубу первого числа, плюс утроенное произведение квадрата первого на второе, плюс утроенное произведение первого на квадрат второго, плюс куб второго числа.

Примеры.

1) (2a + 3b)³ = 8a³ + 3 * 4a² * 3b + 3 * 2a * 9b² + 27b³ = 8a³ + 36a²b + 54ab² + 27b³.

2) 11³ = 10³ + 3 * 10² + 3 * 10 + 1 = 1331.

5. Куб разности.

(a – b)³ = (a – b)²(a – b) = (a² – 2ab + b²)(a – b).

Произведя умножение и приведя подобные члены, получим:

(a – b)³ = a³ – 3a²b + 3ab² – b³.

Куб разности двух чисел равен кубу первого числа, минус утроенное произведение квадрата первого на второе, плюс утроенное произведение первого на квадрат второго, минус куб второго числа.

Примеры.
1) (x – 2)³ = x³ – 6x² + 12x – 8.
2) (3a – 2b)³ = 27a³ – 54a²b + 36ab² – 8b³.

mthm.ru