Как найти вектор по двум точкам?
Если даны две точки плоскости и , то вектор имеет следующие координаты:
Если даны две точки пространства и , то вектор имеет следующие координаты:
То есть, из координат конца вектора нужно вычесть соответствующие координаты начала вектора. Таким
образом, для противоположно направленного вектора формулы запишутся так:
Задача 1
Даны две точки плоскости и . Найти координаты вектора
Решение: по соответствующей формуле:
Как вариант, можно использовать следующую запись:
Эстеты решат и так:
Лично я привык к первой версии записи.
Ответ:
По условию не требовалось строить чертежа (что характерно для задач аналитической геометрии), но в целях пояснения
важного момента, не поленюсь:
в чём различие между координатами точек и координатами векторов?
Координаты точек – это обычные координаты в прямоугольной системе координат (единичные векторы тут
вообще ни при чём). Откладывать точки на координатной плоскости, думаю, все умеют ещё с 5-6 класса. Каждая точка обладает
строгим местом на плоскости, и перемещать их куда-либо нельзя.
Откладывать точки на координатной плоскости, думаю, все умеют ещё с 5-6 класса. Каждая точка обладает
строгим местом на плоскости, и перемещать их куда-либо нельзя.
Координаты же вектора – это его разложение по базису , в данном случае . Любой вектор является свободным, поэтому при желании мы легко можем переобозначить
его через и отложить от какой-нибудь другой точки
плоскости. Следует отметить, что для векторов можно вообще не строить оси, прямоугольную систему координат, нужен лишь базис,
в данном случае ортонормированный базис плоскости .
Дамы и господа, набиваем руку:
Задача 2
а) Даны точки и .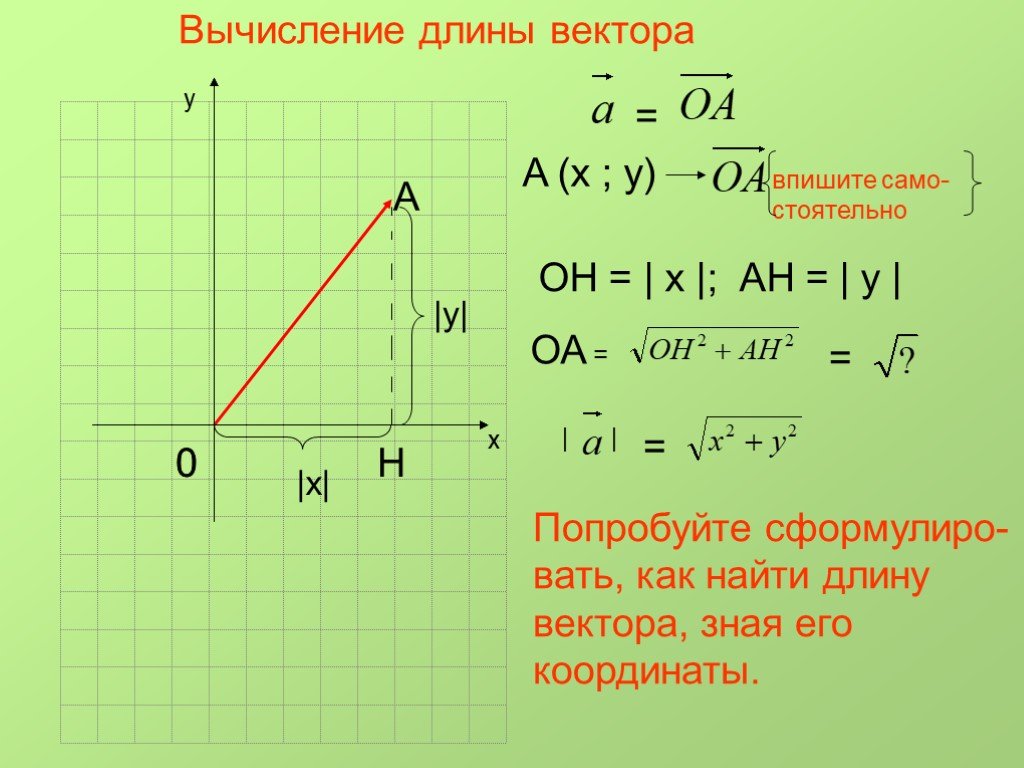 Найти векторы и .
Найти векторы и .
б) Даны точки и . Найти векторы и .
в) Даны точки и . Найти векторы и .
г) Даны точки . Найти векторы .
Пожалуй, достаточно…. Не пропускаем! Решаем письменно и «от руки»! Чертежи делать не нужно (коль скоро, не требовалось). Решения и ответы в конце книги.
Для проверки вычислений удобно использовать Геометрический калькулятор
1.5.2. Как найти длину отрезка?
1.4. Координаты вектора на плоскости и в пространстве
| Оглавление |
Автор: Aлeксaндр Eмeлин
Алгебра векторов, страница 11
Математика \ Аналитическая геометрия и линейная алгебра
Опр. 1.5.6. Направляющими
косинусами вектора а назовём косинусы тех углов , которые этот вектор образует с
базисными векторами, соответственно, i, j, k.
Направляющие косинусы вектора а = (х, у, z) находятся по формулам:
. Сумма квадратов направляющих косинусов равна единице:
.
Направляющие косинусы вектора a являются координатами его орта: .
1.5.4. Декартова прямоугольная система координат.
Пусть базисные орты i, j, k отложены из общей точки О. Будем считать,
что орты задают положительные направления осей Ох, Оу, Oz. Совокупность точки О (начала координат)
и ортонормированного базиса i, j, k называется декартовой прямоугольной системой координат в пространстве. Пусть А – произвольная точка пространства.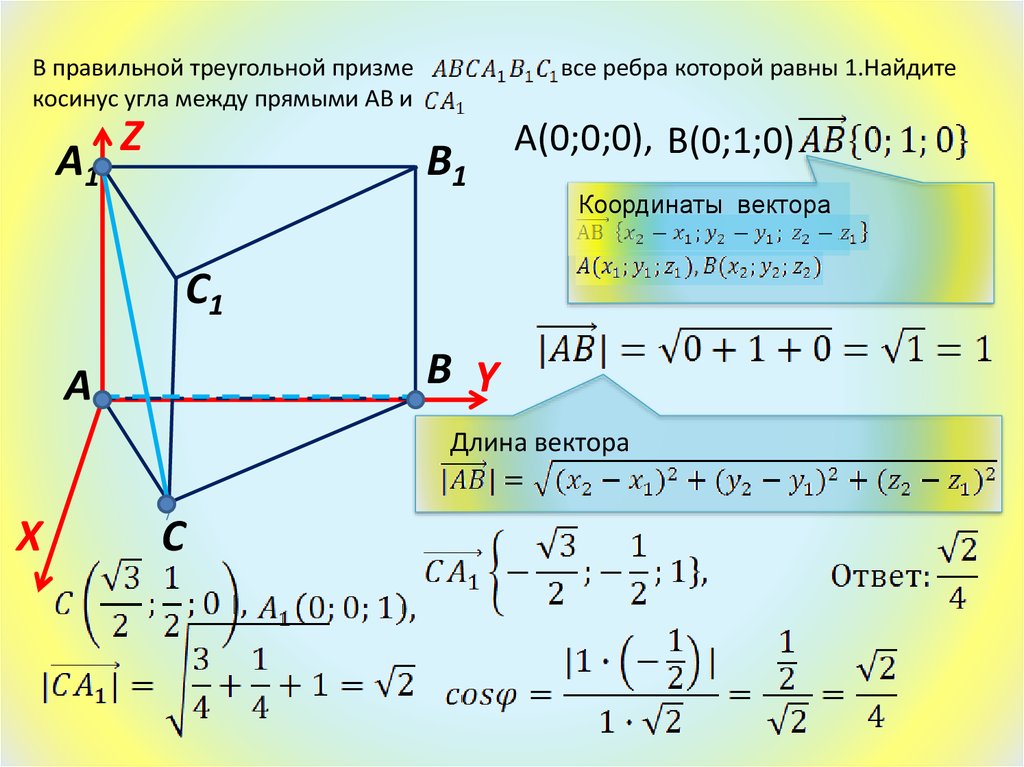 Вектор
Вектор
Если вектор задан координатами своей начальной точки В1(x1, y1, z1)и конечной точки В2(x2, y2, z2), то координаты вектора равны разности координат конца и начала: (так как ).
Декартовы прямоугольные системы координат на плоскости и на прямой определяются совершенно аналогично с соответствующими количественными (в соответствии с размерностью) изменениями.
Решение типовых
задач.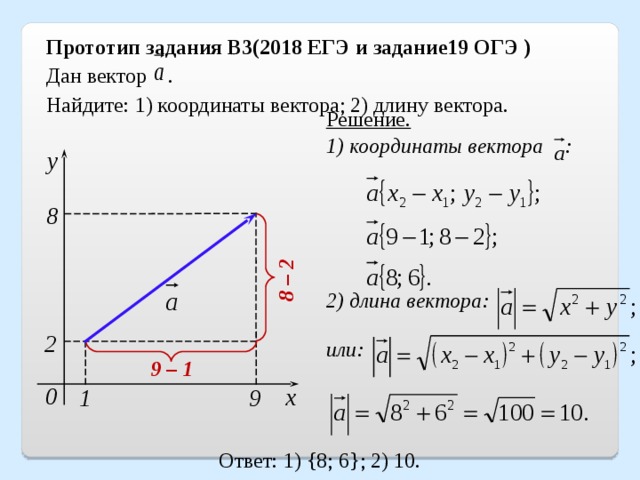
Пример 1. Найти длину и направляющие косинусы вектора а = 6i – 2j -3k.
Решение. Длину вектора: . Направляющие косинусы: .
Пример 2. Найти координаты вектора а, образующего с координатными осями равные острые углы, если длина этого вектора равна .
Решение. Так как , то подставляя в формулу (1.6), получим . Вектор а образует с координатными осями острые углы, поэтому орт . Следовательно, находим координаты вектора .
Пример 3. Заданы три некомпланарных вектора e1 = 2i – k, e2 = 3i + 3j, e3 = 2i + 3k. Разложить вектор d = i + 5j

Скачать файл
Выбери свой ВУЗ
- АлтГТУ 419
- АлтГУ 113
- АмПГУ 296
- АГТУ 267
- БИТТУ 794
- БГТУ «Военмех» 1191
- БГМУ 172
- БГТУ 603
- БГУ 155
- БГУИР 391
- БелГУТ 4908
- БГЭУ 963
- БНТУ 1070
- БТЭУ ПК 689
- БрГУ 179
- ВНТУ 120
- ВГУЭС 426
- ВлГУ 645
- ВМедА 611
- ВолгГТУ 235
- ВНУ им. Даля 166
- ВЗФЭИ 245
- ВятГСХА 101
- ВятГГУ 139
- ВятГУ 559
- ГГДСК 171
- ГомГМК 501
- ГГМУ 1966
- ГГТУ им.
 Сухого 4467
Сухого 4467 - ГГУ им. Скорины 1590
- ГМА им. Макарова 299
- ДГПУ 159
- ДальГАУ 279
- ДВГГУ 134
- ДВГМУ 408
- ДВГТУ 936
- ДВГУПС 305
- ДВФУ 949
- ДонГТУ 498
- ДИТМ МНТУ 109
- ИвГМА 488
- ИГХТУ 131
- ИжГТУ 145
- КемГППК 171
- КемГУ 508
- КГМТУ 270
- КировАТ 147
- КГКСЭП 407
- КГТА им.
 Дегтярева 174
Дегтярева 174 - КнАГТУ 2910
- КрасГАУ 345
- КрасГМУ 629
- КГПУ им. Астафьева 133
- КГТУ (СФУ) 567
- КГТЭИ (СФУ) 112
- КПК №2 177
- КубГТУ 138
- КубГУ 109
- КузГПА 182
- КузГТУ 789
- МГТУ им. Носова 369
- МГЭУ им. Сахарова 232
- МГЭК 249
- МГПУ 165
- МАИ 144
- МАДИ 151
- МГИУ 1179
- МГОУ 121
- МГСУ 331
- МГУ 273
- МГУКИ 101
- МГУПИ 225
- МГУПС (МИИТ) 637
- МГУТУ 122
- ХАИ 656
- ТПУ 455
- НИУ МЭИ 640
- НМСУ «Горный» 1701
- ХПИ 1534
- НТУУ «КПИ» 213
- НУК им.
 Макарова 543
Макарова 543 - НВ 1001
- НГАВТ 362
- НГАУ 411
- НГАСУ 817
- НГМУ 665
- НГПУ 214
- НГТУ 4610
- НГУ 1993
- НГУЭУ 499
- НИИ 201
- ОмГТУ 302
- ОмГУПС 230
- СПбПК №4 115
- ПГУПС 2489
- ПГПУ им. Короленко 296
- ПНТУ им. Кондратюка 120
- РАНХиГС 190
- РОАТ МИИТ 608
- РТА 245
- РГГМУ 117
- РГПУ им.
 Герцена 123
Герцена 123 - РГППУ 142
- РГСУ 162
- «МАТИ» — РГТУ 121
- РГУНиГ 260
- РЭУ им. Плеханова 123
- РГАТУ им. Соловьёва 219
- РязГМУ 125
- РГРТУ 666
- СамГТУ 131
- СПбГАСУ 315
- ИНЖЭКОН 328
- СПбГИПСР 136
- СПбГЛТУ им. Кирова 227
- СПбГМТУ 143
- СПбГПМУ 146
- СПбГПУ 1599
- СПбГТИ (ТУ) 293
- СПбГТУРП 236
- СПбГУ 578
- ГУАП 524
- СПбГУНиПТ 291
- СПбГУПТД 438
- СПбГУСЭ 226
- СПбГУТ 194
- СПГУТД 151
- СПбГУЭФ 145
- СПбГЭТУ «ЛЭТИ» 379
- ПИМаш 247
- НИУ ИТМО 531
- СГТУ им.
 Гагарина 114
Гагарина 114 - СахГУ 278
- СЗТУ 484
- СибАГС 249
- СибГАУ 462
- СибГИУ 1654
- СибГТУ 946
- СГУПС 1473
- СибГУТИ 2083
- СибУПК 377
- СФУ 2424
- СНАУ 567
- СумГУ 768
- ТРТУ 149
- ТОГУ 551
- ТГЭУ 325
- ТГУ (Томск) 276
- ТГПУ 181
- ТулГУ 553
- УкрГАЖТ 234
- УлГТУ 536
- УИПКПРО 123
- УрГПУ 195
- УГТУ-УПИ 758
- УГНТУ 570
- УГТУ 134
- ХГАЭП 138
- ХГАФК 110
- ХНАГХ 407
- ХНУВД 512
- ХНУ им.
 Каразина 305
Каразина 305 - ХНУРЭ 325
- ХНЭУ 495
- ЦПУ 157
- ЧитГУ 220
- ЮУрГУ 309
Видео-вопрос: Использование векторов для нахождения координат вершины квадрата и его площади
𝐴𝐵𝐶𝐷 — это квадрат, в котором координаты точек 𝐴, 𝐵 и 𝐶 равны (1, −8), (3, −10) и (5, −8). Используйте векторы для определения координат точки 𝐷 и площади квадрата.
Стенограмма видео
𝐴𝐵𝐶𝐷 — квадрат, в котором координаты точек 𝐴, 𝐵 и 𝐶 равны единице минус восемь; три, минус 10; и пять, минус восемь. Используйте векторы для определения координат точки 𝐷 и площади квадрата.
Во-первых, важно помнить, что здесь мы имеем дело с квадратом. Мы знаем, что в квадрате противоположные стороны параллельны и равны по длине. Мы также знаем, что соседние стороны находятся под прямым углом друг к другу, хотя это может быть полезно, а может и нет, когда мы будем решать этот вопрос. Нам также говорят, что 𝐴, 𝐵 и 𝐶 — это точки один, минус восемь; три, минус 10; и пять, минус восемь, соответственно. И поэтому мы могли бы нанести эти точки на координатную сетку, как показано.
Мы знаем, что в квадрате противоположные стороны параллельны и равны по длине. Мы также знаем, что соседние стороны находятся под прямым углом друг к другу, хотя это может быть полезно, а может и нет, когда мы будем решать этот вопрос. Нам также говорят, что 𝐴, 𝐵 и 𝐶 — это точки один, минус восемь; три, минус 10; и пять, минус восемь, соответственно. И поэтому мы могли бы нанести эти точки на координатную сетку, как показано.
Отсюда следует, что 𝐷, четвертая вершина квадрата, должна быть где-то здесь. И на самом деле, есть пара способов, которыми мы могли бы использовать векторы для определения точных координат этой точки. Теперь это может выглядеть не так на моей диаграмме, но мы знаем, что векторы, соединяющие 𝐴 с 𝐷 и 𝐵 с 𝐶, должны быть параллельны и равны по длине.
Итак, начнем с поиска вектора 𝐵𝐶. Один из способов сделать это — вычесть вектор 𝑂𝐵 из вектора 𝑂𝐶. В качестве вектора-столбца 𝑂𝐶 равно пяти отрицательным, восьми, а 𝑂𝐵 равно трем, отрицательным 10. Чтобы вычесть векторы, мы просто вычитаем их отдельные компоненты. Пять минус три равно два. И минус восемь минус минус 10 тоже два. Итак, мы видим, что вектор 𝐵𝐶 равен двум, двум.
Пять минус три равно два. И минус восемь минус минус 10 тоже два. Итак, мы видим, что вектор 𝐵𝐶 равен двум, двум.
Это, в свою очередь, означает, что вектор 𝐴𝐷 тоже должен быть два, два. И один из способов, которым мы могли бы путешествовать из точки 𝑂 в 𝐷, чтобы помочь нам найти вектор 𝑂𝐷, состоял бы в том, чтобы путешествовать из 𝑂 в 𝐴 — это вектор 𝑂𝐴 — и затем путешествовать из 𝐴 в 𝐷. Поэтому мы бы добавили вектор 𝐴𝐷. 𝑂𝐴 имеет вектор один, минус восемь. И мы только что обнаружили, что вектор 𝐴𝐷 равен двум, двум. Их сумма равна трем, минус шесть. И мы находим, что вектор 𝑂𝐷 равен трем минус шести. Следовательно, координата 𝐷 должна быть равна трем минус шести.
Во второй части этого вопроса нам нужно найти площадь квадрата. Итак, мы помним, что для нахождения площади квадрата мы просто возводим в квадрат его ширину или высоту. Так как же нам найти ширину или высоту нашего квадрата? Ну, это длина линии, соединяющей любые две соседние вершины. Мы рассмотрим вершины 𝐵 и 𝐶. Мы знаем, что вектор 𝐵𝐶 равен двум, двум. Это означает, что длина отрезка, соединяющего 𝐵 с 𝐶, является величиной этого вектора. И мы находим величину вектора, находя квадратный корень из суммы квадратов каждой из его составляющих.
Мы знаем, что вектор 𝐵𝐶 равен двум, двум. Это означает, что длина отрезка, соединяющего 𝐵 с 𝐶, является величиной этого вектора. И мы находим величину вектора, находя квадратный корень из суммы квадратов каждой из его составляющих.
Итак, это квадратный корень из двух в квадрате плюс два в квадрате, то есть квадратный корень из восьми. И мы видим, что каждая сторона нашего квадрата, следовательно, должна быть квадратным корнем из восьми единиц. Площадь равна квадрату этого значения. Это квадратный корень из восьми в квадрате, что, конечно же, равно восьми. Площадь квадрата равна восьми квадратным единицам.
Вопрос Видео: Использование векторов для нахождения координат вершины в прямоугольнике
𝐴𝐵𝐶𝐷 представляет собой прямоугольник, в котором координаты точек 𝐴, 𝐵 и 𝐶 равны (−18, −2), (−18, −3) и (−8, 𝑘) соответственно. Используйте векторы, чтобы найти значение 𝑘 и координаты точки 𝐷.
Стенограмма видео
𝐴𝐵𝐶𝐷 представляет собой прямоугольник, в котором координаты точек 𝐴, 𝐵 и 𝐶 минус 18, минус два; отрицательный 18, минус три; и минус восемь, 𝑘, соответственно. Используйте векторы, чтобы найти значение 𝑘 и координаты точки 𝐷.
Один из способов решения этой проблемы
было бы нарисовать прямоугольник на координатной плоскости; однако нас просят использовать
векторы. Поэтому имеет смысл
рассмотреть некоторые свойства прямоугольника. В прямоугольнике две пары
равные по длине параллельные стороны. Это означает, что вектор 𝐀𝐁
будет равен вектору 𝐃𝐂. Точно так же вектор 𝐃𝐀 будет
равно вектору 𝐂𝐁. Мы также знаем, что углы в
прямоугольник прямые углы. Это означает, что вектор 𝐀𝐁
перпендикулярно вектору 𝐂𝐁. То же верно и для другого
стороны, сходящиеся под прямым углом.
Напомним, что для вычисления вектора 𝐀𝐁, мы вычитаем вектор 𝐀 из вектора 𝐁. В этом вопросе вектор 𝐀𝐁 равен равно минус 18, минус три минус минус 18, минус два. Отрицательное 18 минус отрицательное 18 равно то же самое, что минус 18 плюс 18. Это равно нулю. Минус три минус минус два равен отрицательной единице. Следовательно, вектор 𝐀𝐁 равен нулю, отрицательный. Вектор 𝐂𝐁 равен вектору 𝐁 минус вектор 𝐂. Это равно минус 18, минус три минус минус восемь, 𝑘. Это равно минус 10, минус три минус 𝑘.
Мы знаем, что если два вектора
перпендикулярно, скалярное произведение равно нулю. Это означает, что скалярное произведение
𝐀𝐁 и 𝐂𝐁 равно нулю. Ноль умножить на минус 10 плюс
минус один умножить на минус три минус 𝑘 равно нулю. Это упрощает до нуля равно
три плюс 𝑘. Вычитание трех с обеих сторон
этого уравнения дает нам 𝑘 равно отрицательным трем.

 Сухого 4467
Сухого 4467 Дегтярева 174
Дегтярева 174 Макарова 543
Макарова 543 Герцена 123
Герцена 123 Гагарина 114
Гагарина 114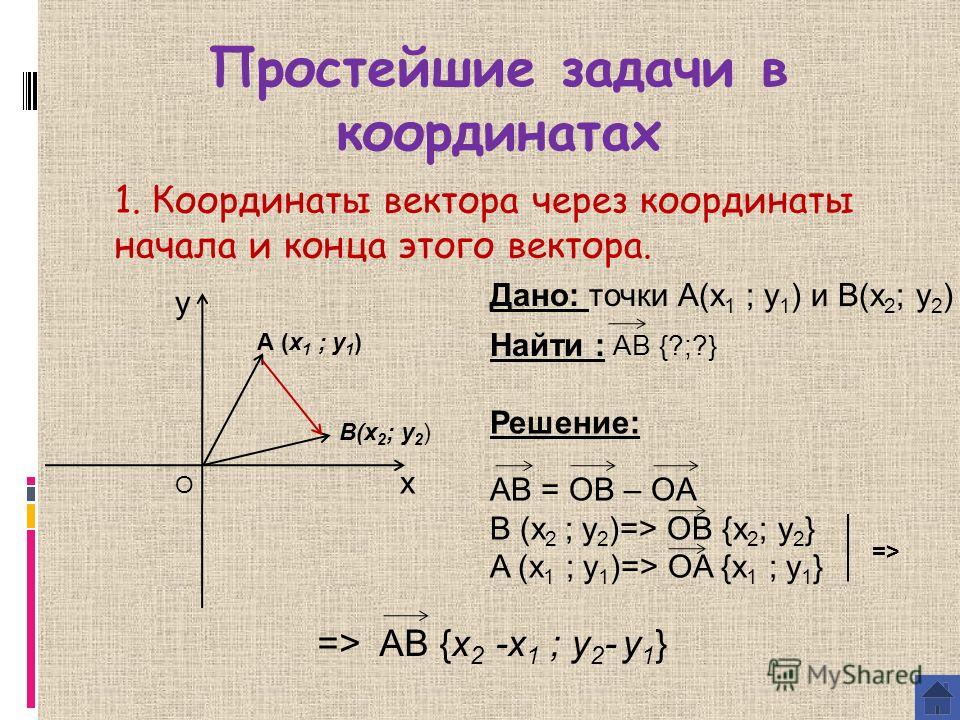 Каразина 305
Каразина 305