Абсолютное значение 1 процента прироста формула пример
ОПРЕДЕЛЕНИЕ СРЕДНЕГО АБСОЛЮТНОГО ПРИРОСТА, СРЕДНИХ ТЕМПОВ РОСТА И ПРИРОСТА
Для обоснованной оценки развития явлений во времени необходимо исчислить аналитические показатели: абсолютный прирост, коэффициент роста, темп роста, темп прироста, абсолютное значение одного процента прироста.
В таблице приведен цифровой пример, а ниже даны формулы расчета и экономическая интерпретация показателей.
Анализ динамики производства продукта «A» по предприятию за 1994-1998 гг.
| Годы | Произведено, тыс. т. | Абсолютные приросты, тыс. т | Коэффициенты роста | Темпы роста, % | Темпы прироста, % | Значение 1% при-роста, тыс. т. | ||
| Цеп-ные | базис-ные | цеп-ные | базис-ные | цеп-ные | базис-ные | цеп-ные | базис-ные | |
| — | — | 1,00 | — | — | — | |||
| 1,050 | 1,05 | 105,0 | 5,0 | 2,00 | ||||
| 1,038 | 1,09 | 103,8 | 3,8 | 9,0 | 2,10 | |||
| 1,055 | 1,15 | 105,5 | 5,5 | 15,0 | 2,18 | |||
| 1,017 | 1,17 | 101,7 | 1,7 | 17,0 | 2,30 |
Абсолютные приросты (Δy) показывают, на сколько единиц изменился последующий уровень ряда по сравнению с предыдущим (гр.3. — цепные абсолютные приросты) или по сравнению с начальным уровнем (гр.4. — базисные абсолютные приросты). Формулы расчета можно записать следующим образом:
При уменьшении абсолютных значений ряда будет соответственно «уменьшение», «снижение».
Показатели абсолютного прироста свидетельствуют о том, что, например, в 1998 г. производство продукта «А» увеличилось по сравнению с 1997 г. на 4 тыс. т, а по сравнению с 1994 г. — на 34 тыс. т.; по остальным годам см. табл. 11.5 гр. 3 и 4.
Коэффициент роста показывает, во сколько раз изменился уровень ряда по сравнению с предыдущим (гр.5 — цепные коэффициенты роста или снижения) или по сравнению с начальным уровнем (гр.6 — базисные коэффициенты роста или снижения). Формулы расчета можно записать следующим образом:
Темпы роста показывают, сколько процентов составляет последующий уровень ряда по сравнению с предыдущим (гр.7 — цепные темпы роста) или по сравнению с начальным уровнем (гр.8 — базисные темпы роста). Формулы расчета можно записать следующим образом:
Так, например, в 1997 г. объем производства продукта «А» по сравнению с 1996 г. составил 105,5 % (
Темпы прироста показывают, на сколько процентов увеличился уровень отчетного периода по сравнению с предыдущим (гр.9- цепные темпы прироста) или по сравнению с начальным уровнем (гр.10- базисные темпы прироста ). Формулы расчета можно записать следующим образом:
Тпр = Тр — 100% или Тпр = абсолютный прирост / уровень предшествующего периода * 100%
Так, например, в 1996 г. по сравнению с 1995 г. продукта «А» произведено больше на 3,8 % (103,8 %- 100%) или (8:210)х100%, а по сравнению с 1994 г. — на 9% (109% — 100%).
Если абсолютные уровни в ряду уменьшаются, то темп будет меньше 100% и соответственно будет темп снижения (темп прироста со знаком минус).
Абсолютное значение 1% прироста (гр. 11) показывает, сколько единиц надо произвести в данном периоде, чтобы уровень предыдущего периода возрос на 1 %. В нашем примере, в 1995 г. надо было произвести 2,0 тыс. т., а в 1998 г. — 2,3 тыс. т., т.е. значительно больше.
Определить величину абсолютного значения 1% прироста можно двумя способами:
§ уровень предшествующего периода разделить на 100;
§ цепные абсолютные приросты разделить на соответствующие цепные темпы прироста.
Абсолютное значение 1% прироста =
В динамике, особенно за длительный период, важен совместный анализ темпов приро
zna4enie.ru
абсолютный прирост; темпы роста и прироста, средний темп роста и прироста Абсолютное значение одного процента прироста.
Абсолютный прирост выражает абсолютную скорость изменения ряда динамики и определяется как разность между данным уровнем и уровнем, принятым за базу сравнения.
Абсолютный прирост (базисный)
где yi — уровень сравниваемого периода; y0 — уровень базисного периода.
Абсолютный прирост с переменной базой (цепной), который называют скоростью роста,
где yi — уровень сравниваемого периода; yi-1 — уровень предшествующего периода.
Средний абсолютный прирост (средняя скорость роста) определяется как средняя арифметическая из показателей скорости роста за отдельные периоды времени:
где yn — конечный уровень ряда; y1 — начальный уровень ряда.
Темп роста
Темп прироста ТП определяется как отношение абсолютного прироста данного уровня к предыдущему или базисному.
Темп прироста базисный
Темп прироста цепной
Темп прироста можно рассчитать и иным путем: как разность между темпом роста и 100 % или как разность между коэффициентом роста и 1 (единицей): 1) Тп = Тр — 100%; 2) Тп = Ki — 1.
Средний темп роста, %. Это средний коэффициент роста, который выражается в процентах:
Средний темп прироста , %. Для расчета данного показателя первоначально определяется средний темп роста, который затем уменьшается на 100%. Его также можно определить, если уменьшить средний коэффициент роста на единицу:
Абсолютное значение одного процента прироста Ai. Этот показатель служит косвенной мерой базисного уровня. Представляет собой одну сотую часть базисного уровня, но одновременно представляет собой и отношение абсолютного прироста к соответствующему темпу роста.
Среднее абсолютное значение 1% прироста
www.ekonomstat.ru
9.7. Абсолютное значение одного процента прироста
При анализе динамических рядов нередко ставится задача: выяснить, какими абсолютными значениями выражается 1 % прироста (снижения) уровней, так как в ряде случаев при снижении (замедлении) темпов роста абсолютный прирост может возрастать. В связи с этим возникает необходимость в расчете абсолютного значения одного процента прироста (снижения).
Абсолютное значение одного процента прироста представляет собой отношение абсолютного прироста к темпу прироста, выраженному в процентах:
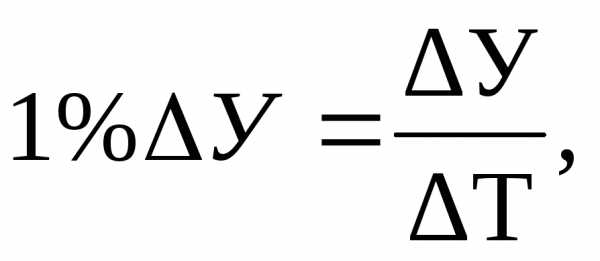(9.16)
где 1 % ΔУ – абсолютное значение 1 % прироста; ΔУ – абсолютный прирост уровня; ΔТ – темп прироста, %.
После несложного преобразования формулы (10.16) получим, что
.
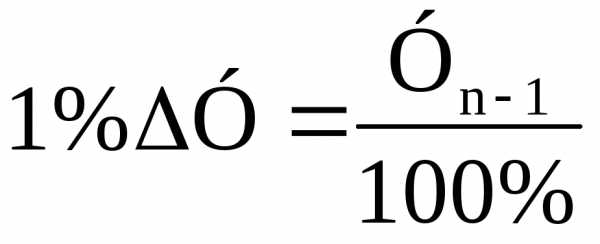(9.17)
Это означает, что абсолютное значение 1 % прироста (снижения) равно 0,01 предыдущего уровня.
Например, известно, что объем выпуска яблочного сока в перерабатывающей организации за 2008 г. составил 1300 т, за 2010 г.–– 1500 т. Необходимо определить абсолютное значение 1 % прироста объема продукции в 2010 г. по отношению к 2008 г. Для расчета искомого показателя прежде всего найдем абсолютный прирост объема продукции в 2010 г. (1500-1300=200),а затем рассчитаем темп прироста продукции за этот же период:
Далее можно найти абсолютное значение 1 % прироста по выпуску яблочного сока:
К такому же результату приходим, рассчитав абсолютное значение 1 % прироста продукции более коротким путем:
Комплексное оформление результатов расчета основных показателей динамического ряда обычно проводится с помощью статистической таблицы. Например, при изучении пятилетней динамики урожайности озимого рапса в сельскохозяйственной организации «Днепр»были получены следующие результаты (табл. 9.6).
Т а б л и ц а 9.6. Основные показатели динамики урожайности
Озимого рапса
Годы | Урожайность, ц/га | Абсолютные приросты урожайности, ц/га | Темп роста, % | Темп прироста, % | Абсолютные значения 1 % прироста, ц/га | |||
базисные | цепные | базисные | цепные | базисные | цепные | |||
У | ΔУб | ΔУц | Тб | Тц | ΔТб | ΔТц | 1 % ΔУ | |
2006 | 35 | 0 | — | 100 | — | 0,0 | — | — |
2007 | 30 | -5 | 85,7 | 85,7 | -14,3 | -14,3 | 0,35 | |
2008 | 25 | -10 | -5 | 71,4 | 83,3 | -29,6 | -16,7 | 0,35 |
2009 | 27 | -8 | 2 | 77,1 | 108 | -22,9 | 8,0 | 0,35 |
2010 | 30 | -5 | 3 | 85,7 | 111,1 | -14,3 | 11,1 | 0,35 |
В среднем: | 29,4 | -1,3 | 96,2 | -3,8 | 0,35 | |||
Данные табл. 9.6 показывают, что для динамики урожайности озимого рапса в сельскохозяйственной организации за изучаемый период характерно снижение текущих уровней по сравнению с начальным (базисным) уровнем. Однако, начиная с серединного уровня, урожайность рапса постепенно повышалась, о чем свидетельствуют цепные темпы роста и прироста. Таким образом, для изучаемого динамического ряда характерна гиперболическая форма развития уровней.
studfiles.net
20 Аналитические (абсолютный прирост, темп роста и прироста, абсолютное значение одного процента прироста) и средние показатели ряда динамики.
Средний уровень ряда определяется: 18
в моментном ряду (равномерном) по формуле средней хронологической простой
;
в моментном (неравномерном ряду) по формуле средней хронологической взвешенной:
в интервальном равномерном
,
в интервальном неравномерном
.
Аналитические показатели ряда динамики представляют собой результат сравнений двух уровней ряда динамики. 9
Сравнение может осуществляться
—базисным способ (каждый последующий уровень сравнивается с первым, принятым за базу)
—цепным способом (каждый последующий уровень сравнивается с предыдущим).
Абсолютный прирост на сколько абсолютных единиц один уровень ряда динамики больше или меньше другого:
абсолютный прирост базисный , абсолютный прирост цепной.
Средний абсолютный прирост определяется только для цепных показателей ()
.
Темп роста –во сколько раз один уровень ряда динамики больше или меньше другого.
Темп роста базисный . Темп роста цепной. Средний темп роста ()
.
Темп прироста на сколько процентов один уровень больше или меньше другого уровня.
Темп прироста базисный .
Темп прироста цепной .
Средний темп прироста ()
.
Абсолютное значение одного процента прироста (А) представляет собой отношение абсолютного прироста к темпу прироста.
21 Методы выравнивания рядов динамики: укрупнение интервалов, сглаживание способом скользящей средней, выравнивание по аналитическим формулам. 4
Укрупнение интервалов – используется редко из-за резкого уменьшения количества исходных данных. При суммировании уровней или выведения ср.значений более четко обнаруживается действие основных факторов и взаимопогашаются и сглаживаются действия случайных причин.
1 у1
2 у2 (у1+у2+у3)/3
3 у3
4 у4
5 у5 (у4+у5+у6)/3
6 у6
7 у7
8 у8 (у7+у8+у9)/3
9 у9
Метод скользящей средней – при определении скользящей средней формируем укрупненные интервалы, состоящие из одинакового числа уровней. Каждый последующий интервал получаем, постепенно сдвигаясь от начала уровня на 1 уровень
у1
у2 (у1+у2+у3)/3 = у1!
у3 (у2+у3+у4)/3 = у2!
у4 (у3+у4+у5)/3 = у3!
у5 (у4+у5+у6)/3 =у4!
у6 (у5+у6+у7)/3 = у5!
у7
заключается в последовательном расчете средних уровней из заданного числа по порядку уровней ряда, каждый раз отбрасывая один уровень в начале и добавляя один следующий.
Аналитическое выравнивание –предполагает представление уровней ряда динамики в виде функции времени , называемойадекватной формулой ряда динамики или аналитическое выражение тренда.
Адекватная формула развития может быть представлена прямолинейной зависимостью для выражения равномерного роста (снижения) и криволинейными зависимостями типа гиперболы, параболы, степенной функции для выражения замедленного или ускоренного роста (снижения).
22 Определение основной тенденции ряда динамики (тренд)
При анализе рядов динамики изучаются основные компоненты рядов:
тренд — основная тенденция развития динамического ряда (к увеличению или снижению его уровней),
периодически (сезонные) колебания,
случайные отклонения.
Изучение тренда включает два основных этапа:
1) ряд динамики проверяется на наличие тренда;
2) производится выравнивание временного ряда и непосредственное выделение тренда с экстраполяцией полученных результатов.
Непосредственное выделение тренда может быть произведено тремя методами.
1. Укрупнение интервалов. Ряд динамики разделяют на некоторое достаточно большое число равных интервалов. Если средние уровни по интервалам не позволяют увидеть тенденцию развития явления, переходят к расчету уровней за большие промежутки времени, увеличивая длину каждого интервала (одновременно уменьшается количество интервалов).
2. Скользящая средняя. В этом методе исходные уровни ряда заменяются средними величинами, которые получают из данного уровня и нескольких симметрично его окружающих. Целое число уровней, по которым рассчитывается среднее значение, называют интервалом сглаживания.
Интервал может быть нечетным (3, 5, 7 и т.д. точек) или четным (2, 4, 6 и т.д. точек).
Недостаток методики сглаживания скользящими средними состоит в условности определения сглаженных уровней для точек в начале и конце ряда. Получают их специальными приемами – расчетом средней арифметической взвешенной.
3. Аналитическое выравнивание — определение основной проявляющейся во времени тенденции развития изучаемого явления. Развитие предстает перед исследователем как бы в зависимости только от течения времени.
Целью аналитического выравнивания динамического ряда является определение аналитической или графической зависимости f(t).
Статистическое прогнозирование динамики социально-экономических явлений основывается на предположении, что закономерность развития, действующая в прошлом (внутри ряда динамики), сохраняется и в прошлом, и в будущем, т.е. прогноз основан на экстраполяции.
Экстраполяция, проводимая в будущее, называется перспективной; в прошлое – ретроспективной.
Методы экстраполяции включают в себя:
-метод среднего абсолютного прироста,
-метод среднего темпа роста,
-метод использования адекватной формулы развития.
Прогнозирование по среднему абсолютному приросту может быть выполнено в том случае, если тенденция может быть представлена равномерным ростом (снижением).
Прогнозирование по среднему темпу роста можно осуществлять в случае, когда есть основание считать, что общая тенденция ряда характеризуется показательной (экспотенциальной) кривой.
В статистике периодические колебания, которые имеют определенный и постоянный период внутри годового промежутка, называются сезонными колебаниями или сезонными волнами.
Сезонные колебания характеризуются показателями, называемыми индексами сезонности (Ус).
Индексом сезонности называют процентное отношение среднемесячного (за три года) уровня к среднегодовому уровню ;
studfiles.net
8.2 Темпы роста, их вычисление
Темпы роста − это отношение уровней ряда одного периода к другому.
Темпы роста могут быть вычислены как базисные, когда все уровни ряда относятся к уровню одного и того же периода, принятому за базу:
Тр= yi/y0 − базисный темп роста
и как цепные,- это отношение каждого уровня ряда к уровню предыдущего периода:
Тр= yi/yi-1 − цепной темп роста.
Темпы роста могут быть выражены коэффициентом или процентом.
Базисные темпы роста характеризуют непрерывную линию развития, а цепные − интенсивность развития в каждом отдельном периоде, причём произведение цепных темпов равно темпу базисному. А частное от деления базисных темпов равно промежуточному цепному.
8.3 Прирост и темп прироста. Абсолютное значение 1% прироста.
Различают понятие абсолютного и относительного прироста. Абсолютный прирост вычисляют как разность уровней ряда и выражают в единицах измерения показателей ряда.
Если из последующего уровня вычитается предыдущий, то мы имеем цепной абсолютный прирост:
Если из каждого уровня вычитается один и тот же уровень − базисный, то это базисный абсолютный прирост:
Между цепными и базисными абсолютными приростами существует следующая взаимосвязь: сумма последовательных цепных приростов равна соответствующему базисному приросту, характеризующему общий прирост за весь соответствующий период времени.
Относительную оценку значения абсолютного прироста по сравнению с первоначальным уровнем дают показатели темпа прироста (Т∆i). Его определяют двумя способами:
Как отношение абсолютного прироста (цепного) к предыдущему уровню:
Это цепной темп прироста.
Как отношение базисного абсолютного прироста к базисному уровню:
Это базисный темп прироста.
2 Как разницу между темпом роста и единицей, если темп роста выражен коэффициентом:
Т∆ = Тр-1, или
Т∆ = Тр— 100, если темп роста выражен в процентах.
Темп прироста показывает, на сколько процентов увеличились размеры явления за изучаемый период. Если темп прироста имеет знак минус, то говорят о темпах снижения.
Абсолютное значение 1-го процента прироста равно отношению абсолютного прироста (цепного) к цепному темпу прироста, выраженному в процентах:
.
Этот показатель можно также вычислить как одну сотую часть предыдущего уровня:
Аi = 0,01хУi;
8.4 Вычисление средних показателей динамики
Средний уровень ряда называется средней хронологической.
Средняя хронологическая − это средняя величина из показателей, изменяющихся во времени.
В интервальном ряду с равными интервалами средний уровень ряда определяется по формуле простой средней арифметической.
Средний уровень ряда в интервальном ряду динамики требует, чтобы было указано, за какой период времени он вычислен (среднемесячный, среднегодовой и т.д.).
Пример 1 Имеются следующие данные о товарообороте, ден.ед.:
Месяц | январь | февраль | март |
Товарооборот | 200 | 195 | 220 |
Вычислить среднемесячный товарооборот за первый квартал.
Т.к. нам дан интервальный ряд с равными интервалами, применим формулу простой средней арифметической:
Если интервальный ряд имеет разные интервалы, то его вначале нужно привести к ряду с равными интервалами, а затем можно будет использовать формулу простой средней арифметической.
Пример 2 Имеются следующие данные о товарообороте, ден.ед.:
Месяц | январь | февраль | март | 2-ой квартал |
Товарооборот | 200 | 200 | 200 | 600 |
Будем считать, что во втором квартале товарооборот распределялся по месяцам равномерно, тогда среднемесячный товарооборот за 1-ое полугодие:
Так как показатели моментных рядов не обладают свойством суммарности, то среднюю нельзя вычислить, применяя формулу простой средней арифметической, в связи с тем, что остатки менялись непрерывно в течение месяца, а данные приводятся на определённый день.
Поэтому мы воспользуемся приближенным методом, основанным на предположении, что изучаемое явление менялось равномерно в течение каждого месяца. Чем короче будет интервал ряда, тем меньше ошибка будет допущена при использовании этого допущения.
Получим формулу :
Эта формула применяется для вычисления среднего уровня в моментных рядах с равными интервалами.
Пример 3 Имеются данные об остатках строительных материалов на начало месяца, ден. ед.:
На дату | 1.01 | 1.02 | 1.03 | 1.04 |
Остатки | 2000 | 1000 | 1600 | 1800 |
Определить средний остаток за 1-й квартал.
Решение.
.
Если интервалы в моментных рядах не равны, то средний уровень ряда вычисляется по формуле:
где — средний уровень в интервалах между датами,
t — период времени (интервал ряда)
Пример 4Имеются данные об остатках сырья и материалов, ден. ед
На дату | 01.01 | 01.02 | 01.03 | 01.04 | 01.07 |
Остатки | 2000 | 1000 | 1600 | 1800 | 1760 |
Найти среднемесячные остатки сырья и материалов за первое полугодие.
Применяем формулу:
Средний абсолютный прирост вычисляется двумя способами:
1 Как средняя арифметическая простая годовых (цепных) приростов, т.е.
.
2 Как частное от деления базисного прироста к числу периодов:
.
Расчет среднего абсолютного значения 1% приростаза несколько лет производится по формуле простой средней арифметической:
При вычислении среднегодового темпа роста нельзя применять простую среднюю арифметическую, т.к. сумма годовых темпов не будет иметь смысла. В этом случае применяют среднюю геометрическую, т.е.:
где Трi − годовые цепные темпы роста;
n − число темпов.
Поскольку произведение цепных темпов равно темпу базисному, то средний темп роста может быть рассчитан следующим образом:
Error: Reference source not found
При расчёте по этой формуле не обязательно знать годовые темпы роста. Величина среднего темпа будет зависеть от соотношения начального и конечного уровня ряда.
Пример 5 Номинальная заработная плата работников народного хозяйства Республики Беларусь характеризуется данными, представленными в таблице 1.
Таблица 1 – Номинальная заработная плата работников народного хозяйства Республике Беларусь
Год | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 |
Размер заработной платы, тыс.р. | 558,9 | 1123,0 | 1189,2 | 2250,7 | 3347,5 | 4463,7 | 5582,2 | 7701,1 |
Для анализа динамики заработной платы определить:
среднегодовой размер заработной платы за 8 лет;
ежегодные и базисные абсолютные приросты, темпы роста и прироста заработной платы;
абсолютное значение 1% прироста;
среднегодовой абсолютный прирост;
среднегодовой темп роста и среднегодовой темп прироста;
среднее значение 1% прироста.
Результаты представить в таблице, сделать выводы.
Решение
1 Среднегодовой размер заработной платы определим по формуле средней арифметической простой
тыс. р.
2 Ежегодный (цепной) абсолютный прирост () определим по формуле
,
где ,– значение показателя соответственно в-м периоде и предшествующем ему.
Например, для 2005 года тыс. р., т. е. заработная плата в 2005 году по сравнению с 2004 годом выросла на 64,1 тыс. р.; для 2006 годатыс. р. и т. д.
Базисный абсолютный прирост () определим по формуле
,
где ,– значение показателя соответственно в-м и базисном (2004 год) периоде.
Например, для 2005 года тыс. р.; для 2006 годатыс. р., т. е. заработная плата в 2006 году по сравнению с 2004 годом увеличилась на 130,3 тыс. р. и т. д.
Цепной темп роста определим по формуле
.
Например, для 2005 года , т. е. заработная плата в 2001 году по сравнению с 2004 годом выросла на 108,8%; для 2006 годаи т. д.
Базисный темп роста определим по формуле
.
Например, для 2001 года ; для 2002 года, т. е. заработная плата в 2002 году по сравнению с 2000 годом выросла на 221,2% и т. д.
Темп прироста найдем по формуле
.
Так, цепной темп прироста
за 2005 год: ;
за 2006 год: .
Базисный темп прироста
за 2005 год: ;
за 2006 год: .
3 Абсолютное значение 1% прироста () найдем по формуле
.
Этот показатель можно также вычислить как одну сотую часть предыдущего уровня:
.
Например, для 2005 года тыс. р.; для 2006 годатыс. р.
Расчеты показателей по пунктам 1, 2, 3 оформим в таблице 2
Таблица 2 – Показатели динамики заработной платы за 2004-2011 гг.
Год | Размер заработной платы, тыс.р. | Абсолютный прирост, тыс. р. | Темп роста, % | Темп прироста, % | Абсолютное значение 1% прироста, тыс.р. | ||||||
Цепной | базисный | цепной | базисный | цепной | базисный | ||||||
2004 | 58,9 | — | — | — | 100 | — | — | — | |||
2005 | 123,0 | 64,1 | 64,1 | 208,8 | 208,8 | 108,8 | 108,8 | 0,589 | |||
2006 | 189,2 | 66,2 | 130,3 | 153,8 | 321,2 | 53,8 | 221,2 | 1,23 | |||
2007 | 250,7 | 61,5 | 191,8 | 132,5 | 425,6 | 32,5 | 325,6 | 1,892 | |||
2008 | 347,5 | 96,8 | 288,6 | 138,6 | 590 | 38,6 | 490 | 2,507 | |||
2009 | 463,7 | 116,2 | 404,8 | 133,4 | 787,3 | 33,4 | 687,3 | 3,475 | |||
2010 | 582,2 | 118,5 | 523,3 | 125,6 | 988,5 | 25,6 | 888,5 | 4,637 | |||
2011 | 701,1 | 118,9 | 642,2 | 120,4 | 1190,3 | 20,4 | 1090,3 | 5,822 | |||
4 Среднегодовой абсолютный прирост вычисляется двумя способами:
– как средняя арифметическая простая годовых (цепных) приростов, т.е.:
;
– как частное от деления базисного прироста к числу периодов
.
Так тыс. р.
или тыс. р.
5 Среднегодовой темп роста найдем по формуле
,
где – число темпов роста цепных;
или
,
где – число периодов.
Так или 143%.
Либо или 143%.
Среднегодовой темп роста заработной платы за 2004-2011 гг. составляет 143%, следовательно, среднегодовой прирост составит 43%.
6 Среднее значение 1% прироста рассчитаем по формуле
.
Так тыс. р.
Таким образом, на протяжении 2004-2011 гг. наблюдается положительная динамика роста заработной платы. Так, среднегодовой абсолютный прирост составил 91,7 тыс. р. или 43%.
studfiles.net
Абсолютное значение 1ого процента прироста
Средний абсолютный прирост
Средний темп роста
— на цепной основе
— на базисной
Аналитическое выравнивание
— Ур-ние
(в системе)
При
, а
Средние величины
—общая формула степенной (аналитической) средней величины
— средняя арифметическая простая
— средняя арифметическая взвешенная
— средняя гармоническая взвешенная
или
или
, где ;
Структурные средние
Нахождение медианы:
— порядковый номер медианы;
; где Xme – нижняя граница медианного интервала, Dme – величина медианного интервала (шаг), Sme-1 – накопленная частота интервала, предшествующего медианному, Fme – частота медианного интервала;
Нахождение моды:
Xmo – нижняя граница модального интервала, d – величина интервала, Fmo-1 – частота интервала, предшествующего модальному, Fmo – частота модального интервала, Fmo+1 – частота интервала, следующего за модальным.
Нахождение квартилей, децилей:
;
;
Показатели вариации
— размах вариации
— коэффициент осцилляции
— простое и взвешенное линейное отклонение
, <100 – относительное линейное отклонение
; — простая и взвешенная дисперсия
— дисперсия в полевых условиях, где ; — средняя из квадратов индивидуальных значений признака, — средняя арифметическая.
;
— коэффициент вариации;
; ;
;
Виды дисперсий (межгрупповая, средняя из внутри групповых и общая дисперсия)
— внутригрупповая дисперсия
— средняя из внутригрупповых дисперсий
— межгрупповая дисперсия
— общая дисперсия
Индексы
Индивидуальные индексы: i1-6=
Общий индекс товарооборота:
Индекс товарооборота:
Общий индекс физического объёма товарооборота:
Общая формула для вычисления всех показателей:
Сводные (общие) индексы
Статистика населения
Обозначения
— численность населения
— число родившихся
— число умерших
— число прибывших на постоянное жительство
— число выбывших
— естественный прирост
— механический (миграционный) прирост
— постоянное население
— наличное население
— временно прибывшие
— временно отсутствующие
Формулы
Среднегодовая численность населения
Численность постоянного населения
Коэффициенты рождаемости, смертности, естественного прироста
— коэффициент рождаемости
— коэффициент смертности
— коэффициент естественного прироста
— коэффициент естественного прироста
Специальный коэффициент рождаемости, коэффициент жизненности
— специальный коэффициент рождаемости
, где — доля женщин в возрасте 15-49 лет в общей численности
— коэффициент жизненности
Коэффициенты прибытия, выбытия, механического (миграционного) прироста
— коэффициент прибытия
— коэффициент выбытия
— коэффициент миграционного прироста
— коэффициент механического (миграционного) прироста
Таблица смертности
Статистика рынка труда
Обозначения
— население трудоспособного возраста
— трудоспособное население
— трудовые ресурсы
— экономически активное население
— среднегодовая численность населения
Формулы
Коэффициенты занятости, безработицы, экономически активного населения
Коэффициенты трудоспособности, трудоспособности в трудоспособном возрасте
Коэффициенты общей нагрузки, пенсионной нагрузки, замещения
Среднесписочная, среднеявочная численность
— среднее число фактически работавших лиц
Коэффициенты оборота по приему, по выбытию, общего оборота
Коэффициент текучести
, где излишний оборот – уволенные ПСЖ, за прогулы, за нарушения дисциплины, по служебному несоответствию
Коэффициенты постоянства, замещения
infopedia.su
Абсолютное значение 1% прироста равно сотой части предыдущего уровня. Оно показывает, какое абсолютное значение скрывается за относительным показателем – одним процентом прироста.
Абсолютное значение 1% прироста равно сотой части предыдущего уровня. Оно показывает, какое абсолютное значение скрывается за относительным показателем – одним процентом прироста.Абсолютное значение 1% прироста вычисляется в том случае, если абсолютный прирост, принятый за базу сравнения, число положительное. Если абсолютные приросты отрицательны, тогда данный показатель не рассчитывают.
Пример, Рассчитанные показатели оформлены в таблице.
Таблица 1 – Динамика посевной площади зерновых культур за 2006 – 2011 годы
| Годы | Посевная площадь зерна, тыс. га | Абсолютный прирост (снижение), тыс. га | Темп роста (снижения), % | Темп прироста, % | Абсолютное значение 1% при- роста, тыс. га | |||
| цепной | базисный | цепной | базисный | цепной | базисный | |||
| 640,2 | - | - | - | - | - | - | - | |
| 629,4 | ||||||||
| 746,9 | ||||||||
| 796,2 | ||||||||
| 781,8 | ||||||||
| 764,7 |
Поэтому определим среднегодовые показатели динамики:
= тыс. га
= %
(%) = (%) – 100% (%) =103,62 – 100=3,62%
Таким образом, за период 2006 – 2011 гг. размер посевных площадей зерновых культур в Орловской области увеличивался в среднем на 24,9 тыс. га или на 3,62% в год.
3. МЕТОДЫ АНАЛИЗА РЯДОВ ДИНАМИКИ
Важным направлением в исследовании закономерностей динамики социально-экономических явлений является изучение общей тенденции развития (тренда). Основная тенденция (тренд) – достаточно плавное и устойчивое изменение уровня явления во времени, более или менее свободное от случайных колебаний. Основную тенденцию можно представить либо аналитически – в виде уравнения (модели) тренда, либо графически.
Выявление тенденции динамики позволяет:
— оценить характер развития изучаемого явления;
— определить эффективность формирующих тенденцию факторов;
— измерить и оценить силу колебаний уровней ряда;
— составить прогнозы уровней ряда на перспективу.
! Основная задача статистического анализа динамики состоит в том, чтобы выявить и количественно измерить основную тенденцию динамики изучаемого явления.
Для этого используется ряд методов анализа рядов динамики:
1. способ укрупнения периодов;
2. метод выравнивания динамического ряда при помощи скользящей средней;
3. методы аналитического выравнивания динамического ряда:
3.1 по среднегодовому абсолютному приросту;
3.2 по среднегодовому коэффициенту роста;
3.3 способом наименьших квадратов по уравнению прямой (или кривой) линии.
Один из наиболее простых методов изучения основной тенденции в рядах динамики является укрупнение интервалов. Он основан на укрупнении периодов времени, к которым относятся уровни ряда динамики (одновременно уменьшается количество интервалов). Средняя, исчисленная по укрупненным интервалам, позволяет выявлять направление и характер (ускорение или замедление роста) основной тенденции развития. Недостатки метода заключаются в следующем:
1. данный метод не дает возможности следить за ходом изменения уровней внутри каждого периода;
2. в результате расчетов исчезает динамический ряд;
3. при использовании этого метода необходимо построить длинный динамический ряд.
Метод выравнивания по скользящей средней.Сущность его заключается в замене абсолютных данных средними арифметическими за определенные периоды. Расчет средних ведется способом скольжения, т.е. постепенным исключением из принятого периода скольжения первого уровня и включением следующего. Скользящая средняя дает более плавные изменения уровней по времени.
Недостатки данного метода:
1) отсутствует возможность следить за изменением уровней внутри каждого периода;
2) при обработке теряются уровни – из трех два и из пяти четыре.
Пример, Проведем выравнивание ряда динамики посевной площади зерновых культур в Орловской области по методом укрупнения интервалов, по трехлетней скользящей средней и методом аналитического выравнивания по среднегодовому абсолютному приросту по данным таблицы 2.
Таблица 2 – Динамика посевной площади зерновых культур в Орловской области
| Годы | Посевная площадь зерновых культур, тыс. га | Укрупнение периодов | По трехлетней скользящей средней | По среднегодовому абсолютному приросту | |||
| сумма | средняя | сумма | средняя | t | средняя | ||
| 641,6 | - | - | - | - | 641,6 | ||
| 711,8 | 2071,2 | 690,4 | 2071,2 | 690,4 | 657,0 | ||
| 717,8 | - | - | 2069,8 | 689,9333 | 672,4 | ||
| 640,2 | - | - | 1987,4 | 662,4667 | 687,8 | ||
| 629,4 | 2016,5 | 672,2 | 2016,5 | 672,1667 | 703,2 | ||
| 746,9 | - | - | 2172,5 | 724,1667 | 718,5 | ||
| 796,2 | - | - | 2324,9 | 774,9667 | 733,9 | ||
| 781,8 | 2342,7 | 780,9 | 2342,7 | 780,9 | 749,3 | ||
| 764,7 | - | - | - | - | 764,7 |
Так, укрупнение периодов по трехлетиям осуществляется по следующим формулам:
,
.
Использование метода укрупнения периодов не позволяет нам сделать вывод о наличии устойчивой тенденции роста или сокращения.
Скользящая средняя за 2003 – 2011 годы определяется следующим образом:
,
и т.д.
где у1 – средняя скользящая,
у0, у1, у2 и т.д. – уровни ряда.
Сравнивая скользящие средние видно, что размер посевной площади зерновых культур имеет тенденцию роста.
Наиболее эффективным способом выявления основной тенденции развития является аналитическое выравнивание, которое позволяет получить аналитическую модель тренда. Тренд динамического ряда – это математическое уравнение, выражающее основную тенденцию динамики изучаемых уровней и позволяющее установить закономерность развития явления во времени.
Аналитическое выравнивание по среднегодовому абсолютному приросту, если изменение уровней ряда идет примерно с одинаковой интенсивностью (колеблемость уровней вызвана случайными факторами), осуществляется по следующему уравнению:
где – теоретические (выровненные) уровни;
уо – уровень года, принятого за начало отсчета;
– среднегодовой прирост;
t – обозначение времени.
Среднегодовой абсолютный прирост:
= тыс. га
Тогда уравнение прямой линии примет вид:
.
Подставляя в данное уравнение значение времени t для каждого года, рассчитывается теоретическая (выровненная) посевная площадь зерновых культур в таблице 2. Изобразим фактический и теоретический уровни графически на рисунке 1.
По теоретически рассчитанным уровням размер посевной площади имеет тенденцию увеличения в среднем на 15,38 тыс. га ежегодно.
Данный метод имеет свои недостатки: ряд посевной площади, выровненный по среднегодовому абсолютному приросту, на графике представляет прямую линию, соединяющую конечный и начальный уровни ряда. Следовательно, выровненные уровни целиком и полностью зависят от значения двух крайних уровней, на формирование которых могут оказывать случайные факторы.
Рисунок 1 – Аналитическое выравнивание динамического ряда посевной площади зерновых культур по среднегодовому абсолютному приросту
Самым точным методом является выравнивание динамического ряда способом наименьших квадратов по уравнению прямой (или кривой) линии.Сущность этого метода заключается в том, что отыскивается аналитическая формула кривой, которая наиболее точно отражает основную тенденцию изменения уровней в течение периода. Эффективность выравнивания по данному способу во многом зависит от правильности выбора математического уравнения, которое наиболее точно может проявить присущую ряду тенденцию.
При аналитическом выравнивании ряда динамики закономерно изменяющийся уровень изучаемого показателя оценивается как функция времени: .
Расчет параметров функции обычно производится методом наименьших квадратов, сущность которого заключается в том, что сумма квадратов отклонений фактических уровней от теоретических была бы минимальной:
.
Если в динамическом ряду наблюдается постоянный абсолютный прирост или снижение, то осуществляют выравнивание по прямой линии по уравнению:
.
Если уровень ряда изменяется неравномерно, а с определенным ускорением, то выравнивание проводят по уравнению параболы второго порядка:
,
где – теоретический уровень ряда, рассчитанный по уравнению;
а – уровень ряда, принятый за базу отсчета;
b – среднегодовой абсолютный прирост в теоретическом или выровненном ряду;
t – порядковый номер периодов или моментов времени;
с – ускорение.
Основанием для выбора вида кривой является содержательный теоретико-экономический анализ сущности развития данного явления. На практике для выбора уравнения прибегают к анализу графического изображения уровней динамического ряда.
Рассмотрим применение способа наименьших квадратов на конкретном примере.
Из расположения точек кривой на рисунке 2 видно, что уровень посевной площади зерновых культур изменяется по годам более менее равномерно, поэтому для установления основной тенденции динамики можно использовать уравнение прямой линии: .
Для определения параметров данного уравнения а и b необходимо решить систему двух нормальных уравнений:
an + bSt = Sy,
aSt + bSt2 = Syt;
Так как значение t – обозначение времени и может принимать любые произвольные значения, то ему можно задать такие значения, чтобы сумма t была равной нулю. Тогда система нормальных уравнений значительно упрощается и принимает вид
(Применим способ расчета фактора времени, таким образом, при котором åt=0. В статистике этот способ отсчета называется расчет от условного нуля, то есть при нечетном числе уровней (как у нас) ряда динамики находится середина ряда и этому значению t придаем значение, равное 0. Тогда ряд делится на два уровня. Отсчет от условного 0 проводим следующим образом: вниз t=1,2,3…, вверх t=-1,-2,-3…)
a n = Sy,
bSt2 = Syt;
Решение данной системы сводится к определению значения параметров а и b по формулам:
где n – число уровней ряда.
В целях анализа ряда динамики проведем аналитическое выравнивание способом наименьших квадратов.
Исходные данные и расчетные величины представлены в таблице 3.
Таблица 3 – Динамика посевной площади зерновых культур в Орловской области
| Годы | Посевная площадь зерновых культур, тыс. га | Аналитическое выравнивание по уравнению прямой линии | |||||
| А | |||||||
| 641,6 | -4 | 16,0 | -2566,4 | 650,1 | 8,5 | 72,2 | |
| 711,8 | -3 | 9,0 | -2135,4 | 666,2 | 45,6 | 2079,9 | |
| 717,8 | -2 | 4,0 | -1435,6 | 682,3 | 35,5 | 1260,8 | |
| 640,2 | -1 | 1,0 | -640,2 | 698,4 | 58,2 | 3386,1 | |
| 629,4 | 0,0 | 0,0 | 714,5 | 85,1 | 7240,1 | ||
| 746,9 | 1,0 | 746,9 | 730,6 | 16,3 | 266,1 | ||
| 796,2 | 4,0 | 1592,4 | 746,7 | 49,5 | 2451,7 | ||
| 781,8 | 9,0 | 2345,4 | 762,8 | 19,0 | 361,6 | ||
| 764,7 | 16,0 | 3058,8 | 778,9 | 14,2 | 201,1 | ||
| Итого | 6430,4 | 60,0 | 965,9 | 6430,4 | 331,9 | 17319,7 |
Рассчитаем параметры уравнения:
a = тыс. га
b = тыс. га
Уравнение тренда имеет вид:
За период с 2003 г. по 2011 г. размер посевной площади зерновых культур в Орловской области ежегодно увеличивается в среднем на 16,1 тыс. га. Средний размер посевной площади зерновых культур за изучаемый период составил 714,49 тыс. га.
Подставим в уравнение тренда значения t для каждого года и осуществим расчет теоретической посевной площади зерна. Например, в 2003 году теоретический (выровненный) уровень размера посевной площади составит:
тыс. га
Изобразим теоретическую посевную площадь, рассчитанную по уравнению тренда, графически на рисунке 2.
Выравнивание размера посевной площади зерновых культур по уравнению прямой линии показывает тенденцию увеличения за последние 9 лет.
Рисунок 2 – Фактический и выровненный уровни посевной площади зерновых культур в Орловской области
В статистике для измерения колеблемости динамического ряда разработана система показателей:
1. амплитуда или размах колебаний:
R(t) = ymax – ymin,
где ymax, ymin – наибольшее и наименьшее значения изучаемого признака.
R(t) = 796,2 – 629,4 = 166,8 тыс. га
Таким образом, в Орловской области разница между максимальным и минимальным размером посевной площади зерновых культур в период с 2003 г. по 2011 г. составила 166,8 тыс. га.
2. среднее линейное отклонение:
,
где – фактический уровень,
– теоретический уровень,
n – число уровней,
p – число параметров уравнения тренда.
тыс. га
В период с 2003 г. по 2011 г. размер посевной площади зерна в Орловской области отклоняется от уровня тренда в среднем на 47,42 тыс. га.
3. среднее квадратическое отклонение:
.
тыс. га
Оно показывает, что в размер посевной площади зерновых культур в отчетном периоде отклонялся от теоретического уровня в среднем на 49, 74 тыс. га.
4. коэффициент колеблемости:
Профессор М.М. Юзбашев рекомендует оценивать колеблемость таким образом: слабой, если ; умеренной, если ; сильной, если ; очень сильной, если .
Следовательно, колебания посевной площади зерна в Орловской области являются слабыми и составляют 6,96% среднего многолетнего уровня. То есть ежегодно размер посевной площади зерновых культур отклоняется от среднего многолетнего уровня в среднем на 6,96 %.
Изучение динамики посевной площади может быть дополнено расчетами показателей устойчивости.
Понятие «устойчивость» используется в различных смыслах:
1) устойчивость как категория, противоположная колеблемости;
2) устойчивость направленности изменений, то есть устойчивость тенденции.
В первом понимании показатель устойчивости характеризует близость фактических уровней к тренду и совершенно не зависит от показателей последнего. Этот показатель устойчивости не выражает эволюции уровней.
Коэффициент устойчивости определяется по формуле:
,
Куст = 1 – 0,07 = 0,93.
В среднем в виду ежегодной колеблемости посевной площади зерна обеспечивается 93% посевной площади, рассчитанной по тренду.
Устойчивость во втором смысле характеризует не сами по себе уровни, а процесс их направленного изменения. С этой точки зрения полной устойчивостью направленного изменения уровней динамического ряда следует считать такое изменение, в процессе которого каждый следующий уровень либо выше всех предшествующих (устойчивый рост), либо ниже всех предшествующих (устойчивое снижение). В качестве показателя устойчивости используют коэффициент корреляции рангов Ч. Спирмена, который вычисляют по формуле:
,
где d – разность между рангом уровня посевной площади и рангом номера лет (d = Py — Pt),
n – число уровней ряда.
При полном совпадении рангов уровней, начиная с наименьшего и номеров периодов (моментов) времени по их хронологическому порядку, коэффициент корреляции рангов равен +1. Это значение соответствует случаю полной устойчивости возрастания уровней. При полной противоположности рангов уровней рангам лет коэффициент Спирмена равен –1, что означает неустойчивость какой-либо тенденции.
Таблица 4 – Расчет коэффициента корреляции рангов Ч. Спирмена
| Годы | Посевная площадь зерновых культур, тыс. га. | Ранг размера посевной площади ру | Ранг лет рл | d=ру — рл | d2 |
| 641,6 | |||||
| 711,8 | |||||
| 717,8 | |||||
| 640,2 | -2 | ||||
| 629,4 | -4 | ||||
| 746,9 | |||||
| 796,2 | |||||
| 781,8 | |||||
| 764,7 | -2 | ||||
| 641,6 | |||||
| Итого | х | х | х |
Коэффициент корреляции Ч. Спирмена показывает, что размер посевной площади зерновых культур в Орловской области имеет высокий устойчивый рост, равный 67%. Таким образом, при значительных колебаниях ежегодных уровней по сравнению со средним за период уровнем в целом в Орловской области наблюдается устойчивый рост размера посевных площадей зерновых культур.
По результатам аналитического выравнивания уровней ряда составляют статистический прогноз.
Статистический прогноз – это вероятная оценка того, какое возможно развитие определенного объекта, процесса и величины его признаков в будущем, полученная на основании выявленной статистической закономерности по данным прошлого периода.
Статистический прогноз предполагает не только верное качественное предсказание, но и достаточно точное измерение вероятных возможностей ожидаемых значений признаков. Объектом статистического прогнозирования могут быть явления и процессы, управление которыми, а тем более планирование их развития затруднено из-за действия многих факторов, влияние которых не может быть однозначно и полностью определено.
В зависимости от продолжительности времени, для которого составляется прогноз, прогнозы бывают долгосрочные и краткосрочные.
Различают точечный и интервальный прогнозы уровня конкретного года. Точечный прогноз показывает, на какой средний уровень выйдет динамический ряд, если будет развиваться с такой же скоростью.
Интервальный прогноз характеризует пределы, в которых находится исследуемый показатель с учетом ежегодной ее колеблемости.
Статистический прогноз, составленный на основе тренда динамического ряда, осуществляется в том случае, если выявлена тенденция увеличения в динамическом ряду. Измерение тенденции динамики и показателей колеблемости позволяют рассчитать уровни ряда на перспективу.
Составим точечный прогноз размера посевной площади зерновых культур в Орловской области на 2013–2014 годы.
Уравнение тренда имеет вид
если в 2011 г. t = 4, то в 2013 году t = 6 и в 2014 г. t = 7, то размер посевной площади будет равен:
тыс. га
тыс. га
На основании точечного прогноза размер посевной площади зерна в Орловской области в 2013г. составит 811,1 тыс.га, а в 2014г. -827,2 тыс.га.
Интервальный прогноз учитывает уровень колеблемости посевной площади и определяется по формуле:
,
Рассчитаем интервальный прогноз:
=811,1±811,1*0,07 т.е. размер посевной площади зерновых культур в 2013г. будет находиться в интервале от 754,3 до 867,9 тыс.га.
=827,2±827,2*0,07 т.е. размер посевной площади зерновых культур в 2014г. будет находиться в интервале от 769,3 до 885,1 тыс.га.
Из точечного и интервального прогнозирования следует, что в дальнейшем среднегодовой размер посевной площади зерновых культур в Орловской области будет иметь тенденцию к росту. Данную тенденцию следует оценить как положительную.
4. МЕТОДЫ ИЗУЧЕНИЯ СЕЗОННЫХ КОЛЕБАНИЙ
Самостоятельно
Дата добавления: 2015-07-18; просмотров: 427 | Нарушение авторских прав
mybiblioteka.su — 2015-2019 год. (0.029 сек.)
mybiblioteka.su