Формула как найти объем – Все формулы объемов геометрических тел

Онлайн калькулятор: Объем геометрических фигур

Данная статья содержит калькуляторы для расчета объема различных геометрических фигур. Основной источник формул: Spiegel, Murray R. Mathematical Handbook of Formulas and Tables. Schaum’s Outline series in Mathematics. McGraw-Hill Book Co., 1968.

Объем куба

Размеры куба

Формула:

Объем куба

Длина ребра куба (H)

Точность вычисления

Знаков после запятой: 5

save Сохранить share Поделиться extension Виджет

Объем прямоугольной призмы

Размеры прямоугольной призмы

Формула:

Объем прямоугольной призмы

Точность вычисления

Знаков после запятой: 5

save Сохранить share Поделиться extension Виджет

Объем пирамиды

Размеры пирамиды

Формула:

Объем пирамиды

Площадь основания

Точность вычисления

Знаков после запятой: 5

save Сохранить share Поделиться extension Виджет

Объем усеченной пирамиды

Размеры усеченной пирамиды

Формула:

Объем усеченной пирамиды

Точность вычисления

Знаков после запятой: 5

planetcalc.ru

формулы и задача :: SYL.ru

Вопрос, как найти объем цилиндра, может возникнуть не только у школьника. Ведь такую форму имеет, к примеру, кастрюля, емкость которой иногда срочно нужно узнать. Вот тогда потребуется знание специальной формулы.

Что нужно знать о цилиндре?

Геометрическое тело, о котором мы говорим, образуется в результате вращения прямоугольника вокруг одной из его сторон, и всегда будет прямым. То есть угол между образующей цилиндра и его основанием в данном случае равен 90 градусам. Если выполнить это простое движение не удается, и угол уже не 90 градусов, то идет речь о наклонном цилиндре.

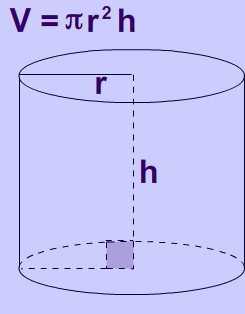
Каким бы ни был вид тела, все равно нужно знать о том, как найти объем цилиндра. Но сначала нужно определиться с некоторыми теоретическими данными.

Как называются отдельные элементы цилиндра и что о них известно?

Отрезки, которые соединяют попарно соответствующие точки на двух основаниях, называются образующими. У любого цилиндра они равны и параллельны друг другу. Если он прямой, то длина образующей совпадает с высотой тела.

В основании может лежать окружность или эллипс, тогда цилиндр будет круговым или эллиптическим соответственно. В формулах этот факт потребуется учесть. Потому что чаще всего они даются для кругового цилиндра. В эллиптическом, до того как вычислить объем цилиндра, нужно будет узнать, по какой формуле определить площадь овала.

Формулы объема для прямого и наклонного цилиндров

Здесь и далее приняты такие обозначения.

Буква-обозначение	математическая величина
V	объем
S	площадь основания
h	высота
r	радиус окружности
l	длина образующей
α	угол между образующей и основанием

В любом случае потребуется формула, в которой высота тела, умножается на площадь основания. Она выглядит так:

V = Sh

Если требуется узнать, как найти объем цилиндра прямого, то здесь высота по длине полностью совпадает с образующей. Основанием чаще всего является круг, тогда его площадь будет сосчитана по формуле:

S = πr².

Когда в задаче идет речь об эллиптическом цилиндре, то потребуется такая формула площади основания:

S = π ab, здесь буквами a и b обозначены малая и большая полуоси овала.

При решении задач о наклонном цилиндре потребуется ввести некоторые дополнения в формулу. Например, если не известна высота, но идет речь об образующей и угле между ней и основанием. Тогда букву h потребуется заменить таким выражением:

h = l * sin α.

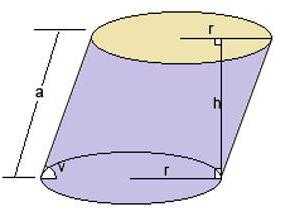
Как быть, если нужно определить объем на практике?

В задачах обычно уже известны значения угла или высоты с образующей. А возможно, какие-то другие элементы, через которые их можно найти. В жизни приходится делать измерения самостоятельно.

Тогда вопрос о том, как определить объем цилиндра, сводится к тому, чтобы правильно сделать измерения его высоты и радиуса. Для этого потребуются: линейка, карандаш и прямоугольный лист бумаги.

Чаще всего в быту нас окружают прямые круговые цилиндры. Измерить их высоту обычно не составляет труда. Нужно просто приложить линейку сбоку и измерить расстояние от низа до верха тела. Это будет высота — h.

С радиусом окружности все не так легко. Нужно немного вспомнить геометрию. Здесь потребуется лист бумаги с прямым углом и карандаш.

Что дает теория по геометрии? Вокруг прямоугольного треугольника можно описать окружность. Причем его прямой угол окажется на ней, а гипотенуза совпадет с диаметром.

Нужно взять лист бумаги и положить его так, чтобы прямой угол касался края основания. Тогда две его стороны, которые образуют этот угол, в некоторых точках пересекутся с окружностью. В этих местах потребуется сделать метки. По ним провести отрезок. Он окажется гипотенузой и искомым диаметром основания цилиндра.

Как найти объем цилиндра, в нашем случае? В формуле фигурирует радиус. Он равен половине диаметра. То есть длину получившегося отрезка нужно разделить на два.

Осталось только подставить результаты измерений в формулу объема и сосчитать. Причем учесть, что ответ получится в см³. Если объем нужно узнать в кубических метрах, то число нужно будет разделить на миллион. Чтобы получить объем в литрах, делителем окажется тысяча.

Задача

Условие. Даны два цилиндра. Высота первого в два раза больше второго. Радиус второго вдвое больше, чем у первого. Необходимо узнать, во сколько раз объем первого цилиндра больше или мегьше объема второго.

Решение. Сначала потребуется ввести обозначения. Пусть высота и радиус первого тела будут иметь индекс 1, а второго — 2.

Теперь можно записать данные в условии значения в виде выражений:

h₁ = 2h₂ и r₂ = 2r₁.

Формулы объемов обоих цилиндров примут такой вид:

v₁ = π r₁² h₁ и v₂ = π r₂² h₂.

В задаче требуется найти:

v₁ : v₂ = (π r₁² h₁) : (π r₂² h₂).

После сокращения πи замены h₁ и r₂введенными выражениями, получается:

v₁ : v₂ = (r₁² 2h₂) : (4r₁² h₂).

То есть v₁ : v₂ = 1 : 2. Это означает, что объем первого цилиндра в два раза меньше.

Ответ. v₁ = v₂ : 2.

www.syl.ru

Как находить объем

Если честно, с геометрией у меня всегда были проблемы, а решить теорему или задачу без использования шпаргалок – это вообще считалось высшим пилотажем. Думаю, со мной согласятся многие, хотя, конечно, есть такие формулы, которые до сих пор сохранились в моей памяти, например, я легко могу найти объем куба.

Уметь вычислять данную величину просто необходимо, поскольку без нее невозможно решение многих математических, физических и прикладных задачек. Итак, находить объем куба можно несколькими путями, все зависит от того, какая величина задана в условии задачи. Рассмотрим пару вариантов.

Вариант №1. По заданной стороне (ребру) а нужно найти объем куба. В данном случае формула для вычисления будет выглядеть так: V=a³, где а – длина ребра, а V – искомый объем. Вместо а написать численное значение ребра, а затем возвести его в куб и получится искомая величина объема.

Вариант №2. Высчитать объем куба по заданной диагонали d. В данном случае пригодится совсем другая формула следующего вида: V=( d/√3)3, где d – диагональ, а V – искомый объем.

В принципе эти формулы я по сей день помню еще со школьной скамьи, но вот в химии находить объем было значительно сложнее, да и вообще данный предмет я никогда не понимала, поэтому каждый раз пользовалась шпаргалкой. Формула для нахождения объема также зависит от условия задачи.

Вариант №1. Найти объемагаза можно так: V = n * Vm, где V – искомый объем, n – количество вещества, а Vm – объем газа (молярный). Формула, конечно простая, но порой решение такой задачи может занять не один час.

Вариант №2. Получить объемараствора гораздо легче, но здесь понадобится совсем другая формула: V = m/p, где m – масса, а p – плотность.

Существует и множество других геометрических формул, но нахождение объемамне больше всего запомнилось, поскольку эту физическую величину я на выпускных экзаменах высчитывала.

kalinka28 13/09/2012 — 13:35

 

Автор kalinka28 это рекомендует потому, что:
объемы различных геомерических фигур имеют свои геометрические формулы, по которым можно найти их численное значение.

www.uso.ru

Как найти объем через массу?

В окружающей нас природе масса взаимосвязана с объемом (мы имеем ввиду точные науки). Совершенно любое тело имеет и массу и объем. Масса представляет тяжесть тела, то есть его величину, а объем тела – это его реальные размеры. И благодаря этим двум параметрам мы можем вычислить или массу или объем. Так как найти объем через массу? Читайте об этом ниже.

Первая формула

Стоит отметить, что приведенные ниже правила пригодны как для физики, так и для химии.

Самая элементарная возможность нахождения нужного объема – это использовать плотность. То есть мы делим нашу массу на имеющийся объем. Вот формула: ρ = m/V. Из нее вытекает, что нужный объем составляет: V = m/ρ.

Запомните, что масса различных веществ в формуле может быть равной, даже если вещества не одинаковы, но объем всегда буде разным, также как и их плотности.

Вторая формула

Наука химия, имеет пример (модель) идеального газа: на одну моль с объемом (этот молярный объем всегда постоянен). Формула выглядит так: V = 22,4 моль на литр. Представленный газ всегда имеет этот объем при давлении и температуре (они постоянны). Если рассматривать этот вопрос со стороны науки физики, то он (объем) может меняться. Вот подходящие формулы: V м — молярный объем равен Vв — объем порции газа деленное на n в — количество вещества. (Vм = Vв/nв). А само количества вещества вычисляется благодаря формуле деления массы нужного вещества на молярную массу (nв = mв/Mв). Из этого следует что: Vв = Vм*mв/Mв.

Третья формула

Когда же в приведенной вам задаче предоставлена концепция самого вещества, то требуемый объем, вы можете легко выразить согласно формуле: c = n/V = m/M/V. В этой формуле М – это масса вещества (молярная).

Мы надеемся, что помогли вам, дорогие читатели, понять, как найти объем, зная массу предоставленного вещества. Желаем вам успехов в химии и физике.

elhow.ru